PRAKIRAAN CURAH HUJAN MENGGUNAKAN MODEL SPACE TIME AUTOREGRESIF ORDE DUA (STAR (1;2))

(1)

PRAKIRAAN CURAH HUJAN MENGGUNAKAN

MODEL SPACE TIME AUTOREGRESIF ORDE DUA (STAR (1;2))

Emah Suryamah, Kankan Parmikanti dan Sugihartini

Jurusan Matematika FMIPA Universitas Padjadjaran Jl Raya Bandung Sumedang Km 21 Bandung 45363

E-mail: emah_suryamah@yahoo.com

ABSTRAK

PRAKIRAAN CURAH HUJAN MENGGUNAKAN MODEL SPACE TIME

AUTOREGRESIF ORDE DUA (STAR (1;2)). Model STAR (Space Time Autoregressive) adalah

model multivariat time series yang merupakan gabungan dari model Autoregressive (AR) dengan model Spasial. Model STAR(1;2) adalah suatu model spasial yang melibatkan dua nilai pengamatan sebelumnya di lokasi tersebut dan lokasi-lokasi lain di sekitarnya yang berada dalam satu kelompok (lag spasial satu). Tujuan penelitian ini adalah mengkaji penurunan model STAR(1;2), serta penerapannya pada prakiraan curah hujan. Metode penelitian dalam makalah ini berdasarkan studi kepustakaan (studi literatur) dan studi eksperimental. Penelitian ini dimulai dengan mengkaji model STAR(1;2), lalu menaksir parameter model dengan menggunakan metode kuadrat terkecil, kemudian menggunakan hasilnya untuk memperkirakan curah hujan dari dua lokasi di Indonesia Barat

Kata kunci: STAR(1;2), MKT, curah hujan

ABSTRACT

STAR (Space Time Autoregressive) model is a model of multivariate time series which is a combination of Autoregressive (AR) with Spatial models. STAR (1, 2) model is a spatial model involving two previously observed values in that location and other locations which are in one group (the first spatial lag).The purpose of this study of STAR (1,2) model, as well as its application to the precipitation forecasts. The research method in this paper is based on literature studies and experimental studies. This study begins by examining the STAR models (1, 2), and then estimating the parameters model using the least squares method, and then use the results to estimate precipitation from two locations at western Indonesia.

Keywords: STAR (1, 2), OLS, precipitation

1. PENDAHULUAN

Data yang berkaitan dengan waktu dinamakan data deret waktu dan prosesnya disebut proses deret waktu. Analisis deret waktu (time series) merupakan salah satu dari metode peramalan kuantitatif yang berdasar-kan pada nilai variabel dimasa lalu. Salah satu model yang digunakan pada masalah time series adalah model univariat linear yang disebut dengan Model Autoregresif dan disingkat dengan AR. Model AR ini menyatakan suatu observasi waktu sekarang yang dipengaruhi oleh waktu

sebelumnya. (Box and Jenkins 1962). Selain data deret waktu terdapat pula data spasial, yaitu data yang diamati berdasarkan lokasi yang berdekatan dan memiliki kemiripan karakteristik sedangkan prosesnya disebut proses spasial.

Data deret waktu dan data spasial berkembang menjadi data lokasi waktu (space

time). Salah satu model space time yang sering

digunakan adalah model STAR (Space Time

Autoregresive). Model STAR diperkenalkan

oleh Pfeifer – Deutsch (1980) yang memper-lihatkan bahwa pengamatan di waktu sekarang di lokasi tertentu dipengaruhi oleh pengamatan

(2)

waktu sebelumnya di lokasi tersebut dan lokasi disekitarnya yang berada dalam satu kelompok. Penelitian mengenai perbandingan matriks bobot model STAR(1;1) dikembangkan Suryamah (2010). Kajian model perlu pengembangan dalam orde spasial maupun waktu, karena itu penulis tertarik mengem-bangkan model STAR(1;1) menjadi model STAR(1;2), yaitu model dengan nilai pengamatam masa mendatang tergantung dari nilai pengamatan dua waktu sebelumnya dan lokasi-lokasi pengamatan berada dalam satu kelompok dengan tingkat perubahan ketergantungan lokasi adalah satu, penaksiran parameter model STAR(1;2) dilakukan meng-gunakan Metode Kuadrat Terkecil (MKT). Hasil kajian model akan digunakan pada data curah hujan dari dua lokasi di Indonesia Barat.

2. LANDASAN TEORI

2.1 Model Autoregresif Orde 2, AR(2)

Model AR(2) adalah model deret waktu yang nilai pengamatannya dipengaruhi oleh nilai pengamatan dua waktu sebelumnya dan unsur galat.

Model AR(2) dinyatakan sebagai berikut:

 

1



1



2



2



 

Z t Z t Z t e t

(2.1) (2.1)

Asumsi galat berdistribusi normal dengan mean nol dan varians konstan( Wei, W.W.S. 1994).

2.2 Model Vektor Autoregresif Orde Dua

2.2.1. Model Vektor Autoregresif Orde Dua VAR(1)

Bentuk umum dari model time series VAR(1), (Wei, W.W.S, 1994) Z

 

t Φ Z1



t1



E

 

t _(2.2) untuk N = 2 adalah:

 









 

1 11 12 1 1 2 21 22 2 2 1 1 z t z t e t z t z t e t                   _            dengan t = 1, 2 , . . , T .

2.2.2 Model Vektor Autoregresif Orde 2, VAR(2)

Model VAR(2) merupakan pengem-bangan dari model AR(2). Jika pada model AR(2) pengamatan waktu sekarang hanya melibatkan pengaruh dua waktu sebelumnya di satu lokasi, maka pada model VAR(2) pengamatan sekarang tidak hanya dipengaruhi oleh satu lokasi tapi juga dipengaruhi oleh lokasi lain di sekitarnya. Model VAR(2) dinyatakan dalam persamaan berikut:

 

t  1



t1



 2



t2





 

t

Z Φ Z Φ Z E

(2.3)

dengan Z

_{ }

t , Z



t 1



, Z



t 2



merupakan matriks yang menyatakan pengamatan untuk setiap waktu t t, 1,t2.

Persamaan di atas dapat pula ditulis

(( ( 1)) 1) 1( ) (( ( 1)) 1) 2( ) (( ( 1)) 1) (( ( 1)) 1)

( )t N T    N N ( 1)t N T   N N ( 2)t N T    ( )t N T  

Z Φ Z Φ Z E

Misalkan terdapat dua lokasi pengamatan, N=2, maka model VAR(2) adalah

((2 ( 1)) 1) 1(2 2) ((2 ( 1)) 1) 2(2 2) ((2 ( 1)) 1) ((2 ( 1)) 1)

( )t _{  }_T  _ ( 1)t _{  }_T  _ (t2) _{  }_T  ( )t _{  }_T

Z Φ Z Φ Z E

, t = 3,4,…,T Model VAR (2) dengan N=2 dan

T=3 menjadi 1 11 12 1 2 21 22 2 11 12 1 1 21 22 2 ((22) 1) ((22) (22)) 2 (3) 0 0 (2) (3) 0 0 (2) (4) 0 0 (3) (4) 0 0 (3) Z Z Z Z Z Z Z Z                                                  _ _ _ __ _ _ _ _ _ _ __ _ _ _                    1 1 11 12 2 2 21 22 11 12 1 1 21 22((22) (22)) 2 ((22)1) ((22) 1) (1) (3) 0 0 0 0 (1) (3) (2) (4 0 0 0 0 (2) Z e Z e Z e Z                                                         _ __ _ _ _  _ __ _ _ _                 2 ((22)1) ) (4) e           _ _ _ _      

2.3 Matriks Bobot Seragam

Matriks bobot merupakan matriks bujur sangkar yang memiliki entri-entri berupa bobot lokasi yang bersesuaian. Bobot untuk entri matriks pada model STAR biasanya ditentukan dengan memperhatikan sifat-sifat fisik atau karakteristik misalnya luas wilayah, kepadatan penduduk, batas antara dua lokasi, atau sarana transportasi, dimana setiap bobot tersebut tidak tergantung pada waktu (Ruchjana, 2002). Asumsi untuk kajian bobot ini adalah bahwa bobot suatu lokasi terhadap dirinya sendiri adalah nol.

Selanjutnya bobot

w

_ij pada lag spasial 1 dinyatakan oleh W berupa matriks bujur sangkar



NxN sebagai berikut:



12 1 21 2 1 2 0 0 0 N N N N w w w w w w                W     

(3)

Salah satu bobot yang sering digunakan adalah bobot seragam. Bobot seragam ditentukan oleh banyaknya lokasi pengamatan lain di sekitar lokasi pengamatan tertentu.

Bobot seragam ditentukan sebagai berikut:

1

, jika dan merupakan tetangga terdekat 0 , jika lainnya ij w i j N      

dengan N menyatakan banyaknya tetangga terdekat dari lokasi i pada lag spasial 1. Sifat-sifat matriks bobot seragam diantaranya:

0

ij

w 

1 1 1

1, untuk setiap dan

N N N ij ij j i j w i w N     





Diagonal matriks bobot W adalah nol.

2.4. Model Space Time Autoregresif Orde 1, STAR(1;1)

Model Space Time Autoregressive (STAR) merupakan hasil kombinasi dari model autoregresif (AR) dari Box-Jenkins (1976) dengan model spasial Cliff-Ord dalam Ruchjana (2002). Persamaan model STAR(1;1) dapat dinyatakan sebagai berikut:

 

t 01



t1



11



t1





 

t

Z Z WZ E

(2.4) dengan:

 t 

Z vektor pengamatan (N x 1) dari N lokasi pada waktu t

(t 1) 

Z vektor pengamatan (N x 1) dari N lokasi pada waktu t-1



W matriks bobot (N x N) pada lag spasial 1

t



waktu pengamatan (2,3,…,T)

01





parameter model pada lag spasial 0 dan

lag waktu 1

11





parameter model pada lag spasial 1 dan lag waktu 1 dengan iid



_0, 2



t

e N 

Persamaan untuk dua lokasi dinyatakan sebagai berikut:

 

1 1 12 1 01 1 2 2 1 2 21 2 2 2 11 2 1 2 2 1 1 0 1 1 0 1 _x x x x Z t Z t w Z t e t Z t Z t w Z t e t



                    _   _               

atau dapat diuraikan sebagai berikut:

3. METODE PENELITIAN

Metode penelitian dalam makalah ini berdasarkan studi kepustakaan (studi literatur) dan studi eksperimental. Studi literatur dilakukan dengan mengkaji literatur tentang proses spasial dan model time series, diantaranya model STAR(1;1), model VAR(2) dan VAR(1). Sedangkan studi eksperimental dilakukan pada data curah hujan pada dua lokasi di Indonesia bagian barat engan penaksiran parameter menggunakan perangkat lunak excel . Data yang digunakan dalam penelitian ini adalah curah hujan dari dua lokasi yaitu Curah Hujan Di Provinsi kepulauan Bangka Belitung dan stasiun pengamatan Tabing Padang Tahun 2004 -2009. Alur/diagram untuk penelitian yang diusulkan: Mulai dengan menentukan data yang akan diolah, untuk mengolah data tersebut perlu kajian teori proses stokastik; Time series , mulai dari Univariat; model AR(2), ACF (fungsi autokorelasi), PACF (fungsi parsial autokorelasi). Untuk menetapkan model AR(2), kemudian menentukan Matriks bobot lokasi W, Matriks bobot seragam, selanjutnya; mempelajari model STAR(1;2), menerapkan model STAR(1;2) pada penaksiran parameter data curah hujan dari 2 lokasi.

4. HASIL DAN PEMBAHASAN

4.1 Model Space Time Autoregresif, STAR(1;2)

Model Space Time Autoregresif orde 1 dalam lokasi dan orde 2 dalam waktu, STAR(1;2) menunjukkan nilai pengamatan masa mendatang tergantung dari nilai pengamatan dua waktu sebelumnya di lokasi tersebut dan di lokasi-lokasi lain disekitarnya yang berada dalam satu kelompok dengan tingkat perubahan ketergantungan lokasi adalah satu. Keterkaitan antara dua lokasi pada model STAR(1;2) dinyatakan oleh matriks bobot W yang entri-entrinya berupa bobot antara dua lokasi yang bersesuaian.

Persamaan model STAR(1;2) dinyatakan dengan:

 

   

01 02 11 12

()

t





t

 

1 

t

 

2 

t

 

1 

t

 

2 t

Z

WZ

E

(4.1)

(4)

Persamaan (4.1) di atas disederhanakan oleh Pfeifer yang menyatakan mengingat kelompok lokasi berada pada lag spasial 1 (dalam satu kelompok lokasi) maka penambahan parameter spasial dan matriks bobot W cukup satu kali yaitu pada lag waktu 1. Model Pfeifer tersebut adalah:

01 02 11

( )

t





( 1)

t

 



(

t



2)





( 1)

t

 

( )

t

Z

WZ

E

(4.2) dengan:

 

t 

Z vektor pengamatan (N x 1) dari N

lokasi pada waktu t

(t 1) 

Z vektor pengamatan (N x 1) dari N lokasi pada waktu t-1



t 2





Z vektor pengamatan (N x 1) dari N lokasi pada waktu t-2



W matriks bobot (N x N) pada lag spasial 1

t



waktu pengamatan (3,4,…,T)

01





parameter model pada lag spasial 0 dan lag waktu 1

11





parameter model pada lag spasial 0

dan lag waktu 2 11





parameter model pada lag spasial 1

dan lag waktu 1 dengan



2



0, iid t

e N 

Selanjutnya untuk dua lokasi pengamatan, persamaan (4.2) dapat dibentuk menjadi

                                                      ) ( ) ( ) 1 ( ) 1 ( 0 0 ) 2 ( ) 2 ( ) 1 ( ) 1 ( ) ( ) ( 2 1 11 02 01 2 1 21 12 2 1 2 1 2 1 t e t e t Z t Z w w t Z t Z t Z t Z t Z t Z    (4.3) (4.2)

Persamaan (4.2) dapat diuraikan menjadi:

 













 













 

1 01 1 02 1 11 12 2 1 2 01 2 02 2 11 21 1 2 1 2 1 1 2 1 Z t Z t Z t w Z t e t Z t Z t Z t w Z t e t



             

Persamaan (4.2) dapat dibentuk menjadi persamaan linear berikut:

YX (4.3) dengan Y Z

_{ }

t , 01 02 11







            , dan



Z t( 1) Z t( 2) Z t( 1)



    X W

4.2 Prosedur Penaksiran Parameter

menggunakan Metode Kuadrat

Terkecil pada Model STAR(1;2)

Penaksiran parameter dengan metode kuadrat terkecil pada prinsipnya adalah untuk meminimumkan jumlah kuadrat galat. Galat model STAR(1;2) adalah sebagai berikut (Sugihartini, , 2010):

    01  1 02  2 11  1

e tZ tZ t  Z t WZ t

( 4.4 ) Jumlah kuadrat galat STAR(1;2) dinyatakan dengan:

 

2

 

01



1



02



2



11



1



2

Se t _Z tZ t Z t WZ t _

Turunan terhadap



₀₁,



₀₂, dan



₁₁ adalah sebagai berikut:

 

01





02





11



 



01 2 1 2 1 1 0 S Z t Z t Z t  Z t Z t   _       _    W ) 1 ( )] 1 ( ) 1 ( ) 2 ( ) 1 ( ) 1 ( ) 1 ( ) ( 11 02 01           t Z t WZ t Z t Z t Z t Z t Z t Z   

 

01





02





11



 



02 2 1 2 1 2 0 S Z t Z t Z t  Z t Z t   _       _    W ) 2 ( )] 1 ( ˆ ) 2 ( ) 2 ( ˆ ) 2 ( ) 1 ( ˆ ) 2 ( ) ( 11 02 01           t Z t WZ t Z t Z t Z t Z t Z t Z   

 

01





02





11









11 2 1 2 1 W 1 0 S Z t Z t Z t  Z t Z t   _       _    W

 



1



01



1





1



02



2





1



Z tWZ t  Z t WZ t  Z t WZ t  › ›     11 Z t 1 Z t 1  W  W  ›

Dalam bentuk matriks menjadi:

                                                 11 02 01 ˆ ˆ ˆ ) 1 ( W ) 1 ( W ) 1 ( W ) 2 ( ) 1 ( W ) 1 ( 2) -1)Z(t -WZ(t ) 2 ( ) 2 ( ) 2 ( ) 1 ( ) 1 ( ) 1 ( W ) 1 ( ) 2 ( ) 1 ( ) 1 ( ) ( W ) ( ) 2 ( ) ( ) 1 ( ) (    t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z (4.5)

Untuk t = 3,4…,T, maka persamaan (4.5) menjadi

(5)

                                                



  11 02 01 3 3 ˆ ˆ ˆ ) 1 ( W ) 1 ( W ) 1 ( W ) 2 ( ) 1 ( W ) 1 ( 2) -1)Z(t -WZ(t ) 2 ( ) 2 ( ) 2 ( ) 1 ( ) 1 ( ) 1 ( W ) 1 ( ) 2 ( ) 1 ( ) 1 ( ) ( W ) ( ) 2 ( ) ( ) 1 ( ) (    t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z T t T t                                                                     



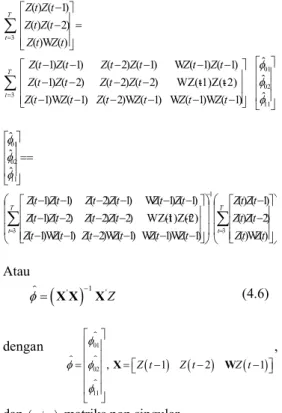
   ) ( W ) ( ) 2 ( ) ( ) 1 ( ) ( ) 1 ( W ) 1 ( W ) 1 ( W ) 2 ( ) 1 ( W ) 1 ( 2) -1)Z(t -WZ(t ) 2 ( ) 2 ( ) 2 ( ) 1 ( ) 1 ( ) 1 ( W ) 1 ( ) 2 ( ) 1 ( ) 1 ( ˆ ˆ ˆ 3 1 3 11 02 01 t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z t Z T t T t    Atau



_'



1 _' Z  X X  X › (4.6) dengan       01 02 11 , Z t 1 Z t 2 Z t 1           _ _ _    _       X W › › › › , dan

_

'

_

X X matriks non singular.

4.3. Prakiraan Curah Hujan dengan Model STAR(1;2)

Di bawah ini disajikan plot data curah hujan pada lokasi 1 dan lokasi 2.

Gambar 4.1 Plot Data curah hujan Lokasi 1 dan Lokasi 2

Data curah hujan yang digunakan pada penelitian ini, data curah hujan di kepulauan Bangka Belitung dan Stasiun Pengamatan Tebing Padang pada periode tahun 2004 -2008.

4.4 Penaksiran Parameter Model STAR(1;2)

Dengan mensubstitusikan nilai-nilai matriks bobot biner ke dalam model STAR(1;2), dapat

dilakukan penaksiran parameter model STAR(1;2) menggunakan metode kuadrat terkecil dengan bantuan software. Parameter-parameter model STAR(1;2) menunjukkan besarnya pengaruh suatu lokasi terhadap lokasi itu sendiri dan pengaruh suatu lokasi terhadap lokasi-lokasi lain disekitarnya. Model taksiran STAR(1;2) merupakan model yang dibentuk dengan parameter-parameternya merupakan parameter hasil taksiran STAR(1;2) dan matriks bobot yang digunakan, yaitu 0 1

1 0

 

  

 

W

Model taksiran STAR(1;2) yang terbentuk adalah 1 1 1 2 2 1 2 2

ˆ ( ) 0.27 ( 1) 0.9 ( 2) 0.05 ( 1)

ˆ ( ) 0.05 ( 1) 0.9 ( 2) 0.27 ( 1)

Z t



 

 





 

 



(4.8)

Artinya curah hujan dilokasi satu dipengaruhi oleh lokasi sendiri 0,27 satu waktu sebelumnya -0,9 dua waktu sebelumnya dan 0,05 satu waktu lokasi lokasi dua, curah hujan dilokasi dua dipengaruhi oleh 0,05 satu waktu sebelumnya dan -0,9 dua waktu sebelumnya dan sebesar 0,27 lokasi dua satu waktu sebelumnya.

5. KESIMPULAN

Model STAR(1;2) adalah sbb:

 













 













 

1 01 1 02 1 11 12 2 1 2 01 2 02 2 11 21 1 2 1 2 1 1 2 1 Z t Z t Z t w Z t e t Z t Z t Z t w Z t e t



             

Model STAR(1;2) dapat diterapkan pada berbagai fenomena riil, seperti data curah hujan. Untuk data curah hujan yang digunakan pada penelitian ini, data curah hujan di kepulauan Bangka Belitung dan Stasiun Pengamatan Tebing Padang pada periode tahun 2004 -2008,Model STAR(1;2) yang terbentuk adalah:

1 1 1 2 2 1 2 2

ˆ ( ) 0.27 ( 1) 0.9 ( 2) 0.05 ( 1)

ˆ ( ) 0.05 ( 1) 0.9 ( 2) 0.27 ( 1)

Z t



 

 





 

 



Artinya curah hujan dilokasi satu dipengaruhi oleh lokasi sendiri 0,27 satu waktu sebelumnya -0,9 dua waktu sebelumnya dan 0,05 satu waktu lokasi lokasi dua, curah hujan dilokasi dua dipengaruhi oleh 0,05 satu waktu sebelumnya dan -0,9 dua waktu sebelumnya dan sebesar

(6)

0,27 lokasi dua satu waktu sebelumnya.

6. UCAPAN TERIMAKASIH

Dalam kesempatan ini penulis mengucapkan terimakasih kepada:Rektor Unpad dan Dekan FMIPA Unpad yang telah memberikan kesempatan kepada Staf Dosen Jurusan Matematika untuk melaksanakan kegiatan penelitian di jurusan dan fakultas MIPA Unpad. Ketua Jurusan Matematika FMIPA Unpad beserta Pengelola Jurusan Matematika yang telah membantu pendanaan kegiatan penelitian ini. Rekan Peneliti Kelompok Bidang Keahlian Pemodelan Stokastik, serta semua pihak yang tidak dapat disebutkan satu per satu. Semoga kegiatan penelitian ini memberikan manfaat bagi kami sebagai tim peneliti untuk melaksanakan kegiatan penelitian sebagai salah satu tridharma perguruan tinggi, agar dapat mendukung pelaksanaan pendidikan maupun pengabdian kepada masyarakat.

7. DAFTAR PUSTAKA

1. WEI, WILLIAM W.S Time Series Analysis, Addison Wesley Publishing Company.Inc.1994.

2. BOX, G.E.E.,AND G.M.JENKINS Time Series Analysis, Forecasting and control, Holden-Day,Inc.,SanFransisco.(1962). 3. PFEIFER,P.E., Spatial Dynamic

Modeling, unpublished Ph.D Dissertation, Georgia Institute of Technologi, Georgia(1979).

4. RUCHJANA, B. N. Suatu Model Generalisasi Space-Time Autoregresi dan Penerapannya Pada Produksi Minyak Bumi, Disertasi S-3, ITB. (2002).

5. SURYAMAH Perbandingan Matriks Bobot Lokasi Model Space Time Autoregresi Orde Satu Tesis Program Pascasarjana UNPAD (2010).

6. SUGIHARTINI, Penaksiran Parameter Model Space Time Autoregresif STAR(1;2) Skripsi Program S1 Matematika FMIPA UNPAD ( 2010).