Analisa Kompleksitas Algoritma. Sunu Wibirama

Analisa Kompleksitas Algoritma

Referensi

✦

Cormen, T.H., Leiserson, C.E., Rivest,

R.L., Stein, C., Introduction to Algorithms

2nd Edition, Massachusetts: MIT Press,

2002

✦

Sedgewick, R., Algorithms in C++ Part

1-4, Massachusetts: Addison-Wesley

Publisher, 1998

✦

Video lecture MIT Opencourseware

ke-1: Introduction

✦

Video lecture IIT Kharagpur, India

Video lecture MIT

Opencourseware ke-1:

Introduction

Video lecture IIT

Kharagpur, India ke-18:

Agenda Hari Ini

•

Pentingnya Analisa Algoritma

•

Prinsip Perbandingan Algoritma

•

Dasar-dasar Matematika dan Teori Big-O

•

Contoh Implementasi

•

Kehandalan dalam menyelesaikan masalah (robustness)

•

Fungsionalitas (functionality)

•

Tampilan grafis (user interface)

•

Daya tahan (reliability)

•

Keamanan (security)

•

Kesederhanaan (simplicity)

•

Kemudahan dalam penggunaan (user friendly)

•

Kemudahan dalam pemeliharaan (maintainability)

Apa yang pertama kali Anda menjadi

pertimbangan Anda saat membeli komputer,

selain PERFORMA?

Algoritma dan Performa

•

Hal-hal yang menjadi pertimbangan utama Anda

tidak muncul dengan gratis

•

Performa sistem menjadi alat tukar seperti

uang

.

•

Algoritma program memegang peran kunci

•

Algoritma adalah teknologi, engineered,

Pentingnya Analisa Algoritma

•

Algoritma membantu kita memahami skalabilitas

program kita

•

Performa terkadang menjadi pembeda antara

yang mungkin dilakukan dan yang

tidak mungkin

dilakukan

•

Analisa algoritma memberi gambaran informasi

tentang ‘perilaku program’ kita

•

Mempelajari

bagaimana menerapkan algoritma

yang baik untuk kasus tertentu

membedakan

profesi system analyst dan programmer

Prinsip Perbandingan Algoritma

•

Apa yang membuat sebuah algoritma dikatakan LEBIH

BAIK dari algoritma yang lain?

•

Kompleksitas waktu (Time Complexity)

•

Kompleksitas ruang (Space Complexity)

•

Kecenderungan saat ini:

•

ruang (hard disk) semakin murah

•

kapasitas data yang diproses semakin besar

•

waktu pemrosesan harus semakin cepat

Penyebab variasi pada hasil analisa algoritma

•

Program aras tinggi diterjemahkan ke bahasa mesin. Setiap

tipe prosesor memiliki prosedur bahasa mesin yang berbeda

•

Aplikasi dijalankan di shared environment, sehingga

terpengaruh oleh penggunaan memori

•

Program sangat sensitif terhadap masukan dan akan

menunjukkan performa yang jauh berbeda untuk rentang

masukan yang tidak terlalu berbeda

•

Program tidak dipahami dengan baik, sehingga analisa

matematika kurang merepresentasikan kondisi yang

sesungguhnya

•

Program tersebut memang tidak bisa dibandingkan dengan

program yang lain karena hanya optimal untuk input-input

tertentu

Hal-hal yang perlu diperhatikan

pada analisa algoritma

•

Memisahkan operasi pada tingkat abstraksi

dan implementasi.

Contoh: menghitung jumlah instruksi

scanf

pada program

lebih diprioritaskan daripada

memahami berapa nanoseconds instruksi

scanf

dieksekusi

•

Mengidentifikasi data masukan:

- Strategi

average

dan

worst case

Dasar Matematika & Teori Big-O

•

Sebagian besar algoritma memiliki parameter primer

N yang sangat mempengaruhi waktu eksekusi

•

Parameter N bisa berupa:

- derajat polinomial

- ukuran berkas (file) yang diproses

- jumlah karakter pada text string

- ukuran data yang diproses

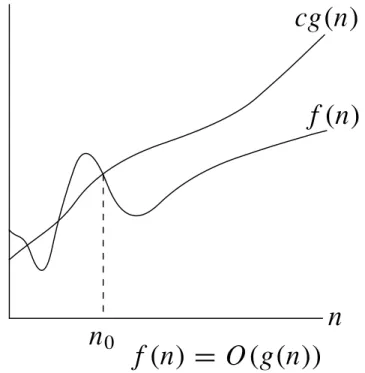
Teori Big-O

O(g(N ))

= { f (N) : jika terdapat konstanta positif c dan N

₀

, sehingga

0

≤ f (N) ≤ cg(N) untuk semua N ≥ N

₀

}

Teorema Matematika:

Engineering:

•

Hilangkan orde yang lebih rendah dan

konstanta. Gunakan hanya orde tertinggi

pada polinomial

Contoh:

3n

3

+ 90n

2

− 5n + 6046 = O(N

3

)

3.1 Asymptotic notation 43 (b) (c) (a) n n n n₀ n₀ n₀ f (n) _{= !(g(n))} f (n) _{= O(g(n))} f (n) _{= "(g(n))} f (n) f (n) f (n) cg(n) cg(n) c₁g(n) c2g(n)

Figure 3.1 Graphic examples of the !, O, and " notations. In each part, the value of n₀ shown is the minimum possible value; any greater value would also work. (a) !-notation bounds a function to within constant factors. We write f (n) _{= !(g(n)) if there exist positive constants n0}, c₁, and c₂ such that to the right of n₀, the value of f (n) always lies between c₁g(n) and c₂g(n) inclusive. (b) O-notation gives an upper bound for a function to within a constant factor. We write f (n) _{= O(g(n))} if there are positive constants n₀ and c such that to the right of n₀, the value of f (n) always lies on or below cg(n). (c) "-notation gives a lower bound for a function to within a constant factor. We write f (n) _{= "(g(n)) if there are positive constants n0} and c such that to the right of n₀, the value of f (n) always lies on or above cg(n).

c₁n2 _≤ 1

2n

2 _{− 3n ≤ c} 2n2

for all n _{≥ n0}. Dividing by n2 yields

c_{1 ≤} 1

2 − 3

n ≤ c2 .

The right-hand inequality can be made to hold for any value of n _{≥ 1 by choosing}

c_{2 ≥ 1/2. Likewise, the left-hand inequality can be made to hold for any value}

of n _{≥ 7 by choosing c1 ≤ 1/14. Thus, by choosing c1 = 1/14, c2 = 1/2, and}

n_{0 = 7, we can verify that} 1₂n2 _{− 3n = !(n}2). Certainly, other choices for the constants exist, but the important thing is that some choice exists. Note that these constants depend on the function 1₂n2_{−3n; a different function belonging to !(n}2) would usually require different constants.

We can also use the formal definition to verify that 6n3 _{$= !(n}2). Suppose for the purpose of contradiction that c₂ and n₀ exist such that 6n3 _{≤ c2}n2 for all n _{≥ n0}. But then n _{≤ c2}/6, which cannot possibly hold for arbitrarily large n, since c₂ is constant.

Intuitively, the lower-order terms of an asymptotically positive function can be ignored in determining asymptotically tight bounds because they are insignificant for large n. A tiny fraction of the highest-order term is enough to dominate the

Macam-macam Parameter N

1

Sebagian besar instruksi dieksekusi satu kali atau dalam

jumlah yang tidak terlalu banyak (waktu eksekusi

konstan)

Pertumbuhan waktu eksekusi program tidak terlalu cepat.

Waktu eksekusi ini terdapat pada program yang

memecahkan masalah dengan kapasitas yang cukup

besar, dipecah-pecah menjadi beberapa bagian

N

Waktu eksekusi program linier. Sebagian besar masukan

_{diproses dalam jumlah yang tidak terlalu banyak}

Waktu eksekusi ini terdapat pada program yang

memecahkan masalah menjadi beberapa bagian,

menyelesaikannya secara terpisah, kemudian

menggabungkannya kembali

log N

Macam-macam Parameter N

(cont’d)

Biasanya digunakan untuk memecahkan masalah dalam

jumlah kecil. Biasanya terdapat pada program yang

memproses pasangan data (quadratic) atau array dua

dimensi secara bersamaan (double-nested loop)

Biasanya digunakan untuk memecahkan masalah dalam

jumlah kecil. Biasanya terdapat pada program yang

memproses tiga buah data (cubic) atau array tiga dimensi

secara bersamaan (triple-nested loop)

Waktu eksekusi program linier. Sebagian besar masukan

diproses dalam jumlah yang tidak terlalu banyak

N

2

N

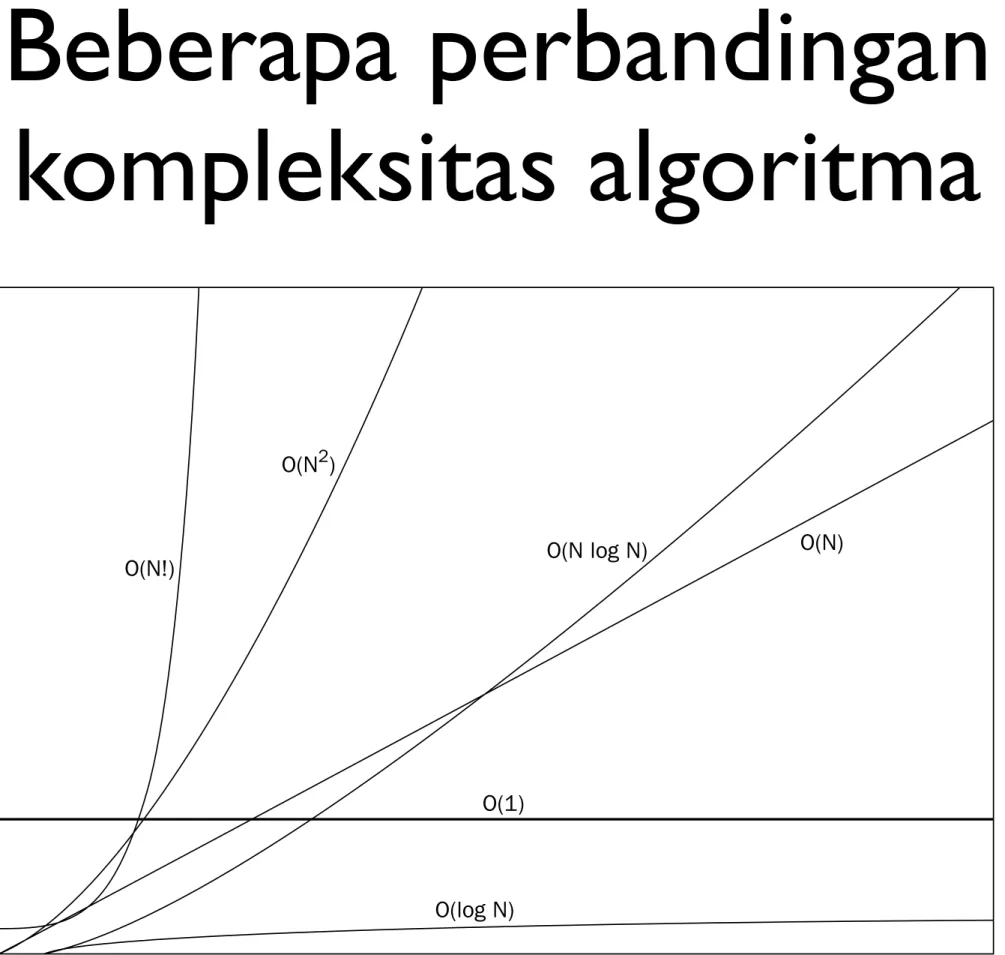
3

Beberapa perbandingan

kompleksitas algoritma

Figure 1-1 shows how the various measures of complexity compare with one another. The horizontal axis represents the size of the problem — for example, the number of records to process in a search algo-rithm. The vertical axis represents the computational effort required by algorithms of each class. This is not indicative of the running time or the CPU cycles consumed; it merely gives an indication of how the computational resources will increase as the size of the problem to be solved increases.

Figure 1-1: Comparison of different orders of complexity.

Referring back at the list, you may have noticed that none of the orders contain constants. That is, if an algorithm’s expected runtime performance is proportional to N, 2×N, 3×N, or even 100×N, in all cases the complexity is defined as being O(N). This may seem a little strange at first — surely 2×Nis better than 100×N— but as mentioned earlier, the aim is not to determine the exact number of operations but rather to provide a means of comparing different algorithms for relative efficiency. In other words, an algo-rithm that runs in O(N) time will generally outperform another algorithm that runs in O(N2₎. Moreover, when dealing with large values of N, constants make less of a difference: As a ration of the overall size, the difference between 1,000,000,000 and 20,000,000,000 is almost insignificant even though one is actu-ally 20 times bigger.

Of course, at some point you will want to compare the actual performance of different algorithms, espe-cially if one takes 20 minutes to run and the other 3 hours, even if both are O(N). The thing to remember,

however, is that it’s usually much easier to halve the time of an algorithm that is O(N) than it is to

change an algorithm that’s inherently O(N2₎to one that is _O(N). O(N!) O(N2) O(N log N) O(log N) O(N) O(1) 5

Getting Started

04_596748 ch01_2.qxd 11/12/07 4:06 PM Page 5

Running Time

(seconds)

Input size (N)

Formula Kondisi Periodik

•

Sebagian besar algoritma terdiri dari proses

penyelesaian masalah dengan memanfaatkan

perulangan (rekursif)

•

Bagian yang berulang tersebut secara tidak

langsung berkontribusi pada kompleksitas

sebuah algoritma

•

Perlu mengetahui formula-formula dasar

Formula Kondisi Periodik

•

Formula 1: kondisi periodik muncul pada program

rekursif yang mengeliminasi satu item input

Formula Kondisi Periodik

•

Formula 2: kondisi periodik muncul pada program rekursif yang

membagi input menjadi dua bagian hanya dengan satu langkah

Formula Kondisi Periodik

•

Formula 3: kondisi periodik muncul pada program rekursif yang

membagi input menjadi dua bagian, namun perlu memeriksa

tiap-tiap input

Formula Kondisi Periodik

•

Formula 4: kondisi periodik muncul pada program rekursif yang

mengolah input secara linear sebelum, pada saat, dan sesudah

membagi input menjadi dua bagian

Formula Kondisi Periodik

•

Formula 5: kondisi periodik muncul pada program rekursif yang

membagi input menjadi dua bagian, kemudian mengerjakan input

lain dengan kapasitas konstan

Jenis analisa waktu eksekusi

•

Strategi

Worst case

(umum digunakan)

T(N) = waktu eksekusi maksimum untuk

jumlah data N

•

Strategi

Average case

(jarang digunakan)

T(N) = waktu yang diharapkan dari sebuah

algoritma untuk mengeksekusi data

sejumlah N. Perlu ada asumsi statistik untuk

distribusi data masukan

Analisa worst case

•

Biasanya mengambil

batas maksimal

(upper bound),

untuk memberi jaminan bahwa program tidak akan

terus berjalan saat batas maksimal waktu eksekusi

tercapai

•

Waktu eksekusi juga tergantung pada kondisi awal

input : data yang sudah terproses akan lebih mudah

dieksekusi daripada yang belum

•

Untuk worst-case, diambil kemungkinan yang paling

buruk (data tidak terproses sama sekali, pada kondisi

yang berlawanan dengan kondisi akhir yang

Machine-independent

Running Time

•

Berapakah waktu eksekusi terburuk (worst-case)

dari sebuah algoritma?

•

Tergantung dari kecepatan mesin kita:

- kecepatan relatif: berjalan di komputer yang sama

- kecepatan absolut: berjalan di komputer yang

berbeda

•

Kita ingin mengukur kecepatan algoritma tanpa

mempertimbangkan kecepatan komputer

Analisa Asymptotic :

Pertumbuhan waktu eksekusi T(N)

saat

N

→ ∞

Performa Asymptotic

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./0+1

!"#$%&'&()*%+,-',$./)+

"

A2"3

"

_,

4

5"(6789:;<=$(>?<8'"(

@6A%#$8$>B@::A(6:8C"'(

@:?8'>$7%6*(78C"D"'0

4

E"@:FC8':;(;"6>?<(

6>$9@$>8<6(8G$"<(B@::(G8'(@(

B@'"G9:(&@:@<B><?(8G(

"<?><""'><?(8&H"B$>D"60

4

I6A%#$8$>B(@<@:A6>6(>6(@(

96"G9:($88:($8(7":#($8(

6$'9B$9'"(89'($7><J><?0

57"<(

"

?"$6(:@'?"("<89?7*(@(

Θ2"

+

₃

_@:?8'>$7%(

?,B?30

&"@$6(@(

Θ2"

1

₃

_@:?8'>$7%0

O(n

2

₎

O(n

3

₎

Pada jumlah data tertentu (> N

0

), algoritma dengan kompleksitas

rendah

O(n

2

₎

bisa saja lebih efisien dibandingkan algoritma

dengan kompleksitas tinggi

Kita tidak boleh meremehkan

sebuah algoritma yang secara

asymptotic lebih lambat

Dalam disain riil, kita perlu

menyeimbangkan proses engineering

dengan melihat algoritma yang

sesuai untuk masalah yang dihadapi

Analisa Asymptotic membantu

kita untuk berlaku lebih adil

terhadap algoritma yang kita

gunakan

Teori Big-O

•

Untuk membandingkan dua buah algoritma,

bandingkan tingkat kompleksitasnya

lim

N

→∞

f (N )

g(N )

→ ∞

Untuk N besar

g(N) lebih efisien dari f(N)

lim

N

→∞

f (N )

g(N )

→ 0

Untuk N besar

Implementasi: Insertion Sort

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0

./0-!"#$%&'()#*$'+$,'&-./0

!"#$%&

1"23"45"((

¢?

_/

*(?

₊

*(6*(?

_"

²

78(43%&"'10

'$%#$%&

#"'%3$9$:74((

¢?A

_/

B*?A

₊

B*6B*?A

_"

²

135;

$;9$((

?A

_/

≤ ?A

₊

≤

6

≤ ?A

_"

0

123*%)#4

!"#$%&

<((+((=((>((?((@

'$%#$%&

+((?((=((@((<((>

Implementasi: Insertion Sort

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./01

!"#$%&'()*(+,-'./+),(-)./

1

+

2

3

4

5

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./01

!"#$%&'()*(+,-'./+),(-)./

2

+

3

1

4

5

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./0/,

!"#$%&'()*(+,-'./+),(-)./

1

+

2

3

4

5

+

1

2

3

4

5

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./0//

!"#$%&'()*(+,-'./+),(-)./

1

+

2

3

4

5

+

1

2

3

4

5

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./0/+

!"#$%&'()*(+,-'./+),(-)./

1

+

2

3

4

5

+

1

2

3

4

5

+

2

1

3

4

5

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./0/1

!"#$%&'()*(+,-'./+),(-)./

2

+

3

4

1

5

+

2

3

4

1

5

+

3

2

4

1

5

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./0/1

!"#$%&'()*(+,-'./+),(-)./

2

+

1

3

4

5

+

2

1

3

4

5

+

1

2

3

4

5

+

1

2

3

4

5

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0

./0/-!"#$%&'()*(+,-'./+),(-)./

1

+

2

3

4

5

+

1

2

3

4

5

+

2

1

3

4

5

+

2

1

3

4

5

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./0/1

!"#$%&'()*(+,-'./+),(-)./

2

+

3

4

5

1

+

2

3

4

5

1

+

3

2

4

5

1

+

3

2

4

5

1

+

5

3

2

4

1

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./0/)

!"#$%&'()*(+,-'./+),(-)./

1

+

2

3

4

5

+

1

2

3

4

5

+

2

1

3

4

5

+

2

1

3

4

5

+

4

2

1

3

5

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./0/1

!"#$%&'()*(+,-'./+),(-)./

1

+

2

3

4

5

+

1

2

3

4

5

+

2

1

3

4

5

+

2

1

3

4

5

+

4

2

1

3

5

+

4

2

5

1

3

&%">

!"#$"%&"'()*(+,,- 1%23$)-.#*4 566789*:$);*<=*<>/?)"> ?"&*1.?$,>0*:=*@>)0>$0%"!"#$%&'(#)%"*#%*+,-%$)#./0 ./0)

!"#$%&'(")#(%&

1

2!345162

7!

645(

8+*("9

ຆ

+:/(0(0(";

*(%

A*ĸ +

&(

"

+(

;>3*ĸ +:(A;

)*ĸ A*B /

,-'.$

)*C*,

<=>(

+:);(?(;>3

+(

+:)D/;(ĸ +:);

)*ĸ )*B /

+:)D/;(@(;>3

A#B"C>DED>"F

BD'$">

)

A

;>3

+G

/

"

Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C., Introduction to Algorithms 2nd Edition, Massachusetts: MIT Press, 2002

24 Chapter 2 Getting Started

In the following discussion, our expression for the running time of INSERTION

-SORT will evolve from a messy formula that uses all the statement costs c_i to a

much simpler notation that is more concise and more easily manipulated. This simpler notation will also make it easy to determine whether one algorithm is more efficient than another.

We start by presenting the INSERTION-SORT procedure with the time “cost”

of each statement and the number of times each statement is executed. For each

j _{= 2, 3, . . . , n, where n = length[A], we let tj} be the number of times the while loop test in line 5 is executed for that value of j. When a for or while loop exits in the usual way (i.e., due to the test in the loop header), the test is executed one time more than the loop body. We assume that comments are not executable statements, and so they take no time.

INSERTION-SORT(A) cost times 1 for j _{← 2 to length[A]} c₁ n

2 _{do key ← A[ j]} c₂ n _{− 1}

3 ! Insert A[ j] into the sorted

sequence A[1 . . j _{− 1].} 0 n _{− 1}

4 i _{← j − 1} c₄ n _{− 1}

5 while i > 0 and A[i] > key c₅ !n_j=2 t_j

6 _{do A[i + 1] ← A[i]} c₆ !n_j=2(t_j − 1) 7 i _{← i − 1} c₇ !n_j=2(t_j − 1) 8 A[i _{+ 1] ← key} c₈ n _{− 1}

The running time of the algorithm is the sum of running times for each statement executed; a statement that takes c_i steps to execute and is executed n times will contribute c_in to the total running time.5 To compute T (n), the running time of INSERTION-SORT, we sum the products of the cost and times columns, obtaining

T (n) _{= c1}n _{+ c2}(n − 1) + c₄(n − 1) + c₅ n " j₌₂ t_{j + c6} n " j₌₂ (t_j − 1) + c7 n " j₌₂ (tj − 1) + c8(n − 1) .

Even for inputs of a given size, an algorithm’s running time may depend on

which input of that size is given. For example, in INSERTION-SORT, the best

5_{This characteristic does not necessarily hold for a resource such as memory. A statement that}

references m words of memory and is executed n times does not necessarily consume mn words of memory in total.

24 Chapter 2 Getting Started

In the following discussion, our expression for the running time of INSERTION

-SORT will evolve from a messy formula that uses all the statement costs c_i to a

much simpler notation that is more concise and more easily manipulated. This simpler notation will also make it easy to determine whether one algorithm is more efficient than another.

We start by presenting the INSERTION-SORT procedure with the time “cost”

of each statement and the number of times each statement is executed. For each

j _{= 2, 3, . . . , n, where n = length[A], we let tj} be the number of times the while loop test in line 5 is executed for that value of j. When a for or while loop exits in the usual way (i.e., due to the test in the loop header), the test is executed one time more than the loop body. We assume that comments are not executable statements, and so they take no time.

INSERTION-SORT(A) cost times 1 for j _{← 2 to length[A]} c₁ n

2 _{do key ← A[ j]} c₂ n _{− 1}

3 ! Insert A[ j] into the sorted

sequence A[1 . . j _{− 1].} 0 n _{− 1}

4 i _{← j − 1} c₄ n _{− 1}

5 while i > 0 and A[i] > key c₅ !n_j=2 tj

6 _{do A[i + 1] ← A[i]} c₆ !n_j=2(tj − 1)

7 i _{← i − 1} c₇ !n_j=2(tj − 1)

8 A[i _{+ 1] ← key} c₈ n _{− 1}

The running time of the algorithm is the sum of running times for each statement executed; a statement that takes ci steps to execute and is executed n times will

contribute cin to the total running time.5 To compute T (n), the running time of

INSERTION-SORT, we sum the products of the cost and times columns, obtaining

T (n) _{= c1}n _{+ c2}(n − 1) + c₄(n − 1) + c₅ n " j₌₂ tj + c6 n " j₌₂ (tj − 1) + c7 n " j₌₂ (tj − 1) + c8(n − 1) .

Even for inputs of a given size, an algorithm’s running time may depend on

which input of that size is given. For example, in INSERTION-SORT, the best

5_{This characteristic does not necessarily hold for a resource such as memory. A statement that}

references m words of memory and is executed n times does not necessarily consume mn words of memory in total.

2.2 Analyzing algorithms 25

case occurs if the array is already sorted. For each j _{= 2, 3, . . . , n, we then find} that A[i] _{≤ key in line 5 when i has its initial value of j − 1. Thus tj = 1 for}

j _{= 2, 3, . . . , n, and the best-case running time is}

T (n) _{= c}1n + c2(n − 1) + c4(n − 1) + c5(n − 1) + c8(n − 1)

= (c1 + c2 + c4 + c5 + c8)n − (c2 + c4 + c5 + c8) .

This running time can be expressed as an _{+ b for constants a and b that depend on} the statement costs c_i; it is thus a linear function of n.

If the array is in reverse sorted order—that is, in decreasing order—the worst case results. We must compare each element A[ j] with each element in the entire sorted subarray A[1 . . j _{− 1], and so tj = j for j = 2, 3, . . . , n. Noting that}

n ! j₌₂ j ₌ n(n + 1) 2 − 1 and n ! j₌₂ (j − 1) = n(n − 1) 2

(see Appendix A for a review of how to solve these summations), we find that in the worst case, the running time of INSERTION-SORT is

T (n) _{= c}1n + c2(n − 1) + c4(n − 1) + c5 "n(n + 1) 2 − 1 # + c6 "_{n(n − 1)} 2 # + c7 "_{n(n − 1)} 2 # + c8(n − 1) = $c_{2 +}5 c_{2 +}6 c₂7%n2 ₊ $c1 + c2 + c4 + c5 2 − c6 2 − c7 2 +c8 % n − (c2 + c4 + c5 + c8) .

This worst-case running time can be expressed as an2 _{+ bn + c for constants a, b,} and c that again depend on the statement costs c_i; it is thus a quadratic function of n.

Typically, as in insertion sort, the running time of an algorithm is fixed for a given input, although in later chapters we shall see some interesting “randomized” algorithms whose behavior can vary even for a fixed input.

Worst-case and average-case analysis

In our analysis of insertion sort, we looked at both the best case, in which the input array was already sorted, and the worst case, in which the input array was reverse sorted. For the remainder of this book, though, we shall usually concentrate on

2.2 Analyzing algorithms 25

case occurs if the array is already sorted. For each j _{= 2, 3, . . . , n, we then find} that A[i] _{≤ key in line 5 when i has its initial value of j − 1. Thus t}j = 1 for

j _{= 2, 3, . . . , n, and the best-case running time is}

T (n) _{= c1}n _{+ c2}(n − 1) + c₄(n − 1) + c₅(n − 1) + c₈(n − 1) = (c1 + c2 + c4 + c5 + c8)n − (c2 + c4 + c5 + c8) .

This running time can be expressed as an _{+ b for constants a and b that depend on} the statement costs ci; it is thus a linear function of n.

If the array is in reverse sorted order—that is, in decreasing order—the worst case results. We must compare each element A[ j] with each element in the entire sorted subarray A[1 . . j _{− 1], and so tj = j for j = 2, 3, . . . , n. Noting that}

n ! j₌₂ j ₌ n(n + 1) 2 − 1 and n ! j₌₂ ( j − 1) = n(n − 1) 2

(see Appendix A for a review of how to solve these summations), we find that in the worst case, the running time of INSERTION-SORT is

T (n) _{= c1}n _{+ c2}(n − 1) + c₄(n − 1) + c₅ "n(n + 1) 2 − 1 # + c6 "_n(n − 1) 2 # + c7 "_n(n − 1) 2 # + c8(n − 1) = $c_{2 +}5 c_{2 +}6 c₂7%n2 ₊ $c_{1 + c2 + c4 +} c5 2 − c₆ 2 − c₇ 2 + c8 % n − (c2 + c4 + c5 + c8) .

This worst-case running time can be expressed as an2 _{+ bn + c for constants a, b,} and c that again depend on the statement costs ci; it is thus a quadratic function

of n.

Typically, as in insertion sort, the running time of an algorithm is fixed for a given input, although in later chapters we shall see some interesting “randomized” algorithms whose behavior can vary even for a fixed input.

Worst-case and average-case analysis

In our analysis of insertion sort, we looked at both the best case, in which the input array was already sorted, and the worst case, in which the input array was reverse sorted. For the remainder of this book, though, we shall usually concentrate on

Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C., Introduction to Algorithms 2nd Edition, Massachusetts: MIT Press, 2002

Implementasi: Insertion Sort

Worst-case (seluruh input diurutkan terbalik):

Apakah Insertion Sort algoritma yang cepat?

- Ya, jika N kecil

- Tidak, jika N besar

Lihat perbandingannya dengan Merge Sort di

slide berikutnya

T (N )

=

O( j)

= O(n

2

)

j=2 N

Contoh komparasi

•

Komputer A:

Insertion Sort, lebih cepat untuk N kecil,

memproses N data dengan waktu eksekusi

Kecepatan eksekusi prosesor 10

9

_{instruksi/detik}

•

Komputer B:

Merge Sort, lebih lambat untuk N kecil,

memproses N data dengan waktu eksekusi

Kecepatan eksekusi prosesor 10

7

_{instruksi/detik}

•

Diketahui:

c

₁

N

2

c

₂

N log N

c

1

 c

2

Jika c

1

=2, c

2

=50, N = 10

6

,

Kesimpulan

•

Analisa algoritma diperlukan untuk

perbandingan algoritma tanpa tergantung

spesifikasi mesin

•

Analisa algoritma membantu kita memecahkan

masalah sesuai kondisi dan data yang kita hadapi

•

Analisa algoritma bukan alat mutlak untuk

memilih algoritma terbaik, tapi membantu

memahami perilaku algoritma saat diterapkan di

dunia nyata