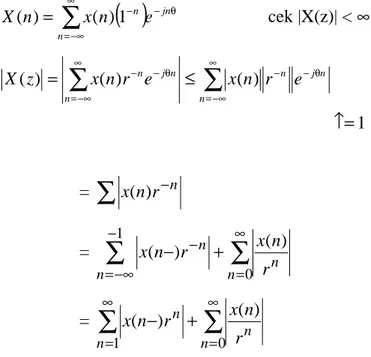Bab 3: Sinyal dan Sistem di Domain z

Bab 3: Sinyal dan Sistem di Domain

z

Analisa sinyal dan sistem bisa dipermudah apabila dilakukan pada domain z. Untuk itu, sinyal dan sistem direpresentasikan ke dalam domain ini kemudian hasilnya dipakai untuk analisa.

1 Transformasi z pada Sinyal

1.1 Definisi Transformasi z

Tujuan Belajar 1

Peserta mengetahui definisi Transformasi z (X(z)) dari sinyal x(n) beserta definisi dan pengertian Region of Convergence (RoC), yakni sebuah polinomial. sequence polinomial x(n) X(z) =

∑

∞ −∞ = − n n z n x( )

Z-transform untuk sinyal x(n) : X(z) = z{x(n)}

( )

n X(z) x ←→z

Region of Converge (ROC) : karena X(z) adalah deret tak hingga maka secara matematis bisa bernilai ∞ untuk z terhingga ⇒ tidak boleh. Oleh sebab itu z yang bisa digunakan adalah z ∈ ROC

Tujuan Belajar 2

Peserta mengetahui bahwa untuk sinyal berdurasi terbatas (finite duration), X(z) adalah polinomial berorde terbatas dengan RoC seluruh

inverse forward Kawasan Z (Z-plane) Kawasan Waktu

x(n) = {1, 2, 5, 7, 0, 1}

⇒ X(z) = 1 + 2z-1 + 5z-2 + 7z-3 + z-5

ROC seluruh z-plane kecuali z = 0, z = ∞

Tujuan Belajar 3

Peserta mengetahui X(z) dari impuls dan versi tergesernya sejauh k sampel.

x(n) = {1, 2, 5, 7, 0, 1}

⇒ X(z) = z2 + 2z+ 5 + 7z-1 + z-3

ROC seluruh z-plane kecuali z = 0, z = ∞ x(n) = δ(n) ⇒ X(z) = 1 ROC : seluruh z-plane

x(n) = δ(n-k), k >0 ⇒ X(z) = z-k ROC : seluruh z-plane, kecuali z = 0

x(n) = δ(n+k), k > 0 ⇒ X(z) = zk ROC : seluruh z-plane, kecuali z = ∞

Tujuan Belajar 4

Peserta mengetahui X(z) untuk sinyal durasi tak hingga x

( ) ( ) ( )

n = a nu n beserta RoC yang sesuai bagi a ≤1.

Cari Z-transform dari x(n) = (1/2)nu(n) Jawab : x(n) = { …, 0, 0, …,

( )

0 2 1 ,

( )

2 2 1 ,

( )

3 2 1 , …}

( )

... 2 1 2 1 2 1 1 2 2 1 _{ +}      +       + + = _z− _z− n_z−n z X

Ingat

∑

∞ =0

=

1

−

1

n n

x

x

, bila |x| < 1 ∞, bila |x| ≥ 1 → X(z) =

( )

2z 1 1 1 − ; ROC : 2z 1 _{< 1} X(z) = 1 2 1 1 1 − − z ; ROC : |z| >1/2 Secara umum berlaku

⇒ x

( )

n =anu

( )

n ⇔

( )

1 1 1 − − = az z X untuk z >a. Tujuan Belajar 5

Peserta mengetahui perbedaan RoC untuk sinyal berdurasi tak hingga kausal (di luar lingkaran), anti-kausal (di dalam lingkaran), dan kombinasinya (cincin).

Konvergensi |X(z)| dari sinyal kausal dan Antikausal

Pertama kita tahu bahwa bilangan kompleks dapat dinyatakan dalam bentuk kartesian atau bentuk polar, misalnya

) Im( ) Re(z j z re z= jθ = + θ _R e I_m z

Gambar 1. Bentuk polar dari bilangan kompleks z.

θ jn n n e r z− = − −

( )

jnθ n n e n x n X − ∞ −∞ = −

∑

= ( )1 ) ( cek |X(z)| < ∞ 1 ) ( ) ( ) ( ↑= ≤ = ∞ − −∞ = − ∞ −∞ = − −

∑

∑

jn n n n n j n e r n x e r n x z X θ θ =

∑

x(n)r−n =

∑

∑

∞ = − −∞ = − ₊ − 0 1 ) ( ) ( n n n n r n x r n x =

∑

∑

∞ = ∞ = + − 0 1 ) ( ) ( n n n n r n x r n x

Term Noncausal : dua term harus konvergen

1 ) ( 1 < −

∑

∞ = n n r n x → r harus kecil, < r1 → n r n x(− ) ≤ 1 →|z| < r1 R_e I_m r₁

Gambar 2. ROC untuk term nonkausal. Term kausal

1

)

(

_<

n

r

n

x

, r>r2, |z|>r2

R_e I_m

r₂

Gambar 3. ROC untuk bagian kausal.

Kalau kedua-dua nya (kausal dan nonkausal) ada dan r2 < r1, maka ROCnya berbentuk

cincin.

Gambar 4. ROC untuk sinyal dengan bagian kausal dan nonkausal. Contoh : x(n) = αnu(n), cari X(z) n n z z X

∑

∞ = − = 0 1₎ ( ) ( α ROC : |αz-1| < 1

1 1 1 − − = z α |z| > α Ctt.

Bila x(n) = u(n) ⇒ x(n) = αnu(n), α = 1

→ 1 1 1 ) ( ₋ − = z z X , |z| > 1 Contoh :    ≤ − ≥ = − − = 1 , 0 , 0 ) 1 ( ) ( n n n u n x n _n α α

∑

∑

−∞ = ∞ = − − ₌₋ − = 1 1 1 ) ( ) ( ) ( n l l n n z z z X α α Ctt.

∑

∞

∑

= ∞ = − = = 1 0 1 n n N n A A A A A , |A| < 1 1 1 1 1 1 1 ) ( _{− −} − − = − − = z z z z X α α α |α-1z| < 1 |z| < |α|

∞ ∞

Gambar 5. ROC untuk sinyal yang finite maupun infinite. One sided

∑

∞ = − + ₌ 0 ) ( ) ( n n z n x z X 1.2 Inversi Transformasi z Tujuan Belajar 6

Peserta mengerti definisi Inverse transformasi z beserta penurunannya dari teorema Cauchy countour integral.

Inverse :

Cauchy Contour Integral

(

)

   ≠ = = −

∫

− − n k n k j dz z z c k n k , 0 , 2 1 π

∫

− − =_ _≠= c k n n k n k j dz z , 0 , 2 1 π

∫

∫ ∑

∞ − − −∞ = − −         = c c k n k k n dz z z k x dz z z X( ) 1 ( ) 1

( )

n j x dz z k x k c k n π 2 ) ( 1 = =

∑

∞

∫

−∞ = − −

∫

− = ⇒ c n _dz z z X j n x ( ) 1 2 1 ) ( π 1.3 Sifat-Sifat Transformasi z Tujuan Belajar 7

Peserta mengetahui dan dapat memanfaatkan sifat linier dari transformasi z, termasuk untuk menghitung transformasi z dari sinyal cos

( ) ( )

ω₀nun dan

( ) ( )

₀nun sinω . Sifat Linear: x1(n) ⇔ X1(z) ROC1 x2(n) ⇔ X2(z) ROC2 α1x1(n) + α2x2(n) ⇔α1X1(z) + α2X2(z) ROC : ∩ ROCi

Contoh : x(n) = [3(2n) - 4(3n)]u(n) = 3x1(n) + (-4)x2(n) ⇓ ⇓ (2n)u(n) (3n)u(n) 1 1 2 1 1 ) ( ₋ − = z z X ROC : |z| > 2 1 2 3 1 1 ) ( ₋ − = z z X ROC : |z| > 3 ⇒ X(z) = 3X1(z) + (-4)X2(z) ROC : |z| > |3| 1 1 _{1 3} 4 2 1 3 − − − ₋ − = Z Z |Z| > 3

Hitung a). x(n) = cos(ωon)u(n) b). x(n) = sin(ωon)u(n) Contoh :

x(n) = ancos(ωon)u(n)

2 2 1 1 cos 2 1 cos 1 − − ₊ − − ⇔ z a az a o o ω ω

x(n) = a3sinωonu(n)

2 2 1 1 cos 2 1 sin − − − + − ⇔ z a az az o o ω ω Tujuan Belajar 8

Peserta mengetahui akibat pergeseran di domain waktu terhadap X

( )

z dan dapat memanfaatkannya.

x(n) ↔ X(z)

⇒ x(n-k) ↔ Z-kX(z)

ROC : sama dengan X(z) kecuali z = 0 k > 0

Contoh :    ≤ ≤ − = elsewhere N n n x , 0 1 0 , 1 ) ( Cari X(z) Perhatikan : x(n) = x1(n) - x2(n) Di mana x1(n) = u(n) x2(n) = u(n-N) = x1(n-N) 1 1 1 1 ) ( − − = z z X |z| > 1 1 1 2 1 ) ( ) ( ₋ − − − = = z z z X z z X N N 1 1 1 1 1 1 1 1 ) ( − − − − − ₋ − = − − − = → z z z z z z X N N ROC |z| > 1 hitung lewat cara lain

) ( ) ( ) ( ) cos( ) ( 2 1 2 1 0n u n e u n e u n n x = ω = jωon + −jωon 1 1 1 ) ( ₋ − ↔ z e n u e o j on j ω ω _{|z| > 1} 1 1 1 ) ( − − − − ↔ z e n u e o j on j ω ω _{|z| > 1}

( )

(

)

(

)

1 z : ROC cos 2 1 cos 1 2 2 1 2 1 1 1 1 1 2 1 1 2 1 1 1 2 1 2 1 1 2 1 1 2 1 1 1 1 1 1 > + − − = + + − + − =         + − − − + − = + − = − − − − − − − − − − − − − − − − − − − z z z z z e e z e e z z e z e z e z e z e z e z X o o j j j j j j j j j j o o o o o o o o o o ω ω ω ω ω ω ω ω ω ω ω ω

) ( ) ( ) ( ) sin( ) ( 2 1 _{e e u n} n u n n x j on j on j o ω ω ω = − − = 2 1 1 cos 2 1 sin ) ( − − − + − = z z z z X o o ω ω ROC : |z| > 1 Tujuan Belajar 9

Peserta mengetahui akibat scaling di domain z terhadap sinyal di domain waktu dan dapat memanfaatkannya.

x(n) ↔ X(z) r1 < |z| < r2

⇒ anu(n) ↔ X(a-1z) |a|r1 < |z| < |a|r2

Bukti:

∑

∞ −∞ = − = n n n n z n x a n x a Z( ( )) ( )

∑

∑

 = ₌      = ∞ − −∞ = − a z n n n z z n a a z n x( ) ( ) ) ( ) ( X a 1z z z X a z = − = = bila X(z) ROC : r1 < |z| < r2 r1 < |z/a| < r2 |a|r1 < |z| < |a|r2 Tujuan Belajar 10

Peserta mengetahui akibat time-reversal di domain waktu terhadap sinyal di domain z dan dapat memanfaatkannya.

) ( ) (n 2 X z x ←→ ROC : r1 < |z| <r2 maka x(−n)↔ X(z−1) ROC : 1/r2 < |z| <1/r1 Bukti :

∑

∞

∑

−∞ = ∞ −∞ = − − − ₌ − = n l l n z l x z n x n x z( ( )) ( ) ( )( 1) 1 ) ( ₋ = = z z z X r1 < |z-1| <r2 1/r2 < z <1/r1 Contoh : x(n) = u(-n) 1 1 ₁ 1 1 )) ( ( ) ( _{− −} = − = = ₋ ↔ − ⇒ z z z z _z n u z n u z − = 1 1 ROC : |z| < 1 Tujuan Belajar 11

Peserta mengetahui akibat diferensiasi di domain z terhadap sinyal di domain waktu dan dapat memanfaatkannya.

) ( ) (n X z x ←→z

[

]

∑

∞

∑

−∞ = − ∞ −∞ = − − − ₌₋ − = n n n n z n nx z z n n x dz z dX ) ( ) )( ( ) ( 1 1 = -z-1Z{nx(n)} dz z dX z n nx Z{ ( )}=− ( ) Contoh : x(n) = nanu(n) = n(anu(n)) ↓ x1(n) ) ( 1 1 ) ( ) ( ₁ 1 1 X z az n u a n x n = − ↔ = ₋ ROC : |z| > |a| ) ( ) 1 ( 1 ) 1 .( ) ( ) ( 2 2 1 1 − − + − − − = − = az az z dz z dX z z X

2 1 1 ) 1 ( − − − = az az |z| > |a| Contoh : 2 1 1 ) 1 ( ) ( ₋ − − ↔ z z n nu |z| > 1 Tujuan Belajar 12

Peserta mengetahui bahwa konvolusi dua sinyal di domain waktu menghasilkan perkalian kedua sinyal di domain z, dan dapat memanfaatkannya. ) ( ) ( ₁ 1 n X z x ↔ ) ( ) ( ₂ 2 n X z x ↔

∑

∞ −∞ = − = ≡ ∗ k k n x k x n x n x n x₁( ) ₂( ) ( ) ₁( ) ₂( )

∑

∞

∑

−∞ = ∞ −∞ = − − ₋         − = k n k k n_{z z x n k} z k n x k x₁( ) ₂( ) . ₂( )

( )

z X z X z X z k x z X k k 1 1 2 1 2 ) ( ) ( ) ( ) ( ↓ = =

∑

∞ −∞ = − Contoh : Hitung x(n) = x1(n) + x2(n) Di mana x1(n) = {1, -2, 1}    ≤ ≤ = elsewhere n n x , 0 5 0 , 1 ) ( 2 jawab : X1(z) = 1- 2z-1+ z-2 X2(z) = 1 +z-1 +z-2 +z-3 + z-4 +z-5

X(z) = X1(z)X2(z)=1 -z-1 -z-6 +z-7 ⇒ x(n) = {1, -1, 0, 0, 0, 0, -1, 1} ↑ Cara lain: X1(z) = (1 - z-1)2 sebelumnya contoh lihat 1 1 ) ( 1 6 2 ₋ − − − = z z z X X1(z) * X2(z) = (1- z-6)(1-z-1) = 1 -z-1 -z-6 +z-7 dst. Tujuan Belajar 13

Peserta mengetahui teorema kondisi awal dan menggunakannya. Teorema Kondisi Awal

x(n) causal (i.e., x(n), n < 0)       _{+ +} = ∞ → ∞ → 2 ) 2 ( ) 1 ( ) 0 ( ) (

_lim

lim

z x_z x z z x z X = x(0) lihat tabel!

2 Bentuk Rasional dari Transformasi z

2.1 Bentuk Rasional dan Plot Pole-Zero

Tujuan Belajar 14

Peserta mengenal bentuk khusus rasional dari X

( )

z , dan mengerti serta dapat mencari pole dan zero dari X

( )

z tersebut. Peserta dapat memplot pole-zero tersebut di bidang z.

Zero dari X(z) adalah nilai-nilai z di mana X(z) = 0 Pole dari X(z) adalah nilai-nilai z di mana X(z) = ∞ X(z) rasional,

∑

∑

= − = − − − − = + + + + + + = = N k k k M k k k o N N a a N M M z a z b a a z z z b z b b z D z N z X 0 0 1 1 1 0 / ... ) ( ... ) ( ) ( ) ( 0 1 Bila a0≠ 0 dan b0≠ 0 o N N o N o M M o M N o M o a a z a a z b b z b b z z a z b X + +     + + +     +         − − − − ... ... 1 1 1 1

karena N(z) dan D(z) polinomial, maka

( )

₍

(

)(

₎₍

) (

_{) (}

)

₎

( )

(

)

(

)

(

)

∏

∏

= = − + − − − = = − − − − − −         = N i i M i i M N N M N M o o p z z z Gz z X p z p z p z z z z z z z z a b z X 1 1 2 1 2 1 ... ... Plot :

Gambar 6. Pole dan zero diletakkan pada z-plane masing-masing dengan lambang x dan o. Tujuan Belajar 15 Im Re zeroes poles

Peserta dapat mencari X(z) dan x(n) berdasarkan plot pole–zero. Contoh :

Plot pole-zero dari sinyal x(n) = anu(n) a > 0 a z z az z X − = − = ₋ 1 1 1 ) ( ROC : |z| > a ⇒ zero ⇒z1 = 0; P1 = a

Gambar 7. Konfigurasi pole dan zero pada sebuah kasus. Contoh : Untuk     _{≤ ≤ −} = elsewhere M n a n x n , 0 1 0 , ) ( ) ( ) ( 1 ) ( 1 1 1 a z z a z az az z X M M M M − − = − = ₋− ₋ M k j k M M

ae

z

a

z

=

→

=

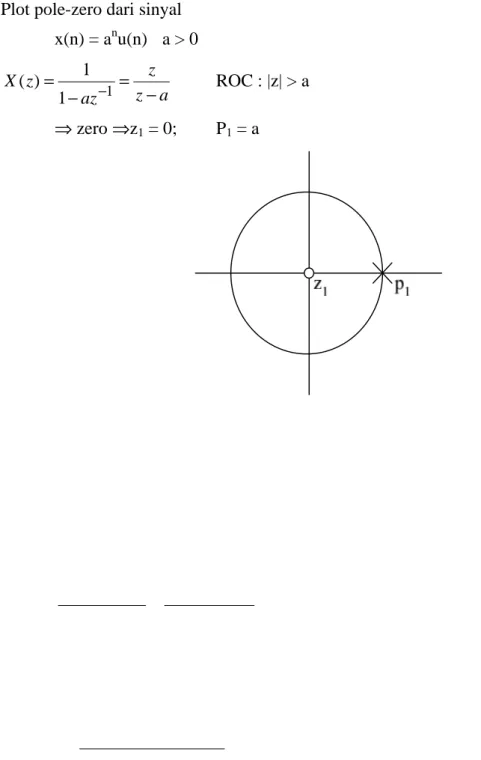
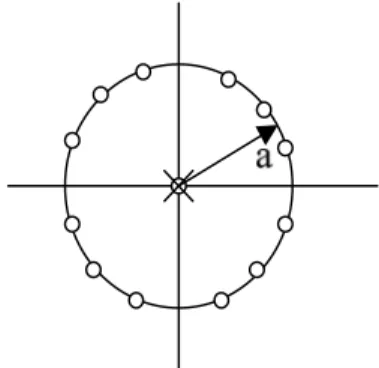
2π / zo = a cancels z = a 1 1 1)...( ) ( ) ( − − − − = ⇒ _M M z z z z z z X M-1 zero M-1 pole

Gambar 8. Konfigurasi pole dan zero.

Soal :

Cari Z-transform dari sinyal dari :

Gambar 9. Konfigurasi pole-zero dalam konjugasi. Jawab:

2 zero : z1 = 0; z2 = rcosωo

2 pole : p1 = rejωo ; p2 = re-jωo

( )

( )

₍

(

)(

₎₍

)

₎

( )

( )

n G

(

r n

)

u

( )

n x r z rz rz G z X re z re z r z z Gz z GX o n o o j j o o o ω ω ω ω ω ω cos z ROC 1 cos 2 1 cos 1 cos 0 2 2 1 1 2 2 = ⇒ > + − − = ⇒         − − − − = ⇒ − − − − −

Tujuan Belajar 16

Peserta memahami sifat sinyal kausal di kawasan waktu akibat lokasi pole, menggunakan kasus satu pole x

( ) ( ) ( )

n = anun , pole ganda

( ) ( ) ( )

n n a un

x = n , dan sepasang pole complex conjugate. Peserta juga mengerti hubungan lokasi pole dengan stabilitas sistem.

Sifat kawasan waktu sinyal kausal akibat lokasi pole Cek pada |z| < 1, |z| = 1, |z| > 1

↑

unit circle

• Kasus 1 pole real

1 1 1 ) ( ) ( ) ( ₋ − = → ← = az z X n u a n x n z |z| > |a|

Gambar 10. Pengaruh posisi pole terhadap dinamika sinyal.

• Kasus z pole real (double)

( )

( )

(

)

a az az n u na n x n > − ↔ = − − z 1 1 2 1

Gambar 11. Pengaruh posisi pole ganda terhadap dinamika sinyal.

Gambar 12. Pengaruh posisi pole ganda konjugate terhadap sifat dinamika sinyal. Jadi:

sinyal dengan pole di dalam unit circle selalu terbatas amplitudanya. Pole dekat origin

→ decay cepat → berlaku untuk sistem stabil

3 Transformasi z Untuk Sistem

Tujuan Belajar 17

Peserta dapat mendefiniskan fungsi sistem H(z) dari h(n) maupun hubungan I/O dari sistem LTI. Peserta juga dapat mencari H(z) dari sistem LCCDE secara cepat, termasuk untuk kasus khusus all-zero dan all-pole.

Y(z) = H(z) X(z) ⇒ H(z) = Y(z)/X(z) Sistem Fungsi ) ( ) ( ↑ =

∑

∞ −∞ = − n h z n h z H Sistem LCCDE:

∑

∞

∑

−∞ = = − + − − = n M k k ky n k b x n k a n y 0 ) ( ) ( ) (

∑

∑

= = − − ₊ − = N k M k k k k kz Y z b z X z a z Y 1 0 ) ( ) ( ) ( ) ( 1 ) ( ) ( 1 0 _{H z} z a z b z X z Y N k k k M k k k = + =

∑

∑

= − = − Kasus khusus -

∑

= − = M k k kz b z H 0 )

( ∈ all zero, FIR

⇒ + =

∑

= − N k k k o z a b z H 1 1 ) ( all pole Contoh :

Cari H(z) dan h(n) dari y(n) = 1/2y(n-1) + 2x(n) Jawab: ) ( ) ( 2 ) ( 1 2 ) ( 2 1 1 2 1_z h n u n z H ⇒ = n − = ₋

4 Inversi dengan Cara

Partial Fraction

Tujuan Belajar 18

Peserta mengerti prinsip inversi transformasi z dengan cara partial fraction, baik untuk X(z) yang proper maupun yang improper.

Inversi partial fraction

∑

→

) (z

X term standar, bergantung pole dan ROC ↓

∑

← ) (n x inverse masing-masing k

Inversi dengan Partial Fraction Definisi

X(z) proper bila bila aN≠0 dan M < N bila tidak proper bisa dibentuk

2 6 1 1 6 5 3 3 1 2 6 1 1 1 3 1 ) ( _{− −} − + + + + − + = z z z z z z X

buat proper + inproper

2 6 1 1 6 1 1 6 1 1 1 2 1 ) ( − − − − + + + + = z z z z z X Tujuan Belajar 19

Peserta dapat melakukan inversi transformasi z dengan cara partial fraction untuk X(z) yang proper dan memiliki pole distink.

aN ≠ 0 M < N N N N N M N M N o N N N N N M N M N N o P z A P z A P z A z z X a z z b z b z z X z z a z a z z b z b z b z x − + + − + − = + + + = = × + + + + + + = − − − − − − ... ) ( proper selalu ... ... ) ( ... ... ) ( 2 2 1 1 1 1 1 1 1 1 Contoh : 2 1 _0,5 5 . 1 1 1 ) ( − − ₊ − = z z z X

) 5 . 0 )( 1 ( 5 . 0 5 . 1 2 2 2 − − = + − = z z z z z z 5 . 0 2 1 1 ) 5 . 0 )( 1 ( ) ( − − + = − − = z A z A z z z z z X ) 5 . 0 )( 1 ( ) 1 ( ) 5 . 0 ( ₂ 1 − − − + − = z z z A z A ) 1 ( ) 5 . 0 ( ₂ 1 − + − = ⇒z A z A z 1 = A1(2 - 0.5) ⇒ A1 = 2 0.5 = A2(0.5 - 1) ⇒ A2 = -1 5 . 0 1 1 2 ) ( − − − = ⇒ z z z z X Ctt. ,...,N k z z X P z A P z A P z A P z A P z z z X P z k P z k k n n k k k k 1 ) ( ) ( ) ( ... ) ( ) ( ) ( 1 1 = − = ⇒ − − + + + − − = − = Contoh : 2 1 1 5 . 0 1 1 ) ( z z z z X + − + = ₋ − 5 . 0 1 ) ( 2_{− +} + = z z z z z X P1 = 1/2 + j1/2 P2 = 1/2 - j1/2 2 2 1 1 2 1)( ) ( 1 ) ( P z A P z A P z P z z z z X − + − = − − + = 2 3 2 1 2 1 1 _{1 1} 1 ) ( ) ( j P z z z z X P z A _{z P z P} = − − + = − = _{= =} 2 3 2 1 1 2 2 _{2 2} 1 ) ( ) ( j P z z z z X P z A _{z P z P} = + − + = − = _{= =}

Tujuan Belajar 20

Peserta dapat melakukan inversi transformasi z dengan cara partial fraction untuk X(z) yang proper dan memiliki pole yang berorde ganda.

2 1 1_{)(1 )} ( 1 ) ( _{− −} − = z Hz z X 2 1 2 ) 1 )( 1 ( ) ( − − + = z z z z z X 2 3 1 ) 1 ( 1 1 ) ( + + − + + = z A z A z A z z X 3 2 2 1 ) 1 ( 1 1 1 ) ( ) 1 ( A z z A z z A z z X z − + + − + + = + 4 1 ) ( ) 1 ( 1 1 = + = z₌₋ z z X z A 2 1 ) ( ) 1 ( 1 2 3 = − = _z= z z X z A 4 3 ) ( ) 1 ( 1 2 2 =         − = = z z z X z dz d A     − − − > → =         − − − − ) 1 ( ) ( | | | | ), ( ) ( 1 1 1 1 n u P P z causal n u P z P z p z k A n k k n k k k i X(z) = (A1P1n + A2P2n + …+ ANPnn)u(n) 2 1 _0.5 5 . 1 1 1 ) ( _{− −} + − = z z z X Contoh : 1 1 _{1 0.5} 1 1 2 ) ( _{− −} − + − = z z z X , ROC |z| > 1, |z| < 0.5, atau 0.5<|z|<1

Ketika |z| > 1 x(n) causal x(n) = 2(1)nu(n)-(0.5)nu(n) |z| < 0.5 → x(n) is non causal x(n) = -2 u(-n-1) +(0.5)nu(-n-1) 1 1 1 ) 1 ( − − = − − − z n u n α α * ROC 0.5 < |z| < 1 |z|<1 anti causal |z| > 0.5 causal x(n) = -2u(-n-1) - (0.5)nu(n) Tujuan Belajar 21

Peserta dapat melakukan inversi transformasi z dengan cara partial fraction untuk X(z) yang proper dan memiliki pasangan pole complex conjugate. Contoh : 2 1 1 5 . 0 1 1 ) ( _{− −} − + − + = z z z z X 1 2 2 1 1 1 1 1 ) ( − − + ₋ − = z P A z P A z X 2 3 2 1 1 j A = − ⇒ 2 3 2 1 1 2 A j A = ∗ = + 2 1 2 1 1 j P = + 2 1 2 1 1 j P = −

( )

( )

( )

( )

( )

[

( ) ( )

]

( )

(

)

[

n

]

u

( )

n r A n u e e r A n x n u p A p A n x k k n k k n j n j n k k n k n k k k k k k k α β α β α β + = + =     ₊ = + − + cos 2 * *

( )

n n u

( )

n x e A o n j       ₋       = → = − = = + = 565 . 71 4 cos 2 1 10 2 1 p 565 . 71 10 2 1 4 9 4 1 4 1 1 π α π Tujuan Belajar 22

Peserta dapat melakukan inversi transformasi z pada X(z) LCCDE melalui perubahan bentuk ke dalam bentuk pole-zero, dan kemudian mendekomposisi X(z) ke dalam beberapa kelompok term (improper, single real pole, conjugate poles, dan multiple poles), kemudian masing-masing diproses sesuai cara masing-masing-masing-masing.

) ( 2 ) 1 ( 1 1 1 _{np u n} pz pz z = n         − − − − _{|z| > |p|} 2 1 1_{)(1 )} 1 ( 1 ) ( _{− −} − + = z z z X 2 1 1 1 1 ) 1 ( 2 1 1 1 4 3 1 1 4 1 − − − − + ₋ + ₋ + = z z z z

x(n) = 1/4(-1)nu(n) + 3/4u(n) + [1/2n(1)n)]u(n) = [1/4(-1)n + 3/4 + n/2]u(n) Dekomposisi

∏

∏

∑

∑

= − = − = − = − − − = + = N k k M k k o N k k k M k k k z p z z b z a z b z X 1 1 1 1 1 0 ) 1 ( ) 1 ( 1 ) (

∑

−

∑

∑

= = − − − = − − ₊ + + + + + + =M N k k k k k k ok k k k k k k multipoles z a z a z b b z a b z c 0 1 1 1 2 2 1 1 1 1 2 1 1 1 Alternatif :

∏

∏

∏

= − − − − = − − − = − + + + + + + = − − M k k k k M k k k o k M k k o kz a z a z b z b z a z b b z p z z b 1 1 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 ) 1 ( ) 1 (

5 Transformasi

z

Satu Sisi

Tujuan Belajar 23

Peserta mengetahui definisi transformasi z satu sisi (X+

( )

z ) beserta sifat-sifat dan persamaan dan perbedaannya dari X

( )

z biasa.

∑

∞ = − + ₌ 0 ) ( ) ( n n z n x z X ) ( ) (n X z x ← →z+ + X+(z) punya sifat-sifat :

• Tidak mempunyai informasi x(n) untuk n<0

• Unik untuk sinyal kausal

• ROC selalu ekterior dari sebuah lingkaran

Tujuan Belajar 24

Peserta dapat menurunkan sifat shifting dari X+

( )

z (baik time delay maupun time advanced) dan mengerti perbedaannya dari sifat shifting

( )

z X .

Semua Z transform properties berlaku kecuali sifat shifting Kasus 1. Time delay ) ( ) (n X z x ← →z+ +

( )

kausal bila 0 0 ] ) ( ) ( [ ) ( 1 n x k z n x z X z k n x k n n k z ↓= > − +   → ← − ⇒

∑

− + − + Bukti :

∑

∞ = − + _{− = −} 0 ) ( )] ( [ n n z k n x k n x Z

( )

0

( ) (

1 1

)

x ... ) 2 ( ) 1 ( ) ( ) ( 0 0 1 2 + − + + + + − + + − + − + − = − − − − − k x x x x k x x k x x k x x k x k

( )

0

( )

1

( )

2 ... x ... ) 2 ( ) 1 ( ) ( [ 1 2 1 + + + + + − + + − + − = − − − − − x x x x x x k x x k x x k x z o k k k         + =

∑

− − = + − − k l l k _{x l z X z} z 1 ) ( ) ( dst. Contoh : 1 1 1 ) ( ) ( ) ( + ₋ − =   → ← = + az z X n u a n x n z x1(n) = x(n-2) di mana x(n) = an ] ) 2 ( ) 1 ( ) ( [ )) 2 ( (x n z 2 X z x z 1 x z2 Z+ − = − + + − + + − ) 2 ( ) 1 ( ) ( 1 2 _{+ − + −} =z− X+ z x z− x karena x(-1) = a-1 x(-2) = a-2 dan 1 1 1 ) ( ₋ + − = az z X 2 1 1 1 1 2 )) 2 ( ( − − − − + _{+ +} − − = − ⇒ a z a az z n x Z

Secara intuitif :

( )

0 z ] ) 1 ( ... ) 1 ( ) ( [ )} ( { k -1 1 > + − + + + − + − = − + + − − + k z X z x z k x k x k n x Z k

Kasus 2. Time Advanced

) ( ) (n X z x ← →z+ + 0 k ) ( ) ( ) ( 1 0 >         −   → ← −

∑

− = − + + k n n k z z n x z x z k n x Bukti :

∑

∞

∑

= ∞ = − − + _{+ = + =} 0 ) ( ) ( )} ( { n l k l k n z l x z z k n x k n x Z sedangkan

∑

∑

∑

∞ = − ∞ = − = − − + _{= = +} k l l l k l l l z l x z l x z l x z X ( ) ( ) ( ) ( ) 0 1 0         − = + ⇒

∑

− = − + + 1 0 ) ( ) ( )} ( { k l l k _{X z x l z} z k n x Z Contoh : Bila x(n) = an, cari Z+{x(n+2)} Jawab: ] ) 1 ( ) 0 ( ) ( [ )} 2 ( { 2 + −1 + _{x n+ =z X z −x −x z} Z z x z x az z ) 1 ( ) 0 ( 1 2 1 2 − − − = ₋ Tujuan Belajar 25

Peserta mengerti sifat asimptotik dari transformasi z satu sisi.

) ( ) (n X z x ← →z+ + ) ( ) 1 ( ) (

_lim

lim

x n z X z n n + ∞ → ∞ → − = ⇒

limit exist bila ROC (z-1)X+(z) mengandung |z| = 1 Contoh : ) ( ) (n d u n h = n |α| < 1

cari nilai step sequence dari n→∞ Y(z) = H(z) X(z) 1 1 1 ) ( − − = z z X 1 1 1 ) ( − − = z z H α 1 : ROC ) ( ) ( ) 1 ( ) )( 1 ( ) ( 2 2 = − = − ⇒ − − = z z z z Y z z z z z Y α α

Karena |α| < 1 → ROC mengandung |z| = 1

α α = − − = → ∞ → 1 1 ) ( ) ( 2 1

lim

lim

y n _zz z n Tujuan Belajar 26

Peserta dapat menerapkan transformasi z satu sisi pada kasus solusi dari deret Fibonacci.

Deret Fibonacci : 1, 1, 2, 3, 5, 8, … Cari close formnya :

y(n) = y(n-1) + y(n-2) Kondisi awal

y(0) = y(-1) + y(-2) = 1 y(1) = y(0) + y(-1) = 1

⇒ y(-1) = 0 dan y(-2) = 1

[

1 _{( ) ( 1)}

] [

2 _{( ) ( 2) ( 1)} 1

]

) ( − + − + − + _{z = z Y z +y − + z Y z +y − +y − z} Y 1 2 2 1 1 1 2 2 2 1 1 1 1 1 1 ) ( − − − − + − + − = − − = − − = ⇒ z P A z P A z z z z z z Y Inversi :

2 5 1 1 + = P 2 5 1 2 − = P 5 1 1 P A = ⇒ 5 2 2 P A =− ) ( 2 5 1 5 3 5 1 2 5 1 5 2 5 1 ) ( 3 n u n y n             − − −     + + = ⇒

(

1 5

) (

1 5

)

( ) 2 1 5 1 y(n) 1 1 1 n u n n n     _{+ − −}       = ⇒ + + + Tujuan Belajar 27

Peserta dapat menerapkan transformasi z satu sisi pada kasus sistem dengan kondisi awal tertentu.

Tentukan respons step dari

y(n) = αy(n-1) + x(n) |α| < 1 dengan kondisi awal y(-1) = 1 jawab :

[

( ) ( 1)

]

( ) ) (z z 1Y z y X z Y+ =α − + + − + + ) 1 ( 1 1 ) ( 1 1 − − + − + − = ⇒ z z z Y α α α ) ( 1 1 ) ( ) ( 1 1_{u n u n} n y n n α α α − − + = + +

(

1

)

( ) 1 1 ₂ n u n+ − − = α α

6 Respons Sistem

Tujuan Belajar 28

Peserta dapat menghitung respons sistem yang memiliki H(z) rasional, berdasarkan analisa pole dan zero dari sinyal input dan fungsi sistem, termasuk mengidentifikasi respons natural dan forced response.

Response dari sistem yang memiliki fungsi-fungsi sistem, yang rasional ) ( ) ( ) ( z Q z N z X = ) ( ) ( ) ( z B z A z H =

Bila kondisi awal = 0, y(-1) = y(-2) = …y(-N) = 0 ) ( ) ( ) ( ) ( ) ( ) ( ) ( z Q z A z N z B z X z H z Y = = ⇒ Bila poles sistem : p1, p2, …, pN sinyal : q1, q2, …, qL pk = qm k = 1, 2, …N m = 1,2,…,L

Bila tidak ada zero yang membuat terjadi pole-zero cancelation, maka

( )

( ) ( )

Response Forced response Natural ) ( ) ( ) ( 1 1 1 1 1 1 1 1 ↓ ↓ + = ⇒ − + − =

∑

∑

∑

∑

= = = − = − L k n k k N k n k k N k L k k k k k n u q Q n u p A z Y z q Q z p A z Y

Perlu dicatat bahwa Ak = f1 (pk,qk)

Qk = f2 (pk,qk)

Zero input → zero output →natural response = 0 Jadi natural response ≠ zero input response untuk nilai relaxed.

Tujuan Belajar 29

Peserta dapat menghitung respons sistem yang mengandung pole order ganda/banyak.

Kasus multiple order poles → kasus seperti pada section 3.4.2, yakni :

⇒ Y(z) mengandung term

(

)

k lz p 1 1 1 − − k = 1, 2, …,m

→ y(n) mengandung term nk-1pln

Tujuan Belajar 30

Peserta dapat menghitung respon sistem yang mengandung pole-zero dan kondisi awal tidak nol (termasuk mengidentifikasi zero state response dan zero input response).

Misalkan x(n) diterapkan pada n = 0 dan y(-1), …, y(-N) ≠ 0 Cari y(n), n ≥ 0 ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 0 1 1 1 0 z X z X z b z n y z Y z a z Y k n x b k n y a n y M k k k k n n N k k k N k M k k k = +         − + − = − + − − =

∑

∑

∑

∑

∑

= + − = + = − + = =

∑

∑

∑

∑

∑

= − = = − = − = − + + − − + = ⇒ N k k k N k k n n k k N k k k M k k k z a z n y z a z X z a z b z Y 1 1 1 1 0 1 ) ( ) ( 1 ) (

( )

z

( )

z z A z N z X z H o + ⇓ ⇓ + = zi zs Y Y ) ( ) ( ) ( ) ( Yzs(z) = H(z)X(z) y(n) y(n) h(n) LCCDE

..., ) ( ) ( 2 1p p p z A z N Y N , , o zi ↓ = + ⇒ y(n) =yzs(n) + yzi(n)

∑

= = N k n k k zi n D p u n y 1 ) ( ) ( ) ( k k ' k L k n k k N k n k k D A A n u q Q n u p A n y + = ↓ + = ⇒

∑

∑

= = ) ( ) ( ) ( ) ( ) ( 1 1 '

⇒ efek dari initial condition adalah mengalter response natural dengan mengubah amplitudo menjadi A1k, tetapi tidak ada efek pada forced response.

Tujuan Belajar 31

Peserta memahami impak dari kondisi awal pada respons. Contoh :

y(n) = 0.9 y(n-1) - 0.81 y(n-2) + x(n) Cari response unit step

Init : y(-1) = y(-2) = 0 y(-1) = y(-2) = 1 Jawab : Relaxed a1 = 0.9 a2 = 0.81 bo=1       −     + − = ⇒ _{− − −} 1 2 1 ₁ 1 81 . 0 9 . 0 1 1 ) ( z z z z Y

(

)(

1

)( )

1 2 1 1 1 1 1 1 1 − − − _{− −} − = z z p z p 3 / 1 0.9ejπ p =

3 / 2 0.9e jπ p = − 1 1 3 / 1 3 / ₁ 099 . 1 9 . 0 1 049 . 0 542 . 0 9 . 0 1 049 . 0 542 . 0 ) ( ) ( − − − − ₋ + ₋ + + − − = = z z e j z e j z Y z Y j j zs _{π π}

→ y(n) =[1.099 + 1.088(0.9)ncos (πn/3 -5.2o)]u(n)

Untuk y(-1) = y(-2) = 1

2 1 1 81 . 0 9 . 0 1 81 . 0 09 . 0 ) ( ) ( ) ( _{− −} − + − − = = z z z z A z N z Y_zi o 1 3 / 1 3 / _{1 0.9} 4936 . 0 026 . 0 9 . 0 1 4936 . 0 026 . 0 − − − ₋ − + − + = z e j z e j j jπ π ⇒ yzi(n) = 0.988(0.9)ncos(πn/3 + 87o)u(n) ⇒ Y(z) = Yzs(z) + Yzi(z) 1 3 / 1 3 / 1 _{1 0.9} 445 . 0 568 . 0 9 . 0 1 445 . 0 568 . 0 1 099 . 1 − − − − ₋ − + − + + − = z e j z e j z jπ jπ

⇒ y(n) = [.099 u(n) + 1.44(0.9)ncos(πn/3 +38o)]

Tujuan Belajar 32

Peserta dapat menghitung transien dan steady state responses dari sistem yang mengandung pole-zero.

∑

= = N k n k k nr n A p u n y 1 ) ( ) ( ) ( |pk| < 1 → ynr(n) decays

In this case → ynr(n) → transient response

Bila pole dekat |z| = 1 → lama decay nya

) ( ) ( ) ( 1 n u q Q n y _k n L k k fr

∑

= =

bila |qk| < 1 → yfr decays → transient response

tapi bila |qk| = 1 → yfr sinusoid → steady state ↓

never decays

→ supaya y(n) ss, x(n) mesti ada terus , n>0 contoh :

Cari transient dan steady state response dari y(n) = 0.5y(n-1) + x(n) x(n) = 10 cos (πn/4)u(n) y(-1)= 0 → relaxed 1 5 . 0 1 1 ) ( − − = → z z H → pole p = 0.5 2 1 1 2 1 2 1 ) 1 ( 10 ) ( _{− −} − + − − = → z z z z X → Y(z) = H(z) X(z) 1 4 / 7 . 28 1 4 / 7 . 28 1 ₁ 78 . 6 1 78 . 6 5 . 0 1 3 . 6 − − − − + ₋ + ₋ − = z e e z e e z j j j j o o π π ↓ ↓ milik H(z) milik X(z) → ynr(n) = 6.3 (0.5)nu(n) → yfr(n)=

[

6.78e−j28.7(ejπn/4)+6.78ej28.7e−jπn/4

]

u(n) = 13.56 cos (πn/4 - 28.7o)u(n) n ≥ 0 → persist

7 Analisa Stabilitas Sistem

Tujuan Belajar 33

Peserta mengerti hubungan antara kondisi pole-zero sistem dengan kausalitas dan stabilitas dari sistem, melalui analisa RoC nya. Termasuk di dalamnya kasus pole-zero cancelation, dan multiple pole (pada unit circle).

h(n) = 0

n < 0 → ROC eksterior dari sebuah lingkaran

LTI causal system ⇔ ROC eksterior dari lingkaran r < ∞, termasuk z = ∞ BIBO ∞ <

∑

∞ −∞ = n n h( )

∑

∞ −∞ = − = n n z n h z H( ) ( ) n n n n z n h z n h z H − ∞ −∞ = ∞ −∞ = −

_∑

∑

= ≤ ⇒ ( ) ( ) ( )

∑

∞ −∞ = ≤ ⇒ n n h z H( ) ( )

Jadi bila BIBO stable, maka |z| = 1 ada di ROC, tebakannya juga benar. BIBO stabil ⇔ |z| = 1 ∈ ROC

Bila causal → ROC eksterior r Stabil → |z| = 1 ∈ ROC

Maka |z| > r < 1

→ semua pole harus ada di dalam unit circle

Contoh : 1 1 2 1 2 1 1 3 1 2 1 1 5 . 1 5 . 3 1 4 3 ) ( _{− − − −} − − + − = + − − = z z z z z z H

Cari ROC dari h(n) agar a) stabil b) causal c) anticausal Jawab :

Systems has poles z = 1/2 & z = 3

a). Stabil → ROC harus termasuk unit circle, 1/2 < |z| < 3 → h(n) = (1/2)nu(n) - 2(3)nu(-n-1)

b). Causal → ROC > |z| > 3 h(n) = (1/2)nu(n) + 2(3)nu(n) c). Anti causal → ROC : |z| < 0.5 h(n) = -(1/2)nu(-n-1)-2(3)nu(-n-1) (the systems is unstable)

* Pole - Zero Cancellations

Contoh :

Cari unit sample response δ(n) dari sistem berikut ini : y(n) = 2.5y(n-1) - y(n-2) + x(n)-5x(n-1) + 6x(n-2) solusi : ) 2 1 )( 1 ( 6 5 1 5 . 2 1 6 5 1 ) ( 1 1 2 1 2 1 2 1 2 1 − − − − − − − − − − + − = + − + − = z z z z z z z z z H ⇒ poles p1 = 1/2, p2 = 2

(

1

)(

1

)

2 1 2 1 2 1 1 6 5 1 ) ( ) ( ) ( − − − − − + − = = z z z z z X z H z Y         − + − = 2 2 1 _z B z A z ⇒ A = 5/2 B = 0

ada zero yang mengcancel z-2 Zeros : z = 2 z = 3 1 2 1 1 2 1 1 2 1 1 1 5 . 2 1 3 1 3 1 ) ( ₋ − − − − − = − − = − − = z z z z z z z H

( )

( ) 5 . 2 ) ( ) ( 1 2 1 _{u n} n n h =δ − n− System System

) 1 ( 3 ) ( ) 1 ( ) ( 2 1 _{− + − −} = y n x n x n n y ⇒ terjadi cancelation Cari response ) ( ) 2 ( ) 1 ( ) ( 2 1 6 5_{y n y n x n} n y = − − − + ) 1 ( ) ( ) ( 3 1 ₋ − = ⇒x n δ n δ n

(

)(

1

)

3 1 1 2 1 2 2 1 1 6 5 _{1 1} 1 1 1 ) ( _{− − − −} − − = + − = z z z z z H 1 3 1 1 ) (z = − z− X

( )

( ) ) ( 1 1 ) ( 2 1 1 2 1_z y n u n z Y → = n − = ₋

⇒ mod (1/3)n ditekankan sebagai hasil dari pole-zero cancellation

* Multiple pole

Pole on unit circle can be dangerous Contoh : ) ( ) 1 ( ) (n y n x n y = − + 1 1 1 ) ( 1→ = − = ⇒ ₋ z_k z z H bila 1 1 1 ) ( ) ( ) ( 1→ = − = → = ₋ z_k z z X n U n X

( )

₁2 1 1 ) ( − − = → z z Y ) ( ) 1 ( ) (n n u n y = + → unstable

kasus multiple pole :

) ( ) (p u n n A_k b _k n

0 ≤ b ≤ m-1, m orde dari pole (pk)n dominates nb

→ bila |pk| < 1 → telah stabil

⇒ yang berguna : digital oscilators (marginaly stable)

Tujuan Belajar 34

Peserta mengerti stability test menurut teknik Schur-Cohn, dan teknik untuk orde 2. Stability test : N nz a z a z A( )=1+ ₁ −1+...+ −

roots dari A(z) harus ada dalam unit circle (lihat Schur-Cohn hal 213!)

* Stabilitas untuk sistem orde-2

⇒ penting karena pembangun ("basic building block") ) ( ) 2 ( ) 1 ( ) (n a₁y n a₂y n b x n y =− − − − + _o 2 2 1 1 1 ) ( ) ( ) ( − − ₊ + = = z a z a b z X z Y z H o 2 1 2 2 a z a z z b_o + + = 4 4 2 , 2 2 1 1 2 1 a a a p p = − ± − determinan 4 ₂ 2 1 a a − = ∆ BIBO stable → |p1| < 1 |p2| < 1 Karena a₁=−(p₁+ p₂)=−(p₁p₁+ p₁p₂) 2 1 2 p p a = maka → a₂ = p₁p₂ = a₁ p₂ <1 dan a1=1+a₂

Gambar 13. Daerah segitiga kestabilan Schur-Cohn. * a₁2 >4a₂ 1 2 2 1 1 1 1 1 ) ( _{− −} − + − = z p A z p A z H 2 1 1 1 p p p b A o − = ⇒ 2 1 2 2 p p p b A o − − =

(

)

( ) ) ( ₁ 1 ₂ 1 2 1 n u p p p p b n h o n+ − n+ − = ⇒

⇒ difference dari two decays exp. Sequence

2 4 2 _{1 2} 1 2 1 a p p p a a = ⇒ = = =−

(

₁

)

2 1 ) ( − − = pz b z H o ) ( ) 1 ( ) (n b n p u n h = _o + n ⇒ ↓

ramp decays exp.

8 Penutup