III PEMBAHASAN
Pada penelitian ini akan dibahas formulasi Hamiltonian bagi gerak gelombang interfacial. Pembahasan dibagi dalam dua kasus yaitu kasus pertama dengan batas atas berupa permukaan rata dan kasus kedua dengan batas atas berupa permukaan bebas. Hamiltonian H didefinisikan sebagai energi total, yaitu penjumlahan energi kinetik K dan energi potensial P yang dinyatakan oleh
.
H K P (3.1)
3.1 Formulasi Hamiltonian 3.1.1 Batas Permukaan Rata
Pada gerak gelombang interfacial dengan batas atas berupa permukaan rata, energi kinetik K dan energi potensial P berturut-turut didefinisikan sebagai berikut 2 1 2 2 ( ) 2 2 1 1 2 2 2 2 1 1 ( ) x h h x K dy dx dy dx , (3.2) 2 1 2 2 2 2 2 1 2 2( ) 2 1 . x h h x P g y dydx g y dydx g x dx (3.3)
Selanjutnya, energi kinetik direduksi menggunakan operator Dirichlet-Neumann untuk lapisan bawah (S t2( , 2)). Misalkan 1( )x 1( ,x 2( ))x dan
2( )x 2( ,x 2( ))x . Definisikan operator Dirichlet-Neumann untuk domain
fluida lapisan bawah sebagai berikut
1 2 2 2 2 2 2 2 1 x 2 G N
(3.4) 1 2 2 1 2 1 2 2 1 x 2 G N , (3.5) dengan 2 2 2 2 1 1 1 T x x
Jadi energi kinetik pada persamaan (3.2) dapat dinyatakan berikut
1 1
2 2 2 2( 2) 2 2 1 1 1( 2) 1
K G G dx . (3.6)
Berdasarkan definisi operator Dirichlet-Neumann, syarat batas kinematik pada persamaan (2.9) dapat dinyatakan oleh
2 2 2 2 2 1 2 1, t t G G (3.7)
dengan penyelesaian masing-masing berbentuk 1 G11( )2 2t dan
1
2 G2 ( )2 2t. Selanjutnya, definisikan Lagrangian L = K - P, maka dengan
menggunakan persamaan (3.3) dan (3.6), diperoleh
1 1 2 2 2 2 2 2 2 1 2 1 2 2 2 2 1 2 1 ( , ) ( ( ) ( ) ) 2 1 ( ) ( ) . 2 t t t t t L G G dx g x dx (3.8) Definisikan peubah 2 2( )x tL , diperoleh 1 1 2 2 2 2 2 1 1 2 2 2 2 1 1 ( ) ( ) ( ) ( ) ( ), t t x G G x x (3.9)
dan berdasarkan persamaan (3.7) dan (3.9), diperoleh
1 2 2 1 2 2 2 1 2 2 2 2 2 2 1 2 1 2 2 1 ( ) ( ( ) ( )) ( ) ( ( ) ( )) , G G G G G G
(3.10) sehingga Hamiltonian H pada persamaan (3.1) menjadi
1 1 2 2 2 2 1 2 1 2 2 2 1 2 2 2 2 2 1 2 2 1 2 ( , ) ( ) ( ) ( ) ( ) ( ) . H G G G G dx g dx (3.11)
Jadi sistem persamaan bagi gerak gelombang interfacial dinyatakan dalam sistem Hamiltonian berikut
2 2
2 , 2
t H t H . (3.12)
Persamaan (3.12) merupakan sistem persamaan tak linear dengan Hamiltonian H diberikan pada persamaan (3.11). Penurunan persamaan (3.8), (3.9), (3.10), dan (3.11) dapat dilihat di Lampiran 1.
3.1.2 Batas Permukaan Bebas
Formulasi Hamiltonian untuk gerak gelombang interfacial dengan batas atas berupa permukaan bebas memiliki Lagrangian yang bergantung pada 1( , )x t
dan 2( , )x t . Energi kinetik K dan energi potensial P pada kasus ini berturut-turut didefinisikan 2 1 1 2 2 ( ) ( ) 2 2 1 1 2 2 2 2 1 1 ( ) x h x h x K dy dy dx, (3.13) 2 1 1 2 2 2 2 2 2 1 1 2 ( 2 1) 2( ) 2 1 1 1( ) . x h x h x P g y dy dx g y dy dx g x g h x dx
(3.14)
Selanjutnya, definisikan 1( )x 1( ,x 2( ))x , 2 2( ,x 2( ))x , dan
3 1( ,x h1 1( ))x . Operator Dirichlet-Neumann untuk domain fluida lapisan
bawah (S t2( , 2)) adalah
1 2 2 2( 2) 2( ) 2 (1 ( x 2) )
G x N dan operator
Dirichlet-Neuman untuk domain fluida lapisan atas (S t1( , 2, 1)) didefinisikan oleh 1 2 1 2 2 1 2 2 1 11 12 2 21 22 3 1 1 1 ( . ) (1 ( ( )) ) ( ) , ( ) ( . ) (1 ( ( )) ) x x N x x G G G G x N x (3.15) dengan 1 1 2 1 1 1 1 T x x N dan 2 2 2 2 1 1 1 T x x N berturut-turut
menyatakan vektor normal satuan di y h1 1 dan y 2. Jadi energi kinetik pada persamaan (3.13) dapat dinyatakan berikut
1 11 12 1 1 1 2 2 2 2 2 2 2 1 21 22 3 3 ( ) T G G K G dx G G . (3.16)
Berdasarkan Operator Dirichlet-Neumann pada persamaan (3.4) dan (3.15), maka syarat batas kinematik (3.7) untuk 2berlaku, sedangkan persamaan (2.9) dan (2.12) berturut-turut menjadi
2 11 1 12 3 1 21 1 22 3 ( ) . t t G G G G (3.17)
Dengan menggunakan persamaan (3.14) dan (3.16), Lagrangian diperoleh dalam bentuk 1 2 11 12 2 1 2 2 2 2 2 1 21 22 1 1 2 2 2 1 2 1 1 1 1 ( ) 2 1 1 ( ) ( ) ( ) . 2 2 T t t t t t t R R G G L G dx dx G G g x dx g h dx (3.18) Definisikan 1
1 tL dan 2 2tL , maka diperoleh
1 1 2 2 2 2 2 11 12 2 1 21 22 1 1 2 2 1 1 1 3 ( ) 0 . t t t G G G G G (3.19)
Dengan menggunakan persamaan (3.19), maka persamaan (3.16) dapat ditulis
2 1 2 2 11 12 21 22 3 1 1 1 1 1 2 2 T T t t G G K dx dx G G . (3.20)
Penyelesaian persamaan (3.15) dan (3.19) untuk 1, 2, dan 3 dalam variabel
2, 1 adalah 2 1 1 1 2 2 2 12 1 1 2 11 2 12 1 1 3 1 ( ( ) ) ( ) B G G B G G (3.21) dengan B 2G11 1G2( 2).
Jadi persamaan (3.20) dapat dinyatakan oleh
2 1 1 1 1 11 2 2 2 2 12 2 2 1 1 1 21 2 2 22 21 12 1 1 ( ) ( ) 1 ( ) 2 T G B G G B G K dx G B G G G B G . (3.22)
Sehingga Hamiltonian diperoleh dalam bentuk
2 1 1 1 1 11 2 2 2 2 12 2 2 1 1 1 21 2 2 22 21 12 1 1 2 2 2 1 2 1 1 1 ( ) ( ) 1 ( ) 2 1 1 ( ) ( ) ( ) . 2 2 T R R G B G G B G H dx G B G G G B G g x dx g h dx (3.23)
Jadi sistem persamaan gerak untuk gelombang interfacial dengan batas atas berupa permukaan bebas dinyatakan oleh sistem Hamiltonian berikut
2 2 1 1 2 2 1 1 , , . t t t t H H H H (3.24)
Persamaan (3.24) merupakan sistem persamaan tak linear dengan Hamiltonian H diberikan pada persamaan (3.23). Penurunan persamaan (3.18), (3.19), (3.20), (3.22), dan (3.23) dapat dilihat di Lampiran 2.
3.2 Gerak Gelombang Interfacial 3.2.1 Batas Permukaan Rata
Berikut ini akan diturunkan persamaan gerak gelombang interfacial dengan batas atas berupa permukaan rata menggunakan asumsi gelombang panjang dan amplitudo kecil sehingga diperkenalkan parameter kecil pada penskalaan berikut
' 2 ' 2
2 2 2
' , ,
x x , (3.25)
yang memberi pengertian bahwa 2 dan u x 2 berorde sama, yaitu O( 2). Parameter dan penskalaan tersebut akan diaplikasikan pada bentuk Hamiltonian persamaan (3.11). Agar bentuk Hamiltonian H dinyatakan secara eksplisit, maka opertor Dirichlet-Neumann pada persamaan (3.4) dan (3.5) dinyatakan dalam uraian deret Taylor yang masing-masing berbentuk
2 2 2 2 2 2 2 2 3 2 1 2 1 2 1 2 1 2 3 2
tanh tanh tanh
,
tanh tanh tanh
, G D h D D D D h D D h D O D G D h D D D D h D D h D O D (3.26)
dengan D i x. Penurunan persamaan (3.26) dapat dilihat pada pustaka [5]. Jika persamaan (3.25) digunakan, maka persamaan (3.26) yang masing-masing berlaku untuk fluida lapisan bawah dan atas menjadi
' ' ' 2 2 2 4 ' ' ' ' ' ' ' ' 8 2 2 2 2 2 ' 2 4 3 ' 4 ' ' ' 2 2 2 6 5 ' 6 2 ' 2 ' ' 2 8 2 2 2 tanh tanh tanh 1 3 2 , 15 G D h D D D D h D D h D O h D h D D D h D h D D O (3.27) dan ' ' ' 1 2 1 4 ' ' ' ' ' ' ' ' 8 2 1 2 1 2 ' 2 4 3 ' 4 ' ' ' 1 1 2 6 5 ' 6 2 ' 2 ' ' 2 8 1 1 2 tanh tanh tanh 1 3 2 . 15 G D h D D D D h D D h D O h D h D D D h D h D D O (3.28)
Selanjutnya definisikan operator B sebagai berikut
2 1( 2) 1 2( 2)
B G G . (3.29)
Berdasarkan persamaan (3.27) dan (3.28), operator B menjadi
2 2 1 2 2 1 4 ' 3 3 4 1 2 2 1 2 2 1 6 5 5 6 2 2 1 2 2 1 1 2 2 1 2 ' 2 8 2 ' 1 ' ' ' 3 2 ' 15 ' ' . B h h D D D h h D h h D h h D D O (3.30)
Sedangkan invers dari operator B adalah
1 1 2 1 2 2 1 3 3 2 1 2 2 1 2 1 2 ' 2 1 2 2 1 1 2 2 1 5 5 2 2 4 ' 1 2 2 1 1 2 2 1 2 1 2 2 1 1 2 2 1 4 2 3 3 2 ' 6 1 2 2 1 1 2 2 1 2 2 1 1 2 2 1 1 ' 1 1 ' 3 2 ' ' ' 15 1 ' 3 B D h h h h D h h h h h h h h D D D h h h h h h D O h h h h 1 ' . D (3.31)
Integrand pada Hamiltonian dalam persamaan (3.11) berupa fungsi dari operator G1 2 B G1 2 2 , sehingga dengan menggunakan penskalaan (3.25)
dan persamaan (3.27), (3.28) dan (3.30), maka persamaan (3.11) menjadi
4 2 2 2 1 2 2 2 2 2 1 2 1 2 2 1 2 4 2 1 1 1 2 2 6 1 2 2 1 7 2 2 2 2 2 1 1 2 2 2 1 2 2 1 , 2 1 3 , 2 h h dx H D h h h h h h D h h dx O h h D D h h
(3.32)
setelah tanda aksen dihilangkan. Dengan mengunakan turunan variasi terhadap Hamiltonian H pada persamaan (3.32), maka persamaan (3.12) menjadi
2 3 2 2 2 1 2 1 2 2 1 2 2 1 2 2 1 1 4 2 2 1 2 2 1 2 2 2 2 1 1 2 2 2 2 1 2 2 1 3 2 2 2 2 2 2 1 1 2 2 1 2 2 2 1 2 2 1 1 3 , . 2 t x x x x t x H h h h h h h h h h h h h h h H h h g h h (3.33)
Penurunan persamaan (3.32) dan (3.33) dapat dilihat di Lampiran 4. Bentuk Hamiltonian H pada persamaan (3.32) dapat dinyatakan dalam peubah 2 dan u sebagai berikut 4 2 2 2 1 2 2 1 2 1 2 2 1 2 6 2 2 1 1 1 2 2 1 2 2 1 2 2 6 2 2 1 1 2 2 2 1 2 2 1 , 2 1 2 3 . 2 x h h dx H u u g h h h h dx h h u h h h h dx u h h
(3.34)
Dengan mengunakan turunan variasi terhadap Hamiltonian H pada persamaan (3.34), maka persamaan (3.33) menjadi
2 1 1 2 2 1 2 2 1 2 2 1 1 2 2 2 1 2 2 1 2 2 2 2 1 1 2 2 2 1 2 2 1 2 2 2 2 1 1 2 2 1 2 2 1 2 2 1 1 3 . 2 x t x t x h h u h h h h h h u h h h h u h h h h u g u h h (3.35)
Persamaan (3.35) merupakan persamaan gerak gelombang interfacial dengan batas atas berupa permukaan rata yang merambat dalam dua arah. Persamaan (3.35) sering disebut sebagai persamaan Boussinesq. Penurunan persamaan (3.34) dan (3.35) dapat dilihat di Lampiran 4.
Berikut ini akan dibahas persamaan gerak gelombang interfacial yang merabat hanya dalam satu arah. Untuk membahas gerak gelombang tersebut, maka berikut ini akan dibahas lebih dahulu bentuk eksplisit persamaan gerak gelombang yang merambat dalam dua arah. Untuk itu, didefinisikan transformasi berikut 2 1 1 2 2 1 2 1 4 4 2 1 2 1 1 2 2 1 2 2 1 1 2 2 1 2 1 4 4 2 1 2 1 1 2 2 1 4 4 4 4 g h h h h h h g h h r s g h h h h u h h g h h , (3.36)
dengan r dan s masing-masing menyatakan simpangan gelombang yang bergerak dalam arah kanan dan kiri. Dengan menggunakan persamaan (3.36), persamaan (3.34) menjadi
3 2 7 4 4 2 1 2 1 2 2 1 2 2 1 6 2 1 2 1 1 2 2 1 1 2 2 1 2 2 2 1 1 2 2 2 1 2 2 1 2 1 3 2 2 3 4 2 1 , 2 1 2 6 1 2 2 2 . x x x x g h h dx H r s r s h h h h g h h h h h h r r s s h h g dx r r s rs s h h (3.37)
Dengan mengunakan turunan variasi terhadap Hamiltonian H pada persamaan (3.37), maka persamaan (3.35) menjadi
3 2 7 4 2 1 2 1 1 2 2 1 2 3 3 2 1 2 1 1 2 2 1 1 2 2 1 2 2 2 2 1 1 2 2 1 2 2 4 2 1 1 2 2 1 6 3 2 , 4 2 t x x x x g h h r r h h h h g h h r s h h h h g r rs s h h h h (3.38) 3 2 7 4 2 1 2 1 1 2 2 1 2 3 3 2 1 2 1 1 2 2 1 1 2 2 1 2 2 2 2 1 1 2 2 1 2 2 4 2 1 1 2 2 1 6 2 3 . 4 2 t x x x x g h h s s h h h h g h h r s h h h h g r rs s h h h h (3.39)
Penurunan persamaan (3.37), (3.38) dan (3.39) dapat dilihat di Lampiran 4. Selanjutnya asumsikan gelombang yang ditinjau bergerak dalam arah kanan, sedangkan arah kiri relatif kecil, sehingga s O( 2). Dengan demikian persamaan gerak gelombang interfacial yang bergerak hanya dalam arah kanan adalah
3 2 7 4 2 1 2 1 1 2 2 1 2 3 2 1 2 1 1 2 2 1 1 2 2 1 2 2 2 2 1 1 2 2 1 4 2 1 1 2 2 1 6 , 2 2 t x x x g h h r r h h h h g h h r h h h h g r r h h h h
atau 2 2 0 0 t x x xxx r c r rr r (3.40) dengan 3 2 7 4 2 1 2 1 0 1 2 2 1 2 1 2 1 1 2 2 1 1 2 2 1 2 2 2 1 1 2 2 1 4 2 1 1 2 2 1 1 6 1 . 2 2 g h h c h h h h g h h h h h h g h h h h (3.41)
Persamaan (3.40) merupakan persamaan gerak gelombang interfacial dengan batas atas berupa permukaan rata yang merambat hanya dalam arah kanan saja. Persamaan (3.40) sering disebut persamaan KdV.
3.2.2 Batas Permukaan Bebas
Berikut ini akan diturunkan persamaan gerak gelombang interfacial dengan batas atas berupa permukaan bebas menggunakan asumsi gelombang panjang dan amplitudo kecil sehingga diperkenalkan parameter kecil pada penskalaan berikut
' 2 ' 2 ' 1 ' 1
2 2 2 1 2 1
' , , , ,
Dengan menggunakan penskalaan (3.42), maka persamaan (3.23) menjadi 3 2 2 2 2 2 2 1 2 1 1 2 2 1 2 2 2 2 2 2 2 1 2 2 1 1 2 2 2 1 1 2 2 1 2 2 2 2 2 2 2 1 2 1 2 1 2 1 2 2 2 2 2 3 3 2 2 2 2 1 1 2 2 1 2 2 1 1 2 1 1 2 2 1 2 2 2 2 2 2 2 2 1 2 2 2 1 2 2 1 3 3 2 6 3 3 3 3 3 2 x x x x h h H g g u u u h h h u h h u h h h h h u u h h h h h h u u u u 2 1 2 12 2 2 7 1 1 1 , u u dx O (3.43)
setelah tanda aksen dihilangkan. Dengan mengunakan turunan variasi terhadap Hamiltonian H pada persamaan (3.43), maka persamaan (3.24) memberikan sistem persamaan berikut
2 2 2 2 2 2 1 2 2 2 1 2 2 2 2 2 3 2 3 2 2 1 2 1 2 1 2 2 2 3 2 2 3 2 1 1 2 1 2 2 1 1 2 2 2 2 2 2 1 2 2 2 2 1 2 2 2 2 1 1 1 2 1 2 1 2 1 2 2 1 1 2 2 1 3 3 2 6 3 6 1 t x x x x x x x t x x x x t x x h h u u u u h h h u u h h h h h u u g u u u u u u h u h h u 2 2 2 2 2 2 1 2 2 1 1 1 2 1 1 2 3 2 2 3 2 2 1 2 1 2 1 2 2 2 2 2 2 3 3 2 2 2 3 2 1 2 1 2 1 2 2 1 1 1 2 1 2 2 1 2 1 1 1 1 1 2 2 6 3 6 3 3 6 . x x x x x t x x u u u h h h h h u h h h h h h u u g u u (3.44)
Selanjutnya didefinisikan transformasi 2 1 ' 2 1 2 ' 1 1 ' 2 2 2 1 ' 1 1 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 g g u u g u u g (3.45) dan 2 2 1 1 2 2 1 1 0 0 0 0 0 0 0 0 a b a b v a b u v a b u , (3.46) dengan 2 2 1 , , 1 1 d a b d d (3.47) dan 2 1 2 1 2 1 1 1 1 1 2 2 2 1 2 2 2 2 2 2 1 2 1 2 1 4 . d h h h h h h h h (3.48)
Misalkan batas atas permukaan bebas berupa gelombang dengan amplitudo yang jauh lebih kecil dari amplitudo gelombang interfacial yang ditinjau, maka diperkenalkan penskalaan berikut
' '
1 1, v1 v . 1 (3.49)
Dengan demikian Hamiltonian H pada persamaan (3.43) menjadi
3 2 2 2 2 0 2 2 2 2 2 2 2 7 1 0 1 2 2 2 2 , x H c v c v D v N v dx O (3.50)
dengan 2 2 0 2 1 2 1 2 1 2 1 2 2 2 2 1 2 2 1 1 2 2 2 2 2 1 2 1 2 2 1 2 1 2 1 2 2 2 2 3 3 2 2 2 2 1 2 1 2 2 1 2 1 1 2 1 2 2 3 2 2 1 1 2 2 2 3 2 1 2 1 1 4 , 2 3 3 2 6 3 3 3 3 , 3 2 , c g h h h h h h gh D h h a gh h h h h a b g h h h h h h b g g N a a b g g a b b (3.51)
setelah tanda aksen dihilangkan. Dengan menggunakan turunan variasi terhadap Hamiltonian H pada persamaan (3.50), maka persamaan (3.44) menjadi
2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 1 0 1 1 1 1 2 . t x x t x t x t x c v D v N v v Nv c v v (3.52)
Persamaan (3.52) merupakan persamaan gerak gelombang interfacial dengan batas atas berupa permukaan bebas yang merambat dalam dua arah (persamaan Boussinesq). Penurunan persamaan (3.50) dan (3.52) dapat dilihat di Lampiran 5.
Berikut ini akan dibahas persamaan gerak gelombang interfacial dengan batas atas berupa permukaan bebas yang bergerak hanya dalam satu arah. Untuk membahas gerak gelombang tersebut, maka berikut ini akan dibahas lebih dahulu bentuk eksplisit persamaan gerak gelombang yang merambat dalam dua arah, sehingga diperkenalkan transformasi berikut
2 0 2 0 2 0 2 0 4 1 4 4 4 2 2 4 1 4 4 4 c c c c r s v , (3.53)
dengan r dan s masing-masing menyatakan simpangan gelombang yang bergerak dalam arah kanan dan kiri.
Selanjutnya asumsikan gelombang yang ditinjau bergerak dalam arah kanan, sedangkan arah kiri relatif kecil, sehingga s O( 2). Sehingga dengan menggunakan persamaan (3.53), Hamiltonian H pada persamaan (3.50) menjadi
3 2 0 5 2 2 2 2 3 1 0 1 0 0 2 . 2 2 x 2 2 H c r dx D N c v r r dx c c (3.54)
Dengan menggunakan turunan variasi terhadap Hamiltonian H pada persamaan (3.54), maka persamaan (3.52) menjadi
2 3 2 0 0 0 2 2 2 t x x x D N r c r r r r c c , atau 2 2 0 0 t x x xxx r c r rr r , (3.55) dengan 0 0 0 0 3 , , 2 2 2 D N c c c c , (3.56)
dimana c , D, dan N diberikan pada persamaan (3.51). Persamaan (3.55) 0 merupakan persamaan gerak gelombang interfacial dengan batas atas berupa permukaan bebas yang merambat hanya dalam arah kanan saja (persamaan KdV). Penurunan persamaan (3.54) dan (3.55) dapat dilihat di Lampiran 5.
3.3 Kajian Numerik
Misalkan penyelesaian persamaan (3.40) dan (3.55) merupakan fungsi periodik dengan perioda 2p dan penyelesaiannya dapat dinyatakan oleh deret Fourier berikut 0 1 ( , ) ( ) k( ) cos( ) k( ) sin( ) k r x t a t a t kx b t kx , (3.57) dengan 1 ( ) ( , ) cos( ) ; 0,1,... 2 k a t r x t kx d x k
dan 1 ( ) ( , ) sin( ) ; 1, 2,... . 2 k b t r x t kx d x k
Persamaan (3.57) merupakan uraian deret Fourier untuk fungsi r dengan koefisien-koefisien ak dan bk tergantung pada variabel waktu t. Dalam realisasinya, perhitungan dilakukan secara numerik dengan bantuan komputer dan dilakukan pemotongan terhadap deret tersebut hingga n suku, yaitu
0 1 ( , ) ( ) ( ) cos( ) ( ) sin( ) n k k k r x t a t a t kx b t kx . (3.58)
Hasil yang diperoleh dengan adanya pemotongan ini tidak akan jauh berbeda dengan penyelesaian eksaknya. Hal ini karena koefisien-koefisien ak dan
bk untuk indeks k yang besar biasanya bernilai sangat kecil. Untuk memudahkan,
maka deret (3.58) ditulis dalam bentuk
( , ) ( ) ( ), n k k k n r x t c t x (3.59) dengan ( ), 0 ( ) ( ), 0. k Cos kx k x Sin kx k
(3.60) Dengan notasi ini, maka
.
x k k k (3.61)
Dalam penerapannya di komputer, deret Fourier untuk fungsi r cukup ditulis komponen ck yang dinyatakan dalam bentuk vektor berikut
1 1 0 1 1
( n, n ,..., , , ,..., n , n)
r c c c c c c c (3.62)
Dengan struktur data di atas, maka turunan r terhadap x juga dapat dinyatakan dalam bentuk vektor, yaitu
1 1 1 1
( , 1 ,..., 1 , 0, ,..., 1 , )
xr ncn n cn c c n c n nc n (3.63)
dan turunan r terhadap t adalah
1 1 0 1 1
( ' , ' ,..., ' , ' , ' ,..., ' , ' )
Selanjutnya untuk mencari koefisien deret Fourier dari r2 ditentukan dengan cara sebagai berikut. Misalkan
0 1 cos( ) sin( ) , n k k k r c c kx c kx maka 2 0 0 1 1 2 2 0 0 0 1 1
cos( ) sin( ) . cos( ) sin( )
2 cos( ) 2 sin( ) cos( ) sin( ) .
n n k k k k k k n n k k k k k k r c c kx c kx c c kx c kx c c c kx c c kx c kx c kx
Dari dua suku pertama diperoleh vektor
2
0 0 1 0 1 0 0 1 0 1 0
(2c c n,c c n ,..., 2c c ,c , 2c c,..., 2c cn , 2c cn).
Suku ketiga, yaitu
2 1 cos( ) sin( ) n k k k
c kx c kx dapat diuraikan sebagai berikut
2
1
1 1
cos( ) sin( )
cos( ) sin( ) cos( ) sin( )
n k k k n n k k k k k k c kx c kx c kx c kx c kx c kx , 1
[ cos( ) cos( ) cos( ) sin( ) sin( ) cos( )
sin( ) sin( )] n k m k m k m k m k m c c kx mx c c kx mx c c kx mx c c kx mx 1 2 , 1
[ cos( ) cos( ) sin( ) sin( )
sin( ) sin( ) cos( ) cos( ) ].
n k m k m k m k m k m c c k m x k m x c c k m x k m x c c k m x k m x c c k m x k m x 1 1 2 2 , 1 1 1 2 2 [ cos( ) sin( ) cos( ) sin( ) ]. n k m k m k m k m k m k m k m k m k m c c c c k m x c c c c k m x c c c c k m x c c c c k m x
= 0 1 cos( ) sin( ) n p p p R R px R px , dengan ketentuan - Jika k + m = p, maka 1 2 p k m k m R c c c c dan 1 2 p k m k m R c c c c
- Jika k - m = p, maka 1 2 p k m k m R c c c c dan 1 2 p k m k m R c c c c
- Jika k - m = -p, maka 1 2 p k m k m R c c c c dan 1 2 p k m k m R c c c c
- Jika k - m = 0 atau k = m, maka diperoleh suku yang tidak mengandung
faktor trigonometri yaitu 1 2 2
2 (ck) (c k) yang menjadi nilai dari R0.
Dengan menerapkan hasil-hasil di atas pada persamaan (3.40) untuk kasus batas atas berupa permukaan rata dan pada persamaan (3.55) untuk kasus batas atas berupa permukaan bebas, maka diperoleh sistem persamaan diferensial biasa orde satu berikut
1 1 0 1 1 ( , ,..., , , ,..., , ) k k n n n n dc f c c c c c c c dt (3.65)
dengan fk suatu fungsi tertentu dan k = 0, ±1, ±2, …, ±n. Sistem persamaan diferensial (3.65) akan diselesaikan secara numerik dengan menggunakan metode Runge-Kutta orde empat. Misalkan syarat awal yang digunakan berupa gelombang soliter persamaan KdV yang dinyatakan oleh
2 ( , 0) sec x r x a h L , dengan 2 12 L
a , dimana µ dan ? merupakan koefisian persamaan KdV (3.41) untuk kasus batas atas berupa permukaan rata dan koefisien persamaan KdV (3.56) untuk kasus batas atas berupa permukaan bebas.
Sebagai contoh kasus untuk gelombang interfacial dengan dengan batas atas berupa permukaan rata, diberikan data dengan kondisi fisis fluida dua lapisan sebagai berikut
1 0.01, 2 0.1
h h dan 1 0.2 2.
Nilai ,c dan diperoleh dari persamaan (3.41), yaitu
0 0.193, 0.0003, 5.803
c .
Misalkan gelombang soliter yang ditinjau memiliki amplitudo a 0.1, maka panjang gelombang soliternya adalah L = 0.774. Jadi syarat awal diberikan oleh fungsi 2 ( , 0) 0.1 sec 0.774 x r x h ,
Uraian deret Fourier dari syarat awal r(x, 0) adalah 0 1 ( , 0) cos( ) sin( ) n k k k r x a a kx b kx dengan 2 0 1 0.1 sec , 2 0.774 x a h dx dan untuk k= 1, 2,3, … 2 2 1 0.1 sec cos( ) ; 2 0.774 1 0.1 sec sin( ) . 2 0.774 k k x a h kx d x x b h kx dx
Nilai-nilai ak diberikan pada Lampiran 6 dan bk 0.
0.00E+00 1.00E-07 2.00E-07 3.00E-07 4.00E-07 5.00E-07 6.00E-07 7.00E-07 8.00E-07 9.00E-07 1.00E-06 0 1 2 3 4 5 6 x H
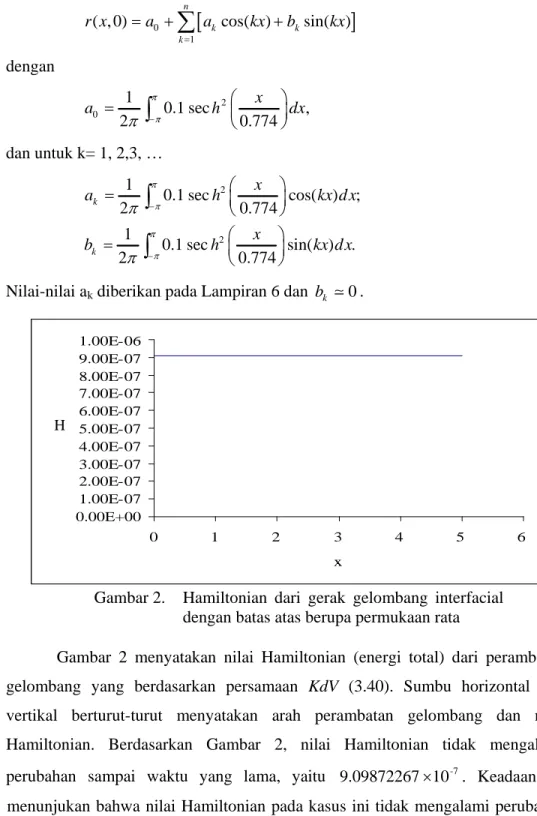
Gambar 2 menyatakan nilai Hamiltonian (energi total) dari perambatan gelombang yang berdasarkan persamaan KdV (3.40). Sumbu horizontal dan vertikal berturut-turut menyatakan arah perambatan gelombang dan nilai Hamiltonian. Berdasarkan Gambar 2, nilai Hamiltonian tidak mengalami perubahan sampai waktu yang lama, yaitu 9.09872267 10 . Keadaan ini -7 menunjukan bahwa nilai Hamiltonian pada kasus ini tidak mengalami perubahan dengan berjalannya waktu. Hal ini menunjukan bahwa energi kekal terhadap waktu. Dengan kata lain Hamiltonian pada gerak gelombang interfacial dengan batas atas berupa permukaan rata bersifat konsisten.
Gambar 2. Hamiltonian dari gerak gelombang interfacial dengan batas atas berupa permukaan rata H
Sebagai contoh kasus untuk gelombang interfacial dengan batas atas berupa permukaan bebas, diberikan data dengan kondisi fisis fluida dua lapisan sebagai berikut
1 0.01, 2 0.1
h h dan 1 0.2 2.
Nilai ,c dan diperoleh dari persamaan (3.56), yaitu
0 0.495, 0.0084, 3.388
c .
Misalkan gelombang soliter yang ditinjau memiliki amplitudo a 0.1, maka panjang gelombang soliternya adalah L = 0.546. Jadi syarat awal diberikan oleh fungsi 2 ( , 0) 0.1 sec 0.546 x r x h ,
Uraian deret Fourier dari syarat awal r(x, 0) adalah
0 1 ( , 0) cos( ) sin( ) n k k k r x a a kx b kx dengan 2 0 1 0.1 sec , 2 0.546 x a h dx dan untuk k= 1, 2,3, … 2 2 1 0.1 sec cos( ) ; 2 0.546 1 0.1 sec sin( ) . 2 0.546 k k x a h kx dx x b h kx dx
Nilai-nilai ak diberikan pada Lampiran 6 dan bk 0.
0.00E+00 2.00E-07 4.00E-07 6.00E-07 8.00E-07 1.00E-06 1.20E-06 1.40E-06 0 1 2 3 4 5 6 x H
Gambar 3. Hamiltonian dari gerak gelombang interfacial dengan batas berupa permukaan bebas
atas berupa permukaan bebas HH
Gambar 3 menyatakan nilai Hamiltonian (energi total) dari perambatan gelombang yang berdasarkan persamaan KdV (3.55). Sumbu horizontal dan vertikal berturut-turut menyatakan arah perambatan gelombang dan nilai Hamiltonian. Berdasarkan Gambar 3, nilai Hamiltonian tidak mengalami perubahan sampai waktu yang lama, yaitu1.2788448 10 . Keadaan ini -6
menunjukan bahwa nilai Hamiltonian pada kasus ini tidak mengalami perubahan dengan berjalannya waktu. Hal ini menunjukan bahwa energi kekal terhadap waktu. Dengan kata lain Hamiltonian pada gerak gelombang interfacial dengan batas atas berupa permukaan rata bersifat konsisten.