UNIVERSITAS INDONESIA. SUDUT ANTARA DUA SUBRUANG DARI SUATU RUANG HASIL KALI DALAM-n TESIS DEBBY SANJAYA

SUDUT ANTARA DUA SUBRUANG DARI SUATU RUANG HASIL KALI DALAM-n

TESIS

DEBBY SANJAYA 1006734546

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM PROGRAM STUDI MATEMATIKA

DEPOK JULI 2012

UNIVERSITAS INDONESIA

SUDUT ANTARA DUA SUBRUANG DARI SUATU RUANG HASIL KALI DALAM-n

TESIS

Diajukan sebagai salah satu syarat untuk memperoleh gelar Magister Sains

DEBBY SANJAYA 1006734546

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM PROGRAM STUDI MATEMATIKA

DEPOK JULI 2012

Puji syukur senantiasa dipanjatkan kepada Tuhan Yang Maha Esa, karena atas berkat dan rahmat-Nya penulis dapat menyelesaikan tesis ini, sebagai salah satu syarat untuk mencapai gelar Magister Sains di Departemen Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Indonesia. Tanpa bantuan dan bimbingan dari berbagai pihak, dari masa perkuliahan sampai pada penyusunan tesis ini, sangatlah sulit bagi penulis untuk menyelesaikan tesis ini. Oleh karena itu, penulis mengucapkan terima kasih kepada:

1. Dr. Hengki Tasman, M.Si. selaku dosen pembimbing tesis dan pembimbing akademis penulis yang telah menyediakan waktu, tenaga, dan pikiran untuk mengarahkan penulis dalam penyusunan tesis ini;

2. Prof. Djati Kerami selaku Ketua Program Studi Magister Matematika UI dan seluruh staf pengajar Departemen Matematika UI yang telah bersedia untuk meluangkan waktunya untuk berbagi ilmu dan berdiskusi dengan penulis selama masa perkuliahan;

3. Prof. Yohanes Surya, Hanna Surya, Surya Wijaya, Emi Nirmala, dan rekan-rekan kerja di Surya Institute dan Sure Indonesia, yang telah banyak memberikan dorongan dan semangat kepada penulis untuk menyelesaikan tesis (dan kuliah) ini;

4. Dr. Sukmawati, Sp.KK yang menolong dalam penyembuhanvasculitispada saat kritis penyelesaian tesis;

5. Seluruh karyawan Departemen Matematika UI yang telah banyak memberikan bantuan dalam pengurusan administrasi;

6. Teman-teman seperjuangan dan seangkatan 2010, baik yang telah lulus ataupun yang masih berjuang untuk lulus, terutama kepada Peter John dan Martin Albert Sulistio;

7. Richard Owen, pelipur lara yang selalu memberikan dukungan kepada penulis untuk memperoleh hasil terbaik selama proses perkuliahan dan penyelesaian tesis;

8. Serta semua pihak yang tidak dapat disebutkan satu-persatu yang telah membantu penulis dalam proses pembuatan dan penyelesaian tesis ini.

Tesis ini ditulis dengan menggunakan LA_{TEX dansettingyang diperoleh dari} internet dan disesuaikan untuk penulisan matematis. Semoga nantinya dapat digunakan sebagai panduan menulis tugas akhir bagi mahasiswa-mahasiswa S1 dan S2 Matematika UI lainnya.

Penulis menyadari bahwa masih terdapat banyak kekurangan dalam penulisan tesis ini. Untuk itu, penulis mengharapkan segala kritik dan saran yang

membangun dari para pembaca untuk menyempurnakan tesis ini. Kritik dan saran dapat dikirimkan lewat email ke debby.sanjaya@gmail.com.

Akhir kata, penulis memohon maaf atas segala kesalahan dan kekurangan dalam tesis ini. Semoga tesis ini dapat berguna bagi siapa saja yang mengkajinya, serta dapat dikembangkan dan disempurnakan agar lebih bermanfaat untuk kepentingan orang banyak.

Depok, Juli 2012 penulis

ABSTRAK

Nama : Debby Sanjaya

Program Studi : Matematika

Judul : Sudut Antara Dua Subruang Dari Suatu Ruang Hasil Kali Dalam-n

Dalam tesis ini diperkenalkan ruang hasil kali dalam-ndan ruang norm-n sebagai perluasan dari ruang hasil kali dalam dan ruang norm. Setiap ruang hasil kali dalam dapat dilengkapi dengan suatu hasil kali dalam-nsederhana

hx0,x1|x2,· · ·,xni= hx0,x1i hx0,x2i · · · hx0,xni hx2,x1i hx2,x2i · · · hx2,xni .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xni .

Hasil kali dalam-nsederhana ini menginduksi suatu norm-nstandar kx1,· · ·,xnk=

p

hx1,x1|x2,· · ·,xni,

yang tak lain merupakan determinan Gram yang merupakan kuadrat dari volume dari paralelotop berdimensi-nyang dibangun olehx1,· · ·,xn.

Tugas akhir ini membahas tentang sudut antara dua subruang dari suatu ruang hasil kali dalam-ndan representasinya secara geometris. Lebih lanjut, dipelajari hubungannya dengan sudut-sudut kanonik yang selama ini telah digunakan untuk mendeskripsikan sudut antara dua ruang.

Kata kunci : hasil kali dalam-n, norm-n, paralelotop berdimensi-n, sudut antara dua subruang

Name : Debby Sanjaya Program : Mathematics

Title : Angle Between Two Subspaces of Ann-Inner Product Space The definitions ofn-inner product space andn-normed space as generalizations of inner product space and normed space are introduced. Every inner product space can form ann-inner product space with a simplen-inner product

hx0,x1|x2,· · ·,xni= hx0,x1i hx0,x2i · · · hx0,xni hx2,x1i hx2,x2i · · · hx2,xni .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xni .

The simplen-inner product induces a standardn-norm kx1,· · ·,xnk=

p

hx1,x1|x2,· · ·,xni,

which is actually the Gram determinant which represents the square root of the volume of then-dimensional parallelotope generated byx1,· · ·,xn.

This thesis discussed the angle between subspaces of ann-inner product space and its geometrical representation. Moreover, its relation to canonical angles, which has been used for describing the angles between two subspaces, is observed too.

Keywords : n-inner product, n-norm, n-dimensional parallelotope, an-gle between two subspaces

DAFTAR ISI

HALAMAN JUDUL i

LEMBAR PERNYATAAN ORISINALITAS ii

LEMBAR PENGESAHAN iii

KATA PENGANTAR iv

LEMBAR PERSETUJUAN PUBLIKASI ILMIAH vi

ABSTRAK vii ABSTRACT viii DAFTAR ISI ix DAFTAR GAMBAR xi 1 PENDAHULUAN 1 1.1 Latar belakang . . . 1 1.2 Perumusan Masalah . . . 2 1.3 Tujuan Penelitian . . . 3 1.4 Batasan Masalah . . . 3 1.5 Metode Penelitian . . . 3 2 TINJAUAN PUSTAKA 4 2.1 Ruang Hasil Kali Dalam dan Ruang Norm . . . 4

2.2 Paralelotop dan Determinan Gram . . . 6

2.3 Ruang Hasil Kali Dalam-ndan Ruang Norm-n. . . 12

3 SUDUT ANTARA DUA SUBRUANG 18 3.1 Temuan Risteski dan Trecevski . . . 18

3.2 Sanggahan oleh Gunawan, Neswan, dan Setya-Budhi . . . 20

3.3 Sudut antara Dua Subruang yang Sederhana . . . 22

3.4 Sudut antara Dua Subruang Sembarang . . . 26

3.5 Sudut-Sudut Kanonik . . . 30

4 Kesimpulan dan Saran 35

DAFTAR GAMBAR

1.1 Sudutθantara vektorudan vektorv . . . 1

1.2 Sudutθantara bidangU dan bidangV . . . 1

2.1 Paralelotop berdimensi-2 dan 3 . . . 7

2.2 Luas jajargenjang = alas×tinggi . . . 8 3.1 Sudut antara subruangU berdimensi-1 dan subruangV berdimensiq 23

PENDAHULUAN 1.1 Latar belakang

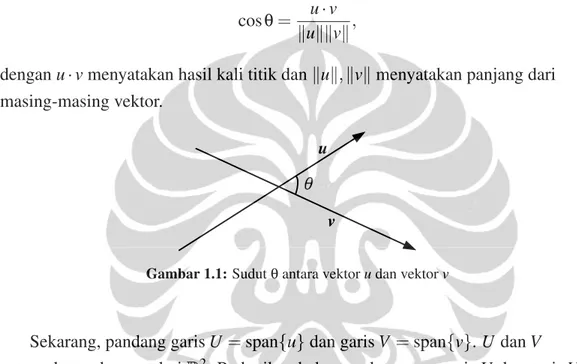
Dalam aljabar linear sudah lazim dikenal dan dipelajari tentang sudut antara dua vektor. Misalnya untuk dua buah vektor tak nolu,v∈_R2(perhatikan Gambar 1.1), sudut antara kedua vektor itu didefinisikan sebagai suatu nilaiθ, 0≤θ≤ π₂, dengan

cosθ= u·v kukkvk,

denganu·vmenyatakan hasil kali titik dankuk,kvkmenyatakan panjang dari masing-masing vektor.

u

v

Gambar 1.1:Sudutθantara vektorudan vektorv

Sekarang, pandang garisU =span{u}dan garisV =span{v}.U danV merupakan subruang dari_R2. Perhatikan bahwa sudut antara garisU dan garisV juga sebesarθ. Sebagai contoh lain perhatikan Gambar 1.2.

Contoh 1.1. Misalkan U dan V adalah dua bidang yang merupakan subruang dari_R3. Sudutθantara U dan V didefinisikan sebagai sudut antara vektor-vektor normalnya (yang tegak lurus terhadap masing-masing bidang).

U

V

Gambar 1.2:Sudutθantara bidangUdan bidangV

2

Biasanya pembahasan tentang sudut antara dua subruang berhenti sampai dengan sudut antara dua bidang di_R3. Hal ini dikarenakan untuk dimensi yang lebih besar, keadaannya tidak dapat digambarkan. Perluasan topik untuk sudut antara dua subruang sebenarnya sudah mulai diteliti sejak pertengahan abad ke-20, namun belum dikenal luas.

Mendefinisikan sudut di antara dua subruang dari_Rn,n>3, tidaklah semudah mengukur sudut di antara dua subruang dari_R2atau_R3. Ada banyak hal yang harus diperhatikan untuk persoalan dengan ruang berdimensi lebih besar, karena tidak adanya bantuan dari ”penglihatan” geometris. Lebih lanjut, pendefinisiannya harus memperhatikan banyak aspek, salah satunya adalah aplikasi/penggunaan dari definisi tersebut. Sampai saat ini, sudut antara dua subruang sudah digunakan dalam bidang komputasi dan statistik. Istilah yang biasanya digunakan adalah sudut-sudut kanonik (canonical angle / principal angle) antara dua subruang. Dalam statistik, sudut-sudut kanonik digunakan sebagai ukuran ketergantungan suatu himpunan peubah acak pada himpunan peubah acak lainnya. Sedangkan dalam komputasi, sudut-sudut kanonik digunakan untuk membandingkan

kesamaan dari dua buah citra (image). Namun, dalam tugas akhir ini, sudut antara dua subruang yang dimaksud lebih secara geometris dan tidak membahas langsung tentang sudut-sudut kanonik. Sebagai penutup, dibandingkan hubungan antara sudut antara dua subruang secara geometris dan sudut-sudut kanonik.

Pada tugas akhir ini, pembahasan diperluas untuk hasil kali dalam dan norm pada suatu ruang hasil kali dalam. Secara sederhana, ruang hasil kali dalam adalah suatu ruang vektor yang disertai dengan suatu hasil kali dalam. Hasil kali titik adalah salah satu contoh dari hasil kali dalam. Idenya adalah untuk me-ngalikan vektor-vektor dan hasilnya adalah skalar.

1.2 Perumusan Masalah

Tesis ini membahas sudut antara dua subruang dari suatu ruang hasil kali dalam-n, terutama untuk dimensi yang lebih besar. Selain itu, juga dibahas mengenai rumus untuk menghitung sudut di antara dua subruang tersebut dan interpretasinya secara geometris. Lebih lanjut, dipelajari hubungannya dengan sudut-sudut kanonik yang selama ini telah digunakan untuk mendeskripsikan sudut antara dua subruang.

1.3 Tujuan Penelitian

Tujuan dari penulisan tesis ini adalah mempelajari generalisasi dari definisi sudut antara dua subruang dan interpretasinya secara geometris.

1.4 Batasan Masalah

Dalam tesis ini, ruang hasil kali dalam-nyang dibahas dibatasi untuk yang berlapangan_R. Untuk hasil kali dalam-nyang dibahas adalah hasil kali dalam-n sederhana.

1.5 Metode Penelitian

Penelitian dilakukan dengan mempelajari karya-karya ilmiah yang disajikan dalam bentuk jurnal dan buku yang berhubungan dengan topik penelitian.

BAB 2

TINJAUAN PUSTAKA

Pada bab ini dibahas tentang topik-topik pendukung yang digunakan dalam pembahasan pada bab-bab berikutnya.

2.1 Ruang Hasil Kali Dalam dan Ruang Norm

Secara sederhana, ruang hasil kali dalam adalah suatu ruang vektor disertai dengan suatu hasil kali dalam. Adapun hasil kali dalam didefinisikan sebagai berikut (Kreyszig, 1978).

Definisi 2.1. Misalkan X adalah sebuah ruang vektor atas lapangan_R. Suatu fungsih•,•idari X2ke_Rdisebut suatu hasil kali dalam jika memenuhi ketiga sifat berikut:

1. Non-negatif

hx,xi ≥0

untuk setiap x∈X danhx,xi=0jika dan hanya jika x=0. 2. Simetris

hx,yi=hy,xi untuk setiap x,y∈X .

3. Linear pada komponen pertama

hαx+βy,zi=αhx,zi+βhy,zi untuk setiap x,y,z∈X danα,β∈_R.

(X,h•,•i)disebut ruang hasil kali dalam (real).

Perhatikan bahwa poin 3 pada Definisi 2.1 mengandung beberapa sifat berikut: 1. Perkalian Skalar

Dengan substitusiβ=0, diperoleh

hαx,yi=αhx,yi, 4

untuk setiapα∈_Rdanx,y∈X. 2. Linear pada komponen kedua

Jelas karena hasil kali dalam real bersifat simetris dan linear pada komponen pertama, maka terpenuhi juga sifat linear pada komponen kedua,

hx,αy+βzi=αhx,yi+βhx,zi untuk setiapα,β∈Rdanx,y,z∈X.

Karena hasil kali dalam real bersifat linear pada komponen pertama dan linear pada komponen kedua, maka dapat dikatakan bahwa hasil kali dalam real bersifat bilinear. Perhatikan bahwa hasil kali dalam pada ruang vektor dengan lapanganC tidak bersifat linear pada komponen kedua, melainkan bersifat linear konjugat.

Berbicara tentang hasil kali dalam, erat hubungannya dengan norm. Definisi dari norm adalah sebagai berikut (Kreyszig, 1978).

Definisi 2.2. Misalkan X adalah sebuah ruang vektor atas lapangan_R. Suatu fungsik•kdari X ke_Ryang memenuhi keempat sifat berikut

1. kxk ≥0

2. kxk=0jika dan hanya jika x=0 3. kαxk=|α| kxk

4. kx+yk ≤ kxk+kyk

untuk setiap x,y∈X danα∈_R, disebut suatu norm dan(X,k•k)disebut ruang norm.

Untuk setiap hasil kali dalamhx,yi,

kxk=phx,xi

membentuk suatu norm padaX, yang biasa disebut sebagai norm terinduksi dari hasil kali dalamhx,yi.

Suatu vektorx∈X dikatakan sebagai vektor satuan jikakxk=1. Teorema berikut ini memuat sifat-sifat dasar dari norm vektor.

Teorema 2.1. Misalkan X ruang hasil kali dalam atas lapangan_Rdengan hasil kali dalamh•,•i.

6

1. (Pertidaksamaan Cauchy-Schwarz) Untuk setiap u,v∈X |hu+vi| ≤ kuk kvk,

dengan kesamaannya diperoleh jika dan hanya jika salah satu dari u dan v merupakan kelipatan (perkalian skalar) dari yang lainnya.

2. (Pertidaksamaan Segitiga) Untuk setiap u,v∈X ku+vk ≤ kuk+kvk,

dengan kesamaannya diperoleh jika dan hanya jika salah satu dari u dan v merupakan kelipatan (perkalian skalar) dari yang lainnya.

3. (Hukum Jajargenjang) Untuk setiap u,v∈X

ku+vk2+ku−vk2=2kuk2+2kvk2.

2.2 Paralelotop dan Determinan Gram

Paralelotop adalah bangun berdimensi hingga yang merupakan generalisasi dari jajargenjang. Definisi 2.3 berikut ini memuat definisi paralelotop secara matematis (John; Courant, 1989).

Definisi 2.3. Paralelotop berdimensi-n yang dibangun oleh vektor-vektor x₁,x₂,· · ·,x_nadalah himpunan titik-titik yang vektor posisinya berbentuk

h= n

∑

i=1

αixi,

dengan0<=αi<=1, untuk setiap i=1,2,· · ·,n. Vektor-vektor x1,x2,· · ·,xn

merupakan rusuk-rusuk dari paralelotop tersebut, sedangkan rusuk-rusuk yang lain sejajar dengan vektor-vektor ini.

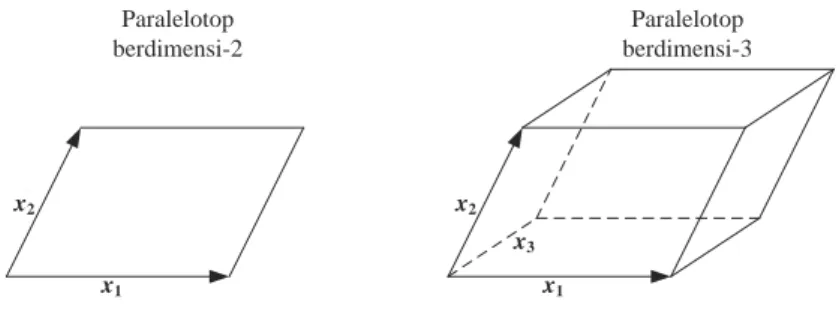
Paralelotop berdimensi-1 tentu saja hanya berupa sebuah vektor. Paralelotop berdimensi-2 merupakan bentuk jajargenjang. Sedangkan paralelotop

berdimensi-3 disebut juga paralelepipedum (parallelpiped), perhatikan Gambar 2.1.

Volume paralelotop dapat dihitung dengan menggunakan determinan Gram (lihat Definisi 2.4 untuk definisi determinan Gram). Kata ”volume” di sini merupakan generalisasi dari panjang vektor pada paralelotop berdimensi-1. Luas

7 x1 x1 x3 x2 x1 x3 x2 x1 Paralelotop berdimensi-3 Paralelotop berdimensi-2

Gambar 2.1:Paralelotop berdimensi-2 dan 3

jajargenjang pada paralelotop berdimensi-2, dan volume bangun ruang paralelepipedum pada paralelotop berdimensi-3.

Definisi 2.4. Misalkan(X,h·,·i)merupakan suatu ruang hasil kali dalam atas lapangan_R. Misalkan pula{x1,x2,· · ·,xn}merupakan suatu himpunan

vektor-vektor di X . Matriks Gram dari{x1,x2,· · ·,xn}didefinisikan sebagai

G(x₁,x₂,· · ·,x_n) =       hx₁,x₁i hx₁,x₂i · · · hx₁,x_ni hx2,x1i hx2,x2i · · · hx2,xni .. . ... ... ... hxn,x1i hxn,x2i · · · hxn,xni       . (2.1)

Determinan dari matriks inilah yang disebut determinan Gram,

Γ(x1,x2,· · ·,xn) =det(G(x1,x2,· · ·,xn)). (2.2)

Teorema 2.2. Determinan GramΓ(x1,x2,· · ·,xn)menyatakan kuadrat dari

volume paralelotop berdimensi-n yang dibangun oleh vektor-vektor x1,x2,· · ·,xn.

Bukti. Berikut ini diberikan bukti secara rekursif. Untukn=1

Misalkan volume dari paralelotop berdimensi-nyang dibangun oleh vektor-vektorx₁,x₂,· · ·,x_ndinotasikan sebagaiV(P_n). Untuk paralelotop berdimensi-1 yang dibangun olehx₁, volumenya adalah

V(P₁) =kx1k= p

hx1,x1i. (2.3)

Untukn=2

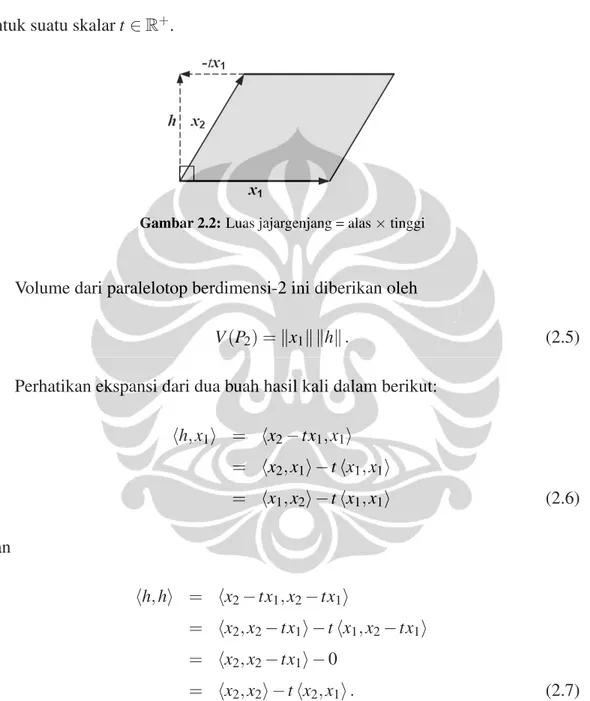
Sekarang kita lihat paralelotop berdimensi-2 yang dibangun oleh vektor-vektor x₁,x₂pada Gambar berikut. Volume dari paralelotop berdimensi-2 sama dengan

8

luas jajargenjang, yaitu alas dikali tinggi. Misalkan alas dari jajargenjang ini adalahx₁dan tingginya adalah

h=x2−tx1, (2.4)

untuk suatu skalart∈_R+_.

Gambar 2.2:Luas jajargenjang = alas×tinggi

Volume dari paralelotop berdimensi-2 ini diberikan oleh

V(P2) =kx1k khk. (2.5)

Perhatikan ekspansi dari dua buah hasil kali dalam berikut: hh,x₁i = hx₂−tx₁,x₁i = hx2,x1i −thx1,x1i = hx1,x2i −thx1,x1i (2.6) dan hh,hi = hx2−tx1,x2−tx1i = hx2,x2−tx1i −thx1,x2−tx1i = hx2,x2−tx1i −0 = hx2,x2i −thx2,x1i. (2.7) Karenahdanx₁saling tegak lurus, makahh,x₁i=0. Dari persamaan 2.6 dapat diperoleh

hx1,x2i −thx1,x1i=0. (2.8) Selanjutnya dari persamaan 2.7 dan persamaan 2.8 dapat dibentuk suatu sistem

persamaan

thx1,x1i+0hh,hi = hx1,x2i (2.9) thx2,x1i+hh,hi = hx2,x2i. (2.10) Untuk berapapun nilait, dengan Aturan Cramer diperoleh solusi dari sistem persamaan (2.9 - 2.10) adalah hh,hi = hx1,x1i hx1,x2i hx2,x1i hx2,x2i hx1,x1i 0 hx2,x1i 1 = Γ(x1,x2) hx1,x1i . (2.11)

Dari persamaan 2.11 diperoleh

khk2= Γ(x1,x2)

kx1k2

. (2.12)

Dengan melakukan substitusi persamaan 2.12 ke persamaan 2.5 diperoleh V(P2) =

p

Γ(x1,x2). (2.13)

Misalkan untukn=kberlaku, bahwa volume paralelotop berdimensi-kyang dibangun oleh vektor-vektorx1,· · ·,xksama dengan akar kuadrat dari

Γ(x1,· · ·,xk), yaitu

V(P_k) =pΓ(x1,· · ·,xk). (2.14)

Pandang bahwa paralelotop berdimensi-kyang dibangun oleh vektor-vektor x₁,· · ·,x_k merupakan ”alas” dari paralelotop berdimensi-(k+1) yang dibangun oleh vektor-vektorx₁,· · ·,x_k,x_k+1, sedangkan tingginya adalah

h=x_k+1−y, (2.15)

dengany=∑kj=1tjxjdantj∈R+. Sehingga, volume dari paralelotop berdimensi-(k+1)yang dibangun oleh vektor-vektorx₁,· · ·,x_k,x_k+1dapat

10

diperoleh dari

V(P_k+1) = V(Pk)khk

= pΓ(x1,· · ·,xk)khk. (2.16)

Perhatikan bahwahtegak lurus terhadap vektor-vektorx₁,· · ·,x_k, sehingga x_k+1−y,x_j=0, (2.17) untuk j=1,· · ·,k. Sementara itu, h2=hh,hi = hxk+1−y,xk+1−yi = hx_k+1−y,xk+1i. (2.18) Dari persamaan 2.16 dan persamaan 2.17 dapat dibentuk sebuah sistem

persamaan k

∑

j=1 tj xi,xj +0hh,hi=hxi,xk+1i, (2.19) untuk setiapi=1,· · ·,k, dan

k

∑

j=1

t_jx_k+1,x_j+hh,hi=hxk+1,xk+1i. (2.20)

Dengan Aturan Cramer, diperoleh

khk2=hh,hi = hx1,x1i hx1,x2i · · · hx1,xk+1i hx₂,x₁i hx₂,x₂i · · · hx₂,x_k+1i .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xk+1i hx1,x1i · · · hx1,xki 0 hx2,x1i · · · hx2,xki 0 .. . ... . .. ... hxn,x1i · · · hxn,xki 1 = Γ(x1,· · ·,xk+1) Γ(x1,· · ·,xk) . (2.21)

Terakhir, dengan melakukan substitusi persamaan 2.21 ke persamaan 2.16

diperoleh V(P_k+1) = p Γ(x1,· · ·,xk)khk = pΓ(x1,· · ·,xk) s Γ(x1,· · ·,xk+1) Γ(x1,· · ·,xk) = Γ(x1,· · ·,xk+1). (2.22)

Jadi, terbukti bahwa determinan GramΓ(x1,· · ·,xn)merupakan kuadrat dari volume paralelotop berdimensi-nyang dibangun oleh vektor-vektorx₁,· · ·,x_n.

Berikut ini adalah beberapa sifat dari determinan Gram. Misalkan {x1,x2,· · ·,xn}merupakan suatu himpunan vektor-vektor diX. Maka

1. Γ(x1,x2,· · ·,xn) =Γ(xi1,xi2,· · ·,xin), dengan{i1,i2,· · ·,in}merupakan permutasi dari{1,2,· · ·,n}. Maksudnya, determinan Gram invarian terhadap permutasi dari{1,2,· · ·,n}.

2. Γ(x1,x2,· · ·,xn)≥0

Bentuk kesamaannya berlaku jika dan hanya jika vektor-vektor {x1,x2,· · ·,xn}bergantung linear.

Volume dari paralelotop berdimensi-nbernilai non-negatif. Kemudian jika vektor-vektor{x1,x2,· · ·,xn}bergantung linear, maka paralelotop yang dibangun sebenarnya mempunyai dimensi kurang darin. Oleh karena itu, volume paralelotop berdimensi-nyang dibangun oleh vektor-vektor {x1,x2,· · ·,xn}yang bergantung linear adalah 0.

3. Pertidaksamaan Hadamard Γ(x1,x2,· · ·,xn)≤∏ni=1kxik2

Bentuk kesamaannya berlaku jika dan hanya jikax_i,x_j=δi,jkxik

x_j, untuk setiapi,j∈ {1,2,· · ·,n}.

Nilai maksimum dari volume paralelotop berdimensi-nyang dibangun oleh {x1,x2,· · ·,xn}diperoleh ketika setiap pasang dari vektor-vektor

{x1,x2,· · ·,xn}saling ortogonal. Sebagai gambaran, paralelotop

berdimensi-2 dengan volume maksimum berbentuk persegi panjang dan paralelotop berdimensi-3 dengan volume maksimum berbentuk balok. Adapun volume maksimum diperoleh dengan menghitung∏n_i=1kxik.

12

2.3 Ruang Hasil Kali Dalam-ndan Ruang Norm-n

Pada tahun 1960-an, Gahler memulai mengembangkan definisi tentang norm-2 (Freese, 2001), yang merupakan perluasan dari norm pada Definisi 2.2. Kemudian melalui studi lebih lanjut, ia mengenalkan definisi tentang norm-n, yang ide awalnya adalah untuk menyeragamkan notasi panjang, luas, dan volume. Definisinya adalah sebagai berikut (Misiak, 1989).

Definisi 2.5. Misalkan n∈N dan X adalah suatu ruang vektor atas lapangan_R dengan dim(X)≥n. Suatu fungsi bernilai realk•,· · ·,•kpada Xnyang memenuhi keempat sifat berikut ini

1. kx1,x2,· · ·,xnk=0jika dan hanya jika x1,x2,· · ·,xnbergantung linear

2. kx1,x2,· · ·,xnkinvarian terhadap setiap permutasi

3. kx1,x2,· · ·,xn−1,αxnk=|α| kx1,x2,· · ·,xn−1,xnkuntuk setiapα∈R

4. kx1,x2,· · ·,xn−1,y+zk ≤ kx1,x2,· · ·,xn−1,yk+kx1,x2,· · ·,xn−1,zk

disebut suatu norm-n dari X dan pasangan(X,k•,· · ·,•k)disebut ruang norm-n. Perhatikan bahwa sembarang hasil kali dalam-nmenginduksi suatu norm-n, dengan

kx₁,x₂,· · ·,x_nk=phx₁,x₁|x2,· · ·,xni.

Selanjutnya pada tahun 1980-an, murid dari Gahler yang bernama A. Misiak (1989) memperkenalkan istilah ruang hasil kali dalam-n, sebagai generalisasi dari ruang hasil kali dalam. Hasil kali dalam-nmengoperasikann+1 buah vektor dan memetakannya ke skalar di lapangan_R. Idenya adalah menambahkan

vektor-vektor lain ke hasil kali dalamhx,yi, namun tetap mempertahankan sifat linearnya. Lebih lanjut, penambahan vektor-vektor lain ini tidak menimbulkan sifat-sifat baru yang signifikan pada hasil kali dalam itu sendiri. Maksudnya, vektor-vektor yang ditambahkan ini tidak bersifat linear.

Definisi 2.6. Misalkan n∈N dan X adalah suatu ruang vektor atas lapangan_R dengan dim(X)≥n. Suatu fungsi bernilai realh•,•|•,· · ·,•ipada Xn+1yang memenuhi keenam sifat berikut ini

1. Non-negatif

hx,x|x2,· · ·,xni ≥0,

untuk setiap x,x₂,· · ·,x_n∈X dan

hx,x|x2,· · ·,xni=0jika dan hanya jika x,x2,· · ·,xnbergantung linear Universitas Indonesia

2. Simetris

hx,y|x2,· · ·,xni=hy,x|x2,· · ·,xni

untuk setiap x,y,x₂,· · ·,x_n∈X . 3. Invarian terhadap permutasi

hx,y|x2,· · ·,xni=hx,y|xi2,· · ·,xini

untuk setiap x,y,x₂,· · ·,x_n∈X dan i₂,i₃· · ·,i_nsembarang permutasi dari 2,3,· · ·,n.

4. Jika n>1, makahx,x|x2,· · ·,xni=hx2,x2|x,· · ·,xniuntuk setiap

x,x₂,· · ·,x_n∈X . 5. Perkalian skalar

hαx,y|x2,· · ·,xni=αhx,y|x2,· · ·,xni

untuk setiap x,y,x2,· · ·,xn∈X .

6. Linear pada komponen pertama

hx+y,z|x2,· · ·,xni=hx,z|x2,· · ·,xni+hy,z|x2,· · ·,xni

untuk setiap x,y,z,x2,· · ·,xn∈X .

disebut suatu hasil kali dalam-n dan(X,h•,•|•,· · ·,•i)disebut ruang hasil kali dalam-n.

Garis vertikal pada notasihx,y|x2,· · ·,xnidigunakan untuk memisahkan komponen-komponen yang bersifat linear (kiri) dan komponen-komponen yang tidak bersifat linear (kanan). Kemudian untukn=1, notasihx,y|x2,· · ·,xni dipahami sebagai hasil kali dalamhx,yi.

Perhatikan bahwa poin 5 dan poin 6 pada Definisi 2.6 mengandung sifat seperti poin 3 pada Definisi 2.1. Lebih lanjut, dengan sifat simetris dan linear pada komponen pertama, dapat diperoleh bahwa hasil kali dalam-njuga bersifat linear pada komponen kedua. Sehingga dapat dikatakan bahwa hasil kali dalam-n bersifat bilinear (pada lapangan_R).

Sebagai contoh adalah hasil kali dalam-nsederhana yang termuat dalam Teorema 2.3 berikut ini.

14

Teorema 2.3. Setiap ruang hasil kali dalam X dapat dilengkapi dengan suatu hasil kali dalam-n sederhana

hx0,x1|x2,· · ·,xni= hx0,x1i hx0,x2i · · · hx0,xni hx2,x1i hx2,x2i · · · hx2,xni .. . ... . . . ... hxn,x1i hxn,x2i · · · hxn,xni . (2.23)

Perhatikan bahwax_i,x_jmenyatakan suatu hasil kali dalam diX. Bukti. Misalkanx,y,x₀,x₁,· · ·,x_n∈X danα∈_R.

1. Untuk membuktikan sifat non-negatif, perhatikan bahwa

hx1,x1|x2,· · ·,xni = hx1,x1i hx1,x2i · · · hx1,xni hx2,x1i hx2,x2i · · · hx2,xni .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xni = Γ(x1,· · ·,xn) (2.24)

merupakan kuadrat dari volume paralelotop berdimensi-nyang dibangun olehx1,· · ·,xn. Nilainya non-negatif dan bernilai nol jika dan hanya jika

x₁,· · ·,x_nbergantung linear.

2. Dengan sifat simetris dari hasil kali dalamx_i,x_j, maka dapat ditunjukkan bahwa matriks yang nilai determinannya adalahhx0,x1|x2,· · ·,xni

merupakan transpose dari matriks yang determinannya adalah

hx1,x0|x2,· · ·,xni. Sehingga terbukti sifat simetrisnya, hx₀,x₁|x₂,· · ·,x_ni = hx0,x1i hx0,x2i · · · hx0,xni hx2,x1i hx2,x2i · · · hx2,xni .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xni = hx1,x0i hx2,x0i · · · hxn,x0i hx1,x2i hx2,x2i · · · hxn,x2i .. . ... . .. ... hx1,xni hx2,xni · · · hxn,xni =       hx₁,x₀i hx₁,x₂i · · · hx₁,x_ni hx2,x0i hx2,x2i · · · hx2,xni .. . ... . .. ... hxn,x0i hxn,x2i · · · hxn,xni       T = hx1,x0i hx1,x2i · · · hx1,xni hx2,x0i hx2,x2i · · · hx2,xni .. . ... . .. ... hxn,x0i hxn,x2i · · · hxn,xni = hx₁,x₀|x₂,· · ·,x_ni.

3. Misalkani2,i3,· · ·,inadalah suatu permutasi dari 2,3,· · ·,n. Misalkan pula

hx,y|x2,· · ·,xnidanhx,y|xi2,· · ·,xinimenyatakan determinan dari

matriks-matriksAdanB. Perhatikan bahwa matriksBdapat diperoleh dari matriksAyang ditukar beberapa baris dan beberapa kolomnya. Perhatikan pula bahwa banyaknya pertukaran adalah genap, sehingga determinannya tetap. Oleh karena itu,

hx,y|x2,· · ·,xni=hx,y|xi2,· · ·,xini. 4. Misalkann>1. hx,x|x2,· · ·,xni = Γ(x,x2,· · ·,xn) = Γ(x2,x,x3,· · ·,xn) = hx2,x2|x,· · ·,xni, Universitas Indonesia

16

untuk setiapx,x2,· · ·,xn∈X. 5. Sifat perkalian skalar:

hαx0,x1|x2,· · ·,xni = hαx0,x1i hαx0,x2i · · · hαx0,xni hx2,x1i hx2,x2i · · · hx2,xni .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xni = αhx0,x1i αhx0,x2i · · · αhx0,xni hx2,x1i hx2,x2i · · · hx2,xni .. . ... . .. ... hx_n,x1i hxn,x2i · · · hxn,xni = α hx0,x1i hx0,x2i · · · hx0,xni hx2,x1i hx2,x2i · · · hx2,xni .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xni = αhx0,x1|x2,· · ·,xni. 6. Sifat linear: hx+y,x1|x2,· · ·,xni = hx+y,x₁i hx+y,x₂i · · · hx+y,x_ni hx2,x1i hx2,x2i · · · hx2,xni .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xni = hx,x1i+hy,x1i hx,x2i+hy,x1i · · · hx,xni+hy,x1i hx2,x1i hx2,x2i · · · hx2,xni .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xni = hx,x₁i hx,x₂i · · · hx,x_ni hx₂,x₁i hx₂,x₂i · · · hx₂,x_ni .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xni + hy,x₁i hy,x₂i · · · hy,x_ni hx₂,x₁i hx₂,x₂i · · · hx₂,x_ni .. . ... . .. ... hxn,x1i hxn,x2i · · · hxn,xni = hx,x₁|x2,· · ·,xni+hy,x1|x2,· · ·,xni.

Jadi, terbukti bahwa fungsi yang didefinisikan dalam persamaan 2.23 adalah suatu hasil kali dalam-n.

Teorema 2.4. Setiap hasil kali dalam-n menginduksi suatu norm-n, dengan kx1,x2,· · ·,xnk=

p

hx1,x1|x2,· · ·,xni. (2.25) Bukti Teorema 2.4 cukup trivial. Sebagai contoh, hasil kali dalam-nsederhana menginduksi norm-n kx1,x2,· · ·,xnk=       hx1,x1i hx1,x2i · · · hx1,xni hx2,x1i hx2,x2i · · · hx2,xni .. . ... . .. ... hx_n,x1i hxn,x2i · · · hxn,xni       1 2 , (2.26)

yang merupakan akar kuadrat dari determinan Gram, yang merepresentasikan volume dari suatu paralelotop berdimensi-nyang dibangun olehx1,x2,· · ·,xn. Hasil kali dalam-nmemenuhi beberapa sifat seperti pada suatu hasil kali dalam. Misalnya saja pertidaksamaan Cauchy-Schwarz yang termuat dalam Teorema 2.5 berikut ini.

Teorema 2.5. (Pertidaksamaan Cauchy-Schwarz)Jika X suatu ruang hasil kali dalam-n, maka berlaku pertidaksamaan

|hx,y|x2,· · ·,xni|2≤ hx,x|x2,· · ·,xni hy,y|x2,· · ·,xni. (2.27)

Bukti. Misalkanx,y,x₂,· · ·,x_n∈X denganx,x₂,· · ·,x_nbebas linear. Misalkan pula u=y−hx,y|x2,· · ·,xni

hx,x|x₂,· · ·,x_nix. Perhatikan bahwahu,u|x2,· · ·,xni ≥0, sehingga diperoleh

0 ≤ hu,u|x2,· · ·,xni 0 ≤ y−hx,y|x2,· · ·,xni hx,y|x2,· · ·,xni x,y−hx,y|x2,· · ·,xni hx,x|x2,· · ·,xni x|x2,· · ·,xn 0 ≤ hy,y|x2,· · ·,xni − |hx,y|x2,· · ·,xni|2 hx,x|x2,· · ·,xni |hx,y|x2,· · ·,xni|2 hx,x|x₂,· · ·,x_ni ≤ hy,y|x2,· · ·,xni |hx,y|x2,· · ·,xni|2 ≤ hx,x|x2,· · ·,xni hy,y|x2,· · ·,xni. (2.28) Universitas Indonesia

BAB 3

SUDUT ANTARA DUA SUBRUANG 3.1 Temuan Risteski dan Trecevski

Tesis ini berawal dari studi jurnal yang dikeluarkan oleh Risteski dan Trencevski (2001), yang memperkenalkan lebih lanjut definisi secara geometris dari sudut antara dua subruang dariRndan menjelaskan hubungannya dengan sudut-sudut kanonik. Definisi yang mereka gunakan didasarkan pada sebuah generalisasi dari pertidaksamaan Cauchy-Schwarz. Namun, Gunawan, Neswan, dan Setya-Budhi (2005) menemukan kesalahan pada teorema landasan yang diberikan oleh Risteski dan Trencevski, dengan memberikan satu contoh penyangkal, dan

memperbaikinya.

Untuk mendefinisikan sudut antara dua subruang (dengan sembarang dimensi) dari ruang vektor Euclid_Rn, Risteski dan Trecevski memberikan Teorema 3.1 berikut ini disertai buktinya.

Teorema 3.1. Misalkan A dan B merupakan subruang dari ruang vektor Euclid

Rndengan hasil kali dalamh•,•i. Misalkan{a1,· · ·,ap}adalah basis dari A dan

{b1,· · ·,bq}adalah basis dari B, dengan p≤q≤n. Maka pertidaksamaan

det(MMT)≤Γ1×Γ2, (3.1) berlaku dengan Γ1 = ha1,a1i ha1,a2i · · · a₁,a_p ha₂,a₁i ha₂,a₂i · · · a₂,a_p .. . ... . .. ... ap,a1 ap,a2 · · · ap,ap , Γ2 = hb1,b1i hb1,b2i · · · b1,bq hb2,b1i hb2,b2i · · · b₂,b_q .. . ... . .. ... b_q,b₁ b_q,b₂ · · · b_q,b_q , serta M=       ha1,b1i ha1,b2i · · · a₁,b_q ha2,b1i ha2,b2i · · · a₂,b_q .. . ... . . . ... a_p,b₁ a_p,b₂ · · · a_p,b_q       , 18

denganΓ1danΓ2menyatakan determinan Gram dari vektor-vektor{a1,· · ·,ap}

dan{b1,· · ·,bq}. Lebih lanjut, kesamaan dalam (3.1) dicapai jika dan hanya jika

A⊆B.

Adapun bukti yang diberikan oleh Risteski dan Trecevski adalah sebagai berikut.

Bukti. Pertidaksamaan (3.1) invarian terhadap setiap operasi baris elementer. Tanpa mengurangi generalitas, diasumsikan{a1,· · ·,ap}adalah vektor-vektor ortonormal dan{b1,· · ·,bq}juga merupakan vektor-vektor ortonormal. (Gunawan, Neswan, dan Setya-Budhi menyanggah pernyataan ini.)

Karena{a1,· · ·,ap}adalah vektor-vektor ortonormal, makahai,aii=1 dan

a_i,a_j=0, untuk setiapi,j∈ {1,· · ·,p}dani6= j.

Γ1= ha1,a1i ha1,a2i · · · a1,ap ha2,a1i ha2,a2i · · · a2,ap .. . ... . .. ... a_p,a₁ a_p,a₂ · · · a_p,a_p =det(I_p) =1 dan Γ2= hb1,b1i hb1,b2i · · · b₁,b_q hb2,b1i hb2,b2i · · · b₂,b_q .. . ... . .. ... b_q,b1 bq,b2 · · · bq,bq =det(Iq) =1

denganI_pdanI_qadalah matriks-matriks identitas berdimensi pdanq. Hanya perlu dibuktikan bahwa det(MMT)≤1.

Misalkanci= (hai,b1i,hai,b2i,· · ·,

ai,bq

)untuk 1≤i≤p. Perhatikan bahwa itu artinyaci∈Rq, untuk 1≤i≤p. Karena{a1,· · ·,ap}dan{b1,· · ·,bq} merupakan sistem-sistem ortonormal, maka untuk 1≤i≤pdan 1≤ j≤qberlaku

ai,bj =cosθi jkaik bj =cosθ_{i j} ≤1.

Lebih lanjut diperoleh bahwa

kc_ik=phc_i,c_ii ≤1 dengan pengukuran Euclid di_Rq, untuk setiap 1≤i≤p.

20

Misalkancp+1,· · ·,cqadalah vektor-vektor ortonormal sedermikian sehingga masing-masing vektor tersebut ortogonal terhadapc₁,· · ·,c_p. Maka diperoleh

det(MMT) = hc1,c1i hc1,c2i · · · c₁,c_q hc2,c1i hc2,c2i · · · c₂,c_q .. . ... . .. ... c_q,c₁ c_q,c₂ · · · c_q,c_q = hc1,c1i hc1,c2i · · · c1,cp hc2,c1i hc2,c2i · · · c2,cp .. . ... . .. ... c_p,c₁ c_p,c₂ · · · c_p,c_p = Γ(c1,c2,· · ·,cq), (3.2)

yang merupakan kuadrat dari volume paralelotop di_Rq, yang dibangun oleh vektor-vektorc₁,c₂,· · ·,c_q. Karenakc_ik ≤1, untuk setiap 1≤i≤q, maka diperoleh det(MMT)≤1.

Lebih lanjut, kesamaan dalam (3.1) dicapai jika dan hanya jikac1,c2,· · ·,cq merupakan sistem ortonormal, dengankcik=1, untuk setiap 1≤i≤q. Namun,

kcik=1 mengakibatkanai∈B, sehinggaA⊆B. Sebaliknya, jikaA⊆B, maka jelas bahwa kesamaan dalam (3.1) tercapai.

Kemudian, dengan asumsi Teorema 3.1 berlaku benar, didefinisikan sudutθ antara subruangAdan subruangBdengan

cos2θ= det(MM

T₎

Γ1Γ2

, (3.3)

dengan matriksMseperti didefinisikan pada Teorema 3.1 danΓ1,Γ2adalah determinan Gram yang diperoleh dari vektor-vektora1,· · ·,apdanb1,· · ·,bq, secara berurutan.

3.2 Sanggahan oleh Gunawan, Neswan, dan Setya-Budhi

Pembuktian Teorema 3.1 yang diberikan oleh Risteski dan Trecevski sekilas terlihat benar. Namun, ada bagian yang tidak tepat menurut Gunawan, Neswan, dan Setya-Budhi pada pembuktian ini. Seperti ditulis pada awal bukti Teorema 3.1, Risteski dan Trecevski menyatakan bahwa ”tanpa mengurangi generalitas,

diasumsikan{a1,· · ·,ap}adalah suatu sistem ortonormal dan{b1,· · ·,bq}juga

merupakan suatu sistem ortonormal.” Hal ini tidak dapat dilakukan karena pada Teorema 3.1 basis dari kedua subruang adalah sembarang. Keadaan pembuktian dengan kedua basis tersebut ortonormal hanyalah merupakan salah satu kasus yang mungkin terjadi dan tidak bisa mewakili semua kasus yang mungkin.

Lebih lanjut, Gunawan, Neswan, dan Setya-Budhi menyatakan bahwa pertidaksamaan (3.1) hanya berlaku jika salah satu kasus ini terjadi

1. p=q

2. {b1,· · ·,bq}juga ortonormal.

Untuk kasus lainnya, masih memungkinkan tanda ”≤” pada pertidaksamaan (3.1) diganti oleh tanda ”>”. Berikut ini adalah contoh dimana ”>” terjadi. Contoh 3.2. Misalkan X =_R3dilengkapi dengan hasil kali dalam biasa. Misalkan pula A=span{a}, dengan a= (1,0,0)dan B=span{b1,b2}dengan b₁= 1₂,1₂,0dan b₂= 1₂,−1₂,1₂.

Berdasarkan Teorema 3.1, ada beberapa nilai berikut ini yang harus diperhatikan.

M=hha,b1i ha,b2i i

. Sehingga ruas kiri dari pertidaksamaan (3.1) diperoleh

det(MMT) = ha,b₁i2+ha,b₂i2 = 1 4+ 1 4 = 1 2.

Sedangkan untuk ruas kanan dari pertidaksamaan (3.1) adalah sebagai berikut.

|ha,ai| × hb1,b1i hb1,b2i hb2,b1i hb2,b2i = kak2kb1,b2k2 = kak2kb₁k2kb₂k2− hb1,b2i 2 3 8. Jadi, diperoleh bahwa

det(MMT)>Γ1×Γ2.

22

Dengan demikian, Teorema 3.1 tidak sah.

Contoh ini membuktikan bahwa pertidaksamaan (3.1) gagal bahkan untuk kasus{a1,· · ·,ap}ortonormal dan{b1,· · ·,bq}ortogonal. Padahal ortogonalitas hampir menyerupai ortonormalitas. Hal ini mengindikasikan bahwa

pertidaksamaan (3.1) berlaku untuk{a1,· · ·,ap}dan{b1,· · ·,bq}yang sama-sama ortonormal.

Melihat kembali formula yang diberikan oleh Risteski dan Trenchevski pada persamaan (3.3), jika kita coba pada kasus di Contoh 3.2, maka akan kita peroleh bahwa cos2θ=det( MMT) Γ1Γ2 = 1 2 3 8 =11 3, (3.4)

yang nilainya lebih besar daripada 1. Dengan demikian, formula pada persamaan (3.3) tidak masuk di akal karena nilai dari ruas kanannya belum tentu berada di interval[0; 1].

Gunawan, Neswan, dan Setya-Budhi memperbaiki formula tersebut dan memperluas ruang semestanya menjadi suatu ruang hasil kali dalam-nsederhana dengan hasil kali dalam yang sembarang.

3.3 Sudut antara Dua Subruang yang Sederhana

Pada subbab ini kita lihat terlebih dahulu dua kasus sudut antara dua subruang yang sederhana. Pengertian sudut di sini sama seperti pengertian sudut yang biasanya. Kemudian perbaikan dari formula pada persamaan (3.3), yang dikemukakan Risteski dan Trenchevski, harus merupakan generalisasi dari dua kasus ini.

MisalkanX merupakan ruang hasil kali dalam-nsederhana atas lapangan real, dengan hasil kali dalam sederhanah•,•i). Diberikan dua subruang dariX, yaituU danV, yang bukan merupakan himpunan nol dan p=dim(U)≤dim(V) =q<∞. Dua kasus yang dibahas pada bab ini adalah

• sudut antara subruang berdimensi 1 dariX dan subruang berdimensiqdariX • sudut antara dua subruang berdimensi pdariX, yang beririsan di suatu

subruang berdimensi p−1 dariX.

Untuk kasus pertama,U dapat dipandang sebagai suatu ”garis” yang

merupakan kumpulan kelipatan dari vektoru. Sudut yang dibentuk antara garisU dan subruangV adalah sudut yang dibentuk oleh vektorudan proyeksi ortogonal dari vektorupada subruangV. Gambar 3.1 menunjukkan ilustrasinya dan Definisi 3.1 memuat formulanya.

Definisi 3.1. Misalkan X adalah ruang hasil kali dalam, U=span{u}adalah sebuah subruang dari X , dan V =span{v1,v2, ...,vq}adalah sebuah subruang

berdimensi q dari X . Maka sudutθantara U dan V didefinisikan oleh cos2θ= hu,uVi

2 kuk2kuVk2

, (3.5)

dengan u_V menyatakan proyeksi ortogonal dari u pada V dank·k=h·,·i12 _adalah

norm yang diinduksi oleh hasil kali dalam di X .

Gambar 3.1:Sudut antara subruangUberdimensi-1 dan subruangVberdimensiq

Pada Definisi 3.1,udapat ditulis sebagaiu=u_V+u_V⊥denganu⊥_V adalah komplemen ortogonal dariupadaV. Maka persamaan (3.5) dapat ditulis menjadi

cos2θ = huV+u ⊥ V,uVi 2 kuk2kuVk2 = huV,uVi+hu ⊥ V,uVi 2 kuk2kuVk2 = huV,uVi+02 kuk2kuVk2 = huV,uVi2 kuk2kuVk2 = kuvk4 kuk2kuVk2 =kuVk2 kuk2 . (3.6)

Sehingga dapat dikatakan bahwa nilai cosθmerupakan perbandingan antara panjang proyeksiupadaV terhadap panjang dariu.

Sedangkan untuk kasus kedua,U danV subruang-subruang berdimensi-pyang beririsan diW yang berdimensi-(p−1). Karena itu, sudut antaraU danV

24

dipengaruhi oleh vektor-vektor pada basis-basisU danV yang tidak berada diW, yaitu vektorudan vektorv. Sudut antaraU danV adalah sudut yang dibentuk oleh proyeksi-proyeksi ortogonal dari vektorudan vektorvpada subruangW. Definisi 3.2 memuat formulanya.

Definisi 3.2. Misalkan X adalah ruang hasil kali dalam dengan

U =span{u,w2, ...,wp}dan V =span{v,w2, ...,wp}adalah subruang-subruang

berdimensi p dari X yang beririsan di suatu subruang berdimensi p−1,

W =span{w2, ...,wp}dengan p≥2. Maka sudutθantara U dan V didefinisikan oleh cos2θ= u_W⊥,v_W⊥2 u_W⊥ 2 v_W⊥ 2, (3.7)

dengan u⊥_W dan v_W⊥ adalah komplemen ortogonal dari u dan v pada W .

Akan ditunjukkan bahwa dari formula pada Definisi 3.2 dapat disimpulkan bahwa nilai dari cosθsama dengan perbandingan antara volume dari paralelotop dimensi-pyang dibangun oleh proyeksi dariu,w2,· · ·,w_ppadaV dan volume dari paralelotop berdimensi-pyang dibangun olehu,w2,· · ·,w_p, yaitu

cos2θ= u_V,w2,· · ·,w_p 2 u,w2,· · ·,wp 2 , (3.8)

denganu_V adalah hasil proyeksi dariupadaV. Pada Definisi 3.2 diberikan

cos2θ= u_W⊥,v_W⊥2 u_W⊥ 2 v_W⊥ 2, (3.9)

denganu⊥_W danv_W⊥ adalah komplemen ortogonal dariudanvpadaW.

Perhatikan bahwaudapat dituliskan sebagaiu=u_W +u_W⊥ , denganu_W adalah proyeksiupadaW danu_W⊥ adalah komplemen ortogonalupadaW. Berdasarkan sifat-sifat norm-ndan norm standar diperoleh

u,w₂,· · ·,w_p = uW+u ⊥ W,w2,· · ·,wp = u_W,w₂,· · ·,w_p+ u ⊥ W,w2,· · ·,wp = 0+ u ⊥ W,w2,· · ·,wp = u ⊥ W w₂,· · ·,w_p. (3.10) Universitas Indonesia

Dengan cara yang serupa dapat dinyatakan bahwa v,w2,· · ·,wp = v ⊥ W w2,· · ·,wp ,

denganv⊥_W adalah komplemen ortogonalvpadaW. Selanjutnya, perhatikan bahwa

u,v|w2,· · ·,wp = D u_W+u⊥_W,v_W+v_W⊥|w2,· · ·,wp E = u_W,v_W|w2,· · ·,wp +Du_W⊥,v_W⊥|w2,· · ·,wp E = 0+Du⊥_W,v⊥_W|w2,· · ·,wp E = Du_W⊥,v⊥_W E w2,· · ·,wp . (3.11)

Lihat kembali persamaan (3.9). Kita kalikan penyebut dan pembilang pada ruas kanan dari persamaan (3.9) masing-masing denganw2,· · ·,wp

4 sehingga diperoleh cos2θ = u_W⊥,v_W⊥2 u_W⊥ 2 v_W⊥ 2 = u_W⊥,v_W⊥2w2,· · ·,wp 4 u_W⊥ 2 v_W⊥ 2 w2,· · ·,wp 4 = u,v|w2,· · ·,wp u,w2,· · ·,wp 2 v,w2,· · ·,wp 2. (3.12)

Selanjutnya, misalkan bahwau_V =αv+∑_kp₌₂βkwk. Dengan menerapkan Aturan Cramer, diperoleh

α= u,v|w2,· · ·,wp v,w2,· · ·,wp 2. (3.13) Universitas Indonesia

26

Oleh karena itu, didapatkan

cos2θ = u,v|w2,· · ·,wp 2 u,w2,· · ·,wp 2 v,w2,· · ·,wp 2 = α u,v|w2,· · ·,wp u,w₂,· · ·,w_p 2 = u,u_V|w2,· · ·,wp u,w₂,· · ·,w_p 2 = u_V,w₂,· · ·,w_p 2 u,w2,· · ·,wp 2 . (3.14)

Jadi, terbukti bahwa pada Definisi 3.2 , nilai dari cosθsama dengan

perbandingan antara volume dari paralelotop berdimensi-pyang dibangun oleh proyeksi dariu,w₂,· · ·,w_ppadaV dan volume dari paralelotop berdimensi-pyang dibangun olehu,w2,· · ·,wp.

3.4 Sudut antara Dua Subruang Sembarang

Pada subbab ini dibahas mengenai formula sudut antara dua subruang dengan dimensi berhingga yang sembarang sebagai perluasan dari formula-formula sudut yang sudah dibahas pada subbab sebelumnya. Gunawan, Neswan, dan

Setya-Budhi mendefinisikan formula sudut antara dua subruang dengan dimensi berhingga yang sembarang dari suatu ruang hasil kali dalam-nsederhana dalam Definisi 3.3 berikut ini.

Definisi 3.3. Misalkan U =span{u1,· · ·,up}suatu subruang berdimensi-p dari

ruang hasil kali dalam-n sederhana X dan V =span{v1,· · ·,vq}suatu subruang

berdimensi-q dari X , dengan p≤q. Sudutθantara U dan V didefinisikan oleh

cos2θ=

proj_Vu1,projVu2,· · ·,projVup

2 u₁,u₂,· · ·,u_p 2 , (3.15)

dengan proj_Vu_iadalah proyeksi dari u_ipada V , untuk i=1,· · ·,p.

Untuk memudahkan dalam membaca indeks, maka notasi proyeksiu_ipadaV tidak ditulisu_iV melainkan proj_Vu_i.

Perhatikan bahwaX merupakan ruang hasil kali dalam-nsederhana, dengan hasil kali dalam yang sembarang. Sedangkan norm dan norm-nyang digunakan adalah yang standar.

Secara sederhana, Gunawan, Neswan, dan Setya-Budhi memformulasikan seperti itu alasannya karena ada dua fakta pendukung. Kedua fakta pendukung ini menjadi dasar untuk mengambil kesimpulan bahwa sudut tersebut bisa

diformulasikan demikian. Fakta 1

Perbandingan pada ruas kanan dari persamaan (3.15) mempunyai nilai dari 0 sampai dengan 1.

Fakta 2

Perbandingan pada ruas kanan dari persamaan (3.15) bebas terhadap basis dari U danV yang dipilih.

Berikut ini adalah bukti bahwa kedua penyataan tersebut benar.

Bukti Fakta 2. Perhatikan bahwa proyeksiuipadaV unik sehingga invarian juga terhadap pemilihan basis dariV yang digunakan. Sedangkan karena proyeksi berupa transformasi linear, maka nilai perbandingan pada persamaan (3.15) tersebut juga invarian terhadap pemilihan basis dariU yang digunakan. Oleh karena itu, perbandingan tersebut bernilai tetap, walaupun

• u_idiganti olehu_j • uidiganti olehui+αuj

• u_idiganti olehαu_i, untukα6=0.

Bukti Fakta 1. Karena nilai norm-nbersifat nonnegatif, maka nilai perbandingan kedua norm-npada persamaan (3.15) juga pasti bernilai nonnegatif. Kemudian bahwa nilai perbandingan kurang dari sama dengan 1, dapat dipahami dengan mudah secara geometris. Perhatikan bahwa dengan norm-nstandar dan hasil kali dalam-nsederhana dapat diperoleh bahwa

proj_Vu₁,proj_Vu₂,· · ·,proj_Vu_p 2

= proj_Vu₁,proj_Vu₁|proj_Vu₂,· · ·,proj_Vu_p

= Γ(proj_Vu1,projVu2,· · ·,projVup), (3.16) yang menyatakan kuadrat dari volume paralelotop berdimensi-pyang dibangun oleh proj_Vu1,projVu2,· · ·,projVup, dan

u1,u2,· · ·,up 2 = u1,u1|u2,· · ·,up = Γ(u1,u2,· · ·,up), (3.17) Universitas Indonesia

28

yang menyatakan kuadrat dari volume paralelotop berdimensi-pyang dibangun olehu₁,u₂,· · ·,u_p.

Perhatikan bahwakproj_Vu_ik ≤ kuik, untuk setiapi=1,· · ·,p. Oleh karena itu, volume paralelotop berdimensi-pyang dibangun oleh

proj_Vu₁,proj_Vu₂,· · ·,proj_Vu_pkurang dari atau sama dengan volume paralelotop berdimensi-pyang dibangun olehu₁,u₂,· · ·,u_p. Akibatnya, jelas bahwa

perbandingan kuadrat dari kedua volume tersebut kurang dari atau sama dengan 1. Untuk membuktikannya secara matematis, boleh diasumsikan bahwa

{u1,· · ·,up}ortonormal. Akibatnya, diperoleh

u1,· · ·,up

=1. Lebih lanjut, karenakproj_Vuik ≤ kuik, untuk setiapi=1,· · ·,p. Oleh karena itu, diperoleh

proj_Vu₁,proj_Vu₂,· · ·,proj_Vu_p ≤1.

Jadi, terbukti bahwa

0≤

proj_Vu₁,proj_Vu₂,· · ·,proj_Vu_p 2 u₁,u₂,· · ·,u_p 2 ≤1. (3.18)

Selanjutnya kita buat persamaan (3.15) dalamu₁,· · ·,u_pdanv₁,· · ·,v_qsecara eksplisit. Misalkan untuk setiapi=1,· · ·,p, proyeksi dariu_ipadaV dapat ditulis sebagai kombinasi linear dariv1,v2,· · ·,vq,

proj_Vu_i= q

∑

k=1 αikvk, (3.19) dengan αik= D u1,vk|vi2(k),· · ·,viq(k) E v₁,v₂,· · ·,v_q 2

untukk=1,2,· · ·,q, dan{i2(k),· · ·,iq(k)}merupakan permutasi dari

{1,2,· · ·,q} \ {k}.

Hasil kali dalam antara dua buah proyeksiui,ujbisa ditulis menjadi

proj_Vui,projVuj = hui,projVuVi = q

∑

k=1 αjkhui,vki, (3.20) untuki,j=1,· · ·,p. Universitas Indonesia

Oleh karena itu, diperoleh

proj_Vu₁,proj_Vu₂,· · ·,proj_Vu_p 2 = ∑q_k=1α1khu1,vki · · · ∑q_k=1αpkhu1,vki .. . . .. ... ∑q_k=1α1k u_p,v_k · · · ∑q_k=1αpk u_p,v_k = det MM˜ T v1,v2,· · ·,vq 2, (3.21) dengan M:= [hu_i,v_ki] dan ˜ M:=hDui,vk|vi2(k),· · ·,viq(k) Ei ,

untukk=1,2,· · ·,q, dan{i2(k),· · ·,iq(k)}merupakan permutasi dari

{1,2,· · ·,q} \ {k}.

MatriksMdan matriks ˜Msama-sama merupakan matriks berukuran(p×q). Oleh karena itu, hasil kaliMM˜T merupakan matriks berukuran(p×p).

Perhatikan bahwa dengan menggunakan norm-nstandar dan hasil kali dalam-n sederhana, kedua norm berikut bisa ditulis dalam bentuk

v₁,· · ·,v_q 2p = v₁,v₁|v2,· · ·,vq p = Γ v1,· · ·,vq p (3.22) dan u₁,· · ·,u_p 2 = u₁,u₁|u₂,· · ·,u_p = Γ(u1,· · ·,up). (3.23)

Jadi, kita peroleh bahwa persamaan (3.15) dapat ditulis sebagai

cos2θ=

det MM˜T Γ(u1,· · ·,up)Γ v1,· · ·,vq

p, (3.24)

yang merupakan perbaikan formula pada persamaan (3.3) yang dikeluarkan oleh Risteski dan Trecevski, yang dikoreksi oleh Gunawan, Neswan, dan Setya-Budhi.

Selanjutnya, persamaan (3.24) dapat disederhanakan untuk dua kasus, yaitu jika

1. {v1,· · ·,vq}ortonormal

30

2. {v1,· · ·,vq}dan{u1,· · ·,up}ortonormal.

Kasus 1

Jika{v1,· · ·,vq}ortonormal, makaΓ v1,· · ·,vq

=1. Kemudian, untuk setiap i=1,· · ·,p, proyeksi dariu_ipadaV dapat ditulis sebagai kombinasi dari

vektor-vektorv₁,· · ·,v_q, yaitu proj_Vu_i= q

∑

k=1 hui,vkivk.

Oleh karena itu, hasil kali dalam dari proyeksi-proyeksu_idanu_jpadaV bisa ditulis sebagai proj_Vu_i,proj_Vu_j= q

∑

k=1 hui,vki u_j,v_k, untuk setiapi,j=1,· · ·,p.

Karenanya kita peroleh dengan norm-nstandar bahwa

proj_Vu₁,proj_Vu₂,· · ·,proj_Vu_p 2 = ∑q_k=1hu1,vki hu1,vki · · · ∑q_k=1hu1,vki u_p,v_k .. . . .. ... ∑q_k=1up,vk hu1,vki · · · ∑q_k=1up,vk up,vk = det MM˜T, (3.25) dengan M:= [hui,vki]. Sehingga, kita peroleh formula

cos2θ=

det MM˜T Γ(u1,· · ·,up)

. (3.26)

Kasus 2

Melanjutkan dari Kasus 1, jika{u1,· · ·,up}juga ortonormal, maka

Γ(u1,· · ·,up) =1, sehingga dapat disimpulkan

cos2θ=det MMT. (3.27)

3.5 Sudut-Sudut Kanonik

Salah satu aplikasi dari sudut antara dua subruang adalah pada bidang statistik. Sudut-sudut kanonik antara dua subruang erat berhubungan dengan ketergantungan

dua kovariansi dari salah satu peubah acak pada peubah acak lainnya.

Selain itu, sudut-sudut kanonik juga digunakan dalam bidang komputasi. Salah satunya adalah untuk mengukur kesamaan citra dari benda-benda 3D yang invarian terhadap rotasi kamera dan perpindahan benda. Yosuke Igarashi dan Kazuhiro Fukui (2010) mengusulkan metode dengan menggunakan sudut-sudut kanonik efektif untuk pengenalan foto-foto wajah.

Adapun definisi dari sudut-sudut kanonik adalah sebagai berikut.

Definisi 3.4. Misalkan U adalah subruang berdimensi-p dan V adalah subruang berdimensi-q dari_Rn, dengan1≤p≤q≤n. Sudut-sudut kanonik di antara U dan V adalahθi, i∈ {1,2,· · ·,p}, yang memenuhi

0≤θ1≤θ2≤ · · · ≤θp≤ π 2 (3.28) dan cosθi = hui,vii kuik kvik (3.29) = max ( hu,vi kuk kvk: u∈U, u⊥uk, v∈V, v⊥vk, k=1,· · ·,i−1 ) , (3.30)

dengan(u_i,v_i)∈U×V , untuk i=1,· · ·,p. Pasangan-pasangan vektor(u_i,v_i)

tersebut disebut pasangan vektor-vektor kanonik.

Adapun langkah-langkah untuk mencarinya adalah sebagai berikut:

1. Langkah pertama kita cari terlebih dahulu vektor-vektor satuanu1∈U1=U danv1∈V1=V yang membuat sudut terkecil (nilai kosinus terbesar) di antaraU₁danV₁. Sudut ini adalahθ1.

2. Kemudian, tentukan komplemen ortogonal dariu₁padaU₁dan komplemen ortogonal dariv₁padaV₁. MisalkanU₂=u⊥₁ ∩U₁danV₂=v⊥₁ ∩V1.

Kemudian cari vektor-vektor satuanu₂∈U₂danv₂∈V₂yang membuat sudut terkecil di antaraU2danV2. Sudut ini adalahθ2.

3. Dan selanjutnya, iterasi ini dilakukan sampaiθp.

Banyak peneliti yang hanya menggunakanθ1untuk estimasi. Namun secara geometris,θ1bukanlah suatu ukuran aproksimasi yang baik. Risteski and Trencevski (2001) menyebutkan bahwa jika kita mengalikan nilai-nilai kosinus dari sudut-sudut kanonik, kita akan memperoleh kosinus dari sudut yang bisa

32

dianggap sebagai sudut ”geometris” antara kedua subruang yang diberikan. Selengkapnya tentang hubungan keduanya bisa dilihat pada teorema berikut. Teorema 3.3. Misalkan U adalah subruang berdimensi-p dan V adalah subruang berdimensi-q dari ruang hasil kali dalam_Rn, dengan1≤p≤q<∞. Misalkan pula{u1,· · ·,up}merupakan basis ortonormal dari U dan{v1,· · ·,vq}merupakan

basis ortonormal dari V . Maka berlaku cosθ=

p

∏

i=1

cosθi, (3.31)

denganθadalah sudut di antara U dan V , sedangkanθi, i=1,· · ·,p, adalah

sudut-sudut kanonik antara U dan V .

Bukti. Perhatikan bahwa karena{u1,· · ·,up}dan{v1,· · ·,vq}orthonormal, maka kita bisa gunakan persamaan (3.27), yaitu

cos2θ=det(MMT), dengan

M=u_i,v_j, untuki=1,· · ·,pdan j=1,· · ·,q.

Lebih lanjut, perkalian matriksM dan matriks transposenyaMT menghasilkan matriks yang terdiagonalkan. Oleh karena itu, nilai dari det(MMT)sama dengan hasil kali dari nilai-nilai eigennya. MatriksMMT mempunyai pbuah nilai eigen. Misalkan nilai-nilai eigen tersebut adalahλ1≥ · · · ≥λp≥0. Klaim bahwa semua kuadrat dari kosinus dari sudut-sudut kanonik di antaraU danV merupakan nilai-nilai eigen dariMMT,

λi=cos2θi, (3.32)

untuki=1,· · ·,p.

Misalkan f(u):=max_v∈V,kvk=1hu,vi. Untuk setiapu∈_Rn_{, nilaihu,viterbesar} diperoleh pada hasil proyeksiupadaV, yaituv=proj_Vu. Sehingga untuk setiap u∈U, dengankuk=1,

f(u) = max

v∈V,kvk=1hu,vi=kprojVuk, (3.33) yang diperoleh ketikav= projVu

kproj_Vuk.

Misalkang= f2, maka g(u):= max v∈V,kvk=1 hu,vi 2 =kproj_Vuk2, (3.34) untuk setiapu∈U dengankuk=1. Lebih lanjut, nilai-nilai kritis darig

merupakan kuadrat dari nilai-nilai kritis dari f, yaitu cos2θi,i=1,· · ·,p.

Sekarang, tulisusebagai kombinasi linear dariu₁,· · ·,u_p, yaituu=∑_ip₌₁βiui. Sehingga diperoleh kproj_Vuk = q

∑

k=1 hu,v_kiv_k = q

∑

k=1 * _p

∑

i=1 βiui,vk + v_k = q

∑

k=1 p

∑

i=1 βihui,vkivk. (3.35) Dengan memandanggsebagai fungsi dariβ1,· · ·,βp, maka didapat nilai fungsigadalah g(β1,· · ·,βp) = kprojVuk 2 = q

∑

k=1 p

∑

i=1 βihui,vkivk 2 = q

∑

k=1 p

∑

i=1 βihui,vki !2 (3.36) dengan∑_ip₌₁β2_i =1.

Lebih lanjut, karenaM= [hu_i,v_ki], maka dapat ditulis g(t) =tTMMTt =MTt

2

q, (3.37)

dengant= [t₁,· · ·,t_p]T ∈_Rp_danktk

p=1. Di sinik·kmenyatakan norm standar di_Rp.

Berikutnya untuk mencari nilai kritisg, kita misalkan fungsi h_λ(t) =MTt

2

q+λ

1− ktk2_p (3.38)

untukt∈_Rp_{denganλadalah pengali Lagrange.}

34

Perhatikan bahwa titik kritist0diperoleh ketika

∇h_λ(t0) =0. (3.39)

Oleh karena itu diperoleh

∇h_λ(t₀) = 0 2MMTt₀−2λt₀ = 0 MMTt0 = λt0 t₀TMMTt₀ = t₀Tλt₀ g(t₀) = λt₀Tt₀ g(t0) = λkt0k g(t₀) = λ. (3.40)

Artinya, setiap pengali Lagrangeλmerupakan nilai kritis darig. Karena itu, sudah dibuktikan bahwa

λi=cos2θi, (3.41)

untuki=1,· · ·,p.

Jadi, dapat disimpulkan bahwa

cos2θ=det(MMT) = p

∏

i=1 λi= p

∏

i=1 cos2θi, (3.42)

atau dengan perkataan lain

cosθ= p

∏

i=1 cosθi. (3.43) Universitas Indonesia

Kesimpulan dan Saran

Formula untuk menghitung sudut antara dua subruang,U =span{u1,· · ·,up}dan

V =span{v1,· · ·,vq}dengan p≤q, dari suatu ruang hasil kali dalam-nsederhana

X adalah

cos2θ=

proj_Vu₁,proj_Vu₂,· · ·,proj_Vu_p 2 u1,u2,· · ·,up 2 ,

yang dikemukakan oleh Gunawan, Neswan, dan Setya-Budhi (2005). Secara geometris, kosinus dari sudut tersebut merupakan perbandingan antara volume paralelotop berdimensi-pyang dibangun oleh proj_Vu_iterhadap volume paralelotop berdimensi-pyang dibangun olehu_i, dengani=1,· · ·,p. Jika{u1,· · ·,up}dan

{v1,· · ·,vq}ortonormal, formula tersebut juga bisa ditulis dalam bentuk cos2θ= det(M

˜ MT)

Γ(u1,· · ·,up)Γ(v1,· · ·,vq) ,

yang merupakan perbaikan dari formula yang dikemukakan oleh Risteski dan Trenchevski (2001).

Selama ini, dalam aplikasi di bidang statistika dan komputasi, untuk mendeskripsikan sudut antara dua subruang digunakan sudut-sudut kanonik. Contohnya dalam statistika, sudut-sudut kanonik digunakan untuk menentukan ketergantungan dan kovariansi dari salah satu peubah acak pada peubah acak lainnya. Sedangkan contohnya dalam komputasi, sudut-sudut kanonik digunakan untuk mengukur kesamaan citra dari benda-benda 3D yang invarian terhadap rotasi kamera dan perpindahan benda.

Telah dibuktikan bahwa formula kosinus sudut antara dua subruang merupakan hasil kali dari semua nilai kosinus sudut-sudut kanonik,

cosθ=

p

∏

i=1

cosθi.

Sebagai saran, formula kosinus sudut antara dua subruang (3.15) ini dapat diteliti lebih lanjut agar dapat digunakan sebagai pengganti sudut-sudut kanonik dalam aplikasinya.

DAFTAR REFERENSI

[1] Courant, R. dan John, F. (1989).Introduction to Calculus and AnalysisII/I. New York: Springer-Verlag.

[2] Freese, R.W. dan Cho, YJ. (2001).Geometry of Linear 2-Normed Spaces. New York: Nova.

[3] Gunawan, H. (2002).Inner Products On n-Inner Product Spaces.Soochow Journal of Mathematics. 28, 4, 389-398.

[4] Gunawan, H., Neswan, O., dan Setya-Budhi, W. (2005).A Formula For Angles Between Two Subspaces Of Inner Product Spaces.Beitrage zur Algebra and Geometrie. 46, 2, 311-320.

[5] Igarashi, Y. dan Fukui, K.3D Object Recognition Based On Canonical Angles Between Shape Subspaces. (2010). ACCV’10 Volume Part IV. 580-591. [6] Jones, F. ”Volumes of Parallelograms”. www.owlnet.rice.edu/fjones/chap8.pdf

(05 Mar. 2012, Pukul 13:13 WIB.)

[7] Kreyzig, E. (1978).Introductory Functional Analysis with Applications. Canada. John Wiley & Sons, Inc.

[8] Misiak, A. (1989).n-Inner Product Spaces.Math. Nachr.. 140, 299-319. [9] Misiak, A. dan Ryz, A. (2000).n-Inner Product Spaces And Projections.

Mathematica Bohemica. 125, 1, 87-97.

[10] Risteski, I. B. dan Trencevski, K. G. (2001).Principal Values And Principal Subspaces Of Two Subspaces Of Vector Spaces With Inner Product.Beitr. Algebra Geom. 42, 289-300.

[11] Roman, S. (2008).Advanced Linear Algebra, 3rd Edition. New York: Springer.