PENYELESAIAN NUMERIK MODEL BLACK-SCHOLES
MENGGUNAKAN METODE BEDA HINGGA UPWIND
IRFAN NUR AFFANDI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2014
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*
Dengan ini saya menyatakan bahwa skripsi berjudul Penyelesaian Numerik Model Black-Scholes Menggunakan Metode Beda Hingga Upwind adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, November 2014
Irfan Nur Affandi
ABSTRAK
IRFAN NUR AFFANDI. Penyelesaian Numerik Model Black-Scholes Menggunakan Metode Beda Hingga Upwind. Dibimbing oleh DONNY CITRA LESMANA dan RUHIYAT.
Produk derivatif adalah instrumen keuangan yang nilainya bergantung pada nilai aset. Salah satu produk derivatif yang diperdagangkan dalam pasar keuangan adalah opsi. Opsi merupakan suatu kontrak antara dua pihak, yaitu pembeli dan penjual yang memberikan hak untuk membeli atau menjual suatu aset tertentu dengan harga dan waktu yang ditentukan. Berdasarkan waktu eksekusinya, opsi dibagi menjadi opsi tipe Eropa dan opsi tipe Amerika. Model yang digunakan untuk menentukan harga opsi tipe Eropa adalah model Black-Scholes yang merupakan persamaan diferensial parsial dengan nilai awal dan syarat batasnya bergantung pada jenis opsinya. Model ini dapat diselesaikan secara numerik dengan menggunakan metode beda hingga. Pada karya ilmiah ini, metode yang akan digunakan adalah metode implisit pada diskretisasi waktu dan metode beda hingga upwind pada diskretisasi ruang. Contoh numerik juga diberikan untuk menunjukkan kekonvergenan metode ini.
Kata kunci: metode beda hingga, model Black-Scholes, opsi
ABSTRACT
IRFAN NUR AFFANDI. Numerical Solution of the Black-Scholes Model Using Upwind Finite Difference Methods. Supervised by DONNY CITRA LESMANA and RUHIYAT.
Derivative product is a financial instrument in which the value was based on certain asset value which is called the underlying asset. One of derivative products traded in the financial market is called option, which is a contract between two parties, the buyer and the seller, in which the parties give a right to buy or sell the underlying asset by a certain price within a certain time frame. Based on the execution time, the time options are divided into two types, the European option and the American option. Models that are used to determine the European option price is called Black-Scholes model. The model is in the form of a partial differential equation with initial and boundary conditions depend on the type of options either call option or put option. This model can be solved numerically using the finite difference method. In this paper, we use implicit method for time stepping and an upwind finite difference method for spatial discretization. Numerical examples are also provided to show the convergence of this method.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
PENYELESAIAN NUMERIK MODEL BLACK-SCHOLES
MENGGUNAKAN METODE BEDA HINGGA UPWIND
IRFAN NUR AFFANDI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2014
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah Subhanahu Wa Ta’ala atas segala karunia-Nya sehingga karya ilmiah yang berjudul Penyelesaian Numerik Model Black-Scholes Menggunakan Metode Beda Hingga Upwind berhasil diselesaikan.
Penulis mengucapkan terima kasih kepada:
1 ayah, ibu, serta seluruh keluarga yang telah memberikan doa, nasehat, dan kasih sayangnya,
2 Dr Donny Citra Lesmana, SSi MFinMath selaku Dosen Pembimbing I dan Ruhiyat, MSi selaku Dosen Pembimbing II yang telah sabar memberikan bimbingan, saran, dan kritik sehingga karya ilmiah ini dapat diselesaikan dengan baik,
3 Dr Berlian Setiawaty, MS selaku moderator dalam seminar dan Dosen Penguji yang telah banyak memberi sarannya,
4 seluruh dosen dan staf Departemen Matematika atas segala ilmu dan bantuan yang diberikan selama perkuliahan,
5 teman-teman Matematika angkatan 47 yang telah membantu dalam kegiatan belajar selama perkuliahan,
6 teman-teman Wisma Uganda (Ayub, Muhjidin, Adit, Nur Fatah, Trias, Danang) yang senantiasa menjadi tempat berbagi,
7 teman-teman OMDA Sragen yang telah menemani perjalanan penulis selama perkuliahan,
8 seluruh mahasiswa matematika Angkatan 46, 48, dan 49 Departemen Matematika IPB yang telah menemani perjalanan penulis selama perkuliahan.
Semoga karya ilmiah ini bermanfaat.
Bogor, November 2014
DAFTAR ISI DAFTAR TABEL vi DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi PENDAHULUAN 1 Latar Belakang 1 Tujuan Penelitian 2 TINJAUAN PUSTAKA 2
Definisi, Jenis, dan Nilai Opsi 2
Barisan 5
Model Black-Scholes 6
Metode Beda Hingga 9
Metode Implisit dan Metode Beda Hingga Upwind 10
Tridiagonal Solver 12
HASIL DAN PEMBAHASAN 12
Menentukan Model Black-Scholes 13
Syarat Awal dan Syarat Batas 13
Diskretisasi 14
Simulasi Numerik 17
SIMPULAN DAN SARAN 26
Simpulan 26 Saran 27 DAFTAR PUSTAKA 27 LAMPIRAN 28 RIWAYAT HIDUP 31
DAFTAR TABEL
1 Hasil perhitungan orde kekonvergenan dari opsi call tipe Eropa 19 2 Hasil perhitungan orde kekonvergenan dari opsi put tipe Eropa 21 3 Hasil perhitungan orde kekonvergenan dari opsi Butterfly 23 4 Hasil perhitungan orde kekonvergenan dari opsi Cash or
Nothing (CoN) 25
DAFTAR GAMBAR
1 Payoff untuk opsi call dengan = 40 pada = 3
2 Payoff untuk opsi put dengan = 40 pada = 3
3 Payoff untuk opsi butterfly dengan = 20, = 40, dan = 60 4 4 Payoff untuk opsi cash or nothing dengan = 40 dan = 1 pada
= 4
5 Harga dari opsi call tipe Eropa 17
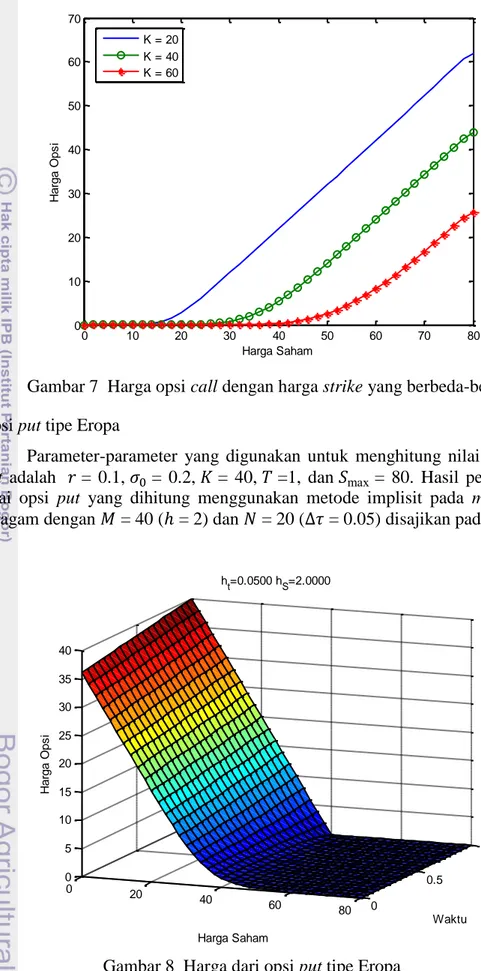
6 Harga opsi call untuk nilai volatilitas yang berbeda-beda 19 7 Harga opsi call dengan harga strike yang berbeda-beda 20
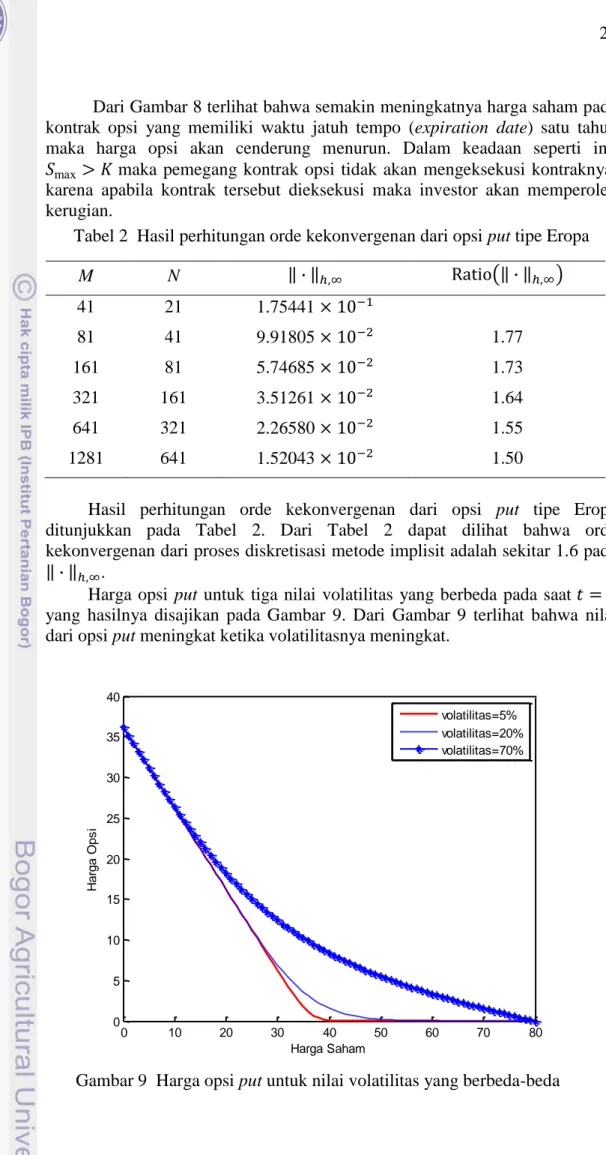
8 Harga dari opsi put tipe Eropa 20
9 Harga opsi put untuk nilai volatilitas yang berbeda-beda 21 10 Harga opsi put dengan harga strike yang berbeda-beda 22
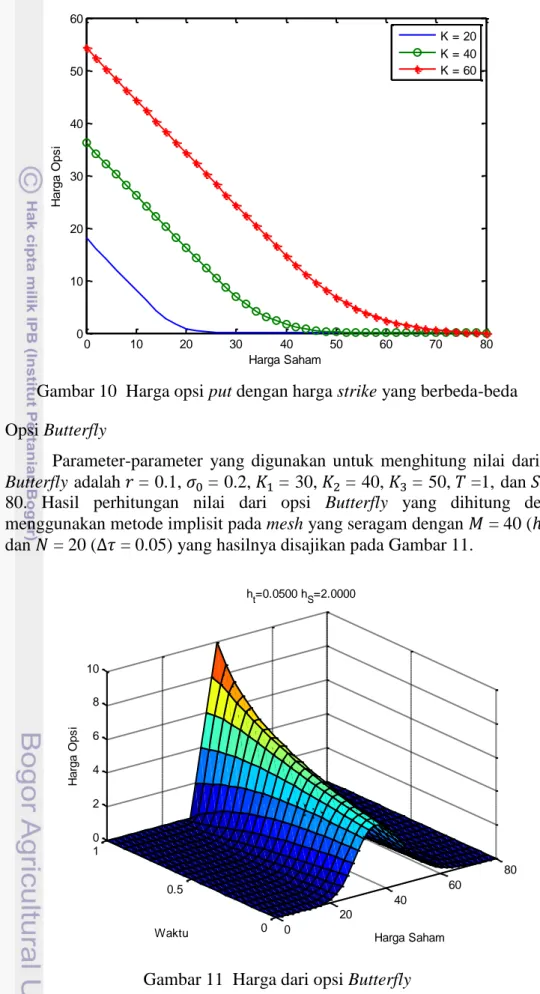
11 Harga dari opsi Butterfly 22
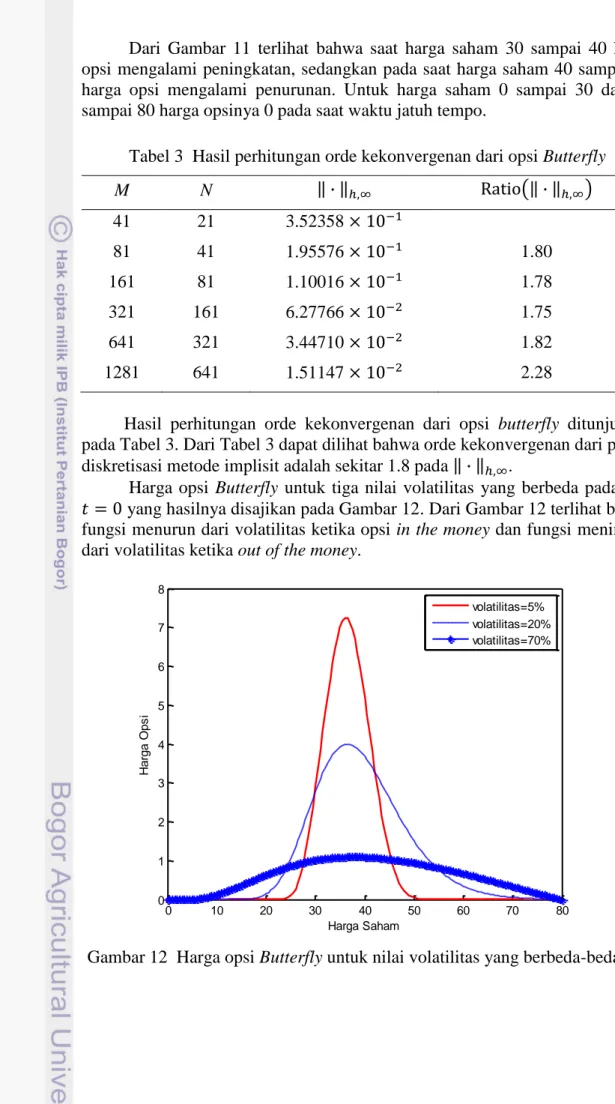
12 Harga opsi Butterfly untuk nilai volatilitas yang berbeda-beda 23 13 Harga opsi Butterfly dengan harga strike yang berbeda-beda 24
14 Harga dari opsi Cash or Nothing (CoN) 24
15 Harga opsi Cash or Nothing (CoN) untuk nilai volatilitas yang
berbeda-beda 25
16 Harga opsi Cash or Nothing (CoN) dengan harga strike yang
berbeda-beda 26
DAFTAR LAMPIRAN
1 Pembuktian persamaan (5) 28
PENDAHULUAN
Latar BelakangSekarang ini minat seseorang terhadap suatu saham atau investasi dalam dunia keuangan semakin berkembang pesat, sehingga semakin banyak orang yang menggunakan produk derivatif. Produk derivatif merupakan instrumen keuangan yang nilainya bergantung pada nilai aset yang mendasarinya (underlying asset). Produk derivatif dapat digunakan untuk mengelola risiko dan spekulasi, serta meminimumkan kerugian yang disebabkan oleh fluktuasi harga dari underlying
asset. Salah satu produk derivatif yang diperdagangkan dalam pasar keuangan
adalah opsi.
Opsi adalah suatu kontrak antara dua pihak, yaitu pembeli dan penjual, yang memberikan hak untuk membeli atau menjual suatu aset tertentu dengan harga yang telah ditentukan, pada atau sebelum waktu yang ditentukan. Harga di mana aset tersebut dapat dibeli atau dijual disebut dengan harga exercise atau harga
strike, sedangkan waktu ketika kontrak berakhir dikenal sebagai expiration date
atau waktu jatuh tempo.
Pada dunia keuangan, opsi dibagi menjadi dua jenis, yaitu opsi call dan opsi
put. Berdasarkan waktu penggunaannya, opsi dikelompokkan menjadi dua, yaitu
opsi tipe Amerika (American option) dan opsi tipe Eropa (European option). Bursa perdagangan opsi saham yang paling besar di dunia untuk produk derivatif yaitu CBOE (Chicago Board Options Exchanges) yang mulai menjual opsi dari 16 saham, dan sekarang CBOE telah menjual opsi lebih dari 1200 saham.
Metode penentuan harga opsi secara umum dapat dilakukan dengan dua metode yaitu metode analitik dan metode numerik. Metode analitik merupakan suatu metode penentuan harga opsi yang menghasilkan nilai yang eksak, sedangkan metode numerik merupakan metode penentuan harga opsi yang menghasilkan nilai aproksimasi sehingga pada metode numerik mungkin akan terdapat error di dalamnya. Pada tahun 1973 dua orang ahli keuangan Fisher Black dan Myron Scholes berhasil mengembangkan model yang dikenal sebagai model Black-Scholes. Model Black-Scholes ini penggunaannya terbatas karena hanya dapat digunakan untuk menentukan harga opsi tipe Eropa saja, sedangkan model ini tidak berlaku untuk opsi tipe Amerika. Salah satu metode numerik yang digunakan untuk menentukan harga opsi adalah metode beda hingga.
Metode beda hingga adalah suatu metode numerik yang digunakan untuk menyelesaikan persamaan diferensial dengan mengaproksimasi turunan-turunan persamaan tersebut menjadi sistem persamaan linear. Secara umum, metode beda hingga yang digunakan antara lain metode eksplisit, metode implisit, metode Crank-Nicholson, metode beda hingga upwind (upwind finite difference method), dan metode volume hingga (finite volume method). Metode yang akan digunakan untuk menyelesaikan model Black-Scholes secara numerik dalam penelitian ini adalah metode implisit pada diskretisasi waktu dan metode beda hingga upwind pada diskretisasi ruang. Pada penelitian ini juga akan digunakan metode faktorisasi Crout untuk menyelesaikan matriks sistem yang berbentuk matriks tridiagonal.
2
Tujuan Penelitian
Tujuan dari penelitian ini adalah:
1 Menyelesaikan persamaan harga opsi Black-Scholes menggunakan metode implisit untuk diskretisasi waktu dan metode beda hingga upwind untuk diskretisasi ruang.
2 Mencari orde kekonvergenan pada metode beda hingga upwind.
TINJAUAN PUSTAKA
Definisi, Jenis, dan Nilai Opsi Definisi 1 (Opsi)Instrumen derivatif adalah kontrak yang nilainya ditentukan oleh satu atau lebih aset yang mendasari (underlying asset). Salah satu instrumen derivatif yang berpotensi untuk dikembangkan adalah opsi. Opsi adalah suatu kontrak antara dua pihak yang memberikan hak untuk membeli atau menjual suatu aset tertentu dengan harga yang telah ditentukan pada waktu yang telah ditentukan (Hull 2009).
Definisi 2 (Underlying Asset)
Aset yang mendasari (underlying asset) adalah aset yang dijadikan sebagai objek atau dasar transaksi.Dalam perdagangan opsi terdapat beberapa underlying asset, antara lain saham (stock), valuta asing (foreign currency), berjangka (future), dan indeks (index). Dalam karya ilmiah ini, underlying asset yang digunakan adalah saham.
Definisi 3 (Jenis Opsi)
Menurut jenisnya opsi terbagi menjadi dua, yaitu opsi call dan opsi put. Opsi call adalah opsi yang memberikan hak kepada pemegang opsi untuk membeli suatu aset tertentu dengan jumlah tertentu pada harga dan jangka waktu tertentu. Opsi
put adalah opsi yang memberikan hak kepada pemegang opsi untuk menjual suatu
aset tertentu dengan jumlah tertentu pada harga dan jangka waktu tertentu.
Hull (2009) menyatakan bahwa strategi trading yang melibatkan dua atau lebih opsi yang sama jenisnya disebut spread. Salah satu strategi spread adalah
butterfly spread. Butterfly spread adalah strategi yang melibatkan 3 buah opsi
dengan harga strike yang berbeda-beda. Strategi ini melibatkan pembelian opsi
call dengan harga strike , pembelian opsi call dengan harga strike yang lebih tinggi dan penjualan dua opsi call dengan harga strike yang merupakan nilai tengah dari dan . Strategi ini dipilih jika investor melihat bahwa harga saham tidak dapat diperkirakan arah kenaikan atau penurunannya.
Payoff adalah imbalan yang diperoleh pada saat opsi jatuh tempo atau pada
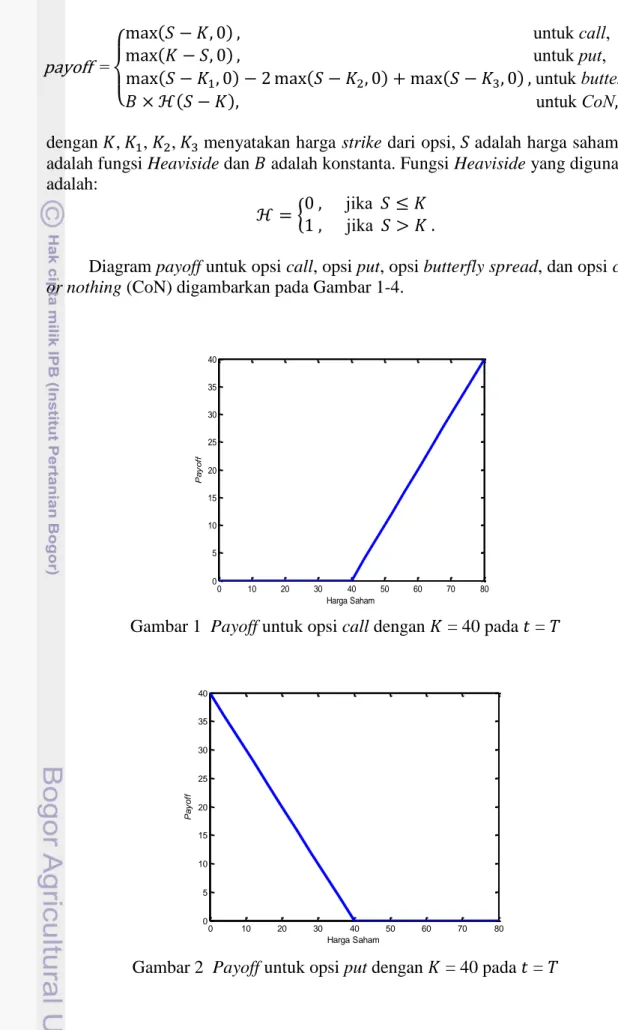
saat opsi dieksekusi. Payoff untuk opsi call, opsi put, opsi butterfly spread, dan opsi cash or nothing (CoN) pada waktu jatuh tempo adalah sebagai berikut:
{ ( ) all ( ) ( ) ( ) ( ) l ( ) dengan , , , menyatakan harga strike dari opsi, adalah harga saham, adalah fungsi Heaviside dan adalah konstanta. Fungsi Heaviside yang digunakan adalah:
{
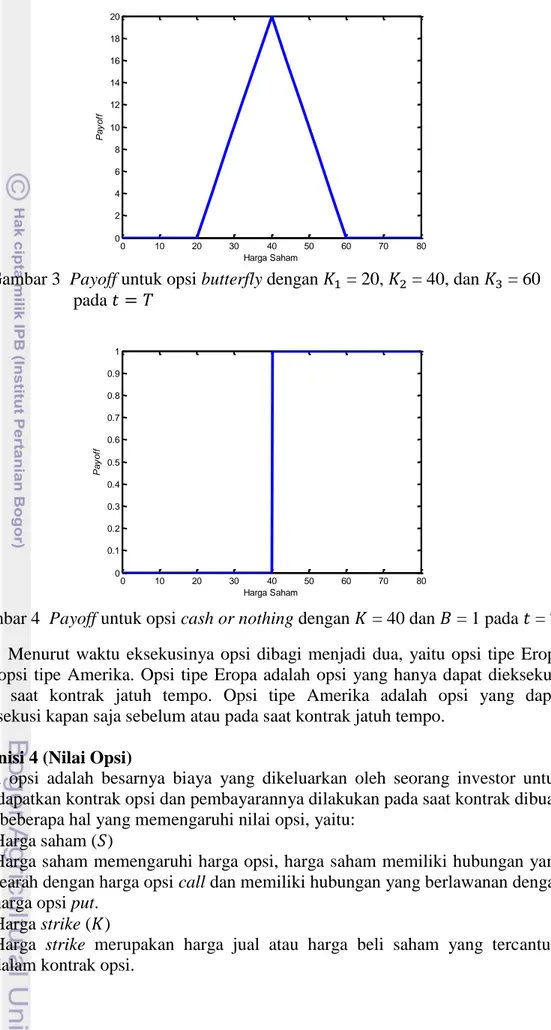
Diagram payoff untuk opsi call, opsi put, opsi butterfly spread, dan opsi cash
or nothing (CoN) digambarkan pada Gambar 1-4.
Gambar 1 Payoff untuk opsi call dengan = 40 pada =
Gambar 2 Payoff untuk opsi put dengan = 40 pada =
0 10 20 30 40 50 60 70 80 0 5 10 15 20 25 30 35 40 Harga Saham P a y o ff 0 10 20 30 40 50 60 70 80 0 5 10 15 20 25 30 35 40 Harga Saham P a y o ff
4
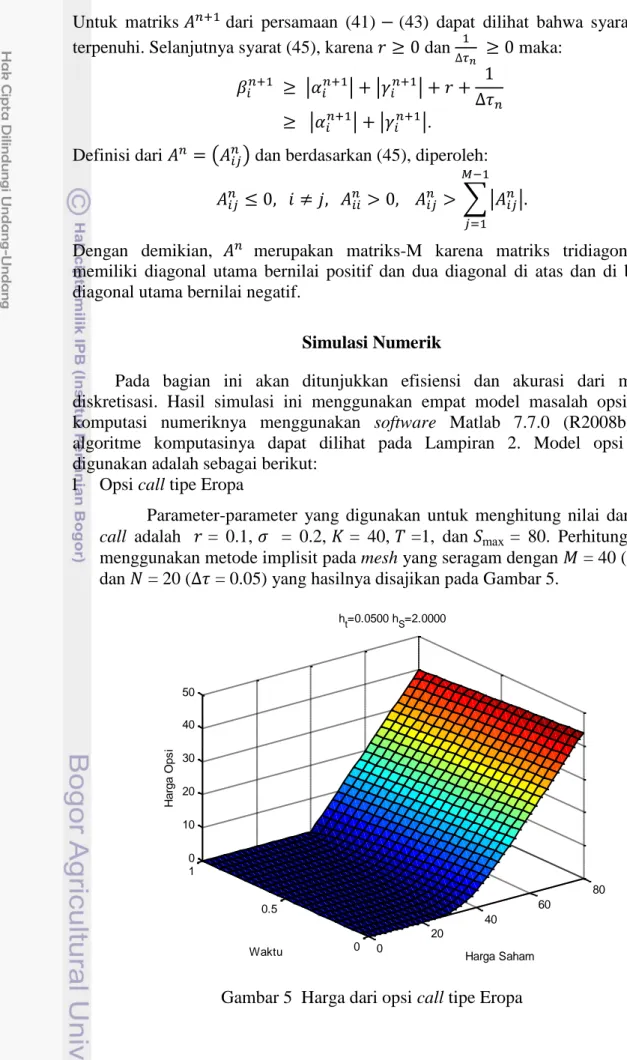
Gambar 3 Payoff untuk opsi butterfly dengan = 20, = 40, dan = 60 pada
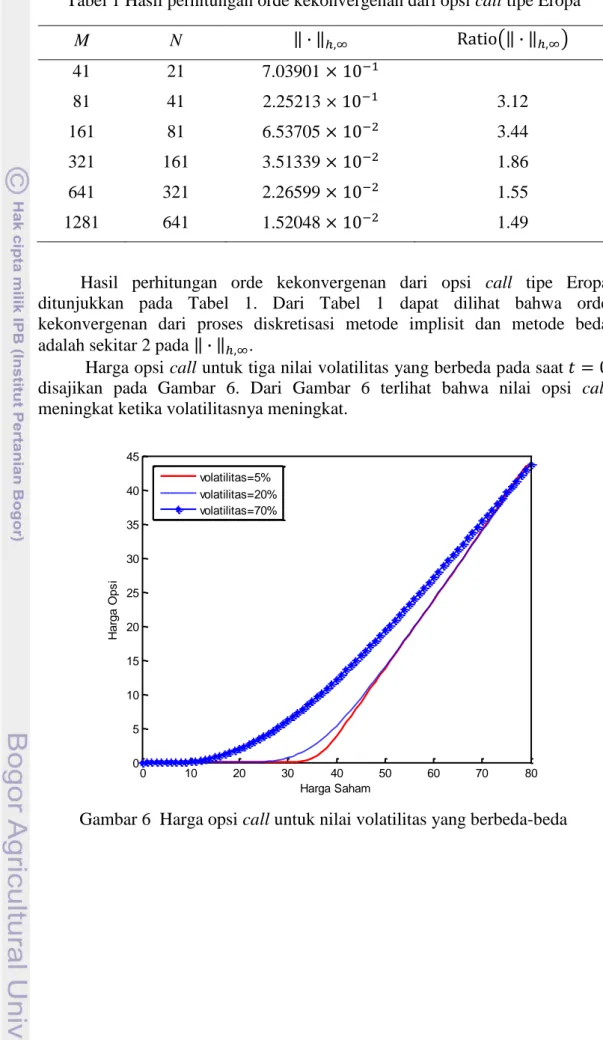
Gambar 4 Payoff untuk opsi cash or nothing dengan = 40 dan = 1 pada = Menurut waktu eksekusinya opsi dibagi menjadi dua, yaitu opsi tipe Eropa dan opsi tipe Amerika. Opsi tipe Eropa adalah opsi yang hanya dapat dieksekusi pada saat kontrak jatuh tempo. Opsi tipe Amerika adalah opsi yang dapat dieksekusi kapan saja sebelum atau pada saat kontrak jatuh tempo.
Definisi 4 (Nilai Opsi)
Nilai opsi adalah besarnya biaya yang dikeluarkan oleh seorang investor untuk mendapatkan kontrak opsi dan pembayarannya dilakukan pada saat kontrak dibuat. Ada beberapa hal yang memengaruhi nilai opsi, yaitu:
1 Harga saham ( )
Harga saham memengaruhi harga opsi, harga saham memiliki hubungan yang searah dengan harga opsi call dan memiliki hubungan yang berlawanan dengan harga opsi put.
2 Harga strike ( )
Harga strike merupakan harga jual atau harga beli saham yang tercantum dalam kontrak opsi.
0 10 20 30 40 50 60 70 80 0 2 4 6 8 10 12 14 16 18 20 Harga Saham P a y o ff 0 10 20 30 40 50 60 70 80 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Harga Saham P a y o ff
3 Waktu jatuh tempo ( )
Pada opsi tipe Amerika, dari kedua macam opsi call maupun opsi put menjadi lebih berharga jika waktu jatuh temponya semakin lama. Opsi tipe Eropa nilai terhadap opsi call maupun opsi put tidak terpengaruh dengan waktu jatuh tempo, hal ini berkenaan dengan waktu eksekusi hak.
4 Volatilitas ( )
Volatilitas merupakan suatu ukuran yang menunjukkan seberapa besar harga berfluktuasi dalam suatu periode (Lo 2003).
Volatilitas atas underlying asset adalah suatu ukuran tingkat ketidakpastian mengenai pergerakan underlying asset tersebut di masa yang akan datang. Jika volatilitas semakin meningkat maka akan semakin meningkat juga peluang undelying asset untuk mengalami peningkatan atau penurunan terhadap suatu opsi.
5 Tingkat suku bunga bebas risiko ( ) 6 Dividen ( )
Dividen merupakan bagian dari keuntungan perusahaan yang dibagikan kepada para pemegang saham.
Ada beberapa istilah dasar yang berhubungan dengan harga saham ( ) dan harga strike ( ):
1 Opsi call
Jika maka opsi call dikatakan dalam keadaan in the money. Pemegang opsi akan mengeksekusi opsi call, yaitu dengan menjual saham dengan harga yang lebih besar dari dan akan mendapatkan hasil sebesar .
Jika , maka opsi call dikatakan dalam keadaan at the money. Jika , maka opsi call dikatakan dalam keadaan out of the money. 2 Opsi put
Jika , maka opsi put dikatakan dalam keadaan out of the money. Jika , maka opsi put dikatakan dalam keadaan at the money. Jika , maka opsi call dikatakan dalam keadaan in the money.
Barisan Definisi 5 (Barisan)
Barisan bilangan real adalah suatu fungsi yang terdefinisi pada himpunan bilangan asli dan memiliki range yang termuat di himpunan bilangan real . Misalkan adalah suatu barisan bilangan real dengan
( ) . Barisan dapat dilambangkan
* + .
Misalkan * + adalah barisan bilangan real. Barisan * + dikatakan memiliki limit untuk menuju takhingga, jika ( ) sehingga | | Barisan * + mempunyai limit ditulis dengan lambang
6
Definisi 6 (Barisan Konvergen)
Jika barisan bilangan * + memiliki limit , maka barisan * + dikatakan konvergen ke .
Model Black-Scholes
Model Black-Scholes merupakan suatu model yang digunakan untuk menentukan nilai opsi yang telah banyak digunakan di dunia keuangan, model ini dikembangkan oleh Fischer Black dan Myron Scholes pada tahun 1973. Penggunaan model Black-Scholes terbatas karena model ini hanya dapat digunakan pada penentuan nilai opsi tipe Eropa yang dijalankan pada waktu jatuh tempo (expiration date), sedangkan model ini tidak berlaku untuk opsi tipe Amerika karena opsi tipe Amerika dapat dijalankan setiap saat sampai waktu jatuh tempo (expiration date).
Ada beberapa asumsi untuk merumuskan nilai opsi yang dikembangkan oleh Fisher Black dan Myron Scholes:
1 Sebaran harga saham adalah lognormal dan ragam dari return pada saham adalah konstan.
2 Tidak ada biaya transaksi dan pajak.
3 Tipe opsi yang digunakan adalah tipe opsi Eropa.
4 Tidak ada kemungkinan arbitrase. Arbitrase adalah tindakan membeli sekuritas yang berharga rendah di suatu pasar dan pada saat yang sama menjualnya dengan harga yang lebih tinggi di pasar yang berbeda sehingga memperoleh keuntungan tanpa risiko.
5 Tingkat suku bunga bebas risiko jangka pendek diketahui dan nilainya konstan. 6 Perdagangan dari aset yang mendasari bersifat kontinu.
7 Penjualan pendek (short selling) diizinkan.
Beberapa definisi atau istilah-istilah yang digunakan untuk memodelkan model Black-Scholes:
Definisi 7 (Proses Stokastik)
Proses stokastik * ( ) + adalah suatu himpunan dari peubah acak dengan himpunan indeks , dengan adalah waktu dan ( ) adalah suatu peubah acak (Niwiga 2005).
Definisi 8 (Gerak Brown)
Proses stokastik * ( ) + disebut gerak Brown jika: 1 ( ) ,
2 Untuk peubah acak ( ) ( ) saling bebas, serta
3 Untuk ( ) menyebar normal dengan rataan 0 dan ragam
Definisi 9 (Proses Wiener)
Proses Wiener adalah suatu proses stokastik * ( ) + yang memenuhi kondisi berikut:
1 ( ) ,
2 Untuk interval , ( ) ( ) menyebar normal ( ) dengan rataan 0 dan ragam ( ),
3 Kenaikan ( ) ( ) , ( ) ( ) … ( ) ( ) dalam interval adalah saling bebas
(Ermogenous 2005).
Proses Wiener umum untuk suatu peubah acak dapat dinyatakan sebagai berikut:
( ) ( )
dengan disebut komponen deterministik dan ( ) disebut komponen stokastik, serta ( ) adalah proses Wiener, sedangkan dan masing-masing menyatakan rataan dan simpangan baku dari (Hull 2009).
Definisi 10 (Proses Itô)
Proses Itô adalah proses Wiener umum dengan dan menyatakan suatu fungsi dari peubah acak dan pada waktu . Proses Itô dapat dinyatakan sebagai berikut: ( ) ( ( ) ) ( ( ) ) ( ) (1) (Hull 2009).
Teorema 1 (Lemma Itô)
Misalkan proses ( ) memenuhi persamaan (1) dan fungsi ( ) ( ( ) ) adalah kontinu, maka ( ) ( ( ) ) memenuhi persamaan berikut:
( ) ( ) ( ) ( ) ( ) , (2) dan
( ) ( ) ( ) , ( ( )) .
Dengan menyubstitusikan persamaan (1) ke persamaan (2) didapat:
( ) ( ( ) ( ) ( ) ) ( ) ( ). (3)
Persamaan (3) merupakan Lemma Itô (Niwiga 2005).
Definisi 11 (Model Harga Saham)
Harga saham yang berubah secara acak menurut waktu diasumsikan sebagai suatu proses stokastik. Selain itu diasumsikan tidak ada pembayaran dividen atas saham.
8
Misalkan ( ) adalah harga saham pada waktu . Mengingat proses Itô, perubahan ( ) akan memiliki nilai harapan drift rate . Parameter menyatakan tingkat rata-rata pertumbuhan harga saham dan ( ) disebut komponen deterministik. Karena harga saham juga dipengaruhi oleh faktor ketidakpastian maka komponen stokastiknya adalah ( ) ( ) dengan menyatakan volatilitas harga saham. Volatilitas harga saham mengindikasikan tingkat risiko dari harga saham. Dengan demikian model dari harga saham dapat dinyatakan sebagai berikut:
( ) ( ) ( ) ( ). (4) Dengan persamaan (4) ini, dapat diterapkan Lemma Itô untuk suatu fungsi ( ), yaitu nilai opsi dengan harga saham pada waktu , sehingga diperoleh:
( ( ) ( )
) ( )
( ). (5)
Bukti dapat dilihat pada Lampiran 1.
Untuk menghilangkan proses Wiener dipilih sebuah portofolio yang diinvestasikan pada saham dan derivatif. Strategi yang dipilih adalah membeli satu opsi dan menjual . Misalkan adalah nilai portofolio yang dimaksud, maka
. (6)
Perubahan nilai portofolio pada selang waktu didefinisikan sebagai:
. (7)
Dengan menyubstitusikan persamaan (4) dan (5) ke persamaan (7) didapat: (
) . (8)
Return dari investasi sebesar pada saham tak berisiko akan memiliki
pertumbuhan sebesar dalam selang waktu , di mana adalah suku bunga bebas risiko. Agar tidak terdapat peluang arbitrase, nilai pertumbuhan ini harus sama dengan ruas kanan dari persamaan (8):
(
) . (9)
Dengan menyubstitusikan persamaan (6) ke persamaan (9) didapat:
. (10)
Metode Beda Hingga
Salah satu metode numerik yang digunakan untuk menyelesaikan persamaan diferensial adalah metode beda hingga. Metode beda hingga adalah suatu metode numerik yang digunakan untuk menyelesaikan persamaan diferensial dengan mengaproksimasi turunan-turunannya, seperti turunan terhadap waktu dan turunan terhadap ruang. Pada umumnya, metode beda hingga digunakan untuk menyelesaikan secara numerik model Black-Scholes. Metode beda hingga yang digunakan antara lain metode eksplisit, metode implisit, metode Crank-Nicholson, metode beda hingga upwind (upwind finite difference method), dan metode volume hingga (finite volume method). Ada beberapa hal yang perlu diperhatikan untuk menerapkan metode beda hingga pada suatu permasalahan persamaan diferensial, yaitu sebagai berikut:
1 Diskretisasi
Misalkan ( ) menyatakan nilai opsi maka model Black-Scholes ditulis:
( ) ( ) ( ) ( ) .
Bidang ( ) dipartisi menjadi mesh, dan panjang untuk subinterval di antara
mesh adalah dan . Kemudian pada dibagi menjadi titik, yaitu
. Titik-titik tersebut untuk mendiskretkan turunan terhadap waktu dengan dan . Misalkan dipartisi menjadi titik, yaitu . Titik-titik tersebut untuk mendiskretkan turunan terhadap harga saham , dengan dan . Dengan demikian, pada bidang ( ) terdapat ( ) ( ) mesh. Selanjutnya, nilai dari opsi pada waktu ketika harga saham dinyatakan oleh:
( ) dengan dan . 2 Aproksimasi
Aproksimasi diperoleh dari ekspansi deret Taylor. Misalkan ekspansi deret Taylor untuk ( ) dan ( ) adalah sebagai berikut:
( ) ( ) ( ) (11) ( ) ( ) ( ) . (12) Menggunakan persamaan (11) diperoleh persamaan beda maju, yaitu:
( ) ( ) ( ) . (13)
10
Menggunakan persamaan (12) diperoleh persamaan beda mundur, yaitu:
. (14)
Hasil pengurangan persamaan (12) dari (11) diperoleh persamaan beda pusat, yaitu:
. (15)
Aproksimasi turunan kedua dapat diperoleh dengan menjumlahkan persamaan (11) dan (12) sehingga diperoleh:
( ) ( ) ( ) ( ) . (16)
Ekspansi deret Taylor untuk ( ) dan ( )
( ) ( ) ( ) (17) ( ) ( ) ( ) . (18) Menggunakan persamaan (17) dan (18), diperoleh:
(19)
(Niwiga 2005).
Metode Implisit dan Metode Beda Hingga Upwind
Metode implisit merupakan salah satu metode beda hingga yang digunakan untuk menyelesaikan secara numerik persamaan diferensial parsial. Metode implisit mengaproksimasi turunannya menggunakan persamaan beda pusat (beda maju dan beda mundur).
Metode beda hingga upwind merupakan metode yang digunakan untuk menyelesaikan suatu persamaan diferensial dengan mengaproksimasi turunan-turunan persamaan tersebut menjadi sistem linear. Metode beda hingga upwind dan metode implisit sama-sama mengaproksimasi turunannya menggunakan persamaan beda pusat. Salah satu contoh kasus yang penyelesaiannya menggunakan metode beda hingga adalah sebagai berikut:
Misalkan
( )
( )
dengan syarat awal:
( ) ( ) (27)
dan syarat batas:
( ) ( ) (28)
( ) ( ) . (29)
Kemudian untuk menyelesaikan sistem persamaan (26)-(29) dilakukan pendiskretan menggunakan metode implisit sebagai berikut:
( ) . (30)
Untuk lebih memudahkan perhitungan, nilai , , dan dijadikan dalam satu sisi dengan menguraikan persamaan (30), sehingga diperoleh persamaan sebagai berikut:
( ) atau (31) dengan
untuk . Dengan menyubstitusikan nilai awal dan nilai batas, maka persamaan (31) akan berbentuk sistem persamaan dalam bentuk matriks berikut: [ ] [ ] = [ ] (32)
12 atau dengan [ ] dan [ ]
asalkan ada (Yang 2005).
Solusi persamaan di atas dapat diselesaikan dengan menggunakan bantuan
software Matlab. Dalam menyelesaikan matriks yang berbentuk matriks
tridiagonal, diperlukan metode seperti metode sapuan ganda Cholesky, Algoritme Thomas, atau Tridiagonal Solver untuk menyelesaikannya.
Tridiagonal Solver
Tridiagonal solver merupakan suatu metode yang digunakan untuk menyelesaikan matriks sistem yang memiliki bentuk matriks tridiagonal. Dalam penyelesaian numerik model Black-Scholes menggunakan metode implisit ini juga dijumpai matriks yang berbentuk matriks tridiagonal, sehingga perlu dilakukan penyelesaian komputasi numeriknya dengan menggunakan Tridiagonal Solver.
Tridiagonal Solver yang digunakan adalah faktorisasi Crout.
Faktorisasi Crout adalah salah satu metode langsung yang digunakan untuk menyelesaikan solusi dari bentuk matriks sistem tridiagonal , di mana adalah matriks tridiagonal berukuran dan adalah sebuah vektor yang berukuran . Dalam menyelesaikan komputasi numeriknya, penyelesaian sistem persamaan linear dengan metode faktorisasi Crout ini menggunakan bantuan software Matlab.
HASIL DAN PEMBAHASAN
Pada bab ini akan dibahas tentang bagaimana langkah-langkah dalam menyelesaikan model Black-Scholes secara numerik. Ada beberapa metode numerik yang digunakan untuk menyelesaikan suatu persamaan diferensial parsial, antara lain metode beda hingga, metode beda hingga upwind, dan metode volume hingga. Dalam karya ilmiah ini metode yang digunakan untuk menyelesaikan model Black-Scholes adalah metode implisit pada diskretisasi waktu dan metode beda hingga upwind pada diskretisasi ruang. Ruang yang dimaksud dalam karya ilmiah ini adalah harga saham. Dalam menyelesaikan komputasi numerik pada penelitian ini digunakan bantuan software Matlab 7.7.0 (R2008b) dengan metode
faktorisasi Crout untuk menyelesaikan sistem persamaan linear yang berbentuk matriks tridiagonal.
Ada beberapa langkah yang perlu diperhatikan dalam menyelesaikan solusi numerik model Black-Scholes, antara lain:
a. Menentukan model Black-Scholes yang akan diselesaikan. b. Menentukan kondisi syarat awal dan syarat batasnya.
c. Melakukan diskretisasi waktu untuk model Black-Scholes dengan menggunakan metode implisit dan diskretisasi ruang menggunakan metode beda hingga upwind.
d. Melakukan simulasi numerik.
Menentukan Model Black-Scholes
Banyak opsi yang diperdagangkan di dalam pasar keuangan. Dalam menentukan nilai opsi, digunakan suatu model yang dikenal sebagai model Black-Scholes. Model ini penggunaannya terbatas karena hanya dapat digunakan untuk menentukan nilai opsi tipe Eropa, sedangkan pada tipe Amerika model ini tidak berlaku.
Secara umum persamaan Black-Scholes adalah sebagai berikut:
Dengan menggunakan transformasi , maka persamaan Black-Scholes menjadi:
(33)
dengan
= volatilitas saham, = harga saham,
= suku bunga bebas risiko, dan = waktu jatuh tempo.
Syarat Awal dan Syarat Batas
Sebelum melakukan proses diskretisasi dengan menggunakan metode implisit terlebih dahulu ditentukan syarat awal dan syarat batas. Adapun syarat awal dan syarat batasnya adalah sebagai berikut:
( ) ( ) ( ), (34)
( ) ( ) ( ], (35)
( ) ( ) ( ]. (36)
Fungsi , , dan dipilih berdasarkan tipe dari opsi. Tipe opsi yang dipilih adalah tipe opsi Eropa untuk opsi Call, Put, Butterfly spread, dan Cash or
14
Nothing (CoN). Syarat awal dan syarat batas dari opsi tipe Eropa tersebut
diberikan sebagai berikut:
{ ( ) all ( ) ( ) ( ) ( ) l ( ) { all l { all l
dengan , , , menyatakan harga strike dari opsi, adalah harga saham, adalah fungsi Heaviside dan adalah konstanta. Fungsi Heaviside yang digunakan adalah:
{ (Lesmana 2013).
Diskretisasi
Metode beda hingga untuk diskretisasi model Black-Scholes menggunakan metode implisit untuk diskretisasi waktu dan metode upwind untuk diskretisasi ruang. Langkah pertama dimulai dengan mendefinisikan mesh untuk waktu berlakunya opsi ( ) dan ruang ( ), di mana mesh untuk dan adalah ( ) ( ).
Misalkan ( ) dibagi menjadi sub-interval ( ) dengan untuk setiap Panjang interval yang digunakan . Misalkan ( ) dibagi menjadi sub-interval dengan mesh * + dengan
untuk setiap dan panjang interval .
Untuk setiap vektor ( ) dan ( ) dengan dan , didefinisikan turunan pertama dan turunan kedua mengikuti operator beda hingga pada mesh di atas, sebagai berikut:
( )( ) ( )( )
( )( )
( )( )
Menggunakan operator di atas untuk mengaproksimasi persamaan (33) mengikuti metode beda hingga upwind:
( )( ) ( ) (
( )
) ( )
( ( )) ( )
Karena persamaan (33) nilai , didapat:
( )( ) ( ) ( ) (37)
untuk setiap dan di mana ( ) dan ( ) dengan menjadi
aproksimasi untuk ( ) . Metode beda hingga upwind digunakan untuk diskretisasi bentuk setelah diaproksimasi mengikuti persamaan beda maju. Diskretisasi waktu juga berdasarkan persamaan beda mundur dan dengan demikian persamaan (37) akan memenuhi skema numerik metode implisit.
( ) ( ) ( ) ( ) ( ) ( ) (38) ( ) ( ) ( ) (39)
16
Persamaan (39) dapat disederhanakan menjadi:
(40)
untuk dan , dengan
(41) (42) . (43)
Dalam bentuk matriks, persamaan tersebut dapat ditulis menjadi:
[ ] [ ] = [ ] + [ ] atau . Teorema 2 (Matriks-M)
Misalkan matriks nonsingular yang berukuran dengan untuk dan untuk serta semua elemen dari matriks taknegatif, maka
matriks disebut Matriks-M.
Untuk sembarang , matriks ( ) adalah suatu matriks-M untuk .
Bukti:
Untuk membuktikan teorema ini, harus ditunjukkan bahwa:
, (44)
| | | | (45)
Untuk matriks dari persamaan (41) (43) dapat dilihat bahwa syarat (44)
terpenuhi. Selanjutnya syarat (45), karena dan maka:
| | | |
| | | |. (46)
Definisi dari ( ) dan berdasarkan (45), diperoleh:
∑| |
Dengan demikian, merupakan matriks-M karena matriks tridiagonal memiliki diagonal utama bernilai positif dan dua diagonal di atas dan di bawah diagonal utama bernilai negatif.
Simulasi Numerik
Pada bagian ini akan ditunjukkan efisiensi dan akurasi dari metode diskretisasi. Hasil simulasi ini menggunakan empat model masalah opsi yang komputasi numeriknya menggunakan software Matlab 7.7.0 (R2008b) dan algoritme komputasinya dapat dilihat pada Lampiran 2. Model opsi yang digunakan adalah sebagai berikut:
1 Opsi call tipe Eropa
Parameter-parameter yang digunakan untuk menghitung nilai dari opsi
call adalah = 0.1, = 0.2, = 40, =1, dan = 80. Perhitungan ini menggunakan metode implisit pada mesh yang seragam dengan = 40 ( = 2) dan = 20 ( = 0.05) yang hasilnya disajikan pada Gambar 5.
Gambar 5 Harga dari opsi call tipe Eropa 0 20 40 60 80 0 0.5 1 0 10 20 30 40 50 Harga Saham ht=0.0500 hS=2.0000 Waktu H a rg a O p s i
18
Dari Gambar 5 dapat ditunjukkan bahwa semakin meningkatnya harga saham pada kontrak opsi yang memiliki waktu jatuh tempo (expiration date) satu tahun maka akan meningkatkan harga opsi call. Dalam keadaan seperti ini, apabila maka pemegang kontrak opsi akan mengeksekusi kontraknya karena investor akan memperoleh keuntungan.
Dalam karya ilmiah ini, untuk menunjukkan orde kekonvergenan perlu dicari perbandingan numeriknya menggunakan rumus berikut:
(‖ ‖ ) ‖ ‖ ‖ ⁄⁄ ‖ ‖ ‖ | ( )|
dengan menunjukkan perhitungan solusi pada mesh dengan ukuran mesh saham dan ukuran mesh waktu. merupakan solusi eksak yang
diperoleh dari solusi analitik. Sejauh ini, tidak diperoleh solusi analitik untuk opsi butterfly dan opsi Cash or Nothing (CoN), sehingga diperlukan aproksimasi yang sangat kecil. Dalam kasus ini digunakan solusi numerik dengan = 2560 dan = 1280 sebagai solusi eksaknya. Solusi analitik untuk opsi call tipe Eropa dan opsi put tipe Eropa menggunakan rumus berikut:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) dengan ( ⁄ ) ( )( ) √ ( ⁄ ) ( ) ( ) √ Keterangan:
= harga opsi call tipe Eropa = harga opsi put tipe Eropa = harga saham
= harga strike
= tingkat suku bunga bebas risiko = jangka waktu berlakunya opsi = volatilitas dari harga saham = mesh dari variabel
= mesh dari variabel
( ) = fungsi sebaran kumulatif normal baku, dengan = , ( ) √ ∫ (Hull 2009).
Tabel 1 Hasil perhitungan orde kekonvergenan dari opsi call tipe Eropa M N ‖ ‖ (‖ ‖ ) 41 21 7.03901 81 41 2.25213 3.12 161 81 6.53705 3.44 321 161 3.51339 1.86 641 321 2.26599 1.55 1281 641 1.52048 1.49
Hasil perhitungan orde kekonvergenan dari opsi call tipe Eropa ditunjukkan pada Tabel 1. Dari Tabel 1 dapat dilihat bahwa orde kekonvergenan dari proses diskretisasi metode implisit dan metode beda adalah sekitar 2 pada ‖ ‖ .
Harga opsi call untuk tiga nilai volatilitas yang berbeda pada saat disajikan pada Gambar 6. Dari Gambar 6 terlihat bahwa nilai opsi call meningkat ketika volatilitasnya meningkat.
Gambar 6 Harga opsi call untuk nilai volatilitas yang berbeda-beda
0 10 20 30 40 50 60 70 80 0 5 10 15 20 25 30 35 40 45 Harga Saham H a rg a O p s i volatilitas=5% volatilitas=20% volatilitas=70%
20
Gambar 7 Harga opsi call dengan harga strike yang berbeda-beda 2 Opsi put tipe Eropa
Parameter-parameter yang digunakan untuk menghitung nilai dari opsi
put adalah = 0.1, = 0.2, = 40, =1, dan = 80. Hasil perhitungan
nilai opsi put yang dihitung menggunakan metode implisit pada mesh yang seragam dengan = 40 ( = 2) dan = 20 ( = 0.05) disajikan pada Gambar 8.
Gambar 8 Harga dari opsi put tipe Eropa
0 10 20 30 40 50 60 70 80 0 10 20 30 40 50 60 70 Harga Saham H a rg a O p s i K = 20 K = 40 K = 60 0 20 40 60 80 0 0.5 1 0 5 10 15 20 25 30 35 40 Waktu ht=0.0500 hS=2.0000 Harga Saham H a rg a O p s i
Dari Gambar 8 terlihat bahwa semakin meningkatnya harga saham pada kontrak opsi yang memiliki waktu jatuh tempo (expiration date) satu tahun maka harga opsi akan cenderung menurun. Dalam keadaan seperti ini,
maka pemegang kontrak opsi tidak akan mengeksekusi kontraknya,
karena apabila kontrak tersebut dieksekusi maka investor akan memperoleh kerugian.
Tabel 2 Hasil perhitungan orde kekonvergenan dari opsi put tipe Eropa
M N ‖ ‖ (‖ ‖ ) 41 21 1.75441 81 41 9.91805 1.77 161 81 5.74685 1.73 321 161 3.51261 1.64 641 321 2.26580 1.55 1281 641 1.52043 1.50
Hasil perhitungan orde kekonvergenan dari opsi put tipe Eropa ditunjukkan pada Tabel 2. Dari Tabel 2 dapat dilihat bahwa orde kekonvergenan dari proses diskretisasi metode implisit adalah sekitar 1.6 pada ‖ ‖ .
Harga opsi put untuk tiga nilai volatilitas yang berbeda pada saat yang hasilnya disajikan pada Gambar 9. Dari Gambar 9 terlihat bahwa nilai dari opsi put meningkat ketika volatilitasnya meningkat.
Gambar 9 Harga opsi put untuk nilai volatilitas yang berbeda-beda
0 10 20 30 40 50 60 70 80 0 5 10 15 20 25 30 35 40 Harga Saham H a rg a O p s i volatilitas=5% volatilitas=20% volatilitas=70%
22
Gambar 10 Harga opsi put dengan harga strike yang berbeda-beda 3 Opsi Butterfly
Parameter-parameter yang digunakan untuk menghitung nilai dari opsi
Butterfly adalah = 0.1, = 0.2, = 30, = 40, = 50, =1, dan =
80. Hasil perhitungan nilai dari opsi Butterfly yang dihitung dengan menggunakan metode implisit pada mesh yang seragam dengan = 40 ( = 2) dan = 20 ( = 0.05) yang hasilnya disajikan pada Gambar 11.
Gambar 11 Harga dari opsi Butterfly
0 10 20 30 40 50 60 70 80 0 10 20 30 40 50 60 Harga Saham H a rg a O p s i K = 20 K = 40 K = 60 0 20 40 60 80 0 0.5 1 0 2 4 6 8 10 Harga Saham ht=0.0500 hS=2.0000 Waktu H a rg a O p s i
Dari Gambar 11 terlihat bahwa saat harga saham 30 sampai 40 harga opsi mengalami peningkatan, sedangkan pada saat harga saham 40 sampai 50 harga opsi mengalami penurunan. Untuk harga saham 0 sampai 30 dan 50 sampai 80 harga opsinya 0 pada saat waktu jatuh tempo.
Tabel 3 Hasil perhitungan orde kekonvergenan dari opsi Butterfly
M N ‖ ‖ (‖ ‖ ) 41 21 3.52358 81 41 1.95576 1.80 161 81 1.10016 1.78 321 161 6.27766 1.75 641 321 3.44710 1.82 1281 641 1.51147 2.28
Hasil perhitungan orde kekonvergenan dari opsi butterfly ditunjukkan pada Tabel 3. Dari Tabel 3 dapat dilihat bahwa orde kekonvergenan dari proses diskretisasi metode implisit adalah sekitar 1.8 pada ‖ ‖ .
Harga opsi Butterfly untuk tiga nilai volatilitas yang berbeda pada saat yang hasilnya disajikan pada Gambar 12. Dari Gambar 12 terlihat bahwa fungsi menurun dari volatilitas ketika opsi in the money dan fungsi meningkat dari volatilitas ketika out of the money.
Gambar 12 Harga opsi Butterfly untuk nilai volatilitas yang berbeda-beda
0 10 20 30 40 50 60 70 80 0 1 2 3 4 5 6 7 8 Harga Saham H a rg a O p s i volatilitas=5% volatilitas=20% volatilitas=70%
24
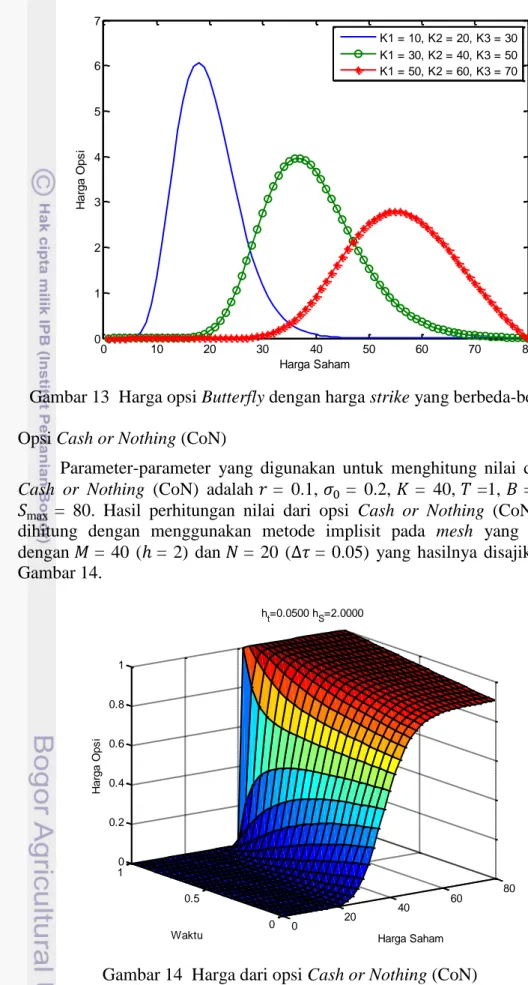
Gambar 13 Harga opsi Butterfly dengan harga strike yang berbeda-beda 4 Opsi Cash or Nothing (CoN)
Parameter-parameter yang digunakan untuk menghitung nilai dari opsi
Cash or Nothing (CoN) adalah = 0.1, = 0.2, = 40, =1, = 1, dan = 80. Hasil perhitungan nilai dari opsi Cash or Nothing (CoN) yang
dihitung dengan menggunakan metode implisit pada mesh yang seragam dengan = 40 ( = 2) dan = 20 ( = 0.05) yang hasilnya disajikan pada Gambar 14.
Gambar 14 Harga dari opsi Cash or Nothing (CoN)
0 10 20 30 40 50 60 70 80 0 1 2 3 4 5 6 7 Harga Saham H a rg a O p s i K1 = 10, K2 = 20, K3 = 30 K1 = 30, K2 = 40, K3 = 50 K1 = 50, K2 = 60, K3 = 70 0 20 40 60 80 0 0.5 1 0 0.2 0.4 0.6 0.8 1 Harga Saham ht=0.0500 hS=2.0000 Waktu H a rg a O p s i
Dari Gambar 14 dapat ditunjukkan bahwa harga opsi bernilai 0 saat harga saham di bawah 40 dan harga opsi akan bernilai 1 saat harga saham di atas 40 pada waktu jatuh tempo (expiration date).
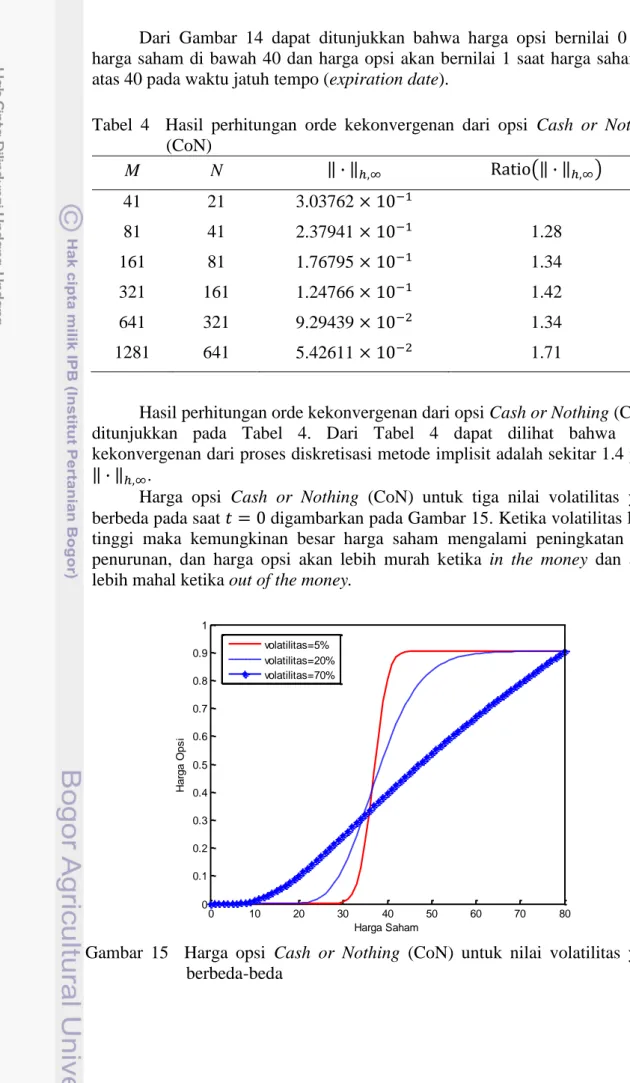
Tabel 4 Hasil perhitungan orde kekonvergenan dari opsi Cash or Nothing (CoN) M N ‖ ‖ (‖ ‖ ) 41 21 3.03762 81 41 2.37941 1.28 161 81 1.76795 1.34 321 161 1.24766 1.42 641 321 9.29439 1.34 1281 641 5.42611 1.71
Hasil perhitungan orde kekonvergenan dari opsi Cash or Nothing (CoN) ditunjukkan pada Tabel 4. Dari Tabel 4 dapat dilihat bahwa orde kekonvergenan dari proses diskretisasi metode implisit adalah sekitar 1.4 pada ‖ ‖ .
Harga opsi Cash or Nothing (CoN) untuk tiga nilai volatilitas yang berbeda pada saat digambarkan pada Gambar 15. Ketika volatilitas lebih tinggi maka kemungkinan besar harga saham mengalami peningkatan atau penurunan, dan harga opsi akan lebih murah ketika in the money dan akan lebih mahal ketika out of the money.
Gambar 15 Harga opsi Cash or Nothing (CoN) untuk nilai volatilitas yang berbeda-beda 0 10 20 30 40 50 60 70 80 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Harga Saham H a rg a O p s i volatilitas=5% volatilitas=20% volatilitas=70%
26
Gambar 16 Harga opsi Cash or Nothing (CoN) dengan harga strike yang berbeda-beda
SIMPULAN DAN SARAN
SimpulanKarya ilmiah ini berhasil menunjukkan bagaimana langkah-langkah dalam menyelesaikan solusi numerik dari model Black-Scholes dengan menggunakan metode implisit pada diskretisasi waktu dan metode beda hingga upwind pada diskretisasi ruang. Solusi yang didapat dari penyelesaian numerik ini berupa matriks sistem yang berbentuk matriks tridiagonal, sehingga dalam menyelesaikannya perlu digunakan metode faktorisasi Crout untuk menyelesaikan matriks tridiagonal tersebut. Software Matlab digunakan untuk membantu menyelesaikan komputasi numeriknya.
Berdasarkan hasil simulasi numerik diperoleh informasi sebagai berikut: 1 Opsi call Eropa
Semakin tinggi harga saham pada kontrak opsi yang memiliki waktu jatuh tempo satu tahun maka harga opsi juga akan semakin meningkat.
Orde kekonvergenan sekitar 2. 2 Opsi put Eropa
Semakin tinggi harga saham pada kontrak opsi yang memiliki waktu jatuh tempo satu tahun maka harga opsi akan cenderung menurun.
Orde kekonvergenan sekitar 1.6.
0 10 20 30 40 50 60 70 80 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Harga Saham H a rg a O p s i K = 20 K = 40 K = 60
3 Opsi Butterfly
Harga opsi akan meningkat saat harga saham 30 sampai 40 dan harga opsi akan menurun saat harga saham 40 sampai 50.
Orde kekonvergenan sekitar 1.8. 4 Opsi Cash or Nothing (CoN)
Harga opsi bernilai 0 saat harga saham di bawah 40 dan harga opsi akan bernilai 1 saat harga saham di atas 40 pada saat jatuh tempo.
Orde kekonvergenan sekitar 1.4.
Saran
Model Black-Scholes merupakan model yang digunakan untuk menentukan nilai opsi tipe Eropa. Selain itu, model ini juga dapat digunakan untuk menentukan rasio lindung nilai untuk opsi tipe Eropa. Dalam karya ilmiah ini hanya digunakan metode implisit dan metode beda hingga upwind untuk menyelesaikan solusi numerik dari model Black-Scholes. Penyelesaian numerik model Black-Scholes juga dapat menggunakan metode beda hingga yang lain, seperti metode eksplisit, metode Crank-Nicholson, dan metode volume hingga.
DAFTAR PUSTAKA
Ermogenous, A. 2005. Brownian Motion and Its Applications In The Stock
Market. Chicago (US): Illinois Institute of Technology.
Hull JC. 2009. Option, Future, and Other Derivatives. Ed ke-7. New Jersey (US): Pearson Education.
Lesmana DC. 2013. An upwind finite difference method for a nonlinear
Black-Scholes equation governing European option valuation under transaction cost
[tesis]. Western Australia (AU): University of Western Australia.
Lo MS. 2003. Generalized autoregressive conditional heterscedasticity time series
model [tesis]. Burnaby (CA): Simon Fraser University.
Niwiga DB. 2005. Numerical method for valuation of financial derivatives [tesis]. South Africa (ZA): University of Western Cape.
Ross SM. 2007. Introduction to Probability Models. Ed ke-9. South California (US): Elsevier.
Yang WY. 2005. Applied Numerical Methods Using Matlab. New Jersey (US): J Wiley.
28
LAMPIRAN
Lampiran 1 Pembuktian persamaan (5)
Diasumsikan bahwa model dari harga saham dapat dinyatakan sebagai berikut:
( ) ( ) ( ) ( ) (1.a) Misalkan ( ) ( ( ) ). Berdasarkan Lemma Itô maka berlaku:
( ) ( ) ( ( )) . (1.b)
Dengan menguadratkan kedua ruas pada persamaan (1.a), diperoleh ( ( )) sebagai berikut:
( ( )) ( ( ) ( ) ( ))
( ) ( ) ( ) ( ) ( ) ( ) ( ( )) Diketahui bahwa ( ) , ( )( ( )) , dan ( ( )) , maka
( ( )) ( ) . (1.c) Dengan menyubstitusikan persamaan (1.a) dan (1.c) pada persamaan (1.b) akan diperoleh: ( ) ( ( ) ( ) ( )) ( ) ( ) ( ) ( ) ( ) ( ( ) ( ) ) ( ) ( ).
Lampiran 2 Program Matlab
function V = EuImplisit(u0,g1,g2,S_end,T,nS,nt)
format long
nS1 = nS+1; % banyaknya mesh ruang (S)
hS = S_end/nS; % panjang dari sub interval S
hS2 = hS*hS;
nt1 = nt+1; % banyaknya mesh dari waktu(t)
ht = T/nt; % panjang dari sub interval t
r = 0.1; % suku bunga bebas risiko
sigma0 = 0.2; % sigma dari model Black-Scholes
rat = 1/ht; % rasio dari panjang ruang dan panjang waktu
% Membangkitkan mesh dari variabel S dan t
Svec = hS*(0:nS); % ukuran = 1x(nS+1)
tvec = ht*(0:nt); % ukuran = 1x(nt+1)
% Mendefinisikan dimensi dari variabel yang tidak diketahui
U = zeros(nt1,nS1); % ukuran = (nt+1)x(nS+1) for k = 1:nS1 U(1,k) = feval(u0,Svec(k)); end for k = 1:nt1 U(k,1) = feval(g1,tvec(k)); U(k,nS1) = feval(g2,tvec(k)); end
for m = 2:nt1 % langkah iterasi waktu
Vtemp = U(m-1,:); Un = U(m-1,:); U_SS = zeros(1,nS1-2); for j = 2:nS1-1 U_SS(j-1) = (Vtemp(j+1)-2*Vtemp(j)+Vtemp(j-1))/hS2; end Svechit = zeros(1,nS1-2); for j = 1:(nS1-2) Svechit(j) = Svec(j+1); end
sigma2 = 0.5*sigma0^2; % ukuran(sigma2) = 1x(nS1-2)
b = r*Svechit; A = zeros(nS1-2,3);
for i = 1:(nS1-2)
A(i,2) = rat + 2*sigma2*(Svechit(i)^2)/hS2+(1/hS)*b(i)+r;
end
for i = 1:(nS1-2)
A(i,1) = -sigma2*(Svechit(i)^2)/hS2;
end
for i = 1:(nS1-2)
A(i,3) = -sigma2*(Svechit(i)^2)/hS2 - (1/hS)*b(i);
end
30
e_1 = sigma2*(Svechit(1)^2)/hS2;
e_n1 = sigma2*(Svechit(end)^2)/hS2 + (1/hS)*b(end); F = zeros(nS1-2,1); F(1) = e_1*U(m,1) + rat*Un(2); F(nS1-2) = e_n1*U(m,nS1) + rat*Un(nS1); for i = 2:(nS1-3) F(i) = rat*Un(i+1); end
% Menyelesaikan matriks tridiagonal A*U = F menggunakan Faktorisasi Crout lamb1 = zeros(nS1-2,1); lamb1(1) = A(1,3)/A(1,2); d = zeros(nS1-2,1); d(1) = F(1)/A(1,2); for k = 2:(nS1-2) lamb1(k) = A(k,3)/(A(k,2)-A(k,1)*lamb1(k-1)); d(k) = (F(k)-A(k,1)*d(k-1))/(A(k,2)-A(k,1)*lamb1(k-1)); end v1 = zeros(nS1-2,1); v1(nS1-2) = (F(nS1-2)-A(nS1-2,1)*d(nS1-3))/(A(nS1-2,2)-A(nS1-2,1)*lamb1(nS1-3)); for k = (nS1-3):-1:1 v1(k) = d(k) - lamb1(k)*v1(k+1); end
% matriks tridiagonal selesai
V1temp = [U(m,1) v1' U(m,end)]; Vfin = V1temp + 0*Vtemp;
for i = 1:nS1
U(m,i) = Vfin(i);
end
end % iterasi waktu selesai
V = zeros(nt1,nS1);
for j = 1:nt1
V(j,:) = U((nt1+1)-j,:);
end
% Plot dari solusi numerik
surf(Svec,tvec,V)
xlabel('Harga Saham');
ylabel('Waktu');
zlabel('Harga Opsi');
s1 = sprintf('h_t=%6.4f h_S=%6.4f', ht, hS);
title(s1);
RIWAYAT HIDUP
Penulis dilahirkan di Sragen pada tanggal 9 Januari 1993 dari ayah Sugito dan ibu Dra Sri Suwarti. Penulis adalah putra pertama dari tiga bersaudara. Tahun 2010 penulis lulus dari SMA Negeri 1 Gondang, Sragen dan pada tahun yang sama penulis lulus seleksi masuk Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB dan diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis aktif di lembaga kemahasiswaan dan memegang amanah sebagai staf Public Relation Gugus Mahasiswa Matematika (Gumatika) IPB selama dua periode kepengurusan yaitu tahun 2012 dan 2013, serta ketua Organisasi Mahasiswa Daerah Sragen tahun 2013. Penulis pernah mengikuti beberapa kegiatan kepanitiaan yang diselenggarakan oleh Gumatika diantaranya adalah kepanitiaan IPB Mathematics Challenge (IMC), Fieldtrip Matematika angkatan 47, studi banding Gumatika, dan berbagai kegiatan lainnya. Penulis juga aktif dalam kegiatan yang diselenggarakan oleh IPB di antaranya