Pemodelan Magnetotellurik 2D Menggunakan Metode Elemen Batas. 2D Magnetotelluric Modelling using Boundary Element Method

 

82

Pemodelan Magnetotellurik 2D Menggunakan Metode Elemen Batas

Imran Hilman Mohammad1,2), Wahyu Srigutomo1), dan Doddy Sutarno1)

1)

Kelompok Keahlian Fisika Sistem Kompleks, Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Teknologi Bandung

2)

Program Studi Geofisika, Universitas Padjadjaran e-mail:imran.hilman@phys.unpad.ac.id

Diterima 10 Maret 2011, disetujui untuk dipublikasikan 6 Juni 2011 Abstrak

Dalam permasalahan elektromagnetik untuk aplikasi geofisika, rangkaian persamaan Maxwell dapat disederhanakan menjadi persamaan Helmholtz, sehingga dapat dicari solusi permasalahan menggunakan berbagai skema numerik. Metode elemen batas merupakan metode numerik untuk memecahkan persamaan diferensial parsial yang telah dikembangkan dalam beberapa dekade ini untuk memecahkan berbagai permasalahan medan elektromagnet. Metode ini memiliki keunikan dibandingkan metode numerik lain untuk memecahkan persamaan diferensial parsial, karena hanya membutuhkan diskretisasi pada bidang-bidang batas domain pemodelan. Solusi pada batas domain dapat digunakan untuk mencari solusi pada seluruh domain pemodelan, membuat metode ini memiliki algoritma numerik yang sangat efisien. Dalam makalah ini, metode elemen batas digunakan untuk menghitung respon magnetotellurik 2D dalam bentuk resistivitas semu dan fasa impedansi modus TE (transverse electric). Pemodelan elemen hingga digunakan sebagai pembanding hasil pemodelan elemen batas yang dikembangkan.

Kata kunci : Metode elemen batas, Magnetotelurik 2D.

2D Magnetotelluric Modelling using Boundary Element Method

Abstract

In most formulations of electromagnetic methods in geophysics, the set of Maxwell’s equations can be simplified into Helmholtz’s equation which leads to possibility of solving electromagnetic problems using various numerical schemes. The boundary element method is a numerical method for solving partial differential problems which in the last several decades has been applied in electromagnetic problems. The method poses unique advantage in comparison to other methods; it requires discretization only on the boundaries of the modeling domain. Solutions in the boundaries can be used to find solutions on the entire modeling domain, which makes the boundary element method a highly efficient numerical method. This paper will discuss 2D magnetotelluric (MT) modeling using boundary element method. The method is applied to calculate 2D MT responses, expressed in apparent resistivity and phase of impedance, for transverse electric (TE) mode. The results obtained by the method are compared to those calculated by analytical solution and finite element modeling to show the accuracy of boundary element method.

Keywords: Boundary-element method, 2D magnetotelluric.

1. Pendahuluan

Fenomena-fenomena fisis yang terjadi di alam semesta dapat dimodelkan secara matematis sebagai suatu sistem dinamis melalui persamaan diferensial parsial (partial differential equation). Solusi persamaan diferensial parsial pada umumnya dapat diselesaikan melalui pendekatan analitik hanya pada kasus-kasus yang sangat sederhana atau sangat disederhanakan. Keberadaan faktor-faktor kompleks di dalam sistem dinamis membuat solusi analitik dari persamaan diferensial parsial terkadang menjadi sangat rumit, atau bahkan tidak tersedia. Berbagai fenomena fisis di alam sangat rumit untuk dimodelkan secara analitik, sehingga digunakan

pendekatan numerik untuk memodelkan fenomena-fenomena tersebut secara matematis.

Salah satu fenomena yang terjadi di alam semesta dan dimanfaatkan dalam aplikasi kebumian adalah fenomena arus tellurik (telluric current). Arus tellurik adalah arus yang dibangkitkan oleh interaksi antara plasma yang dipancarkan matahari dengan medan magnetik bumi. Fenomena arus telurik digunakan dalam aplikasi kebumian melalui metode

magnetotelluric (MT). Dalam metode ini, arus telurik digunakan sebagai sumber untuk menginduksi material bawah permukaan untuk memperoleh informasi struktur konduktivitas bawah permukaan. Metode ini memiliki jangkauan pemetaan struktur bawah permukaan dengan kedalaman bergantung

pada frekuensi. Untuk frekuensi rendah, metode ini dapat memperkirakan struktur konduktivitas bawah permukaan hingga beberapa kilometer (Kauffman dan Keller, 1981; Vozoff, 1986).

Pemodelan respon MT telah dilakukan banyak pihak. Pada awal perkembangannya, pemodelan ke depan dilakukan dengan memecahkan persamaan integral permukaan atau volume. Solusi ke depan untuk model berlapis satu dimensi dinyatakan dalam integral Fourier atau Bessel. Sementara itu, model 2D atau 3D relatif sangat sulit dipecahkan kecuali pada kasus khusus dengan geometri sederhana seperti bola atau silinder. Dengan menggunakan persamaan diferensial, keadaan geologi yang kompleks dapat dimodelkan dengan lebih baik. Beberapa pengembangan pemodelan ke depan metode elektromagnetik menggunakan persamaan diferensial antara lain dilakukan oleh Coggon (1971), Rijo (1977), Wannamaker dkk. (1984), Lee dan Morison (1985) serta Srigutomo dan Sutarno (1998) yang mengembangkan teknik pemodelan elemen hingga. Pengembangan pemodelan elemen hingga pada daerah dengan undulasi topografi yang bervariasi seperti daerah pegunungan juga telah banyak dilakukan, antara lain oleh Wannamaker dkk. (1986) serta Chouteau dan Bouchard (1988).

Salah satu teknik pemecahan persamaan differensial adalah penggunaan metode elemen batas (Brebbia dan Dominguez, 1992). Pemodelan elemen batas untuk persoalan elektromagnetik dalam bidang geofisika diperkenalkan oleh Xu dan Zhao (1987), yang memodelkan kasus MT 2D dengan permukaan flat dan homogen. Selanjutnya Xu dan Zhou (1997) memodelkan persoalan MT 2D dengan efek topografi. Metode elemen batas memiliki keunikan dibandingkan metode elemen hingga, yaitu antara lain memiliki skema diskretisasi elemen yang sederhana, persiapan data yang relatif lebih sedikit dan konfigurasi elemen pada permukaan yang ditinjau sangat bersesuaian dan lebih konsisten dengan kondisi lapangan sesungguhnya.

2. Permasalahan Syarat Batas Metode Magnetotelurik

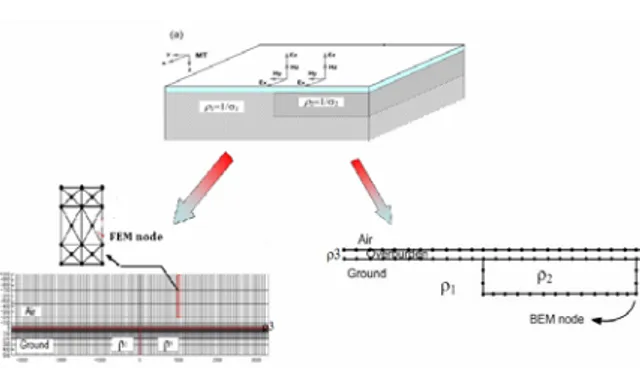
Metode elemen batas menggunakan sifat yang berkaitan dengan harga nilai batas (boundary value problem), dalam hal ini fungsi Green, sehingga suatu persamaan diferensial parsial dapat diselesaikan dengan menggunakan pendekatan integral pada batas domain permasalahan. Persamaan integral pada batas domain (boundary integral equation) yang dihasilkan kemudian didiskretisasi menjadi elemen-elemen batas yang dihitung dalam suatu persamaan matriks sebagaimana dalam metode elemen hingga, hanya matriks yang dihasilkan akan lebih sederhana karena elemen yang diperhitungkan dalam persamaan matriks hanya elemen dari diskritisasi bidang batas. Ini akan menghemat memori komputer dan mempercepat waktu komputasi. Gambar 1

memperlihatkan perbedaan diskretisasi domain antara metode elemen hingga dengan metode elemen batas.

Gambar 1. Perbandingan diskretisasi domain pada kasus MT menggunakan elemen hingga (FEM) dan elemen batas (BEM). Elemen batas mendiskretisasi domain hanya pada batas domain pemodelan, sementara elemen hingga membutuhkan diskretisasi seluruh domain.

Gambar 2. Domain pemodelan dan sistem koordinat untuk kasus rambatan gelombang elektromagnetik 2D. Gelombang diasumsikan menjalar dari udara ke bumi dalam sumbu z negatif dengan arah x

menyatakan arah jurus (strike) geologis.

Asumsikan suatu domain 2D dengan lapisan terdiri dari udara sebagai half space atas dan bawah permukaan sebagai half space bawah sebagaimana ditunjukkan pada Gambar 2. Kita nyatakan dua domain dan sebagai domain untuk halfspace

bawah dan atas Misalkan sumbu x dinyatakan sebagai arah jurus (strike direction), sumbu y tegak lurus terhadap sumbu x dan sumbu z vertikal ke bawah. Gelombang elektromagnetik datang dapat dipisahkan menjadi dua polarisasi yang berbeda, polarisasi Hx dan polarisasi Ex. Asumsikan faktor waktu adalah e-ipersamaan gelombang untuk Hx dan Ex adalah (Xu dan Zhou, 1997):









y z x x y x z E E i H y z H i E z H i E y           _   _       _      _  _ (1) dan





y z x x y x z H H i E y z E i H z E i H y        _{  }    _      _     _  _ (2)

Untuk selanjutnya polarisasi Hx akan dinamakan modus TM dan polarisasi Ex akan dinamakan modus TE. Untuk modus TM, kita dapatkan

y x E z H _   _, z x _E y H _ 

 _{pada batuan konduktif. Berdasarkan}

asumsi  / >> 1, maka harga

z Hx   _dan y Hx   _pada

bagian udara akan bernilai nol, sehingga dapat diasumsikan Hx bernilai konstan pada domain udara. Dengan demikian

1



x

H (3)

pada permukaan. Sedangkan pada domain , medan elektromagnetik dapat didefinisikan sebagai distribusi peluruhan medan elektromagnetik dalam medium homogen:

) exp( ikz

Hx   (4)

Untuk modus TE, berdasarkan kontinuitas pada bidang batas antara lower dan upperhalf space, maka persamaan medan Ex dan turunannya dapat dinyatakan sebagai berikut:

n E n Ex x      0 (5) x x E E  0

dan untuk daerah bawah permukaan, kita dapatkan medan Ex untuk daerah homogen:

) exp( ikz

E_x  (6)

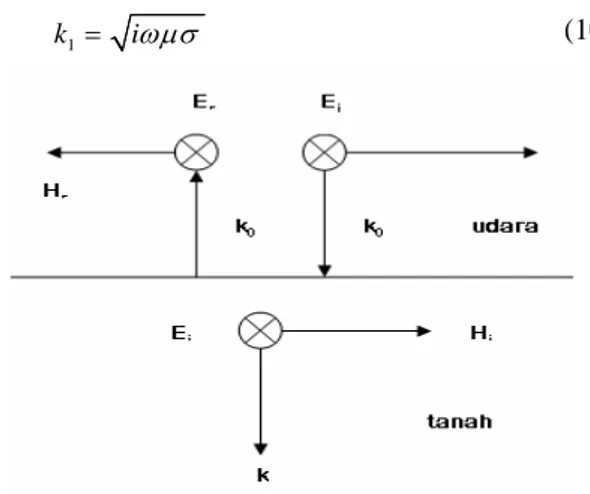
Untuk daerah atas permukaan, medan listrik terdiri dari medan listrik datang (incident field) dan medan listrik terpantul (reflected field) yang dapat dinyatakan dengan (Gambar 3):

z ik reflection z ik incident y z ik reflection z ik incident x e H e H H e E e E E 0 0 0 0 0 0     (7) dimana 2 0 0 0 k     . (8)

Medan listrik yang terdapat pada daerah bawah permukaan merupakan medan listrik transmisi yang diteruskan oleh bidang batas tanah dan udara, sehingga untuk daerah bawah permukaan dapat dituliskan: z ik trans y z ik trans x e H H e E E 2 1   (9) dengan 1 k  i (10)

Gambar 3. Pemantulan dan transmisi medan elektromagnetik modus TE pada bidang batas antara tanah dan udara.

Dari kontinuitas medan elektromagnetik sebagaimana diberikan pada Persamaan (5) dan menggunakan hubungan: 0 0 0 0 1 , , i r t i r t E E E H k H k H k       (11) kita dapatkan: t r i E k k E E 0   (12)

Jika kita set Et = 1 pada permukaan, kita dapat nyatakan E0x pada domain atas permukaan sebagai:

) sin( ) cos( 0 0 0 0 _k k z k i z k E x  (13) Persamaan (3), (4), (5), (6), (7) dan (13) merupakan persamaan syarat batas bagi permasalahan magnetotellurik 2D yang akan dimodelkan pada penelitian ini.

3. Persamaan Elemen Batas

Di dalam metode elemen batas, suatu permasalahan yang diformulasikan dengan persamaan diferensial parsial akan dipecahkan dengan membawa keberlakuan solusi permasalahan dari seluruh domain menuju batas domain. Hal ini dilakukan dengan menggunakan identitas Green dan Teorema Gauss serta menerapkan teknik pembobotan residual (Brebbia dan Dominguez, 1992; Gaul dkk., 1992; Xu dan Zhou, 1997).

Jika kita memiliki fungsi Helmholtz berikut:



_2 _k2



 _ 0 ₍₁₄₎

mula-mula kita gunakan teknik pembobotan residual dengan mengalikan fungsi Helmholtz di atas dengan suatu test function:



2 2



0 *_{  }



 d k   (15)

Selanjutnya, Persamaan (15) diintegrasi parsial untuk mendapatkan:



 





_











_



 

 



   d d d k2 * * 2 *      (16) Penerapan Teorema Gauss untuk suku

pertama ruas kiri persamaan di atas memberikan:





 

 

       

_

_



   d d n d k2 * * 2 *      (17)

Selanjutnya, suku kedua ruas sebelah kanan juga diintegral parsialkan serta diterapkan Teorema Gauss, menghasilkan:





                   

_

_



   d n d n n d k * 2 * * 2 2 *         (18)

Berdasarkan Persamaan (14), suku sebelah kiri Persamaan (18) sama dengan nol. Sehingga Persamaan (18) dapat dituliskan:





                     d n n d n * * * 2 _      (19)

Dengan memilih test function sebagai berikut:



2 2



* 

 

,

x

k 



 (20)

dan menggunakan sifat distribusi Dirac:



  ( ) ) , ( ) (x  x  dx f  f (21)

maka suku sebelah kiri Persamaan (18) dapat kita tuliskan: ) ( * 2    d u n    

_

 (22)

sehingga secara lengkap kita tuliskan Persamaan (18):



                d n n u * * ) (     (23)

Selanjutnya, penguraian ruas kiri Persamaan (22) dapat dinyatakan sebagai berikut:













p p d p d k k        





             2 ) ( 2 2 * * 2 2 (24) atau                               





  d n n d n n S p            * * * * 2 ₍₂₅₎

Suku pertama pada Persamaan (25), p    2 menyatakan nilai potensial pada titik p dikalikan harga sudut yang dibentuk antara titik p dengan bidang batas tempat titik p tersebut berada.

Persamaan (25) merupakan persamaan awal dari metode elemen batas. Selanjutnya persamaan ini akan didiskretisasi menjadi elemen-elemen yang merepresentasikan integral batas persamaan tersebut. Ada beberapa jenis cara pendiskretisasian batas

domain, bergantung pada jenis elemen yang digunakan. Jenis elemen yang biasa digunakan dalam mendiskretisasikan batas domain adalah (Brebbia dan Dominguez, 1992; Gaul dkk., 1992):

1. Elemen batas konstan 2. Elemen batas linier 3. Elemen batas kuadratik 4. Elemen batas kubik

Elemen batas konstan didefinisikan sebagai elemen batas dengan nilai potensial dan turunan potensial yang diasumsikan bernilai konstan sepanjang elemen pengintegrasian. Dalam elemen batas konstan, setiap titik nodal pengintegrasian akan terletak pada titik tengah-tengah antar ujung masing-masing elemen, sehingga sudut yang dibentuk antara titik nodal p dengan bidang batas domain akan bernilai sama diseluruh elemen, yaitu 1800, atau  radian (Gambar 4). Dengan demikian u_p _p _p

  2 1 2  

untuk seluruh simpul pada seluruh elemen.

Gambar 4. Koordinat lokal elemen dan posisi titik simpul pada elemen batas konstan.

Nilai fungsi uji (test function) * dan turunannya

n

 _*

ditentukan berdasarkan solusi fundamental persamaan Helmholtz, yang untuk kasus dua dimensi adalah: ) ( 4 ) 1 ( 0 * kr H i   (26) dan ) ( 4 ) 1 ( 1 * kr H ki n    ₍₂₇₎

dengan r adalah jarak dari titik sumber terhadap titik yang ditinjau, H0(1) adalah fungsi Hankel jenis pertama dan orde nol dan H1(1)merupakan fungsi Hankel jenis pertama orde pertama, yang dapat dituliskan dengan: ) ( ) ( ) ( ) ( ) ( ) ( 1 1 ) 1 ( 1 0 0 ) 1 ( 0 kr iN kr J kr H kr iN kr J kr H     (28)

dengan Jnmerupakan fungsi Bessel jenis pertama dan

Nn merupakan fungsi Bessel jenis kedua atau fungsi Neumann. Subskrip n menyatakan orde fungsi Bessel yang bersangkutan, dengan nilai 0 dan 1.

Nilai potensial dan turunan potensial yang ditinjau adalah harga pada permukaan. Untuk modus

TM potensial yang bersesuaian adalah medan magnet pada permukaan, sedangkan untuk modus TE potensial yang bersesuaian adalah medan listrik pada permukaan. Secara umum untuk kedua modus, kita dapat membagi domain permasalahan sebagai berikut Untuk domain bawah permukaan:

2 S p u u u u d u d n n n n   _  _  _{ }           _  _   _  _         





(29) sedangkan untuk domain atas permukaan:

0 1 2 S p u u u u d u d n n n n   _  _         _  _  _  _{ }  _  _    _{ }   _{ }   



 



  (30) dimana, adalah sudut yang dibentuk oleh titik

nodal p pada domain pemodelan; up potensial pada titik p, u potensial,

n u



 _{turunan potensial, solusi}

fundamental persamaan Helmholtz, n



 _=turunan

solusi fundamental persamaan Helmholtz terhadap arah n, s bidang batas pada permukaan, bidang batas bawah permukaan, 0 bidang batas atas permukaan.

Selanjutnya diskretisasi dilakukan pada domain C dalam batas-batas kecil Cj. Titik-titik yang menghubungkan antar elemen tersebut dinamakan titik ekstrim elemen batas, di mana untuk titik yang memiliki nilai syarat batas dinamakan simpul (nodes).

Dengan memasukkan harga-harga solusi fundamental, maka Persamaan (29) dan (30) diatas dapat dinyatakan dengan

(1) 1 (1) 0 ( ) cos( , ) 2 4 ( ) 4 S S p p kH kr u i u r n d H kr u i d B n   _     _ _      _{ }     





(31) dengan



               d n u n u B_p   dan (1) 0 1 0 0 0 (1) 0 0 0 ( ) 1 cos( , ) 2 4 ( ) 4 S S p p k H k r u i u r n d u H k r i d A n   _     _  _{ }            _{ }     





(32) dengan



              d n u n u A_p 0 0 0 0  

Untuk modus TM, persamaan integral batas pada domain upper halfspace ditiadakan, karena medan Hx relatif konstan pada bidang permukaan yang merupakan batas antara lower dan upper halfspace.

Dengan demikian, persamaan integral batas untuk modus TM dapat dituliskan sebagai berikut

P p d C n u n u d n u u S                        

_

_

       2 (33)          

_

 d n u C S P 

Selanjutnya, diskretisasi dilakukan dengan membuat elemen-elemen di sepanjang garis batas permukaan s . Uraikan integral batas Cp menjadi penjumlahan dari integral tiap-tiap elemen pada s, akan didapatkan untuk nodal (i)

i e C d kr H n u i S          

 

_  4 ) ( ) 1 ( 0 ₍₃₄₎ Dengan mengasumsikan ij D d kr iH j        



 4 ) ( ) 1 ( 0 ₍₃₅₎

kita dapatkan satu set solusi persamaan sebagai berikut : i N j j ij C n u D d kr iH n S e



 

                        1 ) 1 ( 0 4 ) (  (36)

atau dalam bentuk matriks :

C n U D         ₍₃₇₎

Persamaan (37) menentukan harga turunan Hx pada tiap titik di permukaan. Persamaan (3) menyatakan harga Hx konstan pada tiap titik di permukaan, sehingga Persamaan (37) dan (3) dapat digabung untuk memperoleh informasi mengenai resistivitas semu dan fasa impedansi di permukaan untuk modus TM.

Untuk modus TE, diskretisasi suku sebelah kanan Persamaan (31) dinyatakan sebagai berikut:



 

_                     N j j ij n u D d kr iH n S e 1 ) 1 ( 0 4 ) (  ₍₃₈₎





  j iju f d n r kr kH u i e ) , cos( 4 ) ( ) 1 ( 1 ₍₃₉₎

Menggunakan Persamaan (38) dan (39), maka Persamaan (31) untuk kasus TE dapat dituliskan:

1 2 N i ij j ij i j j u F u D B n            _        



(40)

Pada domain atas permukaan modus TE, diskretisasi Persamaan (32) menghasilkan:



 

                     N j j ij n u E d r k iH n S e 1 0 ) 1 ( 0 0 4 ) (  ₍₄₁₎



 

  j iju G d n r r k H k u i e ) , cos( 4 ) ( 0 ) 1 ( 1 0 ₍₄₂₎

Persamaan (41) dan (42) dapat digunakan untuk menyatakan Persamaan (32) menjadi

1 2 N i ij j ij i j j u G u E B n      _{ }     _{ } _     



(43)

Berdasarkan syarat kontinuitas domain bawah dan atas permukaan: n n       0 0 u u u u

kita dapatkan satu set persamaan matriks yang akan mencari semua nilai Ex dan turunannya di sepanjang garis batas permukaan antara domain atas dan bawah permukaan: 2 2 n      _ _{ }  _{  }     _{   }     _{ } _{ }     u F D B u A G I E (44)

Dengan memecahkan Persamaan (44), akan didapatkan semua harga Ex dan turunannya di sepanjang garis batas permukaan antara atas dan bawah permukaan, sehingga dapat dicari nilai resistivitas semu dan fasa impedansi pada permukaan.

Harga resistivitas semu dapat dicari menggunakan hubungan berikut. Dengan memperhatikan syarat batas medan listrik dan magnet pada permukaan (Persamaan 3, 4, 5 dan 13) dan hubungan berikut (Ward dan Hohmann, 1989; Xu dan Zhou, 1997; Srigutomo dan Sutarno, 1989):

n E i H u n u n H E x y x y                1 1 , 1 1 1 1 (45)

maka resistivitas semu untuk modus TM dapat ditulis (Xu dan Zhou, 1997) :

2 2          n u i yx _  (46)

dan fasa impedansinya:

                             n u real n u imag yx arctan  (47)

Resistivitas semu modus TE dapat ditulis:

2           n u u i xy   (48)

dan fasa impedansinya:

 

 

                                     n u real n u imag u real u imag yx arctan arctan 2   (49) 4. Hasil Pemodelan

Pemodelan yang dilakukan terdiri atas :

 Modus TE dan TM bumi homogen

 Modus TE dan TM bumi berlapis

 Modus TE, bumi dengan anomali konduktif

 Modus TE, bumi dengan kontak vertikal Masing-masing model akan dicari responnya berupa resistivitas semu dan fasa impedansi dengan frekuensi 4, 8, 16 dan 32 Hz. Seluruh respon dihitung menggunakan metode elemen batas. Untuk respons pemodelan pada kasus 1D (kasus bumi homogen dan bumi berlapis) akan digunakan hasil perhitungan analitik sebagai pembanding. Hasil pemodelan pada kasus 2D (bumi dengan prisma konduktif dan bumi dengan kontak vertikal) akan dibandingkan dengan respon hasil perhitungan dengan metode elemen hingga. Skema perhitungan analitik yang digunakan adalah skema yang dikembangkan Grandis (1999), sementara skema elemen hingga pembanding adalah skema yang dikembangkan Srigutomo dan Sutarno (1998). Gambar 5, 6, 8 dan 9 menunjukkan respon bumi 1D dihitung dengan skema pemodelan metode elemen batas 2D dibandingkan dengan hasil perhitungan analitik, sementara Gambar 11, 12, 15, dan 16 menunjukkan respon bumi 2D yang dihitung dengan pemodelan elemen batas yang dibandingkan dengan hasil pemodelan metode elemen hingga 2D.

5. Diskusi dan Analisis

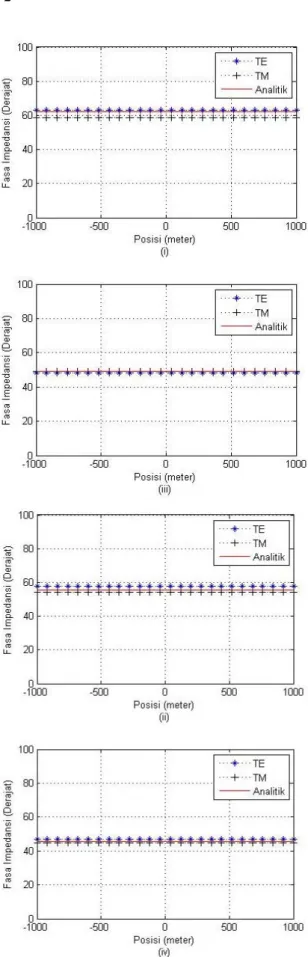
Hasil pemodelan untuk bumi homogen dengan elemen batas modus TE dan TM terhadap solusi analitik (Gambar 5 dan Gambar 6) memperlihatkan bagaimana harga resistivitas semu mendekati harga yang diperkirakan yaitu 100 Ohm meter, sementara fasa impedansi menunjukkan harga pada kisaran 45 derajat. Hal ini mengindikasikan pemodelan yang dilakukan telah sesuai dengan hasil yang diharapkan. Perubahan harga frekuensi tidak menimbulkan perubahan harga resistivitas semu dan fasa impedansi yang berarti baik pada pemodelan dengan modus TE dan TM. Dengan demikian pemodelan elemen batas untuk kasus bumi homogen sesuai dengan hasil yang diperkirakan.

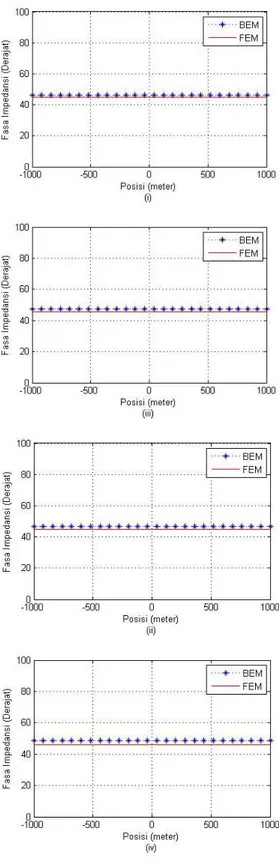
Pemodelan untuk bumi berlapis memperlihat-kan harga resistivitas semu yang relatif dekat antara hasil pemodelan elemen batas dengan solusi analitik (Gambar 8). Pemodelan dengan elemen batas memperlihatkan harga resistivitas semu yang relatif stabil pada kisaran 10 ohm.m untuk semua harga frekuensi yang diujikan, baik pada modus TE maupun modus TM. Sementara nilai fasa impedansi hasil pemodelan elemen batas menunjukkan tingkat kecocokan yang sama dengan hasil analitik. Dengan demikian pengujian dengan solusi analitik 1D memperlihatkan hasil yang diharapkan.

Gambar 5. Perbandingan resistivitas semu bumi homogen 100 ohm.m hasil pemodelan elemen batas modus TE dan TM dengan solusi analitik pada frekuensi (i) 4 Hz, (ii) 8 Hz, (iii) 16 Hz dan (iv) 32 Hz.

Gambar 6. Perbandingan fasa impedansi bumi homogen 100 ohm.m hasil pemodelan elemen batas modus TE dan TM dengan solusi analitik pada frekuensi (i) 4 Hz, (ii) 8 Hz, (iii) 16 Hz dan (iv) 32 Hz.

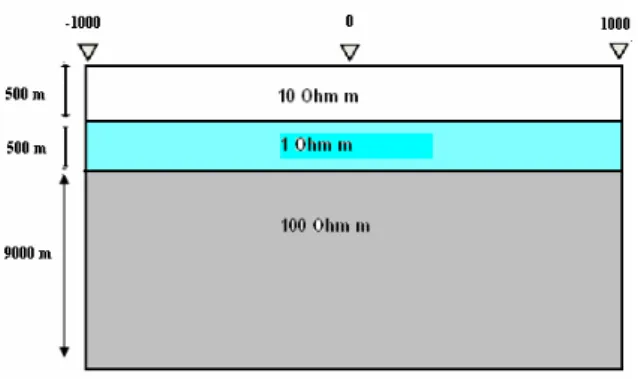
Gambar 7. Model bumi berlapis.

Secara umum, model bumi berlapis diharapkan akan memberikan nilai resistivitas semu yang mewakili harga resistivitas seluruh lapisan, sehingga merupakan representasi kondisi geologis lapisan bawah permukaan. Dengan demikian, nilai yang diharapkan adalah nilai stabil yang merupakan pengaruh dari seluruh lapisan. Pemodelan dengan elemen batas pada seluruh frekuensi memperlihatkan harga resistivitas semu pada kisaran antara 1-10 Ohm meter, atau berada pada dekade yang sama. Sementara respon fasa impedansi cenderung sedikit lebih berfluktuasi pada kisaran dekat dengan harga analitik. Pemodelan elemen batas hanya membutuhkan diskretisasi pada domain, sehingga jumlah elemen yang dibutuhkan jauh lebih sedikit dibandingkan elemen hingga. Namun penggunaan elemen batas konstan membutuhkan pendiskretisasian yang relatif tidak fleksibel terhadap perubahan harga frekuensi. Xu dan Zhou (1997) memodelkan efek topografi dengan menggunakan elemen batas dengan mendiskretisasikan domain dengan panjang elemen lebih kecil dari konstanta panjang gelombang pada daerah domain yaitu sebesar   8 2 2

 . Konstanta tersebut memiliki

kebergantungan pada frekuensi, sehingga metode elemen batas dengan elemen konstan kurang luwes dalam menampilkan perubahan nilai respon akibat perubahan frekuensi. Penggunaan jenis elemen batas yang lain seperti elemen batas linear atau kuadratik lebih fleksibel dalam mengantisipasi perubahan nilai frekuensi.

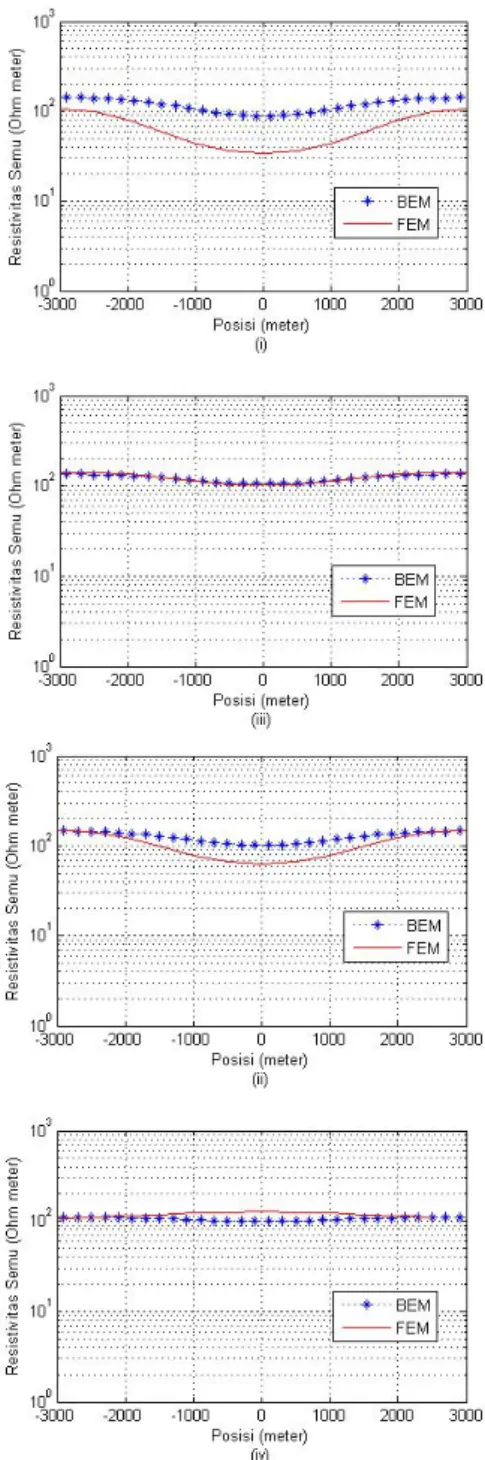
Pemodelan untuk model bumi dengan anomali konduktif memperlihatkan respon yang dihasilkan elemen batas cenderung konstan sedangkan respon elemen hingga cenderung lebih peka terhadap perubahan konduktivitas. Gambar 11 dan Gambar 12 memperlihatkan perubahan resistivitas semu dan fasa impedansi pemodelan elemen batas cenderung stabil dibandingkan pemodelan elemen hingga. Perubahan resistivitas semu pada frekuensi 4 Hz dan 8 Hz memperlihatkan adanya kontras konduktivitas yang dihasilkan anomali konduktif, sedangkan pada frekuensi 16 dan 32 Hz respon lebih memperlihatkan kecenderungan harga stabil yang mendekati harga konduktivitas lapisan penutup (100 Ohm). Untuk

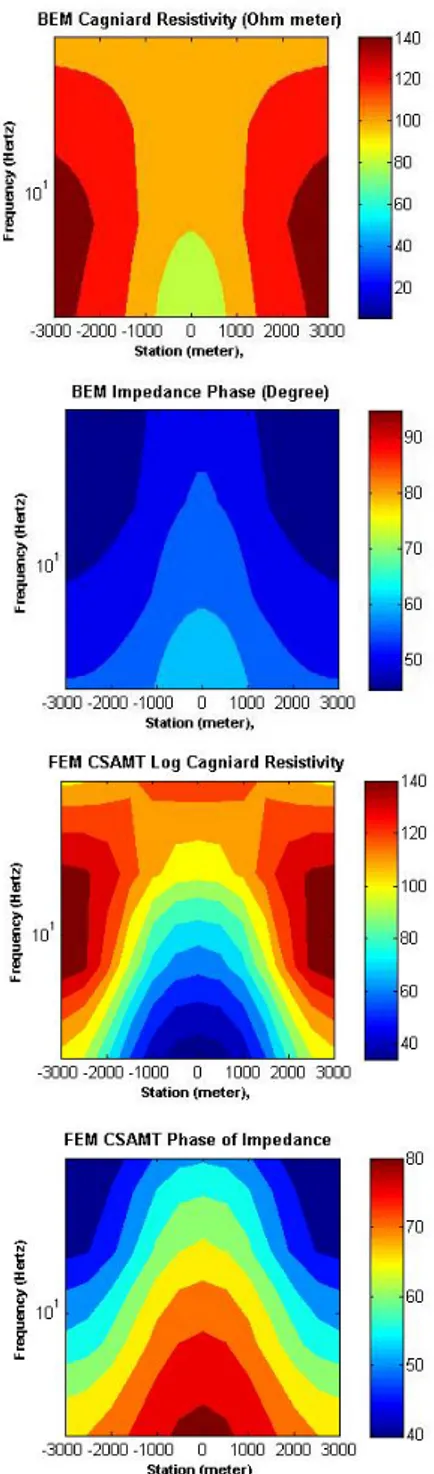
harga fasa impedansi, pemodelan elemen hingga dan elemen batas sama-sama memiliki kecenderungan menurun, namun fasa impedansi untuk elemen hingga lebih memperlihatkan kontras struktur anomali. Pada frekuensi 4 Hz harga fasa impedansi elemen hingga memiliki nilai yang agak jauh dengan nilai elemen batas, namun pada frekuensi setelah 4 Hz harga fasa impedansi elemen hingga dan elemen batas mulai bersesuaian. Penampang semu resistivitas dan fasa impedansi model anomali konduktif (Gambar 13) memperlihatkan bagaimana respon pemodelan elemen batas cenderung stabil dan kurang peka terhadap perubahan struktur bawah permukaan, sedangkan hasil pemodelan elemen hingga memperlihatkan hasil yang cenderung responsif terhadap perubahan struktur bawah permukaan.

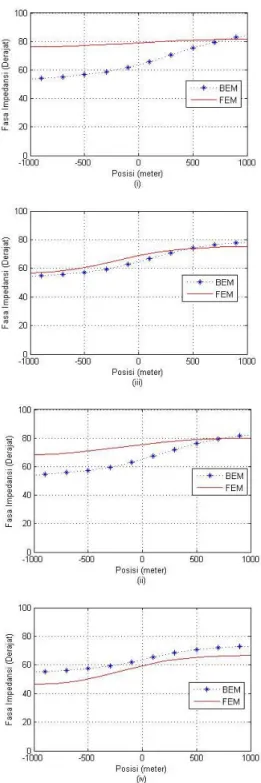
Untuk model bumi berlapis dengan kontak vertikal, trend respon elemen hingga dan elemen batas mirip dengan model bumi berlapis dengan anomali konduktif. Dari Gambar 15 dan 16 terlihat respon resistivitas semu dan fasa impedansi hasil pemodelan elemen batas dan elemen hingga cenderung memiliki trend yang mirip dengan harga yang sedikit berbeda pada frekuensi rendah. Seiring dengan kenaikan frekuensi, harga respon elemen hingga dan elemen batas cenderung saling mendekati. Penampang semu resistivitas dan fasa impedansi yang ditunjukkan Gambar 17 juga memperlihatkan bagaimana respon yang dihasilkan kedua pemodelan cenderung mirip terutama pada frekuensi tinggi.

Secara keseluruhan, elemen batas konstan yang digunakan dalam memodelkan kasus magnetotellurik 2D telah memperlihatkan hasil yang cukup baik. Hasil-hasil pemodelan memperlihatkan adanya kontras harga resistivitas semu pada daerah-daerah yang merupakan anomali konduktif. Pemodelan pada elemen batas konstan ini dilakukan dengan harga mesh berinterval 100 meter pada masing-masing domain pemodelan. Pengintegrasian dilakukan dengan integrasi kuadratur Gaussian-Legendre dengan empat titik pengintegrasian. Hasil yang didapatkan relatif cukup baik meskipun efisiensi komputasinya masih perlu ditingkatkan, baik pada waktu komputasi maupun diskretisasi domain, sehingga keunggulan metode elemen batas dapat dimanfaatkan secara optimal. Selain itu, penggunaan elemen batas konstan juga cenderung kurang fleksibel dalam memodelkan respon bumi dengan banyak frekuensi. Diperlukan modifikasi elemen batas supaya lebih stabil dalam memodelkan respon MT 2D dengan banyak frekuensi. Salah satu upaya yang dapat diusulkan adalah dengan menggunakan elemen batas linear, kubik atau kuadratik yang memiliki tingkat kestabilan dan efisiensi tinggi.

Gambar 8. Perbandingan resistivitas semu bumi berlapis hasil pemodelan elemen batas modus TE dan TM dengan solusi analitik pada frekuensi (i) 4 Hz, (ii) 8 Hz, (iii) 16 Hz dan (iv) 32 Hz.

Gambar 9. Perbandingan fasa impedansi bumi berlapis hasil pemodelan elemen batas modus TE dan TM dengan solusi analitik pada frekuensi (i)4 Hz, (ii)8 Hz, (iii) 16 Hz dan (iv) 32 Hz.

Gambar 10. Model bumi berlapis dengan anomali konduktif.

Gambar 11. Respon resistivitas semu bumi berlapis dengan anomali konduktif hasil pemodelan elemen batas (BEM) dan elemen hingga (FEM) pada frekuensi (i) 4 Hz, (ii) 8 Hz, (iii) 16 Hz dan (iv) 32 H.

Gambar 12. Respon fasa impedansi bumi berlapis dengan anomali konduktif hasil pemodelan elemen batas (BEM) dan elemen hingga (FEM) pada frekuensi (i) 4 Hz, (ii) 8 Hz, (iii) 16 Hz dan (iv) 32 Hz.

Gambar 13. Kontur pseudosection resistivitas semu dan fasa impedansi yang dihasilkan pemodelan BEM dan FEM model bumi berlapis dengan anomali konduktif.

Gambar 14. Model bumi berlapis dengan kontak vertikal.

Gambar 15. Respon resistivitas semu bumi berlapis dengan kontak vertikal hasil pemodelan elemen batas (BEM) dan elemen hingga (FEM) pada frekuensi (i) 4 Hz, (ii) 8 Hz, (iii) 16 Hz dan (iv) 32 H.

Gambar 16. Respon fasa impedansi bumi berlapis dengan kontak vertikal hasil pemodelan elemen batas (BEM) dan elemen hingga (FEM) pada frekuensi (i) 4 Hz, (ii) 8 Hz, (iii) 16 Hz dan (iv) 32 Hz.

Gambar 17. Kontur pseudosection resistivitas semu dan fasa impedansi yang dihasilkan pemodelan BEM dan FEM model bumi berlapis dengan kontak vertikal.

4. Kesimpulan

Dari pembahasan dan hasil pemodelan elektromagnetik modus TM dan TE dengan metode elemen batas, dapat disimpulkan metode elemen batas dengan elemen konstan memiliki keunggulan dalam kesederhanaan dan kepraktisan diskretisasi domain. Hasil validasi pemodelan elemen batas konstan untuk model 1D (bumi homogen dan berlapis) menunjukkan harga respon yang bersesuaian dengan nilai yang diharapkan dari solusi analitik.

Pemodelan dengan elemen batas konstan dilakukan dengan mesh yang relatif rapat dan memperlihatkan hasil yang cukup baik, meskipun terdapat penyimpangan dibandingkan harga pemodelan elemen hingga. Hal ini dikarenakan elemen batas konstan kurang fleksibel dalam memodelkan respon MT dengan banyak frekuensi. Pemodelan dengan elemen batas konstan memerlukan penyesuaian panjang elemen untuk mengakomodasi nilai optimal pada setiap harga frekuensi.

Ketidakluwesan elemen batas konstan dalam memodelkan permasalahan elektromagnetik 2D perlu diantisipasi lebih lanjut dengan mengembangkan pemodelan dngan elemen batas jenis lain seperti elemen batas linear, kubik atau kuadratik. Penggunaan elemen batas jenis lain diharapkan dapat pula meningkatkan efektivitas dan efisiensi pemodelan, meningkatkan akurasi hasil perhitungan, serta baik terhadap bentuk pemodelan sistem yang kompleks, misalnya pemodelan pada sistem geologi gunung api atau situs panas bumi. Pada penelitian lanjutan dari topik ini akan dikembangkan pemodelan elemen batas dengan mesh linear, kuadratik dan kubik untuk mendapatkan hasil respon yang lebih baik.

Daftar Pustaka

Brebbia, C. A. and J. Dominguez, 1992, Boundary Elements: an Introductory Course, 2nd edition, Computational Mechanics Publications.

Chouteau, M. and K. Bouchard, 1988, Two dimensional terrain correction in magnetotelluric surveys, Geophysics, 53, 854-862.

Coggon, J. H., 1971, Electromagnetic and electrical modeling by the finite element method,

Geophysics,36, 132-155.

Gaul, L., M. Kogl, and M. Wagner, 2002, Boundary Element Methods for Engineers and Scientist, An Introductory Course with Advanced Topics, Springer-Verlag, Berlin Heidelberg.

Grandis, H., 1999, An alternative algorithm for one dimensional magnetotelluric response calculation, Computers and Geosciences,25, 119-125

Kauffman, A. and G. V. Keller, 1981, The Magnetotelluric Sounding Method, Elsevier, Amsterdam.

Lee, K. H. and H. F. Morrison, 1985, A numerical solution for electromagnetic scattering by a two dimensional inhomogenity, Geophysics,

50, 1163-1165.

Rijo, L., 1977, Modeling of electric and electromagnetic data, Ph.D. thesis, Univ. of Utah.

Srigutomo, W., 1997, Pemodelan Elektromagnetik 2D Menggunakan Metode Elemen Hingga Untuk Sumber Alami dan Sumber Arus Garis, Tesis Magister, Jurusan Fisika ITB. Srigutomo, W. and D. Sutarno, 1998, 2D

Electromagnetic Modeling using Finite Element Method: Application in Magnetotelluric Case, Kontribusi Fisika Indonesia,9:2, 55-65.

Wannamaker, P. E., G. W. Hohmann, and S. H. Ward, 1984, Magnetotelluric Responses of Three Dimensional Bodies in Layered Earth,

Geophysics, 49:9, 1517-1533

Wannamaker, P. E., J. A. Stodt, and L. Rijo, 1986, Two Dimensional Topografic Responses in Magnetotelluric Modeled Using Finite Element, Geophysics, 51:11, 2131-2145. Xu, S. Z., S. K. Zhao, 1987, Two Dimensional

Magnetotelluric Modeling by the Boundary Element Method, J. Geomagn. Geoelectr.,

39, 677-698.

Xu, S. Z. and H. Zhou, 1997, Modeling of 2D Terrain Effect on MT by the Boundary Element Method, Geophys. Prospect.,45, 931-943. Vozoff, K., (Ed.), 1986, Magnetotelluric Methods,

Society of Exploration Geophysicist, Tulsa, Oklahoma.

Ward, S. H. and G. W. Hohmann, Electromagnetic Theory of Geophysical Applications, in

Nabighian, M. N. Ed., 1989,

Electromagnetic Methods, Theory and Practice vol.1, Society of Exploration Geophysicist.