Analisis Sistem Jaringan Distribusi Air Bersih PDAM Tirtalihou Cabang Parapat Dengan Menggunakan Epanet 2.0 Dan Pipe Flow Expert

(1)

BAB II

TINJAUAN PUSTAKA

2.1 Pengertian Air Bersih

Air adalah senyawa kimia yang sangat penting bagi kehidupan makhluk

hidup di bumi ini. Fungsi air bagi kehidupan tidak dapat digantikan oleh senyawa

lain. Penggunaan air yang utama dan sangat vital bagi kehidupan adalah sebagai

air minum. Hal ini terutama untuk mencukupi kebutuhan air di dalam tubuh

manusia itu sendiri. Kehilangan air untuk 15% dari berat badan dapat

mengakibatkan kematian yang diakibatkan oleh dehidrasi. Karenanya orang

dewasa perlu meminum minimal sebanyak 1,5 – 2 liter air sehari untuk

keseimbangan dalam tubuh dan membantu proses metabolisme (Slamet, 2007). Di

dalam tubuh manusia, air diperlukan untuk transportasi zat – zat makanan dalam

bentuk larutan dan melarutkan berbagai jenis zat yang diperlukan tubuh. Misalnya

untuk melarutkan oksigen sebelum memasuki pembuluh-pembuluh darah yang

ada disekitar alveoli (Mulia, 2005).

Air bersih adalah air yang digunakan untuk keperluan sehari-hari dan akan

menjadi air minum setelah dimasak terlebih dahulu. Sebagai batasannya, air

bersih adalah air yang memenuhi persyaratan bagi system penyediaan air minum.

Adapun persyaratan yang di maksud adalah persyaratan dari segi kualitas air yang

meliputi kualitas fisik, kimia, biologi dan radiologis, sehingga apabila dikonsumsi

tidak menimbulkan efek samping (Ketentuan Umum Permenkes

No.416/Menkes/PER/IX/1990).

2.2 Sistem Distribusi Air Bersih

Sistem distribusi adalah system yang langsung berhubungan dengan

(2)

memenuhi syarat ke seluruh daerah pelayanan. System ini meliputi unsur system

perpipaan dan perlengkapannya, hidran kebakaran, tekanan tersedia, system

pemompaan (bila diperlukan), dan reservoir distribusi menurut Damanhuri, E.,

(1989).

Suplai air melalui pipa induk mempunyai dua macam system menurut Kamala, K. R., (1999), yaitu :

 Continuous system

Dalam system ini air minum yang disuplai ke konsumen mengalir terus

menerus selama 24 jam. Keuntungan system ini adalah konsumen setiap saat pada

memperoleh air bersih dari jaringan pipa distribusi di posisi pipa manapun.

Sedang kerugiannya pemakaian air akan cenderung akan lebih boros dan bila

terjadi sedikit kebocoran saja, maka jumlah air yang hilang akan sangat besar

jumlahn ya.

 Intermitten system

Untuk mendistribusi air minum kepada konsumen dengan kuantitas, kualitas dan

tekanan yang cukup memerlukan system perpipaan yang baik, reservoir, pompa

dan peralatan yang lain. Metode dari pendistribusian air tergantung pada kondisi

topografi dari sumber air dan posisi para konsumen berada.

2.3 Kebutuhan Konsumsi Air Bersih

Kebutuhan air dapat didefenisikan sebagai jumlah air yang dibutuhkan

untuk keperluan rumah tangga, industry, pengelolaan kota dan lain-lain. Dalam

melayani jumlah cakupan pelayanan penduduk akan air bersih, maka

direncanakan kapasitas sistem penyediaan air bersih yang dibagi dalam dua

klasifikasi pemakaian air, yaitu untuk keperluan domestik (rumah tangga) dan non

(3)

2.3.1Kebutuhan Air Domestik

Kebutuhan Air Bersih Untuk Domestik (Rumah Tangga). Menurut

Peraturan Menteri Kesehatan Republik Indonesia No.416/MENKES/PER/IX/1990

menyatakan bahwa kebutuhan domestik dimaksudkan adalah untuk memenuhi

kebutuhan air bersih bagi keperluan rumah tangga yang dilakukan melalui

Sambungan Rumah (SR) dan kebutuhan umum yang disediakan melalui fasilitas

Hidran Umum (HU). Pada Tabel 2.1 dibawah ini menunjukkan besar debit

domestik yang dibutuhkan untuk memenuhi kebutuhan domestik diperhitungkan

terhadap beberapa faktor:

a. Jumlah penduduk yang akan dilayani menurut target tahapan perencanaan

sesuai dengan rencana cakupan pelayanan.

b. Tingkat pemakaian air bersih diasumsikan tergantung pada kategori daerah

dan jumlah penduduknya.

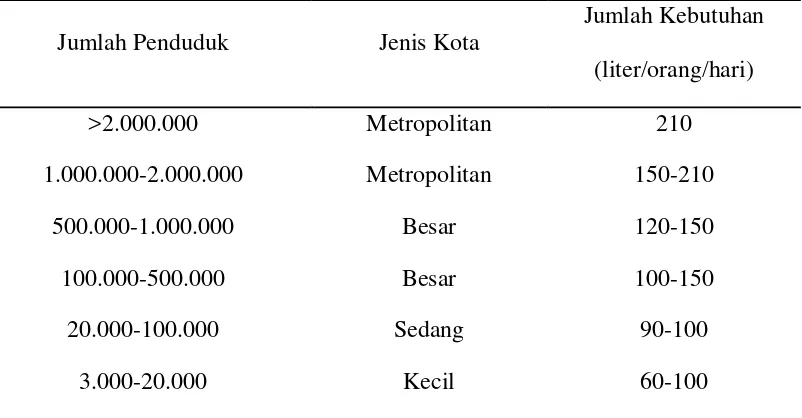
Tabel 2.1 Kebutuhan air domestik berdasarkan jenis kota dan jumlah penduduk

Jumlah Penduduk Jenis Kota

Jumlah Kebutuhan

(liter/orang/hari)

>2.000.000 Metropolitan 210

1.000.000-2.000.000 Metropolitan 150-210

500.000-1.000.000 Besar 120-150

100.000-500.000 Besar 100-150

20.000-100.000 Sedang 90-100

3.000-20.000 Kecil 60-100

(4)

2.3.2Kebutuhan Air Non Domestik

Kebutuhan air non domestik merupakan tahap berikutnya dalam

perhitungan kebutuhan air bersih, besaran pemakaiannya ditentukan oleh jumlah

konsumen non domestik yang terdiri dari fasilitas-fasilitas yang telah disebutkan.

Sebagaimana penjelasan sebelumnya bahwa ada beberapa faktor yang dapat

menentukan perkembangan jumlah fasilitas tersebut, yaitu pertambahan

penduduk, jenis dan perluasan fasilitas serta perkembangan sosial ekonomi.

Perhitungan proyeksi fasilitas dapat dilakukan dengan pendekatan perbandingan

jumlah penduduk.

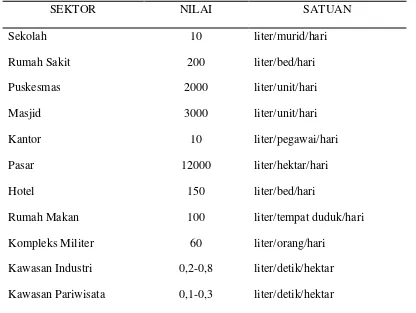
Tabel 2.2 Kebutuhan air non domestik untuk kategori kota

SEKTOR NILAI SATUAN

Sekolah 10 liter/murid/hari

Rumah Sakit 200 liter/bed/hari

Puskesmas 2000 liter/unit/hari

Masjid 3000 liter/unit/hari

Kantor 10 liter/pegawai/hari

Pasar 12000 liter/hektar/hari

Hotel 150 liter/bed/hari

Rumah Makan 100 liter/tempat duduk/hari

Kompleks Militer 60 liter/orang/hari

Kawasan Industri 0,2-0,8 liter/detik/hektar

Kawasan Pariwisata 0,1-0,3 liter/detik/hektar

Sumber : Kriteria Perencanaan Ditjen Cipta Karya Dinas PU, 1996.

(5)

SEKTOR NILAI SATUAN

Sekolah 5 liter/murid/hari

Rumah Sakit 200 liter/bed/hari

Puskesmas 2000 liter/unit/hari

Masjid 3000 liter/unit/hari

Mushola 2000 liter/unit/hari

Pasar 12000 liter/hektar/hari

Komersial/Industri 10 liter/hari

Tabel 2.4 Kebutuhan air non domestik untuk kategori lainnya

SEKTOR NILAI SATUAN

Lapangan Terbang 10 liter/orang/detik

Pelabuhan 50 liter/orang/detik

Stasiun KA dan Terminal

10 liter/orang/detik Bus

Kawasan Insustri 0,75 liter/orang/hektar

2.4 Kapasitas dan Kebutuhan Fluktuasi Air Bersih

Penentuan kebutuhan air mengacu kepada kebutuhan air harian maksimum

(Qmaks) serta kebutuhan air jam maksimum (Qpeak) dengan referensi kebutuhan

air rata-rata.

a. Kebutuhan air rata-rata harian (QAv) adalah jumlah air yang diperlukan

(6)

b. Kebutuhan air harian maksimum merupakan jumlah air terbanyak yang

diperlukan pada satu hari dalam kurun waktu satu tahun berdasarkan nilai Q

rata-rata harian. Diperlukan faktor fluktuasi kebutuhan harian maksimum

dalam perhitungannya.

Qmaks = fmaks x Qav ... (2.1)

Dimana :

Qmaks = Kebutuhan air harian maksimum (ltr/det)

fmaks = Faktor harian maksimum (1 < f maks < 1,5 )

QAv = Kebutuhan air rata-rata harian (ltr/det)

c. Kebutuhan air jam maksimum adalah jumlah air terbesar yang diperlukan

pada jam-jam tertentu. Faktor fluktuasi kebutuhan jam maksimum (fpeak)

diperlukan dalam perhitungannya.

Qpeak = fpeakx Qmaks ... (2.2)

Dimana :

Qpeak = Kebutuhan air jam maksimum (ltr/detik)

fpeak = Faktor fluktuasi jam maksimum ( 1 ,5 - 2,5 )

Qmax = Kebutuhan air harian maksimum (ltr/detik)

Banyak faktor yang mempengaruhi fluktuasi pemakaian air per jam,

dan untuk mendapatkan data ini diperlukan survei dan penelitian terhadap

aktivitas, kebiasaan serta kebutuhan air konsumen. Selain kapasitas

produksi pada unit pengolahan, perlu diperhitungkan juga faktor-faktor lain

yang berpengaruh terhadap perencanaan unit pengolahan.

d. Kehilangan air yaitu selisih antara jumlah air yang diproduksi di unit

pengolahan dengan jumlah air yang dikonsumsi dari jaringan distribusi.

Berdasarkan kenyataan di lapangan, kejadian akan kehilangan air dapat

bersifat teknis dan non teknis.

2.5 Debit Aliran

Jumlah zat cair yang mengalir melalui tampang lintang aliran tiap satu

(7)

aliran biasanya diukur dalam volume zat cair tiap satuan waktu, sehingga

satuannya adalah meter kubik per detik (m3/detik) atau satuan yang lain

(liter/detik, liter/menit).

Di dalam zat cair ideal, dimana tidak terjadi gesekan. Kecepatan aliran V

adalah sama di setiap titik pada tampang lintang. Apabila tampang aliran tegak

lurus pada arah aliran adalah A, maka debit aliran diberikan oleh bentuk berikut:

Q = V x A ... (2.3)

Dimana : Q = Debit aliran (m3/detik)

V = Kecepatan aliran (m/det)

A = luas penampang aliran (m2)

Dalam persamaan kontinuitas zat cair yang tak kompresibel mengalir secara

kontiniu melalui pipa atau saluran terbuka, dengan tampang aliran konstan

ataupun tidak konstan maka volume zat cair yang lewat tiap satuan waktu adalah

semua tampang (Bambang, 1993).

Dipandang dari tabung aliran seperti gambar 2.1 untuk aliran satu dimensi

dan mantap, kecepatan rata dan tampang lintang titik 1 dan 2 adalah V1 dan V2.

Sehingga persamaan kontinuitas melalui medan aliran adalah sebagai berikut:

Q1 = Q2 ... (2.4)

Dimana : Q1 dan Q2 = Debit aliran pada penampang 1 dan 2 (m3/detik)

(8)

2.6 Persamaan Bernoulli

Penurunan persamaan Bernoulli untuk aliran sepanjang garis arus

didasarkan pada hukum Newton II tentang gerak (F=ma). Persamaan ini

diturunkan dengan anggapan bahwa (Bambang, 1993):

1. Zat cair adalah ideal, jadi tidak mempunyai kekentalan (kehilangan energi

akibat gesekan adalah nol);

2. Zat cair adalah homogen dan tidak termampatkan (rapat massa zat cair

adalah konstan);

3. Aliran adalah kontiniu dan sepanjang garis arus;

4. Kecepatan aliran adalah merata dalam suatu penampang;

5. Gaya yang bekerja hanya gaya berat dan tekanan

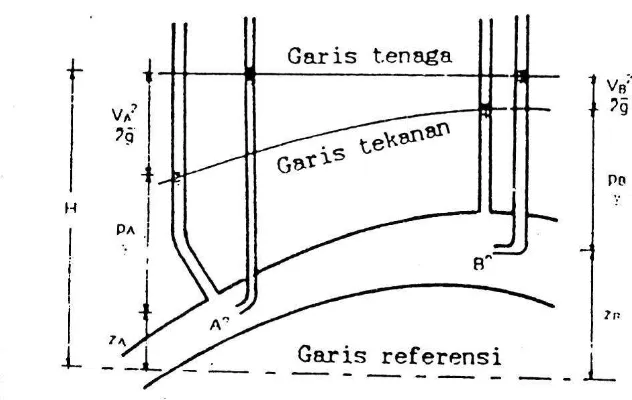
Persamaan Bernoulli dapat digunakan untuk menentukan garis tekanan dan

tenaga (gambar 2.2). Garis tenaga dapat ditunjukkan oleh elevasi muka air pada

tabung pitot yang besarnya sama dengan tinggi total dari konstanta Bernoulli.

Sedang garis tekanan dapat ditunjukkan oleh elevasi muka air di dalam tabung

vertikal yang disambung pada pipa (Bambang, 1993).

� =�+ γ +

�2

2 ... (2.5)

Dimana: p = tekanan pada titik A dan B (kN/m2)

V = kecepatan aliran pada titik A dan B (m/det)

z = perbedaan ketinggian antara titik A dan B (m)

γ = berat jenis fluida (kN/m3

)

g = percepatan gravitasi = 9,81 m/det2

Pada aliran zat cair ideal, garis tenaga mempunyai tinggi tetap yang

(9)

Garis tekanan menunjukkan jumlah dari tinggi elevasi dan tinggi tekanan z + p/

yang bisa naik atau turun pada arah aliran dan tergantung pada luas tampangm

aliran. Di titik A dimana tampang aliran lebih kecil dari titik B, mengingat VA

lebih besar daripada VB. Akibatnya tinggi tekanan di A lebih kecil daripada di B.

Gambar 2.2 Garis Tenaga dan Tekanan Pada Zat Cair Ideal

Aplikasi persamaan Bernoulli untuk kedua titik di dalam medan aliran

adalah:

+

γ +

�2

2 = + γ +

�2

2 ... (2.6)

Dimana:

PA dan PB = tekanan pada titik A dan B (kN/m2)

VA dan VB = kecepatan aliran pada titik A dan B (m/det)

ZA dan ZB = perbedaan ketinggian antara titik A dan B (m)

)

Persamaan di atas digunakan jika diasumsikan bahwa jumlah tinggi elevasi,

(10)

garis tenaga pada aliran zat cair ideal adalah konstan.Untuk zat cair riil (viskos),

dalam aliran zat cair akan terjadi kehilangan tenaga yang harus diperhitungkan

dalam aplikasi persamaan Bernoulli. Kehilangan tenaga hanya dapat terjadi

karena adanya gesekan antara zat cair dan dinding batas (hf) atau karena adanya

perubahan tampang lintang aliran (he). Kehilangan tenaga biasanya dinyatakan

dalam tinggi zat cair. Maka persamaan Bernoulli di atas dapat ditulis menjadi

persamaan baru, dimana dirumuskan sebagai:

+

hf = kehilangan tekanan (m)

PA dan PB = tekanan pada titik A dan B (kN/m2)

VA dan VB = kecepatan aliran pada titik A dan B (m/det)

ZA dan ZB = perbedaan ketinggian antara titik A dan B (m)

)

2.7 Aliran Laminer dan Turbulen

Aliran viskos dapat dibedakan menjadi dua tipe yaitu aliran laminer dan

turbulen. Dalam aliran laminer partikel-partikel zat cair bergerak teratur

mengikuti lintasan yang saling sejajar. Aliran ini terjadi apabila kecepatan kecil

dan kekentalan besar.

Pengaruh kekentalan adalah sangat besar sehingga dapat meredam

gangguan yang dapat menyebabkan aliran menjadi turbulen. Dengan

berkurangnya kekentalan dan bertambahnya kecepatan aliran maka daya redam

terhadap gangguan akan berkurang, yang sampai pada suatu batas tertentu akan

(11)

turbulen gerak partikel-partikel zat cair tidak teratur. Aliran ini terjadi apabila

kecepatan besar dan kekentalan zat cair kecil (Bambang, 1993).

Menurut Reynolds, ada tiga faktor yang mempengaruhi keadaan aliran yaitu

kekentalan zat cair µ(mu), rapat massa zat cair ρ(rho), dan diameter pipa D.

Hubungan antara µ, ρ, dan D yang mempunyai dimensi sama dengan kecepatan

adalah µ/ρD.

Reynolds menunjukkan bahwa aliran dapat diklasifikasikan berdasarkan

suatu angka tertentu. Angka tersebut diturunkan dengan membagi kecepatan

aliran di dalam pipa dengan nilai µ/ρD, yang disebut dengan angka Reynolds

(Bambang, 1993). Angka Reynolds mempunyai bentuk berikut:

Re = �

µ/ρD=

ρDV

µ atau Re = VD

µ ... (2.8)

Dimana : Re = Reynolds number

μ = viskositas dinamik (Pa.det)

ρ = rapat massa zat cair (kg/m3)

D = diameter dalam pipa (m)

v = kecepatan aliran dalam fluida (m/det)

Berdasarkan pada percobaan aliran di dalam pipa, Reynolds menetapkan

bahwa untuk angka Reynolds di bawah 2.000, gangguan aliran dapat diredam oleh

kekentalan zat cair dan aliran dalam kondisi tersebut adalah laminer. Aliran akan

turbulen apabila angka Reynolds lebih besar 4.000. Apabila angka Reynolds

berada diantara kedua nilai tersebut ( 2000 < Re < 4000 ) aliran adalah transisi.

Angka Reynolds pada kedua nilai di atas (Re = 2000 dan Re = 4000) disebut

(12)

2.8 Kehilangan Tinggi Tekanan

Kehilangan tinggi tekanan dapat berupa kehilangan mayor (mayor losses)

dan kehilangan minor (minor losses).

2.8.1 Kehilangan Tinggi Tekanan Mayor

Mayor losses terjadi sebagai akibat gesekan air dengan pipa. Kerugian head

akibat gesekan dapat dihitung dengan menggunakan dari beberapa rumus berikut,

yaitu:

2.8.1.1 Persamaan Darcy – Weisbach

Dalam dinamika fluida, persamaan Darcy-Weisbach adalah persamaan

fenomenologika yang berkaitan dengan head loss, atau kehilangan tekanan akibat

gesekan sepanjang pipa terhadap kecepatan aliran rata-rata. Persamaan ini

terbentuk atas kontribusi Henry Darcy dan Julius Weisbach.

Rumus Darcy-Weisbach merupakan dasar menghitung head turun untuk

aliran fluida dalam pipa-pipa dan saluran (Herman, 1984). Persamaannya adalah:

= � �2

2 ... (2.9)

Dimana:

hf = kerugian head karena gesekan (m)

f = faktor gesekan (diperoleh dari diagram Moody)

D = diameter pipa (m)

L = panjang pipa (m)

V = kecepatan aliran fluida dalam pipa (m/det)

(13)

Tabel 2.5 Kekasaran rata-rata pipa komersil (Frank, 1986)

Bahan (dalam keadaan baru)

Kekasaran (ε)

ft mm

Baja Keling 0,003-0,03 0,9-9,0

Beton 0,001-0,01 0,3-3,0

Bilah tahang kayu 0,0006-0,003 0,18-0,9

Beso Cor 0,00085 0,28

Besi berbalut-seng 0,0005 0,15

Besi-cor beraspal 0,0004 0,12

Baja kkomersial atau besi tempa 0,00015 0,046

Tabung/pipa tarik 0,000005 0,0015

Kaca "halus" "halus"

Gambar 2.3 Diagram Moody

Diagram Moody telah digunakan untuk menyelesaikan permasalahan aliran

fluida di dalam pipa dengan menggunakan faktor gesekan pipa (f) dari rumus

(14)

2000, faktor gesekan dihubungkan dengan bilangan Reynolds, dinyatakan dengan

rumus:

f =64 ... (2.10)

Untuk aliran turbulen dimana bilangan Reynolds lebih besar dari 4000,

maka hubungan antara bilangan Reynolds, faktor gesekan dan kekasaran relatif

menjadi lebih kompleks. Faktor gesekan untuk aliran turbulen dalam pipa

didapatkan dari hasil eksperimen antara lain (Herman, 1986) :

a. Untuk daerah complete roughness, rough pipes yaitu :

1

= 2,0 log 3,7

ε/d ... (2.11)

b. Untuk pipa sangat halus seperti gelas dan plastik, hubungan antara bilangan

Reynolds dan faktor gesekan yaitu :

1. Blasius : f=0,316_0,25 ... (2.12) untuk Re = 3000 – 100.000

2. Von Karman : 1= 2,0 log

2,51 ... (2.13)

= 2,0 log −0.8 ... (2.13)

Untuk Re sampai dengan 3,106

c. Untuk pipa kasar, yaitu :

Von Karman :1 = 2,0 log

ε + 1,74 ... (2.14)

Dimana harga f tidak tergantung pada bilangan Reynolds.

d. Untuk pipa antara kasar dan halus atau dikenal dengan daerah transisi yaitu :

Corelbrook – White : 1 =−2,0 log ε/d

3,7 + 2,51

... (2.15)

Dimana: Re = Bilangan Reynolds

f = faktor gesekan

(15)

2.8.1.2 Persamaan Hazen – Williams

Rumus ini pada umumnya dipakai untuk menghitung kerugian head dalam

pipa yang relatif sangat panjang seperti jalur pipa penyalur air minum. Bentuk

umum persamaan Hazen–Williams, yaitu:

=10.666_1.95 _4.951.95� ... (2.16) Dimana:

hf = kerugian gesekan dalam pipa (m)

Q = laju aliran dalam pipa (m3/det)

L = panjang pipa (m)

C = koefisien kekasaran pipa Hazen – Williams

d = diameter pipa (m)

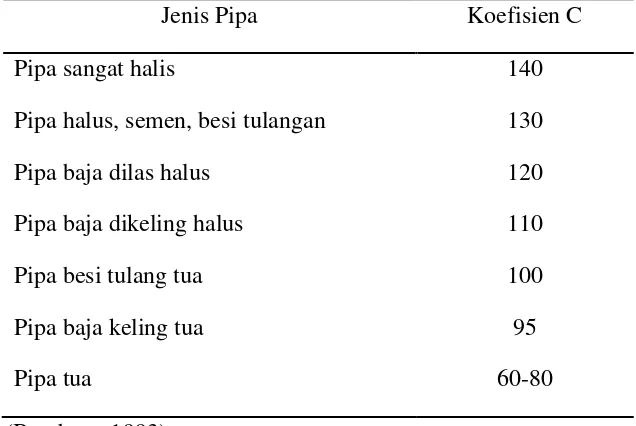
Tabel 2.6 Koefisien kekasaran Hazen–Wiliam, C

Jenis Pipa Koefisien C

Pipa sangat halis 140

Pipa halus, semen, besi tulangan 130

Pipa baja dilas halus 120

Pipa baja dikeling halus 110

Pipa besi tulang tua 100

Pipa baja keling tua 95

Pipa tua 60-80

(Bambang,1993)

2.8.2 Kehilangan Tinggi Tekan Minor

Rerugi kecil disebabkan (Frank, 1986) oleh:

(16)

2. Pemuaian atau penyusutan tiba-tiba;

3. Kelokan, siku, sambungan T, dan piting lain;

4. Katup yang terbuka atau sebagian tertutup;

5. Pemuaian atau penyusutan berangsur.

Rerugi di atas mungkin tidak begitu kecil, misalnya katup yang

tertutupsebagian dapat menyebabkan penurunan tekanan yang lebih besar

daripada pipa yang panjang. Karena pola aliran dalam piting dan katup cukup

rumit, teorinya sangat lemah. Rerugi ini biasanya diukur secara eksperimental dan

dikorelasikan dengan parameter-parameter aliran pipa.

Besarnya kerugian minor dirumuskan sebagai berikut:

= � .�.�2

2 ... (2.17)

Dimana:

g = percepatan gravitasi (9,81 m/det2)

v = kecepatan aliran fluida dalam pipa (m/det)

k = koefisien kerugian

Tabel 2.7 Kehilangan Tinggi Tekanan pada Katup, Alat Penyesuaian dan Pipa

Harga K dalam h= �.�2

2

1. Katup pintu

- Terbuka penuh 0,19

- 3/4 terbuka 1,15

- 1/2 terbuka 5,6

- 1/4 terbuka 24

2. Katup bola, terbuka 10

(17)

4. Bengkokan 90ᵒ

- Jari-jari pendek 0,9

- Jari-jari pertengahan 0,75

- Jari-jari panjang 0,6

5. Lengkungan pengembalian 180ᵒ 2,2

6. Bengkokan 45ᵒ 0,42

7. Bengkokan 22 1/2 ᵒ (45cm) 0,13

8. Sambungan T 1,25

9.

Sambungan pengecil (katup pada ujung yang

kecil) 0,25

10. Sambungan pembesar 0,25 �12− �22 /2

11. Sambungan pengecil mulut lonceng 0,1

12. Lubang terbuka 1,8

2.9 Persamaan Empiris Untuk Aliran Didalam Pipa

Seperti yang diuraikan sebelumnya bahwa permasalahan aliran fluida dalam

pipa dapat diselesaikan dengan menggunakan persamaan Darcy-Weisbach dan

Diagram Moody. Penggunaan rumus empiris juga dapat digunakan untuk

menyelesaikan permasalahan aliran. Dalam hal ini digunakan dua model rumus

yaitu persamaan Hazen Williams dan persamaan Manning.

1. Persamaan Hazen-Williams dengan menggunakan satuan

international yaitu (Robert, 2002):

� = 0.849 0.68 0.84 ... (2.18) Dimana :

(18)

C = koefisien kekasaran pipa Hazen-Williams

R = jari-jari hidrolis ; d/4 untuk pipa bundar

s = slope dari gradient energi (Hl/L)

2. Persamaan Manning dengan satuan international yaitu (Robert,

2002):

� =1 2/3 1/2 ... (2.19)

Dimana :

n = koefisien kekasaran pipa Manning

R = jari-jari hidrolis ; d/4 untuk pipa bundar

s = slope dari gradient energi (Hl/L)

Persamaan Hazen-Williams umumnya digunakan untuk menghitung head

loss dalam pipa yang sangat panjang seperti jalur pipa penyedia air minum.

Persamaan ini tidak dapat digunakan untuk zat cair lain selain air dan digunakan

khusus untuk aliran yang bersifat turbulen. Persamaan Darcy-Weisbach secara

teoritis tepat digunakan untuk semua rezim aliran dan semua jenis zat cair.

Persamaan Manning biasanya digunakan untuk saluran terbuka (open channel

flow).

2.10 Jaringan Pipa

Pemakaian jaringan pipa dalam bidang teknik sipil terdapat pada sistem

jaringan distribusi air minum. Sistem jaringan ini merupakan bagian yang paling

mahal dari suatu perusahaan air minum. Oleh karena itu harus dibuat perencanaan

yang teliti untuk mendapatkan sistem distribusi yang efisien. Jumlah atau debit air

yang disediakan tergantung pada jumlah penduduk dan macam industri yang

dilayani. Analisis jaringan pipa ini cukup rumit dan memerlukan perhitungan

yang besar, oleh karena itu pemakaian komputer untuk analisis ini akan

mengurangi kesulitan. Untuk jaringan kecil, pemakaian kalkulator untuk hitungan

masih dilakukan. Ada beberapa metode untuk menyelesaikan perhitungan sistem

(19)

Aliran keluar dari sistem biasanya dianggap terjadi pada titik-titik simpul.

Metode Hardy-Cross ini dilakukan secara iteratif. Pada awal hitungan ditetapkan

debit aliran melalui masing-masing pipa secara sembarang. Kemudian dihitung

debit aliran di semua pipa berdasarkan nilai awal tersebut. Prosedur hitungan

diulangi lagi sampai persamaan kontinuitas di setiap titik simpul dipenuhi. Pada

jaringan pipa harus dipenuhi persamaan kontinuitas dan tenaga (Bambang

Triatmodjo, 1993: 91-92) yaitu :

1. Aliran di dalam pipa harus memenuhi hukum-hukum gesekan pipa untuk

aliran dalam pipa tunggal.

= 8 � �2 5

2_{... (2.34)}

2. Aliran masuk ke dalam tiap-tiap simpul harus sama dengan aliran yang

keluar.

= 0 ... (2.35)

3. Jumlah aljabar dari kehilangan tenaga dalam satu jaringan tertutup harus

sama dengan nol

= 0 ... (2.36)

2.11 Prosedur Perhitungan Hardy-Cross

(20)

Prosedur perhitungan dengan metode Hardy-Cross adalah sebagai berikut

(Bambang, 1993):

1. Pilih pembagian debit melalui tiap-tiap pipa Qo hingga terpenuhi

kontinuitas;

2. Hitung hf pada tiap pipa, hf = k.Q2

3. Jaringan pipa dibagi menjadi sejumlah jaringan tertutup (tiap pipa

minimal masuk dalam satu jaringan);

4. Hitung Σhf tiap jaringan, jika pengaliran seimbang, Σhf = 0

5. Hitung nilai Σ |2kQ| untuk tiap jaringan

6. Hitung koreksi debit ∆ = � 2

2� ... (2.37)

Dimana : Qo = debit permisalan

7. Koreksi debit, Q = Qo + ΔQ, prosedur 1–6 diulangi hingga diperoleh ∆ ≈0

Pada suatu jaringan perpipaan harus dipenuhi ketentuan berikut:

 Perjumlahan tekanan disetiap circuit = 0 (nol)

 Aliran yang masuk pada setiap titik simpul = aliran keluar

 Persamaan Darcy–Weisbach atau rumus eksponensial berlaku untuk masing-masing pipa.

Analisis jaringan pipa ini cukup rumit dan memerlukan perhitungan yang

besar, oleh karena itu pemakaian komputer untuk analisis ini akan mengurangi

kesulitan.

2.12 Epanet 2.0

Menurut Rossman (2000), Epanet adalah program komputer yang

menggambarkan simulasi hidrolis dan kecenderungan kualitas air yang mengalir

di dalam jaringan pipa. Jaringan itu sendiri terdiri dari Pipa, Node (titik koneksi

pipa), pompa, katub, dan tangki air atau reservoir. Epanet menjajaki aliran air di

(21)

yang mengalir di dalam pipa selama dalam periode pengaliran. Sebagai tambahan,

usia air (water age) dan pelacakan sumber dapat juga disimulasikan.

Epanet di design sebagai alat untuk mencapai dan mewujudkan pemahaman

tentang pergerakan dan nasib kandungan air minum dalam jaringan distribusi.

Juga dapat digunakan untuk berbagai analisa berbagai aplikasi jaringan

distribusi. Sebagai contoh untuk pembuatan design, kalibrasi model hidrolis,

analisa sisa khlor, dan analisa pelanggan. Epanet dapat membantu dalam

memanage strategi untuk merealisasikan qualitas air dalam suatu system. Semua

itu mencakup :

 Alternatif penggunaan sumber dalam berbagai sumber dalam satu sistem  Alternatif pemompaan dlm penjadwalan pengisian/pengosongan tangki.  Penggunaan treatment, misal khlorinasi pada tangki penyimpan

 Pen-target-an pembersihan pipa dan penggantiannya.

Dijalankan dalam lingkungan windows, Epanet dapat terintegrasi untuk

melakukan editing dalam pemasukan data, running simulasi dan melihat hasil

running dalam berbagai bentuk (format), Sudah pula termasuk kode-kode yang

berwarna pada peta, tabel data-data, grafik, serta citra kontur.

2.13 Software Pipe Flow Expert

Menurut Daxesoft (2015), Software Pipe Flow Expert adalah aplikasi

perangkat lunak yang berjalan pada sistem operasi Microsoft Windows. Software

Pipe Flow Expert memiliki antarmuka intuitif yang membuatnya mudah bagi

pengguna untuk mulai bekerja pada desain pipa mereka, yang dapat ditarik keluar

pada grid isometrik 2D atau 3D.

Software Pipe Flow Expert dirancang untuk membantu insinyur hari ini

menganalisa dan memecahkan berbagai masalah hidrolik dimana laju aliran,

kerugian tekanan dan persyaratan memompa seluruh jaringan pipa harus

ditentukan. Software Pipe Flow Expert akan memungkinkan Anda untuk dengan

(22)

terjadi. Pipa Arus Ahli menghitung aliran dan tekanan kondisi stabil seimbang

dari sistem. Software ini akan memungkinkan Anda untuk melakukan analisis

sistem alternatif dalam berbagai kondisi operasi. Hasil yang dilaporkan meliputi:

 Debit aliran untuk setiap pipa  Kecepatan cairan untuk setiap pipa  Nomor Reynolds

 Faktor gesekan

 Kehilangan tekanan gesekan  Tekanan pada setiap node

 HGL nilai (Hydraulic Grade Line)  Nilai Operasi Pompa

Input dan menampilkan informasi sistem pada gambar Pipa Aliran Ahli dan

di tabel hasil dapat ditampilkan dalam satuan metrik atau imperial sesuai

preferensi Anda dan unit khusus untuk setiap item (seperti laju aliran) juga dapat

dikonfigurasi dan diatur pada secara individual seperti yang diperlukan.

Software Pipe Flow Expert telah dirancang untuk insinyur profesional yang

membutuhkan alat yang ampuh yang memiliki terkemuka kelas, mudah digunakan

dan antarmuka yang kuat yang membuatnya mudah untuk merancang dan