Catatan Kuliah
MA2081 Statistika Dasar
“Orang Cerdas Belajar Statistika”Dosen: Khreshna I.A. Syuhada, MSc. PhD.
Kelompok Keilmuan Statistika - FMIPA
Institut Teknologi Bandung
Tentang MAK6281 Topik Statistika IV
Jadwal kuliah: Senin, 13-; Rabu,
9-Silabus:
- Statistika deskriptif
- Peluang
- Peubah acak dan fungsi peluang/distribusi
- Distribusi diskrit dan kontinu
- Distribusi sampel
- Statistika inferensi: selang kepercayaan
- Statistika inferensi: uji hipotesis
- Analisis variansi
- Analisis regresi dan korelasi
Buku teks:
Ronald Walpole, Raymond Myers, Sharon Myers, Keying Ye, 2007, Probability and
Statistics for Engineers and Scienctists.
Penilaian:
- Ujian 2 kali (75%); UTS - 9 Maret 2015, Pukul 13.00
- Kehadiran/PR/Tugas (15%)
Bab 1 - Statistika Deskriptif
Silabus: Jenis data, ukuran pusat/lokasi, ukuran penyebaran, koefisien variasi,
ob-servasi luar, data kelompok, distribusi frekuensi, grafik
Statistika adalah ilmu yang digunakan untuk mengumpulkan, mengorganisasi, melakukan
inferensi dan menafsirkan data. Secara singkat, statistika adalah ilmu/pekerjaan
un-tuk meyimpulkan tentang suatu fenomena pada populasi menggunakan sampel.
Kajian awal dan utama dalam analisis data adalah statistika deskriptif. Kita
da-pat menghitung berbagai statistik dan membuat grafik serta memberikan
interpre-tasi. Kesimpulan yang diberikan dalam statistika deskriptif bersifat subyektif; walau
demikian, kesimpulan yang salah akan terlihat.
Tujuan yang ingin dicapai dalam memahami statistika deskriptif, secara detil, adalah
1. membedakan jenis data dan memahami data
2. menghitung dan memaknai ukuran lokasi/pusat
3. membedakan variansi dan koefisien variasi
4. mengamati observasi luar
5. memahami data kelompok
6. menentukan distribusi frekuensi
7. membuat dan menafsirkan grafik
Data, Jenis Data, Memahami Data
Data adalah hasil observasi tunggal (datum) yang didapat baik secara langsung
(ob-servasi/survey, praktikum) ataupun tidak langsung (buku, koran, internet). Data
merupakan sumber utama analisis data. Pengumpulan, pengorganisasian dan
Dalam praktiknya, data yang kita kumpulkan dapat dikelompokkan menjadi data
kategorik atau data numerik. Hal ini merujuk pada sifat data yang memiliki label
(kategorik) atau memiliki nilai (numerik). Data dapat pula dibedakan menjadi jenis
data berikut:
• nominal (jenis kelamin, golongan darah)
• ordinal (tingkat kecemasan, tingkat nyeri)
• rasio/interval (denyut nadi, tekanan darah, nilai ujian)
Latihan:
Perhatikan kalimat-kalimat berikut. Tentukan jenis datanya (nominal, ordinal,
ra-sio/interval).
(a) “dr. KS, SpD. mengatakan bahwa penyakit Noor sudah kronis, bukan akut”
(b) Wanda dan Windi berdebat tentang harga mobil yang kiranya layak untuk
mo-bil yang hendak mereka beli
(c) “Apakah anda lahir pada bulan September?”
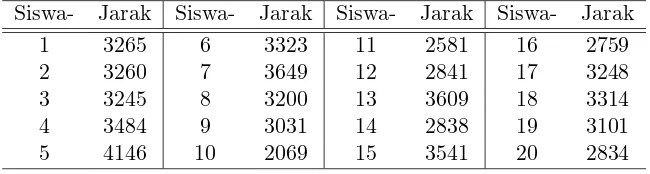
Diskusi: Perhatikan data jarak tempuh (dalam meter) ke sekolah dari beberapa siswa di suatu daerah.
Table 1: Data jarak tempuh ke sekolah dari beberapa siswa.
Siswa- Jarak Siswa- Jarak Siswa- Jarak Siswa- Jarak
1 3265 6 3323 11 2581 16 2759
2 3260 7 3649 12 2841 17 3248
3 3245 8 3200 13 3609 18 3314
4 3484 9 3031 14 2838 19 3101
5 4146 10 2069 15 3541 20 2834
Apakah analisis data rasio/interval akan lebih “kaya” dibandingkan dengan data
nominal/ordinal? Apa yang bisa kita katakan tentang data tersebut? Dapatkah
Diskusi: Data peserta ujian di beberapa sekolah di suatu kecamatan tercatat dalam diagram batang dan daun sebagai berikut. Untuk membaca data, kita perhatikan
kolom disebelah kiri garis yang menyatakan “angka puluhan” dan angka-angka
dise-belah kanan garis yang menyatakan “angka satuan”. Sebagai contoh, “3—5” berarti
jumlah peserta ujian di sekolahg tertentu adalah 35 orang.
0 357889 1 02 2 3 5
Apakah data dalam bentuk diagram batang dan daun cukup informatif? Dapatkah
data numerik tersebut diubah menjadi data kategorik?
Ukuran Pusat/Lokasi dan Penyebaran
Setelah data dikumpulkan dan diorganisasikan, kita dapat memberikan tafsiran
sederhana melalui ukuran atau statistik. Beberapa ukuran yang dikenal antara lain
mean dan variansi/deviasi standar yang menyatakan nilai tengah dan simpangan
data.
Ukuran atau statistik yang melekat pada data dapat dibagi menjadi
• Ukuran pusat/lokasi: mean (aritmetik), median, modus
• Ukuran penyebaran: jangkauan, variansi/deviasi standar, kuartil
Misalkan data sampel adalah
x1, x2, . . . , xn,
dimanaxi menyatakan titik sampel ke-i. Mean (aritmetik) didefinisikan sebagai
¯ x=
n
∑
i=1 xi
Sifat-sifat mean
(a) Untuk suatu konstantak,
n
∑
i=1
k xi=· · ·
(b) Jikayi =xi+k maka ¯y= ¯x+k. Buktikan!
(c) Jika yi =k xi maka ¯y=· · ·.
Median atau median sampel seringkali dikatakan sebagai nilai tengah. Dengan
demikian, menghitung median haruslah dilakukan pada data yang sudah diurutkan.
Definisi median adalah
(a) Observasi ke-((n+ 1)/2), (nganjil), atau
(b) Nilai tengah dari observasi ke-(n/2) dan ke-((n/2) + 1), (n genap)
Diskusi: Bagaimana (perbandingan) nilai mean dan median untuk data yang (i) simetrik, (ii) menceng ke kanan, (iii) menceng ke kiri?
Modus atauModeadalah ukuran pusat yang menyatakan nilai observasi yang paling
sering muncul. Menentukan modus dapat dilakukan pada data tanpa diurutkan
(meskipun lebih mudah apabila diurutkan lebih dahulu).
Latihan:
1. Tentukan ukuran lokasi/pusat dari contoh data diatas
2. Diketahui suatu data tentang jumlah saudara (kandung, angkat, tiri) dari 20
orang siswa sekolah menengah. Apabila setiap titik data ditambah tiga maka nilai
mean dan jangkauan menjadi...
Ukuran penyebaran menyatakan seberapa jauh data menyebar dari mean. Misalkan
kita memiliki dua data sampel. Kedua sampel memiliki mean yang sama, namun
mungkin saja memiliki penyebaran data yang berbeda. Beberapa ukuran
1. Jangkauan (Range):
R=xmaks−xmin
2. Variansi atau variansi sampel:
s2 =
n
∑
i=1
(xi−x)¯ 2
n−1
Catatan:
Deviasi standar atau simpangan baku adalah akar kuadrat dari variansi.
3. Kuartil:
Umumnya kita kenal kuartil pertama dan ketiga, dinotasikan denganK1 dan
K3. Apa yang dapat kita katakan tentang kuartil kedua atauK2?
4. Kuantil atau persentil:...
Sifat-sifat variansi:
Diketahui data sampelx1, . . . , xn memiliki variansis2x. Jika data sampel
(a) yi=xi+k,
(b) yi=k xi,
untuk suatu konstantak, maka
s2y =. . .
Variansi versus Koefisien Variasi: Kita dapat menghitung suatu ukuran yang
men-gaitkan ukuran penyebaran (deviasi standar) dengan ukuran lokasi (mean), yaitu
koefisien variasi (coefficient of variationatau CV):
yang tidak dipengaruhi unit ukuran yang dipakai. CV bermanfaat untuk
memband-ingkan variabilitas beberapa sampel yang berbeda relatif terhadap nilai mean-nya.
Dapat pula kita membanding CV dari beberapa variabel.
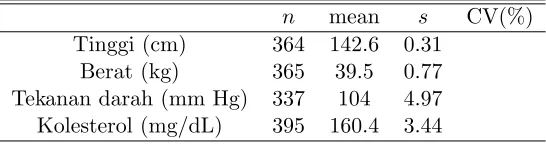
Latihan:
Data pada tabel berikut menyatakan berbagai faktor yang mempengaruhi masalah
pada sistem jantung dan peredaran darah anak. Tentukan CV dan berikan
inter-pretasinya.
Table 2: Faktor risiko kardiovaskular pada anak.
n mean s CV(%) Tinggi (cm) 364 142.6 0.31
Berat (kg) 365 39.5 0.77 Tekanan darah (mm Hg) 337 104 4.97 Kolesterol (mg/dL) 395 160.4 3.44
Mengamati Observasi Luar
Observasi luar atau pencilan atauoutlieradalah nilai/observasi yang “menyimpang”
dari nilai-nilai/observasi yang lain. Observasi luar dapat ditentukan/dihitung
den-gan melihat apakah ada nilai/observasi yang LEBIH BESAR dari
K3+ 1.5 (K3−K1)
atau LEBIH KECIL dari
K1−1.5 (K3−K1),
dengan K1 dan K3 adalah kuartil pertama dan ketiga seperti telah dijelaskan
se-belumnya.
Dalam praktiknya, observasi luar dapat menyatakan sesuatu yang baik/jelek.
Mis-alnya, seseorang dengan tingkat kecerdasan (IQ) yang sangat tinggi (jauh diatas
analisis data meskipun sesungguhnya cara ini tidaklah tepat. Mendeteksi observasi
luar adalah sesuatu yang sangat menantang dalam statistika.
Diskusi: Sekelompok observasix1, . . . , xn memiliki observasi luarxj untuk suatuj.
Dapatkah kita membandingkan mean dengan dan tanpa observasi luar? Mungkinkah
terdapat lebih dari satu observasi luar?
Data Kelompok
Pandang data sampel dengan 275 observasi. Ukuran sampel tersebut terlalu besar
sehingga menampilkan data apa adanya menjadi tidak efisien. Dengan demikian,
data sampel dapat dikelompokkan. Pengelompokan ini dapat pula terjadi (harus
di-lakukan) karena tingkat keakuratan data yang diambil tidak dapat diperoleh dengan
baik.
Pengelompokan data memberikan masalah: Berapa banyak kelompok atau interval
kelas (class intervals) yang ingin kita buat? Berapa lebar interval (interval width)?
Salah satu formula yang bisa kita pakai adalah Formula Sturges, dimana banyaknya
interval kelas adalah
k= 1 + (3.322×log10n),
dimananadalah besar sampel. Lebar intervalnya:
w=R/k,
denganR adalah jangkauan.
Untuk contoh data sampel dengan 275 observasi, kita peroleh:
k≈8, w= (63−18)/8 = 5.625
Dengan demikian, lebar kelas interval adalah 5 atau 10. Diketahui obervasi terkecil
adalah:
10-19
20-29
30-39
40-49
50-59
60-69
Memahami Grafik
Tampilan visual (baca: grafik) dari data merupakan salah satu cara untuk
mema-hami dan menginterpretasi data. Grafik bersifat menarik, memudahkan dalam
mem-bentuk pola, dan prediktif. Beberapa tampilan visualn untuk data adalah diagram
pencar (scatter diagram), diagram bar/batang (bar chart), diagram batang dan daun
(stem-and-leaf plot), histogram, box-plot.
Diagram pencar merupakan bentuk grafik yang sederhana namun cukup informatif.
Diagram ini berupa titik-titik yang menggambarkan nilai observasi. Pola atau
ke-cenderungan data dapat dilihat dengan melihat grafik ini.
Diagram batang dan daun memiliki ke-khas-an berupa tampilan nilai utama/pertama
(batang) dan nilai satuan/kedua (daun). Diagram ini membantu kita untuk
Bab 2 - Peluang
Silabus: Ruang sampel dan kejadian, konsep peluang, peluang bersyarat, Teorema
Bayes.
Setelah kita mempelajari analisis data secara deskriptif, maka kajian berikutnya
adalah melakukan perhitungan secara probabilistik. Hal ini berkaitan dengan
kon-sep distribusi frekuensi relatif yang telah dibahas sebelumnya. Analisis data
se-cara probabilistik memerlukan pemahaman tentang hal-hal yang belum terjadi atau
yang bersifat percobaan. Secara khusus, kita akan membangun ruang sampel dan
mendefinisikan kejadian.
Tujuan yang ingin dicapai dalam mempelajari peluang adalah:
1. Mendefinisikan ruang sampel dan kejadian
2. Menghitung peluang suatu kejadian
3. Mengkaji konsep dan menghitung peluang bersyarat
4. Memanfaatkan Teorema Bayes untuk menghitung peluang bersyarat suatu
ke-jadian
Ilustrasi
Sebagai pengantar, perhatikan ilustrasi-ilustrasi berikut. Pemahaman peluang
memer-lukan pengetahuan tentang cara menyusun atau kombinasi/permutasi. Secara khusus,
kita dituntut untuk dapat membangun pertanyaan peluang.
Ilustrasi-1. Tanti baru saja mengikuti tes mata. Ia masih teringat beberapa huruf yang muncul: A-E-M-R-S. Kini, Tanti mencoba menyusun kata-kata yang mungkin
dari huruf-huruf tersebut.
• Golongan darah yang mungkin untuk Hanin adalah...
• Rupanya Hanin tidak sendirian. Ada Hana dan Hanan disana yang memiliki maksud yang sama dengan Hanin. Jika seorang diantara mereka dipilih secara
acak menjadi pendonor, berapa peluang orang yang terpilih adalah Hana?
• Jika, diantara mereka bertiga, Hanan terpilih menjadi pendonor, berapa pelu-ang golongan darah Hanan adalah B?
Ilustrasi-3. B dan G pergi berburu dengan cara menembak. Pada waktu yang disepakati, B dan G secara bersamaan menembak sasaran tertentu. Peluang
tem-bakan B mengenai sasaran adalah 0.7 sedangkan peluang temtem-bakan G (bebas dari
tembakan B) mengenai sasaran adalah 0.4.
• Berapa peluang sebuah tembakan mengenai sasaran?
• Berapa peluang sasaran tertembak?
Ilustrasi-4. “Ayahku meninggal waktu usiaku tiga tahun. Lalu Ibu kawin lagi. Dengan ayah tiriku, Ibu mendapat dua orang anak tiri dan melahirkan tiga orang
anak. Ketika usiaku lima belas tahun, Ibu pun meninggal. Ayah tiriku kawin lagi
dengan seorang janda yang sudah beranak dua. Ia melahirkan dua orang anak pula
dengan ayah tiriku”
Konsep Peluang
Ruang sampel, S, adalah himpunan semua hasil mungkin dari suatu percobaan.
Kejadian,E, adalah himpunan bagian dari ruang sampel. Peluang suatu kejadian,
P(E), adalah rasio dari banyaknya titik kejadian dan ruang sampel, atau
P(E) = n(E) n(S),
dimanan(E) dan n(S), berturut-turut, adalah banyaknya titik kejadian dan ruang
Peluang suatu kejadian haruslah memenuhi aksioma dan sifat-sifat berikut:
1. 0≤P(E)≤1
2. P({}) = 0
3. P(S) = 1
4. Untuk kejadianA dan B,
P(A∪B) =P(A) +P(B)−P(A∩B)
5. Jika kejadianA danB saling asing maka P(A∩B) = 0
6. KejadianA dan kejadian B dikatakan saling bebas jika
P(A∩B) =P(A)P(B)
Definisi peluang yang lain merujuk pada frekuensi relatif. Misalkan suatu percobaan
dengan ruang sampelS diulang-ulang. Misalkann(E) banyaknya kejadian E yang
terjadi selamanpengulangan. Peluang kejadian E adalah
P(E) = lim
n→∞ n(E)
n
Latihan:
1. Dalam suatu rapat yang terdiri dari 20 orang, setiap orang berjabatan tangan
dengan orang lain diakhir rapat. Ada berapa banyak jumlah ’salaman’ yang
terjadi?
2. Sebuah lift bergerak dari lantai dasar berisi 8 orang (tidak termasuk operator
lift) dan orang-orang tersebut akan keluar hingga lift mencapai lantai paling
tinggi yaitu lantai 6. Dalam berapa cara sang operator dapat mengenali
Bagaimana jika 8 orang tersebut terdiri atas 5 pria dan 3 wanita dan sang
operator membedakan pria dan wanita?
3. Lima orang siswa meletakkan tasnya masing-masing ketika memasuki
perpus-takaan. Kemudian, ketika mereka keluar dari perpustakaan mereka
mengam-bil tasnya secara acak tanpa memperhatikan apakah tas yang diammengam-bil adalah
benar-benar miliknya. Apakah ruang sampel “percobaan” diatas?
4. Setiap pagi Swarna meninggalkan rumahnya untuk berlari pagi. Swarna pergi
lewat pintu depan atau belakang dengan peluang sama. Ketika meninggalkan
rumah Swarna memakai sepatu olah raga atau bertelanjang kaki jika sepatu
tidak tersedia di depan pintu yang dia lewati. Ketika pulang, Swarna akan
masuk lewat pintu atau belakang dan meletakkan sepatunya dengan pelung
sama. Jika dia memiliki 4 pasang sepatu olah raga, akan dihitung berapa
pelu-ang Swarna akan sering berolah raga dengan bertelanjpelu-ang kaki. Pertanyaan
awal, tentukan ruang sampelnya!
5. Bapak Kepala Sekolah mengundang guru-guru yang memiliki setidaknya satu
anak laki-laki (L) ke acara syukuran. Seorang guru yang bernama Pak Jaim
memiliki dua anak. Kita akan menghitung peluang bahwa kedua anak Pak
Jaim adalah laki-laki, diberikan bahwa Pak Jaim diundang ke acara syukuran
tersebut. Pertanyaan awal adalah apa ruang sampel “percobaan” diatas?
Peluang Bersyarat dan Teorema Bayes
Ilustrasi-1. Pandang Ilustrasi-3 diatas.
• Jika sebuah tembakan mengenai sasaran, berapa peluang bahwa itu tembakan G?
• Berapa peluang bahwa, jika sasaran tertembak, kedua tembakan mengenai sasaran?
Ilustrasi-2. Seorang praktikan, Ega, tahu bahwa sebuah lembar kerja praktikum akan berada di salah satu dari tiga buah kotak surat lab yang ada. Misalkan pi
adalah peluang bahwa Ega akan menemukan lembar kerja praktikum setelah
menge-cek kotak surat labidengan cepat jika ternyata surat tersebut berada di kotak surat
labi,i= 1,2,3.
• Misalkan Ega mengecek kotak surat 1 tidak menemukan surat. Berapa peluang hal itu akan terjadi?
• Jika diketahui Ega mengecek kotak surat 1 tidak menemukan surat, berapa peluang bahwa surat itu ada di kotak surat 1?
Peluang kejadian A, apabila kejadian B telah terjadi, adalah peluang bersyarat
P(A|B) yaitu:
P(A|B) = P(A∩B P(B) ,
asalkanP(B)>0. Jelas bahwa jika kejadianAdanB saling bebas makaP(A|B) =
P(A).
Perhatikan bahwa konsep peluang bersyarat dapat digunakan untuk menghitung
peluang total:
P(B) =P(B|A)P(A) +P(B|Ac)P(Ac)
Latihan:
1. Laila memiliki 2 buah koin; satu koin “baik” (memiliki sisi M dan B) dan
satu koin “tidak baik” (memiliki dua sisi M). Sebuah koin dipilih secara acak,
kemudian dilantunkan. Berapa peluang muncul M?
2. Laila memiliki 2 buah koin; satu koin “baik” (memiliki sisi M dan B) dan satu
koin “tidak baik” (memiliki dua sisi M). Sebuah koin dipilih secara acak,
kemu-dian dilantunkan. Muncul M. Berapa peluang bahwa koin yang dilantunkan
TEOREMA BAYES:
Misalkan{B1, B2, . . . , Bn} adalah partisi dari ruang sampel dan misalkanA adalah kejadian yang terobservasi. Peluang kejadianBj diberikan Aadalah
P(Bj|A) =
P(A Bj)
P(A)
= ∑nP(A|Bj)P(Bj)
i=1 P(A|Bi)P(Bi)
Latihan:
Tes darah di suatu laboratorium akan 95% efektif dalam mendeteksi suatu penyakit
tertentu jika penyakit itu ada. Namun demikian, tes tersebut juga memberikan
’hasil positif yang salah’ pada 1% orang sehat yang dites. Jika 0.5% dari populasi
mengidap penyakit tertentu tersebut, tentukan peluang bahwa seseorang menderita
Bab 3 - Peubah Acak dan Fungsi Peluang
Silabus: Konsep peubah acak, fungsi peluang, fungsi distribusi, peluang pada nilai
peubah acak.
Ilustrasi. Maskapai penerbangan mengetahui bahwa lima persen pemesan tiket tidak akan datang untuk membeli tiketnya. Dengan alasan ini, maskapai tidak
ragu untuk menjual 52 tiket penerbangan pada pesawat dengan kapasitas duduk 50
orang. Berapa peluang akan ada kursi yang tersedia untuk setiap pemesan tiket
yang datang?
Apa yang dapat anda katakan tentang soal peluang pada ilustrasi diatas? Mungkinkah
kita mendefinisikan suatu kejadian? ruang sampel? Perlukah cara lain untuk
mema-hami peluang suatu kejadian?
Peubah acak
Apa yang dapat kita katakan tentang peubah acak?
• Peubah acak tidaklah “acak” dan bukanlah “peubah”
• Peubah acak adalah “fungsi” yang memetakan anggotaS ke bilangan realR
Peubah acak X dikatakan diskrit jika terdapat barisan terhitung dari bilangan
{ai, i= 1,2, . . .} sedemikian hingga
Catatan: Sebuah peubah acak diskrit tidak selalu berasal ruang sampel diskrit.
Jika diberikan himpunan terhitung {ai, i = 1,2, . . .} dan bilangan positif {pi, i =
1,2, . . .} sedemikian hingga ∑
i pi = 1, fungsi peluangpX(x) adalah
FX disebut fungsi distribusi (diskrit) dariX jika terdapat barisan terhitung{ai, i=
Fungsi distribusi (kumulatif), F(x) =P(X ≤x), memiliki sifat-sifat:
(a)F fungsi tidak turun
(b) lim
x→∞ F(x) = 1 (c) lim
x→−∞ F(x) = 0
(d)F fungsi kontinu kanan
Catatan:
Misalkan X peubah acak dan fungsi distribusinya FX dapat diturunkan. Fungsi
peluangfX adalah turunan dari fungsi distribusi,
fX(x) =
Peubah acak dengan sifat diatas dikatakan sebagai peubah acak kontinu.
Latihan:
1. Diketahui fungsi peluang sebagai berikut:
f(x) =
2. Tentukan fungsi peluang dari fungsi distribusi berikut:
F(x) =
3. Diketahui fungsi peluang dari peubah acak kontinu:
f(x) =c e−2x, x >0,
Hitung (i)c, (ii) P(X >2)
4. Suatu peubah acakX memiliki fungsi peluang
f(x) =k(1−x2),
Ekspektasi
Nilai harapan/ekspektasi (expected value/expectation) atau ekspektasi dari peubah
acak diskrit/kontinuX adalah
E(X) =∑
x
x pX(x)
dan
E(X) = ∫ ∞
−∞
x fX(x)dx
dimanapX dan fX adalah fungsi peluang dari X.
Catatan:
1. Ekspektasi adalah rata-rata tertimbang (weighted average) dari nilai yang mungkin
dariX
2. Ekspektasi = mean = momen pertama
3. Ekspektasi suatu peubah acak adalah nilai rata-rata (long-run average value)
dari percobaan bebas yang berulang
3. Apakah ekspektasi harus berhingga? (Diskusi!)
Contoh:
1. Rombongan mahasiswa sebanyak 120 orang akan berangkat ke Jogja dengan
menggunakan 3 bis. Ada 36 mahasiswa di bis 1, 40 mahasiswa di bis 2 dan
44 mahasiswa di bis 3. Ketika bis sampai tujuan, seorang mahasiswa dipilih
secara acak. Misalkan X menyatakan banyaknya mahasiswa di bis dimana
seseorang tersebut terpilih. HitungE(X). (Solusi: 40.2667)
2. MisalkanX adalah peubah acak dengan nilai yang mungkin−1,0,1 dan
pelu-ang:
p(−1) = 0.2, p(0) = 0.5, p(1) = 0.3
Sifat-sifat ekspektasi:
1. E(g(X)) =∫∞
−∞ g(x)fX(x)dx
2. E(a X+b Y) =a E(X) +b E(Y)
3. E(XY) =E(X)E(Y), jikaX danY saling bebas.
4. E(X) =∫∞
0 P(X > x)dx, untukX >0 (*)
5. E(Xr) =∫∞
−∞xrfX(x)dx (momen ke-r)
6. E((X−µX)r) =∫−∞∞ (x−µX)rfX(x)dx(momen pusat ke-r)
7. E((X−µX)2) =V ar(X) =E(X2)−(E(X))2
Bab 4 - Distribusi Diskrit dan Kontinu
Silabus: Distribusi peubah acak, distribusi diskrit, distribusi kontinu.
Peubah acak merupakan alat yang dapat digunakan untuk mempelajari konsep pada
tingkat lanjut. Salah satu karakteristik utama peubah acak adalah memiliki distribusi.
Distribusi diskrit adalah fenomena yang digambarkan oleh peubah acak diskrit
melalui fungsi peluang/distribusi. Beberapa distribusi diskrit yang dikenal adalah
binomial, Poisson dan geometrik. Distribusi uniform, eksponensial dan normal
adalah contoh-contoh distribusi kontinu.
Distribusi Binomial
MisalkanS ={sukses,gagal} adalah ruang sampel yang menotasikan ’sukses’ atau
’gagal’ dari suatu percobaan. DefinisikanX(sukses) = 1 danX(gagal) = 0 dan
pX(1) =P(X= 1) =θ;pX(0) =P(X= 0) = 1−θ,
dimana 0 ≤ θ ≤ 1 adalah peluang diperoleh sukses. Peubah acak X dikatakan
peubah acak Bernoulli dengan parameter θ.
Jika dilakukan n percobaan independen dan jikaX menyatakan banyaknya sukses
yang diperoleh makaX dikatakan sebagai peubah acak Binomial dengan parameter
(n, θ), dinotasikan X∼B(n, θ). Fungsi peluangnya adalah
f(x) =pX(x) =Cxnθx(1−θ)n−x
Latihan:
1. MisalkanX∼B(5,0.2). Hitung: (i) P(0< X≤1) (ii) P(X≥1)
2. Maskapai penerbangan mengetahui bahwa lima persen pemesan tiket tidak
untuk menjual 52 tiket penerbangan pada pesawat dengan kapasitas duduk
50 orang. Berapa peluang akan ada kursi yang tersedia untuk setiap pemesan
tiket yang datang?
3. MisalkanXpeubah acak Binomial yang menyatakan banyak orang yang datang
ke toko dan membeli barang. Diketahui nilai parameter “sukses” adalah 0.6.
Jika 10 orang masuk toko, berapa peluang terjadinya maksimal sebuah
“suk-ses”?
4. Tentukan mean dan variansi peubah acak Binomial dengan parameter (n, θ)
5. Suatu hasil produksi (misalkan sebuah TV) akan rusak dengan peluang 0.1.
Hasil produksi saling bebas. Jika terdapat 3 hasil produksi (3 buah TV),
berapa peluang bahwa paling banyak 1 TV rusak?
6. Empat buah koin dilantunkan. Asumsikan bahwa hasil lantunan saling bebas.
Hitung peluang akan muncul 2 Muka dan 2 Belakang?
Distribusi Poisson
Distribusi diskrit lain yang cukup dikenal adalah distribusi Poisson. Umumnya
dis-tribusi ini terlihat pada fenomena banyaknya telfon yang masuk pada suatu hari,
banyaknya kendaraan yang lewat di jalanan pada periode waktu tertentu dsb.
Per-hatian kita adalah pada banyaknya “sukses” pada periode tertentu.
MisalkanX peubah acak dengan fungsi peluang
f(i) =pX(i) =e−λ
λi i!,
untuki= 0,1,2, . . .danλ >0. Peubah acakXdisebut peubah acak Poisson dengan
parameterλ.
Latihan
1. Banyaknya kecelakaan yang terjadi di tol setiap hari berdistribusi Poisson
2. Misalkan X peubah acak Poisson dengan parameter λ. Tunjukkan bahwa
P(X=i) naik secara monoton sebelum kemudian turun secara monoton untuk
isemakin besar.
Apa yang anda ketahui tentang pendekatan Poisson untuk Binomial?
MisalkanX berdistribusi Binomial dengan parameter (n, θ),
P(X=x) =Cxnθx(1−θ)n−x
Untuknbesar dan λmoderat (karenaθ cukup kecil),
(
1. Misalkan peluang sebuah produk susu akan tercemar melamin adalah 0.1.
Ten-tukan peluang bahwa paling banyak 1 produk susu yang tercemar dari sampel
2. MisalkanX∼B(n, θ) danY ∼P OI(λ). Cari hubungan antaraf(k+ 1) dan
f(k) untuk kedua peubah acak.
Distribusi Geometrik
Misalkan percobaan-percobaan dilakukan hingga diperoleh sukses yang pertama.
Percobaan-percobaan tersebut saling bebas dan memiliki peluang sukses α.
Mis-alkanXmenyatakan banyaknya percobaan yang dilakukan untuk mendapatkan
suk-ses pertama tersebut, makaX dikatakan peubah acak Geometrik dengan parameter
α. Fungsi peluangnya adalah
fX(n) =p(n) =P(X=n) = (1−α)n−1α,
untukn= 1,2, . . . dan α >0.
MisalkanY peubah acak yang menyatakan kegagalan yang sudah dialami sebelum
mendapatkan sukses yang pertama; diketahui peluang mendapatkan sukses adalah
α. Fungsi peluang untuk Y adalah
fY(k) = (1−α)kα, k = 0,1,2, . . .
Diskusi:
• Apa yang dapat anda katakan tentang mean dan variansi untuk kedua peubah acakX danY tersebut?
• Apakah nilai mean lebih besar daripada variansi?
Latihan:
1. Hitung momen pertama dan kedua untuk peubah acak Geometrik dengan
2. Tiga remaja makan disuatu restoran. Untuk menentukan siapa yang akan
membayar, mereka sepakat untuk mengundi dengan melantunkan koin.
Sese-orang dengan hasil lantunan yang berbeda dengan yang lain wajib membayar
makanan yang telah dipesan. Jika X menyatakan banyaknya lantunan koin
Bab 5 - Distribusi Sampel
Silabus: Definisi populasi dan sampel, distribusi ¯X dan S2.
Ketika kita “bekerja” dengan statistika, maka pemahaman tentang populasi dan
sampel menjadi penting. Seperti kita ketahui, pekerjaan statistika adalah melakukan
inferensi tentang populasi dengan menggunakan sampel.
Populasi adalah...
Misalkan sampel acak tersebut diambil dari X yang berdistribusi normal dengan
parameter (µ, σ2) maka ¯X∼ · · · dan S2 ∼ · · ·.
Teorema Limit Pusat
Jika ¯Xmean dari sampel acak berukuranndari populasi dengan meanµdan variansi
σ2, maka
Z= X¯ −µ
σ/√n →N(0,1).
Contoh-1. Sebuah perusahaan produsen lampu memberikan klaim bahwa
(jam) dan deviasi standar 40 (jam). Misalkan diambil sampel berukuran 16. Hitung
peluang bahwa sampel acak lampu-lampu tersebut memiliki masa hidup (average
life) kurang dari 775 (jam).
Contoh-2. Perjalanan 2 kampus Ganes dan Jtnanger dengan bis ditempuh selama
28 menit dengan deviasi standar 5 menit. Pada suatu waktu, dilakukan perjalanan
selama 40 kali. Berapa peluang waktu perjalanannya lebih dari 30 menit?
Contoh-3. Dua eksperimen yang saling bebas dilakukan pada pengecatan sebuah
produk; 18 spesimen masing-masing dicat dengan cat jenis A dan B, lalu lama
waktu pengeringan dicatat. Diketahui deviasi standar populasi adalah 1. Asumsikan
bahwa mean waktu pengeringan kedua tipe cat adalah sama. Tentukan peluang
P( ¯XA−X¯B >1).
Latihan: hal. 241-243
Catatan: Pendekatan normal untuk distribusi binomial
Teorema:
Misalkan S2 variansi sampel dari sampel acak berukuran n berdistribusi normal
dengan meanµdan variansiσ2, maka
(n−1)S2 σ2 ∼χ
2
n−1,
denganχ2n−1 adalah distribusi chi-kuadrat dengan derajat kebebasanν =n−1.
Contoh. Batere merk Energiver diklaim memiliki masa hidup 3 tahun dengan deviasi
standar 1 tahun. Pada sampel berukuran 5, diperoleh data masa hidup sebagai
berikut: 1.9, 2.4, 3.0, 3.5, 4.2. Apakah data ini meyakinkan perusahaan batere
tersebut bahwa deviasi standar masa hidup batere 1 tahun? Asumsikan masa hidup
Bab 6 - Inferensi Statistik: Penaksiran Titik dan Selang
Silabus: Distribusit, selang kepercayaan untuk mean dan variansi.
Penaksiran titik dan Selang kepercayaan
Penaksiran titik (point estimate) merupakan langkah awal dalam inferensi statistik
untuk suatu parameter. Pada sampel acak berdistribusi normal dengan parameter
µ dan σ2, maka penaksiran titik untuk kedua parameter tersebut, berturut-turut,
adalah ¯X dan S2. Penaksir ¯X dan penaksir S2 bersifat tak bias (unbiased).
Penaksiran titik seringkali tidak memberikan keleluasaan untuk menafsirkan nilai
parameter. Untuk itu, diberikan penaksiran selang untuk parameter pada tingkat
kepercayaan tertentu. Perhatikan sampel acak normal berukuran n. Kita ketahui
bahwa mean sampel ¯X berdistribusi normal dengan mean µX¯ = µ dan deviasi standar σX¯ = σ/√n. Kita ingin menentukan selang kepercayaan untuk µ, jika σ diketahui. Misalkan zα adalah nilai-zsehingga P(Z < zα). Jadi,
P
Dengan manipulasi aljabar, kita peroleh 100(1−α)%-selang kepercayaan untukµ, :
¯
Contoh. Konsentrasi suatu besi (zinc) di 36 lokasi pada sungai K adalah 2.6 gr/ml.
Tentukan selang kepercayaan untuk mean konsentrasi besi pada tingkatα= 1%,5%.
Asumsikan bahwa deviasi standar populasi adalah 0.3 gr/ml.
Catatan:
• Dapatkah kita menentukan ukuran sampel n agar selang kepercayaan yang kita buat tidak akan melampaui suatu galatetertentu?
Distribusi t
Misalkan kita punyai sampel acak berukurann berdistribusi normal. Asumsikan σ
diketahui tidak dapat dipenuhi. Pandang peubah acak
T = X¯ −µ S/√n
atauT =Z/√
V /ν, denganZ peubah acak normal standar dan V peubah acak
chi-kuadrat dengan derajat kebebasanν. Peubah acakT berdistribusitatau Student-t,
dengan derajat kebebasan ν=n−1, dan memiliki fungsi peluang
f(t) = Γ((ν+ 1)/2)
Selang Kepercayaan Untuk σ Tidak Diketahui
MisalkanT berdistribusi Student-tdengan derajat kebebasann−1. Analog dengan
Z, kita punyai
P(
−tα/2< T < tα/2)
= 1−α.
Karena T = S/X¯−√µn, kita dapat menentukan 100(1−α)%-selang kepercayaan untuk µ, jikaσ tidak diketahui:
¯
Contoh. Isi dari tujuh kontainer barang (yang sejenis) adalah 9.8, 10.2, 10.4, 9.8,
10.0, 10.2, 9.6. Tentukan 95%-selang kepercayaan unutk mean isi kontainer.
Diskusi:
Misalkan ukuran sampel dari suatu sampel acak cukup besar, asumsi normalitas
tidak dapat dipenuhi dan σ tidak diketahui. Dapatkan kita menentukan selang
kepercayaan untukµ?
Hasil tes TPA 500 calon mahasiswa menunjukkan mean dan deviasi standar,
berturut-turut, 501 dan 112. Tentukan 99%-selang kepercayaan untuk mean TPA.
Selang Kepercayaan, Selang Prediksi dan Batas Toleransi
Contoh 9.1. Sebuah mesin memproduksi potongan baja berbentuk silinder. Sampel
potongan-potongan baja diambil dan diameternya (cm) diukur. Diperoleh data
sebagai berikut:
1.01,0.97,1.03,1.04,0.99,0.98,1.01,1.03
Asumsikan distribusi normal, ¯x = 1.0056 dan s = 0.0246, hitung tiga jenis
99%-selang/interval (baca: selang kepercayaan, selang prediksi, selang/batas toleransi).
Petunjuk:
¯
x±t0.005 s
√
n
¯
x±t0.005√s n
√
n+ 1
Selang Kepercayaan Untuk µ1−µ2
Pada dua populasi yang ingin kita bandingkan, kita dapat melakukannya dengan
mengambil sampel dari keduanya. Seperti sebelumnya, ukuran yang kita bandingkan
adalah mean; khususnya selisih dua mean, yaitu µ1−µ2.
Perhatikan bahwa peubah acak
Z= ( ¯X1−√X2)¯ −(µ1−µ2)
Selang kepercayaan untuk selisih dua meanµ1−µ2 adalah
( ¯X1−X¯2)±zα/2
Contoh. Kemampuan produksi zat dari dua mesin A dan B dibandingkan; 50
per-cobaan dengan mesin A dan 75 dengan mesin B. Data menunjukkan mean sampel
A dan B: 36 dan 42. Asumsikan bahwa deviasi standar diketahui yaitu 6 (untuk
mesin A) dan 8 (untuk mesin B). Tentukan 90%-selang kepercayaan untuk selisih
dua mean mesin A dan B.
Diskusi:
Bagaimana kita dapat menentukan selang kepercayaan selisih dua mean pada
• Kasus A: kedua variansi populasi tidak diketahui, - (i) namunσ21 =σ22,
- (ii) danσ12̸=σ22
Selang Kepercayaan Untuk Proporsi
Ukuran atau statistik lain yang dapat kita hitung pada data adalah proporsi p.
Penaksir proporsi adalah ˆp =X/n, dengan X menyatakan banyaknya sukses pada
n percobaan. Untuk n besar, ˆp berdistribusi normal dengan mean dan variansi,
berturut-turut, adalahµpˆ=pdan σp2ˆ= p(1n−p). Dengan demikian, kita peroleh
Selang kepercayaan untuk proporsipdapat diformulasikan dengan manipulasi
pelu-ang diatas. Kita dapatkan,
ˆ
Perhatikan bahwa deviasi standar untuk ˆp adalah fungsi dari p yang harus
ditak-sir oleh ˆp (maksudnya, ini berbeda dengan deviasi standar untuk ¯x yaitu σ yang
“seakan-akan” tidak melibatkan ¯x).
Diskusi:
• Ukuran sampel n pada penentuan selang kepercayaan untuk p dapat diatur se-hingga diperoleh galat tertentu; n=· · ·
•Selang kepercayaan untuk selisih dua proporsi p1−p2 adalah...
Contoh-1. Pada sampel acak berukuran 500 (keluarga) diperoleh informasi bahwa
sejumlah 340 keluarga memiliki TV layar datar. Tentukan selang kepercayaan pada
α= 0.05 untuk proporsi keluarga yang memiliki TV layar datar.
Contoh-2. Dilakukan investigasi menyeluruh terjadi proses produksi, baik pada pada
metode lama dan dengan metode baru. Hasil yang diharapkan adalah perbaikan
kualitas produksi. Data yang ada adalah sebagai berikut: 75 dari 1500 produk
dengan metode lama tidak berkualitas baik; dengan metode baru, 80 dari 2000
produk yang tidak berkualitas baik. Tentukan 90%-selang kepercayaan untuk selisih
Bab 7 - Inferensi Statistik: Uji Hipotesis
Silabus: Konsep uji hipotesis, kesalahan tipe 1 dan 2, uji hipotesis untuk mean (1
dan 2 sampel), uji hipotesis untuk proporsi (1 dan 2 sampel), uji hipotesis 2 sampel
berpasangan.
Konsep Uji Hipotesis
Uji hipotesis (UH) adalah bagian dari statistika inferensi. UH bertujuan untuk
mengambil kesimpulan secara statistik (signifikan) dari hipotesis-hipotesis yang diberikan.
Kesimpulan tersebut didasarkan pada tingkat signifikansi α (yang sesungguhnya
adalah tingkat kesalahan tipe I).
Tahap-tahap dalam pelaksanaan UH adalah
1. Menyatakan hipotesis nol, H0, dan hipotesis alternatif, Ha atauH1,
2. Menentukanα,
3. Menentukan statistik uji (test statistic),
4. Menentukan daerah kritis (critical region) atau daerah penolakan/penerimaan,
5. Menghitung statistik uji dengan data sampel
6. Mengambil kesimpulan: “menolak atau gagal menolakH0”
Contoh:
1. Ini cerita tentang kematian karena kanker yang diduga dimulai dari radiasi
nuklir. Diketahui terjadi 13 kematian pada pekerja di suatu proyek nuklir,
dimana 5 kematian diantaranya disebabkan oleh kanker. Berdasarkan data
statistik, pihak otoritas kesehatan mengklaim bahwa sekitar 20% kematian
2. Misalkan X p.a menyatakan panjang alat suatu pemancar telepon selular.
DiketahuiX berdistribusi normal dengan meanµ. Akan diuji
H0 :µ= 3 vs H1 :µ >3
dengan menggunakan data sampel 6 alat pemancar terpilih acak dengan mean
3.763 dan deviasi standar 0.724. Apakah kesimpulan yang diambil dari uji
hipotesis tersebut?
Kesalahan Tipe-1 dan Tipe-2
Kesalahan-kesalahan dalam UH dibagi atas:
- kesalahan tipe-1 atauα, yaitu kesalahan “menolak H0 yang benar, atau
P(menolakH0|H0benar)
- kesalahan tipe-2 atauβ, yaitu kesalahan “menerima H0 yang salah, atau
P(menerimaH0|H0salah)
Catatan:
• Tidak ada hubungan antaraα danβ
• 1−β adalah kuasa ataupower dari UH
Kaitan antara pengambilan kesimpulan dan kesalahan dapat dilihat dalam tabel
berikut:
Table 3: Pengambilan kesimpulan dan tipe kesalahan.
H0 benar H0 salah H0 gagal ditolak keputusan benar β
Dua jenis uji hipotesis nol vs hipotesis alternatif:
1. Uji hipotesis 2-sisi atautwo-sided:
H0 :µ=µ0 vs H1:µ̸=µ0
2. Uji hipotesis 1-sisi atau one-sided:
H0 :µ=µ0 vs H1:µ > µ0 atau H0:µ=µ0 vs H1 :µ < µ0
Uji Hipotesis Untuk Mean
Uji hipotesis pada 1-sampel
Uji hipotesis untuk mean populasi dapat dilakukan pada kasus (i) pengambilan
sam-pel berasal dari populasi yang berdistribusi normal dengan variansi diketahui atau
tidak diketahui, (ii) pengambilan sampel berasal dari populasi yang tidak
berdis-tribusi normal.
Seorang peneliti tertarik untuk menguji mean umur orang-orang dari suatu
popu-lasi: apakah mean umur orang-orang dari populasi tersebut berbeda dari 30 tahun?
(apakah mean umur orang-orang tersebut 30 tahun?). Untuk itu, diambil sampel
se-banyak 10 orang dan dihitung bahwa ¯x= 27. Asumsikan data berasal dari distribusi
normal dengan σ2 = 20. Tahapan UH-nya adalah
1. Hipotesis:
H0 :µ= 30, Ha:µ̸= 30
2. Tingkat signifikansi: α= 0.05
3. Statistik uji:
Z= X¯ −µ0
4. Daerah kritis:
TolakH0 jika z≥1.96 atauz≤ −1.96
5. Perhitungan:
z= √27−30 20/10 =· · ·
6. Kesimpulan:
· · ·
Pengambilan kesimpulan dapat pula dilakukan dengan menghitung p-value, yaitu
nilai α terkecil untuk menolak H0. Dengan kata lain “tolak H0 jika p-value lebih
kecil dari α”. Pada contoh diatas, nilai p-value adalah
p−value =P(Z ≤z) +P(Z ≥z) = 2×P(Z ≤ −2.12) =· · ·
Jadi,· · ·
Contoh/Latihan:
Lakukan UH untuk soal diatas. Pertanyaan yang diajukan adalah “apakah mean
umur populasi kurang dari 30 tahun?”. Gunakan tingkat signifikansi α = 0.01.
Bagaimana jikan= 20 dan ¯x= 27?
Bagaimana jika σ tidak diketahui?
Gunakan statistik uji:
T = x¯−µ0
s/√n ∼tn−1.
Contoh: Castillo dan Lilioja meneliti suatu teknik untuk mengukur indeks massa
tubuh atau BMI. Mereka ingin menguji apakah mean BMI suatu populasi bukanlah
35. Dilakukan perhitungan pada 14 orang dewasa (laki-laki) dan diperoleh ¯x= 30.5
Tahapan UH-nya adalah
1. Hipotesis:
H0 :µ= 35, Ha:µ̸= 35
2. Tingkat signifikansi: α= 0.05
3. Statistik uji:
T = X¯−µ0
s/√n ∼tn−1
4. Daerah kritis:
TolakH0 jika · · ·
5. Perhitungan:
t=· · ·
6. Kesimpulan:
H0 gagal ditolak (dengan kata lain, diterima), karena −2.16 ≤t ≤2.16 atau
bukan dalam daerah penolakan. Tidak ada alasan untuk mendukung klaim
bahwa mean BMI bukanlah 35.
Diskusi:
• Lakukan pengambilan kesimpulan pada masalah BMI dengan menggunakan
p-value. Bagaimana menurut anda? Manakah yang lebih mudah dilakukan?
(diband-ingkan dengan menentukanz ataut pada tabel)
Uji hipotesis pada 2-sampel
Uji hipotesis untuk mean populasi dapat dilakukan dengan maksud untuk menguji
adanya perbedaan antara mean 2 populasi.
Seorang ahli ilmu tanah meyakini bahwa kerusakan tanah akan lebih masif jika
menggunakan obat B, daripada obat A, dalam proses penggunaan lahan. Untuk
itu, sang ahli memberikan obat A dan B pada 80 bagian lahan (masing-masing obat
diberikan ke 40 bagian lahan). Hasil yang diperoleh adalah:
Obat A:
109,98,103,97,101,102,91,106,
101,98,88,105,100,95,98,98,
97,94,108,102,105,100,113,101
89,99,102,104, 110,95,91,99,
100,104,106,101,96,109,95,96
Obat B:
105,113,106,110,104,122,102,107,
109,111,117,111,102,117,109,107,
110,111,99,103,111,101,103,111,
118,99,107,110,114,109,109,128,
109,112,119,108,114,109,106,109.
Benarkah klaim ahli pertanian tersebut?
Tahapan UH-nya adalah
1. Hipotesis:
H0 :µ1=µ2, Ha:µ1< µ2
atau
H0 :µD = 0, Ha:µD <0,
2. Tingkat signifikansi: α= 0.05
3. Statistik uji:
T = ( ¯X1−X¯2)−0 sp
√
1/n1+ 1/n2 ∼
tn1+n2−2,
jika diasumsikanσ1 =σ2, dimana
s2p = (n1−1)s 2
1+ (n2−1)s22 n1+n2−2
,
atau
T = √( ¯X1−X¯2)−0 s2
1/n1+s22/n2 ,
jika diasumsikanσ1 ̸=σ2
4. Daerah kritis:
TolakH0 jika · · ·
5. Perhitungan:
n1 = 40,x¯1 = 100.15, s1= 5.73
n2 = 40,x¯2 = 109.53, s2= 6.06
t=· · ·
6. Kesimpulan:
· · ·
Catatan:
• Uji mean untuk 2 sampel mengasumsikan bahwa data berasal dari distribusi normal
Uji hipotesis pada 2-sampel Berpasangan
Uji hipotesis untuk mean diatas dilakukan pada 2 mean yang saling bebas atau
independen. Uji untuk mean dapat pula dilakukan pada 2 sampel yang berpasangan.
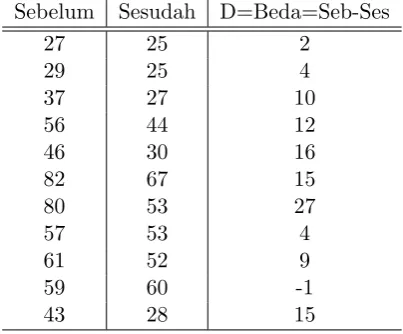
Sebuah studi dimaksudkan untuk melihat apakah merokok dapat menurunkan kadar
“platelet” dalam darah. Sebelas sampel darah diambil dari 11 orang SEBELUM dan
SESUDAH orang-orang tersebut merokok. Data yang diperoleh dalah prosentase
maksimum platelet:
Table 4: Kadar platelet sebelum dan sesudah merokok.
Sebelum Sesudah D=Beda=Seb-Ses
27 25 2
29 25 4
37 27 10
56 44 12
46 30 16
82 67 15
80 53 27
57 53 4
61 52 9
59 60 -1
43 28 15
Apakah data sampel mendukung tujuan studi tersebut?
Tahapan UH-nya adalah
1. Hipotesis:
H0 :µD =µ1−µ2 = 0, Ha:µD >0
2. Tingkat signifikansi: α= 0.05
3. Statistik uji:
T = D¯ −µD0
sD/√n ∼
4. Daerah kritis:
TolakH0 jika · · ·
5. Perhitungan:
nD = 11,D¯ = 10.27, sD = 7.98,
t=· · ·
6. Kesimpulan:
Tolak H0, karena t > 1.812. Dengan kata lain, kadar platelet dalam darah
menurun akibat merokok.
Uji Hipotesis Untuk Proporsi
Pandang 2 proporsi populasi, p1 dan p2. Kita ingin membandingkan, misalnya,
apakah proporsi p1 yang menyatakan proporsi wanita yang bekerja di bidang ilmu
hayati BERBEDA dengan proporsip2 yaitu proporsi wanita yang bekerja di bidang
teknik.
Misalkan
• X1 banyaknya “sukses” dari sampel berukurann1 dari populasi 1
• X2 banyaknya “sukses” dari sampel berukurann2 dari populasi 2
• X1 ∼B(n1, p1) dan X2 ∼B(n2, p2)
• Penaksir proporsinya adalah
ˆ
p1=X1/n1, pˆ2 =X2/n2
Tahapan UH-nya adalah
1. Hipotesis:
H0 :δ=p1−p2 = 0, Ha:δ ̸= 0
2. Tingkat signifikansi: α= 0.05
Contoh/Latihan. Dalam sebuah studi, akan diuji keefektifan suatu perlakuan
ter-hadap persepsi produk mobil listrik. Sampel yang diambil acak berukuran 100
diambil dan diberikan perlakuan tersebut. Sampel lain berukuran 100 tidak diberi
perlakuan. Ditemukan bahwa 35 orang yang diberi perlakuan dan 85 tidak diberi
perlakuan. Apakah data mendukung klaim bahwa perlakuan efektif? Gunakan
α= 0.001.
Solusi:
1. Hipotesis:
H0 :δ=p1−p2 = 0, Ha:δ <0
2. Tingkat signifikansi: α= 0.001
3. Statistik uji:
Z= ˆδ−0
s.e(ˆδ) ∼N(0,1),
dimana ˆ
δ= ˆp1−pˆ2, dan
s.e(ˆδ) = √
ˆ
p1(1−pˆ1) n1
+pˆ2(1−pˆ2) n2
,
4. Daerah kritis:
TolakH0 jika · · ·
5. Perhitungan:
ˆ
p1= 35/100,pˆ2 = 80/100,ˆδ=−0.45, s.e(ˆδ) = 0.06225, z=· · ·
6. Kesimpulan:
Tolak H0 karena z = −7.23 < −3.09. Dengan kata lain, data mendukung