GRAPH, A GENERALIZED WEB GRAPH, AND A GENERALIZED FLOWER GRAPH
Tiffani Arzaqi Putri and Tri Atmojo Kusmayadi Department of Mathematics
Faculty of Mathematics and Natural Sciences Sebelas Maret University
Abstract. LetGbe a connected graph with vertex set V(G) and edge set E(G). The intervalI[u, v] betweenu andv to be the collection of all vertices that belong to some shortestu−v path. A vertexsstrongly resolves two verticesuandv ifubelongs to a shortestv−spath, denoted byu∈I[v, s] orvbelongs to a shortestu−spath, denoted byv ∈ I[u, s]. A vertex set S of G is a strong resolving set of Gif every two distinct vertices ofGare strongly resolved by some vertex ofS. The strong metric basis ofGis a strong resolving set with minimal cardinality. The strong metric dimensionsdim(G) of a graphGis defined as the cardinality of strong metric basis. In this paper we determine the strong metric dimension of lollipopLm,ngraph, generalized webW B(G, m, n) graph, and generalized flowerF L(G, m, n, p) graph.
Keywords : strong metric dimension, strong resolving, lollipop graph, generalized web graph, generalized flower graph
1. Introduction
Let G be a simple connected undirected graph G = (V, E), where V is a set of
vertices, and E is a set of edges. The distance between vertices u and v, i.e. the
length of a shortest u-v path is denoted by d(u, v). A vertex set B={x1, x2, . . . , xk}
of G is a resolving set of G if every two distinct vertices ofG are resolved by some
vertex of B. The metric basis of Gis a resolving set with minimal cardinality. The
metric dimension of G, denoted bydim(G) is the cardinality of its metric basis.
The concept of strong metric dimension was introduced by Seb¨o and Tannier [6]
in 2004. Kratica et al. [2] defined for two vertices u and v in a connected graph
G, if u belongs to a shortest v − s path, denoted by u ∈ I[v, s] or v belongs to a
shortest u − s path, denoted by v ∈ I[u, s] then a vertex s strongly resolves two
vertices u and v. A set of vertices S ⊆ V(G) is strong resolving set for G if every
two distinct vertices u,v ∈ V(G) are strongly resolved by some vertex of S. The
strong metric dimension of G denoted by sdim(G) is the minimum cardinality over
all strong resolving sets of G.
Many researchers have investigated the strong metric dimension to some graph
classes. In 2004 Seb¨o and Tannier [6] observed that the strong metric dimension of
complete graphKn isn - 1, cycle graph Cn is⌈n
denotes the number of leaves of tree. In 2013 Yi [8] determined that the strong
metric dimension of G is 1 if and only if G = Pn. Kusmayadiet al. [3] determined
the strong metric dimension of some related wheel graph such as sunflower graph, t
-fold wheel graph, helm graph, and friendship graph. In this paper, we determine the
strong metric dimension of a lollipop Lm,n graph, a generalized web W B(G, m, n)
graph, and a generalized flower F L(G, m, n, p) graph.
2. Main Result
2.1. Strong Metric Dimension. Let G be a connected graph with vertex set V(G), edge set E(G), and S = {s1, s2, . . . , sk} ⊆ V(G). Oelermann and
Peters-Fransen [5] defined the interval I[u, v] between u and v to be the collection of all
vertices that belong to some shortest u − v path. A vertex s ∈ S strongly resolves
two vertices u and v if u ∈ I[v, s] or v ∈ I[u, s]. A vertex set S of G is a strong
resolving set of G if every two distinct vertices of G are strongly resolved by some
vertex of S. The strong metric basis of G is a strong resolving set with minimal
cardinality. The strong metric dimension of a graph G is defined as the cardinality
of strong metric basis denoted by sdim(G). We often make use of the following
lemma and properties about strong metric dimension given by Kratica et al. [1].
Lemma 2.1. Let u, v ∈ V(G), u ̸= v,
(1) d(w,v) ≤ d(u,v) for each w such that {u,w} ∈ E(G), and (2) d(u,w) ≤ d(u,v) for each w such that {v,w} ∈ E(G).
Then there does not exist vertex a ∈ V(G), a ̸= u,v, that strongly resolves vertices u and v.
Property 2.1. If S ⊂V(G)is a strong resolving set of graph G, then for every two vertices u,v ∈ V(G) which satisfy conditions 1 and 2 of Lemma 2.1, obtained u ∈ S or v ∈ S.
We denotediam(G) as the diameter of graphG, i.e. the maximal distance between
two vertices in G.
Property 2.2. If S ⊂V(G)is a strong resolving set of graph G, then for every two vertices u, v ∈ V(G) such that d(u,v) = diam(G), obtained u ∈ S or v ∈ S.
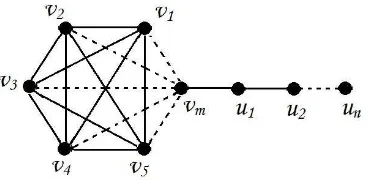
graphKm to a path graphPn with a bridge. We assume that the lollipop graph has
a vertex set V(Lm,n)={v1, v2, . . . , vm, u1, u2, . . . , un}. The lollipop graph Lm,n can
[image:3.595.219.403.222.312.2]be depicted as in Figure 1.
Figure 1. Lollipop graphLm,n
Lemma 2.2. For every integer m ≥ 3 and n ≥ 1, if S is a strong resolving set of lollipop graph Lm,n then |S | ≥ m − 1.
Proof. Consider a pair of vertex (vi, un) withi∈[1,m-1] satisfying conditiond(vi, un) = n+1 = diam(Lm,n). According to Property 2.2, we obtain vi ∈ S or un ∈ S, therefore S has at leastm −1 vertices. Hence |S| ≥ m − 1.
Lemma 2.3. For every integer m ≥ 3 and n ≥ 1, a set S = {v1, v2, . . . , vm−1} is a strong resolving set of lollipop graph Lm,n.
Proof. For every integeri∈[1,m-1] satisfying conditiond(un, vi) =n+1 =diam(Lm,n), we obtain the shortestun−vipath: un, un−1, un−2, . . . , u1, vm, vi. So thatvistrongly resolves a pair of vertices (vm,un). Thus vm ∈ I[un, vi].
For a pair of vertices (uk, ul) withk ̸=l,k, l∈[1,n-1], without loss of generalityk < lwe obtain fori∈[1,m-1], the shortestul −vi path: ul, ul−1, . . . , uk, uk−1, . . . , u1,
vm, vi. So that vi strongly resolves a pair of vertices (uk, ul). Thus uk ∈ I[ul, vi]. Therefore S = {v1, v2, . . . , vm−1} is a strong resolving set of lollipop graph Lm,n.
Theorem 2.1. Let Lm,n be the lollipop graph with m ≥ 3 and n ≥ 1. Then sdim(Lm,n) = m − 1.
Proof. By using Lemma 2.3 a set S = {v1, v2, . . . , vm−1} is a strong resolving set of lollipop graph Lm,n with m ≥ 3 andn ≥1. According to Lemma 2.2, |S| ≥ m - 1 so that S is a strong metric basis of lollipop graph Lm,n. Hencesdim(Lm,n) = m
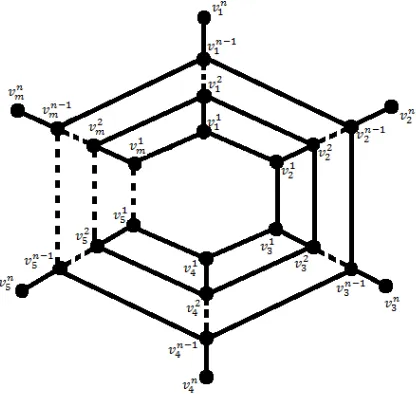
2.3. The Strong Metric Dimension of a Generalized Web Graph. Miller et al. [4] defined the generalized web graph W B(G, m, n) for m ≥ 3, n ≥ 2 is
the graph obtained from the generalized pyramid P(G, m) by taking p copies of
Pn (n ≥ 2) and merging an end vertex of a different copy of Pn with each vertex
of the furthermost copy of G from the apex. In this paper we obtain the strong
metric dimension of generalized web graph withG ∼=Cm and without center vertex
denoted by W B0(Cm, n). We assume that the generalized web graph has a vertex
setV(W Bo)={v1
1, v12, . . . , vm1, v12, v22, . . . , vm2, . . . , v n−1
1 , vn2−1, . . . , vmn−1, v1n, v2n, . . . , vmn}.
[image:4.595.207.415.336.533.2]The generalized web graph W B0(Cm, n) can be depicted as in Figure 2.
Figure 2. Generalized web graphW B0(Cm, n)
Lemma 2.4. For every integer m ≥ 3 and n ≥ 2, if S is a strong resolving set of generalized web graph W B0(Cm, n) then |S | ≥ m.
Proof. LetSis a strong resolving set of generalized web graphW B0(Cm, n). Suppose
thatScontains at mostm- 1 vertices, then|S |< m. LetV1, V2 ⊂V(W B0(Cm, n)),
with V1 ={v11, v21, . . . , vm1 , v12, v22, . . . , v2m, . . . , vn−
1 1 , vn−
1
2 , . . . , vmn−1} and V2 ={vn1, v2n,
. . . , vn
m}. Now we define S1 = V1∩S and S2 = V2 ∩S. Without loss of generality,
we may take |S1 | =p, p≥ 0 and|S2 | =q, q >0. Clearly p+q ≥ m, if not then
there are two distinct vertices va and vb where va ∈ V1 \S1 and vb ∈ V2\S2 such
Lemma 2.5. For every integer m ≥ 3 and n ≥ 2, a set S = {vn
1, v2n, . . . , vmn} is a strong resolving set of generalized web graph W B0(Cm, n).
Proof. We prove that for every two distinct vertices vs
k, vtl ∈ V(W B0(Cm, n)) \ S
with k, l ∈ [1, m] and s, t ∈ [1, n-1], there exists a vertex s ∈ S which strongly resolves vs
k and vtl. There are three possible pairs of vertices.
(1) A pair of vertices (vs
k, vtl) with k, l ∈[1, m], k≠ l and s, t ∈ [1,n-1], s=t. For every integer k, l ∈ [1, m] without loss of generality 1 ≤ k < l ≤ m, we obtain the shortest vt
k −vnl path: vkt, vtk+1, . . . , vtl, v t+1
l , . . . , v n−1
l , vln, and shortestvt
l −vnk path: vlt, vlt−1, . . . , v
t k, v
t+1
k , . . . , v n−1
k , vkn. So thatvtl ∈I[vkt, vln] and vt
k ∈ I[vlt, vnk]. (2) A pair of vertices (vs
k, vtl) with k, l ∈[1, m], k=l and s, t ∈ [1,n-1], s̸=t. For every integer s, t ∈ [1, n-1] without loss of generality 1 ≤ s < t ≤ n-1, we obtain the shortest vt
k − vkn path: vks, v s+1
k , . . . , vtk, v t+1
k , . . . , v n−1
k , vkn. So that vs
k ∈ I[vks, vkn]. (3) A pair of vertices (vs
k, vtl) with k, l ∈[1, m], k≠ l and s, t ∈ [1,n-1], s̸=t. For every integer k, l ∈ [1, m] and s, t ∈ [1, n-1] without loss of generality 1 ≤ k < l ≤ m and 1 ≤ s < t ≤ n-1, we obtain the shortest vs
k − vln path: vs
k, v s+1
k , . . . , v t l−1, v
t l, . . . , v
n−1
l , v n l or v
s k, v
s
k+1, . . . , v
t−1
l , v t l, . . . , v
n−1
l , v n l. So thatvt
l ∈I[v s k, v
n l].
From every possible pairs of vertices, there exists a vertex vn
l ∈ S with l ∈ [1, m] which strongly resolves vs
k,vtl ∈ V(W B0(Cm, n)) \ S. Thus S is a strong resolving
set of generalized web graph W B0(Cm, n).
Theorem 2.2. Let W B0(Cm, n) be the generalized web graph with m ≥ 3 and n ≥
2. Then sdim(W B0(Cm, n)) = m.
Proof. By using Lemma 2.5, we have a setS ={vn
1, v2n, . . . , vmn}is a strong resolving set of W B0(Cm, n) graph. According to Lemma 2.4, | S | ≥ m so that S =
{vn
1, v2n, . . . , vmn} is a strong metric basis ofW B0(Cm, n). Hence sdim(W B0(Cm, n))
= m.
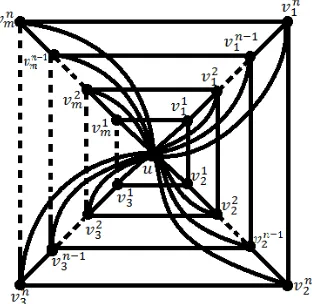
2.4. The Strong Metric Dimension of a Generalized Flower Graph. Miller et al. [4] defined the generalized flower graph with p petals (or simply, generalized
f lower graph) F L(G, m, n, p) for m ≥ 3, n ≥ 2 is the graph obtained from the
generalized web graph W B(G, m, n) by connecting each of the ppendant vertices to
the apex with an edge. A petal ofF L(G, m, n, p) is the subgraphCthat contains the
flower graph has a vertex setV(F L)={u, v1
1, v12, . . . , vm1, v21, v22, . . . , vm2, . . . , v n−1
1 , v
n−1
2 ,
. . . , vn−1
[image:6.595.233.389.209.361.2]m , v1n, v2n, . . . , vmn}. The generalized flower graphF L(Cm, n, p) can be depicted as in Figure 3.
Figure 3. Generalized flower graph F L(Cm, n, p)
Lemma 2.6. For every integer m = 3 and n ≥ 2, if S is a strong resolving set of generalized flower graph F L(C3, n, p) then |S | ≥ 3(n - 1).
Proof. Consider a pair of vertex (vs
k, vlt) with s, t ∈ [1,n], s ̸= t, and k, l ∈ [1,3], satisfying both of the conditions of Lemma 2.1. According to Property 2.1, we obtain vs
k ∈ S or vlt ∈ S, therefore S has at least 3(n−1) vertices. Hence | S | ≥
3(n−1).
Lemma 2.7. For every integer m = 3and n≥2, a set S ={v1
1, v12, v13, v21, v22, v32, . . . ,
vn−1
1 , vn− 1 2 , vn−
1
3 } is a strong resolving set of generalized flower graph F L(C3, n, p).
Proof. We prove that for every two distinct vertices u, v ∈ V(F L(C3, n, p)) \ S,
there exists a vertex s ∈ S which strongly resolvesu and v. There are two possible pairs of vertices.
(1) A pair of vertices (u, vn
k) withk ∈ [1,3].
For every integerk ∈ [1,3], we obtain the shortestvn
k−vk1 path: vkn, u, vk1. So that u ∈ I[vn
k, v1k]. (2) A pair of vertices (vn
k, vln) with k, l ∈ [1,3], k ̸= l.
For every integer k, l ∈ [1,3], without loss of generality 1 ≤ k < l ≤ 3, we obtain the shortestvn
k −v n−1
l path: v n k, v
n l, v
n−1
l . So that v n l ∈ I[v
n k, v
n−1
l ].
From every possible pairs of vertices, there exists a vertex vn−1
l ∈ S or vk1 ∈S with k, l ∈ [1,3] which strongly resolves u, v ∈ V(F L(C3, n, p)) \ S. Thus S is a strong
Lemma 2.8. For every integer m ≥ 4 and n ≥ 2, if S is a strong resolving set of generalized flower graph F L(Cm, n, p) then |S | ≥ mn - 2.
Proof. Consider a pair of vertex (vs
k, vlt) with s, t ∈ [1,n], s ̸=t, and k, l ∈ [1,m], k
̸
= l satisfying both of the conditions of Lemma 2.1. According to Property 2.1, we obtain vs
k ∈ S or v t
l ∈ S, therefore S has at least mn − 2 vertices. Hence | S | ≥
mn − 2.
Lemma 2.9. For every integer m≥4and n≥2, a set S ={v1
1, v21, . . . , v1m, v12, v22, . . . ,
v2
m, . . . , vn1, v2n, . . . , vmn−3, v
n
m−2} is a strong resolving set of generalized flower graph
F L(Cm, n, p).
Proof. We prove that for every two distinct vertices u, v ∈ V(F L(Cm, n, p)) \ S, there exists a vertexs∈S which strongly resolves uandv. There are three possible pairs of vertices.
(1) A pair of vertices (u, vn m−1).
For every integera ∈[1,n] and b ∈[1,m-2], we obtain the shortestvn m−1−v
a b path: vn
m−1, u, v
a
b. So that u ∈ I[vmn−1, v
a b]. (2) A pair of vertices (u, vn
m).
For every integer a ∈ [1,n] and b ∈ [1,m-2], we obtain the shortestvn m−vba path: vn
m, u, vab. So that u ∈ I[vmn, vba]. (3) A pair of vertices (vn
m−1, v
n m). We obtain the shortestvn
m−1−v
n
1 path: vnm−1, v
n
m, vn1. So thatvmn ∈I[vnm−1, v
n
1].
From every possible pairs of vertices, there exists a vertexva
b ∈S witha ∈[1,n] dan b ∈[1,m-2] which strongly resolves u, v ∈ V(F L(Cm, n, p))\ S. Thus S is a strong resolving set of generalized flower graph F L(Cm, n, p).
Theorem 2.3. Let F L(Cm, n, p) be the generalized flower graph. Then for any integer m ≥ 3 and n ≥ 2,
sdim(F L(Cm, n, p)) = {
3(n−1), m = 3; mn−2, m ≥ 4.
Proof. Form= 3 andn≥2, by Lemma 2.6 and Lemma 2.7, we havesdim(F L(Cm, n, p)) = 3(n−1). Next, for m ≥ 4 and n ≥ 2, by Lemma 2.8 and Lemma 2.9, we have
sdim(F L(Cm, n, p)) = mn - 2.
3. Conclusion
According to the discussion above it can be concluded that the strong metric
generalized flower graph F L(Cm, n, p) are as stated in Theorem 2.1, Theorem 2.2,
and Theorem 2.3, respectively.
References
1. Kratica, J., V. Kovaˇcevi´c-Vujˇci´c, and M. ˇCangalovi´c,Minimal Doubly Resolving Sets and The Strong Metric Dimension of Some Complex Polytope, Applied Mathematics and Computation
218(2012), 9790–9801.
2. Kratica, J., V. Kovaˇcevi´c-Vujˇci´c, and M. ˇCangalovi´c, Strong Metric Dimension: A Survey, Yugoslav Journal of Operation Research 24(2)(2014), 187–198.
3. Kusmayadi, T. A., S. Kuntari, D. Rahmadi, and F. A. Lathifah, On The Strong Metric Di-mension of Some Related Wheel Graph, Far East Journal of Mathematical Sciences (FJMS)99
(2016), no. 9, 1325–1334.
4. Miller, M., O. Phanalasy, and J. Ryan,Antimagicness of Some Families of Generalized Graphs, Australasian Journal of Combinatorics53(2012), 179–190.
5. Oelermann, O. and J. Peters-Fransen,The Strong Metric Dimension of Graphs and Digraphs, Discrete Applied Mathematics 155(2007), 356–364.
6. Seb¨o, A. and E. Tannier, On Metric Generators of Graph, Mathematics and Operations Re-search 29(2)(2004), 383–393.
7. Weisstein, Eric W.,CRC Concise Encyclopedia of Mathematics CD-ROM, 2nd ed., CRC Press, Boca Raton, 2003.
8. Yi, E.,On Strong Metric Dimension Graphs and Their Complements, Acta Mathematica Sinica