BAB IV
APLIKASI INTEGRAL GANDA
4.1 Aplikasi Integral Ganda Dua
Integral ganda (rangkap) dua yang bentuk umumnya :
RdA y x f( , )
dapat diaplikasikan untuk beberapa persoalan, diantaranya adalah:
a. Luas suatu Luasan (Bidang)
Luas bidang dapat dipandang sebagai integral ganda dua jika f(x,y) = 1 , sehingga integral ganda dua menjadi :
R dA A
dydx 2
1 2
1 ) ( y
) ( y
b x
a x
x y
x y
A
atau
dxdy 2
1 2
1 ) ( x
) ( x
b y
a y
y x
y x
A
Dalam koordinat polar, bentuk di atas dinyatakan dengan:
2
1 2
1
d d
R
dA A
Contoh :
1. Hitung luas daerah yang dibatasi oleh x + y = 2 dan 2y = x + 4 Jawab :
Sebelum ditentukan luasnya, daerah tersebut digambar terlebih dahulu
Y
2
0 2 2
0 2
0 2
0 y -2
4 -2y
2
0 y -2
4 -2y
6 ) 6 12 ( ) 2 3 -(6y
) 3 6 (
4 2 2
x dxdy
y
dy y
dy y
y
dy d A
A
R
2. Gunakan integral ganda dua untuk menentukan luas suatu luasan yang dibatasi oleh:
3x + 4y = 24, x = 0, y = 0 Jawab
Luas luasan di atas adalah
A(R) =
R dA
=
6
0 3
4 24
0
y
dxdy
= x dy y
3 4 24
0 6
0
=
y dy6
0
4 24 3 1
=
60 22 24 3 1
y y
)6 ,0 (
P
) 0 , 8 (
Q
R 4x3y24
X
4 y x
) 0 , 2 ( )
0 , 2 (
R
X
2 0 2 0 2 2 2
cos ) ( 8
= (24.6 2.6 ) (24.0 2.0 ) 3
1 2 2
= (144 72) 3
1
= 24 satuan luas
b. Pusat Luasan
Misal R adalah suatu luasan yang dibatasi oleh kurva-kurva, maka luasan tersebut mempunyai pusat luasan dan dinyatakan dengan (x, y) dengan hubungan
R R
dA dA x
x dan
R R
dA dA y y
dengan
R
dA adalah luas dari luasan dimaksud.
Contoh
1) Tentukan pusat luasan berikut dengan menggunakan integral ganda dua.y = 2x, y = x, x = 0, dan x = 2
Pusat suatu luasan dinyatakan dengan
x,y
, dengan
R
dA x
x dan
RdA y y
X
2
x x y2
Y
x
y
Luasan di atas dengan menggunakan integral ganda dua didapat:
R
dA R
A( )
22
1 2
0 2 2
0 2
0 2 2
0 2
dydx
y xdx
xdx x xx
x
dan
RdA y
2 9 2
1 4
2 1 2
1 2
0 3 2
0
2 2 2
0
2 2
0 2 2
ydydx
y dx
x x dx x xx x
x
R
dA x
2 9 3
1 2
2
0 3 2
0
2 2 2
0
2 2
0 2
xdydx
xy dx
x x dx x xx x
x
sehingga
9 2 9
x dan
9 2 9
y
diperoleh pusat luasan yang dibatasi oleh y = 2x, y = x, x = 0, dan x = 2
adalah
2 1 , 2 1
2) Tentukan pusat luasan dengan batasanx2y2 4 pada kuadra I.
Pusat suatu luasan dinyatakan dengan
, denganX Y
4 2 2y x
Luasan di atas dengan menggunakan integral ganda dua didapat:
cos 2 . cos 2
cos sin
4 2 dydx
y
cos 2 cos 2 sin 2 4
2
2
tdt t
dydx x cos
3 8 ) (cos cos
8 cos
sin
8 2 tdt
t
Jika S adalah bagian dari permukaan R’ dengan persamaan z=f(x,y). R’ dapat diproyeksikan pada bidang koordinat yang cocok sehingga menghasilkan suatu daerah R pada bidang dalam ruang. Dengan demikian fungsinya terintegralkan pada R.
1. Jika R’ diproyeksikan pada XOY maka
R
dA y z x
z S
2 2
1
2. Jika R’ diproyeksikan pada YOZ maka
R
dA z x y
x S
2 2
1
3. Jika R’ diproyeksikan pada XOZ maka
R
dA z y x
y S
2 2
1
tanda integrasi urutannya menyesuaikan dengan bidang proyeksi, Jika bidang proyeksinya X)Y maka dA berubah menjadi dxdy atau dx.
Contoh
Carilah luas permukaan silinder x2z2 16 didalam silinder x2y2 16 Jawab
Perpotongan kedua selinder menghasilkan bangun
X
Z
Y
16
2 2z
x
16 2 2y x
dengan mengganggap bidang XOY sebagai bidang proyksi, maka
R
dA y z x
z S
2 2
1
0 ,
16 2
y z dan z x x z sehingga x
z sehingga
2
0 16
0
2
2
1 8
x
dydx z
x S
4
0 16
0 2
2
16 4 8
x
dydx x
4
0
128 ) 4 ( 32
32 dx satuanluas
d. Volume Bangun Ruang
Volume bangun suatu ruang dapat dinyatakan dengan menggunakan integral ganda dua dan dituliskan dengan
R
dA y x f V ( , )
dydx y) f(x, 2
1 2
1 ) ( y
) ( y
b x
a x
x y
x y
A
atau
dxdy y) f(x, 2
1 2
1 ) ( x
) ( x
b y
a y
y x
y x
A
Y
Contoh
Dengan melakukan perubahan dA = dydx diperoleh
dydx y
dx Sehingga
dx cos 2 ( ) sin 4 4 ( ) sin 4 ( 9 ) sin 4 cos
2 cos
2
dtdy t
cos
16
cos
Maka
dt t 4 2
cos
16
2
cos sin 4 3 4
cos sin 16
Volume bangun di atas dapat juga dilakukan dengan mengubah urutan tanda integrasi dxdy.
Dengan melakukan perubahan dA = dydx diperoleh
dxdy y
dx sin 9 cos 3 ( ] ) sin 1 ( 9 ) sin 9 ( 9 16 ) sin 1 cos
3 cos
48 cos 48
cos 16
cos
Maka
cos 16
cos sin 4 3 4
cos sin 16
`
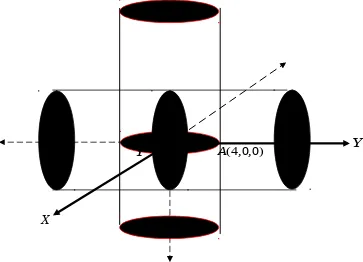
Gambar di oktan I persekutuan silinder di atas adalah
R
dA y x f V ( , )
4
4 16
16
2
2
2
16
2 x dydx
x
x
4
0 16
0
2
2
16
8 x dydx
x
4
0
16 0 2
2
16
8 y x x dx
X X
Y
Y A(4,0,0)
) 0 , 0 , 4 (
A
) 0 , 4 , 0 (
B
Y Z
) 04 , 0 (
4
2
16
8 x dx
4
0 3 3 1 16
8
x x
= 8[(16.4- 43
3 1
)-(16.0- 0 3 1
) = 8(128/3)
= satuanisi
3 1024
3. Dengan menggunakan integral ganda dua, tentukan volume bangun ruang yang dibatasi oleh bidang z = 0, x + y = 4 dan y + z = 4
Jawab
Bangun persekutuan bidang seperti gambar berikut
`
R
dA y x f V ( , )
4
0 4
0
4
y
dxdy y
x yx
ydy
4
0
4 0
4
4
X Z
Y
4
z y
4 y x
) 0 , 0 , 4 (
y yy dy4
0
2)
4 4 16 (
yy dy4
0
2)
8 16 (
4
0 3 2
3 1 3 8
16
y y y
2 3 2 .03
3 1 0 . 3 8 0 . 16 4
. 3 1 4 . 3 8 4 . 16
3 64 3 128
64
4. Tentukan volume bola x2 y2z2 25 menggunakan integral ganda dua.
Jawab
Dengan integral ganda dua diperoleh
r r y
dxdy y x r V
0 0
2 2 2
2 2
8
dxdy x y r y r
2
0 0
2 2 2
2 2
) (
8
Dengan menggunakan substitusi fungsi trigonometri diperoleh
X Z
x = r2 y2 cost dan dx = r2 y2sint
untuk x = 0 didapat t = dan untuk x = r2 y2 didapat t =
2
, sehingga
dxdy x y r y r
2
0 0
2 2 2
2 2
) (
8
dy t y r t y
r y r
2
0 2
0
2 2 2 2 2 2
2 ) ( )sin ( cos )
( 8
2
0 2
0
2 2 2 )cos
( 8
dtdy t y
r
dy t t t y
r
2
0
2
0 2
2
2 1 2
cos sin ) (
8
r
dy y r
0
2 2 )
( 4 .
8
r
y y r
0 3 2
3 1
2
2 3
3 1
2 r r r
3
3 4
r
5. Gambar kurva ruang x2 y2 4x
Jawab
x y x2 2 4
0
4 2
2
x x y
4 )
2
( 2 2
x y
4.2Aplikasi Integral Ganda Tiga
Integral ganda tiga sebagai perluasan integral ganda dua dinyatakan dalam bentuk umum
R
dv V
Sebagaimana telah dinyatakan pada bab III, bahwa integral ganda tiga dapat dinyatakan dalam bentuk koordinat Cartesius, koordinat silider, dan koordinat bola.
Jika dinyatakan dalam bentuk koordinat Cartesius maka
dxdydz z
dxdzdy z
dydzdx z
dzdydx z
dzdxdy z
Jika dinyatakan dalam bentuk koordinat Tabung maka
rdzdrd z
Jika dinyatakan dalam bentuk koordinat Bola maka
Selanjutnya integral ganda tiga dapat digunakan untuk menentukan volume (isi) bendan dan secara umum volume benda dengan
menggunakan integal ganda tiga adalah
R
dv V
dengan menganggap bahwa f(x,y,z)=1
Untuk perhitungan selanjutan dapat menggunakan koordinat Cartesius, koordinat tabung, atau koordinat bola.
Perhatikan beberapa contoh berikut ini.
6. Dengan menggunakan integral ganda tiga tentukan Volume bangun yang dibatasi oleh 6x4y3z12
Volume Limas = Luasalas xtinggi
Dengan integral ganda tiga didapat
dzdxdy
36 36 12
4 31
4.3 Soal-soal
1. Dengan menggunakan integral ganda dua hitunglah luas suatu luasan berikut ini:
a. daerah yang dibatasi oleh 3x + 4y = 24, x = 0, y = 0 b. dibatasi oleh parabola y2 4 x dan y2 4 4x
c. daerah pada kuadran pertama yang dibatasi oleh x2 4 2y` d. dibatasi oleh parabola-parabola y2 x2 dan y 3x2 6x e. dibatasi oleh x + y = 2, 2y = x+4, y = 0
f. dibatasi oleh x2 4y, 8y x2 16
g. dibatasi oleh kurva y2 4x,x2 5 2y danx0
h. di kuadran I yang dibatasi oleh x2 8y40,x2 4y,x0 i. di kuadran I dibatasi oleh y2 6x,y0,danx6
j. diluar r = 4 dan di dalam r = 8 cos θ
k. lingkaran berpusat di titik asal dengan jari-jari 4 satuan. l. di dalam lingkaran r 2(1 cos)
2. Tentukan pusat luasan-luasan berikut dengan batas-batas yang diberikan
a. dibatasi oleh parabola y 6x x2 dan garis y x b. dibatasi oleh parabola y x2 dan garis y 2x3 c. daerah yang dibatasi oleh 3x + 4y = 24, x = 0, y = 0 d. dibatasi oleh y2 4x, x2 5 2y, x 0
e. daerah di atas y = 0 yang dibatasi oleh y2 4x, y2 5 x f. lingkaran x2y2 4
3. Carilah luas bagian bidang x + y + z = 6 dalam silinder x2 y2 4 4. Carilah luas bagian bola x2y2z2 36 dalam silinder x2 y2 6y 5. Tentukan volume benda pejal berikut ini dengan menggunakan
b. di dalam tabung x2y2 9 di atas z = 0 dan dibawah x + z = 4
c. dibatasi oleh bidang-bidang koordinat 6x + 4y + 3z = 12 d. di dalam x2y2 4x di atas z = 0 dan di bawah x2 y2 4z e. dibatasi oleh y0,z0,xy2,2yx6,y2z2 4
6. Tentukan volume berikut dengan menggunakan integral ganda tiga dalam koordinat tabung
a. bola dengan persamaan x2y2z2 9
b. persekutuan silinder x2z2 9 dan silinder x2y2 9
c. benda pejal yang dibatasi oleh zx2y2 dan bidang z = 4 d. benda pejal yang dibatasi oleh x2y2z29,di bawah oleh z
= 0 dan secara menyamping oleh x2y2 4
7. Tulislah integral ganda tiga untuk menentukan isi sebuah bola yang berjari-jari 4 satuan pada tiap kasus dengan: