MODUL PRAKTIKUM FISIKA KOMPUTASI
dengan contoh Bahasa Pemrograman Matlab
JURUSAN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENG ETAHUAN ALAM
UNIVERSITAS BRAWIJAYA
MALANG
2013
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 3
DAFTAR ISI
DAFTAR ISI ... 3
PRACTICE I PENDAHULUAN ... 5
1.1. Pendahuluan... 5
1.2. Perbedaan Kalkulasi Analitis dan Numerik ... 5
1.3. Kode Program Komputer... 5
1.4. Requirement... 6
1.5. Perintah-perintah Dasar ... 6
1.6. Compiling Kode Program ... 11
1.7. Plotting Data ... 12
1.7.1.Plotting GNUPLOT ... 12
1.7.2.Plotting Microsoft Excel ... 13
PRACTICE II ERROR PENDEKATAN ... 17
PRACTICE III AKAR-AKAR POLINOMIAL... 21
PRACTICE IV SOLUSI MATRIKS PERSAMAAN LINIER ... 25
PRACTICE V TRENDLINE ... 31
PRACTICE VI DIFERENSIASI NUMERIK ... 34
PRACTICE VII INTEGRASI NUMERIK ... 37
PRACTICE VIII INTERPOLASI ... 41
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 5
PRACTICE I
PENDAHULUAN
1.1.Pendahuluan
Fisika komputasi pada dasarnya adalah menyelesaikan problem-problem fisika yang tidak dapat diselesaikan secara analitis dengan melakukan pendekatan numerik berdasarkan teori yang sudah ada. Pendekatan numerik tersebut umumnya dilakukan dengan bantuan komputer dan menggunakan bahasa pemrograman tertentu, seperti Pascal, Python, C, C++, Fortran dan lain sebagainya. Hal ini dikarenakan tidak semua problem matematik dapat diselesaikan oleh komputer secara langsung. Problem matematik yang rumit, perlu diubah terlebih dahulu ke bentuk operasi aritmatika ke penambahan, pengurangan, perkalian dan pembagian sederhana agar dapat dikalkulasi oleh komputer. Pengubahan/penurunan tersebut dikenal dengan sebutan pendekatan numerik, di mana hasil perhitungannya identik dengan adanya nilai error.
Problem matematis yang perlu penurunan dengan metode numerik oleh komputer antara lain: problem diferensiasi, integrasi, pencarian akar persamaan polinomial orde tinggi, eigenvalue matrik, boundary value dan lain sebagainya.
1.2.Perbedaan Kalkulasi Analitis dan Nume rik
Salah satu problem matematik yang oleh komputer diselesaikan dengan kalkulasi numerik adalah problem diferensiasi. Dimisalkan terdapat suatu problem fisika dengan persamaan matematis y(x)=2x2-3x+1, yang secara analitis untuk x=5, turunan pertamanya dapat diketahui secara secara langsung dengan penurunan y‟(x)=dy(x)/dx=4x-3, sehingga nilai diferensiai orde satu terhadap x adalah:
Sedangkan untuk perhitungan secara numerik, problem diferensiasi dapat diturunkan dengan metode numerik beda maju (forward different) yang bentuk persamaannya:
(1)
dengan mengambil ∆x=0.1, didapatkan
=17.2
Dari kedua hasil tersebut dapat dibandingkan perbedaan penyelesaian antara numerik dan analitis mempunyai selisih sebesar 0.2, di mana selisih 0.2 ini nantinya akan dikenal sebagai nilai error.
1.3.Kode Program Komputer
Salah satu teknik untuk melakukan komputasi numerik adalah dengan mengimplementasikannya ke bentuk kode program dengan bahasa pemrograman komputer tertentu. Dalam praktikum fisika komputasi ini, tidak disarankan untuk mengacu penggunaan pada salah satu bahasa pemrograman tertentu saja, melainkan praktikan dapat menggunakan bahasa pemrograman Pascal, Python, Matlab atau
6 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
bahasa pemrograman lain, sesuai dengan kemampuan masing- masing. Dengan harapan, praktikan setelah melakukan paraktikum ini dapat menguasai setidaknya salah satu dari macam bahasa pemrograman, sebagai bekal untuk menyelesaikan problem fisika- matematik yang memerlukan penggunaan pendekatan numerik.
1.4.Requirement
Agar semua Kode program yang dituliskan dalam Modul ini dapat berjalan dengan baik, perlu diketahui, semua kode program yang terdapat di dalam modul ini, telah di coba di Matlab v7.0.1. Sehingga praktikan dapat mempunyai gambaran penyesuaian untuk menggunakan compiler Matlab versi diantaranya.
1.5.Perintah-perintah Dasar
Perintah-perintah dasar dalam Matlab yang akan sering digunakan dalam praktikum ini antara lain:
a. Write atau print
Perintah ini digunakan untuk menampilkan huruf atau nilai variabel hasil kalkulasi dari running kode program. Contoh sourcecode-nya:
Kode program 1. Hello world
Matlab
disp(‘Hello World!’);
Untuk menampilkan “Hello World!”, yang merupakan statement standar yang dilakukan bagi pemula untuk mencoba kapabilitas sistem komputer yang digunakan, Matlab menggunakan perintah “disp”, yang juga merupakan perintah dasar ouput, untuk menandai sebuah proses atau mengetahui nilai dari suatu variabel hasil dari suatu perhitungan, sebagaimana ditunjukkan pada Kode program 1.
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 7
b. Read atau Input
Perintah ini digunakan untuk memasukkan suatu nilai atau karakter ke variabel dalam kode program, Contoh source code-nya seperti:
Kode program 2. Input
Matlab
i=input('Masukkan bilangan bulat : '); disp('Hasil: ');
disp(sprintf('Bilangan Bulat : %d',i)); disp(sprintf('Bilangan Asli : %.7f',i)); input('Press any key..');
Dalam praktikum ini, kebanyakan data yang digunakan sebagai variabel input adalah berupa angka, di mana input angka di atas dapat berupa bilangan bulat (integer) atau asli (real). Kode program Matlab di atas menunjukkan teknik untuk inisialisasi type data yang berbeda. Teknik pada Kode program 2 tersebut adalah untuk membedakan antara metode bilangan bulat dan asli, misalnya jika terdapat angka 2 sebagai inputan bilangan asli, beberapa bahasa pemrograman harus menuliskan dengan menambahkan satu angka nol dibelakang koma (Contoh: 2.0), karena jika tidak, bahasa pemrograman secara otomatis menginisialisasikannya sebagai bilangan bulat.
Satu kelebihan Matlab, Matlab merupakan bahasa pemrograman interface. Di mana misalnya ketika bilangan bulat diperlukan menjadi bilangan asli, secara otomatis bilangan tersebut diinisialisasi menjadi bilangan asli oleh Matlab meskipun sebelumnya bertindak sebagai bilangan integer. Sedangkan kode program input pada baris akhir diperlukan agar aplikasi tidak langsung tertutup saat program telah selesai menjalankan perintah-perintah sebelumnya, dan pemberian perintah input ini bersifat optional.
c. Looping for atau while
Pendekatan numerik sering kali melakukan perulangan dalam perhitungannya. Perintah perulangan yang dapat digunakan adalah perintah for dan while. Perintah for digunakan jika tahap perulangannya berupa bilangan bulat. Sedangkan perintah while digunakan jika tahap perula ngannya berupa bilangan asli. Berikut contoh penggunaan perintah for dan while untuk menghitung xy dan mengetahui angka terkecil yang dapat dihitung oleh prosesor. Perintah for:
Kode program 3. Perpangkatan
Matlab x=input('x = '); y=input('y = '); hasil=1; for i=1:y hasil=hasil*x; end
8 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
Perintah while:
Kode program 4. Presisi mesin
Matlab i=1; angka=2; hasil=0; while (hasil~=1) angka=angka/9; hasil=1+angka; disp(sprintf('%3d %.16f',i,hasil)); i=i+1; end;
Kondisi “~=” dalam contoh perulangan while di atas, berfungsi menunjukkan keadaan bahwa selama hasil nilainya tidak sama dengan 1, maka perhitungan nilai “angka” akan dilanjutkan ke nilai berikutnya. Selama ditambahkan dengan nilai “angka”, nilai hasil tidak sama dengan 1, prosesor komputer masih dapat membedakan nilai tersebut sebagai angka yang berbeda dengan selisih yang kecil. Sedangkan ketika nilainya telah dianggap sama, nilai “angka” sebelum perulangan berakhir, nilai “angka” tersebut merupakan hasil pendekatan nilai terkecil yang dapat dihitung oleh prosesor.
d. Kondisi if
Ekspresi kondisi terdiri dari berbagai macam. Untuk bahasa pemrograman yang berbeda, berbeda pula operator pembanding yang digunakan, meskipun mempunyai fungsi yang sama. Perintah yang memerlukan kondisi ini adalah perintah if. Berikut contoh penggunaan perintah tersebut, yang digunakan untuk mencari akar dari fungsi f(x)=x2-4*x-5.
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 9 Kode program 5. Aka r fungsi
Matlab xp=0; x1=15;n=50; p=xp*xp-4*xp-5; disp(sprintf('x y')); for i=0:n x=0.5*(xp+x1); y=x*x-4*x-5; disp(sprintf('%.10f %.10f',x,y)); if (p*y)>0 xp=x; end if (p*y)<0 x1=x; end if (p==y) break; end end disp(sprintf('x mendekati %.10f',x));
Metode numerik yang digunakan untuk mendekati nilai akar parsamaan y=x2-4x-5 di atas adalah metode setengah selisih. Metode ini akan dijelaskan pada bab selanjutnya dan merupakan bagian pokok bahasan pencarian akar persamaan polinomial. Pemakaian perintah if di atas, digunakan untuk mengetahui apakah kedua nilai p dan y berbeda tanda, apakah keduanya positif atau negatif.
e. Membuat fungsi
Seringkali jika dilakukan perlakuan yang sama terhadap suatu data, lebih mudah untuk meringkasnya ke perintah-perintah yang diperlukan ke dalam suatu fungsi. Contoh penggunaan fungsi tersebut adalah seperti dalam Kode program 6:
Kode program 6. Penggunaan fungsi
Matlab
luasbola=@(r)((22/7)*r); bola1=luasbola(5);
bola2=luasbola(0.5);
disp(sprintf('Luas bola1 = %.7f',bola1)); disp(sprintf('Luas bola2 = %.7f',bola2));
Namun di Matlab, jika diperlukan lebih dari satu command yang terdapat dalam fungsi, aturan pendeklarasiannya, fungsi tersebut harus disimpan dalam file lain yang berada satu direktori dan disimpan dengan nama file yang sama dengan nama fungsi itu sendiri. Contoh:
10 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 Matlab %file luasbola.m function output=luasbola(r) output=((22/7)*r); end %file main.m bola1=luasbola(5); bola2=luasbola(0.5);
disp(sprintf('Luas bola1 = %.7f',bola1)); disp(sprintf('Luas bola2 = %.7f',bola2)); f. Output to File
Untuk memudahkan dalam menganalisa hasil program, data hasil perhitungan biasanya disimpan dalam sebuah file. Selain itu, metode penyimpanan ini dapat digunakan jika diperlukan untuk memplot hasil perhitungan ke dalam bentuk grafik, kompiler yang digunakan tidak memiliki fungsi plotter- nya. Contoh kode program untuk penyimpanan data ke file ini adalah:
Kode program 7. Output to file
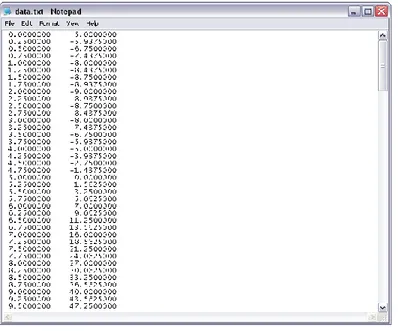
Matlab fp=fopen('data.txt','w'); x=0; while (x<50) y=x*x-4*x-5; fprintf(fp,'%f %f\n',x,y); x=x+0.25; end fclose(fp); disp('Done..');
Kode program di atas digunakan untuk menghitung persamaan
dengan x mulai sama dengan 0 sampai <50 dengan ∆x=0.25. Hasil perhitungannya disimpan dalam bentuk file „data.txt‟ seperti diilustrasikan Gambar 1.1.
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 11 Ga mbar 1.1 File data hasil pe rhitungan
Meskipun demikian di Matlab untuk keperluan plotting data, plotting dapat dilakukan secara langsung menggunakan perintah plot, sehingga penyimpanan data pada Matlab, jarang digunakan untuk keperluan plotting.
1.6.Compiling Kode Program
Gambar 1.6 merupakan contoh tampilan interface Matlab 7.0.1 yang memiliki Command Windows yang fungsinya hampir sama dengan Phython Shell pada compiler Python 2.7x. Agar dalam penulisan kode program lebih mudah untuk dimodifikasi, kode program Matlab dapat ditulis terlebih dahulu ke file yang disebut dengan M-Files. Cara membuat M-File adalah dengan memilih menu FileNewM-File dan akan muncul kotak editor yang merupakan tempat yang digunakan untuk menulis kode program Matlab. Gambar 1.6 juga mengilustrasikan Kode Program 7 sebagai kode program yang akan di-compile. Untuk menjalankannya, klik kanan file yang berisi kode program yang akan dijalankan, pilih Run, dan hasil compilasinya akan ditampilkan di Command Windo ws.
12 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 Ga mbar 1.2 Ta mp ilan user interface Mat lab 7.0.1
1.7.Plotting Data
Plotting data dapat dilakukan dengan berbagai cara, salah satunya dengan menggunakan fungsi yang telah disediakan dalam library compiler itu sendiri, baik 2D maupun 3D. Matlab telah memiliki fungsi plotter sendiri, sedangkan pada umumnya compiler tidak memilikinya. Plotting data dapat dengan menggunakan aplikasi plotter lain, seperti aplikasi khusus pembuat plot, seperti aplikasi GNUPLOT atau Microsoft Excel.
1.7.1. Plotting GNUPLOT
GNUPLOT merupakan aplikasi program interface yang digunakan untuk membuat grafik dari suatu urutan data. Tampilan aplikasi ini seperti ditunjukkan pada Gambar 1.7, yang cara menggunakannya hampir sama dengan Python shell. Contoh penggunaan GNUPLOT untuk membuat grafik 2D dari data hasil running program adalah sebagaimana berikut: Jika data hasil perhitungan Gambar 1.1 diplotkan dengan GNUPLOT, perintah yang digunakan adalah:
Alamat „e:\data\master\lawas\tpw\data.txt‟ merupakan contoh alamat dari file „data.txt‟ yang dapat dilihat pada Address bar windows sebagaimana ilustrasi Gambar 1.8, di mana plot grafik dari file tersebut ditunjukkan pada Gambar 1.9.
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 13 Ga mbar 1.3 Aplikasi GNUPLOT
Ga mbar 1.4 Contoh ala mat file „data.t xt‟
Ga mbar 1.5 Ta mp ilan hasil p lotting file „data.t xt‟
1.7.2. Plotting Microsoft Excel
Untuk plotting file „data.txt‟ dengan Microsoft Excel, caranya adalah seperti membuat grafik pada data Excel biasanya. Perbedaannya adalah ketika membuka file „data.txt‟ terdapat beberapa langkah sebagaimana diuraikan berikut:
14 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
Buka aplikasi Microsoft Excel (di sini digunakan Ms. Excel 2007)
Pilih menu Open, cari folder yang berisi file „data.txt‟ dan seleksi file dengan memilih File Type: Text File. (Gambar 1.10)
Ga mbar 1.6 Kotak d ialog open „data.t xt‟
Klik open maka akan muncul kotak dialog Text Import Wizard seperti ditunjukkan Gambar 1.11.
Ga mbar 1.7 Kotak d ialog Te xt Import W izard file „data.txt‟ step 1
Pilih radio option: Fixed width lalu tekan Next, dan pastikan pada Data Preview data telah terbagi menjadi dua
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 15 Ga mbar 1.8 Kotak d ialog Te xt Import W izard
file „data.txt‟ step 2
Jika data telah terbagi seperti pada Gambar 1.12, selanjutnya dapat ditekan tombol Next atau langsung menekan tombol Finish jika tidak diperlukan untuk mengubah format data dari file „data.txt‟. Data masukan tersebut secara otomatis akan diatur pada kolom-kolom yang telah tersedia oleh Microsoft Excel (Gambar 1.13).
Ga mbar 1.9 Ta mp ilan hasil open file „data.t xt‟ dengan Ms. Exce l
Kemudian untuk memplotkan data-data yang telah dimasukkan diatas, seleksi semua data tersebut, pilih menu InsertScatterScatter with Smooth Lines (Gambar 1.14)
16 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 Ga mbar 1.10 Langkah-langkah plotting scatter
Hasil tampilan plotting grafiknya adalah sebagaimana Gambar 1.15, dan selanjutnya grafik dapat dimodifikasi sesuai dengan kebutuhan.
Ga mbar 1.11 Grafik hasil plotting „data.t xt‟
Tugas
1. Jalankan Kode program 1-7, atau buatlah program serupa dengan bahasa pemrograman yang anda kuasai, sampai dihasilkan plot grafik sebagaimana Gambar 1.9 atau 1.15!
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 17
PRACTICE II
ERROR PENDEKATAN
Teori
Deret Taylor dapat digunakan untuk melakukan pendekatan numerik dari suatu fungsi f(x) berdasarkan nilai f(a) yang telah diketahui. Secara matematis deret Taylor dinotasikan:
(2) Jika f(x)=ex, dengan deret Taylor di atas, nilai f(x) dapat didekati dengan deret seperti ditunjukkan pada persamaan 3 dengan mengambil nilai a=0.
(3)
Begitu juga untuk sin x dan cos x, dengan mengambil nilai a=0, deret pendekatannya adalah:
(4)
(5)
Proble m
Kemampuan komputer impossible untuk melakukan kalkulasi sampai deret tak hingga. Oleh karena itu solusi persamaan 3, 4, dan 5 adalah dengan memotong deret pada nilai n tertentu yang mana nilai error hasil pendekatannya mendekati nol atau bergantung pada kemampuan maksimum komputer yang digunakan. Pertanyaannya adalah berapakah nilai n dari masing- masing persamaan 3, 4, dan 5 agar nilai error pendekatannya mendekati atau sama dengan 0?
18 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
Project I a. Tujuan
Mengetahui nilai error dari pendekatan numerik suatu deret tak hingga berdasarkan model matematis dan kemampuan komputer yang digunakan.
b. Pseudocode
Pseudocode 1. Alur kode progra m e ksponen Input x, n e=1 for i=1 to n do Hitung a=xi Hitung b=i! e= e+(a/b) end for print e
a berfungsi sebagai pembilang dan b berkedudukan sebagai penyebut dari setiap suku deret yang dihitung.
c. ImplementasiKode Program
Kode program 8. Eksponen
Matlab %file faktorial.m function output=faktorial(m) hasil=1; for j=1:m hasil=hasil*j; end output=hasil; end %file eksponen.m x=input('x = '); n=input('n = '); e=1; for i=1:n a=x^i; b=faktorial(i); e=e+(a/b); end
disp(sprintf('e^x = %.10f',e));
Fungsi matematika seperti perpangkatan dan factorial, sebenarnya telah disediakan dalam module math di Python dan di Matlab itu sendiri. Penjabaran fungsi factorial sebagai fungsi di atas, dalam praktikum ini dimaksudkan untuk memberikan contoh bagaimana cara kerja sebenarnya yang dilakukan komputer untuk menyelesaikan problem perpangkatan dan factorial tersebut. Perlu diperhatikan masukan untuk variabel x berupa bilangan asli.
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 19
d. Tugas
1. Salin dan compile kedua kode program, atau buat kode program sendiri sesuai Pseudocode 1 dengan bahasa pemrograman yang anda kuasai!
2. Tentukan nilai n terbaik dan bandingkan antara keduanya, dan juga dengan membandingkan dengan nilai ex dari literatur yang lain (mis. e1= 2.718281828459045), Sertakan juga spesifikasi komputer yang anda digunakan (mis. AMD X2 4800+, P4 1800 MHz, dsb)!
3. Dari salah satu program di atas (sesuai yang anda kerjakan), tunjukkan yang disebut dengan Truncate Error?
Project II a. Tujuan
Mengetahui kelemahan dari model numerik deret tak hingga.
b. Pseudocode
Pseudocode 2. Alur kode progra m sinus Input x, n s=x c=-1 for i=2 to n do if (i mod 2)=1 then Hitung a=xi Hitung b=i! s= s+c*(a/b) c=-1*c endif end for print s
variabel c digunakan sebagai pengubah untuk melakukan penambahan atau pengurangan terhadap hasil penjumlahan nilai s sebelumnya. i mod 2berfungsi agar suku-suku deret yang diambil, hanyalah deret yang berindeks n/suku ganjil.
20 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
c. Implementasi Kode Program
Kode program 9. Deret sinus
Matlab %file sinus.m x=input('x = '); n=input('n = '); s=x; c=-1; for i=2:n if (mod(i,2)==1) a=x^i; b=factorial(i); s=s+c*(a/b); c=-1*c; end end disp(sprintf('sin x = %.10f',s));
Untuk menghitung factorial, pada program Matlab, dapat langsung menggunakan fungsi factorial sebagaimana di tunjukkan pada Kode program 9 di atas.
d. Tugas
4. Bandingkan hasil pendekatan nilai sin x di atas dengan literatur yang anda ketahui (sebutkan sumbernya) dengan nilai x ≥ 1!
5. Bandingkan dan analisa hasil pendekatan kedua kode program di atas! Jika ada tunjukkan kelemahan dari pemodelan nilai sin x tersebut!
6. Buat pseudocode beserta kode program untuk menyelesaikan persamaan 5 (sesuai bahasa pemrograman yang anda kuasai)!
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 21
PRACTICE III
AKAR-AKAR POLINOMIAL
Teori
Bentuk persamaan polinomial untuk orde ≤ n adalah:
(6) dengan nilai koefisien a0, a1, …, an tertentu. Akar-akar persamaannya dapat diketahui dengan beberapa metode seperti metode setengah selisih (biseksi), metode Secant, Newton-Raphson, dan lain sebagainya.
Ide metode setengah selisih adalah mencari nilai xi+1 yang nilai f(xi) mendekati nol berdasarkan nilai f(xi) dan f(xi-1). Ilustrasi pendekatan ini seperti Gambar 3.1 dan nilai xi dan xi-1-nya harus menghasilkan nilai f(xi) dan f(xi-1) yang berbeda tanda.
Ga mbar 3.1 Metode setengah selisih
Metode lain yang serupa dengan metode selisih setengah adalah metode Secant. Tekniknya hampir sama dengan metode setengah selisih, namun metode ini mengambil perbandingan segitiga yang terbentuk dari xi dan xi-1. Ilustrasi pendekatan ini sebagaimana Gambar 3.2.
xi-1 x
f(x)
xi
22 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 Ga mbar 3.2 Metode setengah selisih
Sedangkan untuk metode Newton, atau disebut juga metode Newton-Raphson menggunakan pemotongan deret Taylor pada suku ketiga, yang mana untuk mendekati nilai xi+1 persamaan yang digunakan adalah:
(7)
Proble m
Kode program 5 merupakan contoh pancarian akar dari persamaan polinomial orde 2. Pencarian akar untuk orde <=2 dan akar-akarnya berupa bilangan bulat, mungkin tidak akan menjadi masalah jika dilakukan secara analitis, tetapi bagaimana jika persamaan polinomialnya memiliki orde >2 atau akar-akarnya merupakan bilangan asli?
Project III a. Tujuan
Menentukan akar-akar pada persamaan polinomial orde banyak.
b. Pseudocode
Pseudocode 3. Alur pencarian a kar dengan metode setengah selisih Input x0,x1, n for i=0 to n do x2=0.5*( x0+x1) Hitung f(x2) if f(x2)<0 then x0=x2 else if f(x2)>0 then x1=x2 else break for
end for print x2 xi-1 x f(x) xi xi+1
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 23 Pseudocode 4. Alur kode progra m pencarian a kar dengan metode Secant
Input x0,x1, n f0=f(x0) f1=f(x1) for i=0 to n do Hitung f2=f(x2) x0=x1, x1=x2 f0=f1, f1=f2 end for print x2
c. Implementasi Kode program
Dimisalkan terdapat persamaan polinomial:
(8)
Menggunakan metode Secant, implementasi kode program untuk mencari nilai akar-akar persamaannya adalah:
Kode program 10. Imp le metasi metode Secant
Pascal program secant; uses wincrt; var x0,x1,x2,f0,f1,f2:real; i,n:integer; function f(x:real):real; begin f:=x*x*x*x-31*x*x*x+230*x*x-452*x-144; end; begin write('x0 = ');readln(x0); write('x1 = ');readln(x1); write('n = ');readln(n); f0:=f(x0); f1:=f(x1); for i:=0 to n do begin if((f1-f0)<>0)then x2:=x1-(f1*(x1-x0))/(f1-f0) else begin writeln('Stoped..'); i:=n end; f2:=f(x2); x0:=x1;f0:=f1; x1:=x2;f1:=f2; writeln(i,' ',x2:11:10,' ',f2:11:10); end; end.
24 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 Matlab f=@(x)x*x*x*x-31*x*x*x+230*x*x-452*x-144; x0=input('x0 = '); x1=input('x1 = '); n=input('n = '); f0=f(x0); f1=f(x1); for i=0:n if((f1-f0)~=0) x2=x1-(f1*(x1-x0))/(f1-f0); else disp('Break..'); break; end f2=f(x2); x0=x1;f0=f1; x1=x2;f1=f2; disp(sprintf('%f %f',x2,f2)); end d. Tugas
1. Buatlah grafik hubungan f(x) dan x untuk persamaan 8, berdasarkan contoh pembuatan grafik Gambar 1.9 atau 1.15!
2. Modifikasi Kode program 5, atau buat kode program sendiri sesuai bahasa pemrograman yang anda kuasai dan Pseudocode 3, untuk mencari akar-akar persamaan 8 dengan metode setengah selisih!
3. Bandingkan teknik penentuan nilai awal x0 dan x1 untuk mendekati salah satu nilai akar antara metode setengah selisih dan metode Secant, serta bandingkan jumlah iterasi yang diperlukan antara kedua metode tersebut!
4. Apa yang dimaksud dengan Bracketing Method? Jelaskan apakah yang anda lakukan pada soal no. 3 termasuk metode tersebut?
5. Tentukan nilai keempat akar-akar persamaan 8 dengan kode program yang anda pakai atau yang anda buat, yang mengacu pada grafik soal no. 1!
6. Buatlah Pseudocode atau kode program sesuai bahasa pemrograman yang anda kuasai untuk mencari akar-akar persamaan 8 dengan metode Newton Rapshon! (optional)
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 25
PRACTICE IV
SOLUSI MATRIKS PERSAMAAN LINIER
Teori
Data dalam bentuk matriks sering kali digunakan dalam perhitungan numerik. Dalam persamaan linier, agar lebih mudah, sering kali persamaan-persamaan yang menjadi problem matematik digenerate dalam bentuk matriks untuk mencari solusi penyelesaiannya. Contoh metode numerik yang berbasis matriks antara lain: decomposisi LU, eliminasi Gauss-Jordan, Tridiagonal matriks, dan lain sebagainya.
Penyelesaian eliminasi Gauss-Jordan, seperti dimisalkan terdapat proble m matematis dengan elemen-elemen matriks m x n sebagaimana Gambar 4.1, untuk mencari nilai x1, x2, x3, .., xm langkah- langkahnya adalah sebagaimana berikut:
Ga mbar 4.1 Operasi arit mat ika matriks m x n Rubah matrik a dan b ke bentuk matrik c.
Modifikasi/eliminasi dilakukan pada matrik c ini yang ditujukan untuk mencari matriks identitas dari a
Mengacu pada baris pertama:
Perbaharui nilai c11 dengan membagi semua, mulai kolom 1 sampai n+1 dengan c11 agar nilai c11 bernilai 1.
Untuk baris mulai 2 sampai m, perbaharui nilai mulai kolom 1 sampai n+1 dengan mengurangi c1n yang baru diperbaharui, yang dikalikan dengan cm 1 agar nilai cm 1 bernilai nol.
26 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
Dilanjutkan pada baris kedua:
Karena pada kolom pertama telah bernilai 0, mulai baris kedua sampai ke-m, maka kalkulasi dilakukan pada indeks matriks m≥2 dan n≥2, dengan memperbaharui semua nilai pada baris kedua, dibagi dengan c22 sampai kolom ke n+1.
Untuk baris mulai 3 sampai m, perbaharui nilai mulai kolom 2 sampai n+1 dengan mengurangi c2n yang baru diperbaharui, yang dikalikan dengan cm 2 agar nilai cm 2 bernilai nol.
Dilanjutkan pada baris ketiga dan seterusnya sampai m dengan cara yang sama, sampai didapatkan nilai diagonal matriknya bernilai 1 dan elemen matriks bagian bawah diagonalnya bernilai nol.
Setelah itu, teknik yang dilakukan pada baris satu sampai m di atas dibalik, namun hanya digunakan untuk menghitung agar nilai elemen matriks bagian atas dari diagonal bernilai nol.
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 27
Nilai c1n+1, c2n+1,c3n+1, …, cmn+1 merupakan solusi yang tidak lain adalah nilai x1, x2, x3, .., xm. Langkah- langkah di atas disederhanakan dalam Pseudocode 5.
Proble m
Aplikasi program interface seperti Matlab, Maple, Octave dan Enthought Python, memiliki notasi sendiri untuk mengenerate matriks, yang mana dengan aturan notasi tersebut operasi aritmatika matriks seperti penambahan, pengurangan, perkalian, bahkan untuk mengetahui nilai invers-nya, telah disediakan dalam library dan tinggal memanggilnya saja. Namun bagaimana jika perhitungan numerik membutuhkan operasi matematik atau implementasi numerik yang tidak disediakan dalam library aplikasi tersebut?
Project IV a. Tujuan
Menentukan solusi numerik berdasarkan bentuk matriks suatu persamaan linier.
b. Pseudocode
Pseudocode 5. Alur kode progra m imple mentasi eliminasi Gauss -Jordan
Set matriks a,b Generate matriks c for k=1 to m do p=c[k,k] for j=k to (n+1) do c[k,j]=c[k,j]/p end for for i=k+1 to m do p=c[i,k] for j=k to (n+1) do c[i,j]=c[i,j]-c[k,j]*p end for end for end for for k=m downto 1 do
for i=k-1 downto 1 do p=c[i,k] for j=(m+1) downto 1 do c[i,j]=c[i,j]-c[k,j]*p; end for end for end for print c,x
28 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
c. Implementasi Kode Program
Dimisalkan terdapat suatu persamaan linier yang disusun dalam bentuk matriks sebagaimana berikut:
Ga mbar 4.2 Proble m matriks 3 x 3
Untuk mencari nilai x1, x2, dan x3 dengan metode eliminasi Gauss-Jordan, berdasarkan Pseudocode 5, implementasi kode programnya adalah:
Kode program 11. Imp le metasi untuk metode eliminasi Gauss-Jordan
Matlab m=3;n=m; a=[2 5 7;4 -5 3;8 3 -5]; b=[24 38 -18]; c=[]; %inisialisasi Matriks c for i=1:m for j=1:n c(i,j)=a(i,j); end end for i=1:m c(i,n+1)=b(i); end %proses eliminasi for k=1:m p=c(k,k); for j=k:(n+1) c(k,j)=c(k,j)/p; end for i=k+1:m p=c(i,k); for j=k:n+1 c(i,j)=c(i,j)-c(k,j)*p; end end end for k=m:-1:1 for i=k-1:-1:1 p=c(i,k); for j=(m+1):-1:1 c(i,j)=c(i,j)-c(k,j)*p; end end end %tampilkan matriks c disp(c); for j=1:n disp(sprintf('x %d=%.10f',j,c(j,n+1))); end d. Tugas 1. Analisa Pseudocode 5!
2. Buat program (berdasarkan Pseudocode 5), atau modifikasi Kode program 11, untuk mencari x1, x2, x3,..,x10 problem matriks Gambar 4.3 dengan metode eliminasi Gauss-Jordan! Bandingkan dengan hasil perhitungan x1, x2, x3,..,x10 secara analitis!
3. Buatlah pseudocode dan kode program untuk menyelesaikan problem matriks Gambar 4.3 dengan metode decomposisi LU! Bandingkan hasilnya dengan hasil implementasi Kode Program 11 di atas!
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 29 Ga mbar 4.3 Proble m matriks 10 x 10
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 31
PRACTICE V
TRENDLINE
Teori
Metode yang dapat digunakan untuk mengenerate fungsi dari suatu deret data adalah metode iterasi Jacoby dan Gauss-Seidel. Metode iterasi ini dapat juga digunakan untuk menyelesaikan persamaan linier dan merupakan teknik pendekatan dengan melakukan perulangan substitusi nilai variabel hasil kalkulasi suatu persamaan ke variabel yang sama pada persamaan lain yang segaris.
Iterasi Jacoby dan Gauss-Seidel memiliki bentuk implementasi yang hampir sama, hanya saja yang membedakan adalah teknik substitusi yang dilakukan. Pada iterasi Jacoby obyek variabel yang akan dicari solusinya di kalkulasi terlebih dahulu dan baru disubstitusi pada iterasi selanjutnya. Sedangkan pada iterasi Gauss-Seidel, nilai variabel kalkulasi obyek langsung disubstitusikan menjadi nilai variabel yang sama pada persamaan lain yang segaris.
Untuk berbagai problem matematis, iterasi Gauss-Seidel lebih compatible dibanding iterasi Jacoby. Begitu juga dengan jumlah iterasi yang diperlukan, seringkali jumlah iterasi Gauss-Seidel lebih sedikit dibanding Jacoby. Namun meskipun demikian, untuk keperluan kalkulasi data yang bertautan dalam komputasi paralel, algoritma iterasi Jacoby lebih mudah diimplementasikan daripada Gauss-Seidel.
Untuk menggenerate fungsi dari suatu deret data, dapat dimisalkan terlebih fungsi tersebut sebagai fungsi polinomial (persamaan 9) di mana koefisien-koefisien a0 sampai an adalah variabel yang akan dicari nilainya dengan pendekatan numerik (persamaan 10), yang mana indeks k menunjukkan untuk setiap pendekatan nilai ak menggunakan nilai x yang berbeda pula.
(9)
(10)
Sedangkan nilai error (є) dari metode pendekatan ini disebut dengan RMSE(Root Mean Square Error) yang dirumuskan:
(11)
Proble m
Iterasi Gauss-Seidel di atas berfungsi untuk menghasilkan suatu persamaan fungsi dari f(x), bagaimanakah nilai error fungsi hasil pendekatannya dibandingkan dengan fungsi yang sebenarnya?
32 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
Project V a. Tujuan
Menentukan nilai error hasil pendekatan berdasarkan fungsi yang tergenerate.
b. Pseudocode
Pseudocode 6. Alur kode progra m iterasi Gauss-Seidel Set m Inisialisasi f(x) dan x Inisialisasi n,k for l=0 to m do for k=0 to n do hitung ak (persamaan 10) end for end for hitung RMSE print f(x)
Dimana m menunjukkan jumlah iterasi, n jumlah orde polinomial perkiraan.
c. Implementasi Kode Program
Dimisalkan terdapat deret data sebagaimana berikut:
x 0 0.5π π 1.5π 2π
f(x) 0 1 0 -1 0
Untuk mengenerate fungsi yang melingkupinya, fungsi f(x) dimisalkan sebagai persamaan polinomial. Sehingga berdasarkan jumlah data, persamaan polinomial pemisalannya adalah:
(12) Implementasi kode programnya:
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 33 Kode program 12. Imp le metasi metode iterasi Gauss -Seidel
Matlab
m=1000;n=5; Pi=22/7;
x=[0 (0.5*Pi) Pi (1.5*Pi) (2*Pi)]; f=[0 1 0 -1 0]; a=[0 0 0 0 0]; for l=1:m for k=1:n jum=0; for i=1:n if i~=k jum=jum+a(i)*(x(k)^(i-1)); end a(k)=(f(k)-jum)/((x(k))^(k-1)); end end end e=0; %error for k=1:n jum=0; for i=1:n jum=jum+a(i)*(x(k)^(i-1)); end e=e+(f(k)-jum)^2; end e=sqrt(e/n); disp(sprintf('Error = %.10f',e)); disp(sprintf('a = ')); disp(sprintf(' %.10f ',a)); d. Tugas
1. Jalankan Kode program 12, atau buat kode program sendiri sesuai bahasa pemrograman yang anda kuasai untuk mengenerate fungsi problem di atas, variasi nilai m dan tunjukkan pengaruhnya terhadap hasil fungsi yang tergenerate!
2. Buat grafik hubungan x dan f(x) berdasarkan fungsi polinomial yang tergenerate dari Kode program 12, atau kode program sesuai yang anda kerjakan, dan buktikan bahwa fungsi f(x) sama dengan sin(x)!
3. Tunjukkan pengaruh/hubungan antara jumlah data dengan jumlah suku Polinomial yang diambil?
4. Jelaskan apa yang anda ketahui mengenai Trendline! Apa hubungannya dengan Practice V ini?
5. Cari literatur mengenai iterasi Jacoby dan buatlah pseudocode untuk memodifikasi Kode program 12 dengan metode iterasi Jacoby!
34 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
PRACTICE VI
DIFERENSIASI NUMERIK
Teori
Dalam fisika, penurunan problem diferensiasi numerik dapat menggunakan metode finite difference. Metode ini terdiri dari metode beda maju (forward difference), beda mundur (backward difference) dan beda tengah (central difference) yang persamaan-persamaannya antara lain:
Beda maju
(13)
Beda mundur
(14)
Beda tengah
atau dapat dinotasikan
(15) Persamaan-persamaan di atas digunakan untuk penurunan numerik persamaan diferensiasi orde satu. Sedangkan untuk persamaan diferensiasi orde dua, metode yang digunakan merupakan perpaduan dari metode beda maju, beda mundur dan beda tengah di atas, yang bentuk persamaannya adalah:
(16)
Proble m
Metode beda maju, beda mundur dan beda tengah memiliki ketepatan yang cukup tinggi jika fungsi yang akan didiferensiasikan termasuk persamaan linier. Namun pendekatan akan cukup menyimpang jika fungsinya termasuk fungsi polinomial orde ≥ 2, bagaimanakah nilai error dari pendekatan suatu persamaan diferensiasi yang fungsinya termasuk fungsi polinomial orde ≥ 2?
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 35
Project VI a. Tujuan
Menentukan nilai error dari masing- masing metode differensiasi numerik yang berbeda.
b. Pseudocode
Pseudocode 7. Alur kode progra m perbandingan pendekatan beda ma ju, mundur dan tengah. set x
Set f(x)i, i=0..n for i=1 to n do
bd(x)i=[f(x)i- f(x)i-1]/∆x ---> backward difference end for
for i=0 to n-1 do
fd(x)i=[f(x)i+1- f(x)i]/∆x ---> forward difference end for
for i=1 to n-1 do
cd(x)i=[f(x)i+1- f(x)i-1]/2∆x ---> central difference end for
plot bd(x)i, fd(x)i, cd(x)i, i=0..n
Di mana n jumlah data.
c. Implementasi Kode Program
Dimisalkan terdapat deret data hasil pengamatan gerak bola kasti dalam t, sumbu x dan sumbu y dengan ∆t=0.05 s adalah sebagai berikut:
t (s) 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45
x (m) 0.00 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90
y (m) 0.00 2.51 5.00 7.46 9.90 12.32 14.71 17.07 19.41 21.73
Ga mbar 6.1 Ilustrasi gerak bola kasti
Jika diplotkan berdasarkan letak posisi x dan y, akan didapatkan ilustrasi gerakan bola sebagaimana Gambar 6.1. Untuk mengetahui kecepatan setiap t untuk arah y (vy) implementasi kode program untuk pendekatan nilai kecepatan dengan metode beda maju, beda mundur dan beda tengah adalah:
36 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 Kode program 13. Pendekatan deferensiasi orde s atu dengan beda maju, mundur dan tengah
Matlab fp=fopen('data.txt','w'); n=10;dt=0.05; f=[0 2.49 4.9 7.16 9.2 10.94 12.3 13.21 13.6 13.39]; bd=[];fd=[];cd=[]; %inisialisasi awal bd=f;fd=f;cd=f; %backward difference for i=2:n bd(i)=(f(i)-f(i-1))/dt; end %forward difference for i=1:n-1 fd(i)=(f(i+1)-f(i))/dt; end %central difference for i=2:n-1 cd(i)=(f(i+1)-f(i-1))/(2*dt); end t=0; fprintf(fp,'t BD FD CD\n'); for i=1:n fprintf(fp,'%0.2f %2.7f %2.7f %2.7f\n',t,bd(i),fd(i),cd(i)); t=t+dt; end fclose(fp); disp('Done..'); d. Tugas
1. Jalankan Kode program 13, atau buat kode program sesuai dengan kode program yang anda kuasai berdasarkan Pseudocode 7 untuk mendapatkan data-data seperti yang terdapat pada file “data.txt”!
2. Hitung secara analitik kecepatan arah sumbu y (vy) pada t=0.0, 0.05, 0.10, 0.15,.., 0.90!
3. Plot “data txt” dan bandingkan nilai kecepatan hasil pendekatan metode beda maju, mundur dan tengah, manakah hasilnya yang sesuai dengan perhitungan analitik?
4. Buatlah kode program (atau sesuai bahasa pemrogramanan yang anda kuasai) untuk menghitung percepatan arah y (menggunakan persamaan 16)! Buktikan percepatan tersebut adalah percepatan gravitasi!
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 37
PRACTICE VII
INTEGRASI NUMERIK
Teori
Selain bentuk diferensiasi, problem matematik yang sering ditemui dalam fisika adalah problem integrasi. Untuk pendekatan secara numerik terdapat berbagai metode seperti metode kotak, trapesium, Simpson dan Newton-Cotes. Namun di sini akan dipelajari integrasi numerik dengan mengkhususkan pada metode trapesium.
Secara umum integrasi dapat merupakan luasan yang berada di bawah fungsi. Oleh karena itu dengan metode trapesium dapat diilustrasikan ide integrasi numeriknya sebagaimana Gambar 7.1.
Ga mbar 7.1 Metode trapesium Sehingga solusi persamaan integrasi numeriknya adalah:
,
f(x)<f(x+∆x) (17)Proble m
Teknik untuk memperkecil nilai error untuk metode trapesium adalah dengan memperkecil ∆x, semakin kecil ∆x, nilai error yang diharapkan akan semakin kecil. Dalam matematik, untuk menghitung luas suatu lingkaran dan karena lingkaran mempunyai jumlah sisi tak terhingga, nilai π hanya dapat dicari dengan pendekatan numerik. Bagaimanakah pengaruh variasi ∆x terhadap nilai π?
38 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
Project VII a. Tujuan
Menggunakan integrasi numerik untuk memprediksi nilai suatu konstanta.
b. Pseudocode
Pseudocode 8. Alur kode progra m metode trapesium Set a,b,n dx=(b-a)/n x=a f1=f(x) sum=0 while x<=b do x=x+dx f2=f(x) sum=sum+0.5dx(f1+f2) f1=f2 end while print sum
di mana n jumlah trapesium, semakin banyak jumlah trapesium semakin kecil ∆x-nya
c. Implementasi Kode Program
Kode program 14. Integrasi nume rik dengan metode trapesium
Matlab y=@(r,x)(sqrt(r*r-x*x)); r=5.0;n=1500; a=0;b=r; dx=(b-a)/n; x=a;jum=0; f1=y(r,x); for i=1:n+1 x=x+dx; f2=y(r,x); jum=jum+0.5*dx*(f1+f2); f1=f2; end disp(sprintf('n = %d',n)); disp(sprintf('dx = %.7f',dx));
disp(sprintf('Luas O = %.7f',(4*jum))); disp(sprintf('Pi = %.7f',(4*jum)/(r*r)));
d. Tugas
1. Jalankan Kode program 14, atau buatlah kode program sendiri sesuai bahasa pemrograman yang anda kuasai berdasarkan Pseudocode 8 yang di modifikasi, untuk mendekati nilai π! Berapakah nilai π hasil pendekatan? 2. Analisa variasi ∆x terhadap pendekatan nilai π berdasarkan Kode program 14
atau berdasarkan kode program yang anda buat! Bandingkan dengan nilai π dari literatur lain (mis. π = 3.142857142857143)?
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 39
6. Gunakan metode numerik lain selain metode trapesium untuk mendekati nilai π! Bandingkan hasilnya?
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 41
PRACTICE VIII
INTERPOLASI
Teori
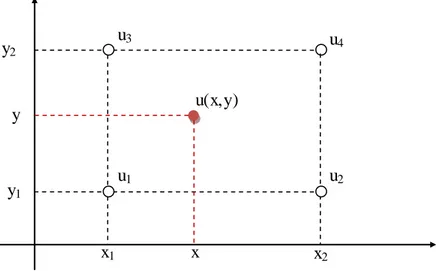
Secara garis besar, interpolasi adalah memprediksi nilai suatu titik berdasarkan titik-titik terdekat yang sudah ada/diketahui nilainya. Salah satu contoh metode interpolasi yang mudah adalah metode interpolasi bilinier, dimana idenya adalah mengambil nilai pendekatan berdasarkan asumsi persamaan gradien terhadap 4 titik terdekat yang sudah diketahui nilainya. Dengan syarat keempat titik tersebut berada membentuk persegi dan nilai titik yang didekati berada dalam 4 titik tersebut. Ilustrasi keberadaan titik tersebut sebagaimana Gambar 8.1.
Ga mbar 8.1 Posisi titik obyek pada interpolasi bilin ier
Persamaan interpolasi bilinier untuk mendekati nilai u di atas adalah sebagaimana persamaan 18.
] (18)
dengan u1, u2, u3, dan u4 yang sudah diketahui.
Proble m
Permasalahan fisis dan matematis seperti apa yang dapat atau cocok digunakan interpolasi bilinier, karena dimungkinkan dengan asumsi titik dalam gradien yang sama dapat memiliki nilai error pendekatan yang besar?
x x2 x1 y1 y y2 u(x,y) u1 u3 u2 u4
42 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
Project VIII a. Tujuan
Menggunakan Interpolasi untuk mendekati suatu nilai berdasarkan dua sumbu koordinat x dan y.
b. Tugas
Salah satu bentuk implementasi interpolasi Bilinier adalah digunakan untuk mendekati nilai kecepatan suatu fluida pada suatu titik x dan y berdasarkan 4 titik yang telah diketahui. Dimisalkan keempat titik tersebut adalah sebagaimana tabel berikut: x y u(x,y) 1 1 2.75 5 1 3.4 1 3 -1.0 5 3 2.2
1. Buatlah Pseudocode beserta Kode program sesuai bahasa pemrograman yang Anda kuasai untuk mendekati nilai u(2.5,1.5) dengan metode interpolasi Bilinier? 2. Analisa hasil pendekatan kecepatan yang Anda peroleh soal no. 1 di atas?
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 43
SOAL UAP (Take home)
1. Simulasikan Gerak Jatuh Bebas suatu benda bermassa m, ke dalam grafik hubungan h (ketinggian) dan t (waktu). Dari ketinggian awal h0 (yang dapat diubah-ubah), dengan syarat ketinggian sebelum dan sesudah menumbuk lantai sama (tumbukan lenting sempurna)! (6)
2. Hampir sama dengan soal no. 1, simulasikan gerak bandul sederhana dalam grafik hubungan x (simpangan) dan t (waktu) dengan syarat gesekan udara diabaikan (gunakan selain metode Verlet)! (6)
3. Buatlah pseudocode beserta kode program untuk menghitung dengan pendekatan numerik dan n berupa pecahan desimal sembarang (tentukan sendiri) dan bernilai negatif?
4. Sebuah mobil bergerak berubah beraturan dengan kecepatan v tercatat di berbagai titik sepanjang jarak x sebagai berikut:
x (m) 0 4 8 12 16 20
44 JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010
Tentukan percepatan mobil dengan menggunakan pendekatan numerik? (6) 5. Suatu gerak projectile diilustrasikan sebagaimana gambar di bawah ini:
di mana sumbu x menunjukkan pergeseran arah mendatar, sedangkan sumbu y menunjukkan perubahan ketinggian (h). Tentukan persamaan posisi projectile sebagai fungsi dari x (h(x)) dengan menggunakan pendekatan numerik?
(2)
Ketentuan menge rjakan soal
Kerjakan dengan ketentuan setiap soal terdapat/meliputi:
1. Tinjauan soal/problem (persamaan/model matematis yang digunakan) 2. Penurunan numerik (Metode yang digunakan, diskritisasi model) 3. Pseudocode
4. Grafik, data hasil kompilasi dan Visualisasi (jika ada) 5. Hasil dan Analisa (pembandingan dengan hasil analitis) 6. Kode program
NB:
Penulisan 1, 2, 4 dan 5 jangan terlalu berbelit-belit. Format bukan laporan, format resume biasa saja.
MODUL PRAKTIKUM FISIKA KOM PUTASI
JURUSAN FISIKA UNIVERSITAS BRAWIJAYA MALANG 2010 45
PUSTAKA
Landau R., et al. Computational Physics.. Problem Solving With Computers (Wiley, 1997)
Kincaid D., Cheney W. Numerical analysis (1991)
Conte, de Boor. Elementary numerical analysis, algorithmic approach Anonymous. 2010. Interpolasi Bilinier. http://wikipedia.org.