Guide for Authors
For a full and complete Guide for Authors, please go to http://www.elsevier.com/locate/regec.
Submissions
For information regarding the submission of manuscripts to the Regional Science & Urban Economics,
please refer to the Guide for Authors at www.elsevier.com/locate/regec.
For specific enquiries on the preparation of electronic artwork, consult http://www.elsevier.com/
artworkinstructions
Author enquiries
For enquiries relating to the submission of articles (including electronic submission where available)
please visit this journal’s homepage at http://www.elsevier.com/locate/regec. You can track accepted
articles at http://www.elsevier.com/trackarticle and set up e-mail alerts to inform you of when an
article’s status has changed. Also accessible from here is information on copyright, frequently asked
questions and more.
Contact details for questions arising after acceptance of an article, especially those relating to proofs,
will be provided by the publisher.
Language services:
Authors who require information about language editing and copyediting services
pre- and post-submission please visit http://www.elsevier.com/locate/languagepolishing or our customer
support site at http://epsupport.elsevier.com.
Please note Elsevier neither endorses nor takes responsibility for any products, goods or services offered
by outside vendors through our services or in any advertising. For more information please refer to our
terms & conditions http://www.elsevier.com/termsandconditions.
The full Guide for Authors can be viewed online at www.elsevier.com/locate/regec.
REGIONAL SCIENCE AND URBAN ECONOMICS
Aims and Scope:
Regional Science and Urban Economics exists to facilitate and encourage high quality scholarship on important
theoretical and empirical issues in urban and regional research. Given a rapidly changing field, the journal’s
empha-sis is on microeconomic analyses of spatial phenomena. The journal solicits original research contributions in
spatial economics, economic geography, and related disciplines. We encourage the submission of theoretical and
empirical contributions related to market organization in space, housing and labor markets, transportation, and
local public economies.
Editors:
DANIEL MCMILLEN, c/o Institute of Government and Public Affairs, Department of Economics (MC 144), University
of Illinois at Chicago, 601 S. Morgan St., Chicago, IL 60607, USA, E-mail: rsue@uic.edu
YVES ZENOU, c/o Department of Economics, Stockholm University, 106 91 Stockholm, Sweden, E-mail:
rsue@ne.su.se
Book review Editor:
ARTHUR O’SULLIVAN, Department of Economics, Lewis & Clark College, Portland, OR 97219, USA
Associate Editors:
S.P. ANDERSON, University of Virginia, Charlottesville, VA; L. ANSELIN, University of Illinois, Urbana, IL; R. ARNOTT,
Boston College, MA 02467-3858; M. BERLIANT, Washington University, St Louis, MO; R. BOADWAY, Queen’s
University, Ontario, Canada; J. BRUECKNER, University of California, Irvine, CA; A. CICCONE, Universitat Pompeu
Fabra, Barcelona, Spain; P.-P. COMBES, GREQAM, Marseille, France; N.E. COULSON, Pennsylvania State University,
PA; R. FORSLID, Stockholm University, Stockholm, Sweden; M. FUJITA, Kyoto Institute of Economic Research, Kyoto;
S. GABRIEL, UCLA, Los Angeles, CA; E. GLAESER, Harvard University, Cambridge, MA; J.V. HENDERSON, Brown
University, Providence, RI; K. IHLANFELDT, Florida State University, Tallahassee, FL; R.P. INMAN, University of
Pennsylvania, Philadelphia, PA; Y. IOANNIDES, Tufts University, Medford, MA; M.E. KAHN, The Fletcher School, Tufts
University, Medford, MA; H. KONISHI, Boston College, MA 02467; K.A. KONRAD, Wissenschaftszentrum Berlin für
Sozialforschung, Berlin, Germany; P. MARTIN, Université de Paris, 1 Panthéon-Sorbonne, Paris, France; T. MAYER,
CEP II, Paris, France; T. MORI, Institute of Economic Research, Kyoto University, Kyoto, Japan; T. NECHYBA, Duke
University, Durham, NC 27708-0097; G. NORMAN, Tufts University, Medford, MA; G.I.P. OTTAVIANO, Universit `a di
Bologna, Bologna, Italy; H.G. OVERMAN, London School of Economics, London, England; E. PATACCHINI, Università
di Roma “La Sapienza”, Rome, Italy; G. PERI, University of California, Davis, CA 95616-8578; J.M. QUIGLEY, University
of California, CA 94720; S. RAPHAEL, University of California, Berkeley, CA 94720-7320; F. ROBERT-NICOUD, LSE,
London, UK; S.L. ROSS, University of Connecticut, CT; E. SHIOJI, Yokohama National University, Yokohama, Japan;
K.A. SMALL, University of California, Irvine, CA; K.O. STAHL, University of Mannheim, D-68131 Mannheim;
J.-F. THISSE, CORE, Catholic University of Louvain, Belgium; P. WANG, Washington University in St. Louis, MO 63130;
B. WEINBERG, Ohio State University, Columbus, Ohio 43210; J.E. ZABEL, Tufts University, MA.
Publication information:
Regional Science & Urban Economics
(ISSN 0166-0462). For 2009, volume 39 is scheduled
for publication. Subscription prices are available upon request from the Publisher or from the Regional Sales Office
nearest you or from this journal’s website (http://www.elsevier.com/locate/regec). Further information is available
on this journal and other Elsevier products through Elsevier’s website (http://www.elsevier.com). Subscriptions are accepted
on a prepaid basis only and are entered on a calendar year basis. Issues are sent by standard mail (surface within
Europe, air delivery outside Europe). Priority rates are available upon request. Claims for missing issues should be
made within six months of the date of dispatch.
Orders, claims, and journal enquiries:
Please contact the Regional Sales Office nearest you:
St. Louis:
Elsevier, Customer Service Department, 11830 Westline Industrial Drive, St. Louis, MO 63146, USA; phone:
(877) 8397126 [toll free within the USA]; (+1) (314) 4537076 [outside the USA]; fax: (+1) (314) 5235153; e-mail:
JournalCustomerService-usa@elsevier.com
Amsterdam:
Elsevier, Customer Service Department, PO Box 211, 1000 AE Amsterdam, The Netherlands; phone:
(+31) (20) 4853757; Fax: (+31) (20) 4853432; e-mail: JournalsCustomerServiceEMEA@elsevier.com
Tokyo:
Elsevier, Customer Service Department, 4F Higashi-Azabu, 1-Chome Bldg, 1-9-15 Higashi-Azabu, Minato-ku,
Tokyo 106-0044, Japan; phone: (+81) (3) 5561 5037; fax: (+81) (3) 5561 5047; e-mail: JournalsCustomerServiceJapan@
elsevier.com
Singapore:
Elsevier, Customer Service Department, 3 Killiney Road, #08-01 Winsland House I, Singapore 239519;
phone: (+65) 6349 0222; Fax: (+65) 67331510; e-mail: JournalsCustomerServiceAPAC@elsevier.com
Advertising information:
Advertising orders and enquiries can be sent to: James Kenney, Elsevier Ltd., 32
Jamestown Road, London NW1 7BY, UK; phone: (+44) 207 424 4216; fax: (+44) 1865 853 136; e-mail: j.kenney@
elsevier.com. Customers in the US and Canada can also contact: Mr Tino deCarlo, Advertising Department, Elsevier
Inc., 360 Park Avenue South, New York, NY 10010-1710, USA; phone: (+1) (212) 633 3815; Fax: (+1) (212) 633 3820;
e-mail: t.decarlo@elsevier.com.
USA mailing notice:
Regional Science and Urban Economics
(ISSN 0166-0462) is published bimonthly by Elsevier
B.V. (P.O. Box 211, 1000 AE Amsterdam, The Netherlands). Periodical postage paid at Rahway NJ and additional
mailing offices.
USA POSTMASTER:
Send change of address: Regional Science and Urban Economics, Elsevier, Customer Service
Department, 11830 Westline Industrial Drive, St. Louis, MO 63146, USA.
AIRFREIGHT AND MAILING
in USA by Mercury International Limited, 365 Blair Road, Avenel, NJ 07001.
The paper used in this publication meets the requirements of ANSI/NISO Z39.48-1992 (Permanence of Paper).
Printed by Henry Ling Ltd., The Dorset Press, Dorchester, UK.
Downtown parking in auto city☆
Richard Arnott
a,⁎
, John Rowse
baDepartment of Economics, University of California, Riverside, 4106, Sproul Hall, Riverside, CA 92521-0427, USA bDepartment of Economics, University of Calgary, Calgary, AB, Canada T2N 1N4
a b s t r a c t
a r t i c l e
i n f o
Article history:
Received 12 December 2007 Received in revised form 11 July 2008 Accepted 12 August 2008
Available online 20 August 2008
JEL classification: R40
Keywords: Parking Traffic congestion Parking garages Parking policy
Arnott and Inci [Arnott, R. and Inci, E., 2006. An integrated model of downtown parking and traffic congestion. Journal of Urban Economics 60, 418–442] developed an integrated model of curbside parking and traffic congestion in a downtown area. Curbside parking is exogenously priced below its social opportunity cost, and the stock of cars cruising for parking, which contributes to traffic congestion, adjusts to clear the market for curbside parking spaces. Denser downtown areas have garage as well as curbside parking. Because of economies of scale in garage construction, garages are discretely spaced. The friction of space confers market power on parking garages. Spatial competition between parking garages, as modeled in Arnott [Arnott, R., 2006. Spatial competition between downtown parking garages and downtown parking policy. Transport Policy 13, 458–469], determines the equilibrium garage parking fee and spacing between parking garages. Also, the stock of cars cruising for parking adjusts to equalize the full prices of curbside and garage parking. This paper combines the ingredients of these two models, hence presenting an integrated model of curbside parking, garage parking, and traffic congestion, and examines curbside parking policy in this context through a numerical example with parameters representative of a medium-sized US city. The central result is that raising the curbside parking fee appears to be a very attractive policy since it generates efficiency gains that may be several times as large as the increased revenue raised.
© 2008 Elsevier B.V. All rights reserved.
1. Introduction
Anyone who has parked in the downtown area of a major city during the business day will attest to its high cost. Parking in a convenient parking garage is expensive, while finding cheaper curbside parking normally entails cruising for parking and walking some distance. To our knowledge, there are no reliable estimates of the proportion of the average full price of a trip with a downtown destination that is associated with parking. Informal estimates of one half seem too high. It seems warranted to say, however, that economists have paid less attention to downtown parking than its importance merits. There is a large literature in economics on urban auto congestion but only a few recent papers on the economics of downtown parking (which will be reviewed below).
Arnott and Inci (2006)constructed an integrated model of curbside parking and traffic congestion in an isotropic downtown area with identical drivers and price-sensitive demand. The curbside meter rate is set below its social opportunity cost. This results in excess demand for curbside parking spaces. Parking is saturated, and cars cruise for parking waiting for a parking spot to open up. The expected time spent cruising for parking adjusts to clear the market, which is achieved via adjustment in the density of cars cruising for parking. The cars cruising for parking contribute to traffic congestion as well. Under reasonable assumptions, Arnott and Inci demonstrated the existence and uniqueness of steady-state equilibrium with saturated parking, and also examined curbside parking policy in the context of the model.
Denser downtown areas have garage as well as curbside parking. Because of economies of scale in garage construction, garages are discretely spaced. The friction of space then confers market power on parking garages. Arnott (2006) developed a model of spatial competition between parking garages, which generates an equili-brium parking fee that is above marginal cost. With underpriced curbside parking and overpriced garage parking, the stock of cars cruising for parking adjusts to equalize their full prices. This paper combines the ingredients of these two models (except, to simplify, it assumes inelastic demand for downtown parking), hence presenting an integrated model of curbside parking, garage parking, and traffic
–
☆ We would like to thank Eren Inci, Robin Lindsey, David Malueg, and seminar participants at Clark University, Emory University, the University of California at Riverside, the University of Colorado at Boulder, the University of Florida at Gainesville, the University of Massachusetts at Amherst, and the University of California at Irvine for helpful comments, and Junfu Zhang for pointing out an error in an earlier draft.
⁎Corresponding author.
E-mail addresses:richard.arnott@ucr.edu(R. Arnott),rowse@ucalgary.ca(J. Rowse). 0166-0462/$–see front matter © 2008 Elsevier B.V. All rights reserved.
doi:10.1016/j.regsciurbeco.2008.08.001
Contents lists available atScienceDirect
Regional Science and Urban Economics
congestion, and examines curbside parking policy in this context through a numerical example with parameters representative of a medium-sized, auto-oriented city such as Winnipeg, Perth, San Diego, Sacramento, or Phoenix.
The addition of garage parking alters the economics of downtown parking in three interesting ways. First, the equilibrium condition determining the stock of cars cruising for parking changes. With only curbside parking, the stock of cars cruising for parking adjusts to clear the market for trips. In contrast, with both curbside and garage parking the stock of cars cruising for parking adjusts to equalize the full prices of curbside and garage parking. Second, even though the overpricing of garage parking does not create inefficiency directly, since overall parking demand is assumed to be inelastic, it does so indirectly in two ways,first, as noted already, by increasing the price spread between curbside and garage parking and hence the stock of cars cruising for parking, and second by causing parking garages to be inefficiently small and too closely spaced. Third, the presence of garage parking magnifies the distortion associated with the under-pricing of curbside parking, or, put alternatively, increases the social benefit of increasing the curbside parking fee. With only curbside parking, the equilibrium full price of a downtown trip is determined by the intersection of the trip demand curve and the curbside parking capacity constraint. Raising the curbside meter rate does not alter this full price oftrips, but simply converts travel time (which includes in-transit and cruising-for-parking time) costs dollar for dollar into meter revenue, so that every extra dollar of revenue raised increases social surplus by one dollar. But with garage parking, there is a magnification effect. Raising the curbside meter rate does not alter the full price of parking. Raising the curbside meter rate converts cruising-for-parking time costs dollar for dollar into meter revenue. But there is the added benefit that the reduction in the stock of cars cruising for parking reduces traffic congestion, which benefits everyone. In our favored numerical example, this magnification effect results in a $3.20 increase in social surplus for every dollar increase in meter revenue.
As noted above, the literature on the economics of parking is small. We start by reviewing the broader literature, and then turn to the small number of papers that distinguish between curbside and/or garage parking or analyze cruising for parking.
Early work on the economics of parking argued that parking, like any other commodity, should be priced at its social opportunity cost (Vickrey, 1954; Roth, 1965).Vickrey (1954)also developed a scheme for demand-responsive pricing of curbside parking. Over the next three decades, parking was largely ignored by economists, in modal choice studies being treated simply as a component of thefixed cost of a trip. Modern interest in the economics of parking started in the early 1990s.Shoup (2005)has led the way in generating interest in the economics of parking. In the 1990s, he championed cashing out employer-provided parking, and has considered many aspects of the economics of parking since then.Arnott et al. (1992)
andAnderson and de Palma (2004)extended the Vickrey bottleneck model (1969) to analyze the temporospatial equilibrium of curbside parking when all drivers have a common destination and desired arrival time, such as for a special event or the morning commute.Arnott and Rowse (1999)examined the steady-state equilibria of cars cruising for parking on a circle when parking is unsaturated.
Arnott et al. (2005, Ch. 2, The basic model) presented a model that examines the interaction between cruising for parking and traffic congestion with only curbside parking. A more thorough treatment of that model was provided inArnott and Inci (2006). Several papers in the literature have recognized that the stock of cars cruising for parking adjusts to equalize the full prices of curbside and garage parking (Calthrop, 2001; Shoup, 2005,1 2006; Arnott et al., 2005;
Calthrop and Proost, 2006). Calthrop (2001) and Arnott (2006)
considered the potential importance of garage market power, Calthrop by assuming a monopoly supplier, Arnott by modeling spatial competition between parking garages. The Los Angeles model of Arnott, Rave, and Schöb includes curbside parking, garage parking, endogenous cruising for parking, and garage market power, but provides an unpersuasive treatment of garage market power.Arnott (2006) contained all four elements as well, but focused on the treatment of garage market power rather than providing a complete analysis of the model. This paper provides a complete analysis with the more satisfactory treatment of garage market power, and also provides calibrated numerical analysis of a variety of parking policies.
In terms of policy insights, our principalfinding –which was noted above– is that, under conditions of even moderate traffic congestion, the social benefits from raising curbside parking rates may be several times the additional meter revenue generated, a double dividend result. Another important finding is that, with realistic parameter values, less space should typically be allocated to curbside parking the larger is the wedge between curbside and garage parking rates.
Section 2 sets the stage by presenting a simplified model in which garage parking is provided at constant unit cost. Section 3 presents and analyzes the central model that takes into account the technology of garage construction and spatial competition between parking garages. Section 4 presents calibrated numerical examples for the central model. Section 5 notes some directions for future research. And Section 6 provides some concluding comments.
2. A simple model
Understanding the central model of the paper will be facilitated by starting with a simplified variant. A broad-brush description is followed by a precise statement.
2.1. Informal model description
The model describes the equilibrium of trafficflow and parking in the downtown area of a major city.2To simplify, it is assumed
that the downtown area is spatially homogeneous (isotropic) and in steady state, and also that drivers are homogeneous. Drivers enter the downtown area at an exogenous uniform rate per unit area-time, and have destinations that are uniformly distributed over it. Each driver travels a fixed distance over the downtown streets to his destination. Once he reaches his destination, he decides whether to park curbside or in a parking garage.3 Both
curbside and garage parking are provided continuously over space. If he parks curbside, he may have to cruise for parking, circling the block until a space opens up. After he has parked, he visits his destination for afixed period of time, and then exits the system. Garage parking is assumed to be provided competitively by the private sector at constant cost, with the city parking department deciding on the curbside meter rate and the proportion of curbside to allocate to parking. The curbside parking fee (the meter rate) is less than the garage fee. Consequently, all drivers would like to park curbside but the demand inflow is sufficiently high that this is impossible. Curbside parking is saturated (the occupancy rate is
1 Shoup, Table 11-5, displays the results of 16 studies of cruising for parking in 11 cities over an eighty- year period. The mean share of traffic cruising was 30% and the average search time was 8.1 min. While the study locations were not chosen randomly, the results do indicate the potential importance of cruising for parking.
2 The model differs from that inArnott and Inci (2006)in two respects. Arnott and Inci consider the situation where all parking is curbside and the demand for trips is sensitive to the full price of a trip. Here, in contrast, the demand for trips is completely inelastic, and there is both curbside and garage parking. The model specification is independent of the form of the street network, but for concreteness one may imagine that there is a Manhattan network of one-way streets.
3 The paper does not consider parking lots. Parking lots are difficult to treat because most are transitional land uses between the demolition of one building on a site and the construction of the next.
100%) and the excess demand for curbside parking spaces is rationed through cruising for parking. In particular, the stock of cars cruising for parking adjusts such that the full price of curbside parking, which is the sum of the meter payment and the cost of time cruising for parking, equals the garage parking payment. The downtown streets are congested by cars in transit and cruising for parking. In particular, travel time per unit distance driven increases with the density of traffic and the proportion of curbside allocated to parking.
2.2. Formal model
Consider a spatially homogeneous downtown area to which the demand for travel per unit area-time is constant,D. Each driver travels a distanceδover the downtown streets to his destination, parks there for a period of timeλ, and then exits.4A driver has a choice between
parking curbside, where the meter rate isfper unit time, and parking in a parking garage, at a ratecper unit time, equal to the resource cost of providing a garage parking space.5Both curbside and garage
parking are continuously provided over space. By assumption (its rationale will be given later),fbc, and the excess demand for curbside parking is rationed through cruising for parking. The stock of curbside parking isPper unit area, so that the number of garage parking spaces per unit area needed to accommodate the exogenous demand is Dλ−P. The technology of traffic congestion is described by the function t=t(T,C,P), wheretis travel time per unit distance,Tthe stock of cars in-transit per unit area, andCthe stock of cars cruising for parking per unit area.6The larger are
CandT, the higher the density of traffic on the city streets, so thattTandtC(subscripts denote partial derivatives) are positive, and the larger isP, the lower the proportion of street space available for traffic, so thattPis positive too. It is assumed as well thattis a convex function ofT,C, andP.
Dis sufficiently high that, even if all curbside is allocated to parking (so thatP=Pmax), there is still a need for garage parking (i.e.,DλNPmax). Due to the underpricing of curbside parking, the stock of cars cruising for parking adjusts such that the full price of curbside parking, the sum of the meter payment and the value of time lost cruising for parking, equals the full price of garage parking.7For the moment, it is assumed
that, even when curbside parking is provided free and all curbside is allocated to parking, the street system can still accommodate the exogenous demand.8
The density of cars per unit area isT+C, their velocity,v, is 1/t, and sinceflow equals density times velocity, the flow in terms of car-distance per unit area-time is (T+C)/t. If there areMdistance units of
one-way streets per unit area, then a person standing on a sidewalk would observe aflow of (T+C)/(Mt) cars per unit time.9
Throughputis defined analogously toflow but includes only cars in transit10; thus,
the throughput in terms of car-distance per unit area-time isT/t. Steady-state equilibrium is described by two conditions. Thefirst, thesteady-state equilibrium condition, is that the input rate into the in-transit pool,D, equals the output rate, which equals the stock of cars in the in-transit pool divided by the length of time each car stays in the pool,T/(δt(T,C,P)):
D¼ T
δt Tð ;C;PÞ: ð
1Þ
This may be written alternatively asDδ=T/t(T,C,P).Dδis the input in terms of car-distance per unit area-time, andT/t(T, C, P) is the throughput. Let ρ be the value of time.11 The second equilibrium
condition, theparking equilibrium condition, is that the stock of cars cruising for parking adjusts to equilibrate the full prices of garage and curbside parking:
cλ¼fλþρCλ
P : ð2Þ
The full price of garage parking iscλ. The full price of curbside parking isfλ plus the (expected) cost of cruising for parking. The expected time cruising for parking12equals the stock of cars cruising
for parking,C, divided by the rate at which curbside parking spots are vacated,P/λ. Thus, holdingfixed the expected time cruising for parking, the stock of cars cruising for parking increases with the number of curbside parking spaces available. The cost of cruising for parking equals the expected time cruising for parking times the value of time. Eq. (2) may be rewritten as
C¼ðc−fÞP
ρ ; ð3Þ
indicating the equilibrium stock of cars cruising for parking as a function ofc,f,P, andρ.
This simple model has two equations in two unknowns,TandC. The equations are recursive. Eq. (3) determinesCand then Eq. (1) determinesT. Resource costs per unit area-time,RC, are simplyρ(T+C), the stock of cars in transit and cruising for parking, times the value of time, plus the resource cost of garage parking,c(Dλ−P).
4One could equally well assume that each driver travels a distanceδ/2 over the downtown streets to his destination, parks there for a period of timeλ, then drives an equal distance over the streets to his entry point.
5The paper neglects the subsidization of garage parking, which is practically very important (Small and Verhoef, 2007, p.113). The bulk of employers, though a smaller proportion of downtown employers, heavily subsidize their employees' garage parking. Furthermore, many shoppers receive subsidized garage parking via“parking validation” whereby a retailer pays for the garage parking of clients who have purchased goods from his store. The subsidization of garage parking reduces the full price of garage parking, hence the price differential between curbside and garage parking, and hence the incentive to cruise for parking.
6Realistically, travel time per unit distance is affected by cars entering and exiting curbside parking spaces as well. This could be incorporated into the analysis by adding the curbside parking turnover rate as an argument to the functiont. The specification of the technology assumes thatPis divisible. This is not completely satisfactory since having only one curbside parking space per block would slow down traffic almost as much, and perhaps even more, as having an entire curb allocated to parking. This objection can be accommodated by having a certain proportion of curbside blocks completely allocated to curbside parking with the remainder being free of curbside parking. But this would violate the spatial symmetry assumed in the model.
7The paper ignores possible safety differences between curbside and garage parking, as well as the search time and walking time inside the parking garage.
8Primitive conditions for this assumption to hold are given in Section 2.6, which examines the congestion technology in detail.
9Flow equals density times velocity is known as the Fundamental Identity of Traffic Flow. Applying this identity in this context requires some care. Ordinarily, density is measured per unit distance, so that, with velocity measured as distance per unit time, the dimension offlow is cars per unit time. Here, however, density is measured as cars per unit area, so that application of the formula givesflow in units of car-distance per unit area-time. WithMmiles of city street per unit area, the density in terms of cars per unit distance is (T+C)/M, and application of the Identity givesflow as cars per unit time on a street, (T+C)/(Mt).
10Since the transportation engineering literature has not analyzed situations in which cars circle the block, it does not make a terminological distinction betweenflow and throughput. It seems intuitive to defineflow as the number of cars that a bystander would count passing by per unit time. Throughput too seems an appropriate choice of term.
11 The large empirical literature on the value of travel time finds it to differ significantly across travel activities and for in-transit travel to differ according to the level of congestion. The analysis could be extended straightforwardly to allow for these considerations.
12This statement takes into account that the service discipline is random access. There are several features of the model that can be interpreted as either stochastic or deterministic. A deterministic interpretation, with FIFO access to curbside parking on each block, is the most straightforward. Stochastic interpretations are more realistic but would need to be solved using queuing theory (see, for example,Breuer and Baum, 2005).
2.3. Full social optimum
The full social optimum entails no cruising for parking. The density of in-transit traffic is then determined by Eq. (1) with C= 0. The social welfare optimization problem is to chooseTand P to mini-mize resource costs per unit area-time, subject to the steady-state equilibrium condition, given by Eq. (1):
min T;P
RC¼ρTþc Dð λ−PÞ s:t: T−δt Tð ;0;PÞD¼0: ð4Þ
The shadow cost of curbside parking is the increase in in-transit travel time cost per unit area-time from having one more curbside parking spot, which, from Eq. (1), isρdT/dP=ρδtPD/(1−δtTD)). If, with P=0, the shadow cost of curbside parking exceedsc, it is optimal to allocate no curbside to parking. And if, withP=Pmax, the shadow cost of curbside parking falls short ofc, it is optimal to allocate all curbside to parking. Otherwise, the optimalPsolves
ρδtPD 1−δtTD−c¼
0; ð5Þ
the level of curbside parking should be chosen to equalize the shadow costs of curbside and garage parking.13
Let⁎denote the value of a variable at the social optimum. The social optimum can be decentralized by settingP=P⁎, T=T⁎, and f=f⁎=c.
2.4. Constrained (second-best) social optimum
Since parking policy is local, it is poorly documented and has been little studied. One empirical regularity stands out, however, at least for US cities. In downtown areas, the curbside parking fee is considerably lower than garage parking fees. In downtown Boston, for example, the meter rate has remained at $1.00 per hour for twenty years, while garage parking fees are as high as $10.00 for thefirst hour. What accounts for this price differential? We have posed this question to several seminar audiences. The common answer is that downtown merchants' associa-tions lobby City Hall to set the meter rate low in order to draw shoppers away from suburban shopping centers, where most parking is provided free. In many downtown shopping areas, merchants pay for shoppers' garage parking by validating their garage parking stubs. Since most curbside parking has time limits, and since merchants cannot pay for their customers' curbside parking, a low meter rate subsidizes the parking of short-term shoppers. If most curbside parking is occupied by shoppers, the result is a form of price discrimination. Shoppers end up paying less for downtown parking than non-shoppers. In this paper, we do not attempt to model the political economy of downtown parking policy, but instead simply assume that that the meter rate is set low– below the marginal cost of a garage parking space – by the local transportation authority, and explore the implications of the price wedge between curbside and garage parking.
The constrained social optimum is now considered, where the constraint is that the curbside parking fee is set belowc, with the stock of cars cruising for parking adjusting so as to satisfy the parking equilibrium condition. The second-best optimal allocation of curb-side to parking minimizes resource costs per unit area, subject to both the steady-state equilibrium condition, (1), and the parking equili-brium condition, (2). Resource costs per unit area-time are given by
ρ(T+C) +c(Dλ−P). Thus, the constrained social welfare optimization problem is to chooseT,C, andPto
min
T;C;PRC¼ρðTþCÞ þc Dð λ−PÞ s:t:
iÞ Dδt Tð ;C;PÞ−T¼0; / iiÞ P
ρðc−fÞ−C¼0; ’ ð6Þ
whereϕ is the Lagrange multiplier on constraint i) andφthat on constraint ii). The second-best optimum may entail no curbside allocated to parking, in which case there is no cruising for parking, or all the curbside allocated to parking. An interior optimum is char-acterized by thefirst-order conditions:
T:ρþ/ðDδtT−1Þ ¼0 ð7aÞ
C:ρþ/DδtC−’¼0 ð7bÞ
P:−cþ/DδtP− ’ðc−fÞ
ρ ¼0 ð7cÞ
Substituting out the Lagrange multipliers yields
ρDδtP 1−DδtTþ
c−f
ð Þ þ DδtC 1−DδtT
c−f
ð Þ−c¼0: ð8Þ
A heuristic derivation is as follows:Pshould be chosen such that dRC/dP= 0. From the objective function, dRC/dP=ρdT/dP+ρdC/dP−c; from constraint ii), dC/dP= (c−f)/ρ; and from constraint i), (dT/dP) (1−DδtT) =DδtCdC/dP+DδtP. The last term in Eq. (8) is the marginal social benefit of P, the reduction in garage costs. The other three terms are components of the marginal cost, all of which relate to travel costs. Thefirst term captures thecapacity reduction effect; this is the increase in aggregate in-transit travel costs that comes about through the reduction in the road space available, holding constant Tand C. The second term captures the cruising-for-parking stock effect; since the stock of cars cruising for parking is proportional to the amount of curbside parking, the increase inPincreases the stock of cars cruising for parking, which, holdingTandPfixed, increases congestion. The third term captures thecruising-for-parking conges-tion effect; via the steady-state equilibrium condition, the increase in the stock of cars cruising for parking causes the stock of cars in transit to increase, which further augments congestion.
Let⁎⁎denote values at the constrained social optimum. With the curbside meter rate set at the exogenous level, the constrained social optimum can be decentralized by settingT=T⁎⁎,C=C⁎⁎, andP=P⁎⁎.
Unless both allocations entail the same corner solution, the optimal amount of curbside to allocate to parking is greater in the full social optimum than in the second-best social optimum with underpriced curbside parking, i.e.P⁎NP⁎⁎. In both allocations, the marginal social benefit of increasingPby one unit is the saving in garage resource costs, c. But the marginal social cost of increasingPis lower in the full social optimum than in the second-best optimum since the costs deriving from the cruising-for-parking stock and congestion effects are absent.
2.5. Revenue multiplier: the effects of raising the curbside parking fee
A principal theme of the paper is that the underpricing of curbside parking is wasteful. To formalize this point, this subsection examines the resource savings from increasing the curbside parking fee by a small amount when it is belowc, holdingPfixed. From the expression for resource costs:
dRC df ¼ρ
dT dfþρ
dC df ¼ρ
½
dTdC
j
ð Þ1 þ1
dCdf:
ð9Þ
where dT/dC|(1) denotes the change in T associated with a unit change inCwhen Eq. (1) is satisfied. Now, the revenue raised from 13Recall that the constraint is that the inflow to the in-transit pool equal the outflow.
In conventional trafficflow theory, there are two densities corresponding to a level of flow. The specification of the minimization problems implies the choice of the lower density. This complication is addressed in Section 2.5. The convexity of the congestion function ensures that there is a unique minimum corresponding to the lower density.
the parking fee,R, isPf, so that dR/df=P. From Eq. (2),ρdC/df=−P. Thus,
− dRC
df ¼
½
dT dCj
ð Þ1þ1
dRdf: ð10Þ
Hence, the resource cost saving per unit area-time from raising the curbside parking fee equals a multiple of the increase in the parking fee revenue raised. We term this themultiplication effect. Since the full price of parking isc, whether a driver parks curbside or in a parking garage, cruising-for-parking costs fall by exactly the amount of the increase in parking fee revenue, and there is the added benefit that in-transit travel costs fall due to the reduction in the stock of cars cruising for parking.
Define
μu− dRC
df dR df
¼1þdT
dCjð Þ1 ð11Þ
to be the (marginal)revenue multiplier. What determines the size of the revenue multiplier? Or put alternatively, by how much does a unit reduction in the stock of cars cruising for parking reduce the total stock of cars on the road? The answer depends on the technology of congestion, as well as its level. The revenue multiplier is even larger if account is taken of the marginal cost of public funds exceeding 1.
2.6. The congestion technology
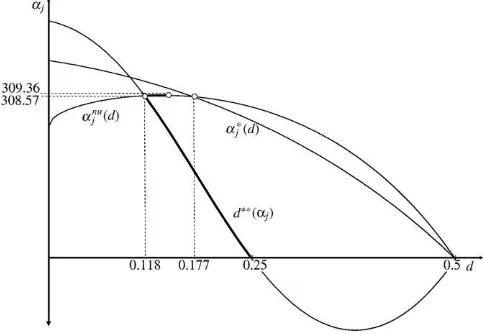
The steady-state equilibrium condition, (1), can be written implicitly asC=C(T;P,D). HoldingfixedPandD, for each level ofT the function gives the stock of cars cruising for parking consistent with steady-state equilibrium. Under the assumption that the functiont(.) is convex inT,C, andP, holdingPfixed the functionCis concave inT. In the absence of cruising for parking, with realistic congestion functions there are normally two densities consistent with a given level of (feasible) flow, i.e. T=δt(T, 0, P)D has two solutions, one corresponding to regular traffic flow, the other to traffic jam conditions.Fig. 1displays the graph of the functionC, termed the steady-state locus, with these two properties. An increase inPcauses the locus to shift down; holding T fixed, Eq. (1) determines an equilibrium travel time, and to offset the increase in travel time due to the increase inPrequires a decrease inC. An increase inDcauses the locus to shift down; holdingPandTfixed, for Eq. (1) to continue to be satisfied the increase inDmust be offset by a decrease int, and hence a decrease inC. IfDincreases sufficiently, there is no (T,C) satisfying Eq. (1) and a steady-state equilibrium does not exist.
It is assumed furthermore that the functiont(.) is weakly separable, specifically thatt=t(T,C,P) =t(V(T,C),P), withVdefined as the effec-tive densityof cars on the road14and normalized in terms of in-transit
car-equivalents in the absence of cruising for parking, i.e.V(T, 0) =T. Defineκ(C,P) = maxTT/t(V(T,C),P) to be thethroughput capacityof the street system as a function ofCandP, so thatκ(0,P) is capacity as conventionally defined. It indicates the maximum entry rate, in terms
of car-distance per unit area-time, the street system can accommodate in steady-state equilibrium for a givenCandP. IfDδexceedsκ(0,P), then the entry rate exceeds throughput capacity even in the absence of cruising for parking, and no steady-state equilibrium exists. IfDδis less than κ(0, P), then the steady-state locus lies in the positive quadrant. The parking equilibrium condition, Eq. (2), can be written as C= (c−f)P/ρ, giving the equilibrium stock of cars cruising for parking. Since the condition is independent ofT, its graph inFig. 1, theparking equilibrium locus, is a horizontal line. If Eq. (2) lies everywhere above Eq. (1), which occurs ifDδNκ((c−f) P/ρ,P), the entry rate exceeds throughput capacity at the equilibrium level of cruising for parking, and no equilibrium exists.15If Eqs. (1) and (2) intersect, they do so
twice. A straightforward stability argument16 can be applied to
establish that the left-hand intersection point is stable while the right-hand one is unstable. Thus, we take the left-hand intersection point to be the equilibrium.
An initial equilibrium is indicated byE1 in Fig. 1. The revenue multiplier equals one plus the reciprocal of the slope of the steady-state locus at the equilibrium point. If the curbside parking fee is lowered, the parking equilibrium locus shifts up, causing the equi-librium to move up along the steady-state locus. Due to the convexity of the congestion technology, the slope of the steady-state locus at the equilibrium point falls, and hence the revenue multiplier increases. Now consider the effect of increasing the amount of curbside allocated to parking. The steady-state locus shifts down and the parking equilibrium locus shifts up. The equilibriumTandCincrease; effective density increases, which, along with the decrease in road capacity, causes traffic congestion to worsen; and the revenue multiplier can be shown to increase.17
2.7. Complications caused by garage construction technology
The above analysis laid out the economics of equilibrium when there is curbside and garage parking, when garage parking is priced at Fig. 1.Steady-state equilibrium. Notes: 1.C(T;P,D) is the steady-state locus, Eq. (1). 2.C¼c−fρPis the parking equilibrium locus, Eq. (2).
14In the numerical examples presented later, it will be assumed that congestion takes the form of a negative linear relationship between velocity and effective density: v=vf(1−V/Vj), wherevfis free-flow speed andVjis effective jam density, which is a slight generalization of Greenshield's Relation. Travel time per unit distance is the reciprocal of velocity. Then lettingt0denote free-flow travel time, this relationship can be rewritten ast=t0/(1−V/Vj). It will also be assumed that a car cruising for parking creates 1.5 times as much congestion as a car in transit, i.e.V=T+ 1.5C. Eq. (1) then becomes T(Vj−T−1.5C) =δDt0Vj. Thus, capacity is Vj/(4t0), the effective density corresponding to this capacity isVj/2, (dC/dT)(1)= (Vj−2T−1.5C)/(1.5T), and the revenue multiplier is µ= (Vj−0.5T−1.5C)/(Vj−2T−1.5C). We shall assume furthermore that effective jam density is linearly decreasing in the proportion of curbside allocated to parking:Vj=Ω(1−P/Pmax), whereΩis the effective jam density with no curbside parking.
15Earlier, to avoid considering non-existence of a solution to the resource cost minimization problems, it was assumed an equilibrium exists even when traffic is as congested as possible, which occurs whenf= 0 andP=Pmax. This condition is thatDδb κ(cPmax/ρ,Pmax). With a positive parking fee and/or less curbside allocated to parking, a solution to the resource cost minimization problems (and the corresponding equilibria) may exist when this condition is not satisfied.
16It is reasonable to assume that the parking equilibrium condition is always satisfied, so that trajectories travel along theĊ= 0 locus.Ṫis positive aboveṪ= 0 and negative below it. If therefore the initial level ofTlies below theṪ= 0 locus,Tdecreases, while if it lies above theṪ= 0 locus,Tincreases. It follows thatE1is a stable equilibrium andE2an unstable equilibrium.
17Substituting Eq. (2) into Eq. (1) givesT=δt(T, (c
−f)P/ρ,P)D =T ^
(P). Also, from Eq. (3), C= (c−f)P/ρ. Then, dT/dC= (dT
^
/dP) ÷ (dC/dP) = [ρ/(c−f)]dT ^
/dP, and so d(dT/dC)/dP= [ρ/(c −f)]d2T
^
constant unit cost, and when curbside parking is priced below this level. Unfortunately, the model is unrealistically simple in assuming that garage spaces are supplied uniformly over space at constant unit cost. The technology of garage construction and other factors result in parking garages being discretely spaced.18To reduce his walking costs, a driver is willing to pay a premium to park in the parking garage closest to his destination. Parking garages therefore have market power and may exercise it by pricing above marginal cost. Further-more, spatial competition between parking garages may result in their being inefficiently spaced. Taking these considerations into account complicates the economics, since there will then be three distortions that need to be taken into account, not only the underpricing of curbside parking but also the overpricing and inefficient spacing of garage parking.
In the next section, the model of this section is extended to take into account the exercise of market power caused by the discrete spacing of parking garages. The exact reason for the discrete spacing of parking garages is secondary. It is assumed that the discrete spacing arises from thefixed land area required for a central ramp, which generates horizontal economies of scale. The optimal spacing minimizes overall resources costs. The equilibrium spacing is the outcome of spatial competition between parking garages.
3. The central model
The primitives of the model differ from those of the simple model of the previous section in three respects. First, the garage cost function incorporates horizontal economies of scale, reflecting thefixed costs associated with the central ramp. Second, to avoid dealing with price discrimination based on parking duration, parking duration rather than visit duration is taken to be exogenous. And third, a grid street network is assumed.
In many cities, there are both public and private parking garages. To keep the analysis manageable, however, it is assumed that all parking garages are private.19The social optimum is solved
first, then the spatial competition equilibrium is solved when the government intervenes only through its curbside parking policy.20
3.1. Social optimum
Since travel demand is perfectly inelastic, the social optimum entails minimizing resource costs per unit area-time. There are three components to resource costs per unit area-time: garage costs per unit area-time (GC), walking costs per unit area-time (WC), and in-transit travel costs per unit area-time (TT):
RC¼GCþWCþTT: ð12Þ
It is assumed that the presence of parking garages does not alter the distance drivers travel over city streets, or the decision of the
individual curbside parker to cruise for parking on his destination block, or the spatial homogeneity of trafficflow.21These assumptions
together imply that the steady-state equilibrium condition for the simple model,T=δt(T, 0,P)D, continues to hold. Denoting the cor-responding equilibrium in-transit density as a function ofPbyT⁎(P) gives TT =ρT⁎(P).
Efficiency entails identical parking garages being symmetrically arrayed over space, with diamond-shaped market areas. Letsbe the grid or Manhattan distance between parking garages,xthe capacity of each parking garage, andK(x) the minimum cost per unit time of a garage as a function of capacity. Each garage services an area ofs2/2. With demand inflowDper unit area-time and parking durationλ, the total number of parking spaces in a garage's service area is Dλs2/2. Since Ps2/2 curbside parking spaces are provided in the service area, garage capacity isx= (Dλ−P)s2/2 and GC =K((Dλ−P)s2/2)÷s2/2. Since the demand for garage parking is uniformly distributed over space, the average distance walked by a garage parker is 2s/3 so that average walking time is 2s/(3w), wherewis walking speed, and WC = 2ρs(D−P/λ)/(3w). Combining the above results gives
RC¼
K ðDλ−PÞs 2 2
s2 2
þ2ρsD− P λ
3wþρT⁎ð Þ:P ð13Þ
Solution of the social optimum entails minimizing Eq. (13) with respect toPands. The optimum may entail no curbside allocated to parking, all curbside allocated to parking, or only a fraction of curbside being allocated to parking. In the last case, thefirst-order condition with respect toPis
−K0− 2ρs 3λwþρ
dT⁎
dP ¼0: ð14Þ
Expanding curbside parking capacity by one unit per unit area results in garage capacity being reduced by one unit per unit area, leading to a saving per unit area-time in garage costs ofK′and in walking costs of 2ρs/(3λw), but in less curbside being allocated to traffic, resulting in an increase in in-transit travel costs ofρdT⁎/dP (an expression for which is provided below Eq. (4)). With a realistic garage construction technology, the optimal spacing between parking garages solves thefirst-order condition of Eq. (13) with respect tos:
2ðDλ−PÞK0
s −
4K s3 þ
2ρD−P λ
3w ¼0:
Dividing through by 2(D−P/λ)/sand usingx= (Dλ−P)s2/2 yields
λK0−λ K x þ
ρs
3w¼0: ð15Þ
The social optimum minimizes resource costs per unit area-time. Since the input rate per unit area is constant, it also minimizes resource costs per driver. And since, in the choice ofs,Pand hence the ratio of garage parkers to drivers arefixed, the optimal choice of s minimizes resource costs per garage parker. Since in-transit travel costs are independent of the spacing between parking garages, the optimal spacing between parking garages minimizes garage plus walking costs per garage parker. Let aGC and mGC be the average and marginal garage costs per garage parker, and define aWC and mWC accordingly. Since an average is minimized where the marginal equals the average, the optimal spacing between parking garages solves
aGCþaWC¼mGCþmWC; ð16Þ
18Suppose, for the sake of argument, that parking garages are continuously distributed over space. It would be cheapest to construct garage parking on the groundfloor of every building, but this space is especially valuable for retail purposes. Constructing below-ground parking may be cost effective at the time the building is constructed, but is expensive for buildings that were originally constructed without underground parking. Constructing above-ground parking in multi-use buildings raises structural issues. In most situations, the cost of constructing garage space is minimized with structures specifically designed as parking garages. Even if parking were distributed continuously over space, parking garage entrances would not be. Because of thefixed width required for a garage entrance and thefixed area required for a central ramp, parking garage entrances would be discretely spaced. Consideration of aesthetics and traffic circulation may play a role as well. Zoning may require that parking garages be located away from major traffic arteries to reduce the congestion and visual nuisance they cause.
19An obvious direction for future research is to investigate the situations where all garage parking is provided by the public sector, and where some is provided publicly and some privately.
20 Less formal derivation of the results is provided inArnott (2006).
which coincides with Eq. (15) since aGC=λK/x, mGC=λK′, aWC=2ρs/(3w), and mWC=ρs/w because the marginal garage parker walks to the boundary of the garage service area.
3.2. Equilibrium
Parking garage structures are prohibitively costly to relocate and very costly to expand. It is also impractical to convert a parking garage to an alternative use, and adding garage capacity to buildings in other uses requires constructing underground parking, which is very costly. Thus, to afirst approximation, a garage's location and capacity can be regarded asfixed. In most downtown areas, the demand for garage parking is increasing over time. The natural way to model spatial competition between parking garages is therefore as a dynamic two-stage game with growing demand. In each period's second two-stage, garages compete in fee schedules, taking the location and capacity of other garages asfixed. In each period'sfirst stage, potential entrants decide simultaneously on entry, capacity, and location, anticipating the future evolution of market equilibrium.
Given the current state of game theory, such a model is intractable. We have chosen instead a particularly simple specification of the parking garage game, which we present below. It is an adaptation of a familiar, two-stage spatial competition game that Tirole (1988)
ascribes toSalop (1979), but which is discussed in Vickrey (1964)
and likely has more distant origins. The friction of space results in parking spaces in different garages being differentiated products. In the second stage, garages play a Bertrand game with differentiated products in mill prices, with mill price undercutting being excluded by assumption, and choose the height of their parking garages to minimize cost. In this stage of the game, garages take as given the location of their neighbors, which are by assumption arrayed sym-metrically, and ignore the effects of their actions on traffic conditions, and capacity constraints are ignored. In thefirst stage of the game, the number of parking garages, and hence the uniform spacing between them, adjusts such that garage profits are zero.
This specification of the parking garage game yields intense competition between parking garages for the same reason that Bertrand competition yields intense competition. In an appendix to the paper, we discuss how treating capacity constraints would alter the game. In particular, we review the game-theoretic literature on duopoly games with capacity constraints,first when products are homogeneous and then when they are differentiated. Two qualitative conclusions emerge. The first is that the addition of capacity constraints makes the analysis of the game much more complicated, so much more that the problem with differentiated products has not yet been solved. The second is that capacity constraints relax com-petition. The intuition is that when my competitors are capacity constrained, I can raise my price without losing customers to them. A well-known result in game theory (Kreps and Scheinkman, 1983) is that, with homogeneous products (and under a reasonable set of assumptions concerning rationing when there is excess demand out of equilibrium in the price sub-game) “Quantity Precommitment (viz., capacity constraints) and Bertrand Competition Yield Cournot Outcomes.”With inelastic demand up to a choke price, duopolists would choose the choke price. The results are considerably more complicated under alternative rationing mechanisms, and include mixed strategy equilibria. And the game when products are dif-ferentiated–as parking garages are–has not been solved. Never-theless, it seems safe to say that the full equilibrium of the parking garage game entails a parking fee between the Bertrand–Nash equilibrium with spatially differentiated products, which is the one we solve for, and the corresponding Cournot–Nash equilibrium, which entails a parking fee equal to the choke price. Thus, our specification of the parking garage game provides a lower bound on the markup of the equilibrium mean price over marginal cost, hence on the mean price differential between curbside and garage parking, hence on the
equilibrium stock of cars cruising for parking, and intuitively22on the
deadweight loss deriving from the market power that the friction of space confers on parking garages.
Arnott (2006) derived the Bertrand–Nash equilibrium parking fee. Here we simply state the result and provide the intuition for it. The Bernard–Nash equilibrium parking fee for parking for a periodλis
Se¼λK0þρs
w ð17Þ
which entails garages charging a markup over marginal garage cost equal to the walking cost incurred by a driver at the boundary between garage service areas. The intuition is as follows. In a Bertrand–Nash equilibrium, a garage must perceive it as unprofitable to either raise or lower its parking fee, taking as given the parking fees charged by its neighbors. If it raises its fee by a small amountΔ, it will gain net revenue from its inframarginal customers but lose custo-mers at the boundary of its market area. Since its service area iss2/2 and since the customer density is D, its revenue gain from infra-marginal customers is s2DΔ/2. Under the Bertrand assumption, it perceives its service area to be 2[s/2−w(S0−S)/(4ρ)]2, whereS0is the fee it charges andSthe common fee charged by its neighbors, so that Δ=S0−S. It therefore perceives that its service area will shrink by an amount wsΔ/(2ρ), and hence that its net revenue will fall by an amountD(S−λK′)wsΔ/(2ρ) from the customers it loses. Equating the gain and the perceived loss gives Eq. (17). In thefirst stage of the game, entry and exit occur, driving profits to zero:
Π¼ D− P λ
λK0þρs w
s2
2−K¼0: ð18Þ
Dividing Eq. (18) through by (D−P/λ)s2/2 yields
aGC¼mGCþmWC: ð19Þ
Comparing Eqs. (16) and (19) implies that, under this form of spatial competition, parking garage market areas are inefficiently small.
It is assumed that, with discrete parking garages, curbside parkers drive to their destination block and then circle that block cruising for parking, as was the case with continuous parking garages, and that at each location (indexed by grid distance from the closest parking garage,m) the in-transit travel time is the same for curbside parkers as for garage parkers.23Under these
assump-tions, the stock of cars cruising for parking at locationmadjusts to equilibrate the full prices of garage and curbside parking there. In contrast to the simple model, the full price of garage parking now includes walking costs. The parking equilibrium condition at locationmis then
Seþ2ρm w ¼fλþ
ρC mð Þλ
P ; ð20Þ
whereC(m) is the density of cars cruising for parking at location m, andSeis given by Eq. (17), so that
C mð Þ ¼ Se þ2ρm
w −fλ
P
ρλ: ð21Þ
To close the model,T(m), the equilibrium density of cars in transit at each location, must be derived. Since there is no nice way to do this,
22The deadweight loss will depend on the equilibrium of the full game–entry, capacity, and location in thefirst stage, and pricing in the second–and not just the pricing game.
23Properly, the equilibrium spatial pattern of trafficflow with drivers optimizing over route and cruising-for-parking strategy should be determined, but this problem is intractable.
it is assumed thatT(m) is the solution to the analog of the steady-state equilibrium condition at locationm:
T mð Þ−δt T mð ð Þ;C mð Þ;PÞD¼0:
In-transit travel costs per unit area (TT) are obtained by averaging ρT(m) over the garage market area, and cruising-for-parking costs per unit area (CP) are obtained analogously.
3.3. Second-best parking policy
Regulation of private garage pricing, capacity, and location is not considered. Government intervention is restricted to curbside parking policy. Since modeling the full game between a local parking autho-rity, with strategy variablesfandP, and private parking garages, with strategy variablesSands. would be complex,24the only policy to be
investigated will be the local parking authority's second-best optimal choice ofP on the assumptions that the government behaves as a Stackelberg leader and that the meter rate is set sufficiently low that parking garages do not have an incentive to undercut it. Relative to the social optimum, there are three sources of distortion. The under-pricing of curbside parking and the overunder-pricing of garage parking induce cruising for parking, which generates cruising-for-parking costs and increases in-transit travel costs. Also, spatial competition between parking garages results in parking garages being inefficiently closely spaced.
Let GC⁎(P) denote garage costs per unit area-time, as a function of P in the social optimum, etc., and GCe(P) the spatial competition equilibrium, etc. The second-best optimal level ofP,P⁎⁎, minimizes RCe(P) = GCe(P) + WCe(P) + TTe(P) + CPe(P). If RCe(P) has a unique local, interior minimum, then [dRCe(P)/dP]
P⁎N0 is a necessary and sufficient condition forP⁎⁎bP⁎. Letting DWL(P) denote the deadweight loss in the spatial competition equilibrium relative to the social optimum, as a function ofP, we have that
DWLð Þ ¼P RCeð ÞP −RC⁎ð ÞP
¼GCeð Þ þP WCeð ÞP−GC⁎ð ÞP−WC⁎ð ÞP þTTeP
ð Þ þCPeP ð Þ−TT⁎ð ÞP
ubDWLð Þ þP DWLbbð Þ:P
ð22Þ
whereDbWLð ÞP is the deadweight loss related to garages being in-efficiently close in the spatial competition equilibrium, and bbDWLð ÞP is that related to cruising for parking. Since [dRC⁎(P)/dP]P⁎= 0, [dDWL (P)/dP]P⁎= [dRCe(P)/dP]P⁎. Thus, if RCe(P) has a unique local, interior minimum, a necessary and sufficient condition for P⁎⁎bP⁎ is that deadweight loss be increasing inPatP⁎. It can be shown thatbbDWLð ÞP is increasing25inP, but the sign of the derivative of bDWLð ÞP is ambiguous,
depending in a complicated way on the properties of the garage cost function. The next section provides several numerical examples in which the second-best level ofPis less than thefirst-best level but also one in which the second-best level exceeds thefirst-best level.
The analysis of this section's model was fairly complete but two thorny game-theoretic issues were sidestepped. Thefirst concerns the modeling of spatial competition between parking garages. Realisti-cally, the price sub-game between parking garages takes place subject
to capacity constraints. But since the game-theoretic literature has not yet solved the price equilibrium in oligopoly games with spatially differentiated products and capacity constraints, we chose to ignore the capacity constraints. Intuitively, ignoring these constraints results in our describing competition between parking garages as fiercer than it actually is. Thus, our analysis tends to understate the markup of garage price over marginal cost, and hence the distortions deriving from the exercise of garage market power, especially those related to cruising for parking. The second thorny game-theoretic issue concerns the modeling of the game between private garage operators and the local parking authority. The paper has considered the choice of the local authorityquaStackelberg leader concerning how much curbside to allocate to parking but took the curbside meter rate asfixed. Modeling the complete game between parking garage operators and the local authority will be difficult. And this difficulty will be compounded when the local authority's policy instruments are expanded to include regulation of parking garage fees, locations, and capacities, and when the political economy considerations that affect the authority's policy choices are taken into account.
4. Numerical examples
4.1. Calibration
Arnott and Inci (2006)present numerical examples for a model similar to the one employed here, except that all parking is curbside and demand is price sensitive. This paper adopts all their values for the common parameters and functions, except for the jam density, and adds a parameterized garage cost function and the level of demand as well.
The following parameters are employed. The units of measurement are hours for time, miles for distance, and dollars for value.
δ¼2:0 λ¼2:0 f ¼1:0 ρ¼20:0 P¼3712
The in-transit travel distance is 2.0 miles; the parking duration is 2.0 h; the curbside parking fee is $1.00 per hour; the value of time is $20.00 per hour; and the number of curbside parking spaces is 3712 per square mile in the base case. We do not know of data on mean non-residential parking duration over the entire downtown area, but 2 h seems reasonable when account is taken of non-work trips and auto trips taken by downtown employees during the working day. Since the model ignores downtown residents, the ratio of 1 mile traveled on downtown streets per hour parked seems reasonable too. The hourly meter rate for curbside parking is that employed in Boston. The value of time of $20.00 per hour might seem high, but the average downtown parker is more highly paid and busier than the typical traveler.26The
value ofPchosen is for the base case, for which parking is on one side of the street, and requires explanation. Assuming 8 city blocks per mile on a Manhattan grid, a street width of 33 ft, a parking space length of 21 ft, and allowance for crosswalks, 29 cars can be parked on one side of a block. With parking on one side of the street, there are 58 curbside parking spaces around each block. And with 64 blocks per square mile, there are 3712 curbside parking spaces per square mile.
The value of D is taken to be 7424 per ml2-h. Since parking duration is 2 h, this implies that the stock of parking spaces needed to accommodate the exogenous demand is 14848 per square mile. Thus, in the base case, one quarter of the cars park curbside and the rest in a parking garage.
24 Calthrop (2001)considers the profit-maximizing pricing of a garage monopolist in the face of an exogenous curbside meter rate, ignoring the discreteness of parking garages. If the meter rate is set above a critical level, it is profitable for the garage monopolist to undercut the meter rate. In the context of the model of this section, the full game between a local parking authority and private parking garages would need to take this undercutting possibility into account, and the equilibrium might involve garages undercutting curbside parking close to the parking garage but not further away.
25 It can be shown that in the spatial competition equilibrium, dC/dP
N0. It then follows from the convexity of the congestion function inT,C, andPthat bbDWLð ÞP is increasing inP.
26 Small et al.(2005)find slightly higher mean values of travel time on the California State Route 91 Freeway in Orange County. The standard rule of thumb, based on many empirical studies, is that the value of travel time is half the wage rate, and the mean effective wage rate in the downtowns being considered must be around $40.00 per hour, corresponding to an annual salary (48 weeks a year and 35 h per week) of $67,200.
The form of the congestion function employed was described earlier, in fn. 14. It is
t¼ t0 1−VVj
with Vj¼X 1− P Pmax
and V¼TþθC: ð23Þ
This congestion function has four parameters. Three are the same as inArnott and Inci (2006)but a different calibration was used to determine jam density (see fn. 14):
t0¼0:05 X¼5932:38 Pmax¼11;136 θ¼1:5
A value oft0, free-flow travel time per mile, of 0.05 corresponds to a free-flow travel speed of 20 mphΩis jam density in the absence of curbside parking.Vjis jam density with curbside parking, which is assumed to equal jam density in the absence of curbside parking times the proportion of street space available for traffic. 1−P/Pmax.Pmax is calculated on the basis that a 33-foot-wide, one-way road can accommodate three lanes of traffic and that parking on one side of the street reduces this to two lanes of traffic. The value ofΩwas calibrated to generate a base case social optimum travel speed of 15 mph, but is also consistent with more basic traffic engineering reasoning.27
θis the in-transit PCEs (passenger car-equivalents) of a car cruising for parking. Since we know of no studies of its value, our estimate is a guess.28
The garage cost function is assumed to have the form
K^
29
x;h
ð Þ ¼R A0þ ax
h
þðk0þk1hÞxþF0þF1h;
where K^ is the amortized (per hour) cost, x garage capacity, h garage height (number offloors of parking),Rland rent,A0the area used for the central ramp,athefloor area needed for each additional car,F0+F1hthe cost of constructing the central ramp in a parking garage with h floors of parking, and k0+k1h the unit cost of an additional parking space in a garage ofhfloors. We assume that an additional car needs 400 square feet offloor space, 200 square feet of parking spaceper seand 200 square feet of added space for traffic circulation, yieldinga= 1.44 × 10−5square miles, and that the parking ramp has a radius of 20 ft and therefore an area of 400πsquare feet, yieldingA0= 4.52 × 10−5. In choosing cost parameter values, we draw heavily onShoup (2005), Chapter 6. Table 6-1 gives an average cost in 2002 dollars per space added for garages constructed on the UCLA Campus between 1977 and 2002 of about30 $28,000. Amortizing
this cost, assuming that the garage is used for 8 h a day, 200 days a year and that the annual user cost of capital is 0.05, which is con-sistent with a real interest rate of 4% and a 40-year life,31yields a
figure
for (k0+k1h) + (F0+F1h)/xof $0.875/h. It is assumed thatk1= 0.125k0, F1= 0.125F0, and F0= 10k0. That leaves two parameters, k0 and R. The values k0= 0.5 and32 R= $2.5 × 105 are chosen. For a parking structure with 1000 spaces, which corresponds to the average at UCLA, the cost-minimizing height is 7.55floors, so that the average amortized construction cost computed according to the above formula is $0.982/h. The amortized cost of land per garage space is $0.488/h. The ratio of land to construction costs seems reasonable. Average garage cost (corresponding toK/xin the theory) is therefore $1.470/h, and marginal garage cost (corresponding toK′in the theory) $1.449/h.33Though the parameters chosen for the garage cost function
yield reasonable results, there is evidently considerable scope for improvement.34
What kind of city does this parameterization correspond to? Parking in Boston(Boston Transportation Department, 2001) reports that in 1997/8 per square mile the number of employees in Downtown Boston was 160,000 and the number of garage, residential, non-hotel parking spaces was 29,000. Downtown Boston Transportation Plan(Boston Transportation Department, 1995) reports that, in 1990, 36% of Downtown workers drove alone and 11% carpooled or vanpooled. On the assumption of no curbside parking, if all downtown workers had commuted by car, the required number of garage parking spaces would have been about 62,000 per square mile. Thisfigure indicates that the calibrated city has a considerably lower employ-ment density than Boston. Furthermore, applying the ratio for Boston of the garage parking spaces if all downtown workers had commuted by car to the number of employees, suggests that a garage parking density of 11,136 per square mile corresponds to an employment density of around 29,000 per square mile. According toDemographia (2007), such downtown employment densities are found in Winnipeg, Perth, San Diego, Sacramento, and Phoenix.
4.2. Numerical results
4.2.1. Base case outcomes
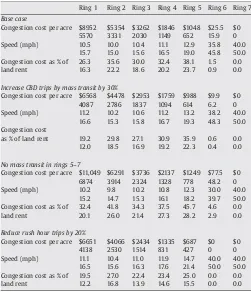
All the numerical exercises are for the central model. Table 1
presents the numerical results with the base case set of parameter values. Each of the columns corresponds to a different exercise. Each row gives the value for a particular variable across the various exercises. Column 1 describes the social optimum with the base case allocation of curbside to parking space ofP= 3712, corresponding to curbside parking on one side of the street. The social optimum is defined to have no cruising for parking. Column 2 provides the numbers for the social optimum with the first-best allocation of curbside to parking. Column 3 presents the base case equilibrium. Column 4 displays results for the same case as column 3 but with the allocation of curbside to parking optimized. Column 5 gives the results for the base case equilibrium, but with the meter rate raised from $1.00 to $1.50 per hour. Finally, column 6 shows the equilibrium for 27With the street geometry assumed, excluding intersections there are about 15.2
street-miles per square mile.Ω= 5932.38 then corresponds to one car every 13.5 ft of street. Since, in the absence of curbside parking, a street has three lanes of traffic, this corresponds to one car every 40 ft in a lane or 132 cars per lane-mile. In the absence of cruising for parking, with the assumed congestion function capacity throughput is achieved at one-half jam density or 66 cars per lane-mile, and the associated velocity andflow are 10 mph and 660 cars per lane-hour, respectively. Thesefigures accord with those given in Table 16-17 of theTransportation and Traffic Engineering Handbook (Institute of Transportation Engineers, 1982),”Maximum Lane Service Volumes on Urban Arterials Based on 50% Cycle Split and Average Density and Speed Criteria.”
28Shoup (2007, p.19)remarks:“Most drivers who are cruising for parking try to avoid following directly behind another car that appears to be cruising, so as to maximize the chance of being thefirst to see a vacant spot.”This suggests that the passenger car equivalent for a cruising car is appreciably greater than one.
29Chapter 14 of the Traffic Engineering Handbook (Institute of Transportation Engineers, 2004),“Parking and Terminals”, discusses the design of parking garages but does not provide engineering cost data. The form of the cost function in (27) was chosen for its ease of interpretation and analysis, and not on the basis of engineering data.
30In calculating this number, Shoup divided construction costs by the number of addedparking spaces, on the assumption that the land was previously used as an on-ground parking lot.
31The real interest rate and the amortization period are those chosen by Shoup, Table 6-3, and he judged these to probably underestimate the user cost of capital.
32This is th