BAB 4. INTEGRAL KOMPLEKS 4.1 Integral Garis Kompleks - BAB 4 INtegral KOMPleks

BAB 4.

INTEGRAL KOMPLEKS

4.1 Integral Garis Kompleks

Misalkan z(t):D→Cadalah fungsi kompleks dengan domain riil

] , [a b

D= , maka integral

∫

b

a

dt t

z( ) , dimana z(t)= x(t)+iy(t) dapat dengan mudah

dihitung, yaitu

∫

b

a

dt t

z() =

∫

+

∫

b

a b

a

dx t y i dx t

x() () . Sebagai

contoh

∫

+ + = +

1

0

2 _.

3 2 3 ] ) 1

[(t it dt i

Masalah kita adalah bagaimana menghitung

∫

b

a

dz z

f( ) , dimana fungsi f :D→C

dengan D ⊂C.

Misalkan f (z) fungsi kompleks pada sub himpunan dari himpunan bilangan kompleks dan C lintasan yang dinyatakan dengan z(t)= x(t)+iy(t), a≤t≤b,

maka pendefinisian dari

∫

b

a

dz z

f( ) sama dengan pendefinisian pada integral fungsi

riil pada suatu interval.

b = z_n

z1 2

z zn−1

Misal P menyatakan partisi pada lintasan terbuka C, yaitu

} ,...,

,

{a z₀ z₁ z b

P= = _n = dan z*_k∈[z_k−1,z_k],k =1,2,...,n, maka jumlah Riemann

yang bersesuaian dengan pariosi P adalah

∑

=

= n

k

k

k z

z f P

S

1 *₎

( )

( ∆ , dengan ∆z_k =z_k −z_k−1.

Jika terdapat bilangan kompleks L sedemikian sehingga untuk sebarang bilangan

0 >

ε terdapat sebuah partisi P_εdari lintasan C sehingga berlaku

ε < −L P

S( ) ,

maka fungsi f(z) dikatakan terintegral pada lintasan C dengan nilai integralnya adalah L. Dengan kata lain

L P S

n→∞ =

) (

lim .

Nilai limit ini dinamakan integral garis f(z) sepanjang kurva C, ditulis

∫

=

C

L dz z

f( ) . Jika C tertutup biasa ditulis dengan

∫

C

dz z f( ) .

Sifat-sifat integral kompleks : 1. Linier, yaitu

∫

∫

∫

+ = +

C C

C

dz z g k dz z f k dz z g k z f

k ( ) ( )] ( ) ( )

[ _{1 2 1 2}

2. Jika C terdiri dari dua bagian kurva C1 dan C2 maka,

∫

∫

∫

= +

2 1

) ( )

( )

(

C C

C

dz z f dz z f dz z

f .

3. Jika z₀dan z₁adalah ujung-ujung lintasan, maka

∫

∫

=− 0

1 1

0

) ( )

(

z

z z

z

dz z f dz z f

4. Jika f(z) terbatas, f(z) ≤M dengan M bilangan positif, maka

∫

∫

≤ ≤

C C

ML dz z f dz z

4.2 Menghitung integral kompleks

Integral bergantung lintasan

Misalkan z(t):[α,β]→C. Lintasan C dapat dipartisi dengan mempartisi inteval ]

,

[α β menjadi n buah sub interval α =t₀ <t₁<...<t_n =b. Dengan demikian

} ) ( ),..., ( ), ( ), (

{a= zα z t₁ z t₂ z β =b merupakan partisi dari lintasan C. Jumlah Riemann yang bersesuaian dengan lintasan C adalah

∑

= − − = n k k k

k z t z t

t z f P S 1 1 * )) ( ) ( ))( ( ( ) (

yang dapat ditulis dalam bentuk

) ( )) ( ) ( ( )) ( ( ) ( ₁ 1 1 1 * − = − − ₋ − −

=

∑

k k

n

k k k

k k

k t t

t t t z t z t z f P S .

Untuk n→∞diperoleh

∫

∑

= − − − = ₋ = − − ∞ → ∞ → β α dt t z t z f t t t t t z t z t z f P

S _{k k}

n

k k k

k k k n n ) ( ' )) ( ( ) ( )) ( ) ( ( )) ( ( lim ) ( lim ₁ 1 1 1 *

Jadi integral f(z) pada lintasan C dapat dinyatakan dengan

∫

∫

= β α dt t z t z f dz z f C ) ( ' )) ( ( ) ( .

Untuk menghitung integral lintasan di atas dilakukan cara sebagai berikut : 1. Nyatakan lintasan C dalam z(t)= x(t)+iy(t), a≤t≤b

2. Cari turunan, z’(t).

3. Substitusikan z(t) ke dalam f(z). 4. Integralkan.

Contoh 1. Tentukan

∫

C

dz z

f( ) jika f(z)=(x+y)+iy dari z = 0 ke z = 1 + i , jika

C adalah :

b. Parabola y= x2.

c. Ruas garis dari z = 0 ke z = 1 , kemudian dari z = 1 ke z = 1 + i.

Penyelesaian.

a. Dalam kasus ini lintasan C adalah z(t)=t+it,0≤t≤1 dan i

t

z'()=1+ . Dengan demikian integral menjadi

∫

=

∫

+ +

C

dt i it t f dz z f

1

0

) 1 )( ( )

(

. 2 3 2 1

] 3 [

) 1 ]( 2 [

1

0 1

0

i dt t i t

dt i it t

+ =

+ =

+ + =

∫

∫

b. Dalam kasus ini lintasan C adalah z(t)=t+it2,0≤t≤1,

ti t

z'()=1+2 , dan f(z(t))=(t+t2)+it2. Dengan demikian integral menjadi

∫

=

∫

+ + +

C

dt i it t t dz z f

1

0

2 2_{) ](1 )}

[( )

(

. 6 7 2 1

) 2 ( [

1

0

2

i

dt t t i t

+ =

c. Dalam kasus ini lintasan C terdiri dua bagian , katakan C₁: z(t) = t, 1

0≤t≤ dan C2 :z(t)=1+it,0≤t≤1.

Pada C₁, z'(t)=1, dan

f

(

z

(

t

))

=

t

. Dengan demikian integral menjadi

∫

=

∫

=

1

. 2 1 )

(

1

0 C

tdt dz z f

Pada C₂, z'(t)=−i, dan

f

(

z

(

t

))

=

−

(

t

+

it

)

. Dengan demikian integral menjadi

∫

=

∫

− + =− +

1

. 2 1 2 1 )

( ) (

1

0 C

i dt

it t dz z f

Jadi

. 2 1 ) ( )

( )

(

2 1

i dz z f dz z f dz z f

C C

C

= +

=

∫

∫

∫

Selanjutnya misalkan ingin ditentukan batas atas nilai mutlak integral, maka perlu

dicari bilangan M sehingga f(z) ≤M untuk semua z∈ C _{dan panjang}

lintasan L. Misalkan untuk C pada kasus (a) kita punyai dan L= 2sehingga

∫

∫

≤ ≤

C C

dz z f dz z

f( ) ( ) 10.

Dari contoh 1 di atas terlihat bahwa nilai integral akan berbeda untuk lintasan yang berbeda.

Integral bebas lintasan

Misalkan D merupakan sub himpunan dari himpunana bilangan riel dan fungsi

C

→ D t

z(): terdiferensial di t. Selanjutnya misalkan fungsi ) , ( ) , ( )

(z u x y iv x y

g = + terdiferensial di z(t). Selanjutnya perhatikan bahwa

g(z(t))=u(x(t),y(t))+iv(x(t),y(t)) dan ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₊ + + = dt dy dy dv dt dx dx dv i dt dy dy du dt dx dx du dt t z g d[ ( ())]

.

Dengan menerapkan persamaan Cauchy Riemann, diperoleh

). ( ' )) ( ( ' ))] ( ( [ t z t z g dt dy i dt dx dx dv i dx du dt dy dy du dt dx dx dv i dt dy dx dv dt dx dx du dt t z g d = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ₊ + − =

Kenyataan di atas dapat digunakan untuk menghitung integral lintasan sebagai berikut. Misalkan F:D→Cdengan )F'(z)= f(z di D. Misalkan juga a dan b di dalam D dan C ⊂D kontur/lintasan dari a ke b. Maka

∫

=

∫

C dt t z t z f dz z f β α , ) ( ' )) ( ( )

( dimanaz(t):[α,β]→C,

) ( ) ( )

(t xt iy t

z = + merupakan representasi lintasan C. Telah diketahui bahwa

) ( ' )) ( ( ) ( ' )) ( ( ' )) (

(z t F z t z t f z t z t F

dt

d _{= =}

, sehingga

∫

=

∫

=

∫

C dt t z F dt d dt t z t z f dz z f β α β α )) ( ( ) ( ' )) ( ( ) (

= F(z(β))−F(z(α))

= F(b)−F(a).

independent). Dari uraian di atas dapat disimpulkan bahwa integral suatu fungsi analitik untuk suatu litasan C di dalam pada domain terhubung sederhana D dari titik a ke titik b adalah

∫

= −

C

a F b F dz z

f( ) ( ) ( )

dengan )F'(z)= f(z untuk z di D.

Dengan demikian jika C adalah lintasan tertutup maka

∫

=

C

dz z

f( ) 0.

Contoh 2.

Tentukan

∫

C

dz

z2 , jika C adalah kurva y= x2 dari z = 1 + i ke z = 2 + 4i.

Penyelesaian. Kita tahu bahwa f(z)=z2adalah fungsi seluruh, jadi analitik untuk

semua z dan 3

3 1 )

(z z

F = . Jadi

[

]

. 3

18 14

) 1 ( ) 4 2 ( 3

1 3 3

2

i

i i

dz z

C

+ − =

+ − + =

∫

Soal latihan :

Tentukan

∫

C

dz z

f( ) jika

1. f(z)= y−x−3ix2, C garis dari 0 ke 1 + i

2. f(z)=z, C parabola y= x2dari 0 ke 1 + i.

3.

z z

f( )=1, C lingkaran jari-jari 2 pusat 0 arah positif (berlawanan

arah jarum jam).

4. f(z)=z+2z, C lintasan dari 0 ke 1 kemudian dari 1 ke 1+ 2i.

5.

z z z

6. f(z)=zez2, C garis dari 0 ke 1 + i

7. f(z)=z3 +2z2 +5z+1, C parabola y= x2dari 0 ke 1 + i.

8. f(z)=cosz, C setengah lingkaran z =π dari z=−πi kez=πi.

9. f(z)=zsinz, C sebarang lintasan dari z = 0 ke z=πi.

10. f(z)=sin2 z, C setengah lingkaran z =π dari z=−πi kez=πi.

4.3 Teorema Cauchy - Goursat

Pada bagian sebelumnya telah dibahas bahwa integral garis fungsi kompleks f(z) bergantung pada ujung-ujung dan bentuk lintasannya. Tetapi jika f(z) analitik maka pada domain terhubung sederhana D maka integral tidak akan bergantung pada bentuk lintasannya dan nilainya nol jika lintasannya tertutup. Pada bagian ini akan dibahas untuk lintasan tertutup. Integral pada lintasan tertutup sederhana sering disebut dengan integral kontur.

Ada beberapa definisi yang akan sering digunakan dalam pembahsan ini.

- Lintasan tertutup sederhana, adalah lintasan yang tidak memotong atau menyinggung dirinya sendiri (gambar 1)

(a) (b) (c)

Gambar 1. Lintasan tertutup, (a) sederhana, (b) sederhana, (c) tidak sederhana

(a) (b) (c)

Gambar 2. Domain terhubung, (a) sederhana, (b) ganda dua, (c) ganda tiga

Teorema Cauchy Goursat. Jika f(z) analitik di dalam suatu domain terhubung sederhana D, maka untuk setiap lintasan tertutup sederhana di dalam D berlaku

0 )

( =

∫

C

dz z

f .

C

D

Gambar 3. lintasan tertutup sederhana C di dalam D

Dengan kata lain integral kontur fungsi kompleks tidak tergantung lintasan yang dilewatinya.

Contoh 3.

∫

( ) =0

C

dz z

f untuk sebarang lintasan tertutup C jika f(z)adalah fungsi

seluruh, misal f(z)= sin z, )f(z = ez.

Contoh 4. Tentukan

∫

C

dz z

f( ) jika

4 1 ) (

2₊

= z z

f dan C linngkaran satuan arah

positif.

Penyelesaian. Titik singular dari

4 1 ) (

2₊

= z z

f adalah z=±2i terletak di luar C.

Jadi

4 1 ) (

2₊

= z z

f analitik pada dan di dalam C, sehingga

∫

( ) =0

C

dz z

Teorema Cauchy-Goursat pada domain berganda

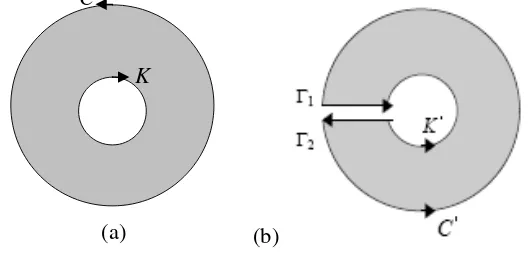
Sebuah anulus adalah daerah cincin, termasuk domain terhubung ganda dua, terdiri dari dua kurva tertutup, C dan K( Gambar 4a). Jika arah kontur dibalik, hasil integral akan menjadi negatifnya. Untuk kurva tertutup arah positif adalah arah yang menyebabkan daerah integrasi berada di sebelah kiri lintasan integrasi. Itulah sebabnya arah lintasan integrasi haruslah ditentukan pada integral kontur fungsi kompleks.

C

K

(a)

Gambar 4. Lintasan integrasi ganda dua

Integrasi menyusuri kurva batas daerah anulus ini dapat dipecah menjadi 4 integral dengan kontur masing-masing C’, Γ1, Γ2, dan –K’ (+K’ didefinisikan searah dengan C). Kontur C’ adalah kontur C setelah terbelah oleh celah lintasan Γ1 dan Γ2 yang masuk dan keluar di antara C dan K. Demikian pula kontur K’

adalah kontur K sesudah diberi celah tersebut di atas (Gambar 4). Celah harus dibuat sedemikian kecil agar C’→ C dan K’→ K. Nilai integral ini adalah

dz z f dz z f dz z f dz z f dz z f

K C

C

∫

∫

∫

∫

∫

= + + +

− 2

1

) ( )

( )

( )

( )

(

'

' Γ Γ

Jika diamati jelaslah bahwa Γ1 = - Γ2 sehingga kedua integralnya saling

menghilangkan.Untuk f(z) yang bersifat analitik di daerah anulus ini berlaku teorema Cauchy-Goursat :

0 ) ( )

( )

(

' '

= +

=

∫

∫

∫

−

dz z f dz z f dz z f

K C

C

.

∫

∫

=

K C

dz z f dz z

f( ) ( ) .

(Dalam hal ini perhatikan bahwa lintasan C dan K memiliki arah yang sama).

Jadi di dalam daerah analitiknya, kontur tertutup integral kompleks boleh mengecil tanpa mengubah nilai integral itu sendiri. Sifat ini dapat diperluas pengertiannya jika anulusnya memiliki banyak lubang, katakanlah lubang K1, K2, ... , Kn (Domain berganda n), sehingga diperoleh

. ) ( ... ) ( )

( )

(

2 1

∫

∫

∫

∫

= + + +

n

K K

K C

dz z f dz

z f dz z f dz z f

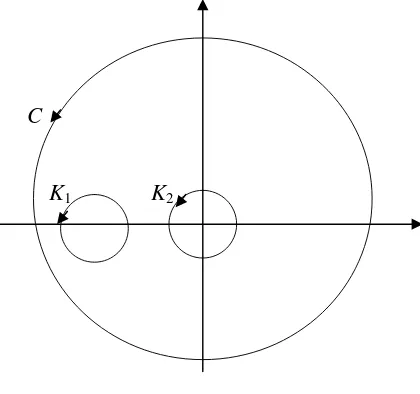
Contoh. Hitunglah

∫

+ +

C

dz z z

z

2

3

, dengan C lingkaran pusat 0, berjari-jari 3 arah

positif. Penyelesaian.

Perhatikan bahwa fungsi

1 2 3 3 )

(

2₊ = − +

+ =

z z z z

z z

f tidak analitik di z = 0

dan z = 1. Kedua titik tersebut ”dibuang” dengan membentuk lingkaran dengan pusat di titik tersebut (gambar 5).

C

K1 K2

-1 0

Dengan demikian f(z) analitik di dalam domain yang dibatasi oleh C, K1, K2

sehingga diperoleh

dz z z dz z z dz z z

z

K K

C

∫

∫

∫

⎟

⎠ ⎞ ⎜

⎝ ⎛

+ − + ⎟ ⎠ ⎞ ⎜

⎝ ⎛

+ − = + +

2 1

1 2 3 1

2 3 3

2

=

∫

∫

∫

∫

+ − +

+ −

2 2

1 1

1 2 3

1 2 3

K K

K

K z

dz z dz z dz

z .

Menurut teorema Cauchy – Goursat maka integral suku pertama dan keempat di ruas kanan adalah nol. Sehingga diperoleh

i i i dz z z

z

C

π π

π 6 2

4 3

2₊ =− + =

+

∫

.

Soal Latihan

1. Buktikan teorema Cauchy-Goursat.

2. Misalkan C daerah persegi dengan titik –titik sudut x=±10,y=±10arah

positif. Tentukan

∫

C

dz z . 1

3. Tentukan

∫

−

C

dz z 1

1

, dengan C sebarang lingkaran berpusat di z = 1 arah

positif.

4. Tentukan

∫

+

C

dz z 1

1

, dengan C sebarang lingkaran berpusat di z = – 1 arah

positif.

5. Tentukan

∫

−

C

dz z 1

1

2 , dengan C ellips 4 36

2 2_{+ y =}

x arah positif.

6. Tentukan

∫

−

C

dz z 1

1

2 , dengan C lingkaran 10 0

2 2_{− x+y =}

x arah positif.

7. Tentukan

∫

− +

−

C

dz z z

z ) 2 )( 1 (

2 7

, dengan C lingkaran 2 3 =

4.4 Rumus integral Cauchy

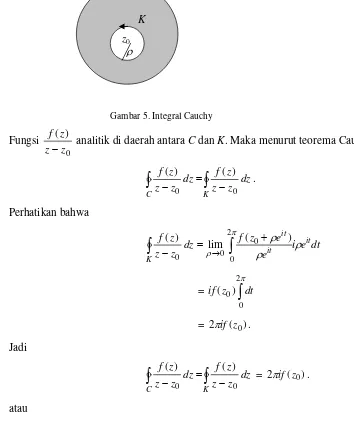
Misalkan fungsi f(z) analitik di dalam suatu daerah yang memuat lintasan tertutup

sederhana C arah positif, dan misalkan z₀ titik interior C.

Karena f analitik maka f kontinu di z₀ sehingga untuk setiap bilangan positif

0 >

ε terdapat δ >0sehingga jika z−z₀ <0maka f(z)− f(z₀) <ε. Misalkan

0 >

ρ sedemikian sehingga ρ <δ dan lingkaran K ={z: z−z₀ =ρ } berada di

dalam C.

C

K z0

ρ

Gambar 5. Integral Cauchy

Fungsi

0

) (

z z

z f

− analitik di daerah antara C dan K. Maka menurut teorema Cauchy

∫

∫

= ₋

−

K C

dz z z

z f dz z z

z f

0 0

) ( )

(

.

Perhatikan bahwa

dt e i e

e z f dz

z z

z

f it

it it

K

ρ ρ

ρ π

ρ

∫

∫

= +

− →

2

0 0 0 0

) (

lim )

(

=

∫

π

2

0 0)

(z dt if

= 2πif(z₀).

Jadi

∫

∫

= ₋

− _K

C

dz z z

z f dz z z

z f

0 0

) ( )

(

= 2πif(z₀).

∫

= −

C

dz z z

z f

0

) (

) ( 2πif z₀

atau

) (z₀

f =

∫

−

C

dz z z

z f

i ₀

) ( 2

1

π .

yang biasa disebut Rumus Integral Cauchy.

Contoh 6. Tentukan

∫

+ −

C

dz z z

z ) 4 )( 1 (

2

, Jika C : z =2arah positif.

Penyelesaian.

Perhatikan bahwa integran tidak analitik di z = 1 dan di z = – 4. Dari kedua titik ini, yang berada di dalam C adalah z = 1. Jadi z = 1

merupakan titik interior dari C, sehingga integran dapat ditulis 1

) ( − z

z f

dengan

4 2 ) (

+ =

z z z

f .

Sekarang fungsi f(z) ini analitik pada dan di dalam lintasan C, sehingga dengan menggunakan rumus integral Cauchy, diperoleh

∫

_{− +}

C

dz z z

z ) 4 )( 1 (

2

= .

5 4 ) 1 ( 2 1

) (

i if

dz z

z f

C

π

π =

= −

∫

Turunan fungsi analitik

Secara umum, jika z0 adalah titik interior pada C maka bentuk integral Cauchy

menjadi f(z₀)=

∫

−

C

dz z z

z f

i ₀

) ( 2

1

π dengan z di dalam C.

Selanjutnya rumus tersebut dapat diperumum dengan mencari turunannya hingga tingkat ke-n. Dalam rumus integral Cauchy, turunan fungsi f di titik z0 adalah

∫

₋

=

C

dz z z

z f i z

f

2 0 0

) (

) ( 2

1 ) ( '

π . (tunjukkan!)

∫

₋ = C dz z z z f i z f 3 0 0 ) ( ) ( 2 ! 2 ) ( ' ' π .

Hingga diperoleh turunan ke-n adalah

∫

₋ + = C n n _dz z z z f i n z f 1 0 0 ) ( ) ( ) ( 2 ! ) ( π .

Yang biasa ditulis dalam bentuk

) ( ! 2 ) ( ) ( 0 ) ( 1 0 z f n i dz z z z f n C n π = −

∫

+ .

Uraian di atas dapat dnyatakan dalam teorema berikut

Teorema. Jika f(z) analitik pada dan di dalam suatu kurva tertutup sederhana C,

maka f(n)(z₀) ada untuk setiap bilangan bulat n, dan dinyatakan dalam rumus

∫

₋ + = C n n _dz z z z f i n z f 1 0 0 ) ( ) ( ) ( 2 ! ) ( π .

Hal ini mengakibatkan jika suatu fungsi analitik di suatu titik maka turunan untuk semua tingkatnya , f’, f’’, ... , juga analitik di titik tersebut.

Contoh 7. Tentukan

∫

− + C dz z z 3 3 ) 2 ( 3

, jika C : z =3arah positif.

Penyelesaian.

Dalam hal ini f(z)=z3+3, z0 = 2, dan n = 2. Dengan menggunakan

rumus integral Cauchy yang telah diperumum, diperoleh,

∫

₋+ C dz z z 3 3 ) 2 ( 3

= ''(2) 2

2 f i π

= 12

π

i.

Soal Latihan

1. Hitunglah g zdz

C

∫

( ) , jika

a. , : 1

2 3 sin )

( ₂ =

+ +

= C z

z z

z z

b. , : 2 2 )

9 ( ) (

2

2₊ − =

= C z

z z z

g .

c. , : 3

2 2 2

) (

2

= −

− −

= C z

z z z z

g .

2. Hitunglah

∫

+

C

dz z

z ) 4

( 2 , jika C seperti pada gambar berikut.

(a) (b)

3. Jika C adalah kontur tertutup dalam arah positif dan

∫

₋ −

=

C

dz z z

z z

g

2 0 2 0

) (

2 2 )

( .

Hitunglah g(z₀)jika (a). z0 di dalam C dan (b). z0 di luar C

4. Jika a bilangan ral positif, hitung integral

∫

+

C z

dz a z

e

2

2 dalam arah positif,

jika