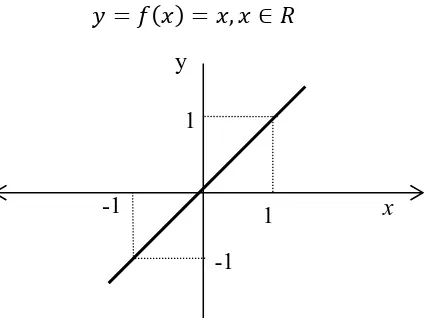1
BAB I
PENDAHULUAN
A. Latar Belakang
Kanker paru adalah tumor ganas paru yang berasal dari saluran napas atau epitel bronkus yang ditandai dengan pertumbuhan sel yang tidak normal, tidak terbatas, dan merusak sel-sel jaringan normal. Kanker paru merupakan penyebab utama keganasan di dunia dan mencapai hingga 13% dari semua diagnosis kanker. Selain itu, kanker paru juga menyebabkan 1/3 dari seluruh kematian akibat kanker pada laki-laki (Kemenkes RI, 2016:1).
Data World Health Organization (WHO) menyebutkan bahwa sebesar 8,8 juta kematian di tahun 2015 disebabkan oleh kanker. Dari jumlah tersebut, kanker paru tergolong menduduki peringkat tertinggi yaitu sebesar 1,69 juta kematian, kanker hati sebesar 788.000 kematian, kanker usus besar sebesar 774.000 kematian, kanker perut 754.000 kematian dan kanker payudara sebesar 571.000 kematian.
International Agency for Research on Cancer (IARC) memperoleh data setidaknya
1,8 juta (12,9%) kasus kanker paru ditemukan di tahun 2012, sehingga menjadi kasus kanker paling umum di dunia. Faktanya, sebagian besar kasus kanker paru (58%) ditemukan di negara-negara berkembang. Berdasarkan data Profil Mortalitas Kanker (Cancer Mortality Profile) yang dirilis oleh WHO menyebutkan, angka kematian yang disebabkan oleh kanker di Indonesia mencapai 195.300 orang, dengan kontribusi kanker paru sebesar 21,8% dari jumlah kematian (Global Burden
2
Kanker paru memang sudah menjadi ancaman yang mematikan bagi kaum laki-laki dan perempuan di seluruh dunia terutama laki-laki. Di Indonesia, kanker paru menjadi penyebab kematian utama kaum laki-laki dan lebih dari 70% kasus kanker itu baru terdiagnosis pada stadium lanjut (UGM Farmasi, 2014). Penyebab utama kanker paru adalah asap rokok karena mengandung lebih dari 4.000 zat kimia, dimana 63 jenis diantaranya bersifat karsinogen dan beracun (Perhimpunan Dokter Paru Indonesia, 2003:2). American Cancer Society mengemukakan bahwa 80% kasus kanker paru disebabkan oleh rokok (perokok aktif) sedangkan perokok pasif berisiko 20% sampai 30% untuk terkena kanker paru. Penyebab kanker paru lainnya adalah radiasi dan polusi udara (American Cancer Society, 2017).
Kanker paru diklasifikasikan menjadi dua kelompok, yaitu kanker paru primer dan kanker paru sekunder. Kanker paru primer adalah sel kanker yang berasal dari paru, sedangkan kanker paru sekunder adalah sel kanker yang menyebar dari anggota tubuh lain, termasuk kanker payudara dan kanker kolorektal. Kanker paru primer dibedakan menjadi dua jenis, yaitu Small Cell Lung
Cancer (SCLC) dan Non Small Cell Lung Cancer (NSCLC) (American Cancer
Society, 2017).
Sebagai langkah awal, umumnya deteksi kanker paru dapat dilakukan dengan pemeriksaan radiologi paru yaitu melalui citra paru. Citra paru atau sering disebut
Chest X-Ray (CXR) adalah suatu proyeksi radiografi dari paru (Perhimpunan
3
pada hasil citra paru namun sebaliknya pada paru yang normal tidak menunjukkan adanya nodul di paru pada hasil citra paru. Nodul yang terdeteksi pada paru dikategorikan menjadi dua yaitu non cancerous nodule (benign atau tumor jinak) dan cancerous nodule (malignant atau tumor ganas) (Japanese Society of Radiology
Technology, 1997). Wajid, et al (2016) melakukan penelitian untuk mendeteksi
kanker paru dengan menggunakan citra paru. Dengan melakukan deteksi dini kanker paru diharapkan dapat memberikan penanganan yang tepat pada penderita kanker paru dan menurunkan angka kematian kanker paru. Penelitian untuk mengklasifikasikan kanker paru biasanya dilakukan dengan mengekstraksi citra paru terlebih dahulu. Fitur hasil ekstraksi citra paru kemudian dapat diklasifikasi dengan berbagai model salah satunya model Jaringan Saraf Tiruan atau Artificial
Neural Networks (ANN).
Beberapa penelitian telah dikembangkan untuk membantu mengklasifikasikan kanker paru dengan beberapa metode yang berbeda-beda, salah satunya klasifikasi sel kanker paru menggunakan Artificial Neural Networks (ANN) yang dilakukan oleh Zhou, et al (2002). Tun & Khaing (2014) mendiagnosis kanker paru dengan menggunakan citra CT Scan dengan menggunakan model Artificial
Neural Networks (ANN) dan mengimplementasikan ekstraksi fitur berupa Gray
Level Co-occurrence Matrix (GLCM) serta mengklasifikasikan kanker paru
menggunakan teknik pengolahan citra.
4
Arsitektur RBFNN adalah jaringan tiga lapisan yaitu lapisan input, lapisan tersembunyi, dan lapisan output. (Seenivasagam & Arumugadevi, 2012). Model RBFNN memiliki beberapa keunggulan, yaitu hanya memiliki satu lapisan tersembunyi. Lapisan tersembunyi pada RBFNN menggunakan fungsi Gaussian atau fungsi aktivasi lainnya (Halici, 2004: 139).
Beberapa penelitian mengenai model RBFNN telah dilakukan, tingkat akurasi yang diperoleh juga menunjukkan bahwa hasil klasifikasinya tergolong baik, diantaranya penelitian yang dilakukan oleh Mandadara (2016) menggunakan model RBFNN dengan K-means clustering untuk mengklasifikasikan stadium kanker paru, input yang digunakan sebanyak 80 citra data gambar yang diekstrak menggunakan GLCM dengan akurasi 88,75% data training dan 80% data testing. Penelitian berikutnya dilakukan oleh Obayya & Ghandour (2015) yang mengklasifikasikan kanker paru yaitu benign dan malignant dengan menggunakan model RBFNN dengan K-means clustering. Pada penelitian tersebut, ekstraksi citra yang digunakan adalah metode GLCM. Pada hasil akhir model diperoleh akurasi akurasi 90% data training dan 84% data testing.
K-5
means dalam mengenali cluster yang secara statistik tidak mampu dikenali karena
beberapa sifat data, seperti tidak adanya korelasi dan tidak berdistribusi normal (Huang & Zao, 2005).
Penggunaan metode SOM Kohonen clustering pada penelitian-penelitian sebelumnya juga menghasilkan nilai akurasi tinggi, diantaranya, penelitian yang dilakukan oleh Chang, et al (2013) mengestimasi perbedaan ikan sungai dari 36 lokasi di Taiwan menggunakan model Self-Organizing Radial Basis Networks (SORBN) dimana tahap pertama pusat dan standart deviation dari lapisan input SOM digunakan pada lapisan tersembunyi RBFNN, dan tahap kedua pada RBFNN menggunakan fungsi gaussian, dengan hasil akurasi data training 80% dan data
testing 20%. Baboo, et al (2009) yang menggabungkan SOM dan RBFNN untuk
mengenali tulisan tangan Tamil dimana lapisan tersembunyi menggunakan jarak antara bobot dan vektor input dari net input, lapisan output menggunakan kombinasi linear sebagai net input, lapisan input menggunakan fungsi aktivasi identitas (linear), lapisan tersembunyi menggunakan radial symmetric basis
functions, dan lapisan output menggunakan fungsi sigmoid, dengan akurasi data
training 99% dan data testing 96,9%. Wu & Chow (2004) mendeteksi kondisi
mesin rusak dan normal menggunakan SOM-Based RBFNN dimana lapisan output dari SOM yaitu pusat dan simpangan baku digunakan pada lapisan tersembunyi RBFNN, dengan akurasi kondisi mesin rusak 96,3% untuk data training dan 85,7% untuk data testing, sedangkan akurasi pada kondisi mesin normal 99,5% untuk data
training dan 96% untuk data testing. Mu & Nandi (2007) mendeteksi biopsi jarum
6
parameter berbeda dan mengklasifikasinya menggunakan SOM-RBF dimana bobot vektor dari neuron-neuron lapisan kompetitif SOM sebagai pusat dan simpangan baku pada lapisan tersembunyi RBFNN, dan tahap RBFNN selanjutnya menggunakan fungsi gaussian, dengan nilai akurasi data traning 98% dan data
testing 94%.
Hal-hal yang telah dijelaskan di atas melatarbelakangi penulis untuk melakukan penyusunan tugas akhir menggunakan metode SOM Kohonen sebagai penentu pusat dan jarak dari setiap fungsi aktivasi model SOM-RBFNN untuk mengklasifikasi citra paru, hal ini yang membedakan antara tugas akhir ini dengan penelitian sebelumnya. Tugas Akhir dengan judul “Klasifikasi Citra Paru Menggunakan Model Self-Organizing Maps Radial Basis Function Neural
Networks (SOM-RBFNN)” diharapkan dapat memberikan manfaat di bidang
matematika dan bidang kesehatan.
B. Rumusan Masalah
Berdasarkan latar belakang yang telah dipaparkan di atas, sehingga diperoleh rumusan masalah sebagai berikut ini:
1. Bagaimana proses klasifikasi citra paru menggunakan model SOM -RBFNN? 2. Bagaimana hasil klasifikasi citra paru menggunakan model SOM-RBFNN?
C. Tujuan Tugas Akhir
Berdasarkan rumusan masalah di atas, tujuan tugas akhir ini adalah:
7
2. Mendiskripsikan hasil klasifikasi citra paru menggunakan model SOM-RBFNN.
D. Manfaat Tugas Akhir
Manfaat dari tugas akhir ini adalah sebagai berikut: 1. Bagi penulis
Bagi penulis sendiri, penulisan skripsi ini dapat menambah pengetahuan dan wawasan tentang aplikasi model SOM-RBFNN dan pemrograman MATLAB dalam kehidupan sehari-hari, khususnya dalam bidang kesehatan.
2. Bagi pembaca
Sebagai salah satu bahan dalam mempelajari model SOM-RBFNN dan MATLAB serta diharapkan tugas akhir ini dapat dijadikan sebagai referensi untuk penelitian selanjutnya.
3. Bagi Universitas Negeri Yogyakarta
Penulisan tugas akhir ini diharapkan dapat menambah koleksi bahan pustaka yang bermanfaat bagi Universitas Negeri Yogyakarta pada umumnya, dan mahasiswa Fakultas Matematika dan Ilmu Pengetahuan Alam pada
8
BAB II
KAJIAN TEORI
Bab II berisi tentang kajian teori yang diantaranya mengenai Kanker Paru, Pengolahan Citra Digital, Ekstraksi Fitur Citra, Artificial Neural Network, SOM Kohonen clustering dan Ketepatan Hasil Klasifikasi.
A. Kanker Paru
Berikut adalah hal-hal mengenai Kanker Paru:
1. Pengertian Kanker Paru
Kanker paru adalah pertumbuhan sel yang tidak normal, tidak terbatas, dan merusak sel-sel jaringan yang normal pada salah satu atau kedua paru. Tumor ganas paru berasal dari saluran napas atau epitel bronkus. Sel kanker dimulai dari mutasi yang terjadi pada DNA sel. Mutasi DNA disebabkan oleh proses penuaan dini atau adanya faktor lingkungan seperti asap rokok, polusi udara, hingga terpapar zat karsinogenik (arsen, asbestos, radon, kadmium) (Kemenkes RI, 2016).
World Health Organization (WHO) berpendapat bahwa kanker paru
9
2. Jenis Kanker Paru
Terdapat dua jenis kanker paru, yaitu (American Cancer Society, 2017): a. Small Cell Lung Cancer (SCLC)
SCLC adalah jenis kanker paru yang tumbuh lebih cepat daripada jenis kanker Non Small Cell Lung Cancer (NSCLC), akan tetapi pertumbuhan SCLC lebih dapat terkendali dengan kemoterapi. Sekitar 20% kasus kanker paru adalah SCLC, atau sekitar 30.000 pasien setiap tahunnya terdiagnosis penyakit tersebut. b. Non Small Cell Lung Cancer (NSCLC)
Sekitar 75%-80% kasus kanker paru adalah NSCLC. Terdapat 3 tipe NSCLC, yaitu:
1) Adenokarsinoma
Adenokarsinoma adalah jenis dari NSCLC yang paling umum dari kanker paru dan lebih banyak muncul pada wanita. Kanker tipe ini berkembang dari sel-sel yang memproduksi lendir pada permukaan saluran udara.
2) Karsinoma skuamosa
Jenis ini paling umum dari kanker paru serta paling banyak terjadi pada pria dan orang tua. Karsinoma skuamosa berkembang dalam sel yang mengisi saluran udara, dan kanker ini tumbuh relatif lambat.
3) Karsinoma sel besar
10
3. Faktor Risiko Kanker Paru
Seperti umumnya penyakit kanker yang lain, penyebab yang pasti dari kanker paru belum diketahui. Namun, faktor risiko seseorang mengalami kanker paru sangat berhubungan erat dengan rokok atau paparan zat yang bersifat karsinogenik. Berikut ini faktor risiko penyebab terjadinya kanker paru (American Cancer
Society, 2017):
a. Merokok
Merokok merupakan faktor yang berperan paling penting. Sekitar 80% kematian kanker paru disebabkan dari kebiasaan merokok. Risiko seorang perokok aktif lebih tinggi dibanding perokok pasif. Kejadian kanker paru pada perokok dipengaruhi oleh lamanya kebiasaan merokok, jumlah rokok yang dihisap setiap hari dan lamanya berhenti merokok.
b. Polusi Udara
Polusi udara menyebabkan risiko kanker paru terutama di daerah perkotaan yang padat kendaraan. Namun, risiko kanker paru yang ditimbulkan lebih rendah dibandingkan dengan kebiasaan merokok. Pada beberapa penelitian, diperkirakan sekitar 5% kematian kanker paru diseluruh dunia disebabkan dari polusi udara. c. Paparan zat karsinogenik
11 d. Genetika
Faktor risiko penyebab kanker paru juga dapat disebabkan oleh genetika. Apabila keluarga memiliki riwayat kanker paru dapat meningkatkan risiko terkena kanker paru, namun belum begitu jelas seberapa besar tingkat risiko yang dialami.
4. Gejala Kanker Paru
Gambaran penyakit kanker paru terdiri dari keluhan subjektif dan gejala objektif. Keluhan utama dapat berupa batuk-batuk atau tanpa dahak, batuk darah, sesak napas, suara serak, sakit dada, sulit menelan, dan terdapat benjolan di pangkal leher. Gejala atau keluhan akibat metastasis di luar paru, seperti kelainan yang timbul karena kompresi hebat di otak, pembesaran hepar, dan berat badan berkurang juga merupakan ciri dari adanya kanker paru. (Perhimpunan Dokter Paru Indonesia, 2003: 3)
5. Deteksi Dini Kanker Paru
Menurut Japanese Society of Radiology Technology, nodul atau benjolan yang terdeteksi pada paru dikategorikan menjadi dua yaitu non cancerous nodule (tumor jinak) dan cancerous nodule (tumor ganas). Tumor jinak yang terdapat pada jaringan paru tidak akan menyerang selain organ paru karena tumor jinak hanya menyerang satu tempat dan tidak menyebar ke organ tubuh lainnya. Gejala awal kanker paru seperti batuk, demam, suara serak dan lain-lain dapat dengan mudah disalah artikan sebagai penyakit flu atau gejala pada orang merokok. sehingga banyak kanker paru pada stadium awal sulit dideteksi (Japanese Society of
12
Berikut ini beberapa cara deteksi dini kanker paru (Modern Cancer Hospital
Guangzhou, 2015):
a. X-Ray
X-Ray adalah metode penting dalam pendeteksian kanker paru, sebagian
besar kanker paru terdeteksi saat melakukan X-Ray dibagian dada. Melalui pemeriksaan ini, dapat diketahui ada tidaknya tumor, letak dan ukuran tumor, serta melihat perubahan inflamasi paru yang disebabkan hambatan tumor pada bronkus yang menimbulkan emfisema lokal atau lesi sekitar.
b. Sitologi dahak
Pemeriksaan sitologi dahak dapat menentukan jenis patologi sel kanker dan kanker paru. Metode ini memiliki tingkat keakuratan lebih dari 80%. Secara klinis, pada pasien yang memiliki risiko lebih besar dapat melakukan sitologi dahak secara berulang.
c. Bronkoskopi
Pengklasifikasian melalui bronkoskopi terhadap pasien kanker paru cenderung lebih tinggi. Melalui cara ini dapat dilihat secara langsung tumor dibagian rongga bronkus, serta mengambil jaringan kecil untuk dilakukan biopsi. d. Biopsi jaringan
13
B. Pengolahan Citra Digital
Citra digital adalah representasi dari citra dua dimensi sebagai sebuah kumpulan nilai digital yang disebut elemen gambar atau pixel. Pixel adalah istilah yang sering digunakan untuk menunjukkan unsur-unsur pada citra digital tersebut (Gonzales & Woods, 2008: 1).
Matriks yang dibentuk oleh citra digital dua dimensi berukuran × , dengan adalah jumlah baris dan adalah jumlah kolom ditunjukkan sebagai berikut,
, = [
, , … , −
, , … , −
⋮
− , − ,⋮ … − , −⋮
] (2.1)
Indeks baris dan indeks kolom menyatakan suatu koordinat titik pada citra, sedangkan , merupakan intensitas atau derajat keabuan pada titik , . Elemen pada matriks merupakan elemen citra digital yang disebut dengan
pixel.
14
1. Citra biner
Citra biner adalah citra digital yang memiliki dua kemungkinan nilai pixel yaitu hitam yang dinyatakan dengan 0 dan putih yang dinyatakan dengan 1. Nilai 0 (hitam) adalah background points, biasanya bukan merupakan bagian dari citra sesungguhnya. Sedangkan nilai 1 (putih) adalah region points, yaitu bagian dari citra sebenarnya (bukan latar belakang). Citra biner juga disebut B&W (black and
white) atau monokrom. Proses pembineran dilakukan dengan membulatkan ke atas
atau ke bawah untuk setiap nilai keabuan dari pixel yang berada di atas atau di bawah nilai batas.
Gambar 2.1 Citra Biner 2. Citra grayscale
Citra grayscale atau abu – abu merupakan citra yang mampu menghasilkan gradasi warna abu-abu dari warna hitam hingga warna putih. Tingkat keabuan disini merupakan warna abu dengan berbagai tingkatan, berupa bilangan antara 0 s.d 255. Nilai ini digunakan untuk menunjukkan nilai intensitas. Nilai 0 untuk warna hitam, nilai 255 untuk warna putih dan nilai antara 0 sd 255 untuk warna antara hitam dan putih (keabuan).
15
3. Citra warna
Citra warna atau yang biasa disebut dengan citra RGB adalah citra digital yang setiap pixelnya mewakili warna kombinasi dari tiga warna dasar yaitu R =
Red, G = Green, dan B = Blue. Citra warna disebut juga true color karena
mempunyai jumlah warna yang cukup besar yaitu mencapai 16 juta warna.
Gambar 2.3 Citra Warna
C. Ekstraksi Fitur Citra
Salah satu teknik ekstraksi citra adalah GLCM. GLCM banyak digunakan dalam klasifikasi citra dan fitur-fitur yang diperoleh dari GLCM dapat membantu memahami rincian gambar secara keseluruhan dalam hal tekstur (Gadkari, 2004).
Ekstraksi citra yang dilakukan dengan metode GLCM dapat menghasilkan 13 fitur ekstraksi yaitu contrast, correlation, energy, homogeneity, sum entropy, sum
of square variance, invers difference moment, sum average, sum variance, entropy,
difference entropy, maximum probability, dan dissimilarity entropy.
1. Contrast
Contrast merupakan perbedaan intensitas antara nilai tertinggi (terang) dan
nilai terendah (gelap) dari pixel yang saling berdekatan. Suatu contrast merupakan ukuran variasi antar derajat keabuan dari suatu daerah citra (Gadkari, 2014: 13). Rumus contrast adalah sebagai berikut (Kalas, 2010: 19):
16 dengan
ℎ , = menunjukkan pixel pada baris ke- dan kolom ke- dengan = , , … , ; = , , … , ,
� = banyak derajat keabuan (grayscale) yang diperoleh dari citra.
Nilai contrast membesar jika dipengaruhi oleh variasi intensitas dalam citra tinggi. Nilai contrast semakin kecil apabila variasi rendah.
2. Correlation
Correlation suatu citra menunjukkan ukuran ketergantungan linear derajat
keabuan (grayscale) citra, sehingga dapat menujukkan adanya struktur linear dalam citra yang dirumuskan sebagai berikut (Mohanaiah, et al, 2013: 2):
= ∑���= ∑���= { � � ℎ �,� }−� �� � (2.3)
dengan
� =∑���= ∑���= { ℎ , }
(nilai rata-rata elemen baris pada histogram citra), � =∑���= ∑���= { ℎ , }
(nilai rata-rata elemen kolom pada histogram citra), � =∑���= ∑���= { − � ℎ , }
(simpangan baku elemen baris pada histogram citra), � =∑���= ∑���= { − � ℎ , }
17
3. Energy
Energy adalah fitur yang bekerja dengan mengukur konsentrasi pasangan
intensitas pada matriks konkurensi. Rumus energy adalah sebagai berikut (Sharma & Mukharjee, 2013: 331):
= ∑���= ∑���= {ℎ , } (2.4) Nilai energi semakin besar apabila pixel yang memenuhi syarat matriks intensitas berkumpul pada beberapa koordinat dan mengecil apabila letaknya menyebar.
4. Homogeneity
Homogeneity memberikan nilai yang merupakan ukuran kedekatan dari
distribusi elemen di GLCM ke diagonal GLCM dan dirumuskan sebagai berikut (Sharma & Mukharjee, 2013: 331):
= ∑ ∑ ℎ �,�
+ �−�2
�� �= ��
�= (2.5)
5. Sum entropy
Sum entropy adalah fitur yang menunjukkan seberapa banyak derajat keabuan
(grayscale) yang acak. Rumus sum entropy adalah sebagai berikut (Haralick, et al, 1973: 619):
= − ∑ =��ℎ + {ℎ + } (2.6)
dengan
18
6. Sum of square (variance)
Variance adalah ukuran statistik yang mengukur tingkat keragaman suatu
pixel pada citra. Rumus sum of square variance adalah sebagai berikut (Anami &
Burkpalli, 2009: 11):
� = ∑���= ∑���= ℎ , − � (2.7)
dengan
� = rata-rata ∑���= ∑���= ℎ , .
7. Inverse Difference Moment
IDM adalah ukuran dari homogenitas lokal. Nilai Inverse Difference Moment tinggi ketika derajat keabuan (grayscale) lokal seragam dan invers dari GLCM tinggi (Mohanaiah, et al, 2013: 2). Rumus IDM adalah sebagai berikut (Sharma & Mukharjee, 2013: 331):
= ∑���= ∑���= + �−�ℎ �,� 2 (2.8)
8. Sum average
Sum average adalah fitur yang menunjukkan seberapa banyak nilai rata-rata
pixel yang ada dalam citra. Rumus sum average adalah sebagai berikut (Haralick,
et al, 1973: 619):
19
9. Sum variance
Sum variance menunjukkan seberapa banyak level keabu-abuan yang
bervariasi dari nilai rata-rata (Sharma & Mukharjee, 2013: 331). Rumus sum
variance adalah sebagai berikut (Haralick, et al, 1973: 619):
= ∑ =�� − ℎ + (2.10)
dengan
= sum entropy.
10. Entropy
Entropy adalah fitur untuk mengukur ketidakteraturan dari distribusi
intensitas. Entropy menunjukkan jumlah informasi dari sebuah citra yang dibutuhkan untuk mengompres (memampatkan) citra (Mohanaiah, et al, 2013: 2). Rumus entropy dari suatu citra adalah sebagai berikut (Haralick, et al, 1973: 619):
= − ∑���= ∑���= ℎ , {ℎ , } (2.11)
11. Difference entropy
Difference entropy adalah fitur yang menunjukkan ketidakteraturan dalam
suatu citra. Rumus difference entropy adalah sebagai berikut (Haralick, et al, 1973: 619):
= − ∑��−= ℎ − { ℎ − } (2.12) dengan
20
12. Maximum probability
Maximum probability menunjukkan derajat keabuan (grayscale) yang
memenuhi relasi pada persamaan entropy dan dirumuskan sebagai berikut (Anami & Burkpalli, 2009: 11):
= �,�{ℎ , } (2.13) 13. Dissimilarity
Dissimilarity menunjukkan perbedaan tiap pixel dan dirumuskan sebagai
berikut (Anami & Burkpalli, 2009: 11):
= ∑���= ∑���= ℎ , | − | (2.14) D. Artificial Neural Network (ANN)
Artificial neural network sederhana diperkenalkan oleh McCulloch dan Pitts
di tahun 1943 yang menyimpulkan bahwa kombinasi beberapa neuron sederhana menjadi sebuah sistem neural akan meningkatkan kemampuan komputasinya. Bobot dalam jaringan yang diusulkan oleh McCulloch dan Pitts diatur untuk melakukan fungsi logika sederhana. Fungsi aktivasi yang digunakan adalah fungsi
threshold. Tahun 1958, Rosenblatt memperkenalkan dan mulai mengembangkan
model jaringan yang disebut perceptron. Metode pelatihan diperkenalkan untuk mengoptimalkan hasil iterasinya. Widrow dan Hoff di tahun 1960 mengembangkan
perceptron dengan memperkenalkan aturan pelatihan jaringan yang dikenal sebagai
aturan delta (kuadrat rata-rata terkecil). Peneliti terdahulu hanya menggunakan jaringan dengan lapisan tunggal. Rumelhart di tahun 1986 mengembangkan
perceptron menjadi backpropagation, yang memungkinkan jaringan diproses
21
dikembangkan oleh Kohonen di tahun 1972, Hopfield di tahun 1982 (Siang, 2009:4).
Suatu artificial neural network ditandai dengan (1) arsitektur yaitu pola dari hubungan antar neuron, (2) algoritma pembelajaran yaitu metode untuk menentukan bobot pada hubungan neuron dan (3) fungsi aktivasi (Fausett, 1994: 3). Sebuah neuron memiliki tiga bagian utama yaitu sel tubuh atau soma (dimana nukleus/inti sel terletak), dendrit, dan akson (gambar 2.4). Dendrit adalah sambungan tunggal berbentuk silinder yang memanjang dari sel tubuh dan membawa impuls (sinyal) dari neuron (Lin & Lee, 1995: 206). Sinyal tersebut berupa impuls elektrik yang dikirim melalui celah sinaptik melalui proses kimiawi. Sinyal yang masuk dimodifikasi (diperkuat/ diperlemah). Selanjutnya, soma atau sel tubuh menjumlahkan semua sinyal yang masuk. Apabila sinyal yang diterima cukup kuat, maka sinyal akan diteruskan ke sel lain melalui akson (Fausett, 1994: 5).
22
Artificial neural network mempunyai karakteristik sebagai berikut (Fausett,
1994:3):
1) Pola hubungan antar neuron (disebut arsitekstur jaringan),
2) Metode untuk menentukan bobot pada penghubung (pelatihan atau pembelajaran, algoritma),
3) Fungsi aktivasi.
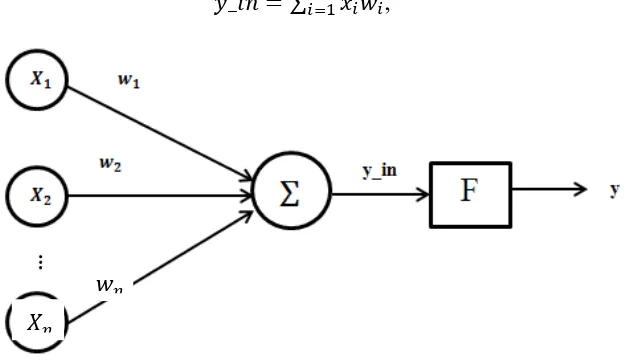
Gambar 2.5 menunjukkan artificial neural network sederhana dengan fungsi aktivasi . Sebuah neuron akan mengolah input = , , … , yang masing-masing memiliki bobot , kemudian fungsi aktivasi akan mengaktivasi _ menjadi output jaringan , dengan rumus (Kusumadewi & Hartati, 2010: 72):
_ = ∑= , (2.15)
Gambar 2.5 Artificial Neural Network Sederhana
Jika artificial neural network pada lapisan output sebanyak ( ) neuron = , , … , , maka proses pengolahan data neuron ke-j adalah sebagai berikut.
_ = ∑ = ∑ = , (2.16)
23
Dalam artificial neural network, informasi yang disebut dengan input akan dikirim ke neuron dengan bobot tertentu. Input ini akan diproses oleh suatu fungsi perambatan yang akan menjumlahkan nilai-nilai semua bobot. Hasil penjumlahan ini kemudian akan dibandingkan dengan suatu nilai ambang (threshold) tertentu melalui fungsi aktivasi setiap neuron. Apabila input tersebut melewati suatu ambang tertentu, maka neuron tersebut akan diaktifkan, tetapi jika tidak, maka neuron tersebut tidak akan diaktifkan. Apabila neuron tersebut diaktifkan, maka neuron tersebut akan mengirimkan output melalui bobot-bobot outputnya ke semua neuron yang berhubungan dengannya, dan demikian seterusnya.
Pada artificial neural network, neuron-neuron akan dikumpulkan dalam lapisan-lapisan (lapisan) yang disebut dengan lapisan neuron (neuron lapisans). Neuron-neuron pada satu lapisan akan dihubungkan dengan lapisan-lapisan sebelum dan sesudahnya (kecuali lapisan input dan output). Informasi yang diberikan pada artificial neural network akan dirambatkan dari lapisan ke lapisan, mulai dari lapisan input sampai ke lapisan output melalui lapisan yang lainnya, yang disebut lapisan tersembunyi (tersembunyi lapisan). Arah perambatan ini sesuai dengan algoritma pembelajaran yang digunakan (Kusumadewi & Hartati, 2010: 69-72). Menurut Fausett (1994:3) karakteristik dari artificial neural network ditentukan oleh beberapa hal, yaitu: arsitektur, fungsi aktivasi, dan learning
24
1. Arsitektur ANN
Hubungan antar neuron dalam artificial neural network mengikuti pola tertentu tergantung pada arsitektur jaringan sarafnya. Menurut Fausett (1994: 12-15) terdapat 3 arsitektur dalam artificial neural network, antara lain:
a. Jaringan Lapisan Tunggal (single lapisan network)
Dalam jaringan ini, sekumpulan input neuron dihubungkan langsung dengan sekumpulan outputnya. Dalam beberapa model (misal perceptron), hanya ada sebuah neuron output.
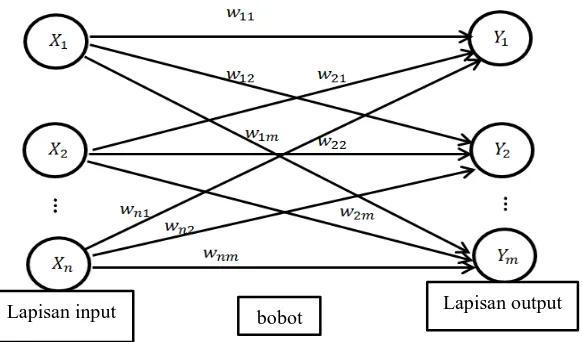
Gambar 2.6 menunjukkan arsitektur jaringan dengan neuron input , , … , dan neuron output , , … , . Dalam jaringan ini, semua neuron input dihubungkan dengan semua neuron output, meskipun dengan bobot yang berbeda-beda. Tidak ada neuron input yang dihubungkan dengan neuron input lainnya. Demikian pula dengan neuron output.
Gambar 2.6 Jaringan Lapisan Tunggal
Lapisan output bobot
25
b. Jaringan Lapisan Jamak (multilapisan network)
Jaringan lapisan jamak merupakan jaringan dengan satu lapisan simpul atau lebih (disebut tersembunyi neuron atau neuron tersembunyi) antara neuron input dan neuron output. Terdapat lapisan bobot antara dua tingkat neuron yang berdekatan (input, tersembunyi, output).
Gambar 2.7 adalah jaringan dengan neuron input , , … , , sebuah lapisan tersembunyi yang terdiri dari neuron � , � , … , � dan neuron output , , … , . Jaringan ini dapat menyelesaikan masalah yang lebih kompleks dibandingkan dengan lapisan tunggal, meskipun kadangkala proses pelatihan lebih kompleks dan lama.
Gambar 2.7 Jaringan Lapisan Jamak
��
Lapisan output Lapisan
input
bobot bobot
26
2. Prosedur Pemodelan ANN
Berikut ini adalah prosedur pemodelan ANN sebagai generalisasi model matemaika dari jaringan saraf biologi (Siang, 2009: 3):
a. Pemrosesan informasi terjadi pada banyak elemen sederhana (neuron), b. Sinyal dikirimkan diantara neuron-neuron melalui penghubung-penghubung,
c. Penghubung antar neuron memiliki bobot yang akan memperkuat atau memperlemah sinyal,
d. Untuk menentukan output, setiap neuron menggunakan fungsi aktivasi (biasanya bukan fungsi linier) yang dikenakan pada jumlahan input yang diterima. Besarnya output ini selanjutnya dibandingkan dengan suatu batas ambang.
3. Fungsi Aktivasi
Pada artificial neural network, fungsi aktivasi digunakan untuk menentukan keluaran suatu neuron. Jika net merupakan kombinasi linear input dan bobot ( = ∑ = �� ), maka fungsi aktivasinya adalah = ∑ = �� (Siang, 2009: 26). Pada beberapa kasus, fungsi aktivasi nonlinear dapat digunakan. Berikut ini adalah fungsi aktivasi non linear yang umum digunakan pada artificial
neural network (Kusumadewi, 2004: 49-61):
a. Fungsi Linear
Fungsi linear sering dipakai apabila menginginkan output jaringan berupa sembarang bilangan riil. Pada fungsi identitas, nilai output yang dihasilkan sama dengan nilai input. Fungsi linear dirumuskan sebagai berikut:
27
Fungsi identitas merupakan fungsi linear dengan nilai = 1 dan = 0. Fungsi identitas dirumuskan sebagai berikut:
= = , ∈ (2.18)
Gambar 2.8 Fungsi Aktivasi Identitas
b. Fungsi Undak Biner (Hard Limit)
Jaringan dengan lapisan tunggal sering menggunakan fungsi undak (step
function) untuk mengkonversikan input dari suatu variabel yang bernilai kontinu ke
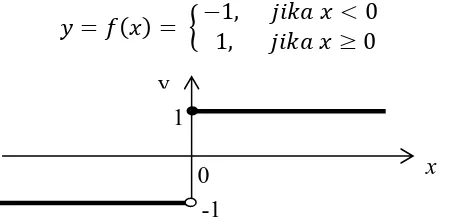
suatu output biner (0 atau 1). Fungsi ini sering digunakan pada jaringan dengan lapisan tunggal. Pada Matlab R2013a, perintah untuk menggunakan fungsi undak biner adalah hardlim. Gambar 2.9 adalah fungsi undak biner (hard limit) dengan rumus sebagai berikut:
= = { , , < ≥ (2.19)
Gambar 2.9 Fungsi Aktivasi Undak Biner (Hard Limit)
1 y
x
-1
-1 1
1 y
28 c. Fungsi Bipolar (Symetric Hard Limit)
Fungsi bipolar mirip dengan fungsi undak biner, perbedaannya terletak pada nilai output yang dihasilkan. Nilai output bipolar berupa 1 atau -1 (gambar 2.10). Pada Matlab R2013a, perintah untuk menggunakan fungsi bipolar adalah hardlims. Fungsi bipolar dirumuskan sebagai berikut:
= = { − , , ≥ < (2.20)
Gambar 2.10 Fungsi Aktivasi Bipolar (Symetric Hard Limit)
d. Fungsi Sigmoid Biner
Fungsi sigmoid biner sering digunakan karena nilai fungsinya terletak antara 0 dan 1 dan dapat diturunkan dengan mudah. Pada Matlab R2013a, perintah untuk menggunakan fungsi sigmoid biner adalah logsig. Fungsi sigmoid biner dirumuskan sebagai berikut:
= = +�−�,, ∈ (2.21)
e. Fungsi Sigmoid Bipolar
Fungsi sigmoid bipolar hampir sama dengan fungsi sigmoid biner, perbedaannya terletak pada rentang nilai outputnya. Rentang nilai output fungsi sigmoid bipolar adalah -1 sampai 1. Pada Matlab R2013a, perintah untuk menggunakan fungsi sigmoid bipolar adalah tagsig. Fungsi sigmoid bipolar dirumuskan sebagai sebagai:
= = − �+�−�−�, ∈ (2.22)
-1 1 y
x
29
4. Algoritma Pembelajaran (Learning Algorithm)
Algoritma pembelajaran adalah prosedur untuk menentukan bobot pada lapisan yang berhubungan dalam artificial neural network (Fausett, 1994: 429). Selama proses pembelajaran akan terjadi perbaikan bobot-bobot berdasarkan algoritma tertentu. Nilai bobot akan bertambah, jika informasi yang diberikan oleh neuron yang bersangkutan tersampaikan, sebaliknya jika informasi tidak tersampaikan oleh suatu neuron ke neuron lain, maka nilai bobot yang menghubungkan keduanya akan dikurangi. Pada saat pembelajaran dilakukan pada input yang berbeda maka nilai bobot akan diubah secara dinamis hingga mencapai suatu nilai yang cukup seimbang. Apabila nilai ini telah seimbang, maka mengindikasikan bahwa tiap-tiap input telah berhubungan dengan output yang diharapkan (Kusumadewi, 2004: 116-117).
Ada 2 metode pembelajaran NN, yaitu pembelajaran terawasi (supervised
learning) dan pembelajaran tak terawasi (unsupervised learning) (Siang, 2009:
28-29):
a. Pembelajaran Terawasi (Supervised Learning)
30
b. Pembelajaran Tak Terawasi (Unsupervised Learning)
Pembelajaran tak terawasi tidak memerlukan target output dan tidak dapat ditentukan hasil yang diharapkan selama proses pembelajaran. Pada metode ini, tidak dapat ditentukan hasil outputnya. Selama proses pembelajaran, nilai bobot disusun dalam suatu range tertentu sesuai dengan nilai input yang diberikan. Tujuan pembelajaran ini adalah untuk mengelompokkan unit-unit yang hampir sama ke dalam suatu area tertentu.
E. SOM Kohonen Clustering
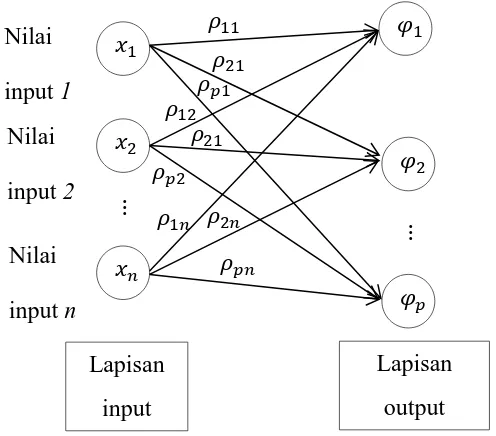
SOM Kohonen diperkenalkan oleh Teuvo Kohonen seorang ilmuwan Finlandia pada tahun 1982, sehingga SOM Kohonen dikenal juga dengan jaringan Kohonen. Jaringan SOM Kohonen merupakan salah satu jaringan saraf tiruan yang dikonfigurasi untuk pengelompokan data. Jaringan SOM Kohonen menggunakan metode pembelajaran unsupervised yang proses pelatihannya tidak memerlukan pengawasan (target output). Jaringan SOM Kohonen terdiri dari 2 lapisan (lapisan), yaitu lapisan input dan lapisan output. Setiap neuron dalam lapisan input terhubung dengan setiap neuron pada lapisan output. Setiap neuron dalam lapisan output merepresentasikan kelompok dari input yang diberikan (Siang, 2009: 141).
Penulisan istilah yang ada pada struktur jaringan SOM Kohonen adalah sebagai berikut :
� : laju pemahaman (learning rate),
: parameter tetangga (radius neighbourhood), � : bobot lapisan kohonen,
31
1. Arsitektur Jaringan SOM Kohonen
Arsitektur Jaringan SOM Kohonen tampak dalam gambar 2.11. Arsitektur ini mirip dengan model lain. Hanya saja Jaringan SOM Kohonen tidak menggunakan perhitungan net (hasil kali vektor masukan dengan bobot) maupun fungsi aktivasi (Siang, 2009: 142).
Gambar 2.11 Arsitektur Jaringan SOM Kohonen
2. Algoritma Jaringan SOM Kohonen
Algoritma pengelompokan data jaringan SOM Kohonen adalah sebagai berikut (Siang, 2009: 143):
Langkah 0 Inisialisasi bobot � dengan nilai random. Mengatur parameter laju pemahaman dan parameter tetangga,
Langkah 1 Jika kondisi penghentian bernilai salah atau kondisi selesai belum terpenuhi maka dilakukan langkah 2 sampai 7,
32
= ∑= � − (2.23)
Langkah 4 Mencari unit pemenang , yaitu unit yang memiliki minimum, Langkah 5 Melakukan perbaikan nilai � dengan nilai tertentu yaitu :
� = � + �[ − � ] (2.24)
Langkah 6 Memperbarui nilai laju pemahaman,
Langkah 7 Menentukan kondisi stop atau kondisi kapan iterasi diberhentikan. Kondisi penghentian iterasi adalah selisih antara � saat itu dengan � iterasi sebelumnya. Apabila semua � hanya berubah sedikit saja, berarti iterasi sudah mencapai konvergensi sehingga dapat dihentikan.
Menghitung pusat dan jarak dengan menggunakan metode SOM Kohonen
clustering dalam penelitian ini dilakukan dengan menggunakan bantuan program
Matlab R2013a, script secara lengkap terlampir pada lampiran (9) halaman (122). Berikut sebagian script terpenting dalam SOM Kohonen clustering (Siang, 2009: 283-291):
net=newc(PR,S,KLR,CLR); net.IW{1,1};
net.b{1};
net.trainParam.epochs=500; net= train(net,p);
b=sim(net,p); ab=vec2ind(b);
dengan
net = Jaringan yang didefinisikan dalam newc
33
newc = Membentuk sebuah jaringan SOM Kohonen dengan spesifikasi tertentu [PR,S,KLR,CLR],
PR = Matriks ukuran Rx2 yang berisi nilai minimum dan maksimum masing-masing nilai vektor masukan,
S = Jumlah neuron target,
KLR = Laju Pemahaman SOM Kohonen (default = , ),
CLR = Laju Pemahaman Conscience (default = , ),
net.IW{1,1} = Menampilkan bobot lapisan, net.b{1} = Menampilkan bobot bias lapisan,
net.trainParam.epochs = Menentukan epoch atau banyaknya iterasi (default=500),
p = Input data,
train = Perintah train akan menghasilkan jaringan (net,p) baru [train(net,p)],
sim = menghitung keluaran jaringan yang berupa matriks B
berordo x ( = jumlah neuron target dan = jumlah vektor masukan). , = menyatakan bahwa vektor masukan ke- masuk ke dalam kelompok ke-1.
vec2ind = Mengetahui secara langsung pengelompokan vektor dari perintah sim,
34
3. Contoh Kasus Cluster Menggunakan Metode SOM Kohonen
Berikut merupakan contoh penerapan SOM Kohonen pada suatu kasus (Siang, 2009: 144-147):
Diketahui 4 buah vektor = , , , , = , , , , = , , , dan = , , , . Menggunakan jaringan SOM Kohonen untuk mengelompokkan 4 buah vektor tersebut ke dalam maksimum 2 kelompok. Diberikan laju pemahaman awal � = , dan � + = , � . Jari-jari vektor sekitar yang dimodifikasi = (berarti hanya vektor pemenang yang dimodifikasi bobotnya pada setiap langkah).
Penyelesaian:
Inisialisasi bobot : Kolom matriks bobot menyatakan jumlah komponen dalam sebuah vektor (dalam kasus ini = ) dan baris menyatakan jumlah maksimum kelompok yang akan dibentuk (dalam kasus = ). Misalkan secara acak didapat bobot awal :
� = ,, ,, ,, ,,
Jari-jari sekitar yang dipakai = dan laju pemahaman awal = , . Berdasarkan persamaan 2.23 pelatihan dilakukan untuk tiap vektor : Untuk vektor = , , , :
= , − + , − + , − + , − = ,
= , − + , − + , − + , − = ,
minimum untuk = , sehingga vektor bobot di baris dimodifikasi menurut aturan persamaan 2.24 yaitu � � = � + , − � ,
35
� = , + , − , = , ; � = , + , − , = ,
Diperoleh vektor bobot baru : � = , , , ,
, , , ,
Untuk vektor = , , , ∶
= , − + , − + , − + , − = ,
= , − + , − + , − + , − = ,
minimum untuk = , sehingga vektor bobot di baris 1 dimodifikasi. Diperoleh:
� = , + , − , = , ; � = , + , − , = , � = , + , − , = , ; � = , + , − , = ,
Vektor bobot baru : � = , , , ,
, , , ,
Untuk vektor = , , , :
= , − + , − + , − + , − = ,
= , − + , − + , − + , − = ,
minimum untuk = , sehingga vektor bobot di baris 2 dimodifikasi. Diperoleh:
� = , + , − , = , ; � = , + , − , = ,
� = , + , − , = , ; � = , + , − , = ,
Vektor bobot baru : � = , , , ,
, , , ,
Untuk vektor = , , , :
= , − + , − + , − + , − = ,
= , − + , − + , − + , − = ,
36
� = , + , − , = , ; � = , + , − , = ,
� = , + , − , = , ; � = , + , − , = ,
Vektor bobot baru : � = , , , ,
, , , ,
Sebelum melakukan iterasi kedua dalam mengubah bobot, terlebih dahulu dilakukan modifikasi laju pemahaman,
� � = , , = ,
Iterasi kedua dilakukan secara analog dengan iterasi pertama. Baris vektor bobot diubah berdasarkan vektor yang saat itu digunakan.
Diperoleh hasil iterasi :
Bobot awal : � = , , , ,
, , , ,
Iterasi-1 : � = , , , ,
, , , ,
Iterasi-2 : � = , − , ,
, , , ,
dan seterusnya,
Iterasi-100 : � = ( , − − ,
, , − − )
Tampak bahwa iterasi tersebut akan konvergen ke vektor bobot � = , ,
Pengelompokan vektor dilakukan dengan menghitung jarak vektor dengan bobot optimal.
Vektor = , , , memiliki
37
= − + , − + − + − = ,
Karena minimum untuk = , sehingga masuk dalam kelompok ke-2. Secara analog, untuk = , , , , = , dan = , , sehingga masuk dalam kelompok ke-1.
Untuk = , , , , = , dan = , , sehingga masuk dalam kelompok ke-2.
Untuk = , , , , = , dan = , , sehingga masuk dalam kelompok ke-1.
F. Ketepatan Hasil Klasifikasi
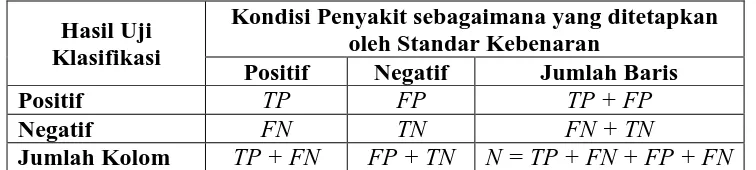
Pengujian ketepatan hasil klasifikasi dilakukan untuk menguji sejauh mana model memberikan ketepatan hasil klasifikasi. Untuk menghitung ketepatan hasil klasifikasi digunakan tiga ukuran statistik. Tiga ukuran statistik tersebut adalah sensitivitas, spesifisitas, dan akurasi. Hasil kemungkinan yang dapat terjadi dalam hasil uji klasifikasi tersaji pada tabel 2.1 di bawah ini (Wong & Lim, 2011: 317):
Tabel 2.1 Hasil Uji Klasifikasi
Hasil Uji Klasifikasi
Kondisi Penyakit sebagaimana yang ditetapkan oleh Standar Kebenaran
Positif Negatif Jumlah Baris
Positif TP FP TP + FP
Negatif FN TN FN + TN
Jumlah Kolom TP + FN FP + TN N = TP + FN + FP + FN
Berdasarkan tabel 2.1, terdapat empat kemungkinan hasil uji klasifikasi yaitu:
True Positive (TP) : klasifikasi asli citra menyatakan kanker dan hasil pembelajaran
38
True Negative (TN) : klasifikasi asli citra menyatakan normal dan hasil
pembelajaran menyatakan normal.
False Positive (FP) : klasifikasi asli citra menyatakan normal dan hasil
pembelajaran menyatakan kanker.
False Negative (FN) : klasifikasi asli citra menyatakan kanker dan hasil
pembelajaran menyatakan normal.
Sensitivitas adalah kemampuan uji untuk mengidentifikasi hasil positif yang tepat. Sensitivitas digunakan untuk mengidentifikasi pasien yang memiliki penyakit kanker dari keseluruhan pasien penyakit kanker. Rumus dari sensitivitas adalah sebagai berikut (Wong & Lim, 2011: 316):
=��+���� x % (2.25)
Spesifisitas adalah kemampuan uji untuk mengidentifikasi hasil negatif yang tepat. Spesifisitas digunakan untuk mengidentifikasi pasien yang normal dari keseluruhan pasien normal. Berikut adalah rumus dari spesifisitas (Wong & Lim, 2011: 316):
=��+���� x % (2.26)
Akurasi adalah kemampuan uji untuk mengidentifikasi hasil yang tepat, baik tepat positif atau tepat negatif dalam sebuah populasi. Berikut adalah rumus dari akurasi:
39
BAB III
PEMBAHASAN
Bab III merupakan pembahasan yang meliputi proses penyusunan tugas akhir yaitu arsitektur dan model SOM-RBFNN, prosedur pemodelan SOM-RBFNN, hasil model SOM-RBFNN untuk klasifikasi citra paru, dan ketepatan hasil klasifikasi.
A. Arsitektur dan Model SOM-RBFNN untuk Klasifikasi Citra Paru
SOM-RBFNN adalah jaringan feed-forward dengan tiga lapisan, sebuah lapisan input dengan � neuron, sebuah lapisan tersembunyi dengan neuron, dan lapisan output dengan satu neuron (Qasem et al, 2013). Lapisan tersembunyi dalam SOM-RBFNN merupakan lapisan output pada SOM Kohonen clustering. Model SOM-RBFNN melakukan pembelajaran jaringan secara hybrid dengan menggunakan pembelajaran tak terawasi (unsupervised learning) dan pembelajaran terawasi (supervised learning). Kinerja SOM-RBFNN tergantung pada pemilihan tiga parameter penting (nilai pusat dari cluster, nilai jarak dan bobot). Nilai parameter ini umumnya diketahui dan dapat ditemukan selama proses pembelajaran jaringan (Pislaru & Shebani, 2014).
1. Arsitektur SOM-RBFNN
40
berfungsi untuk membantu artificial neural network dalam mengolah informasi dengan lebih baik.
Gambar 3.1 Arsitektur model SOM-RBFNN
Pada gambar 3.1, ( �, � = , , , … , � merupakan neuron pada lapisan input, (� , = , , , … , � merupakan neuron pada lapisan tersembunyi, dan merupakan neuron pada lapisan output. Bobot antara lapisan input dan lapisan tersembunyi disimbolkan dengan ��� sedangkan lapisan tersembunyi dan lapisan output disimbolkan dengan .
41
2. Model SOM-RBFNN
Pada SOM-RBFNN, metode SOM Kohonen clustering sebagai penentu pusat dan jarak dari setiap fungsi aktivasi pada lapisan tersembunyi, kemudian dengan fungsi aktivasi � dilanjutkan menuju lapisan output (Pislaru & Shebani, 2014). Fungsi aktivasi yang digunakan yaitu fungsi radial basis. Berikut ini beberapa fungsi radial basis yang dapat digunakan sebagai fungsi aktivasi (Orr, 1996: 40) :
a. Fungsi Gaussian
� = � � [− − ] (3.1)
b. Fungsi Multikuadratik
� = √ − � + � (3.2)
c. Fungsi Invers Multikuadratik
� = √ − + (3.3)
d. Fungsi Cauchy
� = [ − + ]− (3.4)
dengan
� = nilai jarak variabel input ke pusat pada masing-masing cluster,
= nilai input fitur,
� = nilai pusat variabel input pada masing-masing cluster,
42
Output yang dihasilkan dari model SOM-RBFNN merupakan kombinasi linear dari bobot dengan fungsi aktivasi � dan bobot bias . Vektor output dirumuskan sebagai berikut:
= ∑�= � + (3.5)
dan
� = � � [− −�� � −�� ] (3.6)
dengan
[ ] = [ , , , … , �, … , �],
[��] = [� , � , � , … , ��, … , ��],
= vektor nilai input fitur,
�� = vektor nilai pusat cluster ke- ,
= bobot neuron lapisan tersembunyi ke-k menuju neuron pada lapisan output,
= bobot bias pada lapisan tersembunyi menuju neuron pada lapisan output,
� = jarak maksimum pada cluster ke- ,
43
B. Prosedur Pemodelan SOM-RBFNN untuk Klasifikasi Citra Paru
Berikut ini adalah prosedur pemodelan SOM-RBFNN untuk klasifikasi citra paru:
1. Preprocessing Citra
Preprocessing citra adalah proses pengolahan citra sebelum ekstraksi citra
dilakukan. Preprocessing bertujuan untuk menghilangkan noise, memperjelas fitur, memperkecil atau memperbesar ukuran data, dan mengkonversi data asli agar diperoleh data sesuai kebutuhan. Preprocessing citra dapat berupa mengubah citra RGB menjadi grayscale, binerisasi citra, pemotongan citra, mengubah ukuran citra, atau penghilangan background citra.
Preprocessing citra yang digunakan dalam penelitian ini berupa pemotongan
citra, kemudian mengubah citra ke bentuk citra grayscale selanjutnya mengubah ukuran pixel. Selain itu, karena format citra berupa Disk Image File (IMG) dibutuhkan program bantuan yaitu ImageJ untuk mengubah format citra ke bentuk
Joint Photographic Experts Group (JPEG atau JPG).
a. Mengubah format citra dari IMG menjadi (JPEG atau JPG)
Mengubah format file dari Disk Image File (IMG) menjadi Joint
Photographic Experts Group (JPEG atau JPG) sangat penting dilakukan agar file
dapat terbaca oleh program lain. Adapun langkahnya adalah sebagai berikut (Japanese Society of Radiology Technology, 1997), membuka aplikasi imageJ_file menu_import_raw, kemudian mengatur format dengan ketentuan (Image type =
44
bytes, Number of Image = 1, Gap Between Image = 0 bytes, Check “White is Zero”
only).
b. Pemotongan Citra
Proses pemotongan atau penghilangan background citra paru dilakukan dengan bantuan software Adobe Photoshop CS 8.
c. Mengubah citra ke dalam bentuk grayscale
Proses mengubah bentuk citra ke dalam bentuk grayscale dilakukan saat ekstraksi citra menggunakan GCLM dengan program Matlab R2013a. Script selengkapnya terdapat pada lampiran (3) halaman (102). Script yang diketikkan adalah
R=rgb2gray(JPCLN001);
d. Mengubah ukuran pixel
Ukuran pixel citra paru diubah bertujuan untuk menyeragamkan ukuran pixel semua citra foto paru saat di ekstraksi, agar mendapat hasil yang maksimal. Script selengkapnya terdapat pada lampiran (3) halaman (102). Script yang diketikkan pada program Matlab R2013a adalah
Iec=rgb2gray(JPCLN001,[256 256];
2. Ekstraksi Fitur Citra
Setelah melakukan perbaikan kualitas citra dengan operasi titik intensity
adjustment, langkah selanjutnya adalah melakukan ekstraksi citra. Proses ekstraksi
45
citra berupa data-data numerik yang akan digunakan untuk menentukan variabel input dalam klasifikasi SOM-RBFNN.
3. Normalisasi Input Fitur Citra
Normalisasi adalah penskalaan terhadap data input ke dalam suatu range tertentu sehingga data input menjadi lebih merata (seragam). Hal ini dilakukan agar data input sesuai dengan range dari fungsi aktivasi yang digunakan dalam jaringan. Data input dinormalisasi dengan cara membawa data ke bentuk normal baku yaitu dengan mean = 0 dan simpangan baku =1. Berikut adalah rumus normalisasi input fitur citra (Walpole, 1992: 41):
∗ = �− ̅
� (3.7)
dengan
̅ = rata-rata data; ̅ = ∑ = ,
� = simpangan baku data sampel; � = √
− ∑ = − ̅ ,
= , , , . . . , ,
= Jumlah data pengamatan.
Pada MATLAB R2013a normalisasi input fitur citra dapat ditentukan dengan metode dengan fungsi prestd. Script yang digunakan adalah sebagai berikut:
[Pn,meanp,stdp,Tn,meant,stdt]=prestd(P,T)
dengan
P = matriks input,
T = matriks target,
46
Meanp & meant = mean pada matriks input sebelum dinormalisasi P & T ,
stdp & stdt = simpangan baku pada matriks input sebelum dinormalisasi
P & T ,
4. Pembagian Input Fitur Citra
Pembagian input fitur citra input pada jaringan saraf tiruan dibagi menjadi 2, yaitu data training dan data testing. Data training digunakan untuk melatih jaringan dalam mengenali informasi yang diberikan. Sedangkan, data testing merupakan data yang akan digunakan untuk menguji tingkat keakuratan model jaringan dalam mengolah informasi yang telah diberikan. Terdapat beberapa komposisi data
training dan data testing yang digunakan dalam jaringan saraf tiruan (Hota, et al,
2013: 165):
a. 60% keseluruhan data sebagai data training dan 40% keseluruhan data sebagai data testing,
b. 75% keseluruhan data sebagai data training dan 25% keseluruhan data sebagai data testing,
c. 80% keseluruhan data sebagai data training dan 20% keseluruhan data sebagai data testing.
5. Menentukan Variabel Input dan Variabel Output
Variabel input model SOM-RBFNN yang digunakan pada lapisan input fitur adalah 13 fitur hasil ekstraksi citra yang diperoleh dari metode GLCM yaitu,
contrast, correlation, energy, homogeneity, sum entropy, sum of square variance,
invers difference moment, sum average, sum variance, entropy, difference entropy,
47
lapisan input adalah 13 neuron. Variabel output pada model SOM-RBFNN pada tugas akhir ini adalah hasil klasifikasi citra paru yaitu normal dan kanker. Sehingga banyak neuron pada lapisan output adalah 1 neuron. Target jaringan yang digunakan adalah klasifikasi citra paru yaitu kanker dan normal.
6. Pembelajaran SOM-RBFNN
Pembelajaran SOM-RBFNN terbagi menjadi tiga bagian. Bagian pertama menentukan pusat dan jarak menggunakan metode SOM Kohonen.
a. Menentukan nilai pusat dan jarak dengan metode SOM Kohonen
Algoritma pengelompokan data jaringan SOM Kohonen dalam RBFNN adalah sebagai berikut:
Langkah 0 Inisialisasi bobot � � yaitu bobot yang menghubungkan neuron
ke-� pada lapisan input ke neuron ke-( ) pada lapisan tersembunyi dengan nilai random. Berdasarkan contoh kasus, nilai matriks bobot random � � di dalamnya memuat baris sebagai banyaknya cluster yang akan dibentuk dan kolom sebagai banyaknya variabel input fitur citra. Mengatur parameter laju pemahaman (default = 0,01) dan parameter tetangga (default = 0,001),
Langkah 1 Jika kondisi penghentian bernilai salah atau kondisi selesai belum terpenuhi maka dilakukan langkah 2 sampai 7,
Langkah 2 Untuk setiap input fitur citra, dilakukan langkah 3 sampai 5,
Langkah 3 Berdasarkan persamaan 2.23 dilakukan perhitungan jarak matriks tiap-tiap baris pada bobot random � � terhadap input fitur citra,
48
Langkah 5 Melakukan perbaikan nilai bobot random � � berdasarkan persamaan 2.24,
Langkah 6 Memperbarui nilai laju pemahaman,
Langkah 7 Menentukan kondisi stop atau kondisi kapan iterasi diberhentikan. Kondisi penghentian iterasi adalah selisih antara � � saat itu dengan � � iterasi sebelumnya. Apabila semua � � hanya berubah sedikit saja, berarti iterasi sudah mencapai konvergensi sehingga dapat dihentikan.
Menghitung pusat dan jarak dengan menggunakan metode SOM Kohonen
clustering dalam RBFNN dilakukan dengan menggunakan bantuan program
Matlab R2013a. Berikut penjelasan script SOM Kohonen dalam RBFNN:
net=newc(PR,S,KLR,CLR);
net.IW{1,1};
net.b{1};
net.trainParam.epochs=500;
net= train(net,p);
b=sim(net,p);
ab=vec2ind(b);
dengan
net = Jaringan yang didefinisikan dalam newc [net=newc(PR,S,KLR,CLR], newc = Membentuk sebuah jaringan SOM Kohonen dengan spesifikasi tertentu
[PR,S,KLR,CLR],
PR = Matriks input fitur citra yang berisi nilai minimum dan maksimum
masing-masing nilai input fitur citra,
49
KLR = Laju Pemahaman SOM Kohonen (default = , ), CLR = Laju Pemahaman Conscience (default = , ),
net.IW{1,1} = Menampilkan bobot lapisan antara lapisan input dan lapisan
tersembunyi,
net.b{1} = Menampilkan bobot bias lapisan antara lapisan input dan lapisan
tersembunyi,
net.trainParam.epochs = Menentukan epoch atau banyaknya iterasi
(default=500),
p = Matriks input fitur citra,
train = Perintah train akan menghasilkan jaringan (net,p) baru
[train(net,p)],
sim = menghitung keluaran jaringan yang berupa matriks B berordo � x � (� =
banyaknya cluster dan � = banyaknya input fitur citra). , � = menyatakan bahwa input fitur citra masuk ke dalam kelompok 1,
vec2ind = Mengetahui secara langsung pengelompokan vektor dari perintah
sim,
Bobot awal yang dibentuk adalah titik tengah PR.
Setelah diperoleh cluster untuk setiap input fitur citra dengan algoritma SOM Kohonen, kemudian menentukan nilai pusat masing-masing cluster dengan menggunakan rumus sebagai berikut:
� = [
� �
��
50 dan
�� = ∑��= � (3.9)
dengan
= banyaknya input fitur citra dalam setiap cluster.
Selanjutnya menentukan jarak input fitur citra tiap-tiap cluster terhadap nilai pusat tiap-tiap cluster dengan menggunakan jarak Euclidean sebagai berikut:
� = √ − �̅ + − �̅ + + �− �̅̅̅� (3.10) b. Menghitung fungsi aktivasi neuron pada lapisan tersembunyi
Dalam pembelajaran SOM-RBFNN yang kedua adalah menentukan jumlah fungsi aktivasi neuron pada lapisan tersembunyi. Banyak neuron pada lapisan tersembunyi sesuai dengan banyak cluster yang terdapat pada pengelompokan menggunakan SOM Kohonen clustering. Pada lapisan tersembunyi metode SOM-RBFNN, dilakukan perhitungan fungsi aktivasi. Dalam tugas akhir ini, aktivasi fungsi aktivasi dilakukan dengan bantuan Matlab R2013a menggunakan program
rbfDesign (Sutijo, 2008: 156). Program untuk rbfDesign dilampirkan pada lampiran
(13) halaman (133). Cuplikan dari Program rbfDesign adalah sebagai berikut:
Function H = rbfDesign(X’,M,SD,option)
dengan
H = matriks desain SOM-RBFNN,
X’ = matriks input fitur citra,
M = matriks nilai pusat dari setiap cluster,
SD = matriks jarak input terhadap pusat dari setiap cluster,
51
Matriks (‘M’)dan (‘SD’)diperoleh dari hasil proses script SOM Kohonen
clustering pada lampiran (9) halaman (122). Tipe aktivasi yang digunakan pada
tugas akhir ini adalah fungsi Gaussian dengan (‘b’) yaitu neuron bias yang ditambahkan pada jaringan, sehingga matriks � akan mendapatkan satu kolom tambahan. Dipilih fungsi aktivasi gaussian berdasarkan penelitian sebelumnya menghasilkan hasil dan tingkat akurasi yang baik, yaitu pada penelitian yang dilakukan Chang, et al (2013) dan Mu & Nandi (2007).
c. Mengestimasi Bobot Optimum menggunakan Metode Global Ridge
Regression
Pada bagian ketiga dari pembelajaran SOM-RBFNN yaitu menentukan bobot-bobot yang menghubungkan antara lapisan tersembunyi dan lapisan output. Pada tugas akhir ini menggunakan pendekatan metode global ridge regression dalam menentukan bobot-bobot dengan pemilihan kriteria model menggunakan kriteria Global Cross-Validation (GCV). Metode global ridge regression dilakukan dengan bantuan Matlab R2013a. Script secara lengkap terlampir pada lampiran (14) halaman (136). Berikut ini script fungsi globalRidge pada Matlab 2013a (Sutijo, 2008: 156):
lamb = globalRidge(H, T, 0.01)
dengan
l = parameter regulasi,
H = matriks desain SOM-RBFNN,
T = matriks target data training,
52
Metode Global Ridge Regression mengestimasi bobot dengan cara menambahkan parameter regulasi yang bernilai positif � > pada Sum Square
Error (Orr, 1996: 24). Estimasi bobot terbaik diperoleh dari hasil akhir dengan SSE
terkecil. Dengan menggunakan metode kuadrat terkecil (ordinary least square) akan diperoleh bobot optimum. Model linear yang digunakan adalah ( =
∑�= � + ).
�� = ∑ = − ̂ (3.11)
dengan
̂ = hasil variabel output dari data ke- , = target variabel output dari data ke- .
Untuk menentukan nilai optimum bobot , dapat ditentukan dengan mendiferensialkan persamaan (3.11) terhadap bobot-bobotnya sehingga diperoleh,
�
� = ∑ − ̂
� �
= (3.12) Berdasarkan persamaan (3.5) diperoleh,
�
� = � (3.13)
Persamaan (3.13) disubstitusikan ke persamaan (3.12) dengan mengasumsikan bahwa �
� = diperoleh,
= ∑ = − ̂ � (3.14)
= ∑ = � − ∑ = ̂ � (3.15)
∑ = ̂ � = ∑ = � (3.16)
53
Karena, = , , … , � maka akan diperoleh � persamaan seperti persamaan
(3.17) untuk menentukan � bobot. Untuk memperoleh penyelesaian tunggal,
persamaan (3.17) ditulis dalam notasi vektor diperoleh,
� ̂ = � (3.18)
Matriks � adalah matriks desain. Komponen ke- dari saat bobot pada nilai optimum adalah (Orr, 1996: 43),
54
Akibat �� adalah salah satu kolom dari � dan �̅�� adalah salah satu baris dari � . Oleh karena itu, berdasarkan persamaan (3.20) diperoleh,
= [ ] = [ �̅ ̂
�̅ ̂
�̅ ̂]
= �̂ (3.22)
Dengan mensubstitusikan persamaan (3.22) ke persamaan (3.19) maka,
� �̂ = � ̂ (3.23)
� � − � �̂ = � � − � ̂ (3.24)
̂ = � � − � ̂ (3.25)
Selanjutnya pada persamaan SSE yaitu persamaan (3.11) ditambahkan suatu parameter regulasi � > sehingga didapatkan Cost Function (CF) untuk menentukan bobot yang optimal (Orr, 1996: 24):
= ∑ = − ̂ + ∑�= � (3.26)
dengan
= , , . . . , , banyaknya input fitur citra,
̂ = hasil variabel output dari data ke- , = target variabel output dari data ke- ,
� = parameter regulasi,
= bobot dari neuron pada lapisan tersembunyi ke- menuju neuron pada lapisan output.
55 Dengan mengasumsikan bahwa ��
� = pada persamaan (3.28) sehingga akan diperoleh,
= ∑ = �� − ∑ = ̂ �� + � (3.29)
= ∑ = �� − ∑ = ̂ �� + � (3.30)
∑ = ̂ �� = ∑ = �� + � (3.31)
Berdasarkan persamaan (3.5) bahwa �
� = � , maka berdasarkan persamaan (3.31) diperoleh,
∑ = ̂ � = ∑ = � + � ̂ (3.32) Karena, = , , … , � maka akan diperoleh � persamaan seperti persamaan
(3.32) untuk menentukan � bobot. Untuk memperoleh penyelesaian tunggal,
persamaan (3.32) ditulis dalam notasi vektor diperoleh,
56 optimum adalah (Orr, 1996: 43),
= ∑�= � = �̅ ̂ (3.35) Oleh karena itu, berdasarkan persamaan (3.35) diperoleh,
= [ ] =
Dengan mensubstitusikan persamaan (3.37) ke persamaan (3.34) diperoleh,
� �̂ + �̂ = � ̂ (3.38)
57
̂ = � � + � − � ̂ (3.40)
̂ = � � + ���+ − � ̂ (3.41)
Persamaan (3.41) merupakan bentuk persamaan normal untuk bobot-bobot optimum yang diperoleh dari metode global ridge regression.
d. Menentukan jumlah fungsi aktivasi (neuron pada lapisan tersembunyi) dilakukan dengan metode trial and error.
Model SOM-RBFNN menggunakan kriteria pemilihan model untuk memprediksi error. Model terbaik dipilih berdasarkan nilai prediksi error terkecil.
Generalized Cross-Validation (GCV) merupakan salah satu kriteria pemilihan
model. GCV melibatkan semua penyesuaian rata-rata MSE (Mean Square Error) pada data training (Orr, 1996: 20). Berikut ini rumus kriteria pemilihan model dengan GCV.
�̂ �� = ̂
�� ̂
� � (3.42) dan
� = � − � � � − � (3.43)
� = matriks fungsi aktivasi, = banyaknya input fitur citra,
� = matriks proyeksi,
̂ = vektor hasil variabel output.
7. Menentukan Jaringan Optimum
Jaringan optimum pada SOM-RBFNN diperoleh dengan metode trial and
error. Metode ini dilakukan untuk membandingkan nilai akurasi tertinggi yang
58
pada lapisan tersembunyi didapatkan dari banyaknya cluster yang digunakan pada metode SOM Kohonen clustering.
Berdasarkan prosedur pengklasifikasian citra paru menggunakan model SOM-RBFNN adalah preprocessing citra paru dengan cara melakukan cropping,
resize, dan mengubah citra warna (RGB) pada citra paru. Selanjutnya, melakukan
ekstraksi fitur dengan menggunakan metode GLCM untuk memperoleh 13 parameter sebagai input yaitu contrast, correlation, energy, homogeneity, sum
entropy, sum of square variance, invers difference moment, sum average, sum
variance, entropy, difference entropy, maximum probability, dan dissimilarity
entropy. Setelah itu, membagi data menjadi 2 bagian yaitu 80% dari keseluruhan
59
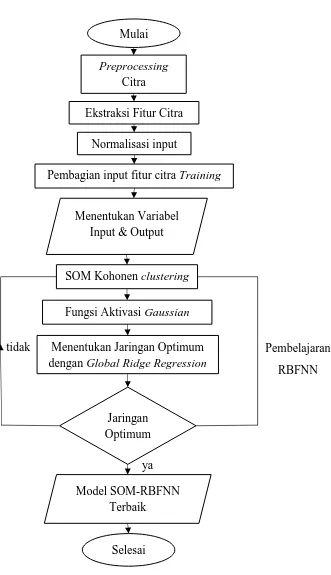
Gambar 3.2 Diagram Alir Pemodelan SOM-RBFNN
Menentukan Jaringan Optimum dengan Global Ridge Regression
Mulai
Preprocessing
Citra
Ekstraksi Fitur Citra
Pembagian input fitur citra Training & Testing
Menentukan Variabel Input & Output
Fungsi Aktivasi Gaussian
Jaringan Optimum
Model SOM-RBFNN Terbaik
Selesai tidak
ya Normalisasi input
SOM Kohonen clustering