Vol. 12, No. 1 (2006), pp. 113–130.
SURVEY OF EDGE ANTIMAGIC LABELINGS
OF GRAPHS
M. Baˇ
ca
1, E.T. Baskoro
2, M. Miller
3, J. Ryan
3,
R. Simanjuntak
2, and K.A. Sugeng
3Abstract.An (a, d)-edge-antimagic total labeling ofGis a one-to-one mappingftaking the vertices and edges onto 1,2, . . . ,|V(G)|+|E(G)|so that the edge-weightsw(uv) =
f(u) +f(v) +f(uv) :uv∈E(G), form an arithmetic progression with initial termaand common differenced. Such a labeling is called super if the smallest possible labels appear on the vertices. In this paper we survey what is known about edge-antimagic total and super edge-antimagic total labelings and provide a summary of current conjectures and open problems.
1. INTRODUCTION
All graphs in this paper are finite, undirected, and simple. A graphG has vertex set V(G) and edge set E(G). We follow the notation and terminology of Wallis [31] and West [33].
A labeling of a graph is any mapping that sends some set of graph elements to a set of positive integers. If the domain is the vertex-set or the edge-set, the labelings are called, respectively,vertex labelingsoredge labelings. Moreover, if the domain isV(G)∪E(G) then the labelings are calledtotal labelings.
Hartsfield and Ringel in [16] introduced the concept of an antimagic graph. In their terminology, a graphG(V, E) is calledantimagicif its edges are labeled with labels 1,2, . . . ,|E(G)| in such a way that all vertex-weights are pairwise distinct, where a vertex-weight of vertexv is the sum of labels of all edges incident withv.
Hartsfield and Ringel [16] point out that among the antimagic graphs are pathsPn,n≥3, cycles, wheels, and complete graphs Kn,n≥3. They conjecture that every connected graph, exceptK2, is antimagic.
Received 13 August 2005, Revised 28 October 2005, Accepted 10 Nov 2005.
2000 Mathematics Subject Classification: 05C78.
Key words and Phrases: Edge-antimagic total labeling, Super edge-antimagic total labeling.
Alon, Kaplan, Lev, Roditty and Yuster [2] used probabilistic arguments with tools from analytic number theory to show that this conjecture is true for all graphs having minimum degree Ω(log|V(G)|). They also prove that ifGis a graph with |V(G)| ≥4 vertices and maximum degree ∆(G)≥ |V(G)| −2 thenGis antimagic and that all complete partite graphs, exceptK2, are antimagic.
It is not difficult to produce many antimagic labelings for most graphs. Thus Bodendiek and Walther [10] introduced further restriction on the vertex-weights. They defined the concept of an (a, d)-antimagic labeling as an edge labeling in which the vertex-weights form an arithmetic progression starting fromaand having common difference d. In [18] this labeling is called (a, d)-vertex-antimagic edge labeling.
For a graph G(V, E), an injective mapping from V(G)∪E(G) onto the set {1,2, . . . ,|V(G)|+|E(G)|}is an (a, d)-vertex-antimagic total labeling if the set of all vertex-weights is {a, a+d, a+ 2d, . . . , a+ (|V(G)| −1)d}. The (a, d )-vertex-antimagic total labeling was introduced by Baˇca et al. [4] as a natural extension of the notion of vertex-magic total labeling defined by MacDougall et al. in [19] and [20]. Results about (a, d)-antimagic labelings and (a, d)-vertex-antimagic total labelings can be found in the general survey of Gallian [14].
In this paper we concentrate on a variation of antimagic labeling, where we consider the sum of all labels associated with an edge. We defineedge-weightof an edge uv under a vertex labeling to be the sum of the vertex labels corresponding to the vertices uandv. Under a total labeling, we also add the label of the edge
uv.
By an (a, d)-edge-antimagic vertex((a, d)-EAV)labelingwe mean a one-to-one mapping f fromV(G) onto{1,2, . . . ,|V(G)|}such that the set of edge-weights of all edges inG,{f(u) +f(v) :uv∈E(G)}is{a, a+d, a+ 2d, . . . , a+ (|E(G)| −1)d}. The equivalent notion of astrongly (a, d)-indexable labeling was defined by Hegde in his Ph.D. thesis (see Acharya and Hegde [1]).
An (a, d)-edge-antimagic total((a, d)-EAT)labelingis defined as a one-to-one mappingf fromV(G)∪E(G) onto the set{1,2, . . . ,|V(G)|+|E(G)|}so that the set {f(u)+f(uv)+f(v) :uv∈E(G)}is equal to{a, a+d, a+2d, . . . , a+(|E(G)|−1)d}, for two integers a >0 andd≥0.
The (a,0)-EAT labelings are usually callededge-magic labelings in the liter-ature (see [12], [17], [24] and [30]).
An (a, d)-EAT labelingf is calledsuperif it has the property that the vertex labels are the integers 1,2, . . . ,|V(G)|, that is, the smallest possible labels, and
f(E(G)) ={|V(G)|+ 1,|V(G)|+ 2, . . . ,|V(G)|+|E(G)|}.
In this paper we extend the survey paper [26] and summarize the results con-cerning (a, d)-EAT and super (a, d)-EAT labelings. We provide several conjectures and open problems for further research.
2. (a, d)-EDGE-ANTIMAGIC TOTAL LABELINGS
Assume that graph G has an (a, d)-EAT labeling f. The sum of all the
In the computation of the edge-weights ofG, each edge label is used once and the label of vertexui is useddeg(ui) times,i= 1,2, . . . ,|V(G)|, wheredeg(ui) is the degree of vertex ui. The sum of all vertex labels and edge labels used to calculate the edge-weights is thus equal to
|V|+|E|
Using parity considerations of the left hand and the right hand sides of (3) we have:
Proposition 1. [25]A graph with all vertices of odd degrees cannot have an(a, d) -EAT labeling withaand dboth even.
Proposition 2. [25]LetGbe a graph with all vertices of odd degrees. If|E(G)| ≡0 (mod4) and|V(G)| ≡2 (mod 4)then Ghas no(a, d)-EAT labeling.
Proposition 3. [25]Suppose Gis a graph whose every vertex has an odd degree. Then in the following cases Ghas no(a, d)-EAT labeling.
For an (a, d)-EAT labeling, the minimum possible edge-weight is at least 1 + 2 + 3. Consequentlya≥6. The maximum possible edge-weight is no more than (|V|+|E| −2) + (|V|+|E| −1) + (|V|+|E|) = 3|V|+ 3|E| −3.
Thus
a+ (|E| −1)d≤3|V|+ 3|E| −3,
d≤ 3|V|+ 3|E| −9
|E| −1 (4)
and we have an upper bound for the parameterdfor an (a, d)-EAT labeling ofG. Next we present some relationships between (a, d)-EAV labeling, (a, d)-EAT labeling and other kinds of labelings, namely, edge-magic vertex ((k,0)-EAV) la-beling and edge-magic total ((k,0)-EAT) labeling.
Theorem 1. [3]IfGhas an edge-magic vertex labeling with magic constantkthen
Ghas a (k+|V|+ 1,1)-EAT labeling.
Theorem 2. [3] Let G be a graph which admits total labeling and whose edge labels constitute an arithmetic progression with differenced. Then the following are equivalent.
(i)Ghas an edge-magic total labeling with magic constantk, (ii)Ghas a (k−(|E| −1)d,2d)-EAT labeling.
LetCn be the cycle with V(Cn) ={vi : 1≤i≤n} and E(Cn) ={vivi+1 :
1 ≤ i ≤n−1} ∪ {vnv1}. It follows from (4) that for every cycle Cn there is no (a, d)-EAT labeling withd >5.
Kotzig and Rosa [17] showed that the cycles Cn, n ≥ 3, are edge-magic ((a,0)-EAT in our terminology) with the common edge-weight 3n+ 1 (fornodd),
5n
2 + 2 (for n≡2 (mod 4)) and 3n (forn≡0 (mod 4)). An edge-magic labeling
forCn with the common edge-weight 5n2+3 (fornodd) and 52n+ 2 (forneven) was described by Godbold and Slater in [15]. Explicit constructions that show that all cycles are edge-magic have been found by Berkman, Parnas and Roditty [9].
Ford≥1, the following results are known.
Theorem 3. [25]Every cycleCnhas(2n+2,1)-EAT and(3n+2,1)-EAT labelings.
Theorem 4. [25]Every even cycle C2k has (4k+ 2,2)-EAT and (4k+ 3,2)-EAT
labelings.
Theorem 5. [25]Every odd cycleC2k+1,k≥1, has(3k+4,3)-EAT and(3k+5,3)
-EAT labelings.
Theorem 6. [3]Every odd cycle C2k+1, k≥1, has (3k+ 4,2)-EAT,(5k+ 5,2)
-EAT, (2k+ 4,4)-EAT and (2k+ 5,4)-EAT labelings.
Theorem 7. [23] Every odd cycleC2k+1,k≥1, has (4k+ 4,1)-EAT,(6k+ 5,1)
Theorem 8. [8]Every cycle Cn, n≥3, has (2n+ 2,3)-EAT and (n+ 4,3)-EAT
labelings.
Open Problem 1. Find (a, d)-EAT labelings for even cycles withd∈ {4,5} and for odd cycles withd= 5.
LetPn be the path with V(Pn) = {vi : 1 ≤i ≤n} and E(Pn) = {vivi+1 :
1≤i≤n−1}. Applying Equation (4) to the paths, we obtain that for every path
Pn there is no (a, d)-EAT labeling withd >6.
Theorem 9. [30] All paths are edge-magic((a,0)-EAT).
Theorem 10. [3]Every pathPnhas (2n+ 2,1)-EAT,(3n,1)-EAT,(n+ 4,3)-EAT
and(2n+ 2,3)-EAT labelings.
Theorem 11. [23] Every odd pathP2k+1,k≥1, has(4k+ 4,1)-EAT,(6k+ 5,1)
-EAT, (4k+ 4,2)-EAT and (4k+ 5,2)-EAT labelings.
Theorem 12. Every odd path P2k+1,k≥1, has(3k+ 4,2)-EAT,(5k+ 4,2)-EAT,
(2k+ 4,4)-EAT and (2k+ 6,4)-EAT labelings.
Theorem 13. [3]Every even pathP2k,k≥1, has(3k+ 3,2)-EAT and(5k+ 1,2)
-EAT labelings.
Theorem 14. [29]Every even path P2k,k≥1, has (2k+ 4,4)-EAT labeling.
Theorem 15. [29]Every pathPn,n≥2, has (6,6)-EAT labeling.
We propose the following open problem.
Open Problem 2. Find (a,5)-EAT labelings for paths Pn, for the feasible values
of a.
3. SUPER (a, d)-EDGE-ANTIMAGIC TOTAL LABELINGS
We start this section by a necessary condition for a graph to be super (a, d )-EAT which will provide an upper bound on the parameterd.
The minimum possible edge-weight in a super (a, d)-EAT labeling is at least 1+2+(|V(G)|+1) =|V(G)|+4. Consequently,a≥ |V(G)|+4. On the other hand, the maximum possible edge-weight is at most (|V(G)| −1) +|V(G)|+ (|V(G)|+ |E(G)|) = 3|V(G)|+|E(G)| −1.
Thus
a+ (|E(G)| −1)d≤3|V(G)|+|E(G)| −1
and we have the following
Theorem 16. If a graphG(V, E)is super(a, d)-EAT then d≤2|V(G|E)|+|(G)|−1E(G)|−5.
Theorem 17. [3]IfGhas an (a, d)-EAV labeling then
The edge-magic labeling for an odd cycleCnwith common edge-weight 5n2+3, described by Godbold and Slater in [15], is super¡5n+3
2 ,0
n to mean the graph constructed from a cycleCn by joining two vertices whose distance in the cycle is t. Forn≥4, 2≤t≤n−2, the graph
Ct
n is of course also the graphC n−t n .
This section provides the values oftfor which there exists a super (a, d)-EAT labeling of Ct
n. If n is odd we can restrict our attention to t either odd or even, while ifnis even we will pay attention only totat most n
2. Suppose the endpoints
of the chord receive labelsxandy. The following result (in the light of Theorem 16) provides the valuesaandx+y under a super (a, d)-edge-antimagic total labeling.
Theorem 20. [6]LetCt
The following results for super (a,0)-EAT labelings were obtained by Mac-Dougall and Wallis [21] and for super (a, d)-EAT labelings,d∈ {1,2}, by Baˇca and Murugan [6].
Theorem 21. [6, 21] For n odd, n = 2k+ 1 ≥ 5, and for all possible values t, every graphCt
(i) super(a,0)-EAT labeling witha= 5k+ 4 ora= 5k+ 5, and (ii) super(a,2)-EAT labeling with a= 3k+ 3or a= 3k+ 4.
Theorem 22. [6, 21]Forn≡0 (mod4),n≥4, the graphCt n has
(i) a super(5n
2 + 2,0)-EAT labeling, and
(ii) a super(3n
2 + 2,2)-EAT labeling,
for allt≡2 (mod4).
Theorem 23. [6, 21] Forn= 10and forn≡2 (mod4),n≥18, the graphCt n has
(i) super(5n
2 + 2,0)-EAT labeling, and
(ii) super(3n
2 + 2,2)-EAT labeling,
for allt≡3 (mod4) and fort= 2andt= 6.
Theorem 24. [6, 21]Forn odd,n≥5, and for all possible values of t, the graph
Ct
n has a super (2n+ 2,1)-EAT labeling.
Theorem 25. [6, 21]Forneven,n≥6, and for t odd,t≥3, the graphCt n has a
super (2n+ 2,1)-EAT labeling.
Theorem 26. [6, 21]Forn≡0 (mod4),n≥4, and fort≡2 (mod4),t≥2, the graph Ct
n has a super(2n+ 2,1)-EAT labeling.
The paper [6] concludes with the following conjecture.
Conjecture 1. There is a super (2n+ 2,1)-EAT labeling ofCt n for
(i)n≡0 (mod4) and fort≡0 (mod4), and (ii)n≡2 (mod4)and fort even.
3.3. Friendship Graphs
Thefriendship graphFnis a set ofntriangles having a common central vertex, and otherwise disjoint. If the friendship graphFn,n≥1, is super (a, d)-EAT then, from Theorem 16, it follows that d <3. The following result characterizes (a, 1)-edge-antimagicness of friendship graphs.
From Lemma 1 and Theorem 17 we obtain
Theorem 27. [7] Forn∈ {1,3,4,5,7}, the friendship graph Fn has super (a,0)
-EAT and super (a,2)-EAT labelings.
Moreover, Baˇcaet al. [7] proved that
Theorem 28. [7]Every friendship graph Fn,n≥1, has super(a,1)-EAT labeling.
For further investigation, we propose the following open problem.
Open Problem 3. For the friendship graph Fn, determine if there is a super (a,0)-EAT or super(a,2)-EAT labeling, forn >7.
3.4. Fans
AfanFn, n≥2, is a graph obtained by joining all vertices of pathPn to a further vertex called the centre. It follows from Theorem 16 that if Fn, n≥2, is super (a, d)-EAT thend <3.
Lemma 2. [7]The fan Fn has(3,1)-EAV labeling if and only if2≤n≤6.
Figueroa-Centeno, Ichishima and Muntaner-Batle [12] showed that fanFn is super edge-magic (super (a,0)-EAT) if and only if 2≤ n ≤6. Then, in light of Lemma 2, we get the following
Theorem 29. [7] The fan Fn is super (a, d)-EAT total if 2 ≤ n ≤ 6 and d ∈ {0,1,2}.
Open Problem 4. For the fan Fn, determine if there is a super (a,1)-EAT or
super (a,2)-EAT labeling for n >6.
3.5. Wheels
AwheelWn,n≥3, is a graph obtained by joining all vertices of cycleCn to a further vertex called the centre. If wheel Wn, n ≥3, is super (a, d)-EAT then
d < 2. Enomoto, Llado, Nakamigawa and Ringel [11] proved that a wheel graph
Wn is not super edge-magic (super (a,0)-EAT). In [7] it is proved that:
Theorem 30. [7]The wheelWn has super(a, d)-EAT labeling if and only ifd= 1
u1 u2 u3 u4 un−1 un
v1 v2 v3 v4 vn−1 vn
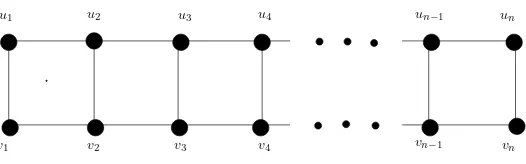
Figure 1: Ladder Ln=Pn×P2.
3.6. Ladders
Let Ln = Pn ×P2 be a ladder with V(Ln) = {ui, vi : 1 ≤ i ≤ n} and
E(Ln) = {uiui+1, vivi+1 : 1≤i ≤n−1} ∪ {uivi : 1≤i ≤n}. See Fig.1. From Theorem 16 it follows that if ladder Ln, n ≥ 2, is super (a, d)-EAT, then the parameterd≤7
3.
Figueroa-Centeno, Ichishima and Muntaner-Batle [12] proved that the ladder
Ln has¡n+52 ,1¢-edge-antimagic vertex labeling. Then, in the light of Theorem 17, the next theorem holds.
Theorem 31. [27] The ladder Ln =Pn×P2 is super (a, d)-EAT if nis odd and d∈ {0,1,2}.
Theorem 32. [27]The ladder Ln=Pn×P2 is super(a,1)-EAT ifnis even.
It is easily verified thatL2is not super (a,0)-EAT. Figueroa-Centeno, Ichishima
and Muntaner-Batle [12] have found super (a,0)-EAT labelings forn= 4 andn= 6. They suspect that a super (a,0)-EAT labeling might be found for larger even values ofn. Thus the following conjecture may hold.
Conjecture 2. The ladder Ln = Pn×P2 is super (a, d)-EAT if n is even and d∈ {0,2}.
Another variation of a ladder graph is specified as follows. A ladder L′
n,
n≥2, is a graph obtained by completing the ladderLn=Pn×P2 by edgesuivi+1
for 1≤i≤n−1.
Lemma 3. [27] The ladderL′n,n≥2, has (a,1)-EAV labeling.
Sugenget al. proved that
Theorem 33. [27]The ladderL′n,n≥2, has super(a, d)-EAT labeling if and only
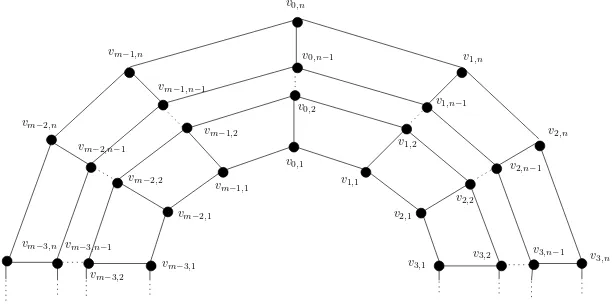
3.7. Generalized Prisms
The generalized prism can be defined as the cartesian productCm×Pn of a cycle on m vertices with a path on n vertices. Let V(Cm×Pn) = {vi,j : 0 ≤
Figure 2: Generalized prismCm×Pn.
Lemma 4. [27] The generalized prism Cm×Pn has (a,1)-EAV labeling if m is
odd,m≥3 andn≥2.
Theorem 34. [27]Ifmis odd,m≥3,n≥2andd∈ {0,1,2}, then the generalized prismCm×Pn has super(a, d)-EAT labeling.
Note that Figueroa-Centeno, Ichishima and Muntaner-Batle [12] have shown that the generalized prism Cm×Pn is super edge-magic (super (a,0)-EAT) ifm is odd and n ≥ 2. The next theorem shows super (a,1)-edge-antimagicness of
Cm×Pn, formeven.
Theorem 35. [27]Ifmis even,m≥4,n≥2, then the generalized prismCm×Pn
has super(a,1)-EAT labeling.
Lemma 5. [27]For prismCm×P2,m even,m≥4, there is no super (a,0)-EAT
labeling and no super (a,2)-EAT labeling.
Applying Theorems 34 and 35 and Lemma 5 for prismCm×P2, we obtain
the following
Theorem 36. [27] The prismCm×P2 has super(a, d)-EAT labeling if and only if
What can be said about super (a, d)-EAT labeling ofCm×Pn for the
remain-m can be obtained by completing the generalized prismCm×Pnby edgesvi,j+1vi+1,j for 0≤i≤m−1, 1≤j ≤n−1, with indicesi
Theorem 37. [27] The generalized antiprism An
m, m≥3,n≥2, is super (a, d)
-EAT if and only if d= 1.
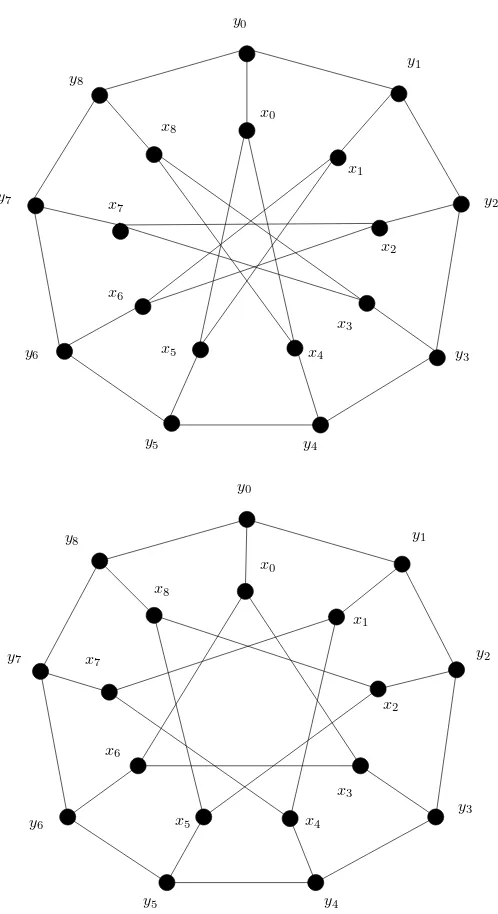
3.9. Generalized Petersen Graphs
Watkins [32] defined a generalized Petersen graph as follows: Thegeneralized Petersen graph P(n, m), n ≥ 3 and 1 ≤ m ≤ ⌊(n−1)/2⌋, consists of an outer
Figueroa-Centeno, Ichishima and Muntaner-Batle [12] and Fukuchi [13] con-structed (a,1)-EAV labelings for the generalized Petersen graphsP(n,1) andP(n,2) which, together with Theorem 17, give the following result.
Theorem 39. [5] Every generalized Petersen graph P(n, m), n odd, n ≥3, 1 ≤
Furthermore, Ngurah and Baskoro [22] proved
y0
y1
y2
y3
y4 y5
y6 y7
y8
x0
x1
x2
x3
x4 x8
x7
x6
x5 y0
y1
y2
y3
y4 y5
y6 y7
y8
x0
x1
x2
x3
x4 x5
x6 x7
x8
Baˇcaet al. [5] put forward the following
Conjecture 4. There is a super (a, d)-EAT labeling for the generalized Petersen graph P(n, m)fornodd,n≥9,d∈ {0,2} and3≤m≤ n−3
2 .
3.10. Complete Bipartite Graphs
Let Kn,n be the complete bipartite graph with V(Kn,n) = {xi : 1 ≤ i ≤
n} ∪ {yj : 1≤j ≤n}and E(Kn,n) ={xiyj : 1≤i≤n and 1 ≤j ≤n}. Using Theorem 16, if the complete bipartite graphKn,n,n≥4, is super (a, d)-EAT then
d <2, while ifKn,n, 2≤n≤3, is super (a, d)-EAT thend <3.
Theorem 42. [7]Every complete bipartite graphKn,n,n≥2, has super(a,1)-EAT
labeling.
Theorem 43. [11] A complete bipartite graph Km,n is super edge-magic (super (a,0)-EAT)if and only if m= 1or n= 1.
Theorem 43 asserts that, forn≥2, there is no super (a,0)-EAT labeling of
Kn,n. ForK2,2andK3,3it was proved that
Theorem 44. [7]For complete bipartite graphKn,n,2≤n≤3, there is no super (a,2)-EAT labeling.
From Theorems 42, 43 and 44, it follows that
Theorem 45. [7]The complete bipartite graphKn,n has super(a, d)-EAT labeling
if and only if d= 1andn≥2.
3.11. Complete Graphs
From Theorem 16, it follows that if the complete graphKn, n≥3, is super (a, d)-EAT thend≤2. In [7], Baˇcaet al. proved that
Theorem 46. [7]The complete graphKn,n≥3, has super(a, d)-EAT labeling if
and only if
(i)d= 0andn= 3, or (ii)d= 1 andn≥3, or (iii)d= 2andn= 3.
3.12. Stars
Letxo denote the central vertex of a starSn, n≥1, and xi, 1 ≤i ≤n, be its leaves. Theorem 16 provides an upper bound on the parameter d, i.e., if a star
Sn, n≥1, is super (a, d)-EAT thend≤3. In [28], Sugenget al. proved that
In light of the preceding lemma and Theorem 17, the next result follows immediately.
Theorem 47. [28] The star Sn, n≥ 1, has super (a,0)-EAT labeling and super (a,2)-EAT labeling.
Applying the construction of (a,1)-EAV labeling from Lemma 6 and com-pleting an edge labeling by a special procedure, it was shown that
Theorem 48. [28]The starSn,n≥1, has super(a,1)-EAT labeling.
To completely characterize super (a, d)-EAT labeling of Sn, it only remains to consider the cased= 3. In [28], it is proved that
Theorem 49. [28]For the starSn,n≥3, there is no super(a,3)-EAT labeling.
Thus from Lemma 6 and Theorems 47, 48 and 49, it follows that
Theorem 50. [28]The starSn has super(a, d)-EAT labeling if and only if
(i)d∈ {0,1,2} andn≥1, or (ii)d= 3 and1≤n≤2.
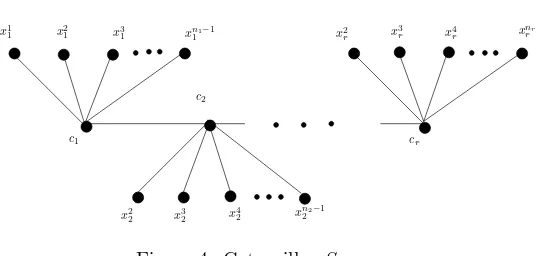
3.13. Caterpillars
Acaterpillaris a graph derived from a path by hanging any number of leaves from the vertices of the path. The caterpillar can be seen as a sequence of stars
S1∪S2∪. . .∪Sr, where eachSi is a star with central vertexci andni leaves for EAT thend≤3. Kotzig and Rosa [17] (see also Wallis [31]) proved that caterpillars have super (a,1)-EAV labeling. This result, together with Theorem 17, gives
Theorem 51. All caterpillars are super(a,0)-EAT and super(a,2)-EAT.
Theorem 52. [28]Every caterpillar with even number of vertices has super(a,1) -EAT labeling.
x11 x21 x31 xn1−1
2⌋denotes the greatest integer smaller than or equal to
r
2. The following theorems
give results for super (a,3)-edge-antimagicness of caterpillarSn1,n2,...,nr.
Theorem 54. [28]If ris even andN1=N2 or|N1−N2|= 1then the caterpillar Sn1,n2,...,nr has super(a,3)-EAT labeling.
Theorem 55. [28] If r is odd and N1 =N2 or N1=N2+ 1 then the caterpillar Sn1,n2,...,nr has super(a,3)-EAT labeling.
For the caterpillarSn1,n2,...,nr, r odd and N2 =N1+ 1, we have not found
any super (a,3)-EAT labeling. So, we propose the following open problem.
Open Problem 5. For the caterpillar Sn1,n2,...,nr, determine if there is a super (a,3)-EAT labeling, forr odd andN2=N1+ 1.
It is an easy consequence of the Theorem 54 that a double starSm,n,m, n≥2, can have super (a,3)-EAT labeling ifm=nor|m−n|= 1. For other cases, it was proved in [28] that
Theorem 56. [28] For the double star Sm,n, m6=n and|m−n| 6= 1, there is no
super (a,3)-EAT labeling.
Sugenget al. [28] suggest the following
Conjecture 5. For the caterpillarSn1,n2,...,nr,N16=N2 and|N1−N2| 6= 1, there
is no super(a,3)-EAT labeling.
4. CONCLUSION
Many researchers have studied edge-magic total and super edge-magic total labelings for many families of disconnected graphs (see the general survey of Gal-lian [14]) and obtained a wealth of results. We believe that these results can be extended to (a, d)-EAT or super (a, d)-EAT labelings.
Acknowledgement The authors would like to thank the referee for his valuable comments.
REFERENCES
1. B.D. Acharya and S.M. Hegde, “Strongly indexable graphs”, Discrete Math. 93 (1991), 275–299.
2. N. Alon, G. Kaplan, A. Lev, Y. Roditty and R. Yuster, “Dense graphs are
antimagic”,J. Graph Theory 47(2004), 297–309.
3. M. Baˇca, Y. Lin, M. Miller and R. Simanjuntak, “New constructions of magic
and antimagic graph labelings”,Utilitas Math. 60(2001), 229–239.
4. M. Baˇca, F. Bertault, J.A. MacDougall, M. Miller, R.Simanjuntak and Slamin, “Vertex-antimagic total labelings of graphs”,Discussiones Mathematicae Graph Theory 23(2003), 67–83.
5. M. Baˇca, E.T. Baskoro, R. Simanjuntak and K.A. Sugeng, “Super edge-antimagic
labelings of the generalized Petersen graphP¡n,n−1
2
¢
”,Utilitas Math., to appear. 6. M. Baˇca and M. Murugan, “Super edge-antimagic labeling of a cycle with a chord”,
Austral. J. Combin., to appear.
7. M. Baˇca, Y. Lin, M. Miller and M.Z. Youssef, “Edge-antimagic graphs”,Discrete Math., to appear.
8. M. Baˇca and M.Z. Youssef, “Further results on antimagic graph labelings”, preprint. 9. O. Berkman, M. Parnas and Y. Roditty, “All cycles are edge-magic”,Ars Combin.,
59(2001), 145–151.
10. R. Bodendiek and G. Walther, “Arithmetisch antimagische Graphen”,in Graphen-theorie III, K. Wagner and R. Bodendiek (eds.), BI-Wiss. Verl., Mannheim, 1993. 11. H. Enomoto, A.S. Llad´o, T. Nakamigawa and G. Ringel, “Super edge-magic
graphs”,SUT J. Math.34(1998), 105–109.
12. R.M. Figueroa-Centeno, R. Ichishima and F.A. Muntaner-Batle, “The place
of super edge-magic labelings among other classes of labelings”, Discrete Math. 231
(2001), 153–168.
13. Y. Fukuchi, “Edge-magic labelings of generalized Petersen graphP(n,2)”,Ars
Com-bin. 59(2001), 253–257.
14. J. Gallian, “A dynamic survey of graph labeling”,The Electronic Journal of Combi-natorics5(2005) #DS6.
16. N. Hartsfield and G. Ringel,Pearls in Graph Theory, Academic Press, Boston -San Diego - New York - London, 1990.
17. A. Kotzig and A. Rosa, “Magic valuations of finite graphs”,Canad. Math. Bull 13 (1970), 451–461.
18. Y. Lin, M. Miller, R.Simanjuntak and Slamin, “Magic and antimagic labelings of
wheels”,Proc. of Eleventh Australian Workshop of Combinatorial Algorithm, Hunter
Valley, Australia (2000), 67–74.
19. J.A. MacDougall, M. Miller, Slamin and W.D. Wallis, “Vertex-magic total
labelings of graphs”,Util. Math. 61(2002), 68–76.
20. J.A. MacDougall, M. Miller and W.D. Wallis, “Vertex magic total labelings of
wheels and related graphs”,Util. Math. 62(2002), 175–183.
21. J.M. MacDougall and W.D. Wallis, “Strong edge-magic labelling of a cycle with
a chord”,Austral. J. Combin. 28(2003), 245–255.
22. A.A.G. Ngurah and E.T. Baskoro, “On magic and antimagic total labeling of
generalized Petersen graph”,Utilitas Math. 63(2003), 97–107.
23. A.A.G. Ngurah, “On (a, b)-edge-antimagic total labeling of odd cycle”, MIHMI 9 (2003), 9–12.
24. G. Ringel and A.S. Llad´o, “Another tree conjecture”,Bull. ICA18(1996), 83–85.
25. R. Simanjuntak, F. Bertault and M. Miller, “Two new (a, d)-antimagic graph
labelings”,Proc. of Eleventh Australian Workshop of Combinatorial Algorithm, Hunter
Valley, Australia (2000), 179–189.
26. R. Simanjuntak and M. Miller, “Survey of (a, d)-antimagic graph labelings”,MIHMI
6(2000), 179–184.
27. K.A. Sugeng, M. Miller and M. Baˇca, “Super edge-antimagic total labelings”,
Utilitas Math., to appear.
28. K.A. Sugeng, M. Miller, Slamin and M. Baˇca, “(a, d)-edge-antimagic total
labelings of caterpillars”,Lecture Notes in Computer Science3330(2005), 169–180.
29. K.A. Sugeng, “Labelings of paths”, preprint.
30. W.D. Wallis, E.T. Baskoro, M. Miller and Slamin, “Edge-magic total labelings”,
Austral. J. Combin. 22(2000), 177–190.
31. W.D. Wallis,Magic Graphs, Birkh¨auser, Boston - Basel - Berlin, 2001.
32. M.E. Watkins, “A theorem on Tait colorings with an application to the generalized
Petersen graphs”,J. Combin. Theory 6(1969), 152–164.
M. Baˇca: Department of Applied Mathematics Technical University, Letn´a 9, 042 00 Koˇsice, Slovak Republic. E-mail: Martin.Baca@tuke.sk.
E.T. Baskoro: Department of Mathematics, Institut Teknologi Bandung, Bandung 40132, Indonesia. E-mail: ebaskoro@math.itb.ac.id.
M. Miller: School of Information Technology and Mathematical Sciences, University of Ballarat, Australia. E-mail: m.miller@ballarat.edu.au.
J. Ryan: School of Information Technology and Mathematical Sciences, University of Ballarat, Australia. E-mail: joe.ryan@ballarat.edu.au.
R. Simanjuntak: Department of Mathematics, Institut Teknologi Bandung, Bandung 40132, Indonesia. E-mail: rino@math.itb.ac.id.