BAB II TINJAUAN PUSTAKA

commit to user

6

BAB II

TINJAUAN PUSTAKA

2.1

Landasan Teori

Dasar-dasar teori yang digunakan sebagai landasan utama dalam penelitian ini,

antara lain sebagai berikut:

2.1.1

Polinomial

Persamaan polinomial (atau persamaan bilangan bulat rasional) diperoleh

apabila suatu polinomial dalam satu variabel ditetapkan sama dengan nol. Bentuk

standar suatu persamaan polinomial adalah sebagai berikut :

ܽ

_଴

ݔ

௡

൅ ܽ

_ଵ

ݔ

௡ିଵ

൅ ܽ

_ଶ

ݔ

௡ିଶ

൅ ǥ ൅ ܽ

_௡ିଶ

ݔ

ଶ

൅ ܽ

_௡ିଵ

ݔ ൅ ܽ

_௡

ൌ Ͳ

(2.1)

dimana a disebut sebagai koefisien polinomial yang merupakan bilangan riil dan n

merupakan derajat polinomial berupa bilangan bulat positif. Suku-suku pangkat

dari

x disusun dalam derajat menurun. Apabila tidak terdapat sebuah suku, maka

nilai koefisien dari suku tersebut adalah nol. Koefisien tidak memiliki faktor umum

kecuali ± 1, dan

ܽ

଴

് Ͳ

. Suku

ܽ

଴

ݔ

௡

disebut sebagai suku terdepan,

ܽ

௡

adalah suku

konstanta, dan

ܽ

_଴

disebut koefisien terdepan (Frank & Schmidt, 2004).

Persamaan polinomial dibedakan menjadi beberapa jenis. Polinomial dengan

koefisien dari variabel x berderajat tertinggi sama dengan 1 disebut sebagai

polinomial monoid. Bentuk polinomial monoid adalah sebagai berikut :

ݔ

௡

_{൅ ܽ}

ଵ

ݔ

௡ିଵ

൅ ܽ

ଶ

ݔ

௡ିଶ

൅ ڮ ൅ ܽ

௡

ൌ Ͳ

(2.2)

Berikut ini merupakan contoh-contoh polinomial berdasarkan derajat

polinomial :

a.

Polinomial kuadrat

Polinomial berderajat dua disebut juga sebagai polinomial kuadrat atau

quadratic polinomial. Polinomial ini memiliki pangkat tertinggi suku x adalah

2 (n = 2). Bentuk polinomial kuadrat adalah sebagai berikut (Harris & Stocker,

1998) :

݂ሺݔሻ ൌ ܽݔ

ଶ

_{൅ ܾݔ ൅ ܿ ൌ Ͳ}

_(2.3)

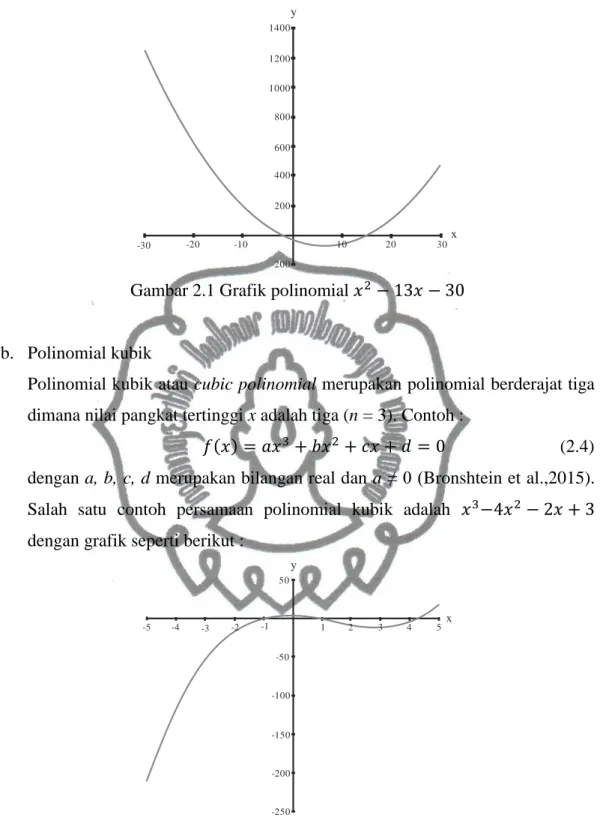
Contoh grafik polinomial derajat dua yaitu

ݔ

ଶ

_{െ ͳ͵ݔ െ ͵Ͳ}

_{terdapat pada}

commit to user

-30 -20 -10 10 20 30 x -200 200 400 600 800 1000 1200 1400 y

Gambar 2.1 Grafik polinomial

ݔ

ଶ

െ ͳ͵ݔ െ ͵Ͳ

b.

Polinomial kubik

Polinomial kubik atau cubic polinomial merupakan polinomial berderajat tiga

dimana nilai pangkat tertinggi x adalah tiga (n = 3). Contoh :

݂ሺݔሻ ൌ ܽݔ

ଷ

_{൅ ܾݔ}

ଶ

_{൅ ܿݔ ൅ ݀ ൌ Ͳ}

_(2.4)

dengan a, b, c, d merupakan bilangan real dan a

≠ 0 (

Bronshtein et al.,2015).

Salah satu contoh persamaan polinomial kubik adalah

ݔ

ଷ

െͶݔ

ଶ

െ ʹݔ ൅ ͵

dengan grafik seperti berikut :

-5 -4 -3 -2 -1 1 2 3 4 5 50 -50 -100 -150 -200 -250 y x

Gambar 2.2 Grafik Polinomial

ݔ

ଷ

െͶݔ

ଶ

െ ʹݔ ൅ ͵

c.

Polinomial kuartik

Polinomial kuartik atau quartic polinomial merupakan polinomial berderajat

empat dimana nilai pangkat tertinggi x adalah empat (n = 4). Contoh :

commit to user

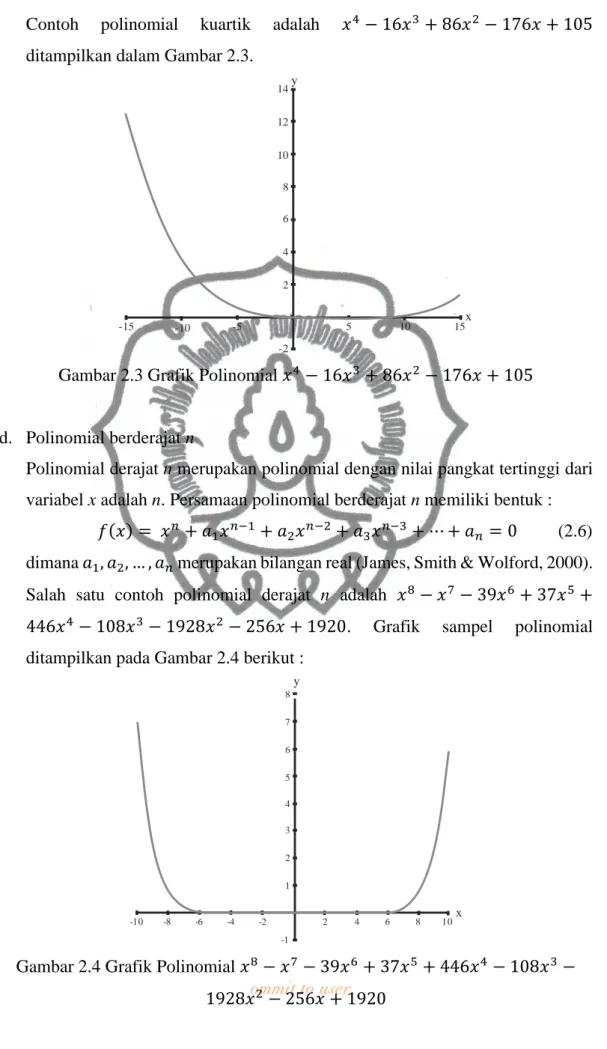
Contoh polinomial kuartik adalah

ݔ

ସ

െ ͳ͸ݔ

ଷ

൅ ͺ͸ݔ

ଶ

െ ͳ͹͸ݔ ൅ ͳͲͷ

ditampilkan dalam Gambar 2.3.

-15 -10 -5 5 10 15 14 8 6 4 2 -2 y x 10 12

Gambar 2.3 Grafik Polinomial

ݔ

ସ

_{െ ͳ͸ݔ}

ଷ

_{൅ ͺ͸ݔ}

ଶ

_{െ ͳ͹͸ݔ ൅ ͳͲͷ}

d.

Polinomial berderajat n

Polinomial derajat n merupakan polinomial dengan nilai pangkat tertinggi dari

variabel x adalah n. Persamaan polinomial berderajat n memiliki bentuk :

݂ሺݔሻ ൌ ݔ

௡

_{൅ ܽ}

ଵ

ݔ

௡ିଵ

൅ ܽ

ଶ

ݔ

௡ିଶ

൅ ܽ

ଷ

ݔ

௡ିଷ

൅ ڮ ൅ ܽ

௡

ൌ Ͳ

(2.6)

dimana

ܽ

ଵ

ǡ ܽ

ଶ

ǡ ǥ ǡ ܽ

௡

merupakan bilangan real (James, Smith & Wolford, 2000).

Salah satu contoh polinomial derajat n adalah

ݔ

଼

െ ݔ

଻

െ ͵ͻݔ

଺

൅ ͵͹ݔ

ହ

൅

ͶͶ͸ݔ

ସ

െ ͳͲͺݔ

ଷ

െ ͳͻʹͺݔ

ଶ

െ ʹͷ͸ݔ ൅ ͳͻʹͲ

. Grafik sampel polinomial

ditampilkan pada Gambar 2.4 berikut :

-10 -8 -6 -4 -2 2 4 6 8 10x 8 4 3 2 1 -1 y 5 7 6

Gambar 2.4 Grafik Polinomial

ݔ

଼

െ ݔ

଻

െ ͵ͻݔ

଺

൅ ͵͹ݔ

ହ

൅ ͶͶ͸ݔ

ସ

െ ͳͲͺݔ

ଷ

െ

commit to user

Sebuah persamaan polinomial f(x) = 0 akan memiliki akar polinomial r jika

dan hanya jika f(r) = 0. Dengan demikian, absis dari titik perpotongan dari grafik y

= f(x) dan sumbu x

adalah akar-akar dari f(x) = 0. Akar-akar sebuah persamaan

polinomial dapat berupa akar-akar kompleks, akar-akar irasional, dan akar-akar

rasional. Berikut ini merupakan penjelasannya :

a.

Apabila persamaan polinomial f(x) = 0 memiliki koefisiean real dan jika

bilangan kompleks a + bi adalah akar dari f(x) = 0, maka konjugasi (sekawan)

kompleks a – bi juga merupakan akar persamaan polinomial tersebut.

b.

Apabila bilangan irasional

ܽ ൅ ξܾ

merupakan salah satu akar dari sebuah

persamaan polinomial f(x) = 0 dimana a dan b adalah bilangan rasional, maka

irasional konjugasi

ܽ െ ξܾ

juga merupakan akar polinomial tersebut.

Berdasarkan bentuk polinomial, maka dapat diketahui bahwa (James, Smith

& Wolford, 2000) :

a.

Setiap persamaan polinomial f(x) memiliki sedikitnya satu akar, bilangan real

atau bilangan kompleks.

b.

Suatu persamaan polinomial derajat n mempunyai tepat n akar. Ke n akar ini

mungkin tidak semuanya berbeda.

c.

Terdapat setidaknya satu akar real jika n merupakan bilangan bulat ganjil

d.

Apabila f(x) = 0 merupakan persamaan polinomial, maka persamaan f(-x) = 0

mempunyai akar-akar negatif dari akar f(x) = 0. Misalnya, persamaan

ݔ

ଷ

൅

͵ݔ

ଶ

െ Ͷݔ െ ͳʹ ൌ Ͳ

mempunyai akar 2, -2, -3; maka persamaan

ݔ

ଷ

െ ͵ݔ

ଶ

െ

Ͷݔ ൅ ͳʹ ൌ Ͳ

adalah -2, 2, 3.

e.

Banyaknya akar positif dari persamaan polinomial f(x) = 0, dengan koefisien

real, sama dengan banyaknya variasi tanda dalam f(x) atau banyaknya bilangan

tersebut dikurangi suatu bilangan genap. Dikatakan variasi tanda yaitu apabila

suatu polinomial disusun dalam variabel dengan derajat menurun, dan terdapat

dua suku berurutan yang memiliki tanda berbeda. Dengan demikian, banyaknya

akar negatif dari f(x)

= 0 sama dengan banyaknya akar positif dari f(-x) =0

(Aturan tanda Descrates). Misalnya,

ݔ

ଷ

_{൅ ͵ݔ}

ଶ

_{െ Ͷݔ െ ͳʹ}

_{mempunyai satu}

variasi tanda, f(-x)

= 0 mempunyai satu akar positif dan f(x) = 0 mempunyai satu

akar negatif.

commit to user

g.

Akar kompleks terjadi pada pasangan konjugasi (pasangan sekawan)

Pencarian akar kompleks polinomial derajat dua dapat dilakukan dengan

menggunakan metode analitik seperti rumus kuadrat dan pembagian horner,

sedangkan untuk menyelesaikan polinomial berderajat tiga atau lebih dapat

dilakukan dengan metode numerik menggunakan algoritma-algoritma khusus

pencarian akar kompleks polinomial. Di bawah ini akan dijelaskan lebih detail

mengenai beberapa metode yang dapat digunakan untuk mencari akar kompleks

polinomial :

2.1.1.1

Rumus Kuadrat

Polinomial berderajat dua atau yang disebut juga persamaan kuadrat

memiliki bentuk seperti yang tertera pada Persamaan 2.3. Dalam penyelesaian

persamaan kuadrat dengan bentuk seperti Persamaan 2.3 memuat bentuk akar

ξܾ

ଶ

_{െ Ͷܽܿ}

_{, bentuk aljabar}

_ܾ

ଶ

_{െ Ͷܽܿ}

_{disebut sebagai diskriminan. Nilai}

diskriminan akan menentukan sifat dan banyaknya akar-akar polinomial yang

dihasilkan.

Persamaan 2.3 dapat dituliskan dalam bentuk lain seperti yang tertera pada

Persamaan 2.6.

ݔ

ଶ

൅ ݌ݔ ൅ ݍ ൌ Ͳ

(2.6)

dimana nilai p

didapat dari

௕

௔

dan nilai q didapat dari

௖

௔

(Harris & Stocker, 1998).

Nilai diskriminan untuk persamaan polinomial kuadrat monoid seperti yang tertera

pada Persamaan 2.6 dapat ditentukan berdasarkan rumus berikut :

ܦ ൌ ቀ

௣

ଶ

ቁ

ଶ

െ ݍ

(2.7)

Berdasarkan nilai diskrimanannya, polinomial kuadrat memiliki sifat-sifat

seperti di bawah ini :

1.

Apabila D > 0, maka

ݔ

ଶ

_{൅ ݌ݔ ൅ ݍ ൌ Ͳ}

_{memiliki dua akar real yang berbeda}

yaitu

ݔ

_ଵǡଶ

ൌ െ݌Ȁʹ േ ξܦ

.

2.

Apabila D = 0, maka

ݔ

ଶ

_{൅ ݌ݔ ൅ ݍ ൌ Ͳ}

_{memiliki dua akar real yang sama yaitu}

ݔ

_ଵǡଶ

ൌ െ݌Ȁʹ

.

3.

Apabila D < 0, maka

ݔ

ଶ

_{൅ ݌ݔ ൅ ݍ ൌ Ͳ}

_{memiliki pasangan penyelesaian yang}

commit to user

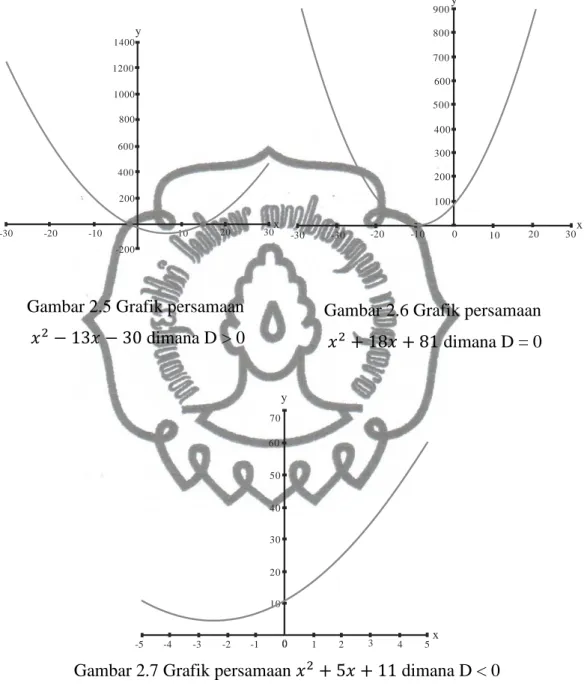
Berikut ini merupakan grafik masing-masing sifat polinomial berdasarkan

nilai diskriminan :

-30 -20 -10 10 20 30 1400 800 600 400 200 -200 y x 1000 1200

Gambar 2.5 Grafik persamaan

ݔ

ଶ

െ ͳ͵ݔ െ ͵Ͳ

dimana D > 0

-30 -30 -20 -10 10 20 30x 900 600 500 300 100 y 700 800 200 400 0

Gambar 2.6 Grafik persamaan

ݔ

ଶ

_{൅ ͳͺݔ ൅ ͺͳ}

_{dimana D = 0}

-5 -4 -3 -2 -1 0 1 2 3 4 5x 70 40 20 10 y 50 60 30 0

Gambar 2.7 Grafik persamaan

ݔ

ଶ

_{൅ ͷݔ ൅ ͳͳ}

_{dimana D < 0}

Penyelesaikan polinomial kuadrat seperti pada Persamaan 2.3 dapat

dilakukan dengan rumus kuadrat berikut :

ݔ

_ଵǡଶ

ൌ

ି௕േξ௕మିସ௔௖

ଶ௔

(2.8)

Berdasarkan rumus kuadrat di atas, maka penyelesaian bentuk standar

polinomial kuadrat yang tertera pada Persamaan 2.6 adalah sebagai berikut :

commit to user

ݔ

ଵǡଶ

ൌ െ

௣ ଶ

േ ටቀ

௣ ଶ

ቁ

ଶ

െ ݍ ൌ െ

௣ ଶ

േ ξܦ

(2.9)

Rumus ini berlaku tanpa ada batasan jika domain variabilitas merupakan

himpunan bilangan kompleks. Apabila dibatasi untuk bilangan real, maka D

≥

0

harus terpenuhi.

Dalam algoritma rumus kuadrat, input yang dimasukkan yaitu berupa

persamaan polinomial seperti pada Persamaan 2.3 dan output yang dihasilkan

berupa dua akar polinomial yaitu

ݔ

_ଵ

dan

ݔ

_ଶ

dimana kedua akar tersebut dapat

berupa bilangan real maupun bilangan kompleks. Langkah-langkah algoritma

rumus kuadrat dijabarkan dalam Alg 2.1 berikut :

1.

Menginputkan persamaan polinomial kuadrat seperti pada Persamaan 2.3.

2.

Mengubah bentuk polinomial menjadi polinomial monoid seperti pada

Persamaan 2.6 serta menentukan nilai p dan q dimana nilai p didapat dari

௕

௔

dan

nilai q didapat dari

௖

௔

.

3.

Menentukan nilai diskriminan menggunakan Persamaan 2.7.

4.

Menghitung akar kompleks polinomial dengan menggunakan Persamaan 2.9

sehingga dihasilkan

ݔ

ଵ

dan

ݔ

ଶ

.

2.1.1.2

Algoritma Cardano

Polinomial kubik merupakan suatu polinomial yang berderajat tiga dengan

bentuk umum seperti yang tertera dalam Persamaan 2.4, yaitu :

ܽݔ

ଷ

൅ ܾݔ

ଶ

൅ ܿݔ ൅ ݀ ൌ Ͳ

dimana a, b, c, d merupakan bilangan real dan a

≠ 0.

Apabila Persamaan 2.4 dibagi

dengan a akan menghasilkan bentuk polinomial monoid derajat tiga seperti berikut:

ݔ

ଷ

_{൅ ݎݔ}

ଶ

_{൅ ݏݔ ൅ ݐ ൌ Ͳ}

_(2.10)

dimana masing-masing nilai r, s, dan t didapat dari perhitungan berikut :

ݎ ൌ

௕ ௔

Ǣ ݏ ൌ

௖ ௔

Ǣ ݐ ൌ

ௗ ௔

Penyelesaian polinomial kubik dapat dilakukan dengan menggunakan

algoritma Cardano. Algoritma Cardano diterbitkan oleh Girolamo Cardano

(1501-1576) dalam tulisannya Ars Magna (Weisstein, n.d). Penyelesaian polinomial kubik

dengan bentuk seperti Persamaan 2.10 dapat diselesaikan dengan menggunakan

algoritma Cardano. Input algoritma Cardano adalah persamaan polinomial seperti

commit to user

yang tertera pada Persamaan 2.10 dan menghasilkan akar-akar polinomial (

ݔ

_ଵ

ǡ ݔ

_ଶ

dan

ݔ

_ଷ

) sebagai outputnya. Langkah-langkah algoritma Cardano dapat dijabarkan

dalam Alg 2.2 berikut (Harris dan Stocker, 1998) :

1.

Menginputkan polinomial yang akan dicari akarnya dalam bentuk Persamaan

2.10 dan menentukan nilai variabel r, s, dan t.

2.

Mensubtitusikan nilai y pada Persamaan 2.10 dimana nilai y didapat dari :

ݕ ൌ ݔ ൅

௥

ଷ

(2.11)

Subsitusi nilai y

akan mengasilkan persamaan tereduksi seperti yang tertera

pada persamaan berikut :

ݕ

ଷ

_{൅ ݌ݕ ൅ ݍ ൌ Ͳ}

_(2.12)

Kemudian menentukan nilai p dan q dengan menggunakan rumus berikut :

ݍ ൌ

ଶ௥య ଶ଻

െ

௥௦ ଷ

൅ ݐ

݌ ൌ

ଷ௦ି௥మ ଷ

3.

Menghitung nilai diskriminan persamaan tereduksi. Nilai diskriminan

direpresentasikan dalam variabel D berikut :

ܦ ൌ ቀ

௣ ଷ

ቁ

ଷ

൅ ቀ

௣ ଶ

ቁ

ଶ

(2.13)

4.

Menentukan cara penyelesaian polinomial kubik menggunakan algoritma

Cardano dan menghitung akar-akar polinomial (

ݔ

ଵ

ǡ ݔ

ଶ

dan

ݔ

ଷ

). Dalam algoritma

Cardano terdapat dua penyelesaian persamaan polinomial. Penyelesaian

tersebut ditentukan berdasarkan nilai diskriminan yang dihasilkan. Berdasarkan

nilai diskriminan, persamaan polinomial kubik memiliki sifat-sifat berikut

(Harris & Stocker, 1998) :

a.

Apabila nilai D > 0 akan menghasilkan satu akar bilangan riil dan dua akar

kompleks sekawan.

b.

Apabila

D = 0 akan menghasilkan tiga akar bilangan riil dengan dua akar

sama (a double solution).

c.

Apabila D < 0 akan menghasilkan tiga akar riil yang berbeda. Pada kondisi

D < 0 disebut sebagai

irreducible case

dimana persamaan polinomial tidak

dapat tereduksi sehingga penyelesaian diselesaikan dengan menggunakan

aturan trigonometri.

commit to user

Penyelesaian polinomial kubik dengan D

≥ 0 dapat dilakukan dengan

menggunakan langkah berikut :

a.

Menghitung nilai u dan v yang didapat dari :

ݑ ൌ ටሺെ

య ௤_ଶ

൅ ξܦ

(2.14)

ݒ ൌ ටሺെ

య ௤_ଶ

െ ξܦ

(2.15)

b.

Menghitung nilai akar polinomial kubik dengan menggunakan persamaan

berikut :

ݔ

_ଵ

ൌ െ

௥ ଷ

൅ ݑ ൅ ݒ

(2.16)

ݔ

ଶǡଷ

ൌ െ

௥ ଷ

െ

௨ା௩ ଶ

േ ξ͵

௨ି௩ ଶ

݅

(2.17)

dimana nilai

݅ ൌ ξെͳ

.

Pada kasus

irreducibe case

dimana nilai D < 0 diterapkan rumus berikut untuk

mencari akar-akar polinomialnya :

ܿ݋ݏ߮ ൌ െ

௤

ଶඥሺȁ௣ȁ ଷΤ ሻయ

(2.18)

sehingga solusi dari persamaan tereduksi Persamaan 2.12 adalah sebagai

berikut :

ݔ

_ଵ

ൌ െ

௥ ଷ

൅ ʹ ή ට

ȁ௣ȁ ଷ

…‘• ቀ

ఝ ଷ

ቁ

(2.19)

ݔ

_ଶ

ൌ െ

௥ ଷ

െ ʹ ή ට

ȁ௣ȁ ଷ

…‘• ቀ

ఝିగ ଷ

ቁ

(2.20)

ݔ

_ଷ

ൌ െ

௥ ଷ

െ ʹ ή ට

ȁ௣ȁ ଷ

…‘• ቀ

ఝାగ ଷ

ቁ

(2.21)

2.1.1.3

Algoritma Viete’s

Penyelesaian polinomial kubik dapat juga dilakukan dengan menggunakan

algoritma Viete’s. Algoritma Viete’s merupakan metode yang diusulkan oleh

matematikawan Perancis, Farnciscus Vieta (1540-

1603). Algoritma Viete’s ini

digunakan untuk mencari akar polinomial derajat tiga bentuk tereduksi seperti yang

tertera pada Persamaan 2.12.

commit to user

Dikutip dari Tutorial Exercises for Solving Cubic Equations yang ditulis

oleh John H. Mathews yang diadopsi dari Henderson (1930), pencarian akar

polinomial dilakukan menggunakan nilai kesatuan akar kubik seperti :

߱

ଵ

ൌ

ିଵା௜ξଷ

ଶ

(2.22)

߱

_ଶ

ൌ

ିଵି௜ξଷ

ଶ

(2.23)

Input algoritma Viete’s merupakan persamaan kubik monoid seperti yang

tertera pada Persamaan 2.10 dan menghasilkan tiga akar polinomial

ሺݔ

ଵ

ǡ ݔ

ଶ

dan

ݔ

ଷ

ሻ

sebagai output. Berikut ini merupakan langkah-

langkah algoritma Viete’s yang

tertuang dalam Alg 2.3 :

1.

Menginputkan persamaan polinomial kubik monoid (Persamaan 2.10) dan

mengubahnya menjadi persamaan tereduksi (Persamaan 2.12) dengan

mensubsitusikan Persamaan 2.11 ke Persamaan 2.10. Kemudian menentukan

nilai p dan q.

2.

Menghitung nilai variabel c

ܿ ൌ െ

௤ ଶ

൅ ට

௣య ଶ଻

൅

௤మ ସ

(2.24)

3.

Menghitung nilai r

ݎ ൌ ܿ

భయ

_(2.25)

4.

Menghitung nilai d

݀ ൌ െ

௣ ଷ

(2.26)

5.

Menentukan akar-akar polinomial

ሺݔ

_ଵ

ǡ ݔ

_ଶ

dan

ݔ

_ଷ

ሻ

dengan menggunakan

Persamaan 2.22 dan Persamaan 2.23 dalam perhitungan akarnya. Berikut

merupakan detail perhitungan pancarian akar polinomial kubik :

ݔ

_ଵ

ൌ ݎ ൅

ௗ ௥

(2.27)

ݔ

ଶ

ൌ ߱

ଵ

ݎ ൅

ௗ ఠభ௥

(2.28)

ݔ

ଷ

ൌ ߱

ଶ

ݎ ൅

ௗ ఠమ௥

(2.29)

2.1.1.4

Algoritma Bairstow

Algoritma Bairstow merupakan metode iteratif yang dapat digunakan untuk

mencari akar polinomial berderajat n. Algoritma melibatkan pencarian faktor

commit to user

kuadrat yaitu

݂ሺݔሻ ൌ ݔ

ଶ

൅ ݑݔ ൅ ݒ

dalam polinomial. Perhitungan mulai dilakukan

dengan menentukan nilai u

dan

v

yang tepat, kemudian proses iterasi akan

terkonvergen pada nilai u dan u yang tepat dimana dengan kedua nilai tersebut yang

membentuk faktor kuadrat akan menghasilkan dua akar polinomial.

Algoritma Bairstow menggunakan persamaan polinomial derajat n dengan

bentuk monoid sebagai input dan akar-akar polinomial

ሺݔ

_ଵ

ǡ ݔ

_ଶ

,

ݔ

_ଷ

ǡ ǥ ǡ ݔ

_௡

ሻ

sebagai

output. Langkah-langkah dalam algoritma Bairstow untuk mencari akar kompleks

polinomial (James, Smith & Wolford, 2000) dijabarkan dalam Alg 2.4 berikut:

1.

Menentukan nilai awal u dan v. Nilai u dan v

yang dipilih harus tepat. Apabila

nilai

u

dan v

tidak tepat, maka ketika iterasi tidak menghasilkan nilai u

dan v

yang konvergen. Untuk menentukan nilai u dan v dapat dilakukan dengan cara

berikut ini :

ݑ ൌ

௔೙షభ

௔೙షమ

݀ܽ݊ݒ ൌ

௔೙

௔೙షమ

(2.30)

dimana a merupakan koefisien dari polinomial derajat n. Namun, pada beberapa

kasus, kebanyakan nilai yang digunakan yaitu

ݑ

_௜

ൌ ݒ

_௜

ൌ Ͳ

2.

Menghitung nilai

ܾ

ଵ

ǡ ܾ

ଶ

ǡ ǥ ǡ ܾ

௡

dengan rumus berikut :

ܾ

_௞

ൌ ܽ

_௞

െ ܾ

_௞ିଵ

ݑ െ ܾ

_௞ିଶ

ݒ

(2.31)

dengan nilai k = 2, 3, ..., n.

Berikut ini merupakan detail perhitungan nilai

ܾ

_ଵ

ǡ ܾ

_ଶ

ǡ ǥ ǡ ܾ

_௡

dengan pembagian sintesis :

ܾ

_଴

ൌ ͳ

ܾ

ଵ

ൌ ܽ

ଵ

െ ݑ

ܾ

_ଶ

ൌ ܽ

_ଶ

െ ܾ

_ଵ

ݑ െ ݒ

ܾ

_ଷ

ൌ ܽ

_ଷ

െ ܾ

_ଶ

ݑ െ ܾ

_ଵ

ݒ

ܾ

ସ

ൌ ܽ

ସ

െ ܾ

ଷ

ݑ െ ܾ

ଶ

ݒ

ڭ

ܾ

௞

ൌ ܽ

௞

െ ܾ

௞ିଵ

ݑ െ ܾ

௞ିଶ

ݒ

ڭ

ܾ

_௡ିଵ

ൌ ܽ

_௡ିଵ

െ ܾ

_௡ିଶ

ݑ െ ܾ

_௡ିଷ

ݒ

ܾ

௡

ൌ ܽ

௡

െ ܾ

௡ିଵ

ݑ െ ܾ

௡ିଶ

ݒ

Dan sisanya =

ሺݔ ൅ ݑሻܾ

_௡ିଵ

൅ ܾ

_௡

commit to user

Konsep dasar algoritma Bairstow adalah untuk mengurangi nilai sisa yang

dihasilkan agar mendekati nol sehingga dapat menghasilkan pendekatan akar

yang memuaskan. Dengan demikian nilai

ܾ

_௡

dan

ܾ

_௡ିଵ

harus mendekati nol.

3.

Dari nilai u, v, dan b, langkah yang harus dilakukan selanjutnya adalah

menghitung nilai

ܿ

_ଵ

ǡ ܿ

_ଶ

ǡ ǥ ǡ ܿ

_௡ିଵ

dengan rumus berikut :

ܿ

௞

ൌ ܾ

௞

െ ܿ

௞ିଵ

ݑ െ ܿ

௞ିଶ

ݒ

(2.32)

dengan nilai k = 2, 3, ..., n-1. Dimana

ܿ

_଴

ൌ ͳ

dan

ܿ

_ଵ

ൌ ܾ

_ଵ

െ ݑ

.

4.

Nilai

οݑ

dan

οݒ

didapat dengan menghitung persamaan berikut:

οݑ ൌ

ฬ ௕೙ ௖೙షమ ௕೙షభ ௖೙షయฬ ቚ௖_௖೙షభ ௖೙షమ ೙షమ ௖೙షయቚ

(2.33)

οݒ ൌ

ฬ ௖೙షభ ௕೙ ௖೙షమ ௕೙షభฬ ቚ௖_௖೙షభ ௖೙షమ ೙షమ ௖೙షయቚ

(2.34)

5.

Menghitung nilai u dan v untuk perhitungan iterasi berikutnya.

ݑ

_௜ାଵ

ൌ ݑ

_௜

൅ οݑ

_௜

(2.35)

ݒ

௜ାଵ

ൌ ݒ ൅ οݒ

௜

(2.36)

6.

Mengulang langkah poin 2 hingga didapat nilai

οݑ

dan

οݒ

mendekati nol dan

memenuhi

nilai ε sebagai berikut:

ȁοݑ

_௜ାଵ

ȁ ൅ ȁοݒ

_௜ାଵ

ȁ ൏ ߝ

(2.37)

7.

Apabila

οݑ

dan

οݒ

mendekati telah mendekati nol dan Persamaan 2.37 telah

terpenuhi, maka nilai u

dan

v yang telah didapat kemudian disubtitusikan ke

dalam persamaan berikut:

ሺݔଶ൅ ݑݔ ൅ ݒሻሺݔ௡ିଶ൅ ܾଵݔ௡ିଷ൅ ܾଶݔ௡ିସ൅ ڮ ൅ ܾ௡ିଷݔ ൅ ܾ௡ିଶሻ ൅ ݎ݁݉ܽ݅݊݀݁ݎ

(2.38)

Menghitung akar dari persamaan kuadrat yang dihasilkan menggunakan rumus

kuadrat seperti yang tertera pada Persamaan 2.8, dengan nilai b merupakan nilai

dari u, nilai

a sama dengan nol, dan nilai c sama dengan v. Dengan demikian,

maka akar 1 dan akar 2 dari persamaan polinomial telah didapat.

8.

Perhitungan akar berikutnya dilakukan dengan mengulangi langkah 1 untuk

persamaan

ሺݔ

௡ିଶ

_{൅ ܾ}

ଵ

ݔ

௡ିଷ

൅ ܾ

ଶ

ݔ

௡ିସ

൅ ڮ ൅ ܾ

௡ିଷ

ݔ ൅ ܾ

௡ିଶ

ሻ

dan sisa yang

dihasilkan pada nilai akhir merupakan nilai b.

commit to user

2.1.1.5

Revisi Algoritma Bairstow

Polinomial berderajat n pada algoritma Bairstow dapat dibagi dengan faktor

kuadrat

ݔ

ଶ

൅ ݑݔ ൅ ݒ

untuk mendapatkan persamaan polinomial berderajat n-2

ditambah sisa. Sisa persamaan tersebut memiliki bentuk :

ሺݔ ൅ ݑሻܾ

௡ିଵ

൅ ܾ

௡

Apabila u dan

v memiliki nilai dimana faktor kuadrat memuat dua akar dari

polinomial derajat n, maka sisanya harus bernilai nol. Nilai u

dan

v

ditemukan

dimana nilai

ܾ

_௡

dan

ܾ

_௡ିଵ

mendekati nol. Berikut ini merupakan pendekatan

alternatif untuk menunjukkan sisa yaitu :

ݔܾ

_௡ିଵ

൅ ሺݑܾ

_௡ିଵ

൅ ܾ

_௡

ሻ ൌ ݎݔ ൅ ݏ

dan mencari nilai u

dan v dimana nilai r dan

s harus mendekati nol. Hal ini dapat

dilakukan dengan menerapkan

ݎሺݑ ൅ οݑǡ ݒ ൅ οݒሻ

dan

ݏሺݑ ൅ οݑǡ ݒ ൅ οݒሻ

dalam

Taylor series. Nilai

οݑ

dan

οݒ

ditentukan dimana niali r

dan

s

mendekati nol,

sehingga :

ݎሺݑ ൅ οݑǡ ݒ ൅ οݒሻ ൌ ܾ

_௡ିଵ

ሺݑ ൅ οݑǡ ݒ ൅ οݒሻ

ൌ Ͳ ؆ ܾ

_௡ିଵ

൅

డ௕೙షభ డ௨

οݑ ൅

డ௕೙షభ డ௩

οݒ

(2.39)

ݏሺݑ ൅ οݑǡ ݒ ൅ οݒሻ ൌ ݑܾ

௡ିଵ

ሺݑ ൅ οݑǡ ݒ ൅ οݒሻ ൅ ܾ

௡

ሺݑ ൅ οݑǡ ݒ ൅ οݒሻ

ൌ Ͳ ؆ ݑܾ

_௡ିଵ

൅ ܾ

_௡

൅

డሾ௨௕೙షభା௕೙ሿ డ௨

οݑ ൅

డሾ௨௕೙షభା௕೙ሿ డ௩

οݒ

(2.40)

Dari persamaan berikut :

డ௕೙

డ௨

ൌ െܾ

௡ିଵ

൅ ܿ

௡ିଶ

ݑ ൅ ܿ

௡ିଷ

ݒ ൌ െܿ

௡ିଵ

dan

߲ܾ

_௡

߲ݒ

ൌ െܾ

௡ିଶ

൅ ܿ

௡ିଷ

ݑ ൅ ܿ

௡ିସ

ݒ ൌ െܿ

௡ିଶ

maka, Persamaan 2.39 menjadi :

ܾ

_௡ିଵ

ൌ ܿ

_௡ିଶ

οݑ ൅ ܿ

_௡ିଷ

οݒ

(2.41)

Sedangkan persamaan 2.40 dapat ditulis sebagai berikut :

Ͳ ൌ ݑܾ

௡ିଵ

൅ ܾ

௡

൅ ቂݑ

డ௕೙షభ డ௨

൅ ܾ

௡ିଵ

൅

డ௕೙ డ௨

ቃ οݑ ൅ ቂݑ

డ௕೙షభ డ௩

൅

డ௕೙ డ௩

ቃ οݒ

(2.42)

Mengubah sebagian turunan dengan nilai c yang berkaitan dengan persamaan di

atas, serta mengubah

ݑܾ

௡ିଵ

dengan

ݑሾܿ

௡ିଶ

οݑ ൅ ܿ

௡ିଷ

οݒሿ

menggunakan

Persamaan 2.41, maka didapat :

commit to user

Solusi untuk

οݑ

dan

οݒ

dari Persamaan 2.41 dan 2.43 pada algoritma Revisi

Bairstow adalah sebagai berikut (James, Smith & Wolford, 2000) :

οݑ ൌ

ฬ ௕೙షభ ௖೙షయ ௕೙ ௖೙షమฬ ቚ_ሺ௖ ௖೙షమ ௖೙షయ ೙షభି௕೙షభሻ ௖೙షమቚ

(2.44)

οݒ ൌ

ฬ ௖೙షమ ௕೙షభ ሺ௖೙షభି௕೙షభሻ ௕೙ ฬ ቚ_ሺ௖ ௖೙షమ ௖೙షయ ೙షభି௕೙షభሻ ௖೙షమቚ

(2.45)

Revisi Algoritma Bairstow menggunakan persamaan polinomial derajat n

dengan bentuk monoid sebagai input dan akar akar polinomial

ሺݔ

_ଵ

ǡ ݔ

_ଶ

,

ݔ

_ଷ

ǡ ǥ ǡ ݔ

_௡

ሻ

sebagai output. Berdasarkan penjelasan di atas, maka langkah-langkah dalam revisi

algoritma Bairstow (James, Smith & Wolford, 2000) dijabarkan dalam Alg 2.5

berikut:

1.

Menentukan nilai awal u dan

v. Nilai u dan

v yang dipilih harus tepat. Nilai u

dan v dapat dilakukan dengan menggunakan Persamaan 2.30 atau menggunakan

nilai yang banyak digunakan dalam beberapa kasus yaitu

ݑ

௜

ൌ ݒ

௜

ൌ Ͳ

2.

Menghitung nilai

ܾ

_ଵ

ǡ ܾ

_ଶ

ǡ ǥ ǡ ܾ

_௡

menggunakan rumus Persamaan 2.31 serta

menghitung nilai

ܿ

_ଵ

ǡ ܿ

_ଶ

ǡ ǥ ǡ ܿ

_௡ିଵ

menggunakan Persamaan 2.32.

3.

Menentukan nilai

οݑ

dan

οݒ

dengan menghitung Persamaan 2.44 dan

Persamaan 2.45.

4.

Menghitung nilai u

dan

v

untuk perhitungan iterasi berikutnya dengan

Persamaan 2.35 dan Persamaan 2.36 seperti berikut :

ݑ

௜ାଵ

ൌ ݑ

௜

൅ οݑ

௜

ݒ

_௜ାଵ

ൌ ݒ ൅ οݒ

_௜

5.

Mengulang langkah poin 2 hingga didapat nilai

οݑ

dan

οݒ

mendekati nol dan

memenuhi Persamaan 2.37 yaitu

ȁοݑ

_௜ାଵ

ȁ ൅ ȁοݒ

_௜ାଵ

ȁ ൏ ߝ

.

6.

Apabila

οݑ

dan

οݒ

mendekati telah mendekati nol dan Persamaan 2.37 telah

terpenuhi, maka nilai u

dan

v yang telah didapat kemudian disubtitusikan ke

dalam Persamaan 2.38. Kemudian menghitung akar dari persamaan kuadrat

yang dihasilkan menggunakan rumus kuadrat seperti yang tertera pada

Persamaan 2.8, dengan nilai b merupakan nilai dari u, nilai a sama dengan nol,

dan nilai c sama dengan v

sehingga akar 1 dan akar 2 dari persamaan polinomial

commit to user

7.

Perhitungan akar berikutnya dilakukan dengan mengulangi langkah 1 untuk

persamaan

ሺݔ

௡ିଶ

_{൅ ܾ}

ଵ

ݔ

௡ିଷ

൅ ܾ

ଶ

ݔ

௡ିସ

൅ ڮ ൅ ܾ

௡ିଷ

ݔ ൅ ܾ

௡ିଶ

ሻ

dan sisa yang

dihasilkan pada nilai akhir merupakan nilai b.

2.1.1.6

Algoritma Muller

Algoritma Muller merupakan algoritma pencarian akar kompleks

persamaan polinomial derajat n

yang diusulkan oleh Muller.

Algoritma Muller

merupakan generalisasi dari metode secant tetapi dalam penerapannya

menggunakan tiga poin interpolasi kuadrat (Press et al., 1989). Algoritma Muller

dapat mencari pasangan akar kompleks dalam menyelesaikan persamaan kuadrat.

Metode iterasi ini konvergen di dekat suatu akar, tidak memerlukan pengevaluasian

turunan fungsinya, dan memperoleh akar-akar nyata maupun kompleks meskipun

akar-akar tersebut tidak sederhana. Selain itu, metode ini bersifat global sehingga

tidak perlu menyediakan suatu pendekatan permulaan (Conte & Boor, 1992).

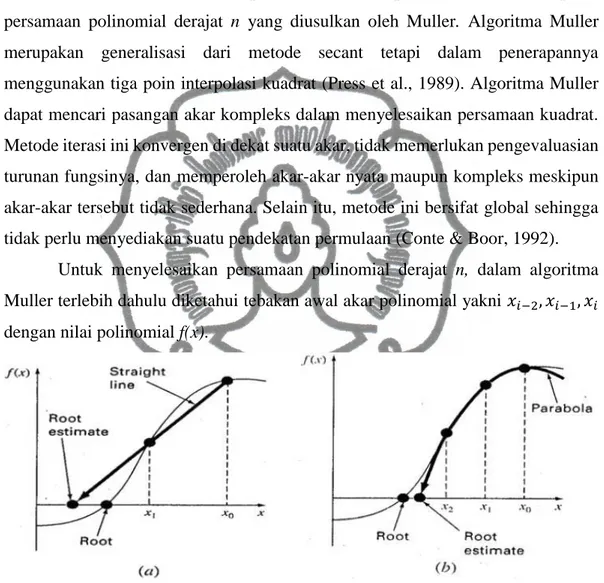
Untuk menyelesaikan persamaan polinomial derajat n,

dalam algoritma

Muller terlebih dahulu diketahui tebakan awal akar polinomial yakni

ݔ

௜ିଶ

ǡ ݔ

௜ିଵ

ǡ ݔ

௜

dengan nilai polinomial f(x).

Gambar 2.8 Grafik perbandingan letak akar antara Metode Secant (a)

dan Metode Muller (b)

Input algoritma Muller merupakan persamaan polinomial derajat n

yang

berupa polinomial monoid. Setelah diproses, algoritma Muller akan menghasilkan

output berupa nilai akar-akar polinomial

ሺݔ

_ଵ

ǡ ݔ

_ଶ

,

ݔ

_ଷ

ǡ ǥ ǡ ݔ

_௡

ሻ

. Algoritma Muller dapat

diterapkan dengan langkah-langkah yang tertuang dalam Alg 2.6 berikut ini (Butt,

2009) :

commit to user

1.

Menentukkan tiga poin tebakan awal yaitu

ݔ

_଴

ǡ ݔ

_ଵ

ǡ ݔ

_ଶ

dan jumlah maksimal

iterasi yaitu

ܯܽݔܫ

2.

Menghitung nilai

݄

଴

ǡ ݄

ଵ

ǡ ݄

ଶ

dimana :

݄

_଴

ൌ ݔ

_଴

െ ݔ

_ଶ

(2.46)

݄

_ଵ

ൌ ݔ

_ଵ

െ ݔ

_ଶ

(2.47)

݄

ଶ

ൌ ݄

଴

כ ݄

ଵ

כ ሺ݄

଴

െ ݄

ଵ

ሻ

(2.48)

3.

Menghitung nilai persamaan fungsi dari masing-masing tebakan awal yaitu

݂ሺݔ

_଴

ሻǡ ݂ሺݔ

_ଵ

ሻǡ ݂ሺݔ

_ଶ

ሻ

.

4.

Menghitung nilai koefisien a, b, c menggunakan perhitungan berikut :

ܽ ൌ

௛భ൫௙ሺ௫బሻି௙ሺ௫మሻ൯ି௛బ൫௙ሺ௫భሻି௙ሺ௫మሻ൯ ௛మ

(2.49)

ܾ ൌ

௛బ మ_൫௙ሺ௫ భሻି௙ሺ௫మሻ൯ି௛భమ൫௙ሺ௫బሻି௙ሺ௫మሻ൯ ௛మ

(2.50)

ܿ ൌ ݂ሺݔ

ଶ

ሻ

(2.51)

5.

Menghitung nilai diskriminan dari perhitungan di atas

ܦ ൌ ξܾ

ଶ

_{െ Ͷܽܿ}

_(2.52)

6.

Menentukan nilai akar polinomial untuk menghasilkan pendekatan baru dari

f(x). Maka, digunakan persamaan berikut :

ݔ

ଷ

ൌ ݔ

ଶ

െ

ଶ௖

௕േ஽

(2.53)

Dimana tanda pada penyebut dipilih untuk mendapatkan nilai absolut atau

modulus yang terbesar mungkin. Dengan demikian, apabila b > 0 dipilih tanda

“+”, sedangkan apabila

b

< 0, maka dipilih tanda “

-

”, dan apabila

b = 0, maka

pilih salah satu tanda “+” atau “

-

”.

Setelah pendekatan baru ditemukan,

ݔ

ଷ

,

maka poin sebelumnya yaitu

ݔ

_଴

diabaikan sehingga tersisa tiga tebakan akar

yaitu

ݔ

_ଵ

ǡ ݔ

_ଶ

ǡ

dan

ݔ

_ଷ

yang kemudian digunakan dalam proses selanjutnya.

7.

Menghitung

ݕ ൌ

dan melakukan pengecekkan terhadap nilai y. Apabila kondisi

tersebut belum terpenuhi

dimana y > ε

, maka dilakukan perulangan langkah 2

hingga 6 sampai mendapatkan nilai

akar yang konvergen dimana y < ε.

Apabila y < ε, maka iterasi dihentikan. Nilai akar polinomial adalah

ݔ

_ଷ

.

Polinomial direduksi dengan cara membagi persamaan polinomial dengan akar

yang ditemukan. Pencarian akar selanjutnya dilakukan dengan menggunakan

persamaan polinomial hasil reduksi kemudian mengulang langkah 1 hingga 7.

commit to user

2.1.2

Bilangan Kompleks

Penyelesaian persamaan polinomial derajat n terkadang menghasilkan akar

kompleks. Akar kompleks disajikan dalam bentuk bilangan kompleks. Bilangan

kompleks dihasilkan dari akar kuadrat suatu bilangan negatif (yaitu

ξെͳǡ ξെͷ

)

yang disebut bilangan imajiner murni. Menurut definisi,

ξെͷ ൌ ξͷ ή ξെͳ

, untuk

menyatakan persamaan ersebut akan lebih mudah menggunakan simbol i dimana

݅ ൌ ξെͳ

, sehingga dapat ditulis

ξെͷ ൌ ݅ξͷ

sebagai bentuk standar bilangan ini.

Bentuk standar bilangan kompleks adalah a + bi dimana a dan b merupakan

bilangan riil. Suku pertama a disebut bagian riil, sedangkan suku kedua bi disebut

sebagai bagian imajiner murni dari bilangan kompleks. Dua bilangan kompleks a

+ bi

dan

c + di dikatakan sama jika a = c dan b = d. Konjugasi (conjugate) dari

bilangan kompleks a +

bi adalah bilangan kompleks a

–

bi (Frank and Schmidt,

2004). Berikut ini merupakan operasi-operasi aljabar bilangan kompleks :

a.

Penambahan, dilakukan dengan menambahkan bagian riil dan menambahkan

bagian imajiner murni, contoh :

ሺʹ ൅ ͵݅ሻ ൅ ሺͶ െ ͷ݅ሻ ൌ ሺʹ ൅ Ͷሻ ൅ ሺ͵ െ ͷሻ݅ ൌ ͸ െ ʹ݅

b.

Pengurangan, dilakukan dengan mengurangi bagian riil dan mengurangi bagian

imajiner murni, contoh :

ሺʹ ൅ ͵݅ሻ െ ሺͶ െ ͷ݅ሻ ൌ ሺʹ െ Ͷሻ ൅ ൫͵ െ ሺെͷሻ൯݅ ൌ െʹ ൅ ͺ݅

c.

Perkalian, dilakukan seperti pada bilangan binomial biasa dan mengganti

݅

ଶ

dengan -1, contoh :

ሺʹ ൅ ͵݅ሻሺͶ െ ͷ݅ሻ ൌ ͺ ൅ ʹ݅ െ ͳͷ݅

ଶ

_{ൌ ͺ ൅ ʹ݅ െ ͳͷሺെͳሻ ൌ ʹ͵ ൅ ʹ݅}

d.

Pembagian, dilakukan dengan mengalikan pembilang maupun penyebut dengan

konjugasi dari penyebut, contoh :

ʹ ൅ ͵݅

Ͷ െ ͷ݅

ൌ

ሺʹ ൅ ͵݅ሻሺͶ ൅ ͷ݅ሻ

ሺͶ െ ͷ݅ሻሺͶ ൅ ͷ݅ሻ

ൌ

ሺͺ െ ͳͷሻ ൅ ሺͳͲ ൅ ͳʹሻ݅

ͳ͸ ൅ ʹͷ

ൌ

͹

Ͷͳ

൅

ʹʹ

Ͷͳ

݅

Jika

z

=

a

+

bi

sebarang bilangan kompleks, maka sekawan (konjugasi) z

dinyatakan oleh

ݖҧ

(dibaca “z garis”), didefinisikan oleh :

ݖҧ ൌ ܽ െ ܾ݅

(2.54)

ݖҧ

diperoleh dengan membalik tanda bagian imajiner z. Secara geometris,

ݖҧ

commit to user

Gambar 2.2 Sekawan bilangan kompleks z

Jika bilangan kompleks z dipandang sebagai vektor di R

2

, maka norma atau

panjang vektor disebut modulus (atau nilai mutlak) z. Modulus bilangan kompleks

z = a+bi, dinyatakan oleh |z|, didefinisikan sebagai berikut (Anton, 1987):

ȁݖȁ ൌ ξܽ

ଶ

_{൅ ܾ}

ଶ

_(2.55)

Apabila z = a+bi direpresentasikan dalam bentuk x, y, maka akan menjadi z

= x+yi. Jika z = x+yi adalah bilangan kompleks tak nol, r = |z|, dan

θ merupakan

sudut dari sumbu riil positif ke vektor z, maka menghasilkan persamaan berikut :

x = r cos

θ

(2.56)

y = r sin

θ

(2.57)

dengan demikian, z = x+yi dapat ditulis sebagai :

z = r (cos

θ

+ i sin

θ

)

(2.58)

Persamaan di atas disebut sebagai bentuk kutub dari z.

Gambar 2.3 Bentuk kutub bilangan kompleks z = x+yi

Sudut θ disebut sebagai argumen

z dan dinyatakan oleh

θ =

arg z

Argumen

z

tidak ditentukan secara unik karena dapat ditambahkan atau

dikurangkan dengan sebarang kelipatan 2π dari θ untuk menghasilkan nilai

argumen yang lain. Namun demikian, hanya terdapat satu nilai argumen dalam

a, b a, -b z = a+bi

ݖҧ ൌ

a-bi

θ

y = r sin

θ

(x,y) r x = r cos

θ

commit to user

radian yang memenuhi -

π < θ < π

yang disebut sebagai argumen utama z dan

dinyatakan oleh

θ

= Arg z

Akar-akar bilangan kompleks dapat diperoleh dengan menggunakan Rumus

DeMoivre. Jika n bilangan bulat positif, dan z sebarang bilangan kompleks, maka

didefinisikan akar ke-n dari z adalah sebarang bilangan kompleks w yang memenuhi

persamaan

w

n

= z (2.59)

Jika

z

≠

0, maka rumus tersebut dapat diturunkan untuk akar ke-n dari z

sebagai berikut :

w =

ρ

(cos

α

+ i sin

α

) dan z = r (cos

θ

+ i sin

θ

)

Jika diasumsikan bahwa w memenuhi Persamaan 49, maka :

ρ

n

_{(cos n}

_α

_{+ i sin n}

_α

_{) = r (cos}

_θ

_{+ i sin}

_θ

_{) (2.60)}

Dengan membandingkan modulus-modulus dari kedua ruas, maka

ߩ ൌ ξݎ

೙

,

dimana

೙

ξݎ

menyatakan akar riil positif ke-n dari r. Agar dalam Persamaan 50

mempunyai cos n

α

= cos

θ

dan sin n

α

= sin

θ

, sudut-sudut n

α

dan

θ

haruslah sama

atau dibedakan oleh suatu kelipatan 2π, yakni :

n

α

=

θ

+ 2k

π, dimana

k = 0, ±1, ±2, ...

Jadi, nilai-nilai w = =

ρ

(cos

α

+ i sin

α

)

yang memenuhi Persamaan 2.59

adalah:

ݓ ൌ ݖ

ଵȀ௡

_{ൌ ξݎ}

೙

ቂܿ݋ݏ ቀ

ఏାଶ௞గ ௡

ቁ ൅ ݅ •‹ ቀ

ఏାଶ௞గ ௡

ቁቃ

(2.61)

Dimana nilai k sama dengan 0, 1, 2, 3, ..., n-1.

2.1.3

Galat

Output dari perhitungan komputasi dengan menggunakan metode numerik

biasanya menghasilkan nilai hampiran atau aproksimasi (approximation) dari nilai

penyelesaian persamaan yang sebenarnya (Esfandiari, 2013). Galat atau kesalahan

(error) didefinisikan sebagai selisih nilai sejati (exact solution) dengan nilai

hampiran. Galat dihitung menggunakan dua cara yakni galat absolut dan galat

relatif. Jika

ݔҧ

merupakan aproksimasi dari nilai sebenarnya x, maka galat absolut

dapat didefinisikan sebagai berikut:

commit to user

Di sisi lain, galat relatif dihitung dengan menggunakan rumus berikut :

݁

_௥௘௟

ൌ

஺௕௦௢௟௨௧௘௘௥௥௢௥ ்௥௨௘௩௔௟௨௘

ൌ

௘ೌ್ೞ ௫

ൌ

௫ି௫ҧ ௫

ǡ ݔ ് Ͳ

(2.63)

Jika nilai sebenarnya sama dengan nol, maka nilai galat relatif tidak

terdefinisikan. Umumnya, galat relatif lebih signifikan dibandingkan dengan galat

absolut.

Perhitungan galat relatif suatu bilangan kompleks tidak dapat dilakukan

dengan menggunakan Persamaan 2.63. Dengan demikian, diperlukan formula

khusus untuk menghitung galat bilangan kompleks. Sebuah usulan baru

menyatakan bahwa dengan memodifikasi Persamaan 2.63, galat relatif suatu

bilangan kompleks dapat dikalkulasi. Perhitungan galat relatif suatu akar kompleks

ݖ

_ଵ

ൌ ݌

_ଵ

൅ ݍ

_ଵ

݅

dengan

i satuan imaginer dari suatu nilai eksak

ݖ ൌ ݌ ൅ ݍ݅

adalah

rasio norm dari selisih eksak dengan hampiran dengan norm dari eksak dan

disajikan dalam bentuk persen.

݈݃ܽܽݐ ൌ

ԡ௭ି௭_ԡ௭ԡభԡ

šͳͲͲΨ

(2.64)

Beberapa jenis galat atau kesalahan adalah sebagai berikut (Salusu, 2008):

a.

Kesalahan relatif (relative error) yaitu kesalahan absolut dibagi dengan nilai

sebenarnya. Karena nilai sebenarnya tidak diketahui maka digunakan nilai

pendekatan.

݅

_௫

ൌ

௘ೣ

௫

(2.65)

b.

Kesalahan bawaan (inheren) yaitu kesalahan dari data sendiri mungkin terjadi

karena pengamatan kurang tepat atau adanya kekeliruan.

c.

Kesalahan pemotongan yaitu kesalahan yang terjadi karena adanya pemotongan

suatu deret sehingga terdapat beberapa suku yang terabaikan.

d.

Kesalahan pembulatan yaitu kesalahan yang terjadi karena adanya pembulatan.

e.

Blunder (Mistakes) Blunder bukanlah suatu error. Misalnya bilangan 6238

dibaca sebagai 6328.

2.1.4

Rekayasa Perangkat Lunak

Rekayasa perangkat lunak merupakan suatu disiplin ilmu yang membahas

semua aspek produksi perangkat lunak, mulai dari tahap awal yaitu analisa

kebutuhan pengguna, menentukan spesifikasi dari kebutuhan pengguna, desain,

commit to user

pengkodean, pengujian hingga pemeliharaan sistem setelah digunakan (Mulyanto,

2008). Perangkat lunak adalah seluruh perintah yang digunakan untuk memproses

informasi yang dapat berupa sebuah program yang dimengerti oleh komputer

maupun prosedur yang dibutuhkan pengguna dalam memproses informasi.

Berbagai model rekayasa perangkat lunak telah dikembangkan untuk

membantu proses pengembangan perangkat lunak. Model rekayasa perangkat lunak

umumnya mengacu pada Software Development Life Cycle (SDLC) yang memiliki

tahapan analisis (analysis), desain (design), implementasi (implementasi),

pengujian (testing), dan perawatan (maintenance) (Mulyanto, 2008).

2.1.4.1

Analisis (analysis)

Analisis sistem merupakan sebuah teknik pemecahan masalah yang

menguraikan sebuah sistem menjadi komponen-komponen dengan tujuan

mempelajari seberapa baik komponen-komponen tersebut bekerja dan berineraksi

untuk mencapai tujuan (Mulyanto, 2008). Tahap analisis dilakukan dengan

menganalisa kebutuhan-kebutuhan perangkat lunak dan lingkungan implementasi.

2.1.4.2

Desain (design)

Desain perangkat lunak merupakan tugas, tahapan, atau aktivitas yang

difokuskan pada spesifikasi rinci dari solusi berbasis komputer. Desain perangkat

lunak fokus pada sisi teknis dan implementasi sebuah perangkat lunak (Mulyanto,

2008). Desain perangkat lunak dapat dilakukan menggunakan flowchart maupun

pemodelan menggunakan UML.

1.

Flowchart

Bagan alir sistem (system flowchart) merupakan bagan yang menunjukkan arus

pekerjaan secara keseluruhan dari sistem. Bagan ini menjelaskan urutan-urutan

dari prosedur-prosedur yang ada dalam sistem (Sikha, 2003). Definisi lain

mengenai

flowchart yaitu bagan-bagan yang mempunyai arus yang

menggambarkan langkah-langkah penyelesaian suatu masalah (Al-Bahra,

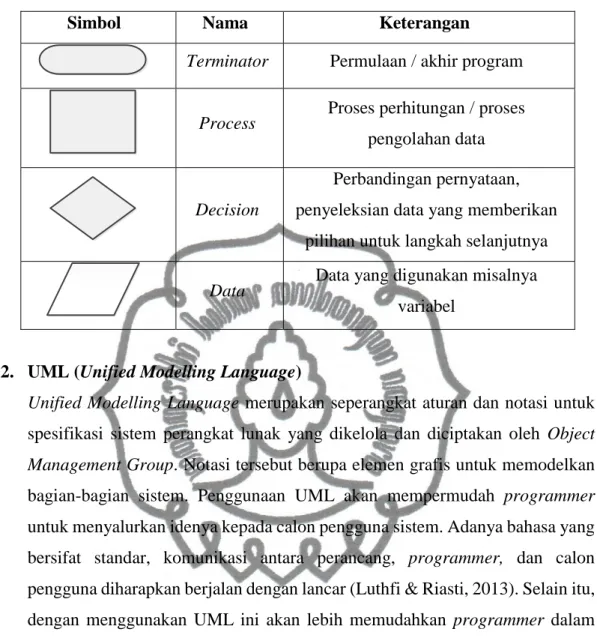
2005). Simbol-simbil atau elemen-elemen pada flowchart

dijabarkan dalam

commit to user

Tabel 2.1 Simbol Elemen Flowchart

Simbol

Nama

Keterangan

Terminator

Permulaan / akhir program

Process

Proses perhitungan / proses

pengolahan data

Decision

Perbandingan pernyataan,

penyeleksian data yang memberikan

pilihan untuk langkah selanjutnya

Data

Data yang digunakan misalnya

variabel

2.

UML (Unified Modelling Language)

Unified Modelling Language merupakan seperangkat aturan dan notasi untuk

spesifikasi sistem perangkat lunak yang dikelola dan diciptakan oleh Object

Management Group. Notasi tersebut berupa elemen grafis untuk memodelkan

bagian-bagian sistem. Penggunaan UML akan mempermudah programmer

untuk menyalurkan idenya kepada calon pengguna sistem. Adanya bahasa yang

bersifat standar, komunikasi antara perancang, programmer,

dan calon

pengguna diharapkan berjalan dengan lancar (Luthfi & Riasti, 2013). Selain itu,

dengan menggunakan UML ini akan lebih memudahkan programmer

dalam

melakukan perancangan perangkat lunak.

a.

Behavioral Diagrams

1.

Use Case Diagram

Use Case Diagram merupakan diagram yang sangat berguna sebagai

alat komunikasi tingkat tinggi yang merepresentasikan kebutuhan

sistem (system requirements). Diagram ini menunjukkan interaksi

antara pengguna dan entitas eksternal dengan sistem yang sedang

dikembangkan. Berikut merupakan elemen use case diagrams:

commit to user

Tabel 2.2 Notasi Use Case Diagram (Sugrue, 2010)

Entitas

Deskripsi

Aktor

Mewakili entitas eksternal dalam sistem, dapat

berupa manusia, perangkat keras, maupun sistem

lainnya.

Use Case

Use case merepresentasikan fungsional sebuah unit

yang dapat berinteraksi dengan aktor eksternal atau

terkait dengan kasus penggunaan lainnya. Use case

digambarkan dengan bentuk elips dengan nama use

case di dalamnya.

Boundary

Use case terdapat dalam batas (boundary)

sistem

yang digambarkan dengan persegi panjang

sederhana. Entitas eksternal tidak harus berada di

dalam batas (boundary) sistem.

Includes

Menggambarkan suatu use case mungkin termasuk

dalam

use case lainnya, yang menyiratkan bahwa

use case tersebut memiliki perilaku yang sama

dengan base use case.

Extends

Menggambarkan suatu use case tertentu

menyediakan fungsional tambahan dari base use

case

lainnya. Hal ini berarti use case target

memperluas perilaku dari use case sumber.

2.

Activity Diagram

Dalam activity diagram dimodelkan alur kerja (workflow) sebuah proses

bisnis dan urutan aktivitas dalam suatu proses. Hampir sama seperti

flowchart, dengan diagram ini dapat dimodelkan sebuah alur kerja dari

satu aktivitas ke aktivitas lainnya atau dari aktivitas ke keadaan state

(Luthfi & Riasti, 2013).

User Trial User

View Errors

System

View Errors

View System Level Error

<<include>>

Print Error Log

Print

commit to user

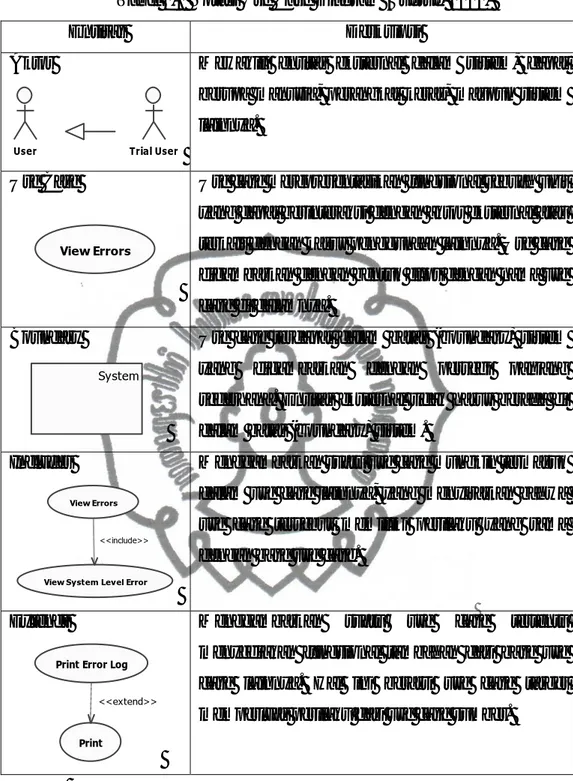
Tabel 2.3 Notasi Activity Diagram (Surgue, 2010)

Entitas

Deskripsi

Action

Merepresentasikan suatu langkah atau aksi

dalam alur program.

Start Node

Digunakan sebagai tanda dimulainya

sebuah alur (flow).

Activity Final Node

Merepresentasikan akhir dari semua alur

kontrol dalam activity.

Control Flow

Merepresentasikan alur kontrol dari satu

action

ke entitas lain seperti action

selanjutnya,

decision point, activity final

node, dan lain sebagainya.

Decision Node

Notasi yang berbentuk diamon digunakan

untuk merepresentasikan keputusan

(decisions) dalam alur kontrol. Selain itu,

notasi tersebut juga dapat digunakan untuk

gabungan alur (merge flows).

Partition

Swimlanes

digunakan dalam activity

diagram

untuk menggambarkan kegiatan

yang dilakukan oleh pelaku yang berbeda.

3.

State Machine Diagrams

State Machine Diagrams digunakan untuk menggambarkan transisi

state dari lifetime objek tunggal dalam menanggapi peristiwa. Diagram

ini dimodelkan hampir sama dengan activity diagram.

View System Events

Start

End

System View System Events

commit to user

b.

Interaction Diagrams

Interaction diagrams adalah subset dari behavioral diagrams yang

berkaitan dengan aliran kontrol seluruh sistem yang dimodelkan.

1.

Sequence Diagrams

Interaksi antar entitas atau objek disusun dalam suatu urutan tertentu dan

akan dijelaskan melalui diagram sequence.

Sequence diagram

menunjukkan tahap-tahap yang seharusnya terjadi untuk menghasilkan

sesuatu dalam use case (uthfi dan Riasti, 2013).

Lifeline Objects

Sequence diagram terdiri dari beberapa lifeline. Masing-masing entitas

memiliki kolomnya sendiri. Berikut ini merupakan beberapa lifeline

untuk masing-masing entitas:

Tabel 2.4 Notasi Lifeline Sequence Diagram (Surgue, 2010)

Entitas

Deskripsi

Actor

Actor mewakili entitas eksternal dalam sistem. Entitas

eksternal meliputi manusia, perangkat keras ataupun

sistem lainnya.

Boundary

Elemen

boundary merupakan antarmuka pengguna,

atau logika back-end yang berhubungan dengan

sistem eksternal secara langsung.

Control

Elemen ini mengelola aliran informasi untuk sebuah

skenario. Perilaku (behavior) dan aturan bisnis

(business rules) biasanya dikelola oleh objek-objek di

dalamnya.

Entity

Elemen

Entity bertanggung jawab mengendalikan

data atau informasi. Elemen ini dianggap sebagai

beans atau model objek.

: User

: Boundary

: Control

commit to user

Pada

sequence diagram, hal yang paling inti yakni pesan antar objek

yang dimodelkan. Pesan tersebut biasanya berbentuk messagename

(parameter). Pesan dapat dikirim dari dua arah, dan memungkinkan

melewati lifelines lainnya untuk menuju lifelines tujuan.

Tabel 2.5 Notasi Message Sequence Diagram (Surgue, 2010)

Entitas

Deskripsi

Synchronous

Digambarkan dengan ujung berupa anak panah

yang solid. Untuk pesan kembalian (return

message) digambarkan dengan anak panah yang

sama namun dengan garis putus-putus.

Asynchronous

Digambarkan dengan ujung berupa garis anak

panah. Untuk return message bentuknya pun

sama tetapi menggunakan garis putus-putus.

Self Message

Biasanya merupakan pesan yang dipanggil

secara rekursif atau panggilan untuk metode lain

milik objek yang sama.

2.

Communication Diagrams

Communication diagrams juga dikenal sebagai collaboration diagram.

Diagram ini hampir sama dengan sqeuence diagrams, tetapi diagram ini

didefinisikan dalam bentuk yang lebih bebas tanpa menggunakan

lifelines.

Communication diagram fokus pada hubungan antara objek

boundary,

control, dan entity. Pesan antar objek diberi nomor untuk

menginformasikan urutannya.

3.

Interaction Overview Diagrams

Interaction Overview Diagrams adalah bentuk activity diagram dimana

setiap node merupakan penghubung ke node lainnya dalam diagram

interaksi. Diagram ini menyediakan ikhtisar atau index yang berguna

dari key diagrams dalam sebuah sistem.

1

1

commit to user

c.

Structural Diagrams

1.

Class Diagrams

Class Diagram merupakan sebuah spesifikasi yang jika diinisiasikan

akan menghasilkan sebuah objek dan merupakan inti dari

pengembangan dan desain berorientasi objek. Diagram ini

menggambarkan keadaan (atribut/properti) sebuah sistem dan

menawarkan layanan untuk memanipulasi keadaan tersebut

(metode/fungsi) (Luthfi dan Ristiana, 2013).

2.

Object Diagrams

Object diagrams memberikan informasi mengenai hubungan antara

contoh kelas pada titik tertentu. Diagram ini menggunakan beberapa

elemen dari class diagram.

3.

Components Diagrams

Components diagrams digunakan untuk menggambarkan bagaimana

komponen sistem yang dihubungkan bersama pada tingkat abstraksi

yang lebih tinggi dari class diagram.

4.

Composite Structure Diagrams

Composite Structure Diagrams menunjukkan struktur internal kelas dan

kolaborasi yang dimungkinkan. Entitas utama dalam diagram ini adalah

parts, ports, connectors, collaboration, sebagai pengklasifikasi.

5.

Deployment Diagrams

Deployment diagrams memodelkan arsitektur runtime dari sistem dalam

pengaturan dunia nyata. Diagram ini menunjukkan bagaimana entitas

perangkat lunak dikerahkan ke node perangkat keras dan devices.

Association

links antar entitas merepresentasikan komunikasi antar

node.

6.

Package Diagrams

Package diagrams menunjukkan organisasi paket dan elemen dalam

memberikan visualisasi dari namespace yang akan diterapkan dalam

class. Diagram ini pada umumnya digunakan untuk mengatur dan

memberikan gambaran class diagram. seperti standar dependensi,

terdapat dua jenis hubungan spesifik yang digunakan untuk package

commit to user

diagram.

Keduanya digambarkan garis putus-putus tergantung pada

stereotip yang sesuai (import or merge).

2.1.4.3

Implementasi (implementation)

Implementasi merupakan tahapan menerjemahkan hasil desain logis dan

fisik ke dalam kode-kode program komputer (Mulyanto, 2008).

2.1.4.4

Pengujian (testing)

Pengujian perangkat lunak merupakan sebuah proses terhadap

aplikasi/program untuk menemukan segala kesalahan dan segala kemungkinan

yang akan menimbulkan kesalahan sesuai dengan spesifikasi perangkat lunak yang

telah ditentukan sebelum aplikasi tersebut diserahkan kepada pelanggan

(Simarmata, 2010).

Terdapat dua jenis pengujian perangkat lunak yaitu manual testing dan

automated testing. Pada manual testing, pengujian perangkat lunak dilakukan

secara manual yaitu dengan menggunakan black box testing ataupun white box

testing.

Black box testing digunakan untuk mengetahui hasil yang diperoleh dari

sebuah sistem. Dalam pengujian black box, data tes diinputkan dalam sistem yang

akan diuji dan kemudian menghasilkan output. Pengujian Black box menguji

kualitas kinerja perangkat lunak, sedangkan pengujian white box menguji kualitas

pembangunan perangkat lunak. Dengan demikian, tidak seperti pengujian black

box, pengujian white box tidak mempertimbangkan hasil yang diperoleh dari sebuah

perangkat lunak, tetapi fokus pada proses yang dilakukan sistem untuk

menghasilkan output (Bennett, McRobb, and Farmer, 2010).

Pelaksanaan pengujian perangkat lunak dilakukan berdasarkan strategi

khusus pengujian perangkat lunak, misalnya big bang testing atau incremental

testing dan bottom-up atau top-down testing (Galin, 2004). Pada automated

testing, pengujian dilakukan dibantu dengan tools CASE (computer aided software

engineering) dalam menganalisa perangkat lunak dan desain tasks.

commit to user

2.1.4.5

Perawatan (maintenance)

Perawatan dapat dilakukan dengan berbagai tipe seperti perawatan

corrective, perawatan routine, dan perawatan system upgrade.

2.2

Penelitian Terkait

Berikut ini merupakan beberapa penelitan-penelitian terkait algoritma-algoritma

pencarian akar kompleks polinomial :

a)

Menentukan Akar kompleks Polinomial dengan Menggunakan Metode

Bairstow

Penelitian yang dilakukan oleh Iges Windra, Minora Longgom Nasution, dan

Meira Parma Dewi pada tahun 2013 membahas cara menentukan akar kompleks

polinomial dengan menggunakan metode Bairstow. Untuk mencari akar kompleks

polinomial dengan menggunakan metode Bairstow, langkah-langkah yang

dilakukan oleh peneliti, seperti yang tertulis dalam jurnalnya yang merupakan

adopsi dari penelitian sebelumnya yang dilakukan oleh Bagheri (n.d) adalah sebagai

berikut:

1.

Menentukan tebakan awal dari variabel

ݔ

ଶ

_{൅ ݑݔ ൅ ݒ}

2.

Menghitung nilai

ܾ

_௡

ൌ ܽ

_௡

3.

Menghitung

ܾ

௡ିଵ

ൌ ܽ

௡ିଵ

൅ ݑܾ

௡

ܾ

_௜

ൌ ܽ

_௜

൅ ݑܾ

_௜ାଵ

൅ ݒܾ

_௜ାଶ

4.

Menghitung nilai

ܿ

_௡

ൌ ܾ

_௡

5.

Menghitung nilai

ܿ

_௡ିଵ

ൌ ܾ

_௡ିଵ

൅ ݑܿ

_௡

ܿ

௜

ൌ ܾ

௜

൅ ݑܿ

௜ାଵ

൅ ݒܿ

௜ାଶ

6.

Mencari

οݑ

dan

οݒ

dengan aturan Cramer sebagai berikut:

οݑ ൌ

ฬ ି௕భ ௖య ି௕బ ௖మฬ ቚ௖_௖మ ௖య భ ௖మቚ

ൌ

ሺ௖_ሺ௖మሻሺି௕భሻିሺି௕బሻሺ௖యሻ మሻሺ௖మሻିሺ௖భሻሺ௖యሻ

οݒ ൌ

ฬ ି௕భ ௖మ ି௕బ ௖భฬ ቚ௖_௖మ ௖య భ ௖మቚ

ൌ

ሺ௖_ሺ௖భሻሺି௕భሻିሺ௖మሻሺି௕బሻ మሻሺ௖మሻିሺ௖భሻሺ௖యሻ

commit to user

7.

Mencari nilai u dan v yang terbaru dengan persamaan :

ݑ

௕௔௥௨

ൌ ݑ

כ

൅ οݑ

ݒ

_௕௔௥௨

ൌ ݒ

כ

_{൅ οݒ}

8.

Melakukan proses iterasi dengan mengulang langkah kedua dan ketiga sampai

memenuhi kriteria penghentian.

9.

Mencari akar kompleks persamaan polinomial dengan bantuan rumus kuadratis.

10.

Menentukan polinomial yang telah terdeflasi, dengan beberapa kemungkinan

berikut:

a.

Jika polinomial yang telah terdeflasi berderajat satu atau dua maka dapat

dicari akarnya dengan rumus analitik.

b.

Jika polinomial yang telah terdeflasi berderajat lebih dari 2 maka

dilanjutkan dengan pencarian akar dengan langkah metode Bairstow.

Dalam penelitian tersebut, peneliti melakukan analisis metode Bairstow secara

detail. Hasil analisis diterapkan untuk menyelesaikan persamaan polinomial. Setiap

akar kompleks polinomial ditemukan, iterasi dihentikan dan dihitung keakuratan

perhitungan berdasarkan estimasi eror. Misalnya iterasi keempat, metode Bairstow

menghasilkan pendekatan

ݔ

ଶ

_{െ ݑݔ െ ݒ}

_{yang sangat akurat dengan estimasi eror}

0.062% untuk u

dan 0.004% untuk v. Kemudian dilanjutkan pencarian akar

kompleks lainnya berdasarkan polinomial terdeflasi. Dengan demikian, hasil analisi

cukup teliti karena dilakukan perhitungan persentase estimasi eror nilai u dan v pada

setiap iterasinya. Namun, pencarian akar kompleks polinomial pada penelitian ini

hanya dilakukan pada satu sampel random yakni

݂ሺݔሻ ൌ ݔ

ହ

െ ͵ǡͷݔ

ସ

൅ ʹǡ͹ͷݔ

ଷ

൅

ʹǡͳʹͷݔ

ଶ

_{െ ͵ǡͺ͹ͷݔ ൅ ͳǡʹͷ}

_{. Selain itu, penelitia yang dilakukan merupakan}

penelitian teoritis sehingga hanya mengujikan teori metode Bairstow yang sudah

ada, tanpa membuat suatu hal yang baru.

Keterkaitan antara penelitian dalam jurnal dengan penelitian yang dilakukan

yaitu memiliki kesamaan metode yang digunakan dalam pencarian akar kompleks

polinomial. Perbedaan dengan peneitian yang diusulkan yaitu objek analisisnya.

b)

Solving Cubic Equations by Viete’s Substitutions

Artikel ditulis oleh OR Chi Ming pada EduMath29

pada tahun 2010. Dalam