2.1. Algoritma
Secara informal, sebuah algoritma adalah prosedur komputasi yang didefinisikan dengan baik yang mengambil beberapa nilai, atau seperangkat nilai sebagai input dan
menghasilkan nilai, atau seperangkat nilai sebagai output[2].
Algoritma yang akan dianalisis dan dibandingkan pada penelitian ini adalah
algoritma Sorting (pengurutan) yaitu algoritma QuickSort, 3 Way QuickSort, dan RadixSort. Algoritma pengurutan adalah algoritma yang menyusun kembali rentetan objek-objek untuk meletakkan objek suatu kumpulan data tersebut ke dalam urutan yang logis [9]. Algoritma adalah prosedur komputasi yang didefinisikan dengan baik yang mengambil beberapa nilai yaitu seperangkat nilai sebagai input dan output yang menghasilkan nilai. Algoritma juga merupakan pola pikir terstruktur yang berisi tahapan penyelesaian, yang nantinya akan diimplementasikan ke dalam suatu bahasa pemrograman [6]. Berdasarkan pengertian algoritma tersebut, dapat disimpulkan bahwa algoritma merupakan suatu istilah yang luas, yang tidak hanya berkaitan dengan dunia komputer.
Menurut Donald E. Knuth, algoritma yang baik memiliki kriteria sebagai berikut:
1. Input
2. Output
Suatu algoritma harus memiliki satu atau lebih algoritma. Suatu algoritma yang tidak memiliki keluaran (output) adalah suatu algoritma yang sia-sia, yang tidak perlu dilakukan. Algoritma dibuat untuk tujuan menghasilkan sesuatu yang diinginkan, yaitu berupa hasil keluaran.
3. Finiteness
Setiap pekerjaan yang dikerjakan pasti berhenti. Demikian juga algoritma harus dapat dijamin akan berhenti setelah melakukan sejumlah langkah proses. 4. Definiteness
Algoritma tersebut tidak menimbulkan makna ganda (ambiguous). Setiap baris aksi/pernyataan dalam suatu algoritma harus pasti, artinya tidak menimbulkan penafsiran lain bagi setiap pembaca algoritma, sehingga memberikan output yang sesuai dengan yang diharapkan oleh pengguna.
5. Effectiveness
Setiap langkah algoritma harus sederhana sehingga dikerjakan dalam waktu yang wajar.[10]
2.2. Kompleksitas Algoritma
Dalam aplikasinya, setiap algoritma memiliki dua buah ciri khas yang dapat digunakan sebagai parameter pembanding, yaitu jumlah proses yang dilakukan dan jumlah memori yang digunakan untuk melakukan proses. Jumlah proses ini dikenal sebagai kompleksitas waktu yang disimbolkan dengan T(n), sedangkan jumlah memori ini dikenal sebagai kompleksitas ruang yang disimbolkan dengan S(n).[12]
2.2.1. Kompleksitas waktu
Kompleksitas waktu T(n), diukur dari jumlah tahapan komputasi yang dibutuhkan untuk menjalankan algoritma sebagai fungsi dari ukuran masukan n. Jumlah tahapan komputasi dihitung dari berapa kali suatu operasi dilaksanakan di dalam sebuah algoritma sebagai fungsi ukuran masukan (n).
Ruang memori yang dibutuhkan untuk menjalankan algoritma yang berkaitan dengan strutur data dari program.[1]Oleh karena itu, pada komputer dan compiler yang berbeda, suatu algoritma yang sama akan memiliki waktu eksekusi yang berbeda.
2.2.2. Kompleksitas waktu asimptotik
Notasi “O” disebut notasi “O-Besar” (Big-O) yang merupakan notasi kompleksitas
waktu asimptotik. Kompleksitas waktu asimptotik merupakan perkiraan kebutuhan algoritma sejalan dengan meningkatnya nilai n. Pada umumnya, algoritma menghasilkan laju waktu yang semakin lama bila nilai n semakin besar. Berikut
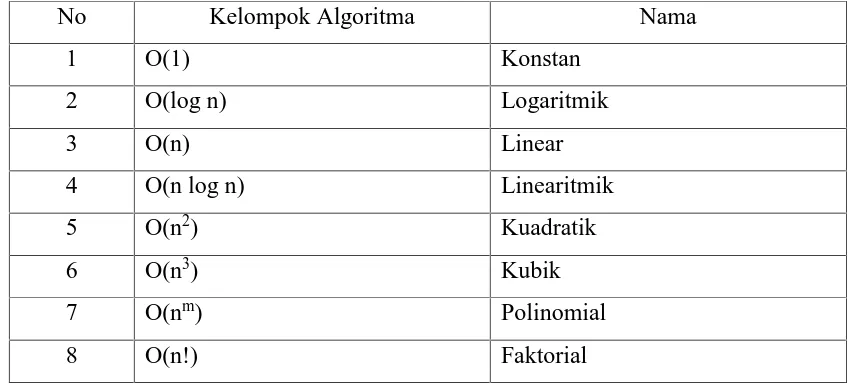
pengelompokan algoritma berdasarkan notasi O-Besar dapat dilihat pada Tabel 2.1.
Tabel 2.1. Pengelompokan algoritma berdasarkan notasi O-Besar
Keterangan Tabel:
1. Konstan O(1): Disebut konstan, karena program hanya dieksekusi dengan suatu nilai yang konstan.
2. Logaritmik O(log n): Disebut algoritma logaritmik, karena peningkatan waktu eksekusi sebanding dengan peningkatan logaritma dari jumlah data.
3. Linear O(n): Disebut linear, karena peningkatan waktu eksekusi sebanding dengan peningkatan data, dan merupakan kondisi optimal dalam membuat algoritma.
4. Linearitmik O(n log n): Disebut linearitmik, karena merupakan gabungan dari linear dan logaritmik. Algortima ini merupakan algoritma log n yang
No Kelompok Algoritma Nama
1 O(1) Konstan
2 O(log n) Logaritmik
3 O(n) Linear
4 O(n log n) Linearitmik
5 O(n2) Kuadratik
6 O(n3) Kubik
7 O(nm) Polinomial
dijalankan sebanyak n kali. Biasanya digunakan untuk memecahkan masalah besar menjadi masalah yang kecil.
5. Kuadratik O(n2): Disebut kuadratik, karena peningkatan waktu eksekusi program akan sebanding dengan peningatan kuadrat jumlah data.
6. Kubik O(n3): Disebut kubik, karena peningkatan waktu eksekusi program akan sebanding dengan peningkatan pangkat tiga jumlah data.
7. Polinomial O(nm): Algoritma yang tidak efisien, karena memerlukan jumlah langkah penyelesaian yang jauh lebih besar daripada jumlah data.
8. Faktorial O(n!): Merupakan algoritma yang paling tidak efisien, karena waktu eksekusi program akan sebanding dengan peningkatan faktorial jumlah data.
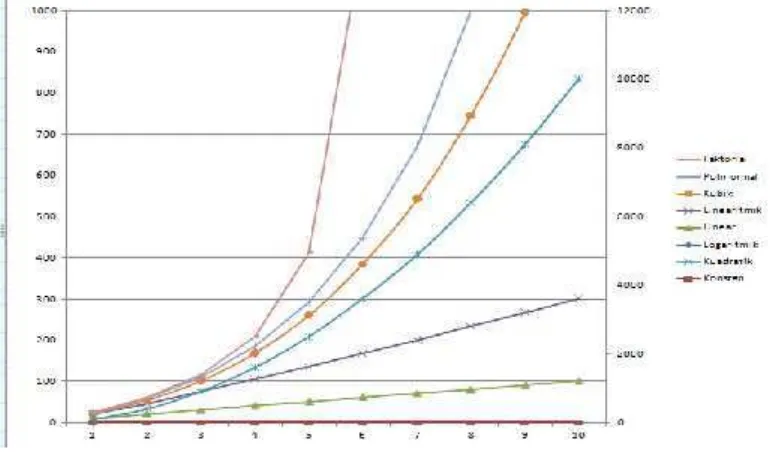
Gambar 2.1. Grafik Perbandingan Pengelompokan Algoritma Berdasarkan Notasi O-Besar
2.2.3. Kompleksitas ruang
2.3. Running Time
Running time adalah waktu yang digunakan oleh sebuah algoritma untuk menyelesaikan masalah pada sebuah komputer paralel dihitung mulai dari saat algoritma mulai hingga saat algoritma berhenti. Jika prosesor-prosesornya tidak mulai dan selesai pada saat yang bersamaan, maka running time dihitung mulai saat komputasi pada prosesor pertama dimulai hingga pada saat komputasi pada prosesor terakhir selesai.
2.4. Pengurutan
Pengurutan merupakan proses yang menyusun kembali rentetan objek-objek untuk meletakkan objek dari suatu kumpulan data ke dalam urutan yang logis. Pada dasarnya, pengurutan (sorting) membandingkan antar data atau elemen berdasarkan kriteria dan kondisi tertentu.[4] Ada dua jenis pengurutan, yakni secara ascending (naik) dan descending (turun).
Ada dua kategori pengurutan, yaitu: 1. Pengurutan internal
Pengurutan internal adalah pengurutan yang dilaksanankan hanya dengan menggunakan memori komputer, pada umumnya digunakan bila jumlah elemen tidak terlalu banyak.
2. Pengurutan eksternal
Pengurutan eksternal adalah pengurutan yang dilaksanakan dengan bantuan memori virtual atau harddisk karena jumlah elemen yang akan diurutkan terlalu banyak.
2.5. Klasifikasi Algoritma Pengurutan
Algoritma pengurutan diklasifikasikan berdasarkan prosesnya menjadi beberapa jenis, yakni,
1. Exchange Sort
Algoritma yang dikategorikan dalam Exchange Sort jika cara kerja algoritma tersebut melakukan pembandingan antar data dan melakukan pertukaran apabila urutan yang didapat belum sesuai. Contohnya adalah bubble sort,
2. Selection Sort
Algoritma yang dikategorikan dalam Selection Sort jika cara kerja algoritma tersebut mencari elemen yang tepat untuk diletakkan pada posisi yang telah diketahui, dan meletakkannya di posisi tersebut setelah data tersebut ditemukan. Contohnya adalah selection sort, heap sort, smooth sort, strand sort.
3. Insertion Sort
Algoritma yang dikategorikan dalam Insertion Sort jika cara kerja algoritma tersebut mencari tempat yang tepat untuk suatu elemen data yang telah diketahui ke dalam subkumpulan data yang telah terurut, kemudian melakukan penyisipan (insertion) data di tempat yang tepat tersebut. Contohnya adalah insertion sort, shell sort, tree sort, library sort, patience sort.
4. Merge Sort
Algoritma yang dikategorikan dalam Merge Sort jika cara kerja algoritma tersebut membagi data menjadi subkumpulan-subkumpulan yang kemudian subkumpulan tersebut diurutkan secara terpisah, dan kemudian digabungkan
kembali dengan metode merging. algoritma ini melakukan metode pengurutan merge sort juga untuk mengurutkan subkumpulandata tersebut, atau dengan kata lain, pengurutan dilakukan secara rekursif. Contohnya adalah merge sort.
5. Non Comparison Sort
Algoritma yang dikategorikan dalam Non Comparison Sort jika proses pengurutan data yang dilakukan algoritma tersebut tidak terdapat pembanding antar data, data diurutkan sesuai dengan pigeon hole principle. Contohnya adalah radix sort, bucket sort, counting sort, pigeonhole sort, tally sort.
2.6. Algoritma QuickSort
karena proses pengurutan menggunakan partisi dan pengurutan dilakukan pada setiap partisi[7].
2.6.1. Langkah-langkah melakukan pengurutan algoritma QuickSort
Tahapan dalam melakukan partisi pada Algoritma QuickSort sebagai berikut: 1. Pilih x Є {A1, A2, ... , An} sebagai elemen pivot (x)
2. Lakukan scanning tabel dari kiri ke kanan sampai ditemukan Ap≥x 3. Lakukan scanning tabel dari kanan ke kiri sampai ditemukan Aq≤x 4. Swap Ap↔ Aq
5. Ulangi langkah ke-2, sampai kedua scanning bertemu di tengah tabel.
Untuk menetukan pivot, ada baiknya dari median tabel. Sebagai contoh, ambil bilangan acak:
523 235 088 880 028 093 002 153
1. Menentukan pivot
A1 A2 A3 A4 A5 A6 A7 A8
523 235 088 880 028 093 002 153 x
2. Melakukan scanning tabel dari kiri ke kanan sampai ditemukan Ap≥x dan scanning tabel dari kanan ke kiri sampai ditemukan Aq≤x
A1 A2 A3 A4 A5 A6 A7 A8
523 235 088 880 028 093 002 153
p x q
3. Swap Ap↔ Aq
A1 A2 A3 A4 A5 A6 A7 A8
002 235 088 880 028 093 523 153
4. Mengulangi langkah ke-2 dari posisi p+1 dan dari posisi q-1, sampai kedua scanning bertemu ditengah tabel.
A1 A2 A3 A4 A5 A6 A7 A8
002 235 088 880 028 093 523 153
p x
q
5. Swap Ap↔ Aq
A1 A2 A3 A4 A5 A6 A7 A8
002 028 088 880 235 093 523 153
p x
q
6. Mengulangi langkah ke-2, karena pivot telah berubah
A1 A2 A3 A4 A5 A6 A7 A8
002 028 088 880 235 093 523 153
p x q
7. Swap Ap↔ Aq
A1 A2 A3 A4 A5 A6 A7 A8
002 028 088 153 235 093 523 880
p x q
8. Mengulangi langkah ke-2 dari posisi p+1 dan dari posisi q-1, sampai kedua scanning bertemu ditengah table
A1 A2 A3 A4 A5 A6 A7 A8
002 028 088 153 235 093 523 880
x p
9. Swap Ap↔ Aq, berhenti karena p≤q di tengah tabel
A1 A2 A3 A4 A5 A6 A7 A8
002 028 088 153 093 235 523 880
x p
q
10. Membagi partisi menjadi 2 tabel: Hasil partisi pertama:
A1 A2 A3 A4 A5
002 028 088 153 093
11. Menentukan pivot
A1 A2 A3 A4 A5
002 028 088 153 093
x
12. Melakukan scanning tabel dari kiri ke kanan sampai ditemukan Ap≥x dan scanning tabel dari kanan ke kiri sampai ditemukan Aq≤x
A1 A2 A3 A4 A5
002 028 088 153 093
x p
q
13. Swap Ap↔ Aq, berhenti karena p≤q di tengah tabel
A1 A2 A3 A4 A5
002 028 088 093 153 x
p
q
Hasil partisi kedua:
A6 A7 A8
14. Menentukan pivot
A6 A7 A8
235 523 880
x
15. Melakukan scanning tabel dari kiri ke kanan sampai ditemukan Ap≥x dan scanning tabel dari kanan ke kiri sampai ditemukan Aq≤x. Dan ternyata, tidak dapat melakukan scanning karena syarat tidak memenuhi. Oleh karena itu, hasil scanning partisi kedua selesai dan merupakan hasil akhir pemartisian.
A6 A7 A8
235 523 880
x
16. Hasil akhir merupakan gabungan antara hasil akhir proses partisi pertama dan kedua
A1 A2 A3 A4 A5 A6 A7 A8
002 028 088 093 153 235 523 880
2.6.2. Pseudocode algoritma QuickSort
Menurut Fachrie Lantera, 2008 pseudocode pada algoritma QuickSort adalah sebagai berikut:
Procedure QuickSort (input/output a : array [1..n] of integer, input i,j : integer )
Deklarasi :
{mengurutkan tabel a[i..j] dengan algoritma QuickSort.
Masukkan: Tabel a[i..j] yang sudah terdefinisi elemen-elemennya. Keluaran: Tabel a[i..j] yang terurut menaik.}
Deklarasi :
if (i<j) then
Partisi(a,i,j,k) {Ukuran (a) > 1}
QuickSort(a,i,k)
QuickSort(a,k+1, j)
End if
Procedure Partisi (input/output: a : array[1..n] of integer, input i, j : integer, output q : integer)
{Membagi tabel a[i..j] menjadi dua tabel a[i..q] dan a[q+1..j]
scanning a[i..q] dan a[q+1..j] Sedemikian sehingga elemen tabel a[i..q] lebih kecil dari elemen tabel a[q+1..j] }
Deklarasi :
Pivot, temp : integer
Algoritma :
while a[p] < pivot do
p <- p + 1
endwhile
{ Ap >= pivot }
while a[q] > pivot do
q <- q – 1
endwhile
{ Aq >= pivot }
if (p >q) then
{ pertukarkan a[p] dengan a[q]}
temp <- a[p]
a[p] <- a[q]
{ tentukan awal pemindaian berikutnya }
p <- p+ 1
q <- q - 1
endif
until p > q
2.6.3. Kompleksitas waktu asimptotik algoritma QuickSort
Terdapat 3 kemungkinan kasus dari performa algoritma QuickSort ini yaitu, terbaik dan rata-rata (best and average case= n log n), serta terburuk (worst case= n2). Kompleksitas waktu asimptotik algoritma QuickSort adalah O (n log n). Oleh karena itu, dapat disimpulkan algoritma ini termasuk “linearitmik”. Karena merupakan
algoritma log n yang dijalankan sebanyak n kali. Dan digunakan untuk memecahkan masalah besar menjadi masalah yang kecil sangat sesuai dengan algoritma QuickSort yang bersifat divide and conquer.
2.7. Algoritma 3 Way QuickSort
Algoritma 3 Way QuickSort pertama kali dikemukakan oleh Sedgewick. 3 Way QuickSort merupakan pengembangan dari algoritma QuickSort dengan membagi array menjadi 3 bagian, yaitu: array < v, array =v, dan array > v. Dimana v merupakan elemen pivot. Dan mempartisinya berdasarkan partisi QuickSort.
2.7.1. Langkah-langkah melakukan pengurutan algoritma 3 Way QuickSort Mekanisme pengurutannya adalah sebagai berikut:
1. Pilih x1, x2, x3Є {A1, A2, ... , An} sebagai elemen pivot (x1, x2, x3) 2. Susun pivot dengan syarat x1 > x2 > x3
3. Atur semua data selain pivot (x1, x2, x3) sesuai urutan kemunculan dengan syarat data yang lebih kecil dari pivot (x1, x2, x3) berada di sebelah kiri pivot dan data yang lebih besar atau sama dengan pivot berada di sebelah kanan pivot.
523 235 088 880 028 093 002 153
002 028 088 093 153 235 523 880
2.7.2. Pseudocode algoritma 3 Way QuickSort
Deklarasi : Algoritma :
if (i<j) then
Partisi(a,l,i,j,r)
{Ukuran (a) > 1}
ThreeWayQuickSort(a,l,j)
ThreeWayQuickSort(a,i, r)
end if
Procedure ThreeWayQuickSort (input/output a : arr [1..r] of integer, input i, lt, gt, v : integer )
if i<pivot then
swap [lt],a[i]
temp <- a[i]
a[i] <- [lt]
a[lt] <- temp
lt<- lt+1
i<- i+1
while pivot=(pivot+1 || pivot-1) && gt>pivot do
Partisi
endwhile
endif
if i>pivot then
swap a[i],[gt]
temp <- a[i]
a[i] <- [gt]
gt<- gt-1
while pivot=(pivot+1 || pivot-1) && gt>pivot do
Partisi
endwhile
endif
if a[i]=pivot then
i<- i+1
while pivot=(pivot+1 || pivot-1) && gt>pivot do
Partisi
endwhile
endif
Procedure Partisi (input/output: a :array[1..r] of integerinput i, j : integer, output q : integer)
{Membagi tabel a[i..j] menjadi dua tabel a[i..q] dan a[q+1..j]
scanning a[i..q] dan a[q+1..j] Sedemikian sehingga elemen tabel a[i..q] lebih kecil dari elemen tabel a[q+1..j] }
Deklarasi :
Pivot, temp : integer
Algoritma :
Pivot <- A[(i+j) div 2]
{ pivot = elemen tengah }
p <- i
q <- j
repeat
while a[p] < pivot do
p <- p + 1
endwhile
{ Ap >= pivot }
endwhile
{ Aq >= pivot }
if (p >q) then
{ pertukarkan a[p] dengan a[q]}
temp <- a[p]
a[p] <- a[q]
a[q] <- temp
{ tentukan awal pemindaian berikutnya}
p <- p+ 1
q <- q - 1
endif
until p > q
2.7.3. Kompleksitas waktu asimptotik algoritma 3 Way QuickSort
Algoritma 3 Way QuickSort ini adalah algoritma yang tidak stabil dan memiliki kompleksitas yang sama dengan QuickSort yaitu, terbaik dan rata-rata (best and average case= n log n), dan kasus terburuk (worst case = n2). Kompleksitas waktu asimptotik algoritma 3 Way QuickSort adalah O (n log n).
2.8. Algoritma RadixSort
2.8.1. Langkah-langkah melakukan pengurutan algoritma RadixSort Langkah-langkah pengurutan RadixSort adalah sebagai berikut:
1. Data dibagi sesuai digit terkanan
523 235 088 880 028 093 002 153
Kategori Digit Isi
0 880
1
-2 002
3 523, 093, 153
4
-5 235
6
-7
-8 088, 028
9
-2. Hasil pengategorian tersebut lalu digabungkan kembali dengan metode kongkatenasi menjadi:
880 002 523 093 153 235 088 028
3. Kemudian pengategorian dilakukan kembali, namun kali ini berdasar digit kedua atau digit tengah, dan jangan lupa bahwa urutan pada tiap subkumpulan data harus sesuai dengan urutan kemunculan pada kumpulan data
880 002 523 093 153 235 088 028
Kategori Digit Isi
0 002
-3 235
4
-5 153
6
-7
-8 880, 088
9 093
4. Kemudian dikongkatenasikan kembali menjadi:
002 523 028 235 153 880 088 093
5. Pengategorian kembali berdasar digit yang terkiri, atau yang paling signifikan
002 523 028 235 153 880 088 093
Kategori Digit Isi
0 002, 028, 088, 093
1 153
2 235
3
-4
-5 523
6
-7
-8 880
9
-6. Dan kemudian kongkatenasikan kembali, yang merupakan hasil akhir dari pengurutan berdasarkan RadixSort
2.8.2. Pseudocode algoritma RadixSort
Menurut Dominikus DP (2005) pseudocode pada Algoritma RadixSort adalah sebagai berikut :
Procedure RadixSort (A : T Array; var B :T Array; d : byte); var
KatRadix : array[0..9] of Queue;
i, x, ctr : integer;
{--- inisialisasi KatRadix ---}
for i:=0 to 9 do
InitQueue (KatRadix[i]);
{--- dikategorikan ---}
for i:=1 to n do
Enqueue (KatRadix [(B[i] div
pembagi) mod 10], B[i]);
B[i] := 0;
while (NOT IsQueueEmpty(KatRadix[i])) do
B[ctr]:=DeQueue (KatRadix [i]);
endwhile
end;
end;
pembagi := pembagi * 10;
end;
end;
2.8.3. Kompleksitas waktu asimptotik algoritma RadixSort
Kompleksitas waktu asimptotik Algoritma RadixSort adalah O(nd). Secara umum, Algoritma RadixSort memiliki kompleksitas waktu asimptotiknya yang sangat kecil (O(kN)). Dimana k merupakan panjang digit terpanjang dalam kumpulan data. Dalam hal ini, dikategorikan ke dalam “linear” karena bentuk O(kN) sebanding dengan O(n),