ESTIMASI INTERVAL SPLINE
DALAM REGRESI NONPARAMETRIK
Muhammad Nafi’
1, I Nyoman Budiantara
2Mahasiswa S2 Jurusan Statistika FMIPA ITS Surabaya1 Email: [email protected]
Dosen Jurusan Statistika FMIPA ITS Surabaya1
Abstraks
Diberikan model regresi nonparametrik yi = f(xi) + εi, xi
∈
[a,b], i=1,2,…,n. Kurva regresi f diasumsikansmooth, dalam arti f termuat di dalam ruang Sobolev . Umumnya estimasi titik diperoleh dari meminimumkan Penalized Likelihood (PL). Untuk menyelesaian optimasi PL ini, para peneliti menggunakan pendekatan Reproducing Kernel Hilbert Space (RKHS) atau Gateaux. Sedangkan untuk persoalan inferensi seperti
estimasi interval (interval konfidensi) untuk f, menggunakan pendekatan Bayesian. Tetapi pendekatan ini memerlukan pengetahuan Matematika yang relatif tinggi dan sulit dipahami oleh banyak pengguna Statistika.
]
,
[
2a
b
W
p ^f
Dalam tulisan ini, penulis mengestimasi titik dengan menggunakan optimasi Likelihood dan mengkonstruksi selang kepercayaan untuk kurva regresi f dengan pendekatan Spline menggunakan Pivotal Quantity, yang merupakan generalisasi regresi parametrik. Inferensi statistik yang dihasilkan secara matematik lebih mudah dan sederhana, serta mudah dipahami oleh pengguna Statistika. Selanjutnya, diberikan suatu ilustrasi numerik model Spline untuk menduga pola hubungan antara umur balita dengan berat badan balita di Kota Surabaya, beserta interval konfidensinya.
^
f
Kata kunci : Regresi Nonparametrik, Penalized Likelihood, Spline, Pivotal Quantity
1. Pendahuluan
Dalam Statistika untuk mengetahui model pola hubungan antara variabel prediktor xi dan variabel
respon yi dapat digunakan analisis regresi. Asumsikan
data berpasangan (xi, yi) mengikuti model regresi yi =
f(xi) + εi, i=1,2,…,n. Fungsi f(xi) merupakan kurva
regresi dan εi error random yang diasumsikan
berdistribusi normal independen dengan mean nol dan variansi σ2. Apabila dalam analisis regresi bentuk kurva regresi diketahui secara jelas, maka model regresi tersebut dinamakan model regresi parametrik (Hardle,1990). Sebagai ilustrasi, jika pola data cenderung mengikuti model linear/kuadratik/kubik, maka pendekatan regresi yang sesuai untuk data tersebut adalah regresi parametrik linear/kuadratik/kubik (Budiantara,2001a).
Dalam kehidupan nyata, sesungguhnya tidak semua data (xi, yi) diketahui pola hubungannya secara
jelas. Apabila pada kasus seperti ini, model parametrik tetap dipaksakan sebagai model pola data, maka akan diperoleh kesimpulan yang menyesatkan. Regresi nonparametrik merupakan pendekatan regresi yang sesuai untuk pola data yang tidak diketahui bentuknya, atau tidak terdapat informasi masa lalu tentang pola data (Budiantara,2001b). Model regresi nonparametrik
yang sering mendapat perhatian dari para peneliti adalah Kernel (Hardle,1990), Spline (Wahba,1990; Craven dan Wahba,1979; Budiantara, et. al.,1997), Deret Fourier dan Wavelets (Antoniadis, et. al.,1994). Dalam pendekatan regresi nonparametrik, data diharapkan mencari sendiri bentuk pendugaannya, tanpa dipengaruhi oleh faktor subyektifitas peneliti.
Diantara model-model regresi nonparametrik di atas, Spline merupakan model regresi yang mempunyai interpretasi Statistik dan Visual sangat khusus dan sangat baik. Model Spline diperoleh dari suatu optimasi Penalized Least Square (PLS) dan memiliki fleksibelitas yang tinggi (Budiantara,2004). Disamping itu Spline mampu menangani karakter data/fungsi yang mulus (smooth). Spline juga memiliki
kemampuan yang sangat baik untuk menangani data yang perilakunya berubah-ubah pada sub-sub interval tertentu (Cox dan O’Sullivan,1996; Eubank,1988; Budiantara,2006).
Dalam regresi nonparametrik Spline, penduga kurva regresi diperoleh dari optimasi PLS atau
Penalized Likelihood (PL)(Craven dan Wahba,1979;
Budiantara, et. al.,1997). Penyelesaian optimasi ini diperoleh dengan menggunakan metode RKHS atau
karena memerlukan pengetahuan tentang Analisis Real dan Analisis Fungsional yang tinggi, sehingga sulit dipahami dan diselesaikan oleh para pengguna regresi nonparametrik Spline. Namun untuk menduga kurva regresi yang diperoleh dari optimasi Likelihood dapat
menjadi pilihan yang cukup baik karena secara matematik mudah dan sederhana.
Sedangkan untuk mengkonstruksi selang kepercayaan pada kurva regresi, beberapa peneliti
seperti Wahba (1983) dan Budiantara (2000b)
menggunakan pendekatan Bayesian dengan
menggunakan prior improper sehingga secara
matematis cukup sulit. Akan tetapi jika selang kepercayaan diperoleh dengan pendekatan Pivotal
Quantity tidak akan melibatkan distribusi prior,
sehingga diperoleh model yang sederhana dan inferensi Statistika yang relatif mudah (Eubank, 1988). Berdasarkan hal diatas, penulis tertarik untuk mempelajari pendekatan spline menggunakan optimasi
Likelihood dan menurunkan interval konfidensi untuk
kurva regresi nonparametrik dengan pendekatan
Pivotal Quantity. Penerapan regresi spline dan interval
konfidensi akan digunakan untuk mengetahui pola rata-rata berat badan dan umur balita, khususnya di kota Surabaya pada tahun 2007.
2. Estimasi Titik Untuk Kurva Regresi
Diberikan model regresi nonparametrik
yi = f(xi) + εi, xi [a,b], i=1,2,…,n. Bentuk kurva
regresi f diasumsikan tidak diketahui, termuat di dalam
ruang Sobolev , dengan :
∈
]
,
[
2a
b
W
pW
2p[
a
,
b
]
={
g
;
∫
(
f
(p)(
x
))
2dx
< }
∞
Selanjutnya estimasi titik untuk kurva f diperoleh dengan menggunakan Optimasi Likelihood. Diberikan suatu Basis untuk ruang Spline (Budiantara,2001(b)) berbentuk : { 1, x, x2,(
x
−
λ
1)
2+, . . . ,(
x
−
λ
m)
2+}, dengan :⎩
⎨
⎧
<
≥
−
=
−
+λ
λ
λ
λ
x
x
x
x
,
0
,
)
(
)
(
2 2dan
λ
1,λ
2,λ
3 merupakan titik-titik knots. Titik knots merupakan titik perpaduan bersama yang memperlihatkan terjadinya perubahan pola prilaku dari fungsi Spline pada interval-interval yang berbeda. Untuk setiap fungsi f dalam ruang Spline dapatdinyatakan menjadi : f(x)= 2, (1) 1 2 2 0
)
(
+ = + =−
+
∑
∑
k m k k j j jx
γ
x
λ
γ
dengan
γ
j merupakan konstanta yang bernilai real. Model regresi Spline dapat ditulis menjadi :yi = f(xi) + εi. = 2 + ε 1 2 2 0
)
(
+ = + =−
+
∑
∑
i k m k k j j i jx
γ
x
λ
γ
i.Apabila diasumsikan sesatan random εi berdistribusi
normal independen dengan mean nol dan variansi , maka y
2
σ
i juga berdistribusi normal dengan mean f(xi)dan variansi
σ
2. Akibatnya diperoleh fungsi Likelihood:)
,
(
y
f
L
=∏
= −⎟
⎠
⎞
⎜
⎝
⎛
−
−
n i i if
x
y
Exp
1 2 2 / 1 2))
(
(
2
1
(
)
2
(
σ
πσ
= 2 2 2 / 2))
(
(
2
1
(
)
2
(
i i nx
f
y
Exp
−
−
−σ
πσ
Estimasi titik untuk f diperoleh dengan menyelesaikan Optimasi Likelihood
Max
{
L
(
y
,
f
)
}
f = 1 2+ + ∈
Max
R m γ {−
∑
=−
− n i i ny
Exp
1 2 2 / 2(
2
1
(
)
2
(
σ
πσ
2 1 2 2 0)
(
+ = + =−
−
∑
∑
k m k k j j jx
γ
x
λ
γ
)2)}Apabila diambil transformasi Logaritma dan mengingat persamaan (1) maka diperoleh fungsi :
Log
L
(
y
,
λ
,
γ
)
=−
−
∑
−
= n i iy
n
1 2 2(
2
1
)
2
log(
2
πσ
σ
2 1 2 2 0)
(
+ = + =−
−
∑
∑
k m k k j j jx
γ
x
λ
γ
)2.Dengan penyajian matriks, diperoleh : Log
L
(
y
,
λ
,
γ
)
=log(2
2)
2
n
πσ
−
(
(
,
)
)
(
(
,
)
)
2
1
2λ
γ
λ
γ
σ
y
−
T
x
′
y
−
T
x
−
, (2) denganγ
=(
γ
0,
γ
1,
γ
2,
γ
3,
γ
4,
γ
5,
γ
6)
′
,y=
(
y
1,...,
y
n)
′
, danT
(
x
,
λ
)
matriks berukurannx(m+3), diberikan oleh :
)
,
(
x
λ
T
= .⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−
−
−
−
−
+ + + + + + 2 2 1 2 2 2 2 1 2 2 2 2 2 1 2 1 1 2 1 1)
(
)
(
1
)
(
)
(
1
)
(
)
(
1
m n n n n m mx
x
x
x
x
x
x
x
x
x
x
x
λ
λ
λ
λ
λ
λ
L
M
O
M
M
M
M
L
L
Apabila persamaan (2) diderivatifkan parsial terhadap
γ
γ
λ
∂
∂
Log
L
( y
,
,
)
=)]
)
,
(
(
)
)
,
(
(
2
1
[
2λ
γ
λ
γ
σ
γ
−
y
−
T
x
′
y
−
T
x
∂
∂
= 0. Dengan sedikit penjabaran dan mengingat)
,
(
x
λ
T
merupakan matriks dengan rank penuh, makadiperoleh estimasi Likelihood untuk
γ
adalah :γ
ˆ
(
x
,
λ
)
=[
T ′
(
x
,
λ
)
T
(
x
,
λ
)
)]
−1T ′
(
x
,
λ
)
y. Estimator kurva regresif
(x
)
diberikan oleh :)
,
(
^λ
x
f
=T
(
x
,
λ
)
[
T ′
(
x
,
λ
)
T
(
x
,
λ
)
)]
−1T ′
(
x
,
λ
)
y. =W
(
x
,
λ
)
y, dengan :W
(
x
,
λ
)
=T
(
x
,
λ
)
[
T ′
(
x
,
λ
)
T
(
x
,
λ
)
)]
−1T ′
(
x
,
λ
)
.Terlihat bahwa merupakan estimator linear
dalam observasi y dan sangat tergantung pada titik
knots
)
,
(
^λ
x
f
λ
= {λ
1,λ
2, . . .,λ
m}. Dalam model Spline titik knots harus dipilih dengan berbagai metode sepertiGeneralized Cross Validation (GCV) (Budiantara,2000a
dan Wahba,1983), Cross Validation (CV) (Craven dan
Wahba,1979), Generalized Maximum Likelihood (GML) (Wang,1998), atau metode-metode yang lainnya. Estimator linear ini sangat membantu dalam membangun inferensi Statistik, seperti interval konfidensi untuk kurva regresi f.
3. Interval Konfidensi Untuk Kurva Regresi
Persoalan inferensi yang sangat penting dalam regresi Spline, adalah interval konfidensi untuk kurva regresi , i = 1,2,...,n. Untuk memperolehinterval konfidensi, umumnya digunakan pendekatan Bayesian (Wahba,1983 ; 1990 dan Wang,1998). Dalam tulisan ini digunakan pendekatan lain, yaitu Pivotal
Quantity. Karena
)
(
x
if
ε
= (ε
1,...,ε
n)′
berdistribusi N(0,σ
2I
) maka : y berdistribusi N(f
(x
)
,σ
2I
). Selanjutnya variabel randomγ
ˆ
(
x
,
λ
)
berdistribusi N(f
(x
)
,[
T ′
(
x
,
λ
)
T
(
x
,
λ
)
)]
−1σ
2).Ekspektasi dan Variansi dari , berturut-turut
diberikan oleh :
)
,
(
^λ
x
f
E((
,
)
)= ^λ
x
f
T
(
x
,
λ
)
[
T ′
(
x
,
λ
)
T
(
x
,
λ
)
)]
−1T ′
(
x
,
λ
)
T
(
x
,
λ
)
γ
=T
(
x
,
λ
)
γ
=f
(x
)
, dan Var((
,
)
)= ^λ
x
f
σ
2T
(
x
,
λ
)
[
T ′
(
x
,
λ
)
T
(
x
,
λ
)
)]
−1T ′
(
x
,
λ
)
=σ
2W
(
x
,
λ
)
.Karena sifat linearitas dari distribusi normal maka variabel random :
(
,
)
berdistribusi N( , ^λ
x
f
f
(x
)
σ
2W
(
x
,
λ
)
).Jika diambil Transformasi :
U
(
x
,
λ
)
=(
σ
W
(
x
,
λ
)
)
−1( - ), atau :)
,
(
^λ
x
f
f
(x
)
U
(
x
i,
λ
1,
λ
2,
.
.
.,
λ
m)
=)
.,
.
.
,
,
,
(
)
(
)
.,
.
.
,
,
,
(
2 1 2 2 1 ^ m i i i m ix
x
f
x
f
λ
λ
λ
ω
σ
λ
λ
λ
−
, i = 1,2,...,n. =)
.,
.
.
,
,
,
(
)
(
)
(
ˆ
ˆ
2 1 2 2 1 2 2 0 m i i i k i m k k j i j jx
x
f
x
x
λ
λ
λ
ω
σ
λ
γ
γ
+
−
+−
= + =∑
∑
dengan
ω
i(
x
i,
λ
1,
λ
2,
.
.
.,
λ
m)
elemen diagonal ke-idari matriks
W
(
x
,
λ
)
. Variabel random)
.,
.
.
,
,
,
(
x
i 1 2 mU
λ
λ
λ
berdistribusi N(0,1). Dengandemikian
U
(
x
i,
λ
1,
λ
2,
.
.
.,
λ
m)
merupakan PivotalQuantity untuk Kurva regresi . Interval Konfidensi
)
(
x
if
α
−
1
diperoleh dari menyelesaikanpersamaan:
P
(
a
≤
U
(
x
i,
λ
1,
λ
2,
.
.
.,
λ
m)
≤
b
)
=
1
−
α
,
dengan
a
∈ ,
R
b
∈
R
, dan a < b, i = 1,2,...,n.Persamaan di atas dapat dinyatakan menjadi :
α
λ
λ
λ
ω
σ
λ
γ
γ
−
=
≤
−
−
+
≤
+ = + =∑
∑
1
)
)
.,
.
.
,
,
,
(
)
(
)
(
ˆ
ˆ
(
2 1 2 2 1 2 2 0b
x
x
f
x
x
a
P
m i i i k i K k k j i j jDengan sedikit penjabaran, diperoleh interval konfidensi
1
−
α
untukf
(
x
i)
, untuk i = 1,2,...,nα
λ
λ
λ
ω
σ
λ
γ
γ
λ
λ
λ
ω
σ
λ
γ
γ
−
=
⎟
⎟
⎟
⎟
⎠
⎞
−
⎥
⎦
⎤
⎢
⎣
⎡
−
+
⎜
⎜
⎜
⎜
⎝
⎛
≤
≤
−
⎥
⎦
⎤
⎢
⎣
⎡
−
+
∑
∑
∑
∑
= = + + = = + +1
)
.,
.
.
,
,
,
(
)
(
ˆ
ˆ
)
(
)
.,
.
.
,
,
,
(
)
(
ˆ
ˆ
2 1 2 2 0 1 2 2 2 1 2 2 0 1 2 2 m i i j K k k i k j i j i m i i j K k k i k j i jx
a
x
x
x
f
x
b
x
x
P
(3)Dengan menggunakan konsep Interval konfidensi terpendek, harus ditentukan nilai
a
∈
R
danb
∈
R
,sehingga panjang dari interval pada
Persamaan (3) terpendek. Untuk tujuan ini, dicari penyelesaian optimasi bersyarat berikut.
)
,
( b
a
l
={
(
,
)
}
,a
b
Min
R b R a∈ ∈l
{
(
)
2(
,
1,
2,
.
.
.,
)
}
,b R i i m R a∈Min
∈b
−
a
σ
ω
x
λ
λ
λ
, (4) Dengan syarat :∫
=
−
b aatau
du
u
)
1
,
(
α
ϕ
Φ
(
b
)
−
Φ
(
a
)
−
(
1
−
α
)
=
0
(5) Fungsiϕ
merupakan distribusi probabilitas N(0,1) danmerupakan distribusi probabilitas Kumulatif N(0,1). Optimasi (4) dan (5) dapat diselesaikan dengan
menggunakan metode Lagrange Multiple. Dibentuk
fungsi Lagrange :
Φ
)
.,
.
.
,
,
,
(
)
(
)
,
,
(
a
b
c
=
b
−
a
σ
2ω
ix
iλ
1λ
2λ
mΩ
+∫
=
−
−
. b adu
u
c
[
ϕ
(
)
(
1
α
)
]
umur bayi berat bayi 0 10 20 30 40 50 46 8 1 0 1 2 1 4 umur bayi berat bayi 0 10 20 30 40 50 46 8 1 0 1 2 1 4Selanjutnya dengan menderivatifkan fungsi terhadap a, b, dan c diperoleh:
)
,
,
(
a
b
c
Ω
=
⇒
∂
Ω
∂
0
)
,
,
(
a
c
b
a
−
σ
2ω
i(
x
i,
λ
1,
λ
2,
.
.
.,
λ
m)
−
c
ϕ
(a
)
= 0. (6)=
⇒
∂
Ω
∂
0
)
,
,
(
b
c
b
a
σ
2ω
i(
x
i,
λ
1,
λ
2,
.
.
.,
λ
m)
+
c
ϕ
(b
)
= 0. (7)⇒
=
∂
Ω
∂
0
)
,
,
(
c
c
b
a
0
)
1
(
)
(
)
(
−
Φ
−
−
=
Φ
b
a
α
(8)Persamaan (6) dan (7) menghasilkan penyelesaian :
ϕ
(
a
)
=
ϕ
(
b
)
. (9)Mengingat persamaan (8) dan maka
penyelesaian Persamaan (9) adalah , atau
(
~
0,1
U
N
)
b
a
=
b
a
=
−
. Tetapi persamaan tidak memenuhi.Jadi agar diperoleh interval konfidensi terpendek harus diambil nilai a dan b yang memenuhi persamaan :
b
a
=
∫
∫
∞ − ∞=
=
a bdu
u
du
u
(
)
2
)
(
α
ϕ
ϕ
(10)Jika tingkat konfidensi
1
−
α
diberikan, maka nilai adan b dapat dilihat dalam tabel distribusi N(0,1). Interval konfidensi
1
−
α
untuk kurva regresif
(
x
i)
,i = 1,2,...,n diberikan oleh Persamaan (3), dengan a
dan b memenuhi Persamaan (10).
4. Aplikasi Model dan Interval Konfidensi
Spline
Pada umumnya pola pertumbuhan balita tidaklah konstan, tetapi terjadi perubahan pola pertumbuhan pada umur-umur tertentu. Sejak kelahiran sampai umur 6 bulan pertumbuhan balita umumnya sangat pesat, tetapi setelah umur 6 bulan pertumbuhannya agak perlahan. Hal ini dapat dilihat dengan memodelkan pola hubungan antara umur dan berat badan balita di Kota Surabaya dengan model spline polinomial truncated :
f(x) = k p, m k p k p j j j
x
x
+ = + =−
+
∑
∑
(
)
1 0λ
γ
γ
untuk berbagai nilai p yang menunjukan orde spline dan berbagai m yang menunjukan banyak titik knot.
Untuk memilih titik knot optimal dalam model spline digunakan metode GCV. Dengan menggunakan Program S-Plus 2000 didapatkan nilai GCV terkecil 0,02526942 terjadi pada model spline kuadratik dengan tiga titik knot pada umur 4 bulan, umur 8 bulan, dan umur 14 bulan.
Gambar 1. Plot data dan spline kuadratik dengan titik
Setelah diperoleh titik – titik knot optimum selanjutnya dilakukan pendugaan pada model:
2 3 5 2 2 4 2 1 3 2 2 1 0
)
(
)
(
)
(
)
(
+ + +−
+
−
+
−
+
+
+
=
λ
γ
λ
γ
λ
γ
γ
γ
γ
x
x
x
x
x
x
f
Secara lengkap model regresi spline setelah diperoleh nilai – nilai estimasi dari γj yang signifikan adalah
sebagai berikut : 2 2 2 2 ^
)
14
(
4
0.00724217
)
8
(
0.01593129
)
4
(
0.03508034
0.05900713
-0.9431169
3.556999
)
(
+ + +−
+
−
+
−
+
+
=
x
x
x
x
x
x
f
Dari hasil pemilihan titik–titik knot optimal 4, 8, 14, diperoleh R2 = 0.9968227, atau R2 = 99,682%
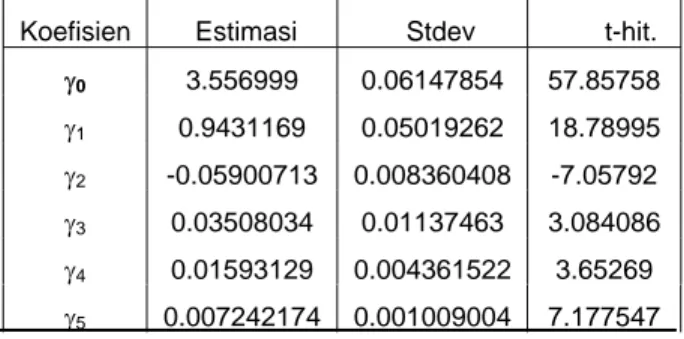
Tabel 1. Ringkasan statistik estimasi parameter model
spline kuadratik.
Koefisien Estimasi Stdev t-hit.
γ0 3.556999 0.06147854 57.85758 γ1 0.9431169 0.05019262 18.78995 γ2 -0.05900713 0.008360408 -7.05792 γ3 0.03508034 0.01137463 3.084086 γ4 0.01593129 0.004361522 3.65269 γ5 0.007242174 0.001009004 7.177547 umur bayi ber at bayi 0 10 20 30 40 50 46 8 1 0 1 2 1 4 umur bayi ber at bayi 0 10 20 30 40 50 46 8 1 0 1 2 1 4 umur bayi ber at bayi 0 10 20 30 40 50 46 8 1 0 1 2 1 4
Jadi berdasarkan Tabel 1, dapat disimpulkan pula bahwa model spline kuadratik dengan titik-titik knot 4, 8 dan 14 dengan nilai GCV = 0.02526942 adalah memadai sebagai model pendekatan untuk data.
Setelah mendapatkan model spline terbaik dengan model kuadratik tiga titik knot 4, 8 dan 14 bulan, akan dibangun interval konfidensi 95%. Kurva berwarna hitam adalah kurva spline dengan titik knot optimal dan kurva lain berturut-turut merupakan interval konfidensi spline bawah dan atas.
Gambar 2. Interval Konfidensi Spline
5. Kesimpulan
1. Untuk memperoleh estimasi titik kurva regresi dalam regresi nonparametrik spline, umumnya
digunakan optimasi Penalized Likelihood.
Disamping itu dapat pula menggunakan optimasi
Likelihood yang memberikan hasil relatif mudah.
2. Untuk membangun interval konfidensi dalam regresi nonparametrik spline, umumnya digunakan pendekatan Bayesian. Pendekatan
Pivotal Quantity juga dapat digunakan dan
memberikan hasil yang relatif sederhana.
3. Model Spline kuadrat sangat memadai untuk digunakan menduga pola hubungan antara umur balita dan berat badan balita di Kota Surabaya.
6. Referensi
Antoniadis, A., Gregorire, G. and Mackeagu, W., 1994, Wavelets Methods for Curve Estimation, Journal
of the American Statistical Association., 89,
1340-1353.
Budiantara, I.N, Subanar, and Soejoeti, Z., 1997, Weighted Spline Estimator, Bulletin of the
International Statistical Insitute, 51, 333-334.
Budiantara, I.N, 2000a, Metode U, GML, CV dan GCV Dalam Regresi Nonparametrik Spline, Majalah Ilmiah Himpunan Matematika Indonesia (MIHMI),
6, 285-290.
Budiantara, I. N., 2000b, Optimasi dan Proyeksi Dalam
Regresi Nonparametrik Spline, Majalah Berkala
Matematika dan Ilmu Pengetahuan Alam (BMIPA), Universitas Gadjah Mada, 10, 35-44.
Budiantara, I.N, 2001(a), Regresi Nonparametrik dan Semiparametrik Serta Perkemba-ngannya,
Makalah Pembicara Utama pada Seminar Nasional Alumni Pasca Sarjana Matematika Universitas Gadjah Mada, Yogyakarta.
Budiantara, I.N, 2001(b), Estimasi Parametrik dan Nonparametrik untuk Pendekatan Kurva Regresi,
Makalah Pembicara Utama pada Seminar nasional Statistika V, Jurusan Statistika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Teknologi Sepuluh Nopember (ITS), Surabaya.
Budiantara, I.N, 2004, Spline : Historis, Motivasi, dan Perannya Dalam Regresi Nonparametrik,
Makalah Pembicara Utama pada Konferensi Nasional Matematika XII, Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana (UNUD), Denpasar.
Budiantara, I.N, 2006, Regresi Nonparametrik Dalam
Statistika, Makalah Pembicara Utama pada
Seminar Nasional Matematika, Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Negeri Makasar (UNM), Makasar.
Cox, D. D. and O’Sullivan, F.,1996, Penalized Type Estimator for Generalized Nonparametric
Regression, 1983, Journal of Multivariate
Analysis, 56, 185-206.
Craven, P. and Wahba, G.,1979, Smoothing Noise
Data with Spline Functions, Numerische
Eubank, R.L.,1988, Spline Smoothing and Nonparametric Regression, Marcel Deker, New
York.
Hardle, W.,1990, Applied Nonparametric Regression, Cambridge University Press, New York.
Soetjiningsih, (1995), Tumbuh Kembang Anak,
Laboratorium Ilmu Kesehatan Anak Universitas Airlangga, Surabaya.
Supariasa, I.N.,Bakri, B., dan Fajar, I., (2002), Penilaian Status Gizi, Penerbit Buku Kedokteran EGC,
Jakarta.
Wahba, G.,1983, Bayesian Confidence Interval for the Cross Validated Smoothing Parameter in the Generalized Spline Smoothing Problems, The Annals of Statistics, 13, 1378-1402.
Wahba, G.,1990, Spline Models for Observasional Data, SIAM Pensylvania.
Wang, Y., 1998, Spline Smoothing Models With Correlated Errors, Journal of the American