Regresi Linear dan Metode Grafik

Regresi Linear dan Metode Grafik

Eko Sulistya

Laboratorium Fisika Dasar - Departemen Fisika FMIPA UGM Yogyakarta

sulistya@ugm.ac.id

27 Oktober 2017

Artikel ini membahas tentang metode regresi linear dan cara penarikan garis

lurus pada grafik yang diperlukan oleh mahasiswa yang mengambil

prakti-kum fisika dasar.

1

Pendahuluan

Pada praktikum Fisika Dasar diperlukan penggambaran grafik data pengamatan yang berupa kurva linier. Grafik linier (gari lurus) adalah grafik yang memberikan informasi yang diperluk-an, yaitu kemiringan garis dan titik potong, yang merupakan parameter yang diperlukan untuk menentukan variabel yang akan ditentukan dalam eksperimen.

Persamaan garis lurus yang mewakili relasi (hubungan) antara variabelx dany dituliskan dalam bentuk persamaan (1):

y=A+Bx, (1)

variabelyadalah besaran yang diukur.

AdanB bisa ditentukan dengan cara manual, yaitu dengan menggambarkan grafik (mem-plot) data-data pengamatan antaraxversusy. Kemudian dengan cara manual juga menarik ga-ris lurus yang diusahakan melewati sebanyak mungkin data. Cara kedua adalah dengan metode regresi linear yang berdasarkan pada metode kuadrat terkecil. Penjabaran bagaimana mempe-roleh nilaiAdanB dengan metode kuadrat terkecil tidak dibahas dalam tulisan ini, hanya akan disajikan hasil akhirnya. Untuk penjabaran silahkan baca di buku teks (1) dan (2).

2

Regresi Linear

Hubungan linier antarax dany diharapkan berbentuk seperti persamaan (1), yang dinamakan persamaan hasil fit linier, sehingga untuk setiap nilai xi bisa dihitung nilai yf it = A+Bxi. Sementara itu hasil pengukuran untuk nilaixiadalahyi. Jika hasil pengukurannya akurat, tidak ada ralat, makayi = yf it, namun dalam prakteknya, selalu ada ralat dalam hasil pengukuran yi. Data-data hasil pengukuran tersebar mengikuti distribusi normal, dengan nilai tengah adalah yi dan deviasi standarσi. Deviasi standar ini merupakan ukuran ralat dari hasil pengukurany. Jika ada sejumahN nilaiy, maka ada sejumlahN distribusi Gauss, dan ada sejumlahNdeviasi standar.

Tinjau salah satu pengukuran ke-i. Kebolehjadian (probability) memperoleh hasil ukur yi, dengan deviasi standarσiadalah (distribusi Gauss):

Pi = 1 σi

√

2π exp (

−1₂

yi−yf it σi

2)

(2)

Kebolehjadian menemukan satu set hasil sejumahN pengukuran adalah hasil kali dari masing-masing kebolehjadian-i,

Y Pi =

Y 1

σi √

2π exp (

−1₂X

yi−yf it σi

2)

Dengan mengingat persamaan (1), persamaan (3) dapat ditulis menjadi

Nilai terbolehjadi, atau nilai maksimum kebolehjadian persamaan (4) diperoleh jika nilai pada eksponensial minimum. Dengan menuliskan

χ2 =X

maka kebolehjadian pada persamaan (4) maksimum jikaχ2 _minimum.

2.1

Menentukan parameter

A

dan

B

Untuk mendapatkan parameterAdanB yang bisa membuat persamaan (5) minimum, makaχ2

Persamaan (6) dapat dituliskan menjadi

dan persamaan (7) dapat dituliskan menjadi

AX xi

Persamaan (8) dan persamaan (9) adalah persamaan simultan dengan 2 nilai yang akan dicari, yaituAdanB. Dua persamaan tersebut ditulis dalam bentuk matriks:

P ₁

Penyelesain persamaan (10) dengan metode determinan:

A=

Dengan menuliskanwi = 1/σi2, maka persamaan (11) dan (12) dapat ditulis menjadi:

Jika deviasi standar padayisemua sama, yaituσi =σ, maka

dan persamaan (11) dan (12) menjadi:

A= w2

Ralat dalamAdanBberasal dari sumbangan ralat dalamyiyaituσi(dianggap tidak sama untuk seluruhy), dihitung dengan rumus perambatan ralat.

σA2 =

Penyebut pada persamaan (11) dan (12) tidak bergantung kepada nilaiyi sehingga tidak terpe-ngaruh oleh derivasi ke-yisehingga bisa dikeluarkan dari derivatif dan dituliskan sebagai:

Selanjutnya,

Kemudian dari persamaan (17) dan (18),

2.3

Ralat dalam

A

dan

B

jika

σ

i

=

σ

Jika dalam pengukuran y terdapat ralat (absolut) yang sama, maka A dan B diberikan oleh persamaan 15 dan 16, dan ralatnya (buktikan!)

σA=σy

r P x2

∆ , (23)

σB =σy

r N

∆, (24)

dengan

σy =

v u u

t 1

N ₋2

N

X

i=1

(yi−A−Bxi)2 (25)

3

Contoh Penerapan Regresi Linier

Pengukuran suhu nol-mutlak dengan termometer gas volume konstan.

Jika volume dari suatu gas ideal dibuat tetap, maka suhunya merupakan fungsi linier dari teka-nannya. Bisa ditulis

T =A+BP (26)

Aadalah suhu pada saat tekanan mencapai nol, yang disebut dengan suhu nol-mutlak, dengan nilai yang diterima secara teoritis

A=₋273,15oC

KonstantaB bergatung kepada sifat alami gas, yaitu massa dan volumenya1. Dengan melakuk-an beberapa pengukurmelakuk-an akmelakuk-an diperoleh pasmelakuk-angmelakuk-an dataT dan P yang dapat digunakan untuk mengestimasi nilai-nilaiAdanB. Data-data yang diperoleh disajikan pada kolom 2 dan 3 tabel berikut.

Pengukuran

ke-Tekanan Pi

Suhu

Ti A+BPi

1 65 -20 -22,2

2 75 17 14,9

3 85 42 52,0

4 95 94 89,1

5 105 127 126,2

Perhitungan untuk mencari A dan B dengan persamaan (15) dan (16) telah dilakukan di buku (1) halaman 191. Dalam tulisan ini, pencarian nilai parameterAdanB dilakukan dengan pemrograman python. Listing program python untuk regresi linear adalah sebagai berikut.

#program r e g r e s i l i n i e r dengan bobot import matplotlib . pyplot as plt

from math import sqrt

import numpy as np

d e f inisialisasi ():

namafile = raw_input(’ F i l e yang akan d i b a c a ? ’) sumbux = raw_input(’Nama sumbu X ? ’)

sumbuy = raw_input(’Nama sumbu Y ? ’) judul = raw_input(’ J u d u l g r a f i k ? ’)

r e t u r n namafile , sumbux , sumbuy , judul

d e f bacafiledata ( datafile ):

filedata = open( datafile ,’ r ’)

datax = []; datay = []; datae = []; i = 0

f o r baris i n filedata : i +=1

datanya = baris . split () x = f l o a t( datanya [0]) datax . append (x)

y = f l o a t( datanya [1]) datay . append (y)

e = f l o a t( datanya [2]) datae . append (e)

p r i n t(" x = %5.2 f y = %5.2 f e = %5.2 f ") % (x , y , e) filedata . close ()

jumlahdata = i

p r i n t(" Jumlah d a t a = "), jumlahdata

r e t u r n jumlahdata , datax , datay , datae

plt . title ( judul ) plt . xlabel ( sumbux ) plt . ylabel ( sumbuy )

plt . legend ( loc =’ upper l e f t ’) plt . plot (x , y , ’ ko ’)

plt . errorbar (x , y , xerr = None , yerr =e , fmt = ’ ’) plt . show ()

d e f regresilinear (x , y , e ):

sum1 =0.0; sum2 =0.0; sum3 =0.0; sum4 =0.0; sum5 =0.0

f o r i i n range(0 , jumlahdata ):

sum1 = sum1 +( x[i ]_∗∗2/ e[i ]_∗∗2) #wx^2

sum2 = sum2 +( y[i ]/ e[i ]_∗∗2) #wy

sum3 = sum3 +( x[i ]/ e[i ]_∗∗2) #wx

sum4 = sum4 +( x[i]∗y[i ])/ e[i ]∗∗2 #wxy

sum5 = sum5 +1/ e[i ]_∗∗2 #w # h i t u n g determinan

det = ( sum5∗sum1)−sum3∗∗2 # (w) ( wx ^ 2 ) − ( wx ) ^ 2 # parameter a dan b

a = (( sum1_∗sum2)₋(sum3_∗sum4 ))/ det # ( ( wy ) ( wx ^ 2 ) ₋ ( wx ) ( wxy ) ) / d e t

b = (( sum5∗sum4)−(sum3 )∗( sum2 ))/ det # ( (w) ( wxy ) − ( wx ) ^ 2 ) / d e t

sigmaa2 = sum1 / det sigmab2 = sum5 / det

sigmaa = sqrt ( sigmaa2 ) # s q r t ( ( wx ^ 2 ) / d e t )

sigmab = sqrt ( sigmab2 ) # s q r t (w/ d e t ) r e t u r n a , b , sigmaa , sigmab

# p l o t g r a f i k

d e f plotregresi (x , a , b ):

f o r i i n range(0 , l e n(x )): y = a + b_∗x

plt . plot (x ,y ,’ g ’, label =’ H a s i l f i t ’)

d e f fitploterror (x ,a ,b ):

f o r i i n range(0 , l e n(x )): y = a + b_∗x

plt . plot (x ,y ,’ g ’, linestyle =’₋₋’)

d e f korelasi (x , y ):

sum1 = 0; sum2 = 0; sum3 = 0; sum4 = 0; sum5 = 0

sum5 += y[i ]_∗∗2

r1 = l e n(x)_∗sum1 ₋ sum2_∗sum3

r2 = sqrt ((l e n(x)_∗sum4 ₋ sum2_∗∗2)_∗(l e n(x)_∗sum5 ₋ sum3_∗∗2)) r = r1 / r2

r e t u r n r

namafile , sumbux , sumbuy , judul = inisialisasi ()

jumlahdata , datax , datay , datae = bacafiledata ( namafile )

r = korelasi ( datax , datay )

p r i n t(" K o e f i s i e n k o r e l a s i = %.2 f ") % (r)

a , b , sigmaa , sigmab = regresilinear ( datax , datay , datae )

p r i n t(" a= %8.6 f , sigmaa= %8.6 f ") % (a , sigmaa )

p r i n t(" b= %8.6 f , sigmab= %8.6 f ") % (b , sigmab )

xfit = np . arange (0 , max( datax ), 1) plotregresi ( xfit , a , b)

fitploterror ( xfit ,a₋sigmaa ,b+ sigmab ) fitploterror ( xfit ,a+ sigmaa ,b−sigmab ) gambar ( datax , datay , datae )

Untuk menjalankan program regresi-linier python di atas, data-data dituliskan dalam file txt 3 kolom dengan dibatasi spasi antar kolom. Kolom pertama adalah nilaix, kolom ke-2 adalah nilaiydan kolom ke-3 adalah nilaiσi.

Sebagai contoh, data-data pada tabel di atas dituliskan dalam file txt dengan σi = 7, dan disimpan dengan nama file : contoh.txt.

65 ₋20 7

75 17 7

85 42 7

95 94 7

105 127 7

Jalannya program adalah sebagai berikut:

C :\ Kuliah Metode Pengukuran Fisika > python regresi_linear_2 . py File yang akan dibaca ? contoh . txt

Nama sumbu Y ? T

Judul grafik ? Menentukan suhu nol mutlak x = 65.00 y = ₋20.00 e = 7.00

x = 75.00 y = 17.00 e = 7.00 x = 85.00 y = 42.00 e = 7.00 x = 95.00 y = 94.00 e = 7.00 x = 105.00 y = 127.00 e = 7.00 Jumlah data = 5

Koefisien korelasi = 1.00

a= ₋263.350000 sigmaa = 19.074197 b= 3.710000 sigmab = 0.221359

Grafik hasil program:

Gambar 1: Hasil program regresi linier python untuk file: contoh.txt

Dari hasil program di atas dapat dituliskan:

4

Metode Grafik

Pada dasarnya penentuanA danB tidak menjadi masalah jika dihitung dengan menggunakan metode regresi linier. Yang menjadi permasalahan adalah jika mahasiswa harus menggambark-an grafik dmenggambark-an menemukmenggambark-anAdanB secara manual, beserta dengan ketidakpastiannya. Masalah tersebut muncul karena tidak ada kejelasan mengenai bagaimana menerapkan metode mencari garis terbaik dengan bantuan dua garis maksimum dan minimum. Satu hal yang jelas adalah bahwa garis terbaik harus melewati titikcentroid2, yaitu nilai rata-rata dari variabelxdan vari-abely, titik(¯x,y)¯ .

4.1

Garis bantu ditarik dari ujung-ujung ralat

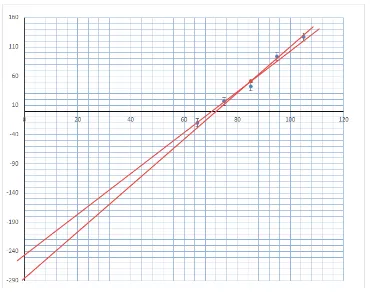
Cara ini yang biasanya digunakan oleh mahasiswa. Cara yang praktis, namun mengandung resiko bahwa garis terbaik tidak melewati titik centroid. Ingat, bahwa meskipun dinamakan garis bantu, namun garis tersebut adalah juga garis "terbaik" yang masih mungkin. Sebagai contoh ditunjukkan pada Gambar 2. Menentukan titik centroid:

¯ x=

P xi

N =

65 + 75 + 85 + 95 + 105

5 = 85

¯ y=

P yi

N =

(₋20) + 17 + 42 + 94 + 127

5 = 52

Titik merah adalah titik centroid, dua garis bantu digambarkan dengan menerapkan metode tarik garis dari ujung-ujung batang ralat. Dapat dilihat bahwa garis terbaik, yang merupakan rata-rata dari dua garis bantu tersebut tidak melewati titikcentroid. Grafik pada Gambar 2 ada-lah plot dari data-data pada contoh yang dibahas di depan, sehingga bisa dibandingkan hasilnya jika kita mencari persamaan garis lurus dengan metode grafik manual ini.

Kemiringan, atau gradien (slope) garis ditentukan secara manual dengan mencari dua titik

2

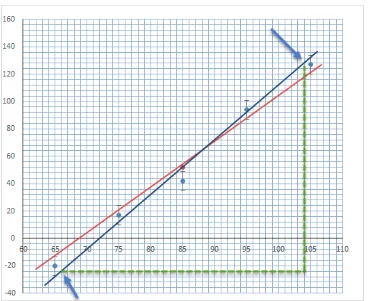
Gambar 2: Dua garis bantu ditarik dari ujung-ujung batang ralat

pada garis yang memotong garis grid. Semakin jauh jarak antara dua titik tersebut, hasil gradien semakin baik.

Lihat Gambar 3. Untuk garis-1 dari grafik diperoleh gradien:

B₁ = ∆y

∆x =

(128)₋(₋24)

104₋66 =

152 38 = 4

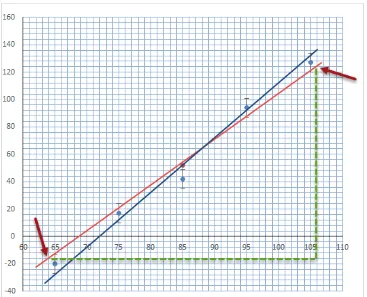
Dengan cara yang sama, gradien untuk garis-2 adalah (Lihat Gambar 4)

B₂ = ∆y

∆x =

(124)₋(₋16)

106₋64 =

140

42 = 3,33

Dengan demikian diperoleh gradien garis terbaiknya adalah:

¯

B = B1+B2

2 =

4,00 + 3,33

Gambar 3: Cara manual menentukan gradien garis

dan ralatnya:

σB¯ = |

B₁₋B_2|

2 =

|4,00₋3,33_|

2 = 0,335

Bisa juga dihitung dengan :σB¯ =

B₁−B¯=|4,00−3,665|= 0,335. Bisa dikatakan bahwa hasil penentuan gradien dengan cara grafik manual ini sama dengan hasil dari metode regresi linear, hanya ralatnya yang lebih besar.

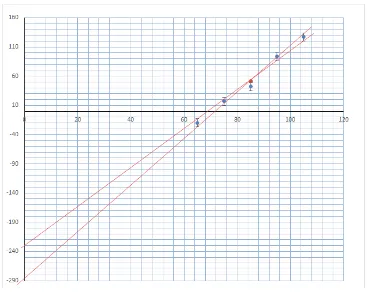
Selanjutnya adalah menentukanAdari grafik, yaitu titik potong garis dengan sumbu tegakl. Ditunjukkan pada Gambar 5. Gambar di-zoom untuk menunjukkan perpotongan garis dengan sumbuy. (Lihat Gambar (6)).

Gambar 4: Cara manual menentukan gradien garis

potong terbaiknya : ¯

A= A1+A2

2 =

(₋285) + (₋230)

2 =−257,5

dan ralatnya:

σA¯ =

A₁−A¯=|−285−(257,5)|= 27,5

Hasilnya dapat dituliskan:

¯

A_±σA= (−258±30)◦C

Gambar 5: Mencari titik potong garis dengan sumbuy

tidak akurat. Hal ini sudah terlihat bahwa garis-garis bantu tidak melewati titikcentroid yang menyebabkan garis terbaik juga tidak melewati titikcentroid, yang merupakan kekeliruan.

Pada contoh di atas, titik potong diperoleh dengan cara ekstrapolasi, yang memberikan efek pada membesarnya ralat pada titik potong. Semakin jauh ekstrapolasi, kedua garis bantu ak-an semakin menyebar. Dengak-an membuat garis bak-antu yak-ang melewati ujung-ujung batak-ang ralat (maksimum dan minium) maka pemisahan dua garis bantu juga akan besar, dan jika dilakukan ekstrapolasi, ralatnya akan semakin membesar. Sebagai contoh, ralat pada titik potong dengan menggunakan regresi linier sebesar

20

261 ∼= 7,7%

sedangkan dari hasil metode grafik

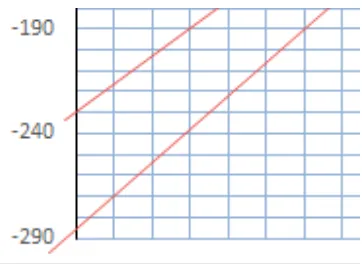
30

Gambar 6: Gambar titik-titik potong diperbesar

4.2

Garis bantu ditarik melewati titik

centroid

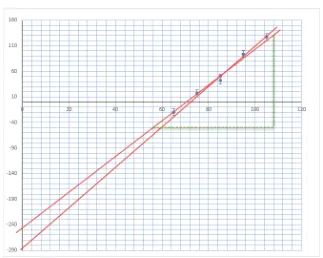
Karena garis-garis bantu adalah juga garis yang mungkin bisa mewakili titik-titik data, maka garis-garis tersebut juga harus melalui titikcentroid. Seperti ditunjukkan pada Gambar 7.

Dari Gambar 8 diperoleh gradien garis-1: 140₋(₋50)

108₋60 =

190

48 = 3,958

dan dari Gambar 9 diperoleh gradien garis-2: 130₋(₋50)

108₋56 =

180

52 = 3,462

Nilai terbaik gradien:

3,958 + 3,462

2 =

7,42

2 = 3,71

dengan ralat

3,958₋3,462

2 =

0,496

2 = 0,248

Dari gambar tersebut diperoleh nilai terbaik untukAadalah −245 + (₋285)

2 =−265

Gambar 7: Garis bantu melewati titik centroid

Hasil penentuanAdanB dengan ketiga metode dirangkum dalam tabel berikut:

Metode Regresi Garis bantu

dari ujung-ujung batang ralat

Garis bantu melewati titik centroid

A= (₋263_±19)◦_{C A= (}

−258_±30)◦_{C A= (}

−265_±20)◦_C B = (3,7_±0,2)◦_{C/mmHg B = (3,7±0,3)}◦_{C/mmHg B = (3,7±0,2)}◦_C/mmHg

Gambar 8: Menentukan gradien garis-1

5

Penutup

Dari uraian dan contoh-contoh yang telah diberikan, maka sebaiknya cara menarik garis bantu yang dilakukan dari ujung-ujung batang ralat sebaiknya dihindari. Selain cara itu bisa menyala-hi aturan penggambaran garis terbaik jika garis yang ditarik tidak melewati titik centroid, hasil perhitungannya juga menyimpang dari metode standar untuk menentukan parameter persamaan linear.

Pustaka

1. Taylor, J. R., 1992,An Introduction to Error Analysis, University Science Book.California.