d mtk 0808077 chapter3

(1)

BAB III

METODE PENELITIAN

A. Jenis dan Desain Penelitian

Jenis penelitian ini adalah eksperimen semu karena dilakukan dalam seting

sosial, dengan memberikan suatu perlakuan kepada sekelompok sampel dan

mengkaji dampak dari perlakuan tersebut. Adapun perlakuan yang diberikan

adalah pembelajaran generatif. Agar dampak perlakuan yang diberikan tidak bias,

peneliti berupaya semaksimal mungkin mengontrol variabel-variabel luar yang

tidak menjadi fokus kajian dalam penelitian.

Dampak dari pemberian perlakuan yang menjadi fokus kajian dalam

penelitian ini adalah kemampuan penalaran matematis (KPM), kemampuan

komunikasi matematis (KKM) dan kemandirian belajar siswa dalam matematika

(KBS) yang disebut sebagai variabel terikat (dependent variable), sedangkan

perlakuan yang diberikan kepada kelompok sampel penelitian disebut variabel

bebas (dependent variable), yaitu pembelajaran generatif.

Untuk melihat dampak dari perlakuan yang diberikan pada kelompok

eksperimen, dampak tersebut perlu dibandingkan dengan kelompok yang tidak

dikenakan perlakuan (kelompok kontrol). Dalam penelitian ini kelompok kontrol

tidak diberikan perlakuan khusus, sehingga siswa yang termasuk ke dalam

kelompok ini hanya mendapat pembelajaran biasa (konvensional).

Desain penelitian yang digunakan adalah Pretest and Postest Control

Group Design (Tuckman, 1978; Ruseffendi, 2005). Secara singkat, desain

(2)

O X O

O O (Ruseffendi, 2005)

Keterangan:

O : Pretes dan Postes (tes KPM dan KKM)

X : Perlakuan berupa pembelajaran generatif.

Dalam implementasinya, peneliti menggunakan tiga level sekolah, yaitu

level sekolah atas, level sekolah tengah, dan level sekolah bawah. Dari

masing-masing sekolah dipilih dua kelas, satu kelas untuk eksperimen dan satu kelas lagi

untuk kontrol. Kelompok eksperimen diberi perlakuan (X) yaitu pembelajaran

generatif, sedangkan kelompok kontrol tidak diberi perlakuan khusus.

Penetapan kelompok sampel penelitian atas kelompok eksperimen dan

kelompok kontrol mempertimbangkan pengelompokan siswa dalam rombongan

belajar yang ada di sekolah. Setiap kelas penelitian diberikan pretes dan postes

untuk mengukur KPM, KKM dan KBS. Skor hasil pretes dan postes merupakan

data penelitian yang digunakan untuk menguji hipotesis penelitian yang diajukan.

B. Variabel Penelitian

Sejalan dengan rumusan masalah yang dikemukakan sebelumnya, variabel

penelitian yang menjadi pokok kajian terdiri dari variabel bebas dan variabel

terikat. Variabel bebas adalah pembelajaran generatif (PG) dan variabel terikat

adalah KPM, KKM dan KBS. Selain itu penelitian ini juga melibatkan level

sekolah (atas, tengah, bawah) dan kemampuan awal matematis (tinggi, sedang,

rendah) sebagai variabel kontrol.

Keterkaitan antar variabel bebas, variabel terikat, dan variabel kontrol

(3)

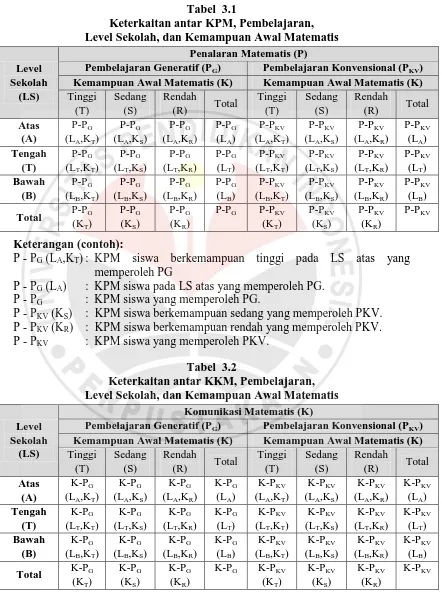
Tabel 3.1

Keterkaitan antar KPM, Pembelajaran, Level Sekolah, dan Kemampuan Awal Matematis Level

Sekolah (LS)

Penalaran Matematis (P)

Pembelajaran Generatif (PG) Pembelajaran Konvensional (PKV)

Kemampuan Awal Matematis (K) Kemampuan Awal Matematis (K)

Tinggi Level Sekolah, dan Kemampuan Awal Matematis Level

Sekolah (LS)

Komunikasi Matematis (K)

(4)

K - PG (LA) : KKM siswa pada LS atas yang memperoleh PG Level Sekolah, dan Kemampuan Awal Matematis

Level Sekolah

(LS)

Kemandirian Belajar Siswa (KBS)

Tinggi

Populasi dalam penelitian ini adalah seluruh siswa SMA Kota Pekanbaru

tahun pelajaran 2010/2011. Pemilihan siswa SMA sebagai populasi penelitian

didasarkan pada pertimbangan:

(1) Perkembangan intelektual siswa kelas X secara umum masih belum formal

(5)

(2) Pada umumnya KBS SMA lebih tinggi daripada siswa SMP.

(3) Berdasarkan studi terdahulu, penerapan model pembelajaran generatif di

jenjang sekolah menengah (SMP dan SMA) memberikan dampak positif

terhadap keaktifan siswa, sikap, dan hasil belajar siswa.

2. Sampel Penelitian

Sampel penelitian ditentukan berdasarkan teknik strata (stratified

sampling). Teknik ini dipilih karena sampel yang terambil dari

kelompok-kelompok yang berbeda akan mewakili karakteristik masing-masing kelompok-kelompok

populasi. Sampel penelitian adalah siswa SMA kelas X pada level sekolah atas,

tengah, dan bawah di Kota Pekanbaru. Dalam menetapkan sampel penelitian,

ditempuh langkah-langkah sebagai berikut:

a. Meminta daftar sekolah dari Dinas Pendidikan Kota Pekanbaru berdasarkan

jumlah nilai ujian nasional SMA tahun pelajaran 2009/2010 kelompok IPA

(Bahasa Indonesia, Inggris, Matematika, Fisika, Kimia, Biologi) dan IPS

(Bahasa Indonesia, Inggris, Matematika, Ekonomi, Sosiologi, Geografi).

b. Menetapkan ranking SMA Kota Pekanbaru berdasarkan nilai rata-rata dari total

kelompok (IPA, IPS), yang didasarkan pada hasil UN 2009/2010.

c. Menentukan pengkategorian level sekolah dengan menggunakan kriteria:

(1) level sekolah atas : skor total nilai UN > X + SD

(2) level sekolah tengah : X – SD  skor total nilai UN ≤ X + SD

(3) level sekolah bawah : skor total nilai UN < X – SD

d. Setelah pengkategorian level sekolah ditentukan, maka berdasarkan

pertimbangan diperoleh 3 sekolah, yakni: satu level sekolah atas, satu level

(6)

e. Dari setiap sekolah yang dipilih menjadi sampel, berdasarkan pertimbangan

diambil dua kelas dengan asumsi kemampuannya sama.

f. Dari dua kelas yang dipilih sebagai sampel, ditetapkan satu kelas kontrol dan

satu kelas eksperimen berdasarkan pertimbangan.

Berdasarkan data UN SMA tahun pelajaran 2009/2010 diperoleh bahwa

rata-rata total nilai (X) mata pelajaran yang diujikan untuk kelompok (IPA, IPS)

sebesar 49,21 dengan simpangan baku 1,78 (Adaptasi dari Diknas Kota

Pekanbaru, 2011). Dengan menggunakan aturan di atas, maka kategori level

sekolah yang digunakan adalah sebagai berikut:

(1) level sekolah atas : skor total nilai UN > 50,98

(2) level sekolah tengah : 47,43  skor total nilai UN ≤ 50,98

(3) level sekolah bawah : skor total nilai UN < 47,43

Pada level sekolah atas, sekolah yang dipilih sebagai tempat penelitian

adalah SMAN 5 Pekanbaru dari lima sekolah yang ada (SMA Plus Provinsi Riau,

SMAN 8, SMAN 1, SMAN 5, dan SMAN 4 Pekanbaru), dengan siswa kelas X.10

sebagai kelas eksperimen dan siswa kelas X.8 sebagai kelas kontrol. Level

sekolah tengah dipilih SMAN 7 Pekanbaru dari dua puluh empat sekolah yang ada

(SMAN 3, SMAN 7, ... , SMAN 11), dengan siswa kelas X.7 sebagai kelas

eksperimen dan siswa kelas X.6 sebagai kelas kontrol. Pada level sekolah bawah,

dipilih SMA Nurul Falah Pekanbaru dari tujuh sekolah yang ada (SMA Datuk

Batu Hampar, SMAN 13, SMA An-Nur, SMA Taruna Mandiri, SMA Widya

Graha, SMA Insan Terpuji, dan SMA Nurul Falah Pekanbaru), dengan siswa

kelas X.1 sebagai kelas eksperimen dan siswa kelas X.3 sebagai kelas kontrol.

(7)

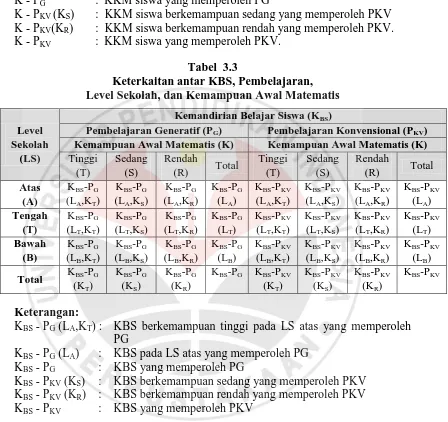
Tabel 3.4.

Sampel Penelitian berdasarkan Level Sekolah

Level Sekolah Sekolah Kelompok Subjek Ukuran Sampel

Atas SMAN 5

Siswa Kelas X.10

(Kelompok Generatif) 32

Siswa Kelas X.8

(Kelomp. Konvensional) 30

Tengah SMAN 7

Siswa Kelas X.7

Siswa Kelas X.6

Bawah SMA Nurul

Falah

Siswa Kelas X.1

Siswa Kelas X.3

Jumlah 192

D. Instrumen Penelitian dan Pengembangannya

Untuk mengumpulkan data yang diperlukan dalam penelitian ini,

digunakan dua jenis instrumen, yaitu tes dan non-tes. Instrumen dalam bentuk tes

terdiri dari seperangkat tes untuk mengukur kemampuan awal matematis,

kemampuan penalaran dan komunikasi matematis, sedangkan instrumen dalam

bentuk non-tes terdiri dari skala kemandirian belajar siswa dalam matematika,

lembar observasi aktivitas guru dan siswa selama pembelajaran, dan pedoman

wawancara siswa.

Langkah awal yang dilakukan adalah membuat kisi-kisi dan merancang

instrumen penelitian yang selanjutnya divalidasi (muka dan isi) oleh penimbang

atau validator yang berlatar belakang mahasiswa S3 pendidikan matematika yang

dianggap ahli. Pertimbangan validitas muka didasarkan pada kejelasan soal dari

segi bahasa atau redaksional dan dari segi gambar atau representasi. Pertimbangan

(8)

diberikan, indikator pencapaian hasil belajar, aspek kemampuan awal matematis

siswa yang diukur dan tingkat kesukaran siswa SMA kelas X. Setelah instrumen

direvisi berdasarkan masukan para ahli, kemudian diujicobakan kepada siswa

yang sudah mempelajari materi itu.

Ujicoba instrumen tes bertujuan untuk mengetahui validitas dan reliabilitas

tes, sementara ujicoba instrumen non tes, dilakukan untuk pembobotan pada tiap

butir skala kemandirian belajar. Kemudian dilakukan analisis instrumen untuk

mengetahui apakah perangkat tes sudah memenuhi syarat untuk penelitian atau

belum. Apabila perangkat tes sudah memenuhi syarat, maka instrumen tersebut

dapat diterapkan di lapangan.

Berikut ini merupakan uraian dari masing-masing instrumen yang

digunakan.

1. Tes Kemampuan Awal Matematis (KAM)

Tes KAM digunakan untuk mengukur kemampuan yang dimiliki siswa

sebelum diberikan pembelajaran (perlakuan). Pemberian tes KAM dimaksudkan

untuk pengelompokan siswa berdasarkan kategori KAM ke dalam tiga kelompok

kemampuan, yaitu kelompok siswa berkemampuan tinggi, sedang dan rendah.

Pengelompokan siswa didasarkan pada kriteria seperti terlihat pada Tabel 3.5.

Tabel 3.5

Kriteria Pengelompokan Siswa berdasarkan KAM Interval Skor Tes KAM Kategori

xi ≥ 18 Tinggi

13 < xi < 18 Sedang

xi ≤ 13 Rendah

Keterangan: Skor ideal adalah 24

(9)

Tes KAM menggunakan bentuk pilihan ganda dengan empat pilihan.

Jumlah butir soal pada awalnya 32, tetapi setelah melalui tahap ujicoba ada 8 butir

soal yang tidak valid sehingga jumlah soal yang digunakan sebanyak 24 butir

soal. Uji validitas setiap butir tes KAM dilakukan melalui pertimbangan para ahli

tentang validitas muka dan isi dari butir tes KAM. Penskoran terhadap jawaban

siswa untuk setiap butir soal dilakukan dengan aturan bahwa untuk setiap jawaban

benar diberi skor 1, dan untuk setiap jawaban salah atau tidak menjawab diberi

skor 0.

Hasil pertimbangan validitas muka dan isi oleh lima penimbang secara

lengkap disajikan pada lampiran C-1 halaman 473 dan 474. Hipotesis yang diuji:

Ho : Para penimbang memberikan pertimbangan yang sama

H1 : Para penimbang memberikan pertimbangan yang tidak sama

Untuk menguji keseragaman hasil pertimbangan validitas muka dan isi

kelima penimbang, dianalisis dengan menggunakan ststistik Q-Cochran. Analisis

statistik ini bertujuan untuk mengetahui apakah para penimbang memberikan

pertimbangan terhadap setiap butir tes KAM secara sama atau tidak. Kriteria

pengujiannya: jika nilai probabilitas (sig.) lebih besar dari 0,05, maka Ho diterima

dan dalam keadaan lainnya Ho ditolak. Hasil uji statistik hasil pertimbangan

terhadap validitas muka dan isi disajikan pada Tabel 3.6 dan Tabel 3.7.

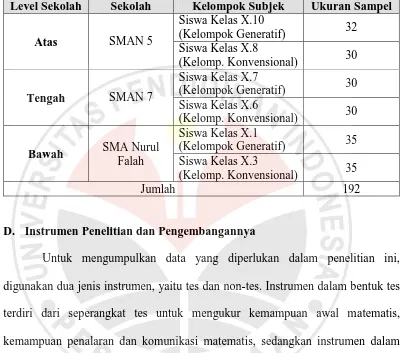
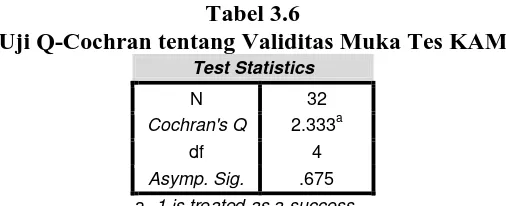
Tabel 3.6

Uji Q-Cochran tentang Validitas Muka Tes KAM

Test Statistics

N 32

Cochran's Q 2.333a

df 4

(10)

Tabel 3.7

Uji Q-Cochran tentang Validitas Isi Tes KAM

Test Statistics

N 32

Cochran's Q 2.333a

df 4

Asymp. Sig. .675 a. _{1 is treated as a success}.

Berdasarkan Tabel 3.6 dan Tabel 3.7 di atas, terlihat bahwa harga statistik

Q-Cochran untuk validitas muka dan isi adalah 2,33 dengan angka signifikansi

asimtotis 0,68 lebih besar dari 0,05 sehingga Ho diterima. Dengan demikian, para

penimbang memberikan pertimbangan yang sama terhadap validitas muka dan isi

setiap buitr tes KAM. Selanjutnya soal diujicobakan kepada 32 siswa untuk

mengetahui validitas dan reliabilitas butir soal. Validitas butir soal dihitung

menggunakan rumus korelasi Product Moment Pearson. Reliabilitas tes KAM

dihitung menggunakan rumus KR-21. Analisis validitas dan reliabilitas tes KAM

selengkapnya dapat dilihat pada lampiran C-1 halaman 328. Hasil perhitungan

reliabilitas dan validitas tes KAM disajikan pada Tabel 3.8.

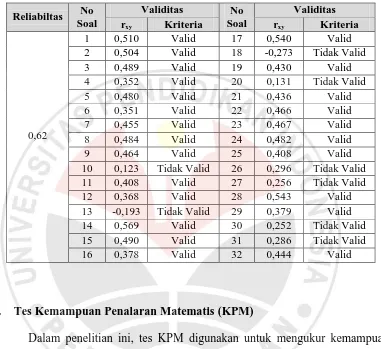
Dari Tabel 3.8 terlihat bahwa besarnya koefisien reliabilitas adalah 0,62.

Menurut Guildford (Ruseffendi, 2005), suatu tes dengan koefisien reliabilitas

sebesar 0,62 tergolong sedang. Dari Tabel 3.8 terlihat juga bahwa 24 butir soal

koefisien rhitung (rxy) lebih besar dari rtabel (0,349) berarti Ho ditolak, sehingga

terdapat korelasi positif yang signifikan antara skor butir soal dengan skor total

untuk 24 butir soal tersebut. Dengan demikian, untuk 24 butir tes KAM

(11)

Tabel 3.8

Hasil Perhitungan Reliabiltas dan Validitas Tes KAM Reliabiltas No

Soal

Validitas No

Soal

Validitas

rxy Kriteria rxy Kriteria

0,62

1 0,510 Valid 17 0,540 Valid

2 0,504 Valid 18 -0,273 Tidak Valid

3 0,489 Valid 19 0,430 Valid

4 0,352 Valid 20 0,131 Tidak Valid

5 0,480 Valid 21 0,436 Valid

6 0,351 Valid 22 0,466 Valid

7 0,455 Valid 23 0,467 Valid

8 0,484 Valid 24 0,482 Valid

9 0,464 Valid 25 0,408 Valid

10 0,123 Tidak Valid 26 0,296 Tidak Valid 11 0,408 Valid 27 0,256 Tidak Valid

12 0,368 Valid 28 0,543 Valid

13 -0,193 Tidak Valid 29 0,379 Valid 14 0,569 Valid 30 0,252 Tidak Valid 15 0,490 Valid 31 0,286 Tidak Valid

16 0,378 Valid 32 0,444 Valid

2. Tes Kemampuan Penalaran Matematis (KPM)

Dalam penelitian ini, tes KPM digunakan untuk mengukur kemampuan

penalaran matematis siswa sebelum dan sesudah pembelajaran dilaksanakan, baik

untuk kelas eksperimen maupun kelas kontrol. Materi pokok yang diujikan adalah

sistem persamaan linear dan pertidaksamaan satu variabel (SPLDV, SPLTV,

SPLK, PtK, PtL). Tes kemampuan ini berbentuk uraian yang terdiri dari enam

butir soal.

Tes KPM disusun dan dikembangkan oleh peneliti berdasarkan prosedur

penyusunan instrumen yang baik dan benar. Penyusunan tes diawali dengan

pembuatan kisi-kisi tes yang mencakup kompetensi dasar, indikator yang diukur,

(12)

Indikator yang diukur dalam tes KPM adalah (1) kemampuan menyatakan

situasi masalah dengan menggunakan gambar dan fakta dalam menyelesaikan

soal; (2) kemampuan menyelesaikan situasi masalah dengan mengikuti

argumen-argumen logis; dan (3) kemampuan menyelesaikan situasi masalah dengan

mengikuti argumen-argumen logis dan menarik kesimpulan logis dari

penyelesaian yang diperoleh. Kemudian menyusun tes beserta kunci jawaban.

Aturan pemberian skor untuk setiap jawaban siswa ditentukan berdasarkan

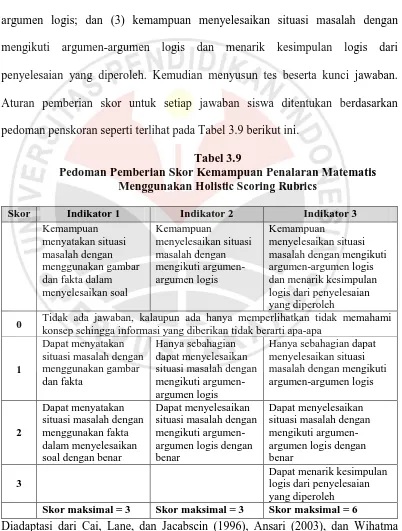
pedoman penskoran seperti terlihat pada Tabel 3.9 berikut ini.

Tabel 3.9

Pedoman Pemberian Skor Kemampuan Penalaran Matematis Menggunakan Holistic Scoring Rubrics

Skor Indikator 1 Indikator 2 Indikator 3

Kemampuan konsep sehingga informasi yang diberikan tidak berarti apa-apa

(13)

Tes KPM, terlebih dahulu divalidasi oleh lima orang penimbang berlatar

belakang S3 pendidikan matematika yang dianggap ahli dalam pendidikan

matematika. Para penimbang diminta untuk menilai atau mempertimbangkan dan

memberikan saran atau masukan mengenai validitas muka dan isi dari tes tersebut.

Pertimbangan validitas muka didasarkan pada kejelasan soal dari segi

bahasa atau redaksional dan kejelasan soal dari segi gambar atau representasi.

Pertimbangan vaditas isi didasarkan pada kesesuaian butir soal dengan materi

pokok yang diberikan, indikator pencapaian hasil belajar, aspek KPM yang diukur

dan tingkat kesukaran untuk siswa SMA kelas X. Hasil pertimbangan validitas

muka dan isi dari lima penimbang disajikan pada lampiran C-2 halaman 479.

Hipotesis yang diuji adalah sebagai berikut.

Kriteria pengujian yang digunakan adalah: jika nilai probabilitas (sig.) lebih

besar dari α = 0,05, maka Ho diterima dan dalam keadaan lainnya Ho ditolak.

Hasil perhitungan validitas muka dan isi tes KPM dengan menggunakan

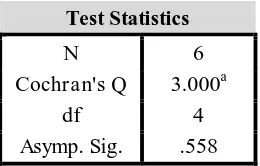
statistik Q-Cochran disajikan pada Tabel 3.10 dan Tabel 3.11.

Tabel 3.10

Uji Hasil Pertimbangan Validitas Muka Tes KPM

Test Statistics

N 6

Cochran's Q 3.000a

df 4

(14)

Tabel 3.11

Uji Hasil Pertimbangan Validitas Isi Tes KPM Test Statistics

N 6

Cochran's Q 3.000a

df 4

Asymp. Sig. .558

a. 1 is treated as a success.

Berdasarkan Tabel 3.10 dan Tabel 3.11 di atas terlihat bahwa harga

ststistik Q-Cochran untuk validitas muka dan isi adalah 3 dengan angka

signifikansi asimtotis 0,56 lebih besar dari 0,05, sehingga Ho diterima. Jadi para

penimbang memberikan pertimbangan yang sama terhadap validitas muka dan isi

setiap butir tes KPM.

Setelah tes diperbaiki berdasarkan masukan para penimbang, dilakukan uji

coba pada siswa kelas XI SMA Negeri 5 Pekanbaru sebanyak 40 siswa. Data hasil

uji coba tes KPM serta perhitungan reliabilitas instrumen dan validitas butir soal

selengkapnya dapat dilihat pada lampiran C-2 halaman 482.

Selanjutnya untuk menguji validitas butir soal, skor setiap butir soal

dikorelasikan dengan skor total. Hipotesis diajukan sebagai berikut.

Ho : Tidak terdapat korelasi positif yang signifikan antara skor butir soal dan skor

total.

H1 : Terdapat korelasi positif yang signifikan antara skor butir soal dan skor total.

Untuk menguji hipotesis ini digunakan rumus product moment dari Karl Pearson.

Kriteria pengujian yang digunakan, yakni: jika rhitung (rxy) ≥ rtabel, maka Ho ditolak,

dalam keadaan lainnya Ho diterima. Pada taraf α = 0,05 dengan N = 40

(15)

Hasil perhitungan koefisien reliabilitas dan koefisien korelasi setiap butir

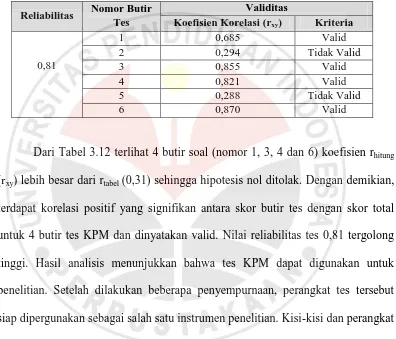
soal tes KPM disajikan pada Tabel 3.12.

Tabel 3.12

Hasil Perhitungan Reliabilitas dan Validitas Butir Tes KPM Reliabilitas Nomor Butir

Tes

Validitas

Koefisien Korelasi (rxy) Kriteria

0,81

1 0,685 Valid

2 0,294 Tidak Valid

3 0,855 Valid

4 0,821 Valid

5 0,288 Tidak Valid

6 0,870 Valid

Dari Tabel 3.12 terlihat 4 butir soal (nomor 1, 3, 4 dan 6) koefisien rhitung

(rxy) lebih besar dari rtabel (0,31) sehingga hipotesis nol ditolak. Dengan demikian,

terdapat korelasi positif yang signifikan antara skor butir tes dengan skor total

untuk 4 butir tes KPM dan dinyatakan valid. Nilai reliabilitas tes 0,81 tergolong

tinggi. Hasil analisis menunjukkan bahwa tes KPM dapat digunakan untuk

penelitian. Setelah dilakukan beberapa penyempurnaan, perangkat tes tersebut

siap dipergunakan sebagai salah satu instrumen penelitian. Kisi-kisi dan perangkat

tes selengkapnya disajikan pada lampiran B-5 halaman 445.

3. Tes Kemampuan Komunikasi Matematis (KKM)

Dalam penelitian ini, tes KKM digunakan untuk mengukur kemampuan

komunikasi matematis siswa sebelum dan sesudah pembelajaran dilaksanakan,

baik untuk kelas eksperimen maupun kelas kontrol. Materi pokok yang diujikan

adalah sistem persamaan linear dan pertidaksamaan satu variabel (SPLDV,

SPLTV, SPLK, PtK, PtL). Tes kemampuan ini berbentuk uraian yang terdiri dari

(16)

Tes KKM disusun dan dikembangkan oleh peneliti berdasarkan prosedur

penyusunan instrumen yang baik dan benar. Penyusunan tes diawali dengan

pembuatan kisi-kisi tes yang mencakup kompetensi dasar, indikator yang diukur,

aspek yang diukur, dan tes.

Indikator yang diukur dalam tes KKM adalah (1) kemampuan menyatakan

situasi masalah ke dalam model matematika dan menyelesaikannya secara tertulis

ke dalam gambar atau grafik (menggambar); (2) kemampuan menyatakan situasi

masalah ke dalam model matematika dan menyelesaikannya (ekspresi matematis);

dan (3) kemampuan menjelaskan konsep dan ide dari suatu gambar yang

diberikan ke dalam model matematika secara tertulis dan menyelesaikannya

(menulis). Kemudian menyusun tes beserta kunci jawaban. Aturan pemberian

skor untuk setiap jawaban siswa ditentukan berdasarkan pedoman penskoran

seperti terlihat pada Tabel 3.13.

Sebelum digunakan, tes KKM terlebih dahulu divalidasi oleh lima

penimbang berlatar belakang S3 pendidikan matematika yang dianggap ahli

dalam pendidikan matematika. Para penimbang diminta untuk menilai atau

mempertimbangkan dan memberikan saran atau masukan mengenai validitas

muka dan isi dari tes tersebut.

Pertimbangan validitas muka didasarkan pada kejelasan soal dari segi

bahasa atau redaksional dan kejelasan soal dari segi gambar atau representasi.

Pertimbangan vaditas isi didasarkan pada kesesuaian butir soal dengan materi

pokok yang diberikan, indikator pencapaian hasil belajar, aspek KKM yang

(17)

Tabel 3.13

Pedoman Pemberian Skor Kemampuan Komunikasi Matematis Siswa Menggunakan Holistic Scoring Rubrics

Skor Indikator 1 Indikator 2 Indikator 3

Kemampuan menyatakan konsep dan ide dari suatu gambar yang diberikan ke konsep sehingga informasi yang diberikan tidak berarti apa-apa

1 konsep dan ide dari suatu

gambar yang diberikan,

3 Dapat menggambar grafik dengan benar

Skor maksimal = 6 Skor maksimal = 3 Skor maksimal = 4

Diadaptasi dari Cai, Lane, Jacabscin (1996), Ansari (2003), dan Wihatma (2004)

Hasil pertimbangan validitas muka dan isi dari lima penimbang disajikan

pada lampiran C-3 halaman 483. Hipotesis yang diuji adalah sebagai berikut.

Untuk menguji keseragaman hasil pertimbangan validitas muka dan isi oleh lima

penimbang, dianalisis dengan menggunakan ststistik Q-Cochran. Kriteria

pengujian yang digunakan, yakni: jika nilai probabilitas (sig.) lebih besar dari

(18)

Hasil perhitungan validitas muka dan isi tes KKM menggunakan statistik

Q-Cochran disajikan pada Tabel 3.14 dan Tabel 3.15.

Tabel 3.14

Uji Hasil Pertimbangan Validitas Muka Tes KKM Test Statistics

N 6

Cochran's Q 3.000a

df 4

Asymp. Sig. .558

Tabel 3.15

Uji Hasil Pertimbangan Validitas Isi Tes KKM Test Statistics

N 6

Cochran's Q 3.000a

df 4

Asymp. Sig. .558

Tabel 3.14 dan Tabel 3.15 menunjukkan bahwa harga statistik Q-Cochran

untuk validitas muka dan isi adalah 3 dengan nilai asymp. sig. 0,56 lebih besar

dari 0,05, sehingga Ho diterima. Dengan demikian, para penimbang memberikan

pertimbangan yang sama terhadap validitas muka dan isi setiap buitr tes KKM.

Setelah tes diperbaiki berdasarkan masukan para penimbang, dilakukan

ujicoba pada siswa kelas XI SMA Negeri 5 Pekanbaru sebanyak 40 siswa. Data

hasil ujicoba tes KKM, perhitungan reliabilitas instrumen dan validitas butir tes

selengkapnya dapat dilihat pada lampiran C-3 halaman 486. Selanjutnya untuk

menguji validitas butir tes, skor setiap butir tes dikorelasikan dengan skor total.

(19)

Ho : Tidak ada korelasi positif yang signifikan antara skor butir tes dan skor total.

H1 : Ada korelasi positif yang signifikan antara skor butir tes dan skor total.

Untuk menguji hipotesis ini digunakan rumus product moment dari Karl

Pearson. Kriteria pengujian yang digunakan adalah: jika rhitung (rxy) ≥ rtabel,

maka Ho ditolak; dalam keadaan lainnya Ho diterima. Pada taraf α = 0,05 dengan

N = 40 diperoleh rtabel = 0,31. Dalam perhitungan reliabilitas tes digunakan

Cronbach-Alpha. Hasil perhitungan koefisien reliabilitas dan koefisien korelasi

setiap butir tes KKM disajikan pada Tabel 3.16.

Tabel 3.16

Hasil Perhitungan Reliabilitas dan Validitas Butir Tes KKM

Reliabilitas Nomor Butir Tes

Validitas

Koefisien Korelasi (rxy) Kriteria

0,66

1 0,468 Valid

2 0,696 Valid

3 0,844 Valid

4 0,823 Valid

5 0,298 Tidak Valid

6 0,610 Valid

Pada Tabel 3.16 dapat dilihat bahwa pada lima butir tes (butir nomor 1,

2, 3, 4, dan 6) koefisien rhitung (rxy) lebih besar dari rtabel (0,31) sehingga Ho ditolak.

Jadi, ada korelasi positif yang signifikan antara skor butir tes dengan skor total

untuk lima butir tes tersebut. Dengan demikian, lima butir tes KKM dinyatakan

valid. Hasil analisis tersebut menunjukkan bahwa tes KKM dapat digunakan

untuk penelitian. Setelah dilakukan beberapa penyempurnaan, perangkat tes

KKM siap dipergunakan sebagai salah satu instrumen penelitian. Kisi-kisi dan

(20)

4. Skala Kemandirian Belajar Siswa dalam Matematika

Skala kemandirian belajar siswa (KBS) dalam matematika digunakan

untuk mengetahui tingkatan kemandirian belajar siswa dalam matematika. Skala

ini dijaring melalui angket tertutup, disusun dan dikembangkan berdasarkan

sepuluh aspek kemandirian belajar, yakni: (1) inisiatif belajar; (2) mendiagnosis

kebutuhan belajar; (3) menetapkan tujuan belajar; (4) mengatur dan mengontrol

belajar; (5) mengatur dan mengontrol kognisi, motivasi, perilaku (diri); (6)

memandang kesulitan sebagai tantangan; (7) mencari dan memanfaatkan sumber

belajar yang relevan; (8) memilih dan menerapkan strategi belajar; (9)

mengevaluasi proses dan hasil belajar; dan (10) self-efficacy (konsep diri).

Skala KBS dalam matematika terdiri dari 74 item pernyataan dengan

empat pilihan jawaban, yaitu: SS (Sangat Setuju), S (Setuju), TS (Tidak Setuju),

dan STS (Sangat Tidak Setuju). Pilihan jawaban N (Netral) tidak digunakan untuk

menghindari keraguan siswa. Penyusunan skala KBS diawali dengan membuat

kisi-kisi skala tersebut mencakup aspek yang diukur dan pernyataan positif dan

negatif.

Sebelum skala ini digunakan dalam penelitian, dilakukan ujicoba terbatas

pada 5 siswa SMA diluar sampel tetapi setaraf. Tujuan ujicoba adalah untuk

mengetahui tingkat keterbacaan bahasa dan sekaligus memperoleh gambaran

apakah pernyataan-pernyataan yang terdapat pada angket kemandirian belajar

dapat dipahami oleh siswa SMA kelas X dengan baik (sudah layak digunakan).

Setelah dilakukan perbaikan berdasarkan hasil ujicoba terbatas,

selanjutnya skala KBS dalam matematika diujicobakan pada siswa kelas X SMA

(21)

validitas setiap item pernyataan dan sekaligus untuk menghitung skor setiap

pilihan (SS, S, TS, STS) dari setiap pernyataan. Pemberian skor setiap pilihan dari

pernyataan skala KBS ditentukan berdasarkan distribusi jawaban responden atau

dengan kata lain menentukan nilai skala dengan deviasi normal. Dengan

menggunakan cara ini, skor SS, S, TS, dan STS dari setiap pernyataan dapat

berbeda-beda, tergantung pada sebaran respon siswa terhadap masing-masing

pernyataan.

Proses perhitungan skor setiap pilihan (SS, S, TS, STS) dari

masing-masing pernyataan pada skala kemandirian, data hasil ujicoba dan perhitungan

reliabilitas dan validitas butir skala secara lengkap dapat dilihat pada lampiran C

halaman 491. Untuk menguji validitas butir pernyataan, skor setiap butir

pernyataan dikorelasikan dengan skor total. Hipotesis yang diajukan adalah

sebagai berikut:

Ho : Tidak terdapat korelasi positif yang signifikan antara skor butir pernyataan

dan skor total.

H1 : Terdapat korelasi positif yang signifikan antara skor butir pernyataan dan

skor total.

Selanjutnya mengukur koefisien korelasi antara skor butir pernyataan

dengan skor total dengan menggunakan rumus product moment dari Karl Pearson.

Kriteria pengujian yang digunakan adalah: jika thitung (txy) ≥ ttabel, maka Ho

ditolak; dalam keadaan lainnya Ho diterima. Pada taraf α = 0,05 dengan N = 40

dan dk = 38 diperoleh ttabel = 1,68, sedangkan untuk menghitung reliabilitas tes

digunakan Cronbach-Alpha. Hasil perhitungan koefisien reliabilitas dan koefisien

(22)

Tabel 3.17

Hasil Perhitungan Reliabilitas dan Validitas Skala KBS Reliabilitas Nomor

Dari Tabel 3.17 terlihat bahwa besarnya koefisien reliabilitas adalah 0,88.

Menurut Guildford (Ruseffendi, 2006), koefisien reliabilitas sebesar 0,88

tergolong tinggi. Dari tabel itu juga terlihat bahwa setiap butir skala kemandirian

(23)

60, 64, 68, 70, dan 74, koefisien thitung (txy) lebih besar dari ttabel (1,68) sehingga Ho

ditolak. Jadi, terdapat korelasi positif yang signifikan antara skor butir pernyataan

dan skor total. Dengan demikian untuk setiap butir skala kemandirian belajar,

kecuali butir 3, 8, 9, 14, 20, 23, 28, 29, 36, 37, 41, 42, 46, 49, 55, 56, 57, 60, 64,

68, 70, dan 74, dinyatakan valid. Selanjutnya untuk butir pernyataan yang tidak

valid tidak dipakai dalam penelitian.

5. Lembar Observasi Aktivitas Pembelajaran

Lembar observasi digunakan untuk mengamati situasi didaktis dan

pedagogis yang terjadi selama proses pembelajaran. Lembar ini juga digunakan

untuk mendapatkan gambaran tentang kualitas proses pembelajaran guru dan

aktivitas siswa selama berlangsungnya proses pembelajaran. Hal ini dipandang

perlu untuk dideskripsikan secara rinci untuk memperkuat pembahasan hasil

penelitian yang akan diperoleh nantinya.

Lembar observasi yang dimaksud yaitu lembar observasi aktivitas guru

dan lembar observasi aktivitas siswa. Lembar observasi guru bertujuan untuk

memeriksa apakah prosedur pembelajaran sudah sesuai dengan teorinya; dalam

hal ini sudah sesuai dengan tahap-tahap pembelajaran generatif, yaitu tahap

orientasi, tahap pengungkapan ide, tahap tantangan dan restrukturisasi, tahap

penerapan, dan tahap memeriksa kembali. Lembar observasi aktivitas siswa

berfungsi untuk mengumpulkan data kemampuan siswa dalam bernalar dan

berkomunikasi sesuai dengan tahap-tahap pembelajaran generatif.

Lembar observasi pembelajaran (aktivitas guru dan siswa) berupa daftar

cek dengan lima pilihan dimulai dari sangat kurang (1) sampai ke sangat baik (5)

(24)

-putus, jika pada proses pembelajaran berlangsung (guru dan siswa) tidak

melakukan/memunculkan aktivitas sesuai dengan tahap-tahap yang ada. Kedua

lembar observasi tersebut harus diisi oleh observer sesuai dengan pembelajaran

yang sedang berlangsung di kelas. Observasi dilakukan oleh dua orang yang

dianggap telah memahami dengan baik cara dan objek yang akan diobservasi.

Lembar observasi (pedoman observasi) aktivitas guru dan siswa dapat dilihat pada

Lampiran B-1 halaman 427.

6. Pedoman Wawancara

Wawancara berfungsi untuk menggali permasalahan yang ditemui siswa

pada pembelajaran generatif dan dilakukan pada beberapa siswa yang dianggap

dapat membantu mengungkapkan sikap maupun apresiasi mereka terhadap

peningkatan kemampuan penalaran dan komunikasi matematis siswa dalam

pembelajaran generatif. Wawancara dilakukan dengan beberapa siswa yang

mewakili kelas eksperimen dan mempertimbangkan kegagalan siswa dalam

menyelesaikan soal-soal kemampuan penalaran dan komunikasi matematis yang

dianggap kurang. Setiap kelas dipilih 3 sampai 5 siswa pada masing-masing kelas

eksperimen dan level sekolah.

Pemilihan siswa yang diwawancarai berdasarkan pertimbangan berikut.

a. Memilih siswa berdasarkan tingkat kemampuan mereka dalam menjawab

soal-soal yang diujikan (tinggi, sedang, rendah).

b. Memperhatikan jawaban siswa terhadap tes yang diujikan.

c. Meminta siswa untuk mencermati kembali soal-soal yang tidak tuntas dijawab,

salah menggunakan konsep dan operasi atau jawaban akhir yang salah.

(25)

1) Apa yang membuat kamu salah dalam menjawab soal itu?

2) Apa yang membuat kamu tidak tuntas dalam menjawab soal itu?

3) Mengapa menggunakan cara itu? Apa ada cara lain?

4) Mengapa mengambil sikap “seperti itu” ketika berinteraksi dengan siswa

lain atau guru di kelas pada pelajaran matematika?

Bentuk pertanyaan bisa berkembang selama wawancara sesuai dengan

temuan di lapangan ketika melakukan diskusi dengan siswa.

e. Mencatat hasil wawancara dalam format wawancara.

Hasil wawancara dengan siswa ditriangulasi melalui wawancara dengan

siswa lainnya dan guru yang mengetahui karakteristik siswa yang diteliti.

Wawancara dengan guru juga dilakukan untuk memperoleh gambaran lebih lanjut

tentang pelaksanaan proses pembelajaran dalam mengungkap kemampuan

penalaran dan komunikasi matematis siswa yang diteliti.

Selain itu, wawancara dilakukan untuk menggali pandangan siswa

terhadap pembelajaran generatif dalam pembelajaran matematika. Item-item yang

terdapat pada pedoman wawancara merupakan modifikasi dari pedoman

wawancara yang dikembangkan Hulukati (2005), dan jawaban yang dikehendaki

adalah jawaban secara bebas dari siswa.

Adapun hal-hal yang diwawancarai adalah sebagai berikut.

(1) Setelah mengikuti pembelajaran yang diberikan guru, bagaimana pandangan

anda tentang pembelajaran generatif dalam pembelajaran matematika, jika

dibandingkan dengan pendekatan lain?

(2) Apakah dalam pembelajaran ini, anda termotivasi mempelajari materi yang

(26)

(3) Apakah dalam pembelajaran ini, guru memberikan kesempatan kepada anda

untuk mengajukan ide atau gagasan secara bebas?

(4) Adakah anda menyadari ada gagasan dan pendapat anda yang berbeda dengan

teman lain?

(5) Apakah anda mempunyai keberanian mengajukan pendapat dan

berargumentasi dengan teman, jika ada jawaban yang tidak sesuai dengan

pendapat anda?

(6) Adakah anda menyadari dalam pembelajaran ini, anda terdorong untuk

meningkatkan kemampuan anda dalam bernalar dan mengkomunikasikan

konsep-konsep matematika?

(7) Adakah kesulitan yang anda temui dalam meningkatkan kemampuan

penalaran dan komunikasi pada pembelajaran yang telah dilakukan guru?

(8) Apa kelebihan dan kekurangan yang anda rasakan dalam pembelajaran

dengan menggunakan pembelajaran generatif dalam matematika?

(9) Apa saran anda terhadap pembelajaran generatif dalam matematika?

E. Perangkat Pembelajaran dan Pengembangannya

Perangkat pembelajaran merupakan salah satu komponen pembelajaran

yang turut menentukan keberhasilan implementasi suatu model pembelajaran.

Penelitian ini mengimplementasikan pembelajaran generatif. Oleh karena itu

perangkat pembelajaran yang digunakan, dirancang dan dikembangkan sesuai

dengan karakteristik dari pembelajaran generatif dan kemampuan siswa yang akan

dicapai, yaitu kemampuan penalaran dan komunikasi matematis. Selain itu,

(27)

tuntutan kurikulum tingkat satuan pendidikan (KTSP) supaya siswa mencapai

kompetensi matematis yang relevan dengan tuntutan kurikulum.

Perangkat pembelajaran yang dikembangkan peneliti adalah perangkat

pembelajaran untuk siswa SMA kelas X yaitu rencana pelaksanaan pembelajaran

(RPP), lembar aktivitas siswa (LAS). Perangkat pembelajaran meliputi dua materi

pokok yaitu sistem persamaan linear dan pertidaksamaan satu variabel (SPLDV,

SPLTV, SPLK, PtK, PtL), disampaikan selama 20 jam pelajaran atau sepuluh kali

tatap muka (satu kali tatap muka dua jam pelajaran).

Sebelum digunakan, perangkat pembelajaran terlebih dahulu divalidasi

oleh lima penimbang berlatar belakang mahasiswa S3 pendidikan matematika

yang dianggap ahli dalam pendidikan matematika. Para penimbang diminta untuk

menilai atau menimbang dan memberikan saran atau masukan mengenai format,

(sistemmatematika penyajian, kejelasan bahasa yang digunakan, kejelasan

ilustrasi atau gambar); baik untuk RPP maupun LAS; isi (keseseuaian dengan

standar kompetensi dan kompetensi dasar, kesesuaian dengan tingkat

perkembangan siswa, keruntutan penyajian, kesesuaian dengan alokasi waktu) dan

proses (tahap orientasi, pengungkapan ide, penerapan, melihat kembali) untuk

RPP. Untuk LAS, isi (kesesuaian dengan uraian materi pokok, kesesuaian dengan

tingkat perkembangan siswa, keruntutan penyajian, kesesuaian dengan alokasi

waktu) dan proses (tahap tantangan dan restrukturisasi).

Selain itu juga kesesuaian masalah dan tugas yang terdapat pada LAS

dengan tujuan yang akan dicapai pada RPP, peran LAS untuk membantu siswa

(28)

untuk membantu siswa membangun konsep-konsep/prinsip-prinsip matematika

dengan kemampuan mereka sendiri.

Setelah perangkat pembelajaran diperbaiki berdasarkan masukan para

penimbang, kemudian dilakukan ujicoba pada siswa SMA kelas X. Dalam ujicoba

diamati situasi didaktis dan pedagogis yang terjadi selama proses ujicoba

berlangsung. Hal ini bermanfaat untuk memperbaiki prediksi respon yang terdapat

dalam skenario pembelajaran karena mungkin saja prediksi respon yang disusun

peneliti pada draf awal belum lengkap sehingga akan membingungkan guru dalam

melakukan antisipasi didaktis untuk memperlancar proses pembelajaran melalui

pembelajaran generatif.

Selain itu, ujicoba dilakukan dengan tujuan untuk mengetahui keterbacaan

LAS dan sekaligus untuk memperoleh gambaran apakah LAS dapat dipahami

siswa dengan baik. Perbaikan perangkat pembelajaran setelah ujicoba diharapkan

akan menghasilkan suatu perangkat pembelajaran yang baik sehingga akan

memperlancar jalannya proses pembelajaran pada saat eksperimen dilakukan.

Pembelajaran generatif dikembangkan melalui RPP dan LAS dalam

meningkatkan kemampuan penalaran dan komunikasi matematis. Di dalam RPP,

untuk setiap materi baru, guru memberikan gambar (berupa media) dari situasi

dan kondisi (permasalahan yang diberikan) yang dapat menghubungkan atau

mengaitkan materi dengan pengalaman siswa sehari-hari, sehingga mempermudah

siswa untuk memahami materi yang akan dipelajari. Demikian juga dengan

kemampuan awal (KAM) yang dimiliki siswa sangat membantu untuk memahami

materi yang dipelajari; seperti memahami konsep fungsi, menggambar grafik

(29)

pertidaksamaan kuadrat, melakukan manipulasi aljabar dalam perhitungan yang

berkaitan dengan persamaan dan pertidaksamaan kuadrat, merancang model

matematika dari masalah yang berkaitan dengan persamaan dan/atau fungsi

kuadrat, dan menyelesaikan model matematika dari masalah yang berkaitan

dengan persamaan dan/atau fungsi kuadrat dan penafsirannya. Semuanya ini

merupakan prasyarat untuk memahami materi SPLPtSV.

Pada RPP-01 (tahap orientasi) siswa diberi kesempatan untuk membangun

kesan mengenai topik atau konsep yang akan dibahas dengan mengaitkan materi

dan pengalaman mereka sehari-hari. Kegiatan dilakukan dengan tanya jawab.

Guru memberikan masalah dari kehidupan sehari-hari yang berkaitan dengan

SPLDV. Untuk jelasnya, berikut diberikan gambar situasi orang yang sedang

berbelanja buah-buahan di Pasar Buah Pekanbaru dengan permasalahan yang

diberikan.

Gambar 3.1: Situasi Orang yang sedang Berbelanja

(30)

Pernahkah kalian pergi ke Pasar Buah Pekanbaru? Jika pernah, apakah

kalian memperhatikan harga dari beberapa barang tertentu yang ada di

pasar tersebut? Misalkan kalian tidak mengetahui harga dari suatu

barang, tetapi kalian mengetahui berapa banyak dua orang pembeli

membeli dua jenis barang yang jumlahnya berbeda dan total uang yang

harus dibayarkan atas barang itu. Apakah kalian dapat mengetahui tiap

harga dari kedua jenis barang tersebut?

Siswa diminta mengajukan pertanyaan-pertanyaan yang kurang dipahami

mengenai masalah di atas. Setelah siswa memahami permasalahan yang

diberikan, siswa diharapkan dapat menggali kemampuan penalaran dan

komunikasi matematis.

SPLTV. Untuk jelasnya, berikut diberikan gambar situasi orang yang sedang

membeli kebutuhan sekolah sehari-hari untuk anak-anak mereka di Toko Buku

Budi Pekanbaru dengan permasalahan yang diberikan; disajikan pada Gambar 3.2.

Pernahkah kalian pergi ke Toko Buku Budi Pekanbaru? Jika pernah,

apakah kalian memperhatikan harga dari beberapa barang tertentu yang

ada di Toko Buku itu? Misalkan kalian tidak mengetahui harga dari suatu

barang, tetapi kalian mengetahui berapa banyak tiga orang pembeli

membeli tiga jenis barang yang jumlahnya berbeda dan total uang yang

harus dibayarkan atas barang itu. Apakah kalian dapat mengetahui tiap

(31)

diberikan, siswa diharapkan dapat menggali KPM dan KKM.

Gambar 3.2: Situasi Orang yang sedang Membeli Kebutuhan Sekolah

Sehari-hari untuk Anak-anak di Toko Budi Pekanbaru

(32)

Gambar 3.3: Mobil Patroli Polisi yang sedang parkir di kawasan pertokoan di

Pekanbaru

Gambar 3.4: Mobil Patroli Polisi yang sedang mengejar mobil Pengebut Pernahkah kalian melihat peristiwa yang terjadi seperti pada gambar di

atas? Jika pernah, apakah kalian memperhatikan mobil patroli polisi

mengejar mobil pengebut itut? Misalkan kalian tidak mengetahui waktu

yang diperlukan mobil patroli polisi untuk menangkap mobil pengebut itu,

(33)

percepatan konstan mobil patroli polisi tepat setelah mobil pengebut itu

melewatinya. Apakah kalian dapat menentukan waktu yang diperlukan

mobil patroli polisi untuk menangkap mobil pengebut itu? Berapa jarak

yang ditempuh mobil patroli polisi saat mobil pengebut tertangkap?

pertidaksamaan satu variabel (PtSV). Untuk jelasnya, berikut diberikan gambar

pertandingan bola basket di suatu sekolah; ketika seorang pemain basket sedang

melempar masuk bola ke dalam jaring basket.

(34)

Pernahkah kalian menonton pertandingan bola basket di sekolah? Jika

pernah, apakah kalian memperhatikan seorang pemain basket melempar

masuk bola ke dalam jaring basket? Bagaimana bentuk lintasan bola itu?

Misalkan kalian tidak mengetahui lamanya waktu yang diperlukan

seorang pemain basket melempar masuk bola ke dalam jaring basket,

tetapi kalian mengetahui posisi bola itu pada ketinggian tertentu. Apakah

kalian dapat menghitung waktu yang diperlukan pemain basket melempar

masuk bola itu ke dalam jaring basket?

Dalam lembar aktivitas siswa (LAS) untuk beberapa permasalahan,

diberikan petunjuk atau langkah-langkah yang dapat membantu siswa dalam

menyelesaikan soal-soal yang diberikan (tidak semua informasi yang dibutuhkan

ada pada buku paket); sehingga mempermudah siswa memperoleh informasi

(konsep) yang diperlukan untuk menyelesaikan permasalahan yang diberikan.

Pada tahap ini (tahap tantangan dan restrukturisasi), semua siswa telah

dikondisikan dalam beberapa kelompok (setiap kelompok terdiri dari beberapa

siswa yang mempunyai KAM tinggi, sedang dan rendah) dengan tujuan agar

siswa yang pandai dapat membantu siswa yang lemah, sehingga diskusi dapat

berjalan secara efektif. Dalam diskusi (baik diskusi kelompok maupun diskusi

kelas) diharapkan terjadi konflik kognitif, sehingga dimungkinkan siswa dapat

(35)

Pada LAS-01 siswa diberi permasalahan atau soal sebagai berikut.

Daniel membeli 2 buah kue A dan 3 buah kue B dengan harga Rp 14.000,00. Pada

tempat yang sama, Giok membeli 3 buah kue A dan 4 buah kue B dengan harga

Rp 19.500,00.

a. Buatlah model matematika dari pernyataan di atas!

b. Selidiki apakah sistem persamaan linear yang diperoleh mempunyai solusi

tunggal! Jelaskan jawaban anda!

c. Hitunglah harga 1 buah dari masing-masing jenis kue!

d. Gambarlah grafiknya untuk menunjukkan bahwa kesimpulan yang diberikan

pada (b) benar!

Untuk menyelesaikan permasalahan (a), siswa diberi petunjuk atau

langkah-langkah sebagai berikut.

Model matematika adalah hasil penerjemahan kasus-kasus yang umum terjadi

dalam kehidupan sehari-hari ke dalam bentuk matematika (sistem persamaan),

sehingga dapat diperoleh formulasi untuk mendapatkan solusi atas kasus yang

terjadi. Untuk membuat model matematika yang berkaitan dengan sistem

persamaan (SPLDV, SPLTV, atau SPLK), ada beberapa langkah:

1. Identifikasi karakteristik masalah yang akan diselesaikan berkaitan dengan

sistem persamaan.

2. Nyatakan besaran yang ada dalam masalah sebagai variabel (dilambangkan

dengan huruf-huruf) sistem persamaan.

3. Rumuskan sistem persamaan yang merupakan model matematika dari

masalah.

4. Tentukan penyelesaian dari model matematika sistem persamaan yang

diperoleh pada langkah 2.

(36)

Untuk menyelesaikan permasalahan (b), siswa diberi petunjuk atau

Untuk menyelesaikan permasalahan (c), siswa diberi petunjuk atau

Beberapa jenis penyelesaian SPLDV di atas, dibedakan menjadi 3 kelompok:

1. Jika ≠ dengan a2 ≠ 0 dan b2≠ 0, maka SPL ini mempunyai tepat satu

pasang anggota dalam himpunan penyelesaiannya (solusi tunggal). Dalam

hal ini grafik persamaan a1x +b1y = c1 berpotongan dengan grafik a2x + b2y = c2 . SPL ini dikatakan konsisten (bergantung linear).

2. Jika = ≠ dengan a2 ≠ 0, b2 ≠ 0, dan c2 ≠ 0, maka SPL ini tidak

mempunyai anggota dalam himpunan penyelesaiannya. Himpunan

penyelesaiannya dikatakan himpunan kosong, ditulis dengan Ø atau { }.

Dalam hal ini grafik a1x +b1y = c1 sejajar dengan grafik a2x + b2y = c2 dan SPL ini dikatakan tidakkonsisten.

3. Jika = = dengan a2 ≠ 0, b2 ≠ 0, dan c2 ≠ 0, maka SPL ini

mempunyai tak terhingga banyaknya penyelesaian. Dalam hal ini

grafik a1x + b1y = c1 berimpit dengan grafik a2x + b2y = c2 atau (a1x +b1y– c1) – k(a2x + b2y– c2) = 0, k € R,dan SPL ini dikatakan sangat

konsisten (bergantungan).

Metode Eliminasi

Mengubah SPLDV menjadi sebuah persamaan linear satu variabel dapat juga

dilakukan dengan mengeliminir (menghilangkan) satu variabel untuk

menentukan nilai variabel yang lainnya.

Langkah-langkah menyelesaikan sistem persamaan menggunakan metode

eliminasi:

1. Perhatikan koefisien x (atau y). Jika sama, kurangi persamaan yang satu

oleh persamaan yang lain. Jika angkanya sama tetapi tandanya berbeda,

jumlahkan kedua persamaan itu.

2. Jika koefisiennya berbeda, samakan koefisiennya dengan mengalikan kedua

persamaan dengan bilangan yang sesuai, kemudian jumlahkan atau

(37)

Untuk menyelesaikan permasalahan (d), siswa diberi petunjuk atau

Kadir, Nikolas, dan Ikhsan berbelanja di sebuah toko buku. Kadir membeli 2 lusin

buku tebal, 3 lusin pena faster, dan 4 lusin pensil warna dengan membayar

Rp 270.000,00. Nikolas membeli 1 lusin buku tebal, 2 lusin pena faster, dan 1

lusin pensil warna dengan membayar Rp 130.000,00. Ikhsan membeli 2 lusin

buku tebal, dan 1 lusin pena faster dengan membayar Rp 130.000,00.

b. Hitung harga 1 lusin buku tebal, 1 lusin pena faster dan 1 lusin pensil warna!

c. Bagaimana bentuk umum model matematika di atas dan tentukan

penyelesaiannya!

Untuk menyelesaikan permasalahan (a), siswa dapat melihat petunjuk

seperti soal nomor (1a) pada LAS-01; hanya saja disini persamaannya berbentuk

tiga variabel (SPLTV).

Langkah-langkah untuk menggambar grafik fungsi linear:

1. Tentukan titik potong dengan sumbu-x, syaratnya: y = 0, sehingga

diperoleh koordinat titik potong dengan sumbu-x.

2. Tentukan titik potong dengan sumbu-y, syaratnya: x = 0, sehingga

diperoleh koordinat titik potong dengan sumbu-y.

3. Gambarlah kedua koordinat titik potong itu pada bidang kartesius.

4. Hubungkan kedua koordinat titik potong itu dengan garis lurus.

Cara lain untuk menentukan penyelesaian SPLDV adalah dengan metode

grafik. Langkahnya: Lakukan langkah 1 sampai 4 pada kedua persamaan

linear yang diberikan. Titik potong kedua garis dari persamaan-persamaan

(38)

langkah-langkah sebagai berikut.

Metode Eliminasi-Substitusi (Gabungan)

Langkah-langkah untuk menyelesaikan SPLTV:

1. Eliminasikan sebuah variabel dari dua persamaan.

2. Selesaikan hasil yang diperoleh, yaitu SPLDV dengan metode substitusi

atau eliminasi atau eliminasi-substitusi.

3. Substitusikan variabel-variabel yang diperoleh pada langkah 2 ke

persamaan awal untuk memperoleh nilai variabel lainnya.

Sistem persamaan linear dengan tiga variabel (SPLTV) adalah sistem

persamaan yang mempunyai bentuk:

Pertama ax + by + cz = d atau Kedua a1x + b1y + c1z = d1

ex + fy + gz = h a2x + b2y + c2z = d2

ix + jy + kz = l a3x + b3y + c3z = d3

dengan a, b, c, d, e, f, g, h, i, j, k, dan l atau a1, b1, c1, d1, a2, b2, c2, d2, a3, b3,

c3, dan d3 merupakan konstanta real. Untuk selanjutnya digunakan bentuk

umum SPLDV yang kedua.

Jika nilai x = x0, y = y0, z = z0, ditulis sebagai pasangan terurut (x0, y0, z0),

memenuhi SPLTV tersebut, maka haruslah berlaku hubungan:

a1x0 + b1y0 + c1z0 = d1

a2x0 + b2y0+ c2z0 = d2

a3x0 + b3y0+ c3z0 = d3

Dalam hal demikian, (x0, y0, z0) disebut penyelesaian SPLTV itu dan

himpunan penyelesaiannya ditulis sebagai {(x0, y0, z0)}. SPLTV dapat

diselesaikan dengan metode substitusi, eliminasi dan gabungan eliminasi

substitusi. Metode grafik tidak digunakan karena keterbatasan dalam

menentukan titik persekutuan antara tiga bidang datar, sedangkan metode

(39)

1. Sebuah mobil bergerak dengan kecepatan konstan 20 m/dtk. Mobil lain

bergerak dengan arah yang sama dari keadaan diam dengan percepatan konstan

10 m/dtk2 tepat setelah mobil pertama melewatinya.

b. Hitunglah waktu yang diperlukan mobil kedua untuk mendapatkan mobil

pertama!

c. Hitunglah jarak yang ditempuh mobil kedua untuk mendapatkan mobil

pertama!

d. Gambarlah grafiknya untuk menunjukkan posisi mobil kedua mendapatkan

mobil pertama!

Untuk menyelesaikan permasalahan (a, b, dan c), siswa diberi petunjuk

atau langkah-langkah sebagai berikut.

Gerak lurus beraturan (GLB) didefinisikan sebagai gerak suatu benda pada

lintasan lurus dengan kecepatan tetap (konstan), yang artinya baik besar

maupun arahnya tetap. Formula yang dipakai adalah s = so + v.t atau

x = xo + v.t dengan s = x adalah jarak yang ditempuh, so =xo adalah jarak

awal sebelum bergerak, v adalah kecepatan, dan t adalah waktu yang

diperlukan. Karena jarak awal atau so = 0, maka formulanya berubah menjadi

s = v. t atau s = vo. t. Demikian juga dengan xo = 0, maka formulanya berubah menjadi x = v. t atau x = vo. t.

Gerak lurus berubah beraturan (GLBB) didefinisikan sebagai gerak suatu

benda pada lintasan lurus dengan percepatan tetap. Formula yang dipakai

adalah s = vo. t + ½ .a .t 2

, dengan s adalah jarak yang ditempuh, vo adalah kecepatan awal, t adalah waktu yang diperlukan dan a adalah percepatan.

(40)

Untuk menyelesaikan permasalahan (d), siswa diberi petunjuk atau

2. Diberikan sistem persamaan linear dan kuadrat (SPLK), 2x + y + 1 = 0 dan

y =

a. Selidiki apakah SPLK tepat mempunyai satu anggota dalam himpunan

penyelesaiannya! Jelaskan jawaban anda!

b. Tentukan himpunan penyelesaiannya (HP)!

c. Gambarlah grafiknya!

Langkah-langkah untuk menggambar grafik fungsi linear:

1. Tentukan titik potong dengan sumbu-x, syaratnya: y = 0, sehingga diperoleh koordinat titik potong dengan sumbu-x.

2. Tentukan titik potong dengan sumbu-y, syaratnya: x = 0, sehingga diperoleh koordinat titik potong dengan sumbu-y.

3. Gambarlah kedua koordinat titik potong itu pada bidang kartesius. 4. Hubungkan kedua koordinat titik potong itu dengan garis lurus. Langkah-langkah untuk menggambar grafik fungsi kuadrat: 1. Ikuti langkah 1 sampai 3.

2. Tentukan koordinat titik puncak, P (�= − 2 , y =

�

−4 ) dengan D = b

2_– 4ac. 3. Gambarlah koordinat titik puncak itu pada bidang kartesius.

Sistem persamaan linear dan kuadrat (SPLK) adalah sistem persamaan yang terdiri dari sebuah persamaan linear dan sebuah persamaan berbentuk kuadrat yang masing-masing memuat dua variabel. Berdasarkan karakteristik dari bentuk bagian kuadratnya, SPLK dapat dikelompokkan menjadi:

1. SPLK dengan bagian kuadrat berbentuk eksplisit. 2. SPLK dengan bagian kuadrat berbentuk implisit.

Persamaan dua variabel x dan y disebut berbentuk eksplisit, jika persamaan itu dapat dinyatakan dalam bentuk y = f(x) atau x = f(y). Bentuk umum SPLK dengan bagian kuadrat berbentuk eksplisit dinyatakan sebagai:

y = ax + b ... (bagian linear)

(41)

Pak Anwar akan membuat kolam renang berbentuk persegi panjang dengan

keliling 140 m dan luasnya minimal 1.200 m2.

b. Hitunglah batasan untuk kolam renang tersebut!

c. Bagaimana bentuk umum model matematika di atas?

Langkah-langkah penyelesaian atau HP dari SPLK, y = ax + b dan

y = px2 + qx + r, adalah sebagai berikut:

1. Substitusikan bagian linear y = ax + b ke bagian kuadrat y = px2 + qx + r, sehingga diperoleh: ax + b = px2 + qx + r

px2 + qx –ax + r –b = 0

px2 + (q–a)x + (r –b) = 0, merupakan persamaan kuadrat dalam x. 2. Tentukan akar-akar persamaan kuadrat yang terbentuk, yakni x1 dan x2.

3. Substitusikan nilai-nilai x1 dan x2 ke persamaan bentuk linear untuk mendapatkan nilai-nilai y1 dan y2, sehingga diperoleh himpunan penyelesaian {(x1, y1), (,x2, y2)}.

Model matematika adalah hasil penerjemahan kasus-kasus yang umum terjadi dalam kehidupan sehari-hari ke dalam bentuk matematika (sistem pertidaksamaan), sehingga dapat diperoleh formulasi untuk mendapatkan solusi atas kasus yang terjadi. Untuk membuat model matematika yang berkaitan dengan pertidaksamaan satu variabel (berbentuk kuadrat atau linear), ada beberapa langkah:

1. Identifikasi karakteristik masalah yang akan diselesaikan berkaitan dengan

pertidaksamaan kuadrat atau linear. 2. Nyatakan besaran yang ada dalam masalah sebagai variabel (dilambangkan

dengan huruf-huruf) sistem pertidaksamaan.

3. Rumuskan sistem pertidaksamaan yang merupakan model matematika dari masalah.

(42)

Untuk menyelesaikan pertidaksamaan kuadrat (menentukan himpunan penyelesaian dari pertidaksamaan kuadrat) dapat ditentukan dengan dua cara, yaitu dengan menggunakan sketsa grafik fungsi kuadrat dan garis bilangan. A.Menyelesaikan Pertidaksamaan Kuadrat dengan menggunakan Sketsa

Grafik Fungsi Kuadrat.

Langkah-langkah untuk menentukan penyelesaian pertidaksamaan kuadrat dengan menggunakan sketsa grafik fungsi kuadrat:

1. Gambarlah sketsa grafik fungsi kuadrat f(x) = ax2 + bx + c atau parabola

y = ax2 + bx + c. Jika ada, carilah titik-titik potong dengan sumbu X.

2. Berdasarkan sketsa grafik yang diperoleh pada langkah 1, tetapkan selang atau interval yang memenuhi pertidaksamaan kuadrat ax2 + bx + c 0, ax 2+ bx + c ≤ 0, ax2 + bx + c 0, atau ax2 + bx+ c ≥ 0.

B.Menyelesaikan Pertidaksamaan Kuadrat dengan menggunakan Garis Bilangan.

Mencari penyelesaian pertidaksamaan kuadrat f(x) 0 artinya mencari interval nilai x yang mengakibatkan f(x) bernilai 0 (positif). Karena negatif dan positif dibatasi angka nol maka lebih dahulu dicari pembuat nol f(x).

Pembuat nol ini (x1 dan x2) biasanya menghasilkan tiga interval.

x1 x2

x x1 x1 x x2 x x2

Selanjutnya tentukan nilai f(x) di setiap interval dengan cara mensubstitusikan sembarang nilai x yang termuat dalam interval tersebut.

Langkah-langkah untuk menentukan penyelesaian pertidaksamaan kuadrat dengan menggunakan garis bilangan:

1. Jika ruas kanan tidak nol maka pindahkan semua suku ke ruas kiri sehingga pertidaksamaan menjadi f(x) 0, f(x) 0, f(x) ≤ 0, atau f(x) ≥ 0.

2. Tentukan pembuat nol f(x) dan gambar pada garis bilangan. Pembuat nol itu akan membagi garis bilangan menjadi tiga interval.

3. Substitusikan sembarang nilai x ke f(x) untuk menentukan tanda f(x) pada setiap interval.

4. Arsir garis bilangan yang sesuai sebagai penyelesaian. Sesuai artinya, jika f(x) 0 maka yang diarsir interval bertanda positif. Jika f(x) 0 maka yang

(43)

Pada kegiatan akhir dari pembelajaran generatif, guru tidak hanya

melakukan tahap melihat kembali dan memberi PR; tetapi juga melakukan

generalisasi. Dengan bimbingan guru, siswa membuat generalisasi dari materi

yang sudah dipelajari selama pembelajaran dan mengelaborasi pemahaman dan

penguasaan siswa terhadap materi-materi yang telah dipelajari.

Apabila dibandingkan dengan pembelajaran generatif yang telah dilakukan

oleh Hulukati (2005) dapat dijelaskan bahwa dalam RPP (tahap orientasi), guru

langsung memberikan permasalahan atau soal-soal yang harus dikerjakan;

sedangkan pada RPP yang peneliti lakukan; untuk setiap materi baru, guru

memberikan gambar (berupa media) dari situasi dan kondisi (permasalahan yang

diberikan) yang dapat menghubungkan atau mengaitkan materi dengan

pengalaman siswa sehari-hari, sehingga mempermudah siswa untuk memahami

materi yang akan dipelajari.

Dalam LKS pada penelitian Hulukati, guru hanya memberikan soal-soal

saja tanpa ada petunjuk atau langkah-langkah yang dapat membantu siswa dalam

menyelesaikan soal-soal yang diberikan. Pada LAS yang peneliti lakukan; untuk Pertidaksamaan kuadrat adalah pertidaksamaan yang variabelnya paling tinggi

berderajat dua. Pertidaksamaan kuadrat dalam variabel x dapat berbentuk

(Bentuk Umum):

1. ax2 + bx+ c 0,

2. ax2 + bx+ c 0,

3. ax2 + bx+ c ≥ 0, dengan a, b, c konstata real dan a ≠ 0.

(44)

beberapa permasalahan, diberikan petunjuk atau langkah-langkah yang dapat

membantu siswa dalam menyelesaikan soal-soal yang diberikan (tidak semua

informasi yang dibutuhkan ada pada buku paket); sehingga mempermudah siswa

memperoleh informasi atau konsep yang diperlukan untuk menyelesaikan

permasalahan yang diberikan.

Pada kegiatan akhir dari pembelajaran generatif yang dilakukan oleh

Hulukati, guru hanya melakukan tahap melihat kembali dan memberi PR,

sedangkan yang peneliti lakukan; guru tidak hanya melakukan tahap melihat

kembali dan memberi PR saja; tetapi juga melakukan generalisasi, yakni dengan

bimbingan guru, siswa membuat generalisasi dari materi yang sudah dipelajari

selama pembelajaran dan mengelaborasi pemahaman dan penguasaan siswa

terhadap materi-materi yang telah dipelajari. Sampel yang diambil pada penelitian

yang dilakukan oleh Hulukati adalah siswa kelas 8 SMP negeri Gorontalo dengan

level sekolah tinggi dan rendah, sedangkan sampel yang peneliti ambil adalah

siswa SMA kelas X pada level sekolah atas dan tengah dan bawah di Kota

Pekanbaru.

Apabila dibandingkan dengan pembelajaran generatif yang telah dilakukan

oleh Fahinu (2007) dapat dijelaskan bahwa dalam RPP (tahap orientasi), dosen

memberikan kesempatan kepada mahasiswa (1) untuk mengenali topik atau

materi melalui observasi secara induktif sehingga menemukan generalisasinya

secara umum dan (2) untuk mengemukakan gagasannya secara tertulis tentang

aksioma lapangan bilangan real dan sifat-sifat (teorema) aljabar bilangan real.

(45)

mahasiswa memahami topik atau materi yang akan (sedang) dipelajari; sedangkan

pada RPP yang peneliti lakukan; untuk setiap materi baru, guru memberikan

gambar (berupa media) dari situasi dan kondisi (permasalahan yang diberikan)

yang dapat menghubungkan atau mengaitkan materi dengan pengalaman siswa

sehari-hari, sehingga mempermudah siswa untuk memahami materi yang akan

dipelajari.

Dalam LKM pada penelitian Fahinu, dosen hanya memberikan soal-soal

saja tanpa ada petunjuk atau langkah-langkah yang dapat membantu mahasiswa

dalam menyelesaikan soal-soal yang diberikan. Pada LAS yang peneliti lakukan;

untuk beberapa permasalahan, diberikan petunjuk atau langkah-langkah yang

dapat membantu siswa dalam menyelesaikan soal-soal yang diberikan (tidak

semua informasi yang dibutuhkan ada pada buku paket); sehingga mempermudah

siswa memperoleh informasi atau konsep yang diperlukan untuk menyelesaikan

permasalahan yang diberikan.

Dari beberapa pernyataan di atas, dapat dilihat bahwa yang menjadi

perbedaan pembelajaran generatif yang peneliti lakukan dengan pembelajaran

generatif yang dilakukan oleh Hulukati dan Fahinu adalah sebagai berikut.

1. Dalam RPP, untuk setiap materi baru, guru memberikan gambar (berupa

media) dari situasi dan kondisi (permasalahan yang diberikan) yang dapat

menghubungkan atau mengaitkan materi dengan pengalaman siswa sehari-hari,

sehingga mempermudah siswa untuk memahami materi yang akan dipelajari.

2. Dalam LAS untuk beberapa permasalahan, diberikan petunjuk atau