III. DISTRIBUSI FREKUENSI
3.1 Pendahuluan
· Tujuan dari pembuatan tabel distribusi frekuensi adalah untuk mengatur data mentah (data yang belum dikelompokkan) ke dalam bentuk yang rapi tanpa mengurangi inti informasi yang ada.
· Pembuatan tabel distribusi frekuensi dapat dimulai dengan menyusun data mentah ke dalam urutan yang sistematis (dari nilai terkecil ke nilai yang lebih besar atau sebaliknya) atau lebih sering disebut data terurut.
· Keuntungan dari pengurutan data mentah ke dalam urutan data yang sistematis, diantaranya
1. Dapat melihat jarak antara nilai terkecil dan terbesar dari kumpulan data tersebut. 2. Dapat mengetahui distribusi data.
3. Dapat mengetahui di sekitar mana data terkonsentrasi.
· Untuk mendapatkan distribusi frekuensi, kumpulan array data dikumpulkan ke dalam sejumlah kelas (kelompok) yang relatif sedikit, sehingga distribusi frekuensi adalah suatu pengelompokkan data berdasarkan pada kemiripan ciri.
3.2 Penyusunan Distribusi Frekuensi
· Beberapa Istilah
Sebelum membuat tabel distribusi terlebih dahulu akan diperkenalkan istilah yang digunakan dalam sebuah tabel distribusi frekuensi.
Tabel 3.1 Nilai Ujian Statistik Untuk 50 Mahasiswa Politeknik Nilai Ujian Frekuensi (f) Batas Kelas Titik Tengah Kelas
50 – 59 8 49,5 - 59,5 54.5
Dari tabel 3.1 dapat dilihat bahwa :
« Kelas Interval
- Nilai Ujian 50–59, 60–69, ..dst disebut kelas interval.
- Dalam daftar distribusi frekuensi, data dibuat menjadi beberapa kelompok dalam interval-interval tertentu. Urutan kelas interval disusun mulai dari data terkecil sampai dengan data terbesar atau sebaliknya.
- Urutan kelas interval 50–59 disebut kelas interval pertama, 60–69 disebut kelas interval kedua,..., 90–99 disebut kelas interval kelima/terakhir.
« Ujung Kelas Interval
- Nilai-nilai di kiri kelas interval (50,60,70,80 dan 90) disebut ujung bawah kelas (UBK).
- Nilai 50 disebut ujung bawah kelas pertama, nilai 60 disebut ujung bawah kelas kedua,..., 90 disebut ujung bawah kelas kelima/terakhir.
- Nilai-nilai di kanan kelas interval (59,69,79,89 dan 99) disebut ujung atas kelas (UAK).
- Nilai 59 disebut ujung atas kelas pertama, nilai 69 disebut ujung atas kelas kedua,..., nilai 99 disebut ujung kelas kelima/terakhir.
« Panjang Kelas Interval (p)
Selisih positif antara tiap dua ujung bawah kelas berurutan disebut panjang kelas interval. Daritabel diperoleh panjang kelas interval= 60 – 50 = 70 – 60 =...= 90 – 80 =10.
« Frekuensi (f)
- Bilangan yang menunjukkan banyaknya data yang terdapat dalam setiap kelas interval disebut frekuensi.
- Nilai f = 8, artinya jumlah mahasiswa yang nilai ujian statistiknya antara 50 – 59 ada 8 orang. Jumlah seluruh frekuensi sama dengan jumlah seluruh data (N).
« Batas Kelas Interval
- Nilai 49,5 , 59,5 ,..., 89,5 disebut batas bawah kelas (BBK). Nilainya bergantung pada ketelitian data yang digunakan. Jika data dicatat hingga satuan BBK = UBK – 0,5. Jika data dicatat hingga satu desimal BBK = UBK – 0, 05....dst.
- Nilai 59,5 , 69,5 ,..., 99,5 disebut batas atas kelas (BAK). Nilainya bergantung pada ketelitian data yang digunakan. Jika data dicatat hingga satuan BAK = UAK + 0,5. Jika data dicatat hingga satu desimal BAK = UAK + 0, 05....dst.
- Nilai batas bawah kelas berikutnya sama dengan nilai batas atas kelas sebelumnya.
« Titik Tengah Kelas (m)
- Nilai 54,5 , 64,5 ,..., 94,5 disebut titik tengah kelas
- Titik tengah kelas/tanda kelas adalah suatu nilai yang diambil sebagai wakil dari kelas itu, yakni rata-rata setiap kelas interval .
-- Untuk kelas interval pertama, 54,5
2
· Langkah-langkah Membuat Daftar Distribusi Frekuensi
Berikut adalah langkah-langkah untuk membuat Daftar Distribusi Frekuensi : 1. Tentukan nilai dari data terkecil, data terbesar, dan banyak data.
2. Tentukan Rentang/Range, yaitu nilai data terbesar dikurangi nilai data terkecil.
Rentang = Data Terbesar – Data Terkecil (3.2)
3. Tentukan banyak kelas interval yang diperlukan.
Pada umumnya, banyak kelas interval ini antara 5 sampai 15 kelas, dipilih sesuai keperluan. Namun yang ideal, banyak kelas interval dapat dihitung dengan menggunakan aturan Sturges, yaitu :
Banyak Kelas = 1 + 3,3 log N ; dengan N menyatakan banyak data (3.3)
4. Tentukan panjang kelas interval (p).
kelas
banyak
rentang
p
=
(3.4)5. Tentukan ujung bawah kelas interval pertama.
Biasanya diambil data terkecil atau nilai yang lebih kecil dari data terkecil, akan tetapi selisihnya harus kurang dari panjang kelas interval yang telah didapat.
6. Selanjutnya kelas interval pertama dihitung dengan cara menjumlahkan ujung bawah kelas dengan p dikurangi 1. Demikian seterusnya.
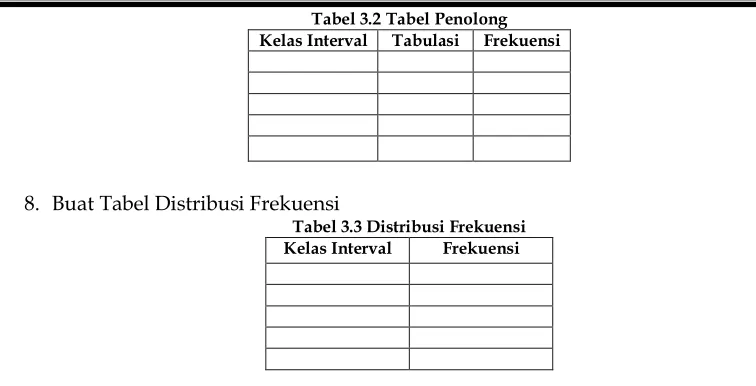
Tabel 3.2Tabel Penolong Kelas Interval Tabulasi Frekuensi
8. Buat Tabel Distribusi Frekuensi
Tabel 3.3 Distribusi Frekuensi Kelas Interval Frekuensi
· Contoh 3.1
Buatlah daftar distribusi frekuensi dari data pengeluaran per hari (ribu rupiah) untuk 30 keluarga di suatu daerah berikut ini :
Data Pengeluaran Per Hari (Ribu Rupiah) Untuk 30 Keluarga
50 67 70 74 60 70
60 69 71 72 65 72
72 75 78 85 75 80
63 71 56 58 58 73
69 76 64 65 65 85
Catatan : Data Rekaan Jawab :
1. Tentukan nilai dari data terkecil, data terbesar, dan banyak data.
Data terkecil (DK) = 50 Data terbesar (DB) = 85 Banyak data (N) = 30
2. Tentukan rentang, yaitu nilai data terbesar dikurangi nilai data terkecil.
Rentang = DB – DK = 85 – 50 = 35
3. Tentukan banyak kelas interval yang diperlukan. Dengan menggunakan aturan Sturges :
Banyak kelas = 1 + 3,3 log N = 1 + 3,3 log (30) = 5,87 ~ 6 kelas
4. Tentukan panjang kelas interval (p).
kelas
banyak
rentang
p
=
= 35 / 6 = 5,83 ~ 65. Tentukan ujung bawah kelas interval pertama.
UBK Pertama = 50
6. Selanjutnya kelas interval pertama dihitung dengan cara menjumlahkan ujung bawah kelas dengan p dikurangi 1.
Kelas ke- Kelas Interval Tabulasi Frekuensi
1. 50 – 55 I 1
8. Sehingga Daftar Distribusi Frekuensinya adalah
Tabel 3.5 Distribusi Frekuensi Pengeluaran Per Hari (Ribu Rupiah) Untuk 30 Keluarga Pengeluaran Frekuensi
Sedapat mungkin hindari kelas terbuka. Meskipun kelas terbuka diperlukan jika ada beberapa nilai yang sangat besar atau sangat kecil dibandingkan nilai-nilai lain yang ada disekitar pemusatan, sebaiknya kelas terbuka jarang digunakan sebab akan menimbulkan persoalan dalam penyajian grafik dan kesulitan perhitungan ukuran-ukuran statistik deskriptif yang penting lainnya, seperti rata-rata hitung, deviasi, dll.
· Contoh 3.2
Berikut adalah contoh daftar distribusi frekuensi dengan kelas terbuka, mengenai banyak penduduk di daerah A menurut kelompok umur (dalam tahun).
Tabel 3.6 Distribusi Frekuensi Banyak penduduk di daerah A menurut kelompok umur (dalam tahun) Umur (tahun) Frekuensi
3.3 Distribusi Frekuensi Relatif
· Dalam daftar distribusi frekuensi yang dibuat, frekuensi dinyatakan dengan banyaknya data yang terdapat dalam tiap kelas (berbentuk absolut). Jika frekuensi tersebut dinyatakan dalam bentuk persen, maka akan diperoleh daftar distribusi frekuensi relatif.
· Jadi distribusi frekuensi relatif disusun melalui pembagian masing-masing frekuensi kelas dengan seluruh frekuensi dan dinyatakan dalam persen. Distribusi frekuensi relatif terutama berguna dalam membandingkan beberapa distribusi yang memiliki jumlah frekuensi yang berbeda.
· Untuk mendapatkan nilai f (%) /frekuensi relatif dihitung dengan rumus berikut :
%
· Contoh 3.3 (Berdasarkan Contoh 3.1)
Buatlah daftar distribusi frekuensi relatif dari data Pengeluaran Per Hari (Ribu Rupiah) Untuk 30 Keluarga, berdasarkan daftar distribusi frekuensi yang diperoleh sebelumnya.
Jawab : Tabel 3.7 Distribusi Frekuensi dan Distribusi Frekuensi Relatif Pengeluaran Per Hari (Ribu Rupiah) Untuk 30 Keluarga
Pengeluaran Frekuensi Frekuensi Relatif (%) 50-55 1 (1/30) x 100 = 3,33
· Daftar distribusi frekuensi kumulatif adalah distribusi frekuensi biasa yang nilai frekuensi kumulatifnya didapat dengan jalan menjumlahkan frekuensi demi frekuensi.
· Daftar distribusi frekuensi kumulatif ada 2 macam, yaitu kumulatif kurang dari (<) dan
kumulatif atau lebih (≥).
· Contoh 3.4 (Berdasarkan Contoh 3.3)
Buatlah daftar distribusi kumulatif kurang dari dan daftar distribusi kumulatif atau lebih dari data Pengeluaran Per Hari (Ribu Rupiah) Untuk 30 Keluarga.
Jawab :
Perhatikan Tabel 3.7 !
« Distribusi frekuensi kumulatif kurang dari “<”
- Diperolehdengan cara menjumlahkanfrekuensi setiap kelas.
- Kelas pertama selalu bernilai 0 (nol).
- Kelas terakhirselalu bernilai sama dengan banyak data.
Frek. Absolut Frek. Relatif
Tabel 3.8 Distribusi Frekuensi Kumulatif Kurang Dari
« Distribusi frekuensi kumulatif atau lebih
- Diperolehdengan cara mengurangkan frekuensi setiap kelas. - Kelas pertama selalu bernilai sama dengan banyak data. - Kelas terakhir selalu bernilai 0 (nol).
Frek. Absolut Frek. Relatif
Pengeluaran F. Kum F. Kum
Tabel 3.9 Distribusi Frekuensi Kumulatif Atau Lebih
3.5 Penyajian Distribusi Frekuensi Dengan Grafik
· Pola data yang disajikan dalam diagram/grafik dapat lebih mudah ditangkap maknanya dibandingkan dengan memperhatikan tabel frekuensi. Dua bentuk penyajian grafik dari seperangkat data yang disajikan dalam daftar distribusi frekuensi adalah
Histogram dan Poligon Frekuensi.
· Histogram
Histogram adalah penyajian data distribusi frekuensi yang diubah menjadi diagram batang, namun sisi-sisi batang yang berdekatan harus berimpitan. Untuk menggambarkan histogram digunakan sumbu mendatar yang menyatakan batas-batas kelas interval dan sumbu tegak menyatakan frekuensi absolut atau frekuensi relatif.
· Poligon Frekuensi
Polygon frekuensi adalah diagram garis dari suatu distribusi frekuensi. Polygon frekuensi diperoleh dengan menghubungkan titik-titik yang merupakan pasangan koordinat titik tengah dan frekuensi setiap kelas. Titik tengah kelas diperoleh dengan membagi dua jumlah antara batas bawah dan batas atas kelas itu atau dengan menggunakan rumus (3.1).
· Contoh 3.5 (Berdasarkan Contoh 3.1)
Gambarkan histogram dan poligon dari data Pengeluaran Per Hari (Ribu Rupiah) Untuk 30 Keluarga.
Jawab :
Untuk menggambarkan histogram dan poligon maka diperlukan batas-batas kelas dan titik tengah kelas.
Gambar 3.1 Histogram dan Poligon Pengeluaran Per Hari (Ribu Rupiah) Untuk 30 Keluarga
Frekuensi
Batas Kelas
· Ogive
Ogive merupakan penyajian secara grafis dari suatu distribusi frekuensi kumulatif (berupa diagram garis).
Distribusi frekuensi kumulatif “kurang dari “ mempunyai ogive yang naik dari kiri bawah ke kanan atas, sedangkan distribusi frekuensi kumulatif “atau lebih” mempunyai ogive yang turun dari kiri atas ke kanan bawah.
· Contoh 3.6 (Berdasarkan Contoh 3.4)
Gambarkan ogive dari data pendapatan (juta rupiah) untuk 30 toko komputer.
Jawab :
Perhatikan kembali Tabel 3.8 dan 3.9 !
Gambar 2 Ogive Distribusi Kumulatif “ kurang dari “ dan Ogive Distribusi Kumulatif “ atau lebih Untuk Pengeluaran Per Hari (Ribu Rupiah) Untuk 30 Keluarga
Frek.kumulatif
Ujung Bawah Kelas (Pengeluaran)
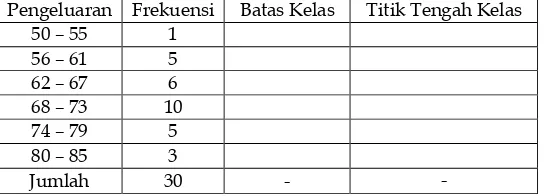
Pengeluaran Frekuensi Batas Kelas Titik Tengah Kelas 50 – 55 1 49,5 – 55,5 (50+55) / 2 = 52,5 56 – 61 5 55,5 – 61,5 (56+61) / 2 = 58,5
62 – 67 6 61,5 – 67,5 64,5
68 – 73 10 67,5 – 73,5 70,5
74 – 79 5 73,5 – 79,5 76,5
80 – 85 3 79,5 – 85,5 82,5
· Kurva Frekuensi
Jika garis patah-patah yang terbentuk dari poligon frekuensi didekati oleh sebuah lengkungan halus yang bentuknya secocok mungkin dengan poligon tersebut, akan diperoleh sebuah kurva frekuensi. Kurva ini dapat mencerminkan/menjelaskan secara umum ciri-ciri dari populasi data.
· Jenis-jenis kurva ferkuensi
Kurva distribusi frekuensi yang telah dihaluskan dan yang sering dijumpai dalam praktek mempunyai bentuk dengan ciri-ciri tertentu seperti berikut:
1. Model Normal, selalu simetrik dan mempunyai satu puncak/modus (unimodal). 2. Model Simetrik, unimodal. Perhatikan bahwa model normal itu selalu simetrik, namun
tidak berlaku sebaliknya (simetrik belum tentu normal).
Gambar 3.3 Model Normal Gambar 3.4 Model Simetrik
3. Model Tidak Simetris secara moderat atau model condong/miring dengan ciri bahwa ekor kurva yang satu lebih panjang dari ekor kurva yang lainnya. Model miring ada 2 yakni miring positif dan miring negatif.
Gambar 3.5 Model Miring Positif Gambar 3.6 Model Miring Negatif
4. Bentuk J atau J terbalik, dengan ciri bahwa salah satu nilai ujung kurva mempunyai frekuensi maksimum
Gambar 3.7 Bentuk J Gambar 3.8 Bentuk J Terbalik
5. Bentuk U dengan ciri bahwa kedua ujung kurva mempunyai frekuensi maksimum.
Gambar 3.9 Bentuk U
6. Model Bimodal, bila kurva mempunyai dua nilai maksimum/2 modus, dan multimodal bila mempunyai lebih dari dua nilai maksimum.
Gambar 3.10 Model Bimodal Gambar 3.11 Model Multimodal
7. Model Uniform, jika nilai-nilai variabel dalam suatu interval mempunyai frekuensi sama.