BAB II
TINJAUAN PUSTAKA 2.1 Tinjauan Umum
Untuk mendapatkan kesempurnaan dalam perencanaan pekerjaan diperlukan suatu tinjauan pustaka. Dengan tinjauan pustaka diharapkan mampu memberi kontribusi yang besar terhadap sebuah perancangan suatu pekerjaan. Dengan demikian dapat dikatakan bahwa semakin banyak tinjauan pustaka yang dibutuhkan semakin mendekati sempurna pula sebuah perencanaan pekerjaan.
Analisis tinggi muka air dan daerah genangan banjir sungai Krueng Pase Kabupaten Aceh Utara menggunakan software HEC-RAS, memerlukan tinjauan pustaka untuk mengetahui dasar-dasar teori dalam berbagai analisa yang diperlukan. Dasar-dasar teori ini nantinya akan menjadi acuan dalam analisis muka air banjir.
2.2 Analisa Hidrologi
Untuk menyelesaikan permasalahan banjir pada pada saluran-saluran (drainase) dibutuhkan analisa hidrologi khususnya masalah hujan sebagai sumber air yang akan dialirkan pada sistem saluran dan limpasan sebagai akibat tidak mampunya saluran menampung air hujan tersebut. Desain hidrologi sangat diperlukan untuk mengetahui debit pengaliran.
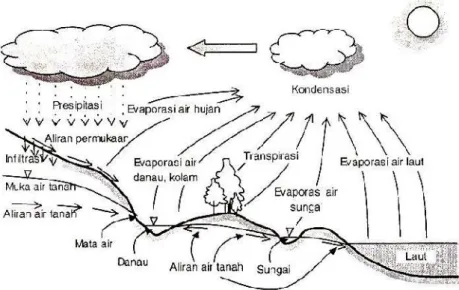
2.2.1 Siklus Hidrologi
matahari merupakan kunci proses siklus hidrologi tersebut dapat berjalan secara kontinu. Air berevaporasi, kemudian jatuh sebagai presipitasi dalam bentuk hujan, salju, hujan batu, hujan es dan salju (sleet), hujan gerimis atau kabut. Pada perjalanan menuju bumi beberapa presipitasi dapat berevaporasi kembali ke atas atau langsung jatuh yang kemudian diintersepsi oleh tanaman sebelum mencapai tanah. Setelah mencapai tanah, siklus hidrologi terus bergerak secara kontinu dalam tiga cara yang berbeda:
Evaporasi / transpirasi; Air yang ada di laut, di daratan, di sungai, di tanaman, dan sebagainya kemudian akan menguap ke angkasa (atmosfer) dan kemudian akan menjadi awan. Pada keadaan jenuh uap air (awan) itu akan menjadi bintik-bintik air yang selanjutnya akan turun (precipitation) dalam bentuk hujan, salju dan es.
Infiltrasi/ perkolasi ke dalam tanah; Air bergerak ke dalam tanah melalui celah-celah dan pori-pori tanah dan batuan menuju muka air tanah. Air dapat bergerak akibat aksi kapiler atau air dapat bergerak secara vertikal atau horizontal di bawah permukaan tanah hingga air tersebut memasuki kembali sistem air permukaan.
Air Permukaan; Air bergerak di atas permukaan tanah dekat dengan aliran utama dan danau, makin landai lahan dan makin sedikit pori-pori tanah, maka aliran permukaan semakin besar. Aliran permukaan tanah dapat dilihat biasanya pada daerah urban. Sungai-sungai bergabung satu sama lain dan membentuk sungai utama yang membawa seluruh air permukaan disekitar daerah aliran sungai menuju laut. Air permukaan, baik yang mengalir
permukaan akan terkumpul dan mengalir membentuk sungai dan berakhir ke laut. Proses perjalanan air di daratan itu terjadi dalam komponen-komponen siklus hidrologi yang membentuk sistem Daerah Aliran Sungai (DAS).
2.2.2 Analisa Curah Hujan Rencana
Hujan merupakan komponen yang sangat penting dalam analisis hidrologi. Pengukuran hujan dilakukan selama 24 jam baik secara manual maupun otomatis,
Gambar 2.4 Siklus Hidrologi
(Suripin, 2004, Sistem Drainase Perkotaan yang Berkelanjutan: 20)
dengan cara ini berarti hujan yang diketahui adalah hujan total yang terjadi selama satu hari. Dalam analisa digunakan curah hujan rencana, hujan rencana yang dimaksud adalah hujan harian maksimum yang akan digunakan untuk menghitung intensitas hujan, kemudian intensitas ini digunakan untuk mengestimasi debit rencana.
atau menitan. Hal ini akan membawa konsekuen dalam pemilihan data, dan dianjurkan untuk menggunakan data hujan hasil pengukuran dengan alat ukur otomatis.
2.2.3 Analisa Frekuensi Curah Hujan
Dalam ilmu statistik dikenal beberapa macam distribusi frekuensi yang banyak digunakan dalam bidang hidrologi. Berikut ini empat jenis distribusi frekuensi yang paling banyak digunakan dalam bidang hidrologi: - Distribusi Normal
- Distribusi Log Normal - Distribusi Log Person III - Distribusi Gumbel. 2.2.3.1 Distribusi Normal
Distribusi normal atau kurva normal disebut juga distribusi Gauss. Perhitungan curah hujan rencana menurut metode distribusi normal, mempunyai persamaan sebagai berikut:
X = X + K S (2.1) Dimana : S X X K T T (2.2) Dimana :
XT = perkiraan nilai yang diharapkan terjadi dengan periode ulang T tahunan.
KT = faktor frekuensi, merupakan fungsi dari peluang atau periode ulang dan tipe model matematik distribusi peluang yang digunakan untuk analisis peluang.
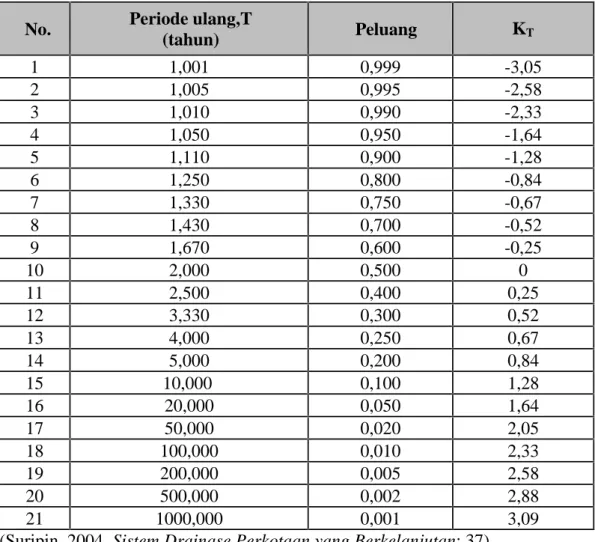
Untuk mempermudah perhitungan, nilai faktor frekuensi KT umumya sudah tersedia dalam tabel, disebut sebagai tabel nilai variabel reduksi Gauss (Variable reduced Gauss), seperti ditunjukkan dalam Tabel 2.1.
Tabel 2.1 Nilai Variabel Reduksi Gauss
No. Periode ulang,T
(tahun) Peluang KT 1 1,001 0,999 -3,05 2 1,005 0,995 -2,58 3 1,010 0,990 -2,33 4 1,050 0,950 -1,64 5 1,110 0,900 -1,28 6 1,250 0,800 -0,84 7 1,330 0,750 -0,67 8 1,430 0,700 -0,52 9 1,670 0,600 -0,25 10 2,000 0,500 0 11 2,500 0,400 0,25 12 3,330 0,300 0,52 13 4,000 0,250 0,67 14 5,000 0,200 0,84 15 10,000 0,100 1,28 16 20,000 0,050 1,64 17 50,000 0,020 2,05 18 100,000 0,010 2,33 19 200,000 0,005 2,58 20 500,000 0,002 2,88 21 1000,000 0,001 3,09
(Suripin, 2004, Sistem Drainase Perkotaan yang Berkelanjutan: 37) 2.2.3.2 Distribusi Log Normal
dikatakan mengikuti distribusi Log Normal. Untuk distribusi Log Normal perhitungan curah hujan rencana menggunakan persamaan berikut ini:
S K Y YT T (2.3) S Y Y K T T (2.4) Dimana:
YT= perkiraan nilai yang diharapkan terjadi dengan periode ulang T-tahunan,
Y = nilai rata-rata hitung variat,
S = deviasi standar nilai vatiat,dan
KT= Faktor Frekuensi, merupakan fungsi dari peluang atau periode ulang dan tipe model matematik disrtibusi peluang yang digunakan untuk analisis peluang.
2.2.3.3 Distribusi Log Pearson III
Perhitungan curah hujan rencana menurut metode Log Pearson III, mempunyai langkah-langkah perumusan sebagai berikut:
- Ubah data dalam bentuk logaritmis, X = Log X - Hitung harga rata-rata:
n logX X log n 1 i i
(2.5)- Hitung harga simpangan baku :
0.5 n 2 i logX logX
- Hitung koefisien kemencengan :
3 n 1 i 3 i s 2 n 1 n X log logX G
(2.7)- Hitung logaritma hujan atau banjir dengan periode ulang T dengan rumus : K.s
X log
logXT (2.8)
Dimana K adalah variabel standar ( standardized variable) untuk X yang besarnya tergantung koefisien kemencengan G. tabel 2.2 memperlihatkan harga k untuk berbagai nilai kemencengan G.
Interval kejadian (Recurrence interval), tahun (periode ulang)
1,0101 1,2500 2 5 10 25 50 100
Koef,G Persentase peluang terlampaui (Percent chance of being exceeded)
99 80 50 20 10 4 2 1 3,0 2,8 2,6 2,4 2,2 -0,667 -0,714 -0,769 -0,832 -0,905 -0,636 -0,666 -0,696 -0,725 -0,752 -0,396 -0,384 -0,368 -0,351 -0,330 0,420 0,460 0,499 0,537 0,574 1,180 1,210 1,238 1,262 1,284 2,278 2,275 2,267 2,256 2,240 3,152 3,114 3,071 3,023 2,970 4,051 3,973 2,889 3,800 3,705 2,0 1,8 1,6 1,4 1,2 -0,990 -1,087 -1,197 -1,318 -1,449 -0,777 -0,799 -0,817 -0,832 -0,844 -0,307 -0,282 -0,254 -0,225 -0,195 0,609 0,643 0,675 0,705 0,732 1,302 1,318 1,329 1,337 1,340 2,219 2,193 2,163 2,128 2,087 2,192 2,848 2,780 2,706 2,626 3,605 3,499 3,388 3,271 3,149 1,0 0,8 0,6 0,4 0,2 -1,588 -1,733 -1,880 -2,029 -2,178 -0,852 -0,856 -0,857 -0,855 -0,850 -0,164 -0,132 -0,099 -0,066 -0,033 0,758 0,780 0,800 0,816 0,830 1,340 1,336 1,328 1,317 1,301 2,043 1,993 1,939 1,880 1,818 2,542 2,453 2,359 2,261 2,159 3,022 2,891 2,755 2,615 2,472 0,0 -0,2 -0,4 -0,6 -0,8 -2,326 -2,472 -2,615 -2,755 -2,891 -0,842 -0,830 -0,816 -0,800 -0,780 0,000 0,033 0,066 0,099 0,132 0,842 0,850 0,855 0,857 0,856 1,282 1,258 1,231 1,200 1,166 1,751 1,680 1,606 1,528 1,448 2,051 1,945 1,834 1,720 1,606 2,326 2,178 2,029 1,880 1,733 -1,0 -1,2 -1,4 -1,6 -1,8 -3,022 -2,149 -2,271 -2,388 -3,499 -0,758 -0,732 -0,705 -0,675 -0,643 0,164 0,195 0,225 0,254 0,282 0,852 0,844 0,832 0,817 0,799 1,128 1,086 1,041 0,994 0,945 1,366 1,282 1,198 1,116 1,035 1,492 1,379 1,270 1,166 1,069 1,588 1,449 1,318 1,197 1,087 -2,0 -2,2 -2,4 -2,6 -2,8 -3,0 -3,605 -3,705 -3,800 -3,889 -3,973 -7,051 -0,609 -0,574 -0,537 -0,490 -0,469 -0,420 0,307 0,330 0,351 0,368 0,384 0,396 0,777 0,752 0,725 0,696 0,666 0,636 0,895 0,844 0,795 0,747 0,702 0,660 0,959 0,888 0,823 0,764 0,712 0,666 0,980 0,900 0,830 0,768 0,714 0,666 0,990 0,905 0,832 0,769 0,714 0,667 Tabel 2.2 Nilai K untuk distribusi Log-Person III
2.2.3.4 Distribusi Gumbel
Perhitungan curah hujan rencana menurut Metode Gumbel, mempunyai perumusan sebagai berikut:
S.K X
X (2.9)
Dimana :
X = harga rata-rata sampel,
S = standar deviasi (simpangan baku) sampel.
Nilai K (faktor probabilitas) untuk harga-harga ekstrim Gumbel dapat dinyatakan dalam persamaan:
n n Tr S Y Y K (2.10) Dimana :
Yn = reduced mean yang tergantung jumlah sample/ data n (Tabel 2.3) Sn = reduced standard deviation yang juga tergantung pada jumlah sample/
data n (Tabel 2.4)
YTr= reduced variate, yang dapat dihitung dengan persamaan berikut ini.
r r Tr T 1 T ln ln Y (2.11)
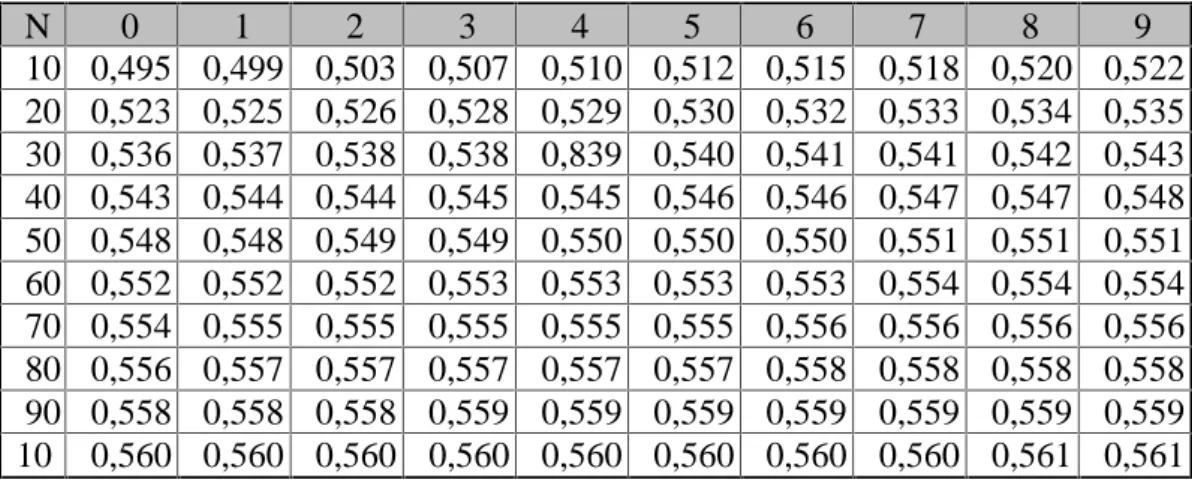
Tabel 2.3 Reduced Mean, Yn
(Suripin, 2004, Sistem Drainase Perkotaan yang Berkelanjutan: 51) Tabel 2.4 Reduced Standard Deviation, Sn
(Suripin, 2004, Sistem Drainase Perkotaan yang Berkelanjutan: 52)
Tabel 2.5 Reduced variate, YTrsebagai fungsi periode ulang Periode Ulang, Tr (tahun) Reduced variate YTr Periode ulang, Tr (tahun) Reduced variate Ytr 2 0,3668 100 4,6012 5 1,5004 200 5,2969 10 2,2510 250 5,5206 20 2,9709 500 6,2149 25 3,1993 1000 6,9087 50 3,9028 5000 8,5188 75 4,3117 10000 9,2121
(Suripin, 2004, Sistem Drainase Perkotaan yang Berkelanjutan: 52)
N 0 1 2 3 4 5 6 7 8 9 10 0,495 2 0,499 6 0,503 5 0,507 0 0,510 0 0,512 8 0,515 7 0,518 1 0,520 2 0,522 0 20 0,523 6 0,525 2 0,526 8 0,528 3 0,529 6 0,530 9 0,532 0 0,533 2 0,534 3 0,535 3 30 0,536 2 0,537 1 0,538 0 0,538 8 0,839 6 0,540 3 0,541 0 0,541 8 0,542 4 0,543 6 40 0,543 6 0,544 2 0,544 8 0,545 3 0,545 8 0,546 3 0,546 8 0,547 3 0,547 7 0,548 1 50 0,548 5 0,548 9 0,549 3 0,549 7 0,550 1 0,550 4 0,550 8 0,551 1 0,551 5 0,551 8 60 0,552 1 0,552 4 0,552 7 0,553 0 0,553 3 0,553 5 0,553 8 0,554 0 0,554 3 0,554 5 70 0,554 8 0,555 0 0,555 2 0,555 5 0,555 7 0,555 9 0,556 1 0,556 3 0,556 5 0,556 7 80 0,556 9 0,557 0 0,557 2 0,557 4 0,557 6 0,557 8 0,558 0 0,558 1 0,558 3 0,558 5 90 0,558 6 0,558 7 0,558 9 0,559 1 0,559 2 0,559 3 0,559 5 0,559 6 0,559 8 0,559 9 10 0 0,560 0 0,560 2 0,560 3 0,560 4 0,560 6 0,560 7 0,560 8 0,560 9 0,561 0 0,561 1 N 0 1 2 3 4 5 6 7 8 9 10 0,949 6 0,967 6 0,983 3 0,997 1 1,009 5 1,020 6 1,031 6 1,041 1 1,049 3 1,056 5 20 1,062 8 1,069 6 1,075 4 1,081 1 1,086 4 1,091 5 1,096 1 1,100 4 1,104 7 1,108 0 30 1,112 4 1,115 9 1,119 3 1,122 6 1,125 5 1,128 5 1,131 3 1,133 9 1,136 3 1,138 8 40 1,141 3 1,143 6 1,145 8 1,148 0 1,149 9 1,151 9 1,153 8 1,155 7 1,157 4 1,159 0 50 1,160 7 1,162 3 1,163 8 1,165 8 1,166 7 1,168 1 1,169 6 1,170 8 1,172 1 1,173 4 60 1,174 7 1,175 9 1,177 0 1,178 2 1,179 3 1,180 3 1,181 4 1,182 4 1,183 4 1,184 4 70 1,185 4 1,186 3 1,187 3 1,188 1 1,189 0 1,189 8 1,190 6 1,191 5 1,192 3 1,193 0 80 1,193 8 1,194 5 1,195 3 1,195 9 1,196 7 1,197 3 1,198 0 1,198 7 1,199 4 1,200 1 90 1,200 7 1,201 3 1,202 0 1,202 6 1,203 2 1,203 8 1,204 4 1,204 9 1,205 5 1,206 0 10 0 1,206 5 1,206 9 1,207 3 1,207 7 1,208 1 1,208 4 1,208 7 1,209 0 1,209 3 1,209 6
2.2.4 Uji Distribusi Probabilitas
Uji distribusi probabilitas dimaksudkan untuk mengetahui apakah persamaan distribusi probabilitas yang dipilih dapat mewakili distribusi statistik sampel data yang dianalisis.(I.M.Kamiana, 2011)
2.2.4.1 Metode Chi-Kuadrat
Rumus yang digunakan dalam perhitungan dengan metode uji chi-kuadrat adalah sebagai berikut :
n 1 i f 2 f f 2 E E O χ (2.12) Dimana :χ2 = Parameter chi-kuadrat terhitung.
Ef = Frekuensi yang diharapkan sesuai dengan pembagian kelasnya.
Of = Frekuensi yang diamati pada kelas yang sama.
n = jumlah sub kelompok.
Derajat nyata atau derajat kepercayaan (α) tertentu yang sering diambil adalah 5%. Derajat kebebasan (Dk) dihitung dengan rumus :
Dk = K – (p+1) (2.13)
Dimana :
Dk = derajat kebebasan.
P = banyaknya parameter, untuk uji chi-kuadrat adalah 2 K = jumlah kelas distribusi
n = banyaknya data
Selanjutnya distribusi probabilitas yang dipaki untuk menentukan curah hujan rencana adalah distribusi probabilitas yang mempunyai simpangan maksimumterkecil dan lebih kecildari simpangan kritis atau dirumuskan sebagai berikut :
χ2< χ2cr (2.15)
Dimana :
χ2 = parameter chi-kuadrat terhitung.
χ2cr = parameter chi-kuadrat kritis (tabel 2.6)
Prosedur perhitungan dengan menggunakan dengan metode chi-kuadrat adalah sebagai berikut :
Urutkan data dari besar ke kecil atau sebaliknya. Menghitung jumlah kelas.
Menghitung derajat kebebasan (Dk) dan χ2cr Menghitung kelas distribusi.
Menghitung interval kelas. Perhitungan nilai χ2.
Tabel 2.6 tabel nilai parameter Chi-Kuadrat Kritis, χ2cr Dk (α) Derajat Kepercayaan 0,995 0,99 0,975 0,95 0,05 0,025 0,01 0,005 1 0,0000393 0,000157 0,000982 0,00393 3,841 5,024 6,635 7,879 2 0,0100 0,0201 0,0506 0,103 5,991 7,378 9,210 10,597 3 0,0717 0,115 0,216 0,352 7,815 9.,48 11,345 12,838 4 0,207 0,297 0,484 0,711 9,488 11,143 13,277 14,860 5 0,412 0,554 0,831 1,145 11,070 12,832 15,086 16,750 6 0,676 0,872 1,237 1,635 12,592 14,449 16,812 18,548 7 0,989 1,239 1,69 2,167 14,067 16,013 18,475 20,278 8 1,344 1,646 2,18 2,733 15,507 17,535 20,09 21,955 9 1,735 2,088 2,7 3,325 16,919 19,023 21,666 23,589 10 2,156 2,558 3,247 3,940 18,307 20,483 23,209 25,188 11 2,603 3,053 3,816 4,575 19,675 21,492 24,725 26,757 12 3,074 3,571 4,404 5,226 21,026 23,337 26,217 28,300 13 3,565 4,107 5,009 5,892 22,362 24,736 27,688 29,819 14 4,075 4,660 5,629 6,571 23,685 26,119 29,141 31,319 15 4,601 5,229 6,161 7,261 24,996 27,488 30,578 32,801 16 5,142 5,812 6,908 7,962 26,296 28,845 32,000 34,267 17 5,697 6,408 7,564 8,672 27,587 30,191 33,409 35,718 18 6,265 7,015 8,231 9.,90 28,869 31,526 34,805 37,156 19 6,844 7,633 8,907 10,117 30,144 32,852 36,191 38,582 20 7,434 8,260 9,591 10,851 31,410 34,17 37,566 39,997 21 8,034 8,897 10,283 11,591 32,671 35,479 38,932 41,401 22 8,643 9,542 10,982 12,338 33,924 36,781 40,289 42,796 23 9,260 10,196 11,689 13,091 36,172 38,076 41,638 44,181 24 9,886 10,856 12,401 13,848 36,415 39,364 42,980 45,558 25 10,52 11,524 13,120 14,611 37,652 40,646 44,314 46,928 26 11,16 12,198 13,844 15,379 38,885 41,923 45,642 48,290 27 11,808 12,879 14,573 16,151 40,113 43,194 46,963 49,645 28 12,461 13,565 15,308 16,928 41,337 44,461 48,278 50,993 29 13,121 14,256 16,047 17,708 42,557 45,722 49,588 52,336 30 13,787 14,953 16,791 18,493 43,773 46,979 50,892 53,672 Sumber : Soewarno (1995)
2.2.4.2 Metode Smirnov-Kolmogorof
Pengujian distribusi probabilitas dengan Metode Smirnov-Kolmogorof dilakukan dengan langkah-langkah perhitungan sebagai berikut:
Urutkan data (Xi) dari besar ke kecil atau sebaliknya.
Tentukan peluang empiris masing-masing data yang sudah diurut tersebut P(Xi) dengan rumus tertentu, rumus Weibull misalnya :
1 n i ) P(Xi (2.16) Dimana : n = jumlah data.
i = nomor urut data (setelah diurut dari besar ke kecil atau sebaliknya.
Tentukan peluang teoritis masing – masing data yang sudah di urut
tersebut P’ (Xi) berdasarkan persamaan distribusi probabilitas yang diplih
(Gumbel, Normal, dan sebagainya).
Hitung selisih (∆Pi ) antara peluang empiris dan teoritis untuk setiap data yang sudah diurut :
∆Pi= P(Xi) –P’ (Xi) (2.17)
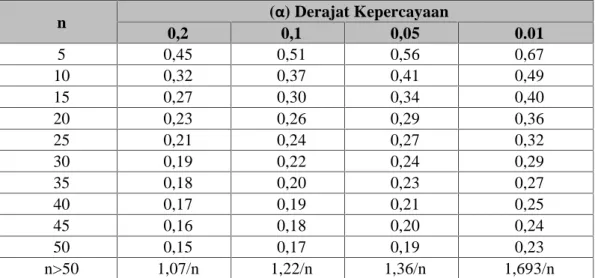
5. Tentukan apakah ∆Pi < ∆P kritis, jika “tidak” artinya distribusi probabilitas yang dipilih tidak dapat diterima, demikian sebaliknya.
n (α) Derajat Kepercayaan 0,2 0,1 0,05 0.01 5 0,45 0,51 0,56 0,67 10 0,32 0,37 0,41 0,49 15 0,27 0,30 0,34 0,40 20 0,23 0,26 0,29 0,36 25 0,21 0,24 0,27 0,32 30 0,19 0,22 0,24 0,29 35 0,18 0,20 0,23 0,27 40 0,17 0,19 0,21 0,25 45 0,16 0,18 0,20 0,24 50 0,15 0,17 0,19 0,23 n>50 1,07/n 1,22/n 1,36/n 1,693/n Sumber : Soewarno (1995)
2.3 Intensitas Hujan Rencana
Intensitas hujan adalah jumlah hujan yang dinyatakan dalam tinggi hujan atau volume hujan tiap satuan waktu. (Wesli, 2008). Sifat umum hujan adalah makin singkat hujan berlangsung intensitasnya cenderung makin tinggi dan makin besar periode ulangnya makin tinggi pula intensitasnya.(Suripin, 2004).
Intensitas hujan diperoleh dengan cara melakukan analisis data hujan baik secara statistik maupun secara empiris. Biasanya intensitas hujan dihubungkan dengan durasi hujan jangka pendek misalnya 5 menit, 30 menit, 60 menit dan jam- jaman. Data curah hujan jangka pendek ini hanya dapat diperoleh dengan menggunakan alat pencatat hujan otomatis. Apabila data hujan jangka pendek tidak tersedia, yang ada hanya data hujan harian, maka intensitas hujan dapat dihitung dengan rumus Mononobe.
Dimana:
I = Intensitas hujan (mm/jam) t = Lamanya hujan (jam)
R24 = Curah hujan maksimum dalam 24 jam (mm). 2.5.4 Waktu Konsentrasi
Waktu konsentrasi suatu DAS adalah waktu yang diperlukan oleh air hujan yang jatuh untuk mengalir dari titik terjauh sampai ketempat keluar DAS (Titik Kontrol) setelah tanah menjadi jenuh dan depresi-depresi kecil terpenuhi. Salah satu rumus untuk memperkirakan waktu konsentrasi (tc)adalah rumus yang
dikembangkan oleh Kirpich (1940), yang ditulis sebagai berikut.
tc= 0,87 x L 21000 x S x 0,385 (2.19)
dimana:
L: Panjang saluran utama dari hulu sampai penguras (km). S: Kemiringan rata-rata saluran utama dalam (m/m).
Waktu konsentrasi dapat juga dihitung dengan membedakan menjadi dua komponen yaitu:
1. Inlet time (t0) yakni waktu yang diperlukan air untuk mengalir di permukaan lahan sampai saluran terdekat.
2. Conduit time (td)yakni waktu perjalanan dari pertama masuk sampai titik keluaran.
dimana:
t0 : 23 x 3,28 x L x nS (menit) td : Ls60 V (menit),
n : Angka kekasaranManning,
Ls : Panjang lintasan aliran di dalam salura/sungai (m). 2.5.5 Koefisien Aliran Pengaliran
Koefisien pengaliran (C) didefinisikan sebagai nisbah antara aliran permukaan terhadap intensitas hujan (Suripin, 2004). Faktor ini merupakan variabel yang paling menentukan hasil perhitungan debit banjir. Pemilihan harga C yang tepat memerlukan pengalaman hidrologi yang luas. Berikut disajikan koefisien pengaliran (C) pada tabel 2.8.
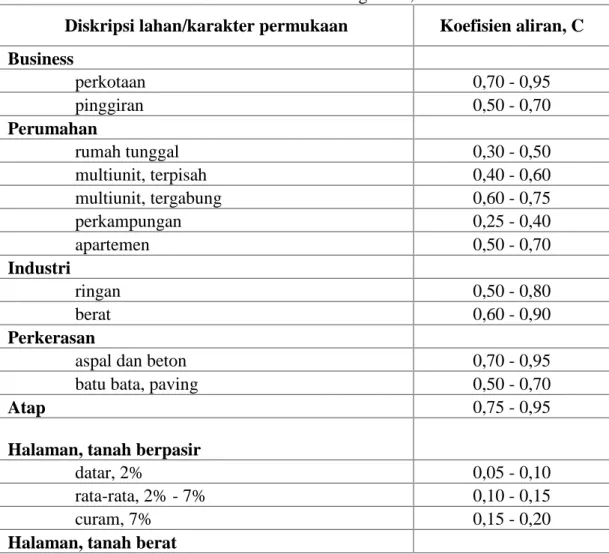
Tabel 2.8 Koefisien Pengaliran, C
Diskripsi lahan/karakter permukaan Koefisien aliran, C Business perkotaan 0,70 - 0,95 pinggiran 0,50 - 0,70 Perumahan rumah tunggal 0,30 - 0,50 multiunit, terpisah 0,40 - 0,60 multiunit, tergabung 0,60 - 0,75 perkampungan 0,25 - 0,40 apartemen 0,50 - 0,70 Industri ringan 0,50 - 0,80 berat 0,60 - 0,90 Perkerasan
aspal dan beton 0,70 - 0,95
batu bata, paving 0,50 - 0,70
Atap 0,75 - 0,95
Halaman, tanah berpasir
datar, 2% 0,13 - 0,17
rata-rata, 2% - 7% 0,18 - 0,22
curam, 7% 0,25 - 0,35
Halaman kereta api 0,10 - 0,35
Taman tempat bermain 0,20 - 0,35
Taman, perkuburan 0,10 - 0,25 Hutan datar, 0 - 5% 0,10 - 0,40 bergelombang, 5% - 10% 0,25 - 0,50 berbukit, 10% - 30% 0,30 - 0,60 Sumber : Suripin (2004)
2.6 Perhitungan Debit Banjir Hidrograf Satuan Sintesis Nakayasu
Stasiun pengukur debit dan tinggi muka air sungai (stasiun hidrometri) pada umumnya hanya dipasang di tempat tempat tertentu yang dipandang oleh pengelolanya mempunyai arti yang cukup penting. Hal tersebut disebabkan karena tidak mungkin memasang stasiun hidrometri disembarang tempat dan biaya pemasangannya juga tidak murah. Namun masalah yang banyak timbul adalah ketidak-cocokan antara rencana pengembangan jaringan stasiun hidrometri. Pengembangan suatu daerah sering tidak dapat diketahui sebelumnya, atau kalau rencana itu diketahui tidak selekasnya diikuti dengan keiatan pengumpulan data. Hingga pada saat dibutuhkan untuk analisis data tidak tersedia, atau tersedia dalam jangka waktu yang sangat pendek.
Untuk mengatasi hal ini sebenarnya di Indonesia telah dikenal dan banyak digunakan cara cara untuk memperkirakan banjir rancangan yang didasarkan atas persamaan rasional. Cara ini mengandalkan data curah hujan sebagai dasar hitungan.Namun dari penelitian terbukti bahwa cara cara seperti Melchior, Der
Selain itu tercatat pula bahwa 77% dari kasus yang ditinjau menunjukkan perkiraan lebih (overestimated). Cara - cara rasional untuk memperkirakan banjir yang mendapatkan kritikan tajam, karena pemakaian koefisien limpasan (runoff coefficient) mengundang subjektivitas yang sangat besar dan merupakan salah satu faktor penyebab penyimpangannya. Penyebab lainnya adalah koefisien reduksi (reduction coefficient). Persamaan rasional hanya dianjurkan untuk DAS kecil, kurang dari 80 hektar, atau untuk DAS yang memiliki unsur unsur penyusun yang seragam. Dalam perancangan diharapkan perkiraan banjir rancangan yang menyimpang sekecil mungkin. Sudah barang tentu perkiraan yang tepat tidak akan dapat diharapkan, karena proses pengalihragaman hujan menjadi banjir merupakan proses alam yang sangat kompleks yang tidak dapat diungkapkan dengan persamaan matematik secara tuntas. Cara cara lain yang lebih baik hampir seluruhnya menuntut ketersediaan data pengukuran sungai yang memadai. Hidrograf Satuan Sintetik Nakayasu ini merupakan salah satu upaya untuk mengatasi kesulitan kesulitan tersebut.Cara ini dapat digunakan disembarang lokasi yang dikehendaki dalam suatu DAS tanpa tergantung ada atau tidaknya data pengukuran sungai. Akan tetapi, perlu ditegaskan bahwa kegiatan hidrometrik masih tetap merupakan pilihan utama, sehingga walaupun telah ditemukan cara pendekatan yang akan banyak mengatasi masalah kelangkaan data, namun prioritas pengukuran sungai ditempat mutlak masih diperlukan. Hidrograf satuan ini secara sederhana dapat disajikan sebagai berikut ini:
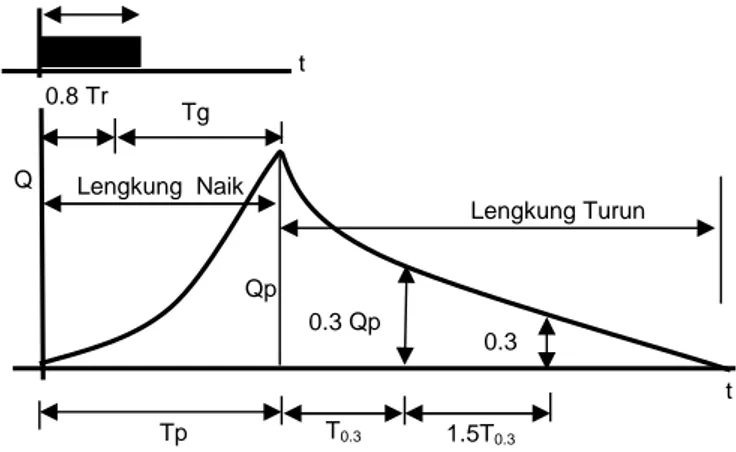
Gambar 2.4 Hidrograf Satuan Sintetik Nakayasu
Nakayasu (1950) telah menyelidiki hidrograf satuan di Jepang dan memberikan seperangkat persamaan untuk membentuk suatu hidrograf satuan sebagai berikut:
1. Waktu kelambatan (tg), rumusnya:
untuk L > 15 : = 0,4 + 0, 058 (2.22)
untuk L < 15 : = 0,21 , (2.23)
2. Waktu pucak dan debit puncak hidrograf satuan sintetis dirumuskan sebagai berikut:
= + 0,8 (2.24)
3. Waktu saat debit sama dengan 0,3 kali debit puncak:
, = (2.25) 4. Waktu puncak = + 0,8 Lengkung Turun Lengkung Naik 0.8 Tr Tg t Q t Qp 0.3 Qp 0.3 Qp2 Tp T0.3 1.5T0.3
5. Debit puncak hidrograf satuan sintetis dirumuskan sebagai berikut:
= , ( ,
, ) (2.27)
6. Bagian lengkung naik (0 < t < tp)
= , (2.28)
7. Bagian lengkung turun Jika < < , = 0,3 , (2.29) Jika > > , = 0,3 , , , , (2.30) Jika > 1,5 , = 0,3 ,, , (2.31)
2.7 Prediksi Tinggi Muka Air Banjir Rencana Manual
Tinggi banjir ini dihitung dengan cara coba-coba dengan menggunakan metode tahapan langsung (dirrect step method). Debit yang digunakan adalah debit banjir rencana, dalam penelitian ini digunakan metode HSS Nakayasu.
Karena penampang sungai yang tidak beraturan untuk memudahkannya dalam melakukan perhitungan maka diasumsikan penampang sungai menjadi penampang trapesium dengan kemiringan 1:1 seperti terlihat pada Gambar 2.5. Pada Gambar 2.5 garis putus-putus menunjukkan tampang pendekatan yang
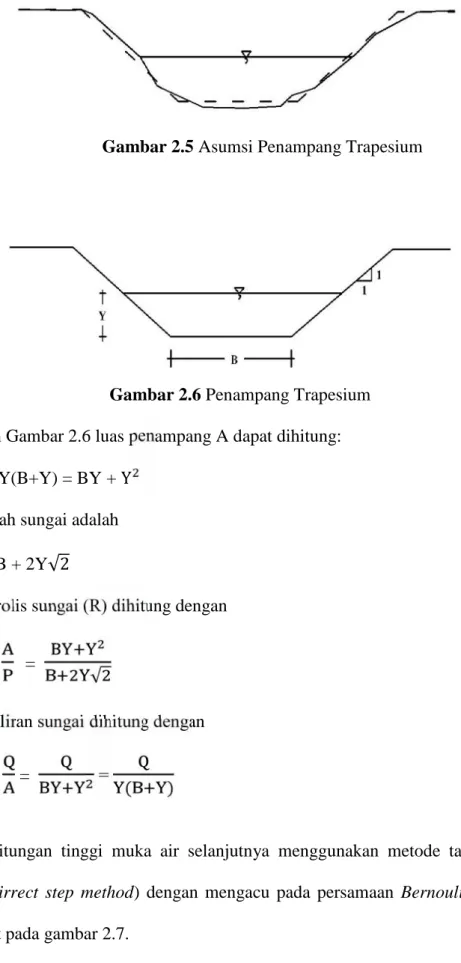
Gambar 2.5 Asumsi Penampang Trapesium
Gambar 2.6 Penampang Trapesium Berdasarkan Gambar 2.6 luas penampang A dapat dihitung:
A = Y(B+Y) = BY +Y Keliling basah sungai adalah
P = B + 2Y√2
Jari-jari hidrolis sungai (R) dihitung dengan
R = =
√
Kecepatan aliran sungai dihitung dengan
V = = =
( )
Perhitungan tinggi muka air selanjutnya menggunakan metode tahapan langsung (dirrect step method) dengan mengacu pada persamaan Bernouli yang dapat dilihat pada gambar 2.7.
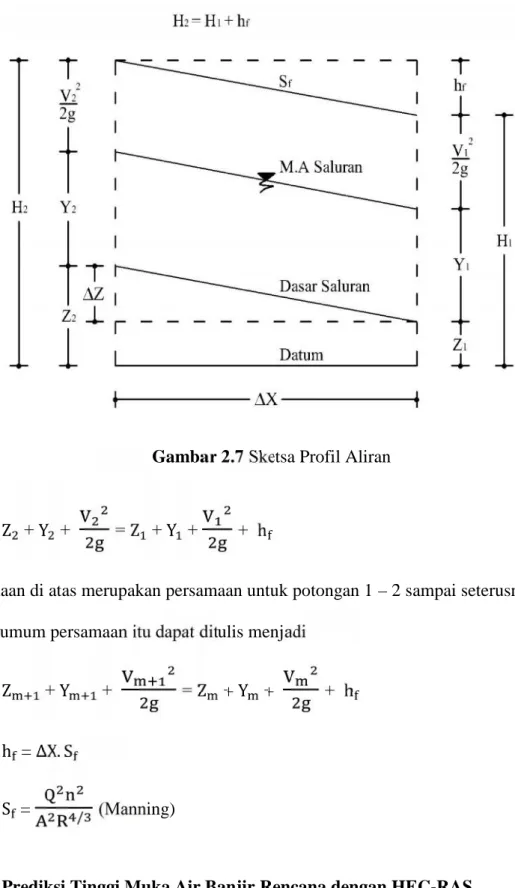
Gambar 2.7 Sketsa Profil Aliran
Z + Y + =Z + Y + + h
Persamaan di atas merupakan persamaan untuk potongan 1 – 2 sampai seterusnya. Secara umum persamaan itu dapat ditulis menjadi
Z +Y + =Z + Y + + h
h = ∆X. S
S = / (Manning)
(HEC) yang merupakan satuan kerja di bawah US Army Corps of Engineers (USACE).HEC-RAS merupakan model satu dimensi aliran permanen maupun tak-permanen (steady and unsteady one-dimensional flow model). HEC-RAS memiliki empat komponen model satu dimensi: (1) Hitungan profil muka air aliran permanen, (2) Simulasi aliran tak permanen, (3) Hitungan transport sedimen, dan (4) Hitungan kualitas (temperatur) air.
Satu elemen penting dalam HEC-RAS adalah keempat komponen tersebut memakai data geometri yang sama, routine hitungan hidraulika yang sama, serta beberapa fitur desain hidraulik yang dapat diakses setelah hitungan profile muka air dilakukan.
HEC-RAS merupakan program aplikasi yang mengintegrasikan fitur graphical user interface, analisis hidraulik, manajemen dan penyimpanan data, grafik, serta pelaporan.
Dengan menggunakan software HEC-RAS ini dapat memberikan prediksi tinggi muka air banjir sungai deli dengan banjir pasang muara sungai deli.
2.8.1 Graphical User Interface
Interface ini berfungsi sebagai penghubung antara pemakai dan HEC-RAS. Graphical interface dibuat untuk memudahkan pemakaian HEC-RAC dengan tetap mempertahankan efisiensi. Melalui graphical interface ini, dimungkinkan untuk melakukan hal-hal berikut ini dengan mudah:
Melakukan analisis hidraulik
Menampilkan data masukan maupun hasil analisis dalam bentuk tabel dan grafik
Penyusunan laporan, dan Mengakses On-Line help
2.8.2 Penyimpanan Data dan Manajemen Data
Penyimpanan data dilakukan ke dalam “flat” files (format ASCII dan
biner), serta file HEC-DSS. Data masukan dari pemakai HEC-RAS disimpan kedalam file-file yang dikelompokkan menjadi: project, plan, geometry, steady flow, unsteady flow, dan sediment data. Hasil keluaran model disimpan kedalam binary file. Data dapat ditransfer dari HEC-RAS ke program aplikasi lain melalui HEC-DSS file.
Manajemen data dilakukan melalui user interface. Pemakai diminta untuk menuliskan satu nama file untuk project yang sedang dia buat. HEC-RAS akanmenciptakan beberapa file secara automatik (file-file: plan, geometry, steady flow, unsteady flow, output, etc.) dan menamainya sesuai dengan nama file project yang dituliskan oleh pemakai. Penggantian nama file, pemindahan lokasi penyimpanan file, penghapusan file dilakukan oleh pemakai melalui fasilitas interface; operasi tersebut dilakukan berdasarkan project-by-project. Penggantian nama, pemindahan lokasi penyimpanan, ataupun penghapusan file yang dilakukan dari luar HEC-RAS (dilakukan langsung pada folder), biasanya akan
operasi atau modifikasi file-file harus dilakukan melalui perintah dari dalam HEC-RAS.
2.8.3 Grafik dan Pelaporan
Fasilitas grafik yang disediakan oleh HEC-RAS mencakup grafik X-Y alur sungai, tampang lintang, rating curves, hidrograf, dan grafik-grafik lain yang merupakan plot X-Y berbagai variabel hidraulik. HEC-RAS menyediakan pula fitur plot 3D beberapa tampang lintang sekaligus. Hasil keluaran model dapat pula ditampilkan dalam bentuk tabel.Pemakai dapat memilih antara memakai tabel yang telah disediakan oleh HEC-RAS atau membuat/mengedit tabel sesuai kebutuhan. Grafik dan tabel dapat ditampilkan di layar, dicetak, atau dicopy ke clipboard untuk dimasukkan kedalam program aplikasi lain (word processor, spreadsheet). Fasilitas pelaporan pada HEC-RAS dapat berupa pencetakan data masukan dan keluaran hasil pada printer atau plotter.
Untuk mulai pekerjaan HEC-RAS klik File terus New Project, kemudian simpan dengan nama Sungai Deli pada direktori atau folder .
Langkah selanjutnya adalah membuat dan mengisi geometri data. Dengan cara klik tool bar Edit/Enter Geometric Data dari tampilan awal HEC RAS. Seperti tampilan berikut ini:
Gambar 2.9 Tampilan menu geometri data.
Setelah muncul tampilan Geometric Data, langkah selanjutnya adalah membuat layout Sungai Deli dengan cara klik tool bar River Reach dari tampilan Geometric Data, kemudian mulai menggambar layout Sungai Deli dengan memberi nama River dan Reach nya.Kemudian masukkan data geometry muara Suara Deli pada tampilan ini dimasukkan data long section (penampang memanjang muara Sungai Deli) dengan cara klik ikon Cross Section padatampilan Geometric Data , sehingga selanjutnya akan muncul tampilan seperti ini:
Gambar 2.10 Menu Cross Section Pada Geometri Data
Untuk memasukkan data-data potongan melintang, klik Optionterus Add a New Cross Section, masukkan nomor stationing (Sta) atau nomor patok. Pada bagian kiri tampilan Cross Section Data terdapat dua buah kolom, yaitu station dan elevation.Yang dimaksud dengan station adalah jarak pias potongan melintang (sumbu X), sedangkan yang dimaksud dengan elevation adalah elevasi pias potongan melintang (sumbu Y).kemudianmasukkan Downstream Reach Length atau jarak antar potongan melintang yang kini sedang dibuat dengan potongan melintang dihilirnya, angka Manning, dan Main Channel Bank Station yang berada pada bagian tengah tampilan Cross Section Data. Pada Reach Length, kemudian masukkan data berupa jarak pada LOB (Left Over Bank) atau tebing kiri, Channel atau bagian tengah, dan ROB (Right Over Bank). Angka Manning dimasukkan berdasarkan kekasaran material dinding saluran, sedangkan data Bank Stationing dimasukkan berdasarkan tebing yang ada pada data potongan melintang.
Gambar 2.11 Tampilan Data Cross Section
Setelah semua geometri data selesai dimasukkan, selanjutnya di savedengan klik File terus Save Geometric Data As.
Langkah selanjutnya adalah memasukkan data aliran, untuk memasukkan data aliran, klik Edit/Unsteady Flow Data.Pada tabBoundary Condition, klik tampilan flowhydrographmasukkan data debit banjir yang dihitung dengan metode HSS Nakayasu, seperti tampilan berikut:
Selanjutnya masukkan data pasang surut yang dihitung dengan metode Admiraltyklik tampilanstage/flow hydrograph, seperti gambar 2.13.
Gambar 2.13 Unsteady Flow Data yang dimasukkan data hasil perhitungan Pada aliran unsteady, selain data boundary condition, kita juga harus memasukkan data initial condition. Data initial condition ini merupakan asumsi aliran pada jam ke-nol.Setelah data aliran telah selesai dimasukkan, klik filekemudian save unsteady flow data as.
Selanjutnya running aliran unsteady klik item-item pada Programs to Run, mengisi waktu atau tanggal simulasi pada Simulation Time Windowdan menyetting interval waktu perhitungan pada Computation Setting. Pada tampilan Flow Analysis, pilih Geometry File dan Flow File yang akan dirunning, dan menamai Plan. Selanjutnya klik Compute,seperti gambar 2.14.