Bab ini khusus membahas mengenai definisi serta sifat – sifat dari line digraph yang dapat digunakan untuk mengenali line digraph. Jika suatu graf memenuhi sifat – sifat yang akan dibahas kemudian, maka graf tersebut adalah suatu line digraph dan dapat dibentuk graf lain sebagai graf asalnya, dimana lintasan Hamilton pada line digraph merupakan lintasan Euler pada graf asal.
3.1. Definisi
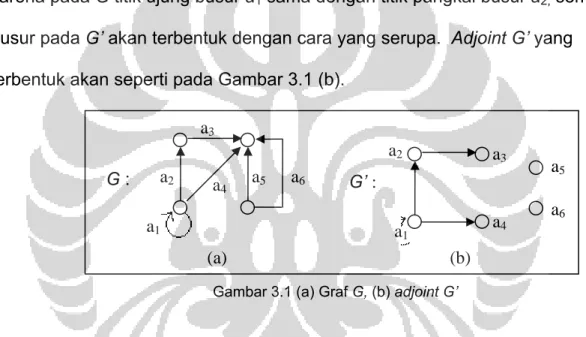
Suatu graf disebut graf-p jika untuk setiap pasangan terurut simpul x,y (x boleh sama dengan y), terdapat paling banyak p busur sejajar dari x ke y. Jika suatu graf tidak memiliki busur sejajar (p = 1) maka graf tersebut disebut graf-1. Seperti yang telah dibahas pada Bab II, adjoint G’= (V,U) dari suatu graf berarah G = (X,V) merupakan graf-1 dengan himpunan simpul V dan terdapat busur dari simpul x ke y di G’ jika dan hanya jika titik ujung dari busur x di G merupakan titik pangkal dari busur y di G. Suatu graf G’ merupakan adjoint jika terdapat suatu graf G sedemikian sehingga G’ merupakan adjoint dari G. Suatu graf dikatakan directed line graph (atau
Gambar 3.1 (a) Graf G, (b) adjoint G’
disebut line digraph) jika dan hanya jika graf tersebut merupakan adjoint dari graf-1.
Pada Gambar 3.1(a) diberikan contoh graf berarah G dengan empat simpul dan enam busur {a1, a2, a3, a4, a5, a6}. Pada adjoint G’, akan ada enam simpul {a1, a2, a3, a4, a5, a6} dan akan ada busur dari simpul a1 ke a2 karena pada G titik ujung busur a1 sama dengan titik pangkal busur a2, semua busur pada G’ akan terbentuk dengan cara yang serupa. Adjoint G’ yang terbentuk akan seperti pada Gambar 3.1 (b).
Secara garis besar, sifat – sifat dari line digraph dapat dilihat dari hubungan antara adjoint dan graf asal serta dari pelabelan pada suatu graf. Ketika mempelajari sifat – sifat dari line digraph yang melihat dari hubungan adjoint dan graf asal akan dipergunakan istilah lingkungan untuk menyatakan simpul – simpul yang bertetangga dengan suatu simpul. Jika suatu simpul y merupakan titik ujung dari suatu busur yang memiliki titik pangkal di x maka simpul y merupakan anggota lingkungan kanan dari x. Jika suatu simpul y merupakan titik pangkal dari suatu busur yang memiliki titik ujung di x maka simpul y merupakan anggota lingkungan kiri dari x. Definisi formal dari
a1 a2 a3 a4 a5 a6 a1 a2 a3 a4 a5 a6 G : G’ : (a) (b)
lingkungan kanan N+(x) dan lingkungan kiri N-(x). MisalkanG=( , )V U dan x V∈ , maka N+( )x ={y V∈ | ( , )x y ∈U} dan N−( )x ={y∈V| ( , )y x ∈U}.
Sifat – sifat dari line digraph juga dapat dilihat dengan memberikan suatu pelabelan pada simpul graf tersebut. Pelabelan yang digunakan merupakan tuple dengan panjang k dan komponen label 1,…,α. Label dari setiap simpul harus berbeda dan jika dua simpul x dan y terhubung maka k-1 label paling kanan simpul x harus sama dengan k-1 label paling kiri dari simpul y. Pelabelan seperti ini disebut dengan pelabelan ( , )α k . Definisi formal dari pelabelan ( , )α k diberikan pada Definisi 3.1.
Definisi 3.1 Misalkan α > 0 dan k > 1 merupakan dua bilangan bulat. Suatu graf-1 H =( , )V U diketahui dapat dilabel dengan pelabelan- ( , )α k jika
dimungkinkan untuk memberi label ( ( ), ( ),..., ( ))l x l x1 2 l x dengan panjang k k pada tiap simpul x dari H sedemikian sehingga
1. ( ) {1,..., } l xi ∈ α ∀ ∈x V i=1,...,k
2. Semua label berbeda, yakni ( ( ), ( ),..., ( ))l x l x1 2 l xk ≠( ( ), ( ),..., ( ))l y l y1 2 l yk jika x≠ y.
3. ( , )x y ∈ ⇔U ( ( ),..., ( ))l x2 l xk =( ( ),...,l y1 lk−1( ))y
Graf-1 yang dapat dilabel dengan pelabelan- ( , )α k akan masuk ke dalam kelas L kα dengan α > 0 dan k > 1. Karena line digraph adalah graf-1 maka line digraph yang dapat dilabel dengan pelabelan- ( , )α k termasuk kelas
α
L k . Setelah membahas mengenai definisi dari line digraph dan pelabelan, pada subbab selanjutnya akan dibahas sifat – sifat dari line digraph.
3.2. Sifat – sifat dari line digraph
Telah disinggung bahwa secara garis besar, sifat – sifat dari line digraph dapat dilihat dari hubungan antara adjoint dan graf asal serta dari pelabelan pada suatu graf. Sifat – sifat dari line digraph yang dilihat dari hubungan antara adjoint dengan graf asal dapat dilihat pada teorema – teorema berikut.
Teorema 3.1 Misalkan graf H adalah adjoint dari graf G. Maka terdapat lintasan/lingkaran Euler di G jika dan hanya jika terdapat lintasan/lingkaran Hamilton di H.
Bukti. Berdasarkan definisi adjoint, dimana simpul pada graf H merupakan busur pada graf G. Oleh karena itu, jika terdapat lintasan/lingkaran yang melalui tiap busur pada graf G maka terdapat juga lintasan/lingkaran yang melewati tiap simpul pada graf H dan berlaku sebaliknya.
Karena line digraph merupakan adjoint dari graf-1 maka diperoleh akibat sebagai berikut :
Akibat 3.1 Misalkan H adalah line digraph dari graf-1 G. Maka terdapat lintasan/lingkaran Euler di G jika dan hanya jika terdapat lintasan/lingkaran Hamilton di H.
Telah dijelaskan pada Bab II, permasalahan pada graf DNA yang dibentuk dari spektrum adalah mengubah pencarian lintasan Hamilton menjadi pencarian lintasan Euler sehingga graf DNA dapat dipandang sebagai line digraph. Telah dijelaskan pula bahwa masalah mencari lintasan/lingkaran Euler (jika ada) dapat ditemukan dalam waktu polinomial maka masalah mencari lintasan/lingkaran Hamilton pada adjoint mungkin juga dapat
ditemukan dalam waktu polinomial. Akan menarik untuk mengetahui apakah adjoint dapat dikenali dalam waktu polinomial. Teorema – teorema berikut dapat digunakan untuk membuktikannya. Pertama akan ditunjukan sifat dari adjoint yang dapat digunakan untuk mengenali apakah suatu graf merupakan adjoint.
Teorema 3.2 Suatu graf-1H =( , )V U adalah adjoint dari suatu graf jika dan hanya jika N+( )x ∩N+( )y ≠ ∅ ⇒N+( )x =N+( )y berlaku untuk setiap pasang simpul x,y di V.
Bukti. (⇒ ) Misalkan H = (V,U) adalah suatu graf-1 dan terdapat graf G = (X,V) sedemikian sehingga H adalah adjoint dari G. Ambil x,y sembarang simpul di H. Akan dibuktikan N+( )x ∩N+( )y ≠ ∅ ⇒N+( )x =N+( )y berlaku. Misalkan N+( )x ∩N+( )y ≠ ∅ berarti terdapat simpul p sedemikian sehingga
( ) ( )
p∈N+ x ∩N+ y . Karena H adjoint dari G, maka simpul p di H
berkorespondensi dengan suatu busur p di G. Simpul p bertetangga dengan simpul x di H (p∈N+( )x ) berarti terdapat busur x di G dan simpul a
sedemikan sehingga simpul a merupakan titik ujung bagi busur x dan titik pangkal bagi busur p. Begitu juga p∈N+( )y , berarti bahwa terdapat busur y di G yang berkorespondensi dengan simpul y di H, yang juga memiliki titik ujung di simpul a. Ambil sebarang simpul c di N+( )y , yang berarti bahwa c bertetangga dengan simpul y di H. Dengan demikian, terdapat busur c di G sedemikian sehingga titik ujung y dan titik pangkal c sama. Karena dari yang telah diketahui bahwa titik ujung y adalah a dan terminal suatu busur itu tunggal, maka titik pangkal dari busur c juga simpul a. Dengan demikian, titik pangkal busur c dan titik ujung busur x sama sehingga c∈N+( )x . Karena
( ) ( )
c∈N+ y ⇒ ∈c N+ x maka N+( )y ⊆N+( )x . Dengan cara yang sama, dapat dibuktikan bahwa N+( )y ⊇N+( )x . Dengan demikian terbukti bahwa
( ) ( ) N+ x =N+ y .
(⇐ ) Misalkan H = (V,U) adalah graf-1 dan N+( )x ∩N+( )y ≠ ∅ ⇒N+( )x = N+( )y berlaku untuk setiap pasang simpul x,y di V pada graf H. Akan dibuktikan terdapat graf G = (X,V) sedemikian sehingga graf H adalah adjoint dari G. Graf G dapat dibangun dengan cara, setiap simpul di H menjadi busur di G. Busur x, y di G dihubungkan oleh sebuah simpul jika dan hanya jika simpul x, y di H terhubung. Dengan demikian, menurut definisi graf H adalah line digraph dari graf G.
Selanjutnya untuk mengenali suatu graf yang merupakan adjoint adalah line digraph dapat digunakan sifat berikut:
Teorema 3.3 Sebuah adjoint adalah line digraph jika dan hanya jika tidak mengandung graf S, S’, S” dalam Gambar 3.2 sebagai subgraf parsialnya.
Bukti. (⇒ ) Misalkan H adalah line digraph dari graf-1 G yang mengandung S dan S’ sebagai subgrafnya.Berarti busur b dan c di G berkorespondensi dengan simpul b dan c di S dan S’. Busur b dan c ini harus memiliki titik pangkal yang sama (karena busur (a,b) dan (a,c) ada di S dan S’) yang juga
c a b S’ : S” : b c (a) (b) (c) Gambar 3.2 S, S’, S” a c d b S:
merupakan titik ujung bagi busur a. Tetapi karena busur (b,d) dan (c,d) di S serta busur (b,a) dan (c,a) di S’ maka busur b dan c juga harus memiliki titik ujung yang sama. Sehingga graf G yang diperoleh bukan graf-1. Hal ini kontradiksi dengan yang diketahui bahwa G adalah graf-1, maka pasti graf H tidak mengandung S dan S’ sebagai subgrafnya. Selanjutnya, misalkan pula graf H mengandung S” sebagai subgraf, maka pada simpul b dan c terdapat loop. Hal itu berarti pada graf G, busur b dan c adalah loop, dan loop
tersebut ada pada simpul yang sama. Sehingga kontradiksi juga dengan kenyataan G adalah graf-1. Oleh karena itu graf H tidak akan mengandung S, S’ dan S” sebagai subgraf.
(⇐ ) Misalkan H adalah adjoint dari graf G dan H tidak mengandung S, S’ maupun S” sebagai subgrafnya. Jika graf G adalah graf-1 maka berdasarkan definisi line digraph, graf H adalah suatu line digraph. Jika G bukan graf-1, bangun graf-1 G’ sedemikian sehingga H adalah adjoint dari G’. Bentuk G’ dengan cara, pertama anggap G’ = G. Selama G’ bukan graf-1, pasti ada pasangan simpul x,y di G’ dengan paling tidak dua busur sejajar yang
menghubungkan x dengan y. Karena S” bukan subgraf dari H, maka x dan y merupakan simpul yang berbeda. Selain itu diperoleh N−( )x = ∅ atau
( )
N+ y = ∅ . Jika N−( )x dan N+( )y bukan himpunan kosong maka di G’ akan memuat suatu busur, misalkan busur a, menuju x dan busur d yang
meninggalkan x dan menuju y. Jika a≠d, busur a, b, c dan d membentuk subgraf S pada graf H dan jika a=d akan terbentuk subgraf S’ pada graf H. Hal ini bertentangan dengan yang diketahui. Jadi N−( )x = ∅ atau N+( )y = ∅ pasti terpenuhi dan dapat dilakukan perubahan berikut pada G’ dimana
1, 2,..., p( 1)
e e e p> adalah busur sejajar dari x ke y. If N−( )x = ∅ then
Gantikan x dengan x x1, 2,...,x dan setiap busur ep i dengan busur (xi,y),
i = 1,…,p;
Gantikan tiap busur (x,z), z≠ y, dengan busur (xi,z) untuk suatu i.
else (N+( )y = ∅ )
Gantikan y dengan y y1, 2,...,y dan setiap busur ep i dengan busur (x,yi),
i = 1,…,p;
Gantikan tiap busur (z,y), z x≠ , dengan busur (z,yi) untuk suatu i.
Setelah perubahan ini, H tetap adjoint dari G’, karena perubahan tersebut tidak menghilangkan setiap lintasan yang ada di G’. Perubahan ini juga membuat banyaknya busur sejajar yang ada berkurang. Jadi dengan sejumlah langkah yang hingga, graf G dapat membentuk graf-1 yang
diinginkan. Sehingga H merupakan adjoint dari graf-1, yang berarti H adalah line digraph.
Akibat 3.2 Sebuah graf-1 H merupakan line digraph jika dan hanya jika
(
)
( ) ( ) ( ) ( ) ( ) ( )
N+ x ∩N+ y ≠ ∅ ⇒ N+ x =N+ y dan N− x ∩N− y = ∅ terpenuhi untuk tiap pasang simpul x, y di H.
Bukti. (⇒ ) Karena graf H adalah line digraph, berarti H merupakan adjoint dari suatu graf-1. Berdasarkan Teorema 2, N+( )x ∩N+( )y ≠ ∅
mengakibatkan N+( )x =N+( )y . Jika untuk tiap pasang simpul x, y terpenuhi
( ) ( ) ( ) ( )
N+ x =N+ y ≠ ∅ dan N− x ∩N− y ≠ ∅ , graf tersebut pasti mengandung S pada Gambar 3.2(a) sebagai subgraf, jika a sama dengan d graf G akan mengandung S’ atau, jika a sama dengan b dan d sama dengan c (atau sebaliknya) graf G akan mengandung S”. Oleh karena itu graf G akan mengandung S, S’ atau S” sebagai subgraf bila
( ) ( ) ( ) ( )
N+ x =N+ y ≠ ∅ dan N− x ∩N− y ≠ ∅ terpenuhi yang berarti kontradiksi dengan Teorema 3. Sehingga jika H adalah line digraph maka
(
)
( ) ( ) ( ) ( ) ( ) ( )
N+ x ∩N+ y ≠ ∅ ⇒ N+ x =N+ y dan N− x ∩N− y = ∅ terpenuhi untuk tiap pasang simpul x, y di H.
(⇐ ) Dari Teorema 2, diketahui bahwa graf H harus adjoint. Karena pada graf S, S’, dan S” terdapat sepasang simpul b dan c sedemikian sehingga
( ) ( ) ( ) ( )
N+ b ∩N+ c ≠ ∅dan N− b ∩N− c ≠ ∅ , maka graf yang ada tidak mungkin memiliki S, S’, dan S” sehingga H merupakan line digraph.
Dari Akibat 2 diketahui bahwa proses untuk mengenali suatu line digraph dapat dilakukan dalam waktu 3
(n ) Ο .
Selain sifat – sifat yang telah dibahas sebelumnya, suatu line digraph juga dapat dikenali dengan menggunakan pelabelan pada suatu graf. Aturan pelabelan yang digunakan adalah aturan yang ada pada subbab 3.1. Sifat dari line digraph yang dapat digunakan ada pada Teorema berikut:
Teorema 3.4 Misalkan G adalah graf yang termasuk dalam kelas L ∞
k dengan
k > 1, dan misalkan H adalah line digraph dari G. Maka H termasuk dalam kelas ∞
+1 L k .
Bukti. Perhatikan sebarang pelabelan- ( , )∞ k dari G, dan setiap busur ( , )x x i j di G. Misalkan ( ( ), ( ),..., ( ))l x1 i l x2 i l xk i dan ( (l x1 j),...,lk−1(xj), (l xk j)) adalah label untuk simpul xi dan simpul xj. Gunakan label ( ( ), ( ),..., ( ), (l x1 i l x2 i l xk i l xk j))
sebagai label simpul v = ( , )x x di H. Akan dibuktikan bahwa pemberian i j label ini merupakan pelabelan- ( ,∞ + dari H. Pertama, perlu diperhatikan k 1) bahwa pelabelan tersebut memiliki panjang k + 1. Karena G termasuk dalam kelas L k∞, dari definisi kelas L k∞ maka dipastikan bahwa setiap label di H berbeda. Selanjutnya akan ditunjukan bahwa (va,vb) adalah busur di H jika
dan hanya jika k komponen label paling akhir simpul va sama dengan k
komponen label paling awal simpul vb.
Misalkan va =(x xp, q) dan vb =( ,x xr s) merupakan dua simpul di H. Karena xp
adalah lingkungan kiri dari xq di G, maka( (l x2 p),..., (l xk p))=( (l x1 q),...,lk−1(xq)).
Jadi diperoleh beberapa pernyataan setara: (a) ( , )v v busur di H. a b
(b) simpul xq dan xr sama.
(c) label( ( ), ( ),..., ( ), ( ))l x1 r l x2 r l xk r l xk s dari vb sama dengan
1 2 1
( (l xq), (l xq),...,lk−(xq), (l xk q), ( ))l xk s , yang juga sama dengan
2
( (l xp),..., (l xk p), (l xk q), ( ))l xk s menurut pernyataan di atas.
(d) k label komponen paling akhir dari label ( (l x1 p), (l x2 p),..., (l xk p), (l xk q)) dari simpul va sama dengan k label komponen paling awal dari simpul vb.
Khusus untuk k = 2 maka diperoleh Teorema berikut:
Teorema 3.5 Sebuah graf merupakan line digraph jika dan hanya jika termasuk dalam kelas L 2∞
Bukti. (⇒ Misalkan H adalah line digraph dari graf G, maka setiap simpul v ) di H berkorespondensi dengan busur ( , )x x di G. Dengan memberi label (i,j) i j
pada simpul v = ( , )x x , akan diperoleh pelabelan- ( , 2)i j ∞ dari H, dimana semua labelnya berbeda karena G tidak memiliki busur sejajar.
(⇐ Misalkan terdapat suatu pelabelan- ( , 2)) ∞ dari H∈L . Tanpa 2∞ menghilangkan keumuman, asumsikan bahwa semua komponen label merupakan anggota dari himpunan A={1,..., }α dimana α ≤2n. Bangun
sebuah graf G = (A,V) dengan cara sebagai berikut: busur dari simpul i ke simpul j ada di G jika dan hanya jika terdapat simpul dengan label (i,j) di H. G adalah graf-1 karena setiap label dari H berbeda, dan dari pembentukan graf tersebut graf H merupakan line digraph dari G.