21
BAB V
DISTRIBUSI NORMAL Deskripsi:
Pada bab ini akan dibahas mengenai konsep distribusi normal dalam pengukuran.
Manfaat:
Memberikan metode distribusi normal yang benar saat melakukan proses pengukuran.
Relevansi:
Pertemuan ini membenaran teoritis untuk ide-ide statistik dan memberikan bukti beberapa hasil yang dinyatakan tanpa bukti dalam bab-bab sebelumnya.
Learning Outcome:
Mahasiswa memahami dan mampu mengimplementasikan metode distribusi normal hasil pengukuran dengan benar.
MATERI:
Bab ini melanjutkan pembahasan kita tentang analisis statistik pengukuran ulang. Bab 4 memperkenalkan ide-ide penting dari rerata, standar deviasi, dan deviasi standar dari rerata, kita melihat signifikansi mereka dan beberapa kegunaan mereka. Bab ini memasok pembenaran teoritis untuk ide-ide statistik dan memberikan bukti beberapa hasil dinyatakan tanpa bukti dalam bab-bab sebelumnya.
Masalah pertama dalam membahas pengukuran berulang kali adalah untuk menemukan cara untuk menangani dan menampilkan nilai-nilai yang diperoleh. Salah satu metode yang nyaman adalah dengan menggunakan distribusi atau histogram, seperti yang dijelaskan dalam Bagian 5.1. Bagian 5.2 memperkenalkan gagasan terbatas distribusi, distribusi hasil yang akan diperoleh jika jumlah pengukuran menjadi besar tak berhingga. Pada Bagian 5.3, saya mendefinisikan distribusi normal, atau distribusi Gauss, adalah distribusi terbatas hasil untuk setiap subjek pengukuran banyak kesalahan acak kecil.
Setelah sifat matematika dari distribusi normal dipahami, kita dapat melanjutkan untuk membuktikan beberapa hasil penting cukup mudah. Bagian 5.4 memberikan bukti bahwa, seperti yang diharapkan dalam Bab 4, sekitar 68 % dari semua pengukuran (semua satu kuantitas dan semua menggunakan teknik yang sama) harus berada dalam satu standar deviasi dari nilai sebenarnya. Bagian 5.5 membuktikan hasil, digunakan kembali dalam Bab 1, bahwa jika kita melakukan N pengukuran xl, x2,…, xN dari beberapa kuantitas x, maka
22 perkiraan terbaik kami xterbaik berdasarkan nilai rerata 𝑥̅ = ∑ 𝑥𝑖/𝑁. Bagian 5.6 membenarkan
penggunaan penambahan dalam quadrature ketika menyebarkan kesalahan yang independen dan acak. Pada Bagian 5.7, saya membuktikan bahwa ketidakpastian dari rerata 𝑥̅ , bila digunakan sebagai estimasi terbaik dari x, diberikan oleh deviasi standar dari rerata 𝜎𝑥 = 𝜎𝑥/√𝑁, sebagaimana tercantum dalam Bab 4. Akhirnya, Bagian 5.8 membahas bagaimana menetapkan kepercayaan numerik untuk hasil eksperimen.
Matematika yang digunakan dalam bab ini lebih maju daripada yang digunakan sejauh ini. Secara khusus, Anda akan perlu memahami ide dasar integrasi integral sebagai daerah di bawah grafik, perubahan variabel, dan (kadang-kadang) integrasi parsial. Namun, setelah Anda telah bekerja melalui Bagian 5.3 pada distribusi normal (akan lebih dari perhitungan dengan pensil dan kertas, jika perlu) Anda harus mampu mengikuti sisa bab tanpa banyak kesulitan.
5.1 Histogram dan Distribusi
Harus jelas bahwa analisis statistik percobaan mengharuskan kita untuk membuat banyak pengukuran. Jadi, pertama kita perlu merancang metode untuk merekam dan menampilkan sejumlah besar nilai yang terukur. Anggaplah, misalnya, kami membuat 10 pengukuran beberapa panjang x. Sebagai contoh, x mungkin jarak dari lensa ke bayangan yang dibentuk oleh lensa. Kita mungkin mendapatkan nilai-nilai (semua dalam cm)
26, 24, 26, 28, 23, 24, 25, 24, 26, 25. (5.1)
Sebagai langkah pertama, kita dapat mengatur ulang nomor (5,1) dalam urutan menaik, 23, 24, 24, 24, 25, 25, 26, 26, 26, 28.
(5.2)
Selanjutnya, daripada merekam tiga bacaan 24, 24, 24, kita hanya dapat merekam bahwa kami memperoleh nilai 24 tiga kali, dengan kata lain, kita dapat merekam nilai yang berbeda x diperoleh, bersama dengan jumlah kali setiap nilai adalah ditemukan, seperti pada Tabel 5.1.
23 Tabel 5.1. Diukur panjang x dan jumlah mereka kejadian.
Nilai yang berbeda, xk 23 24 25 26 27 28
Jumlah kali ditemukan, nk
1 3 2 3 0 1
Di sini telah memperkenalkan notasi xk (k = 1, 2,...) untuk menunjukkan berbagai nilai yang berbeda ditemukan: x1 = 23, x2 = 24, x3 = 25, dan seterusnya. Dan nk (k = 1, 2,...) menunjukkan jumlah kali nilai xk yang sesuai ditemukan: n1 = 1, 2 = 3, dan seterusnya.
Jika kita merekam pengukuran seperti pada Tabel 5.1, kita dapat menulis ulang definisi rerata x dalam apa yang terbukti menjadi cara yang lebih nyaman. Dari definisi lama kita, kita tahu bahwa
𝑥̅ = ∑ 𝑥𝑘 𝑘 / 𝑁 = 23+24+24+24+25+ . . .+ 28 10 (5.3)
Persamaan ini sama dengan
𝑥̅ = 23 +(24 x 3) + ( 25 x 2 ) + . . .+2810 atau secara umum
𝑥̅ =∑ 𝑥𝑖 𝑖
𝑁 (5.4)
∑ 𝑛𝑖 𝑖 = N (5.5)
(Misalnya, untuk Tabel 5.1 persamaan ini menyatakan bahwa jumlah dari angka di baris bawah adalah 10.)
Cepat Periksa 5. I. Dalam dua tahun pertamanya di perguruan tinggi, Joe mengambil 20 program (semua dengan jumlah kredit yang sama) dan menghasilkan 7 A, 4 B, 7 C, dan 2 E. Untuk tujuan menghitung nilai rata-rata (IPK), setiap huruf kelas diberi skor numerik dengan cara yang biasa, sebagai berikut :
Nilai : F D C B A
24 Mengatur tabel seperti Tabel 5.1 menunjukkan kemungkinan perbedaan skor sk dan berapa
kali nk mereka peroleh. Gunakan Persamaan (5.4) untuk menghitung IPK Joe, 𝑠.
Fk = 𝑛𝑁𝑘 (5.6) 𝑥̅ = ∑ 𝐹𝑘 𝑘 (5.7) Hasil (5,5) menunjukkan bahwa
∑ 𝐹𝑘 𝑘 = 1 (5.8)
Artinya, jika kita menjumlahkan fraksi Fk untuk semua hasil yang mungkin xk, kita harus 1.
Setiap himpunan bilangan yang jumlahnya adalah 1 dikatakan dinormalisasi, dan hubungan (5,8) karena itu disebut kondisi normalisasi.
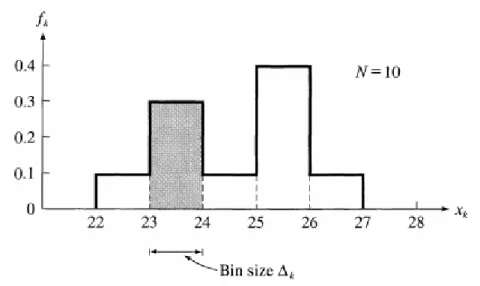
Distribusi pengukuran kami dapat ditampilkan secara grafis dalam histogram, seperti pada Gambar 5.1. Angka ini hanya sebidang Fk terhadap xk, di mana perbedaan nilai yang terukur
xk diplot sepanjang sumbu horisontal dan fraksi kali setiap xk diperoleh ditunjukkan dengan
ketinggian vertikal yang ditarik di atas xk. (Kita juga bisa plot nk melawan xk, namun untuk
tujuan kita plot Fk terhadap xk lebih nyaman). Data ditampilkan dalam histogram seperti ini
dapat komprehensif cepat dan mudah, karena banyak penulis untuk surat kabar dan majalah.
Gambar 5.1 Histogram untuk 10 pengukuran panjang x. Sumbu vertikal menunjukkan fraksi kali Fk bahwa setiap nilai xk diamati
Sebuah histogram seperti itu pada Gambar 5.1 dapat disebut sebuah histogram batang karena distribusi hasil ditunjukkan dengan ketinggian batang vertikal di atas xk tersebut. Ini jenis
histogram yang sesuai bila nilai-nilai xk yang rapi spasi, dengan nilai integer. (Misalnya, nilai
25 histogram.) Kebanyakan ukuran, bagaimanapun, tidak memberikan hasil bulat rapi karena jumlah fisik yang paling memiliki berbagai berkesinambungan nilai yang mungkin. Sebagai contoh, daripada 10 panjang dilaporkan dalam Persamaan (5.1), Anda akan jauh lebih mungkin untuk mendapatkan nilai-nilai seperti 10.
26,4, 23,9, 25,1, 24,6, 22,7, 23,8, 25,1, 23,9, 25,3, 25,4 (5.9)
Sebuah batang histogram dari 10 nilai akan terdiri dari 10 bar yang terpisah, semua sama tinggi, dan akan menyampaikan relatif sedikit informasi. Mengingat pengukuran seperti di (5.9), jalan terbaik adalah untuk membagi rentang nilai menjadi beberapa nyaman interval atau "bin" dan untuk menghitung berapa nilai masing-masing jatuh ke "bin" Sebagai contoh, kita bisa menghitung jumlah pengukuran (5.9) antara x = 22 dan 23, antara x = 23 dan 24, dan seterusnya. Hasil penghitungan dengan cara ini ditunjukkan pada Tabel 5.2. (Jika pengukuran kebetulan jatuh tepat pada batas antara dua sampah, Anda harus memutuskan di mana tempat itu. Sebuah kursus sederhana dan masuk akal adalah untuk menetapkan setengah pengukuran untuk masing-masing dua bin).
Tabel 5.2 10 pengukuran (5.9) dikelompokkan dalam bins
Bin pengamatan
dalam bin
22 - 23 23 - 24 24 – 25 25 - 26 26 – 27 27 - 28
1 3 1 4 1 0
Hasil pada Tabel 5.2 dapat diplot dalam bentuk yang dinamakan histogram bin, seperti yang ditunjukkan pada Gambar 5.2. Dalam plot ini, fraksi pengukuran yang jatuh setiap bin ditunjukkan dengan luas persegi panjang digambar di atas tempat sampah. Dengan demikian, berbayang persegi panjang di atas interval dari x = 23 sampai x = 24 memiliki luas 0,3 x 1 = 0,3, menunjukkan bahwa 3/10 dari seluruh pengukuran jatuh dalam interval ini. Secara umum, kami menunjukkan lebar bin kth oleh Δk. (Ini lebar biasanya semua sama, meskipun
mereka pasti tidak harus.) Ketinggian fk persegi panjang yang ditarik di atas bin ini dipilih
sehingga daerah fkΔk adalah
26 Gambar 5.2 Bin histogram di mana berbeda nilai yang terukur xk diplot sepanjang sumbu
horisontal dan fraksi kali setiap xk diperoleh ditunjukkan dengan ketinggian vertikal yang ditarik di atas xk. (Kita juga bisa plot nk melawan xk, namun untuk tujuan kita plot Fk
terhadap xk lebih nyaman). Data ditampilkan dalam histogram seperti ini dapat komprehensif
cepat dan mudah, karena banyak penulis untuk surat kabar dan majalah.
Gambar 5.2 Histogram untuk 10 pengukuran panjang x. Sumbu vertikal menunjukkan fraksi kali Fk bahwa setiap nilai xk diamati
Sebuah histogram seperti itu pada Gambar 5.1 dapat disebut sebuah bar histogram karena distribusi hasil ditunjukkan dengan ketinggian bar vertikal di atas xk tersebut. Ini jenis histogram yang sesuai bila nilai-nilai xk yang rapi spasi, dengan nilai integer. (Misalnya, nilai siswa pada ujian biasanya bilangan bulat dan ditampilkan nyaman menggunakan bar histogram.) Kebanyakan ukuran, bagaimanapun, tidak memberikan hasil bulat rapi karena jumlah fisik yang paling memiliki berbagai berkesinambungan nilai yang mungkin. Sebagai contoh, daripada 10 panjang dilaporkan dalam Persamaan (5.1), Anda akan jauh lebih mungkin untuk mendapatkan nilai-nilai seperti 10
27 26,4, 23,9, 25,1, 24,6, 22,7, 23,8, 25,1, 23,9, 25,3, 25,4 (5.9)
Sebuah bar histogram dari 10 nilai akan terdiri dari 10 bar yang terpisah, semua sama tinggi, dan akan menyampaikan relatif sedikit informasi. Mengingat pengukuran seperti di (5.9), jalan terbaik adalah untuk membagi rentang nilai menjadi beberapa nyaman interval atau "bin" dan untuk menghitung berapa nilai masing-masing jatuh ke "bins" Sebagai contoh, kita bisa menghitung jumlah pengukuran (5.9) antara x = 22 dan 23, antara x = 23 dan 24, dan seterusnya. Hasil penghitungan dengan cara ini ditunjukkan pada Tabel 5.2. (Jika pengukuran kebetulan jatuh tepat pada batas antara dua sampah, Anda harus memutuskan di mana tempat itu. Sebuah kursus sederhana dan masuk akal adalah untuk menetapkan setengah pengukuran untuk masing-masing dua sampah).
Tabel 5.2 10 pengukuran (5.9) dikelompokkan dalam bin
Bin pengamatan
dalam bin
22 - 23 23 - 24 24 – 25 25 - 26 26 – 27 27 - 28
1 3 1 4 1 0
Hasil pada Tabel 5.2 dapat diplot dalam bentuk kita dapat memanggil histogram bin, seperti yang ditunjukkan pada Gambar 5.2. Dalam plot ini, fraksi pengukuran yang jatuh setiap bin ditunjukkan dengan luas persegi panjang digambar di atas tempat sampah. Dengan demikian, berbayang persegi panjang di atas interval dari x = 23 sampai x = 24 memiliki luas 0,3 x 1 = 0,3, menunjukkan bahwa 3/10 dari seluruh pengukuran jatuh dalam interval ini. Secara umum, kami menunjukkan lebar bin kth oleh Δk. (Ini lebar biasanya semua sama, meskipun
mereka pasti tidak harus.) Ketinggian fk persegi panjang yang ditarik di atas bin ini dipilih sehingga daerah fkΔk adalah
28 Gambar 5.2 Bin histogram yang menunjukkan sebagian kecil dari 10
pengukuran (5.9) x yang jatuh dalam "bin2" 22 dan 23, 23 - 24, dan seterusnya. Luas persegi panjang di atas setiap interval memberikan fraksi pengukuran yang jatuh dalam interval tersebut. Dengan demikian, daerah persegi panjang yang diarsir adalah 0,3, menunjukkan bahwa 3/10 dari semua pengukuran berada di antara 23 dan 24
Jelas, lebar bin harus dipilih sehingga beberapa bacaan jatuh pada beberapa bin. Dengan demikian, ketika jumlah total dari pengukuran N kecil, kita harus memilih bin kita relatif luas, tetapi jika kita meningkatkan N, maka kita biasanya dapat memilih tempat sempit. Cepat Periksa 5.2. Sebuah kelas 20 siswa mengambil ujian, yang dinilai dari 50 poin, dan memperoleh hasil sebagai berikut:
26, 33, 38, 41, 49, 28, 36, 38, 47, 41 32, 37, 48, 44, 27, 32, 34, 44, 37, 30
(Skor ini diambil dari daftar abjad dari siswa.) Pada selembar kertas memerintah persegi, menggambar histogram bin dari nilai, menggunakan batas bin pada 25, 30, 35, 40, 45, dan 50. Label skala vertikal sehingga daerah masing-masing persegi panjang adalah sebagian kecil dari mahasiswa di tempat yang sesuai.
5.2 Distribusi Terbatas
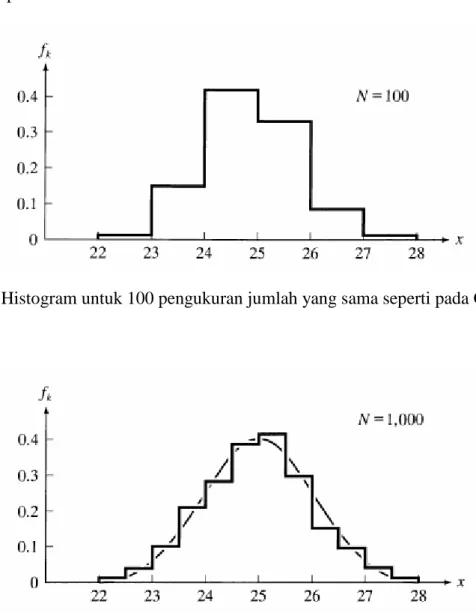
Di sebagian besar percobaan, karena jumlah pengukuran meningkat, histogram mulai mengambil bentuk sederhana pasti. Ini bentuk berkembang jelas terlihat pada Gambar 5.3 dan 5.4, yang menunjukkan 100 dan 1.000 pengukuran jumlah yang sama seperti pada Gambar
29 5.2. Setelah 100 pengukuran, histogram telah menjadi puncak tunggal, yang kira-kira simetris. Setelah 1.000 pengukuran, kami telah mampu untuk mengurangi separuh ukuran bin, dan histogram telah menjadi sangat halus dan teratur. Ketiga grafik menggambarkan sifat penting dari kebanyakan pengukuran. Karena jumlah pengukuran mendekati tak terhingga, distribusi mereka mendekati beberapa pasti, kurva kontinu. Ketika ini terjadi, kurva kontinu disebut distribusi terbatas tampaknya menjadi dekat dengan simetris kurva berbentuk lonceng ditumpangkan pada Gambar 5.4.
Gambar 5.3 Histogram untuk 100 pengukuran jumlah yang sama seperti pada Gambar 5.2.
Gambar 5.4. Histogram untuk 1.000 pengukuran jumlah yang sama seperti pada Gambar 5.3. Kurva rusak adalah distribusi terbatas
Sebuah distribusi terbatas, seperti kurva mulus pada Gambar 5.4, mendefinisikan fungsi-tion, yang kita sebut f(x). Pentingnya fungsi ini ditunjukkan oleh Gambar 5.5. Seperti kita membuat semakin banyak pengukuran kuantitas x, histogram kami akhirnya akan dibedakan
30 dari terbatas kurva f(x). Oleh karena itu, fraksi pengukuran yang jatuh dalam interval x kecil untuk x + dx sama daerah f(x) dx dari strip diarsir pada Gambar 5.5 (a):
f(x) dx = fraksi pengukuran yang
jatuh antara x dan x + dx
(5.10)
Secara umum, fraksi pengukuran yang jatuh antara dua nilai a dan b adalah total daerah di bawah grafik antara x = a dan x = b (Gambar 5.5b).
Gambar 5.5. Sebuah distribusi terbatas f(x). (a) Setelah sangat banyak pengukuran, fraksi yang jatuh antara x dan x + dx daerah f(x) dx dari jalur sempit. (b) Fraksi yang jatuh antara x = a dan x = b adalah daerah yang teduh
Daerah ini hanya integral tertentu dari f(x). Dengan demikian, kita memiliki hasil penting yang
� 𝑓(𝑥)𝑑𝑥 = fraksi pengukuran yang 𝑏
𝑎
jatuh antara x dan x + dx
(5.11)
f(x) dx = probabilitas bahwa setiap pengukuran satu
akan memberikan jawaban antara x dan x + dx (5.12)
Demikian pula, integral ∫ 𝑓(𝑥) 𝑑𝑥𝑎𝑏 memberitahu kita probabilitas bahwa setiap pengukuran yang akan jatuh antara x = a dan x = b. Kami telah sampai pada satu kesimpulan penting berikut : Jika kita tahu terbatas distribusi f(x) untuk pengukuran kuantitas x diberikan dengan
31 alat tertentu, maka kita akan mengetahui kemungkinan memperoleh jawaban dalam interval a ≤ x ≤ b.
Karena probabilitas total untuk memperoleh jawaban manapun antara -∞ dan +∞ harus menjadi salah satu, terbatas distribusi f(x) harus memenuhi
� 𝑓(𝑥)𝑑𝑥∞ −∞
= 1 (5.13)
Identitas ini adalah analog alami dari jumlah normalisasi (5.8), ∑ 𝐹𝑘 𝑘 = 1, dan fungsi f(x) memuaskan (5.13) dikatakan dinormalisasi.
Batas-batas ±∞ dalam integral (5.13) mungkin tampak membingungkan. Mereka tidak berarti bahwa kita benar-benar berharap untuk mendapatkan jawaban mulai sepanjang jalan dari -∞ dan +∞. Justru sebaliknya. Dalam sebuah percobaan sesungguhnya, pengukuran semua jatuh dalam beberapa interval terhingga cukup kecil. Sebagai contoh, pengukuran Gambar 5.4 semua terletak antara x = 21 dan x = 29. Bahkan setelah tak terhingga banyaknya pengukuran, fraksi tergeletak di luar x = 21 sampai x = 29 akan sepenuhnya diabaikan. Dengan kata lain, f(x) pada dasarnya adalah nol di luar kisaran ini, dan tidak ada bedanya apakah integral (5.13) berjalan dari -∞ sampai +∞ atau 21-29. Karena kita umumnya tidak tahu apa batas-batas terbatas adalah, untuk kenyamanan kita meninggalkan mereka sebagai ±∞.
Jika pengukuran dalam pertimbangan sangat tepat, semua nilai yang diperoleh akan mendekati nilai sebenarnya dari x, sehingga histogram hasil, dan karenanya terbatas distribusi, akan memuncak sempit seperti kurva solid dalam Gambar 5.6. Jika pengukuran presisi rendah, maka nilai-nilai yang ditemukan akan menyebar luas dan distribusi akan luas dan rendah seperti kurva putus-putus pada Gambar 5.6.
32 Gambar 5.6. Dua distribus terbatas i, satu untuk pengukuran presisi tinggi,
yang lain untuk pengukuran presisi rendah
Distribusi terbatas f(x) untuk pengukuran kuantitas x diberikan menggunakan alat tertentu menggambarkan bagaimana hasilnya akan dibagikan setelah banyak, banyak langkah- surements. Jadi, jika kita tahu f(x), kita bisa menghitung nilai rata-rata x yang akan ditemukan setelah bertahun- pengukuran. Kami melihat di (5.7) bahwa rata-rata sejumlah pengukuran adalah jumlah dari semua nilai yang berbeda xk, masing-masing berbobot oleh fraksi kali
didapatkan :
𝑥̅
= � 𝑥𝑘𝐹𝑘 (5.14) 𝑘
Dalam kasus ini, kami memiliki sejumlah besar pengukuran dengan distribusi f(x). Jika kita membagi seluruh rentang nilai ke dalam interval kecil xk ke xk + dxk, fraksi nilai dalam setiap
interval adalah Fk = f(xk) dxk dan dalam batas bahwa semua interval pergi ke nol, (5.14)
menjadi
𝑥̅
= � 𝑥𝑓(𝑥)𝑑𝑥 (5.15)∞ −∞
Ingat bahwa formula ini memberikan x rata-rata diharapkan setelah tak terhingga banyaknya percobaan.
Demikian pula, kita dapat menghitung deviasi standar σx diperoleh setelah banyak
pengukuran. Karena kita prihatin dengan batas N →∞, tidak ada bedanya yang definisi σx
kita gunakan, asli (4.6) atau "diperbaiki" (4.9) dengan N digantikan oleh N - 1. Dalam kedua kasus, ketika N →∞, σx2 adalah rata-rata deviasi kuadrat (x - x)2. Jadi, tepatnya argumen yang
mengarah ke (5.15) memberikan, setelah banyak percobaan, 𝜎𝑥2
= � (𝑥 − 𝑥)∞ 2
−∞ 𝑓(𝑥)𝑑𝑥 (5.16)
5.3 Distribusi Normal
Berbagai jenis pengukuran memiliki distribusi terbatas berbeda. Tidak semua distribusi terbatas memiliki bel bentuk simetris digambarkan dalam Bagian 5.2.
33 Gambar 5.7. Distribusi terbatas untuk subjek pengukuran banyak kesalahan
acak kecil. Distribusi adalah bel dibentuk dan berpusat pada nilai sebenarnya dari pengukuran kuantitas x
Gambar 5.8. Fungsi Gauss (5.17) yang berbentuk lonceng dan berpusat pada x = 0. Kurva lonceng lebar jika σ besar dan sempit jika σ kecil. Meskipun untuk saat ini kita akan melihat σ hanya sebagai parameter yang mencirikan lebar kurva lonceng itu, σ dapat ditampilkan (seperti pada Soal 5.13) menjadi jarak dari pusat kurva ke titik di mana kelengkungan perubahan tanda. Jarak ini ditampilkan dalam dua grafik.
Fungsi matematika yang menggambarkan kurva berbentuk lonceng yang disebut distribusi normal, atau fungsi Gauss . Prototipe fungsi ini adalah
𝑒−𝑥2/2𝜎2
(5.17) dimana σ parameter tetap yang disebut parameter lebar.
Fungsi Gauss (5.17) adalah kurva berbentuk lonceng berpusat pada x = 0. Untuk mendapatkan kurva berbentuk lonceng berpusat pada beberapa titik lainnya x = X, kita hanya mengganti x dalam (5.17) dengan x - X. Dengan demikian, fungsi
𝑒−(𝑥−𝑋)2/2𝜎2
34 memiliki maksimum pada x = X dan jatuh simetris pada kedua sisi x = X, seperti pada Gambar 5.9.
Gambar 5.9. Fungsi Gauss (5.18) adalah bel dibentuk dan berpusat pada x = X Fungsi (5.18) tidak cukup dalam bentuk final untuk menggambarkan distribusi terbatas yang karena distribusi apapun harus dinormalisasi, yaitu, harus memenuhi
∫ 𝑓 (𝑥)−∞∞ 𝑑𝑥 = 1 (5.19) Untuk mengatur normalisasi ini, kita menetapkan
f(x) = 𝑁𝑒−(𝑥−𝑋)2/2𝜎2 (5.20)
(Perkalian dengan faktor N tidak berubah bentuk, juga tidak menggeser maksimum pada x = X.) Kami kemudian harus memilih "faktor normalisasi" N sehingga f (x) menjadi normal seperti pada (5.19). Ini melibatkan beberapa manipulasi dasar integral, yang saya berikan dalam beberapa detail:
� 𝑓(𝑥) 𝑑𝑥 =∞
−∞ � 𝑁𝑒
−(𝑥−𝑋)2/2𝜎2
∞
−∞ 𝑑𝑥 (5.21)
(Perkalian dengan faktor N tidak berubah bentuk, juga tidak menggeser maksimum pada x = X.) Kami kemudian harus memilih "faktor normalisasi" N sehingga f (x) menjadi normal seperti pada (5.19). Ini melibatkan beberapa manipulasi dasar integral, yang saya berikan
dalam beberapa detail:
= 𝑁 � 𝑒∞ −𝑦2/2𝜎2
−∞ 𝑑𝑥 (5.22) Selanjutnya, kita dapat mengatur y/𝜎 = z = (dalam hal dy = 𝜎dz) dan diperoleh
35 = 𝑁𝜎 � 𝑒∞ −𝑧2/2
−∞ 𝑑𝑧 (5.23)
Sisanya terpisahkan adalah salah satu integral standar fisika matematika. Hal ini dapat dievaluasi dengan metode dasar, tetapi rincian tidak terutama illuminat-ing, jadi saya hanya akan mengutip hasil; Selanjutnya, kita dapat mengatur y/𝜎 = z = (dalam hal dy = 𝜎dz) dan diperoleh
� 𝑒∞ −𝑧2/2
−∞ 𝑑𝑧 = √2𝜋 (5.24) Kembali ke (5.21) dan (5.23), kita menemukan bahwa
� 𝑓(𝑥) 𝑑𝑥∞
−∞ = 𝑁𝜎√2𝜋
Karena integral ini harus sama dengan 1, kita harus memilih faktor normalisasi N untuk menjadi
𝑁 = 1
𝜎√2𝜋
Dengan pilihan ini untuk faktor normalisasi, kita sampai pada bentuk akhir untuk Gauss, atau, fungsi distribusi normal, yang kita dilambangkan dengan Gx, Dengan pilihan ini untuk faktor normalisasi, kita sampai pada bentuk akhir untuk Gauss, atau, fungsi distribusi normal, yang kita dilambangkan dengan 𝐺𝑋,𝜎(𝑥):
Distribusi Gauss, atau Normal
𝐺𝑋,𝜎(𝑥) = 1
𝜎√2𝜋𝑒(𝑥−𝑋)
2/2𝜎2
36 Gambar 5.10 Dua distribusi normal, atau Gauss
Cepat Periksa 5.3. Di atas kertas persegi yang dikuasai, sketsa Gauss fungsi 𝐺𝑋,𝜎(𝑥) untuk X = 10 dan 𝜎 = 1. Gunakan kalkulator untuk menemukan nilai-nilai pada x = 10, 10,5, 11, 11,5, 12, dan 12,5. Anda tidak perlu untuk menghitung nilai x <10 karena Anda tahu fungsi
tersebut simetris terhadap x = 10.
Kami melihat dalam Bagian 5.2 bahwa pengetahuan tentang distribusi terbatas untuk pengukuran memungkinkan kita menghitung nilai rata-rata 𝑥̅ diharapkan setelah berbagai percobaan. Menurut (5,15), rata-rata ini diharapkan untuk distribusi Gauss f (x) = 𝐺𝑋,𝜎(𝑥) adalah
𝑥̅ = ∫ 𝑥 𝐺−∞∞ 𝑋,𝜎(𝑥) 𝑑𝑥 (5.26) Sebelum kita mengevaluasi integral ini, kita harus mencatat bahwa jawabannya hampir jelas akan X, karena simetri fungsi Gauss tentang X menunjukkan bahwa jumlah yang sama hasil akan jatuh setiap jarak di atas X akan jatuh sebagai jarak yang sama di bawah X. Jadi , rata-rata harus X.
Kita bisa menghitung integral (5.26) untuk distribusi Gauss sebagai berikut: 𝑥̅ =
∫ 𝑥 𝐺−∞∞ 𝑋,𝜎(𝑥) 𝑑𝑥 = 𝜎√2𝜋1 ∫ 𝑥𝑒−∞∞ −(𝑥−𝑋)2/2𝜎2𝑑𝑥 (5.27)
Jika kita membuat perubahan variabel y = x - X, maka dx = dy dan x = y + X. Dengan demikian, integral (5.27) menjadi dua entuk,
𝑥̅ = 1 𝜎√2𝜋 (∫ 𝑦𝑒−𝑦 2/2𝜎2 ∞ −∞ 𝑑𝑦 + X∫ 𝑥𝑒−𝑥 2/2𝜎2 ∞ −∞ 𝑑𝑥 ) (5.28) Integral pertama di sini adalah persis nol karena kontribusi dari setiap titik y adalah persis dibatalkan dari titik-y. Integral kedua adalah integral normalisasi ditemui dalam (5.22) dan memiliki nilai √2𝜋 . Integral ini membatalkan dengan 𝜎√2𝜋 pada
penyebut dan meninggalkan jawaban yang diharapkan bahwa
𝑥̅ = X (5.29)
Dan sesuai dengan (5.16) menjadi
𝜎𝑥2 = ∫ (𝑥 − 𝑥)−∞∞ 2 𝐺𝑋,𝜎(𝑥) 𝑑𝑥 (5.30)
37 𝜎𝑥2 = 𝜎2 (5.31)
Bagian 5.4 Standar Deviasi sebagai Keyakinan 68%
jauh lebih banyak uji coba. Jika kita membuat beberapa jumlah terbatas pengukuran (10 atau 20, misalnya) x, standar deviasi diamati harus beberapa pendekatan untuk o-, tapi kami tidak punya alasan untuk berpikir itu akan persis u. Bagian 5.5 alamat apa lagi yang bisa dikatakan tentang rerata dan deviasi standar setelah jumlah terbatas percobaan.
5.4 Standar Deviasi sebesar 68% Batas Keyakinan
Prob (dalam 𝜎) = ∫𝑋−𝜎𝑋+𝜎 𝐺𝑋,𝜎(𝑥) 𝑑𝑥 = 1 𝜎√2𝜋 ∫ 𝑥𝑒−(𝑥−𝑋) 2/2𝜎2 𝑋+𝜎 𝑋−𝜎 𝑑𝑥 Integral ini diilustrasikan dalam Gambar 5.11. Hal ini dapat disederhanakan dengan
mengganti (x - X) / 𝜎 = z. Dengan substitusi ini, dx = 𝜎dz, dan batas-batas integrasi menjadi z = ± 1. Oleh karena itu,
Prob (dalam 𝜎) = 1
√2𝜋 ∫ 𝑒−𝑧
2/2
+1
−1 𝑑𝑥 Integral ini di tunjukkan dalam Gambar 5.12
Gambar 5. 11 Daerah yang diarsir antara X ± σ adalah probabilitas pengukuran dalam satu standar deviasi dari X
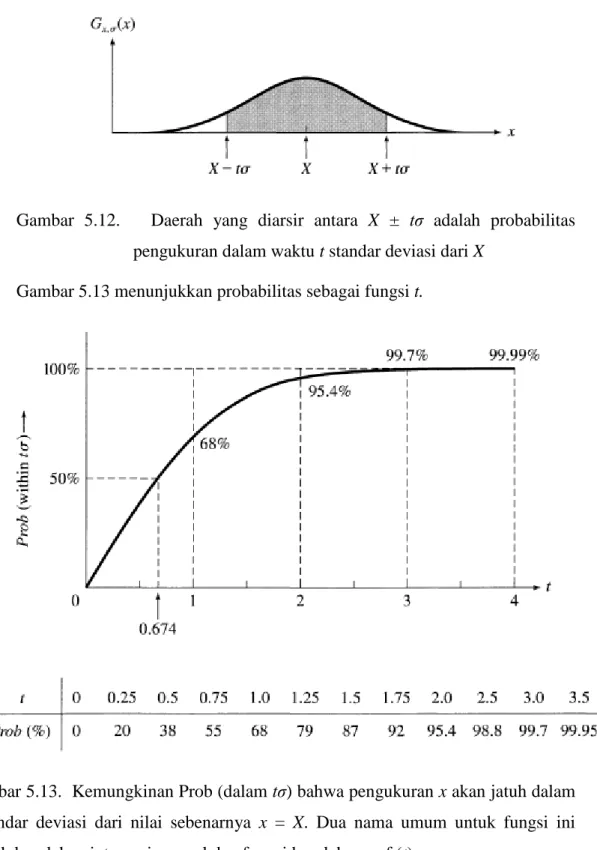
38 Gambar 5.12. Daerah yang diarsir antara X ± tσ adalah probabilitas
pengukuran dalam waktu t standar deviasi dari X Gambar 5.13 menunjukkan probabilitas sebagai fungsi t.
Gambar 5.13. Kemungkinan Prob (dalam tσ) bahwa pengukuran x akan jatuh dalam t standar deviasi dari nilai sebenarnya x = X. Dua nama umum untuk fungsi ini adalah kesalahan integrasi normal dan fungsi kesalahan, erf (t).
5.5 Pembenaran Rerata sebagai Taksiran Terbaik
Tiga bagian terakhir telah dibahas membatasi distribusi terbatas f (x), distribusi yang diperoleh dari jumlah tak terbatas pengukuran kuantitas x.
39 Prob (x antara x1 dan x1 + dxi) = 1
𝜎√2𝜋 𝑥𝑒−(𝑥1−𝑋)
2/2𝜎2
𝑑𝑥1 Dalam prakteknya, kita tidak tertarik pada ukuran interval Dalam prakteknya, kita tidak tertarik pada ukuran interval 𝑑𝑥1 (atau factor √2𝜋), jadi kami menyingkat persamaan ini menjadi
Prob (x1) α 𝜎1 𝑒−(𝑥1−𝑋)
2/2𝜎2
(5.36)
Probabilitas mendapatkan pembacaan kedua x2, adalah
Prob (x2) α 1𝜎 𝑒−(𝑥2−𝑋) 2/2𝜎2
dan kita sama bisa menuliskan semua probabilitas berakhir dengan Prob (xN) α 1𝜎 𝑒−(𝑥𝑁−𝑋)
2/2𝜎2
(5.38)
Probabilitas bahwa kita mengamati seluruh rangkaian N pembacaan hanya produk dari probabilitas terbatas, Prob x, 𝜎 (𝑥R1, . . . , xN) α 1 𝜎𝑁𝑒− (𝑥𝑁−𝑋) 2/2𝜎2 (5.39) Prob x, 𝜎 (𝑥R1, . . . , xN) α 1 𝜎𝑁𝑒− (𝑥𝑁−𝑋) 2/2𝜎2 (5.40) Dengan menggunakan prinsip ini, kita dapat dengan mudah menemukan estimasi terbaik untuk nilai sebenarnya X. Jelas (5.40) maksimal jika jumlah dalam eksponen minimum. Dengan demikian, estimasi terbaik untuk X adalah bahwa nilai X dengan
∑ (𝑥𝑁𝑖=1 𝑖 –
)2/ σ2 (5.41) minimum. Untuk menemukan minimum ini, kita mendeferensialkannya terhadap X dan
mengatur derivatifnya sama dengan nol, memberikan ∑ (𝑥𝑁𝑖=1 𝑖 − 𝑋) = 0 atau
(Nilai terbaik untuk X) = =∑ 𝑥𝑖
𝑁
40 (Estimasi terbaik untuk σ ) = ∑ 1
𝑁(𝑥𝑖− 𝑋)2 𝑁
𝑖=1 (5.43)
Nilai sebenarnya X tidak diketahui. Dengan demikian, dalam prakteknya, kita harus mengganti X pada (5.43) dengan perkiraan terbaik kami untuk X, yaitu rata-rata x. Penggantian ini menghasilkan perkiraan
σ = ∑𝑁 𝑖=1 𝑁1(𝑥𝑖− 𝑥̅ )2 (5.44) Artinya, estimasi terbaik untuk σ, standar deviasi dari nilai yang terukur xl, x2,. , xN, dengan (N - 1) dalam penyebutnya,
(Estimasi terbaik untuk σ ) = ∑ 1
𝑁−1(𝑥𝑖− 𝑋)2 𝑁
𝑖=1 (5.45) (Ketidakpastian fraksional dalam σ x ) = 1
�2(𝑁−1) (5.46)
Latihan Soal: