i
PENENTUAN WAKTU TEMPUH BUS TRANS JOGJA DENGAN MENGGUNAKAN SISTEM INFERENSI KABUR TSUKAMOTO
Skripsi
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Kresentia Aprilia Kurniawati NIM: 163114028
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA 2021
ii
DETERMINING TRAVEL TIME OF TRANS JOGJA BUS USING TSUKAMOTO FUZZY INFERENCE SYSTEM
Paper
Presented as a Partial Fulfillment of the
Requirements to Obtain the Degree of Sarjana Matematika Mathematics Study Program
Written by:
Kresentia Aprilia Kurniawati Student ID: 163114028
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY 2021
v
HALAMAN PERSEMBAHAN
“Janganlah takut, sebab Aku ini menyertai engkau, janganlah bimbang, sebab Aku ini Allahmu; Aku akan meneguhkan, bahkan akan menolong engkau; Aku akan memegang engkau dengan tangan kanan-Ku yang membawa kemenangan.”
Yesaya 41:10
Skripsi ini aku persembahkan untuk: Tuhan Yesus Kristus yang senantiasa memberikan berkat dan petunjuk-Nya dalam setiap langkah yang aku jalani, untuk kedua orangtuaku tercinta, Heribertus Susilo dan Anastasia Sumarni, serta kedua kakakku, mbak Tina dan mas Dian yang selalu mendukungku.
vi
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya, bahwa skripsi ini yang saya tulis ini tidak memuat karya atau bagian dari karya orang lain kecuali yang disebutkan dalam daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 26 Juli 2021
vii
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma
Nama : Kresentia Aprilia Kurniawati NIM : 163114028
Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:
PENENTUAN WAKTU TEMPUH BUS TRANS JOGJA DENGAN MENGGUNAKAN SISTEM INFERENSI KABUR TSUKAMOTO
beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma untuk menyimpan, mengalihkan ke dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu meminta izin dari saya maupun memberikan royaliti kepada saya selama tetap mencantumkan nama saya sebagai penulis.
Demikian pernyataan ini saya buat dengan sebenarnya.
Di buat di Yogyakarta Pada tanggal 26 Juli 2021 Yang menyatakan
viii ABSTRAK
Sistem inferensi kabur adalah sistem komputasi yang bekerja atas dasar penalaran kabur. Dalam tugas akhir ini, salah satu metode dari sistem inferensi kabur, yaitu metode Tsukamoto, akan dipakai dalam menentukan waktu tempuh bus Trans Jogja. Faktor-faktor yang akan dipertimbangkan dalam menentukan waktu tempuh bus Trans Jogja, yaitu jarak tempuh dan volume kendaraan. Kedua faktor tersebut yang akan menjadi variabel masukan dan diproses menggunakan metode Tsukamoto sehingga menghasilkan keluaran berupa nilai tegas. Keluaran inilah yang merupakan waktu tempuh bus Trans Jogja. Proses penentuan waktu tempuh dapat dilakukan dengan menerapkan masukan pada aplikasi berbasis GUI pada MATLAB, yang dapat menyederhanakan komputasi, sehingga prosesnya menjadi lebih mudah dan cepat.
Kata kunci: sistem inferensi kabur, metode Tsukamoto, penentuan waktu tempuh bus Trans Jogja.
ix ABSTRACT
A fuzzy inference system is a computational system that works based on fuzzy reasoning. In this final project, one of the fuzzy inference system methods, namely the Tsukamoto method, will be used in determining the travel time of the Trans Jogja bus. The factors that will be considered in determining the travel time of the Trans Jogja bus are the distance traveled and the volume of the vehicles. These two factors will be input variables and processed using the Tsukamoto method to produce crips value output. This output is the travel time of the Trans Jogja bus. The process of determining travel time can be done by applying the input to a GUI-based application in MATLAB, which can simplify the computation, so that the process becomes easier and faster.
Keywords: fuzzy inference system, Tsukamoto method, determining Trans Jogja
bus travel time.
x
KATA PENGANTAR
Puji syukur penulis panjatkan ke hadirat Tuhan Yang Maha Esa, yang senantiasa mencurahkan berkat, kasih dan karunia-Nya sehingga di tengah pandemi virus covid-19 ini penulisdapat menyelesaikan tugas akhir yang berjudul “Penentuan Waktu Tempuh Bus Trans Jogja Dengan Menggunakan Sistem Inferensi Kabur Tsukamoto” dengan baik.
Tugas akhir yang telah diselesaikan penulis, merupakan salah satu syarat guna memperoleh gelar Sarjana Matematika pada program studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma. Selama penulisan tugas akhir ini, penulis tidak lepas dari bantuan, dukungan serta bimbingan dari banyak pihak. Oleh karena itu, penulis mengucapkan terima kasih kepada:
1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D. selaku Dekan Fakultas Sains dan Teknologi.
2. Bapak YG. Hartono, S.Si., M.Sc., Ph.D. selaku Ketua Program Studi Matematika.
3. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc. selaku Dosen Pembimbing Akademik.
4. Romo Prof. Dr. Frans Susilo, SJ selaku Dosen Pembimbing yang selalu sabar dan mau membimbing penulis sehingga penulis dapat menyelesaikan tugas akhir ini dengan baik.
5. Romo/Bapak/Ibu dosen Program Studi Matematika Universitas Sanata Dharma yang telah membimbing dan membagikan ilmu selama masa perkuliahan penulis.
6. Bapak/Ibu karyawan Fakultas Sains dan Teknologi yang telah berdinamika selama masa perkuliahan penulis.
7. Bapak, Ibu, mbak Tina, mas Dian dan keluarga yang telah membantu, memberi semangat dan mendukung penulis selama masa penulisan tugas akhir.
xi
8. Keluarga Study Soft/Hard/Tour yang selalu membantu, memberi semangat dan mendukung penulis selama masa perkuliahan dan pengerjaan tugas akhir.
9. Teman-teman Prodi Matematika Angkatan 2016 yang telah mendukung dan membantu penulis selama masa perkuliahan dan penulisan tugas akhir. 10. Kakak dan adik angkatan Prodi Matematika yang telah memotivasi dan memberi saran penulis selama masa perkuliahan dan penulisan tugas akhir. 11. Semua pihak yang telah mendoakan, membantu, memotivasi dan memberi saran penulis selama masa perkuliahan maupun penulisan tugas akhir yang tidak dapat disebutkan satu per satu.
Semoga Tuhan Yesus Kristus membalas segala bentuk bantuan, semangat, dukungan, perhatian dan kasih sayang yang telah penulis terima. Penulis menyadari bahwa masih banyak kekurangan dalam penulisan tugas akhir ini. Oleh karena itu, penulis mengharapkan kritik dan saran yang dapat membangun dan menyempurnakan tugas akhir ini. Penulis juga berharap tugas akhir ini dapat bermanfaat bagi para pembaca.
Yogyakarta, 26 Juli 2021 Penulis
xii DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... v
PERNYATAAN KEASLIAN KARYA ... vi
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... vii
ABSTRAK ... viii
ABSTRACT ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
DAFTAR GAMBAR ... xiv
BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 4 C. Batasan Masalah ... 5 D. Tujuan Penulisan ... 5 E. Manfaat Penulisan ... 5 F. Metode Penulisan ... 5 G. Sistematika Penulisan ... 5
BAB II HIMPUNAN DAN LOGIKA KABUR ... 7
A. Himpunan Kabur ... 7
B. Fungsi Keanggotaan ... 12
xiii
D. Perampatan Operasi Baku pada Himpunan Kabur ... 15
E. Relasi Kabur ... 16
F. Logika Kabur ... 18
1. Konsep Logika Kabur ... 18
2. Variabel Linguistik ... 18
3. Pengubah Linguistik ... 19
4. Proposisi Kabur ... 20
5. Implikasi Kabur ... 22
6. Penalaran Kabur ... 25
G. Sistem Inferensi Kabur... 30
BAB III PENENTUAN WAKTU TEMPUH BUS TRANS JOGJA DENGAN MENGGUNAKAN SISTEM INFERENSI KABUR TSUKAMOTO ... 36
A. Sistem Inferensi Kabur Tsukamoto ... 36
B. Implementasi Sistem Inferensi Kabur Tsukamoto dalam Penentuan Waktu Tempuh Bus Trans Jogja ... 37
1. Menyusun Basis Data ... 39
2. Menyusun Basis Kaidah... 42
3. Unit pengaburan ... 43
4. Unit Penalaran Kabur ... 44
C. Implementasi pada Aplikasi Matlab berbasis GUI ... 55
BAB IV PENUTUP ... 59
A. Kesimpulan ... 59
B. Saran ... 60
DAFTAR PUSTAKA ... 62
xiv
DAFTAR GAMBAR
Gambar 2.1 Fungsi Keanggotaan Himpunan Kabur “Jauh” ... 8
Gambar 2.2 Pendukung, Teras, Pusat dan Titik Silang dari Suatu Himpunan Kabur ... 11
Gambar 2.3 Potongan- dari suatu himpunan kabur ... 12
Gambar 2.4 Fungsi keanggotaan Segitiga (x; 2, 6, 9) ... 13
Gambar 2.5 Penarikan Kesimpulan dalam Modus Ponens Rampat ... 28
Gambar 2.6 Struktur Dasar Suatu Sistem Inferensi Kabur ... 31
Gambar 2.7 Nilai Fungsi Pengaburan Segitiga di ... 32
Gambar 2.8 Fungsi Keanggotaan Himpunan-himpunan Kabur yang Terkait dengan Nilai-nilai Linguistik untuk Variabel x pada Semesta [0,100] ... 33
Gambar 3.1 Grafik Fungsi Keanggotaan Variabel Jarak Tempuh ... 40
Gambar 3.2 Grafik Fungsi Keanggotaan Variabel Volume Kendaraan ... 41
Gambar 3.3 Grafik Fungsi Keanggotaan Variabel Waktu Tempuh ... 42
Gambar 3.4 Menunjukkan Derajat Keserasian ... 46
Gambar 3.5 Menunjukkan Derajat Keserasian ... 47
Gambar 3.6 Menunjukkan Derajat Keserasian ... 49
Gambar 3.7 Menunjukkan Derajat Keserasian ... 50
Gambar 3.8 Menunjukkan Derajat Keserasian ... 51
Gambar 3.9 Menunjukkan Derajat Keserasian ... 53
Gambar 3.10 Sistem Inferensi Kabur Tsukamoto Berbasis GUI dalam Penentuan Waktu Tempuh Bus Trans Jogja ... 56
Gambar 3.11 Hasil perhitungan waktu tempuh dengan masukan jarak tempuh dan volume kendaraan yang diberikan ... 56
1 BAB I PENDAHULUAN
A. Latar Belakang
Trans Jogja merupakan salah satu alat transportasi umum berupa bus yang digunakan masyarakat Yogyakarta. Keuntungan menggunakan Trans Jogja adalah tarif perjalanan yang murah dan fasilitas bus yang cukup lengkap. Sistem yang digunakan oleh Trans Jogja adalah sistem tertutup, dalam arti penumpang tidak dapat memasuki bus tanpa melewati gerbang pemeriksaan. Selain itu, sistem pembayaran menggunakan tiket atau secara langsung kepada petugas di setiap halte. Tiket yang digunakan berupa kartu pintar yang akan diperiksa secara otomatis melalui suatu mesin yang akan membuka pintu masuk Trans Jogja secara otomatis. Penumpang dapat berganti bus tanpa harus membayar biaya tambahan apabila masih dalam satu tujuan. Tarif Trans Jogja saat ini, sebesar Rp 3.500 per satu tujuan. Saat ini, semakin banyak tersedia bus Trans Jogja dengan jalur berbeda-beda pula. Penumpang dapat menggunakan bus Trans Jogja dengan berbagai macam pilihan jalur yang akan dilewati. Hal ini kadang kala membuat penumpang bingung untuk memilih jalur yang akan dilewati dengan memperhitungkan waktu tempuhnya.
Menurut MKJI (1997), waktu tempuh adalah waktu total yang diperlukan untuk melewati suatu panjang jalan tertentu, termasuk waktu berhenti dan tundaan.
Dalam tugas akhir ini, akan digunakan dua faktor dalam menentukan waktu tempuh, yaitu jarak tempuh dan volume kendaraan. Menurut MKJI (1997), jarak adalah panjang dari segmen jalan. Sedangkan volume kendaraan adalah jumlah kendaraan bermotor yang melalui suatu titik pada jalan per satuan waktu, yang dinyatakan dalam lalu lintas harian rata-rata tahunan (LHRT). Lalu lintas harian rata-rata tahunan merupakan rata-rata volume selama 24 jam pada suatu lokasi pengamatan selama 365 hari pengamatan yang dinyatakan dengan kendaraan/hari. Volume
kendaraan dapat dihitung dengan menggunakan rumus sebagai berikut (Sukirman, 1999):
dengan
LHRT = Lalu lintas Harian Rata-Rata Tahunan N = Jumlah kendaraan dalam setahun
Masalah dalam penentuan waktu tempuh bus Trans Jogja dapat diselesaikan dengan menggunakan konsep logika kabur, yaitu logika dengan tak hingga banyak nilai kebenaran yang dinyatakan dengan bilangan real dalam selang tertutup [0,1]. Konsep logika kabur dikembangkan oleh Lotfi Asker Zadeh, seorang guru besar pada University of California, yang pada tahun 1965 mempublikasikan suatu karya ilmiah berjudul “Fuzzy Sets”. Dalam karya ilmiah tersebut, Zadeh memperluas konsep himpunan tegas menjadi himpunan kabur. Himpunan tegas adalah himpunan yang terdefinisi secara tegas dalam arti bahwa untuk setiap elemen dalam semestanya selalu dapat ditentukan secara tegas apakah ia merupakan anggota dari himpunan itu atau tidak. Tetapi dalam kenyataannya, tidak semua himpunan yang kita jumpai dalam kehidupan sehari-hari terdefinisi secara demikian itu, misalnya himpunan orang yang kurus, himpunan orang yang gemuk, dan sebagainya. Untuk mengatasi permasalahan himpunan dengan batas tidak tegas itu, Zadeh menciptakan konsep himpunan kabur. Ia mengaitkan himpunan dengan batas yang tidak tegas itu dengan suatu fungsi yang menyatakan derajat kesesuaian unsur-unsur dalam semestanya dengan ciri yang merupakan syarat keanggotaan himpunan tersebut. Fungsi itu disebut fungsi keanggotaan dan nilai fungsi itu disebut derajat keanggotaan suatu unsur dalam himpunan itu. Himpunan itulah yang oleh Zadeh disebut himpunan kabur (fuzzy set). Fungsi keanggotaan dari suatu himpunan kabur ̃ dalam semesta adalah pemetaan ̃ dari ke selang tertutup[0,1], yaitu:
̃ [ ].
Nilai fungsi ̃ menyatakan derajat keanggotaan unsur dalam himpunan kabur ̃.
Dari konsep fungsi keanggotaan tersebut, setiap anggota dalam suatu himpunan kabur tidak lagi merupakan sesuatu yang tegas antara anggota atau bukan anggota, tetapi sesuatu yang mempunyai derajat keanggotaan tertentu.
Berdasarkan konsep himpunan kabur tersebut, dikembangkanlah konsep logika kabur. Logika kabur adalah ilmu yang mempelajari secara sistematis kaidah-kaidah penalaran yang sah (valid) dari pernyataan-pernyataan yang memuat predikat kabur, yaitu predikat yang direpresentasikan dengan suatu himpunan kabur.
Salah satu penerapan logika kabur adalah sistem inferensi kabur, yaitu sistem komputasi yang bekerja atas dasar penalaran kabur. Terdapat beberapa variasi sistem inferensi kabur, yaitu sistem inferensi kabur Mamdani, sistem inferensi kabur Takagi-Sugeno-Kang, dan sistem inferensi kabur Tsukamoto.
Dalam sistem inferensi kabur Tsukamoto, himpunan kabur yang dipakai untuk menyatakan predikat kabur pada bagian konsekuen dari kaidah-kaidah sistemnya mempunyai fungsi keanggotaan yang monoton (naik monoton atau turun monoton), sehinggamasing-masing kaidah akan menghasilkan keluaran berupa nilai tegas yang diimbas oleh daya sulut pada kaidah yang bersangkutan. Bentuk umum kaidah ke-i sistem tersebut adalah sebagai berikut:
di mana adalah predikat kabur yang direpresentasikan dengan himpunan kabur ̃ dengan fungsi keanggotaan yang monoton (untuk dengan m adalah banyaknya kaidah dalam sistem itu). Setiap masukan ( ) akan menghasilkan daya sulut yang mengimbas keluaran tegas untuk kaidah ke-i. Kesimpulan akhir y
diperoleh dengan menghitung rerata terbobot dari semua keluaran tersebut dengan bobot daya sulutnya, yaitu:
∑ ∑
di mana adalah daya sulut untuk kaidah ke-i. Model Tsukamoto ini, menyederhanakan komputasi karena keluarannya berupa nilai tegas sehingga tidak memerlukan fungsi penegasan.
Pada tugas akhir ini, sistem inferensi kabur Tsukamoto akan diterapkan pada penentuan waktu tempuh bus Trans Jogja dengan menggunakan data jumlah kendaraan bermotor provinsi Yogyakarta yang terdaftar pada tahun 2018 berdasarkan data yang diperoleh dari Badan Pusat Statistik serta data yang diperoleh dari Dinas Perhubungan Yogyakarta. Adapun variabel-variabel yang akan digunakan adalah jarak tempuh dan volume kendaraan sebagai variabel masukan, dan waktu tempuh sebagai variabel keluaran. Selanjutnya, akan dibahas proses menentukan waktu tempuh bus Trans Jogja dengan menyusun kaidah-kaidah yang akan diberlakukan, misalnya:
Jika jarak tempuh dekat dan volume kendaraan rendah, maka waktu tempuh cepat.
Proses dilanjutkan dengan menghitung rerata terbobot dengan bobot daya sulutnya sebagai keluaran akhir. Hasil akhir inilah yang akan digunakan dalam penentuan waktu tempuh bus Trans Jogja.
B. Rumusan Masalah
Permasalahan yang akan dibahas dalam tugas akhir ini adalah bagaimana menentukan waktu tempuh bus Trans Jogja dengan menggunakan sistem inferensi kabur Tsukamoto dengan masukan jarak tempuh dan volume kendaraan?
C. Batasan Masalah
Dalam tugas akhir ini, akan dibatasi metode yang digunakan, yaitu metode Tsukamoto. Selain itu, akan dibatasi juga variabel-variabel yang digunakan dalam proses penentuan waktu tempuh bus Trans Jogja, yaitu jarak tempuh dan volume kendaraan sebagai variabel masukan, serta waktu tempuh sebagai variabel keluaran.
D. Tujuan Penulisan
Tujuan penulisan tugas akhir ini adalah menyelesaikan permasalahan dalam penentuan waktu tempuh bus Trans Jogja dengan menggunakan sistem inferensi kabur Tsukamoto.
E. Manfaat Penulisan
Manfaat penulisan tugas akhir ini adalahmengetahui suatu metode dalam menentukan waktu tempuh bus Trans Jogja, yaitu metode sistem inferensi kabur Tsukamoto.
F. Metode Penulisan
Metode penulisan yang akan digunakan dalam tugas akhir ini adalah metode studi pustaka, yaitu dengan mempelajari buku-buku dan jurnal-jurnal yang berhubungan dengan sistem inferensi kabur Tsukamoto dan penerapannya. G. Sistematika Penulisan BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan
E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan
BAB II HIMPUNAN DAN LOGIKA KABUR A. Himpunan Kabur
B. Fungsi Keanggotaan
C. Operasi Baku pada Himpunan Kabur
D. Perampatan Operasi Baku pada Himpunan Kabur E. Relasi Kabur
F. Logika Kabur
G. Sistem Inferensi Kabur
BAB III PENENTUAN WAKTU TEMPUH BUS TRANS JOGJA DENGAN MENGGUNAKAN SISTEM INFERENSI KABUR TSUKAMOTO
A. Sistem Inferensi Kabur Tsukamoto
B. Implementasi Sistem Inferensi Kabur Tsukamoto dalam Penentuan Waktu Tempuh Bus Trans Jogja
C. Implementasi pada Aplikasi Matlab berbasis GUI
BAB IV PENUTUP A. Kesimpulan B. Saran
DAFTAR PUSTAKA LAMPIRAN
7 BAB II
HIMPUNAN DAN LOGIKA KABUR
A. Himpunan Kabur
Sebelumnya kita telah mengenal dan menggunakan konsep himpunan dalam kehidupan sehari-hari, misalnya Himpunan Mahasiswa Matematika (HMM), Himpunan Mahasiswa Jurusan Teknik Elektro (HMJTE), dll. Himpunan adalah suatu kumpulan atau koleksi obyek-obyek (konkret maupun abstrak) yang mempunyai kesamaan sifat tertentu. Tetapi dalam kenyataannya, tidak semua himpunan dapat terdefinisi secara tegas, misalnya pada himpunan makanan manis. Dalam hal ini kita tidak dapat menentukan secara tegas apakah suatu makanan dapat dikatakan manis atau tidak.
Untuk mengatasi permasalahan himpunan dengan batas yang tidak tegas itu, Lotfi Asker Zadeh, seorang guru besar di University of California, Barkeley, Amerika Serikat menciptakan konsep himpunan kabur. Ia mengaitkan himpunan semacam itu dengan suatu fungsi yang menyatakan derajat kesesuaian unsur-unsur dalam semestanya dengan ciri yang merupakan syarat keanggotaan himpunan tersebut. Fungsi itu disebut fungsi keanggotaan dan nilai fungsi itu disebut derajat keanggotaan suatu unsur dalam himpunan itu, yang selanjutnya disebut himpunan kabur (fuzzy set). Fungsi keanggotaan dari suatu himpunan kabur ̃ dalam semesta adalah pemetaan ̃ dari ke selang [0,1], yaitu ̃ [ ] Nilai fungsi ̃ menyatakan derajat keanggotaan unsur dalam himpunan kabur ̃ Nilai fungsi sama dengan 1 menyatakan keanggotaan penuh, dan nilai fungsi sama dengan 0 menyatakan sama sekali bukan anggota himpunan kabur tersebut.
Himpunan kabur merupakan perluasan dari himpunan tegas, atau himpunan tegas dapat dipandang sebagai kejadian khusus dari himpunan kabur dengan fungsi kenggotaan hanya bernilai 1 untuk unsur-unsur yang merupakan anggota himpunan atau 0 untuk unsur-unsur yang tidak
merupakan anggota himpunan tersebut. Suatu himpunan tegas A dalam semesta dapat dinyatakan dengan fungsi karakteristik yang didefinisikan dengan aturan
{ untuk setiap .
Pada himpunan jarak jauh dalam semesta [0,100], himpunan jarak jauh dapat dinyatakan dengan fungsi keanggotaan dengan grafik seperti disajikan dalam Gambar 2.1.
Misalnya jarak 20 km mempunyai derajat keanggotaan 0.2, yaitu
, dan jarak 50 km mempunyai derajat keanggotaan 0.5,
yaitu , dalam himpunan kabur “jauh” tersebut.
Gambar 2.1 Fungsi Keanggotaan Himpunan Kabur “Jauh”
Definisi 2.1.1
Secara matematis suatu himpunan kabur ̃ dalam semesta X dapat dinyatakan sebagai himpunan pasangan terurut
̃ ̃
di mana ̃ adalah fungsi keanggotaan dari himpunan kabur ̃ , yang merupakan suatu pemetaan dari himpunan semesta X ke selang tertutup [0,1].
Suatu himpunan disebut kitaran dari titik a, jika terdapat selang I yang memuat a dan terdapat dalam N, yaitu . Himpunan diskret adalah himpunan yang terdiri dari bilangan real
0 1 0.5 0.2 20 50 100 km 𝝁𝒋𝒂𝒖𝒉 𝝁𝒋𝒂𝒖𝒉 𝒙
sedemikian rupa sehingga setiap bilangan dalam himpunan tersebut adalah titik terisolasi, yaitu titik yang memiliki kitaran yang tidak mengandung titik-titik lain dari himpunan tersebut. Apabila semesta X adalah himpunan diskret himpunan kabur ̃ seringkali dinyatakan dengan
̃ ∑ ̃
di mana lambang “∑” di sini tidak melambangkan operasi jumlahan seperti yang dikenal dalam aritmetika, tetapi melambangkan keseluruhan unsur-unsur bersama dengan derajat keanggotaannya dalam himpunan kabur ̃. Sedangkan lambang “ ” bukan lambang pembagian seperti dikenal dalam aritmetika, tetapi lambang pemisah antara unsur-unsur dan derajat keanggotaannya dalam himpunan kabur ̃.
Apabila semesta X adalah himpunan yang kontinu, yaitu himpunan yang tidak diskret, maka himpunan kabur ̃ seringkali dinyatakan dengan
̃ ∫ ̃
di mana lambang “∫” di sini bukan lambang integral seperti dikenal dalam kalkulus, tetapi melambangkan keseluruhan unsur-unsur bersama dengan derajat keanggotaannya dalam himpunan kabur ̃ . Sedangkan lambang “ ” bukan lambang pembagian seperti dikenal dalam aritmetika, tetapi lambang pemisah antara unsur-unsur dan derajat keanggotaannya dalam himpunan kabur ̃.
Contoh 2.1.1: Dalam semesta , jika ̃ adalah himpunan “bilangan yang jauh dari nol”, maka himpunan kabur ̃ tersebut dapat dinyatakan misalnya sebagai
̃ ∑ ̃
Contoh 2.1.2: Dalam semesta himpunan semua bilangan real , jika ̃ adalah himpunan “bilangan real yang dekat dengan nol”, maka himpunan kabur ̃ tersebut dapat dinyatakan sebagai
̃ ∫
Definisi 2.1.2
Pendukung (support) dari suatu himpunan kabur ̃ , yang dilambangkan dengan Pendukung ( ̃ ), adalah himpunan tegas yang memuat semua unsur dari semesta yang mempunyai derajat keanggotaan taknol dalam ̃, yaitu:
( ̃) ̃
Definisi 2.1.3
Teras (core) dari suatu himpunan kabur ̃, yang dilambangkan dengan Teras ( ̃), adalah himpunan tegas yang memuat semua unsur dari semestanya yang mempunyai derajat keanggotaan sama dengan 1, yaitu:
( ̃) ̃
Definisi 2.1.4
Titik silang (crossover point) dari suatu himpunan kabur ̃ adalah unsur (titik) dari semesta yang mempunyai derajat keanggotaan sama dengan 0.5, yaitu titik sedemikian sehingga ̃ .
Definisi 2.1.5
Tinggi (height) dari himpunan kabur ̃, yang dilambangkan dengan Tinggi ( ̃), didefinisikan sebagai batas atas terkecil dari himpunan semua derajat keanggotaan unsur-unsur semesta dalam himpunan kabur ̃ yaitu:
( ̃)
̃
Himpunan kabur yang tingginya sama dengan 1 disebut himpunan kabur normal, sedangkan himpunan kabur dengan tinggi kurang dari 1 disebut himpunan kabur subnormal.
Definisi 2.1.6
Pusat dari himpunan kabur ̃ dalam semesta yang dilambangkan dengan Pusat ( ̃), adalah titik yang merupakan purata dari semua titik di mana fungsi keanggotaan himpunan kabur itu mencapai maksimum.
1) Jika nilai purata itu berhingga, maka pusat himpunan kabur itu adalah titik dengan nilai purata tersebut.
2) Jika nilai purata itu takhingga positif, maka pusat himpunan kabur itu adalah titik terkecil di antara semua titik yang mencapai nilai fungsi keanggotaan maksimum.
3) Jika nilai purata itu takhingga negatif, maka pusat himpunan kabur itu adalah titik terbesar di antara semua titik yang mencapai nilai fungsi keanggotaan maksimum.
Gambar 2.2 menyajikan ilustrasi pendukung, teras, pusat dan titik silang dari suatu himpunan kabur.
Gambar 2.2 Pendukung, Teras, Pusat dan Titik Silang dari Suatu Himpunan Kabur titik silang 1 0.5 0 X titik silang teras
pusat
Definisi 2.1.7
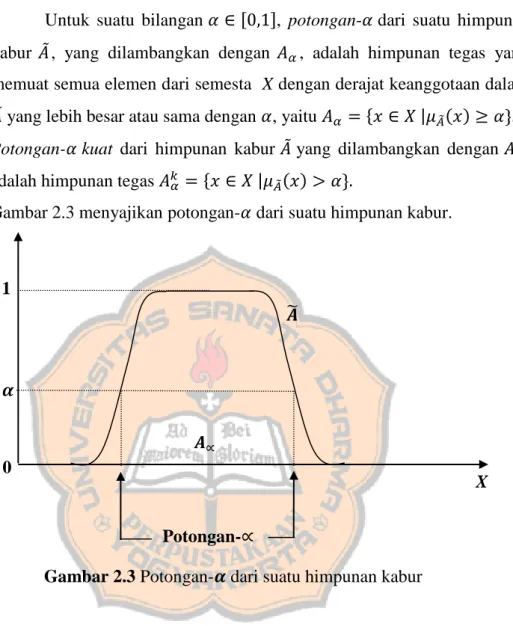
Untuk suatu bilangan [ ], potongan- dari suatu himpunan kabur ̃, yang dilambangkan dengan , adalah himpunan tegas yang memuat semua elemen dari semesta X dengan derajat keanggotaan dalam ̃ yang lebih besar atau sama dengan , yaitu ̃ Potongan- kuat dari himpunan kabur ̃ yang dilambangkan dengan , adalah himpunan tegas ̃
Gambar 2.3 menyajikan potongan- dari suatu himpunan kabur.
Gambar 2.3 Potongan- dari suatu himpunan kabur
B. Fungsi Keanggotaan
Setiap himpunan kabur dapat dinyatakan dengan suatu fungsi keanggotaan. Fungsi keanggotaan adalah suatu fungsi yang menyatakan derajat kesesuaian unsur-unsur dalam semestanya dengan ciri yang merupakan syarat keanggotaan himpunan tersebut. Berikut beberapa cara untuk menyatakan himpunan kabur dengan fungsi keanggotaannya:
1. Cara daftar:
Cara daftar digunakan untuk semesta berhingga yang diskret, misalnya seperti pada Contoh 2.1.2.
𝑨̃ 1 𝜶 0 X 𝜶 Potongan-∝ 𝑨∝
2. Cara analitik
Cara analitik digunakan untuk semesta takhingga yang kontinu dan semesta takhingga yang diskret, misalnya seperti pada contoh 2.1.1.
Definisi 2.2.1
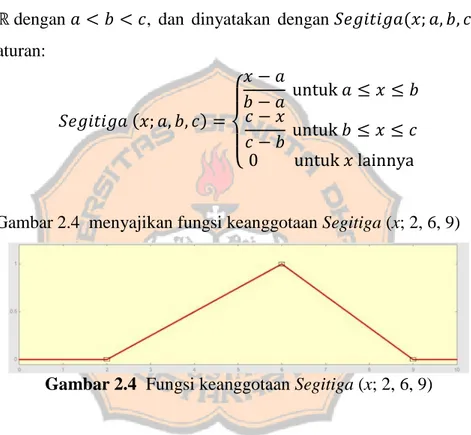
Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan segitiga jika mempunyai tiga buah parameter, yaitu dengan , dan dinyatakan dengan dengan aturan: {
Gambar 2.4 menyajikan fungsi keanggotaan Segitiga (x; 2, 6, 9)
Gambar 2.4 Fungsi keanggotaan Segitiga (x; 2, 6, 9)
C. Operasi Baku pada Himpunan Kabur
Pada himpunan tegas, didefinisikan operasi uner yaitu komplemen dan operasi-operasi biner yaitu gabungan dan irisan. Pada subbab sebelumnya telah dijelaskan bahwa himpunan kabur merupakan perluasan dari himpunan tegas. Oleh karena itu, operasi-operasi pada himpunan kabur dapat didefinisikan sesuai dengan operasi-operasi pada himpunan tegas.
Definisi 2.3.1
Komplemen Baku dari suatu himpunan kabur ̃ adalah himpunan kabur ̃ dengan fungsi keanggotaan
̃ ̃
untuk setiap
Definisi 2.3.2
Gabungan Baku dua buah himpunan kabur ̃ dan ̃ adalah himpunan kabur ̃ ̃ dengan fungsi keanggotaan
̃ ̃ ̃ ̃
untuk setiap
Definisi 2.3.3
Irisan Baku dua buah himpunan kabur ̃ dan ̃ adalah himpunan kabur ̃ ̃ dengan fungsi keanggotaan
̃ ̃ ̃ ̃
untuk setiap
Contoh 2.3.1: Misalkan dalam semesta diketahui himpunan kabur ̃ dan ̃ maka ̃ ̃ ̃ ̃ ̃ ̃
D. Perampatan Operasi Baku pada Himpunan Kabur
Definisi operasi-operasi baku pada himpunan kabur dapat dirampatkan sedemikian sehingga definisi operasi-operasi baku tersebut merupakan kejadian khusus dari operasi pada himpunan kabur.
Definisi 2.4.1
Komplemen kabur adalah suatu pemetaan k: [0,1] [0,1] dengan syarat sebagai berikut:
1) k(0) = 1 dan k(1) = 0 (syarat batas)
2) Jika , maka ) umtuk semua [ ] (syarat tak naik)
Contoh 2.4.1: Suatu kelas pemetaan yang merupakan komplemen kabur adalah kelas Sugeno yang didefinisikan sebagai berikut:
dengan parameter Untuk diperoleh operasi komplemen baku, yaitu
di mana x adalah derajat keanggotaan suatu elemen dalam suatu himpunan kabur ̃ , yaitu ̃ dan adalah derajat keanggotaan elemen tersebut dalam himpunan kabur ̃ (komplemen dari himpunan kabur ̃), yaitu ̃ .
Definisi 2.4.2
Gabungan kabur (norma-s) adalah suatu pemetaan [ ] [ ] [ ] dengan syarat sebagai berikut:
1) (syarat batas) 2) (syarat komutatif)
4) Jika dan , maka untuk semua [ ] (syarat takturun)
Contoh 2.4.2:
Contoh-contoh norma-s adalah sebagai berikut: 1) Gabungan baku: 2) Jumlah Aljabar:
Definisi 2.4.3
Irisan kabur (norma-t) adalah suatu pemetaan [ ] [ ] [ ] dengan syarat sebagai berikut:
1) (syarat batas) 2) (syarat komutatif)
3) ( ) (syarat asosiatif)
4) Jika dan , maka untuk semua [ ] (syarat takturun)
Contoh 2.4.3:
Contoh-contoh norma-t adalah sebagai berikut: 1) Irisan Baku:
2) Darab Aljabar:
E. Relasi Kabur Definisi 2.5.1
Relasi kabur (biner) ̃ antara elemen-elemen dalam himpunan X dengan elemen-elemen dalam himpunan Y didefinisikan sebagai himpunan bagian kabur dari darab Cartesius , yaitu himpunan kabur
Relasi kabur ̃ tersebut juga disebut relasi kabur pada himpunan (semesta) Jika maka ̃ disebut relasi kabur pada himpunan X.
Contoh 2.5.1: Misalnya X = {47, 78, 93}, Y = {2, 40, 70} dan ̃ adalah relasi kabur “jauh lebih besar” antara elemen-elemen dalam X dengan elemen-elemen dalam Y. Maka relasi ̃ tersebut dapat disajikan sebagai berikut:
̃ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄
Definisi 2.5.2
Jika ̃ adalah relasi kabur pada dan ̃ adalah relasi kabur pada , maka komposisi relasi kabur ̃ ̃ , yang dinotasikan dengan ̃ ̃ , adalah relasi kabur pada dengan fungsi keanggotaan
̃ ̃
̃ ̃
di mana t adalah suatu norma-t.
Jika sebagai norma-t diambil operator “min”, maka diperoleh relasi komposit ̃ ̃ dengan fungsi keanggotaan
̃ ̃
̃ ̃
Komposisi tersebut disebut komposisi sup-min.
Jika sebagai norma-t diambil operator “darab aljabar”, maka diperoleh relasi komposit ̃ ̃ dengan fungsi keanggotaan
̃ ̃
̃ ̃
F. Logika Kabur
1. Konsep Logika Kabur
Logika adalah ilmu yang mempelajari secara sistematis kaidah-kaidah penalaran yang sah. Dalam kehidupan sehari-hari logika yang biasanya kita pakai adalah logika dwinilai, di mana setiap proposisi mempunyai dua kemungkinan nilai, yaitu benar atau salah, dan tidak kedua-duanya. Logika dwinilai dapat dikembangkan menjadi logika n-nilai, yaitu logika dengan tak hingga banyak nilai kebenaran yang dinyatakan dengan bilangan real dalam selang [0,1]. Logika inilah yang menjadi dasar dari logika kabur.
2. Variabel Linguistik
Variabel adalah suatu lambang atau kata yang menunjuk pada sesuatu yang tidak tertentu dalam semesta wacananya. Jika semesta wacananya adalah himpunan kata-kata atau istilah-istilah dari bahasa sehari-hari, maka variabel itu disebut variabel linguistik. Jika semesta wacananya adalah himpunan bilangan-bilangan, maka variabel itu disebut variabel numeris.
Definisi 2.6.1
Variabel linguistik adalah suatu rangkap-5 (x,T,X,G,M) di mana x adalah lambang variabelnya, T adalah himpunan nilai-nilai linguistik yang dapat menggantikan x, X adalah semesta wacana (numeris) dari nilai-nilai linguistik dalam T, G adalah himpunan aturan sintaksis yang mengatur pembentukan istilah-istilah anggota T, dan M adalah himpunan aturan semantik yang mengaitkan setiap istilah dalam T dengan suatu himpunan kabur dalam semesta X.
Contoh 2.6.1: Misalkan variabel linguistik x adalah “tinggi”, maka sebagai himpunan nilai-nilai linguistiknya dapat diambil himpunan istilah-istilah T = {sangat tinggi, agak tinggi, tinggi, rendah, agak rendah, sangat
rendah}, dengan semesta X = [0,200], himpunan aturan sintaksis G yang mengatur pembentukan istilah-istilah anggota T, dan himpunan aturan semantik { ̃ ̃ }.
3. Pengubah Linguistik
Pengubah linguistik (linguistic hedge / modifier) adalah suatu kata yang dipergunakan untuk mengubah suatu kata/istilah menjadi kata/istilah yang baru dengan makna yang baru pula. Pengubah linguistik paling sering dipakai adalah “sangat” dan “agak”.
Definisi 2.6.2
Jika suatu istilah dikaitkan dengan himpunan kabur ̃ dalam semesta , maka istilah “sangat A” dikaitkan dengan himpunan kabur Konsentrasi dari ̃, dengan lambang ( ̃) dan fungsi keanggotaan
̃ ̃
untuk setiap , sedangkan istilah “agak A” dikaitkan dengan himpunan kabur Dilasi dari ̃, dengan lambang ̃ dan fungsi keanggotaan
̃ ̃
untuk setiap .
Contoh 2.6.2: Misalkan X = {2,4,6,8,10} dan istilah “dekat dengan 10” dikaitkan dengan himpunan kabur ̃ . Maka istilah berikut:
“sangat dekat dengan 10” dikaitkan dengan himpunan kabur ( ̃) “sangat dekat sekali dengan 10” dikaitkan dengan himpunan kabur
( ̃ )
“agak dekat dengan 10” dikaitkan dengan himpunan kabur ( ̃) “tidak sangat dekat dengan 10” dikaitkan dengan himpunan kabur
( ( ̃))
“dekat tetapi (dan) tidak sangat dekat dengan 10” dikaitkan dengan himpunan kabur
̃ ( ( ̃))
4. Proposisi Kabur
Proposisi kabur adalah kalimat yang memuat predikat kabur, yaitu predikat yang dapat direpresentasikan dengan suatu himpunan kabur. Proposisi kabur yang mempunyai nilai kebenaran tertentu disebut pernyataan kabur dengan nilai kebenaran yang disajikan dengan suatu bilangan real dalam selang [0,1]. Nilai kebenaran itu disebut juga derajat kebenaran dari pernyataan kabur itu.
Bentuk umum dari suatu proposisi kabur adalah x adalah A
di mana x adalah suatu variabel linguistik dan predikat A adalah suatu nilai linguistik dari x. Bila ̃ adalah himpunan kabur yang dikaitkan dengan nilai linguistik A dan adalah suatu elemen tertentu dalam semesta X dari himpunan kabur ̃ , maka mempunyai derajat keanggotaan ̃ dalam himpunan kabur ̃. Derajat kebenaran dari pernyataan kabur
adalah A
didefinisikan sama dengan derajat keanggotaan dalam himpunan kabur ̃, yaitu ̃
Logika kabur merupakan perluasan dari logika tegas, sehingga dapat dibentuk proposisi kabur majemuk dari proposisi-proposisi kabur
tunggal dengan menggunakan operator-operator logika. Beberapa contoh proposisi kabur majemuk misalnya:
Film itu bagus dan ceritanya menarik
Siswa itu kurang pandai atau tingkat kesulitan soal yang tinggi Jika permintaannya rendah, maka harga jual menjadi murah Anak itu gemuk bila dan hanya bila nafsu makannya tinggi
Secara umum terdapat empat macam proposisi kabur majemuk dengan operator logika biner, yaitu:
Konjungsi kabur : x adalah A dan y adalah B Disjungsi kabur : x adalah A atau y adalah B Implikasi kabur : Bila x adalah A, maka y adalah B
Ekivalensi kabur : x adalah A bila dan hanya bila y adalah B
Pada empat macam proposisi di atas, variabel-variabel linguistik dalam proposisi-proposisi tunggal penyusunnya tidak harus dalam semesta numeris yang sama.
Jika x adalah variabel linguistik dengan semesta numeris X, dan A adalah suatu predikat kabur yang dikaitkan dengan himpunan kabur ̃ dalam X, maka negasi kabur:
x adalah tidak A
adalah proposisi kabur dengan predikat kabur “tidak A” yang dapat dikaitkan dengan komplemen kabur dari himpunan kabur ̃, yaitu ̃ , dengan fungsi keanggotaan
̃ ( ̃ )
di mana k adalah suatu komplemen kabur.
Jika x adalah variabel linguistik dengan semesta numeris X dan y adalah variabel linguistik dengan semesta numeris Y, maka konjungsi kabur:
x adalah A dan y adalah B
di mana A dikaitkan dengan himpunan kabur ̃ dalam X, dan B dikaitkan dengan himpunan kabur ̃ dalam Y, dapat dipandang sebagai suatu relasi kabur ˄ dalam dengan fungsi keanggotaan
( ̃ ̃ )
dengan t adalah suatu norma-t. Sedangkan disjungsi kabur: x adalah A atau y adalah B
dapat dipandang sebagai suatu relasi kabur ˅ dalam dengan fungsi keanggotaan
( ̃ ̃ )
dengan s adalah suatu norma-s.
5. Implikasi Kabur
Implikasi kabur adalah proposisi kabur majemuk yang paling sering digunakan dalam aplikasi teori kabur. Bentuk umum suatu implikasi kabur adalah
Bila x adalah A, maka y adalah B
di mana A dan B adalah predikat-predikat kabur yang dikaitkan dengan himpunan-himpunan kabur ̃ dan ̃ dalam semesta X dan Y berturut-turut. Implikasi kabur dapat dipandang sebagai suatu relasi kabur dalam , yang dilambangkan dengan →.
Beberapa cara menginterpretasikan implikasi kabur sebagai relasi kabur → dalam , sebagai berikut:
a. Implikasi Dienes-Rescher
Dalam logika dwinilai, implikasi tegas ekivalen dengan . Bila proposisi p dan q tersebut diganti dengan proposisi kabur berturut-turut “x adalah A” dan “y adalah B”, maka implikasi kabur tersebut dapat diinterpretasikan sebagai relasi kabur → dalam dengan fungsi keanggotaan
( ̃ ) ( ̃ )
di mana s adalah suatu norma-s dan k adalah suatu komplemen kabur. Bila sebagai norma-s dan komplemen kabur diambil operasi-operasi gabungan dan komplemen baku, maka diperoleh
b. Implikasi Zadeh
Dalam logika dwinilai, implikasi tegas juga ekivalen dengan sehingga implikasi kabur juga dapat diinterpretasikan sebagai relasi kabur → dalam dengan fungsi keanggotaan
( ( ̃ ̃ ) ( ̃ ))
di mana s adalah suatu norma-s, t adalah suatu norma-t dan k adalah suatu komplemen kabur. Bila sebagai norma-s, norma-t dan komplemen kabur diambil operasi-operasi gabungan, irisan dan komplemen baku, maka diperoleh
( ( ̃ ̃ ) ̃ )
c. Implikasi Mamdani
Implikasi Mamdani merupakan salah satu implikasi kabur yang paling sering digunakan. Implikasi ini didasarkan pada asumsi bahwa dalam implikasi kabur
Jika x adalah A, maka y adalah B
hanya dibahas mengenai x adalah A dan y adalah B saja. Oleh karena itu, implikasi kabur dapat dipandang sebagai suatu konjungsi kabur, sehingga diperoleh
̃ ̃
Terdapat beberapa jenis implikasi Mamdani, antara lain: 1) Implikasi Mamdani Min
Bila sebagai norma-t diambil operasi baku “min”, maka diperoleh
( ̃ ̃ )
2) Implikasi Mamdani Darab
Bila sebagai norma-t diambil operasi “darab aljabar”, maka diperoleh
̃ ̃
Implikasi kabur dapat diperluas menjadi implikasi dengan bentuk umum:
di mana dan berturut-turut adalah proposisi kabur dalam semesta dan .
Contoh 2.6.3: Misalkan diketahui semesta X = {20, 25, 30, 35, 40} dan Y = {4, 5, 6} dan implikasi kabur
di mana predikat “muda” dan “cepat” berturut-turut dikaitkan dengan himpunan kabur ̃ ⁄ ⁄ ⁄ ⁄ dan ̃ ⁄ ⁄ Maka diperoleh 1) Implikasi Dienes-Rescher ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ 2) Implikasi Zadeh ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ 3) Implikasi Mamdani ⁄ ⁄ ⁄ ⁄
⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ atau ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ ⁄ 6. Penalaran Kabur
Penalaran kabur (fuzzy reasoning), yang juga disebut penalaran hampiran (approximate reasoning), adalah suatu cara penarikan kesimpulan berdasarkan seperangkat implikasi kabur dan suatu fakta yang diketahui (premis). Penalaran kabur merupakan suatu perampatan dari penalaran tegas. Berikut ini suatu contoh penalaran tegas:
Premis 1 : Bila hari ini hari Minggu, maka Alex pergi ibadah Premis 2 : Hari ini hari Minggu
Kesimpulan : Alex pergi ibadah
Aturan dalam penalaran tegas dapat dirampatkan menjadi aturan kabur dengan premis dan kesimpulannya adalah proposisi-proposisi kabur. Berikut ini suatu contoh penalaran kabur:
Premis 1 : Bila toko penuh, maka antrian kasirnya lama Premis 2 : Toko agak penuh
Kesimpulan : Antrian kasirnya agak lama
Penalaran tersebut dapat dirumuskan secara umum dengan skema sebagai berikut:
Premis 1 (Kaidah) : Bila x adalah A, maka y adalah B Premis 2 (Fakta) : x adalah A′
Penalaran kabur dengan skema seperti di atas disebut modus ponens rampat (generalized modus ponens). Kesimpulan yang sah dalam penalaran kabur tersebut diperoleh dengan menggunakan suatu aturan penarikan kesimpulan yang merupakan komposisi relasi dan disebut “kaidah inferensi komposisional” (compositional rule of inference), yaitu sebagai berikut:
Premis 1 : Bila x adalah A, maka y adalah B
(yang merupakan relasi/implikasi kabur di ) Premis 2 : x adalah A′
(yang dapat direpresentasikan dengan himpunan kabur ̃ dalam X)
Kesimpulan : y adalah B′
(yang diperoleh dengan menentukan himpunan kabur ̃ ̃ dalam Y dengan fungsi keanggotaan
̃
̃
di mana t adalah suatu norma-t).
Bila A′ misalnya predikat kabur “sangat A”, untuk norma-t diambil operasi baku “min”, dan untuk implikasi kabur dipakai implikasi Mamdani , maka kesimpulan “y adalah B′ ” di atas kita peroleh dengan menentukan himpunan kabur ̃ dengan fungsi keanggotaan
̃
̃ ̃ ̃
Bila ̃ dan ̃ adalah himpunan-himpunan tegas dan ̃ ̃, maka
̃
̃ ̃ ̃
̃ ̃ ̃
untuk setiap . Jadi ̃ ̃ , yang berarti dalam kasus ini aturan penalaran tersebut adalah modus ponens tegas.
Teorema 2.1
Bila dalam modus ponens rampat di atas, predikat kabur A dikaitkan dengan himpunan kabur ̃, predikat kabur B dikaitkan dengan himpunan kabur ̃, predikat kabur A′ dikaitkan dengan himpunan kabur ̃ , untuk norma-t diambil operasi baku “min”, dan untuk implikasi kabur dipakai implikasi Mamdani , maka predikat kabur B′ dalam kesimpulan terkait dengan himpunan kabur ̃ dengan fungsi keanggotaan ̃ ̃ di mana
̃ ̃
Bukti:
Dengan menggunakan kaidah inferensi komposisional, predikat kabur B′ dalam kesimpulan terkait dengan himpunan kabur ̃ ̃ dengan fungsi keanggotaan
̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ( ̃ ̃ ̃ ) ̃ di mana ̃ ̃ ̃ ̃ ∎
Bilangan dalam Teorema 2.1 disebut derajat keserasian (degree of compatibility) antara predikat A′ dengan predikat A.
Gambar 2.5 menunjukkan proses memperoleh himpunan kabur ̃ tersebut.
Gambar 2.5 Penarikan Kesimpulan dalam Modus Ponens Rampat
Modus ponens rampat dapat digeneralisasikan menjadi modus ponens rampat multikondisional, yang terdiri dari m buah premis kabur berupa kaidah, sebuah premis kabur berupa fakta, dan kesimpulan. Adapun skema umumnya adalah sebagai berikut:
Premis 1 : Bila adalah dan … dan adalah , maka y
adalah
Premis 2 : Bila adalah dan … dan adalah , maka y adalah
Premis m : Bila adalah dan … dan adalah , maka y adalah
Fakta : adalah dan … dan adalah Kesimpulan : y adalah B′
Teorema 2.2
Bila dalam modus ponens rampat multikondisional di atas dan
adalah predikat kabur yang dikaitkan dengan himpunan kabur ̃ dan ̃ dalam semesta , dan adalah predikat kabur yang dikaitkan dengan himpunan kabur ̃ dalam semesta Y ( ),
𝐴 ̃ w 𝐴̃ 𝐵 ̃ 𝐵̃ X Y
masing-masing kaidah dipandang sebagai relasi kabur ̃ dalam , dan ̃ ⋃ ̃ , faktanya adalah himpunan kabur ̃ ̃ ̃ dalam , dan untuk implikasi kabur ̃ diambil implikasi Mamdani maka predikat kabur B′ dalam kesimpulannya terkait dengan himpunan kabur ̃ dengan fungsi keanggotan ̃ =
[ ] ̃ di mana [ ] dan
̃ ̃ ,
Bukti:
Kesimpulan “y adalah B′ ” diperoleh dengan menentukan himpunan kabur ̃ yang berkaitan dengan predikat kabur B′ dengan menggunakan kaidah inferensi komposisional, yaitu ̃ ̃ ̃ dalam semesta Y dengan fungsi keanggotaan
̃ ⋃ ̃ ̃ [ ] ̃ ̃ ( ̃ ̃ ̃ ) [ ] [ ] ̃ [ ] ̃ ̃ [ ] [ ] [ ] ̃ ( ) ̃ ̃ [ ] ̃ di mana [ ] dan [ ] ̃ ( ) ̃ ̃ ̃ , . ∎
Bilangan disebut derajat keserasian (degree of compatibility) antara fakta ̃ yang diberikan dengan anteseden ̃ dari premis/kaidah ̃ , sedangkan bilangan yang merupakan minimum dari semua untuk disebut daya sulut (firing strength), yang menyatakan
sejauh mana anteseden dari kaidah ̃ dipenuhi oleh fakta ̃ yang diberikan dan menyulut konsekuen dari kaidah tersebut.
Dengan menggunakan Teorema 2.2, kesimpulan ̃ dapat ditentukan dengan empat langkah sebagai berikut:
Langkah 1: Untuk setiap dan tentukan derajat keserasian , yaitu supremum dari ̃ ̃
untuk semua
Langkah 2 : Untuk setiap i, tentukan daya sulut yaitu minimum
dari semua derajat keserasian .
Langkah 3 : Untuk setiap i, tentukan irisan dengan ̃
Langkah 4 : Tentukan gabungan semua irisan tersebut (langkah 3) yang menghasilkan himpunan kabur ̃ .
G. Sistem Inferensi Kabur
Sistem inferensi kabur adalah sistem komputasi yang bekerja berdasarkan penalaran kabur. Sistem inferensi kabur semacam itu terdiri dari empat unit, yaitu:
1. Unit pengaburan (fuzzification unit)
2. Unit penalaran logika kabur (fuzzy logic reasoning unit)
3. Unit basis pengetahuan (knowledge base unit), yang terdiri dari dua bagian:
a. Basis data (data base), yang memuat fungsi-fungsi keanggotaan dari himpunan-himpunan kabur yang terkait dengan nilai dari variabel-variabel linguistik yang dipakai. b. Basis kaidah (rule base), yang memuat kaidah-kaidah
berupa implikasi kabur. 4. Unit penegasan (defuzzification unit).
Sistem inferensi semacam itu mempunyai cara kerja sebagai berikut: 1. Mula-mula akan diukur nilai-nilai tegas dari semua masukan yang
terkait dalam proses inferensi tersebut.
2. Selanjutnya oleh unit pengaburan nilai-nilai yang sudah didapatkan tersebut akan diubah ke nilai kabur yang sesuai.
3. Hasil pengukuran yang sudah dikaburkan tersebut akan diproses oleh unit penalaran dengan menggunakan unit basis pengetahuan dan menghasilkan himpunan kabur sebagai keluarannya.
4. Himpunan kabur keluaran tersebut akan diterjemahkan ke dalam nilai yang tegas oleh unit penegasan.
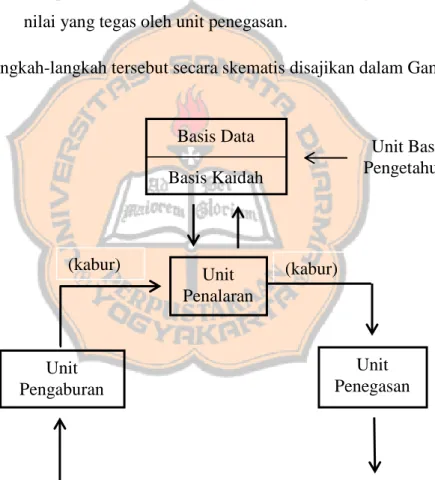
Langkah-langkah tersebut secara skematis disajikan dalam Gambar 2.6.
Gambar 2.6 Struktur Dasar Suatu Sistem Inferensi Kabur Basis Data Basis Kaidah Unit Penalaran Unit Penegasan Unit Pengaburan Unit Basis Pengetahuan Masukan (tegas) Keluaran (tegas) (kabur) (kabur)
Keempat unit dalam sistem inferensi kabur tersebut akan dijelaskan sebagai berikut:
1. Unit Pengaburan
Langkah pertama yang dilakukan adalah mengubah masukan tegas yang diterima menjadi masukan kabur. Hal tersebut dilakukan karena sistem inferensi kabur bekerja dengan kaidah dan masukan kabur. Itulah yang dikerjakan oleh unit pengaburan dengan menggunakan suatu fungsi yang disebut fungsi pengaburan (fuzzification function), yaitu pemetaan , di mana K adalah suatu kelas himpunan kabur dalam semesta .
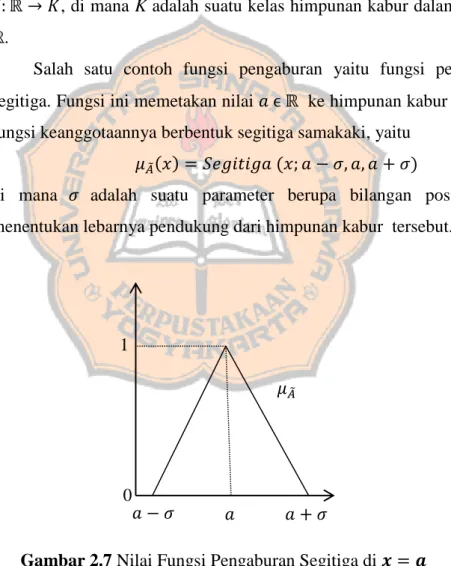
Salah satu contoh fungsi pengaburan yaitu fungsi pengaburan segitiga. Fungsi ini memetakan nilai ke himpunan kabur ̃ dengan fungsi keanggotaannya berbentuk segitiga samakaki, yaitu
̃
di mana adalah suatu parameter berupa bilangan positif yang menentukan lebarnya pendukung dari himpunan kabur tersebut.
Gambar 2.7 Nilai Fungsi Pengaburan Segitiga di
2. Basis Pengetahuan
Basis pengetahuan dari suatu sistem inferensi kabur terdiri dari basis data dan basis kaidah.
1
0
𝑎 𝜎 𝑎 𝑎 𝜎 𝜇𝐴̃
a. Basis Data
Basis data adalah himpunan fungsi-fungsi keanggotaan dari himpunan-himpunan kabur yang terkait dengan nilai-nilai linguistik dari variabel-variabel yang terlibat dalam sistem inferensi kabur tersebut.
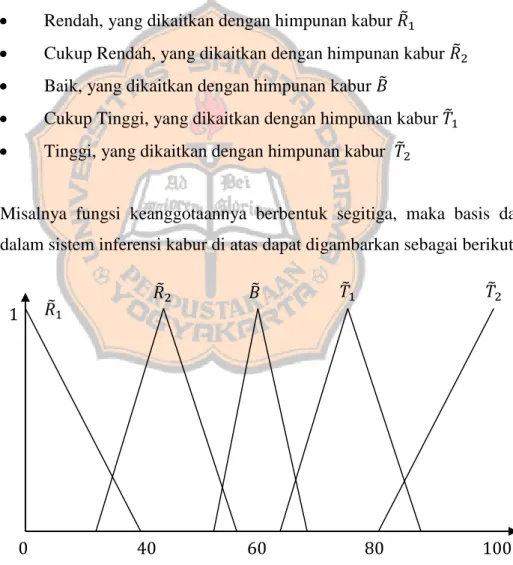
Contoh 2.7.1: Misalnya dalam suatu sistem inferensi kabur variabel x menyatakan nilai akademik seorang pelajar dengan semesta selang tertutup [0,100] mempunyai lima nilai linguistik sebagai berikut:
Rendah, yang dikaitkan dengan himpunan kabur ̃
Cukup Rendah, yang dikaitkan dengan himpunan kabur ̃
Baik, yang dikaitkan dengan himpunan kabur ̃
Cukup Tinggi, yang dikaitkan dengan himpunan kabur ̃
Tinggi, yang dikaitkan dengan himpunan kabur ̃
Misalnya fungsi keanggotaannya berbentuk segitiga, maka basis data dalam sistem inferensi kabur di atas dapat digambarkan sebagai berikut:
Gambar 2.8 Fungsi Keanggotaan Himpunan-himpunan Kabur yang Terkait dengan Nilai-nilai Linguistik untuk Variabel x pada Semesta
[0,100] 𝑇̃ 𝑇̃ 𝐵̃ 𝑅̃ 𝑅̃
b. Basis Kaidah
Basis kaidah adalah himpunan implikasi-implikasi kabur yang berlaku sebagai kaidah dalam sistem inferensi kabur. Bila sistem inferensi kabur tersebut mempunyai m buah kaidah dengan (n+1) variabel, maka bentuk umum kaidah ke-i adalah sebagai berikut:
di mana adalah variabel linguistik dengan semesta numeris
Contoh 2.7.2: Misalkan implikasinya melibatkan tiga variabel sebagai berikut:
di mana x menyatakan nilai akademik siswa, y menyatakan nilai ektrakurikuler siswa dan z menyatakan nilai prestasi siswa adalah variabel-variabel dengan semesta selang tertutup [0,100], dan dengan lima nilai linguistik seperti Contoh 2.7.1. Maka basis kaidah dari sistem inferensi kabur ini terdiri dari 25 kaidah, yang secara lengkap dapat disajikan dalam bentuk matriks sebagai berikut:
z y ̃ ̃ ̃ ̃ ̃ x ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃ ̃
Misalnya salah satu kaidahnya berbunyi:
Bila nilai akademik siswa cukup tinggi dan nilai ekstrakurikuler siswa cukup tinggi, maka nilai prestasi siswa tinggi
3. Unit Penalaran Kabur
Masukan kabur hasil pengolahan unit pengaburan diterima oleh unit penalaran untuk disimpulkan berdasarkan kaidah-kaidah yang tersedia dalam basis pengetahuan. Penarikan kesimpulan itu dilaksanakan berdasarkan aturan modus ponens rampat multikondisional dengan skema umum seperti yang telah dijelaskan pada bagian subbab F. Pada unit ini keluaran yang dihasilkan berupa suatu himpunan kabur.
4. Unit Penegasan
Unit penegasan berfungsi untuk mengubah nilai kabur keluaran menjadi nilai yang tegas. Fungsi penegasan adalah suatu pemetaan , di mana adalah suatu kelas himpunan-himpunan kabur, yang memetakan suatu himpunan kabur ke suatu bilangan real yang tegas. Keluaran dalam sistem inferensi kabur Takagi-Sugeno-Kang (TSK) dan sistem inferensi kabur Tsukamoto berupa nilai tegas, sehingga tidak diperlukan suatu fungsi penegasan. Sedangkan keluaran dalam sistem inferensi kabur Mamdani masih berupa himpunan kabur, sehingga diperlukan suatu fungsi penegasan untuk mengubah himpunan kabur tersebut menjadi nilai tegas. Salah satu fungsi penegasan yang sering dipakai adalah Rerata Pusat.
36 BAB III
PENENTUAN WAKTU TEMPUH BUS TRANS JOGJA DENGAN MENGGUNAKAN SISTEM INFERENSI KABUR TSUKAMOTO
A. Sistem Inferensi Kabur Tsukamoto
Y. Tsukamoto mengembangkan suatu variasi sistem inferensi kabur yang disebut sistem inferensi kabur Tsukamoto. Dalam sistem inferensi kabur Tsukamoto, predikat kabur pada bagian konsekuen dari kaidah-kaidah sistemnya mempunyai fungsi keanggotaan yang monoton (naik monoton atau turun monoton).
Definisi 3.1
Fungsi f: ℝ ℝ dikatakannaik monoton jika dan hanya jika ℝ) ⇒
dan turun monoton jika dan hanya jika
ℝ) ⇒
Dalam sistem inferensi kabur Tsukamoto, masing-masing kaidah menghasilkan keluaran berupa nilai tegas yang diimbas oleh daya sulut pada kaidah yang bersangkutan. Bentuk umum kaidah ke-i sistem tersebut adalah sebagai berikut:
di mana adalah predikat kabur yang direpresentasikan dengan himpunan kabur ̃ dengan fungsi keanggotaan yang monoton untuk (dengan m adalah banyaknya kaidah dalam sistem tersebut). Setiap masukan akan menghasilkan daya sulut untuk kaidah ke-i, yang mengimbas keluaran tegas , yang memenuhi:
di mana ̃ adalah fungsi keanggotaan yang monoton pada konsekuen kaidah ke-i. Kesimpulan akhir y diperoleh dengan menentukan rerata terbobot dari semua keluaran dengan bobot daya sulutnya, yaitu:
∑∑
di mana adalah daya sulut pada kaidah ke-i.
Berikut adalah cara kerja sistem inferensi kabur Tsukamoto: Langkah 1 : Menentukan derajat keserasian (untuk setiap
dan yaitu supremum dari ̃ ̃ untuk semua
Langkah 2 : Untuk setiap i, menentukan daya sulut yaitu minimum dari semua derajat keserasian .
Langkah 3 : Untuk setiap i, menentukan nilai tegas yang memenuhi
̃
di mana ̃ adalah fungsi keanggotaan yang monoton pada konsekuen kaidah ke-i.
Langkah 4 : Menentukan keluaran akhir , yaitu ∑∑
di mana adalah daya sulut untuk kaidah ke-i.
B. Implementasi Sistem Inferensi Kabur Tsukamoto dalam Penentuan Waktu Tempuh Bus Trans Jogja
Pada tugas akhir ini, metode Tsukamoto akan dipakai dalam menentukan waktu tempuh bus Trans Jogja. Berikut adalah langkah-langkah penyusunan sistem inferensi kabur Tsukamoto dalam penentuan waktu tempuh bus Trans Jogja:
Langkah 1: Menentukan variabel-variabel masukan terkait dalam proses pencarian nilai dari variabel keluaran. Dalam implementasi sistem inferensi kabur untuk menentukan waktu tempuh bus
Trans Jogja, terdapat dua variabel yang akan digunakan sebagai variabel masukan, yaitu jarak tempuh dan volume kendaraan, serta satu variabel yang akan digunakan sebagai variabel keluaran, yaitu waktu tempuh. Kemudian menentukan semesta numeris dari masing-masing variabel tersebut. Selanjutnya menentukan nilai-nilai linguistik untuk masing-masing variabel tersebut, himpunan-himpunan kabur yang terkait, serta fungsi keanggotaan untuk setiap himpunan kabur tersebut.
Langkah 2: Menyusun basis kaidah.
Langkah 3: Untuk setiap kaidah ke- ( ), menentukan daya sulut dan nilai tegas .
Langkah 4: Menentukan keluaran akhir .
Berdasarkan data yang diperoleh dari Badan Pusat Statistik, jumlah kendaraan bermotor provinsi Yogyakarta yang terdaftar pada tahun 2018 adalah sebanyak 4.764.418 kendaraan. Volume kendaraan dapat dihitung denganmenggunakan rumus sebagai berikut (Sukirman, 1999):
dengan
LHRT = Lalu lintas Harian Rata-Rata Tahunan N = Jumlah kendaraan dalam setahun
yaitu:
Maka diperoleh selang volume kendaraan, yaitu [ ] dengan satuan kendaraan/hari. Variabel “jarak tempuh” berada dalam selang [ ] dengan satuan km, dan variabel “waktu tempuh” berada dalam selang [ ] dengan satuan menit.
1. Menyusun Basis Data
Dalam implementasi sistem inferensi kabur untuk menentukan waktu tempuh bus ini, terdapat dua variabel yang akan digunakan sebagai masukan, yaitu jarak tempuh dan volume kendaraan, serta satu variabel yang akan digunakan sebagai keluaran, yaitu waktu tempuh. Ketiga variabel tersebut mempunyai nilai-nilai linguistik yang merupakan himpunan-himpunan kabur yang akan didefinisikan dengan menggunakan fungsi keanggotaan segitiga. Berikut penjelasan mengenai masing-masing variabel:
a. Jarak tempuh
Nilai-nilai linguistik untuk variabel jarak tempuh dengan semesta selang [0,
60
] adalah sebagai berikut: “dekat” yang dinyatakan dengan himpunan kabur ̃
“sedang” yang dinyatakan dengan himpunan kabur ̃
“jauh” yang dinyatakan dengan himpunan kabur ̃
Fungsi keanggotaan dari himpunan-himpunan kabur tersebut:
̃ { ̃ { ̃ {
Gambar 3.1 menyajikan grafik fungsi-fungsi keanggotaan himpunan kabur di atas.
Gambar 3.1 Grafik Fungsi Keanggotaan Variabel Jarak Tempuh
b. Volume Kendaraan
Nilai-nilai linguistik untuk variabel volume kendaraan dengan semesta selang [ ] adalah sebagai berikut:
“rendah” yang dinyatakan dengan himpunan kabur ̃
“sedang” yang dinyatakan dengan himpunan kabur ̃
“tinggi” yang dinyatakan dengan himpunan kabur ̃ Fungsi keanggotaan dari himpunan-himpunan kabur tersebut:
̃ { ̃ { ̃ { 𝜇𝐷̃ 𝜇𝐷̃ 𝜇𝐷̃
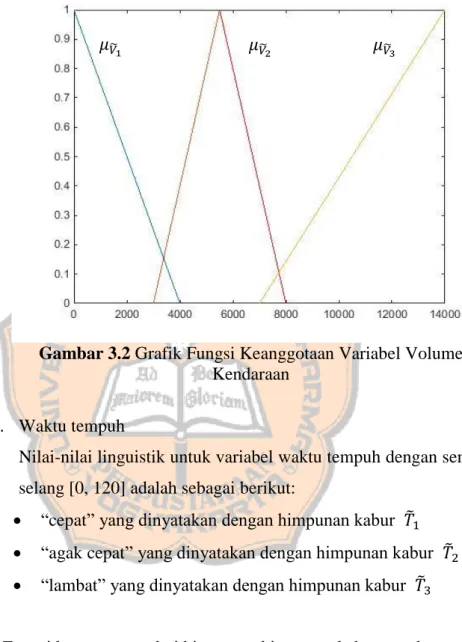
Gambar 3.2 menyajikan grafik fungsi-fungsi keanggotaan himpunan kabur di atas.
Gambar 3.2 Grafik Fungsi Keanggotaan Variabel Volume Kendaraan
c. Waktu tempuh
Nilai-nilai linguistik untuk variabel waktu tempuh dengan semesta selang [0, 120] adalah sebagai berikut:
“cepat” yang dinyatakan dengan himpunan kabur ̃
“agak cepat” yang dinyatakan dengan himpunan kabur ̃
“lambat” yang dinyatakan dengan himpunan kabur ̃
Fungsi keanggotaan dari himpunan-himpunan kabur tersebut:
̃ { ̃ { ( ) 𝜇𝑉̃ 𝜇𝑉̃ 𝜇𝑉̃
̃ {
Gambar 3.3 menyajikan grafik fungsi-fungsi keanggotaan himpunan kabur di atas (yang monoton).
Gambar 3.3 Grafik Fungsi Keanggotaan Variabel Waktu Tempuh
2. Menyusun Basis Kaidah
Kaidah-kaidah yang disusun dalam basis kaidah, berupa implikasi kabur yang antesedennya memuat dua variabel kabur masukan, yaitu jarak tempuh (dengan tiga nilai linguistik) dan volume kendaraan (dengan tiga nilai linguistik), dan konsekuennya memuat variabel kabur keluaran, yaitu waktu tempuh (dengan tiga nilai linguistik). Oleh karena ketiga variabel tersebut memiliki tiga nilai linguistik, maka diperoleh 33 = 27 kaidah. Akan tetapi tidak semua dari kaidah tersebut dapat diterima, misalnya kaidah
“Jika jarak tempuh jauh dan volume kendaraan tinggi, maka waktu tempuh cepat”
merupakan kaidah yang tidak dapat diterima. Oleh karena itu, dipilih kaidah berupa kombinasi dari varibel jarak tempuh dan volume
𝜇𝑇̃
𝜇𝑇̃
kendaraan dengan masing-masing vaiabel tersebut mempunyai tiga nilai linguistik, yaitu diperoleh 32 = 9 kaidah yang dapat diterima sebagai berikut:
[K1] Jika jarak tempuh dekat dan volume kendaraan rendah, maka waktu tempuh cepat
[K2] Jika jarak tempuh dekat dan volume kendaraan sedang, maka waktu tempuh agak cepat
[K3] Jika jarak tempuh dekat dan volume kendaraan tinggi, maka waktu tempuh lambat
[K4] Jika jarak tempuh sedang dan volume kendaraan rendah, maka waktu tempuh cepat
[K5] Jika jarak tempuh sedang dan volume kendaraan sedang, maka waktu tempuh agak cepat
[K6] Jika jarak tempuh sedang dan volume kendaraan tinggi, maka waktu tempuh lambat
[K7] Jika jarak tempuh jauh dan volume kendaraan rendah, maka waktu tempuh agak cepat
[K8] Jika jarak tempuh jauh dan volume kendaraan sedang, maka waktu tempuh lambat
[K9] Jika jarak tempuh jauh dan volume kendaraan tinggi, maka waktu tempuh lambat
3. Unit pengaburan a. Masukan
Misalnya seseorang akan pergi dari Sindu Kusuma Edupark (SKE) menuju Candi Prambanan dengan rute bus Trans Jogja: TPB (Tempat Perhentian Bus) Diamond 2 – Halte TJ (Trans Jogja) Jl Solo (SMA De Britto) – Halte Jl Solo Janti – Halte TJ (Trans Jogja) Prambanan. Jarak yang ditempuh adalah 17 km dan volume kendaraan adalah 3500 kendaraan/hari.
b. Unit Pengaburan
Dengan menggunakan fungsi pengaburan segitiga, masukan jarak tempuh akan dikaitkan dengan himpunan kabur ̃ dan masukan volume kendaraan akan dikaitkan dengan himpunan kabur ̃ dengan fungsi keanggotaan sebagai berikut:
̃ { ̃ {
4. Unit Penalaran Kabur
a. Menentukan daya sulut dan nilai tegas
Untuk masing-masing dari 9 kaidah di atas, akan dicari daya sulut dan nilai tegas untuk .
Derajat keserasian adalah
( ̃ ( ) ̃ ( ))
̃ ̃ untuk setiap i = 1,…,9 dan j = 1,2.
Untuk setiap i = 1,…,9 daya sulut adalah
̃
untuk k = 1,2,3.
Berikut ini proses perhitunganuntuk setiap kaidah.
[K1] Jika jarak tempuh dekat dan volume kendaraan rendah, maka waktu tempuh cepat
[ ] ̃ ̃
̃ ̃ [ ]
Akan dicari titik perpotongan grafik ̃ dan ̃ : ̃ ̃ ̃ ̃ [ ] ̃ ̃ ̃ ̃ [ ] [ ] = 0.2273