FOSTERING STUDENTS’ UNDERSTANDING ABOUT ANGLE MAGNITUDE
THROUGH REASONING ACTIVITIES
Boni Fasius Hery, S.Pd, M.Sc. Sriwijaya University
Abstract
The purpose of this study is to support seventh-grade students learning about angle magnitude. Realistic Mathematics Education (RME) is employed as the design heuristic of the educational design. Design research is considered as the appropriate research approach to investigate how the design lesson can help students to comprehend the important concepts of angles magnitude through reasoning activities. The data such as, the collection of students written work, interview with students, and video recording from the whole teaching experiments were analyzed using task-oriented method to continually improve the design. The results from the analysis suggest that the use of reasoning activities in the teaching experiments could help the students to retrieve their prior-knowledge about angle, negate their misconceptions about angle and allow them to reinvent the relation between angles magnitudes in a parallel-transversal situation. It was shown how production tasks and reasoning activities supported the learning of important concepts of angles and its magnitude. In the teaching experiments, several students came to reason about the angle magnitude using informal measurement, overlapping and reshaping strategy.
Keywords: educational design, realistic mathematics education, design research, angle
magnitude, reasoning activity
INTRODUCTION
Asking students to memorize the definition and the concepts of the angle seems to be a fairly simple activity. For instance, teacher claims the angle as the sub-figure of polygon (the vertices), diagrammatically explains the definitions of angle, or uses a protractor to show what is being measured referring to angle magnitude. Unfortunately, the students interpreted this knowledge in so many different ways and a traditional teaching
approach couldn t help us to gain a better understanding about how the students learnt the concepts (Keiser, 2004; Mitchelmore and White, 2000; Devichi and Munier, 2013).
Keiser (2004) claimed that this approach allowed the concept to be introduced quickly
but it robbed students opportunities to experience angles that could help them to be more flexible on this area. Telling the definitions to the students is a typical approach in a traditional mathematics classroom, which Mitchelmore and White (2000) confirmed by stating that the definitions of angle are unlikely to help the young students. In addition to that, Devichi and Munier (2013) stated that production tasks are relevant
to identify pupils representations of the concept of angle. (owever, these tasks are
rarely proposed in the traditional mathematics classroom, which is mainly based on reproduction and comparison tasks.
Mitchelmore, 1997). For example, Keiser (2004) in his study found many students thought that a sharper angle was the larger angle in turning contexts, some thought that the longer the rays the greater the measure of the angle was, others thought that the more space between the rays the larger the angle was, and some really struggled to adapt their concept image for angle so that it could include specifically the 0°, 180° and 360° angles. In addition to that, a study conducted by Mitchelmore and White (2000) revealed an interesting finding that even with a contextual classroom environment there is still a significant proportion of students who could not make the connection between the angles concepts.
Those studies stressed their attention on how young students perceived the definitions of angle related to the presented angles situations such as intersection, corner, bend, slope, turn, and rotation. Some contexts may produce the intended outcomes but others
may not, depend on many external factors. An example from Mitchelmore s study about
children s informal knowledge of physical angle situations found that some
specific features of each angle situation strongly hindered recognition of the common features which defined the angle concept (e.g. in turns context, and size of small angles involve the fraction concept). Of course we cannot be absolutely sure about which angle situations that can be employed to create the best learning environment for the students. Nonetheless, we still can carefully choose and calibrate the angle situations that can provide the students with a meaningful learning environment and give them the opportunity to gain the intended knowledge.
It seems that we lack of studies that focus on how students comprehended the concept of angle magnitude, especially in the secondary level. Devichi and Munier (2013) suggested that it would be interesting to analyze the link between the type of angle produced and the ability to change its size in countries where the right angle, the other angles, and the measurement of angles are introduced simultaneously. This study conducted in Indonesia, where these concepts was introduced simultaneously as it is clear from the national curriculum and the standard mathematical text books that have been used recently.
The purposes of the present paper are to investigate how seventh-grade students grasp the sense of angle magnitude, and comprehend some important concepts of angles. We also want to contribute to mathematics education literature by providing ideas in teaching and learning geometry, in particular about angle magnitude for the secondary school level.Therefore, our intentions in this study can be condensed into a general angle is a difficult task due to all definitions have their own limitations in describing the concept by emphasizing one aspect more heavily than others (Keiser, 2004). The teacher may have several definitions of angle at hand before s/he enters the classroom, in order
interpretation of Euclid and one definition from Hilbert. However, it is not favorable for this study to analyze the nine interpretations in order to investigate how seventh
graders perceive the angle and its magnitude. Therefore, we use Schotten s classification
of the definitions that concentrate mostly on three particular classes of definitions of this concept: angle as the portion of a plane included in between two rays in the plane which meet in a point, angle as the difference of direction between two rays, and angle as the amount of turn/rotation between two rays (Schotten, 1893, pp. 94–183; cited by Dimitric, 2012).
Promoting learning about angles
It was obvious that several studies on this area utilized the power of contexts to create a
meaningful learning environment to promote students learning about angle.
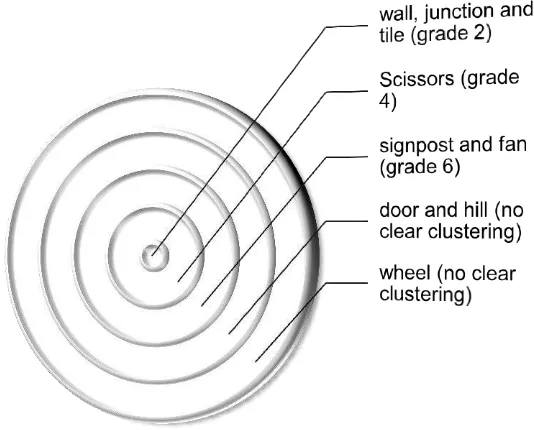
Mitchelmore and White (2000) for example utilized real world objects that were commonly associated with or had strong relations with the attribute of angles, such as: a wheel, door, scissors, fan, signpost, hill, junction, tile and wall. Their study revealed that there was a hierarchical relationship between students recognition of angles and their
grade level as was shown in figure . Furthermore, they claimed that the students
conception of angle developed from a physical angle domain and grew steadily to be more abstract concepts of angle.
Figure 1.The hierarchical of students' recognition of angle
Munier and Merle (2009, p. 1889-1891) investigated how their designed teaching
sequence supported students understanding about the concepts of angle. They
employed three learning contexts; a mirror, compass, and visual field. In the mirror sequence, the students had to determine which of three objects would be lit up by a
reflected ray from a mirror that was put in a random orientation. )n the compass
not given a diagram. They had to state whether the hidden area would get bigger, smaller, or stay the same when the distance between the child and the screen changed, or when the screen was made wider. They found that the visual field sequence which brought out the sector conception of the angle was beneficial to third-grade students. However, the mirror and compass sequence appear to be more complex, which suggests
that they might be more suitable for students in grade or . Similar to Munier s and Merle s study, Bustang used visual field activities to promote students learning
about angle in grade 3. In his study, he found that the activities made the concept of angles meaningful for students and it was breakaway from the conventional teaching method that did not allow students to experience physical situations.
Fyhn (2008) studied students in a higher grade level (grade 7) in recognizing the largest and smallest angles via an indoor climbing activity. She gave three examples of how the students mathematized the climbing activity into the concept of angle; the students could recognize the angles even with only one visible side, could recognize the acute angles, and could recognize the dynamic aspect of angles.
The findings in those studies converge to explain the power of contexts in teaching and learning about angles. The use of contexts and a meaningful learning environment has been used in Realistic Mathematics Education (RME) for decades. The use of contexts in the teaching and learning process plays an important role in successful learning outcomes. In order to explain and investigate how the lesson sequence developed in this study helps the students to understand the angle and its magnitude, we use the domain specific instructional theory on the teaching and learning of RME as a heuristic approach. Here we apply the five characteristics of RME that Treffers (1987) described as a framework of thinking about the process of designing the learning sequence. The five characteristics are; the use of context, model, students own productions and constructions, interactivity, and intertwinement of various learning strands.
METHOD
Research approach
In general we can say the aim of this study is to develop a local instructional theory to
support students comprehension about angle magnitude in grade seven. In the development process, we iteratively calibrate the materials to make it fit with practices. By iterative calibrating, we want to make sure those materials can be used in more general educational practices. Therefore, in this study, design research is employed as the appropriate research approach to achieve the aim. Barab and Squire (2004; cited by
van den Akker, et al., defined a design research approach as a series of
approaches, with the intent of producing new theories, artifacts, and practices that
account for and potentially impact learning and teaching in naturalistic settings . Design
Data collection and analysis
Three Indonesian seventh grade classes participated in this study. The students who involved in this study could be categorized as average learners based their performances during the test, the interviews, and their teacher s assessment. The collected data include video recording from the whole teaching experiments, student work, field notes, and interview with students. We have identified the similarity of
students reactions in the teaching experiments. In the following section, we highlight the most representative observations that we observed during the actual teaching experiments.
The lesson
The aim of the lesson is to support students reasoning about angles similarity that formed by a straight line that falling across two parallel lines (parallel-transversal situation). In the first task, the students should make a poster of upper case letters using matchsticks. The aim of this activity is to give the students a hand on experience in constructing the angles with various magnitudes. The students performed well during the activity. They could easily reconstruct the upper case letters without hesitations. In the follow-up activity of the first task, the students should decide which letter in their reconstruction that has the smallest angle. The students came up with different solutions such as, A, V, W, N, and M. The following fragment from the classroom discussion reveals how students reason about the angle magnitude to explain the similarity between angles.
[1]Researcher: Okay, between V and A Reconstruct the letters according to the students constructions; V with 4 sticks and A with 3 sticks) How we
compare the sizes of these angles?
After few moments of thought, Giga came up with a strategy. He removed two sticks
from the very ends of the V s arms and put one of the stick to turn the letter V into an
inverted letter A. He managed to convince their fellow students that the angles on letters V and A were in the same magnitude.
[2]Researcher: Now we agree that the angles on A and V have the same
magnitude. (ow about the letters W, N, and M?
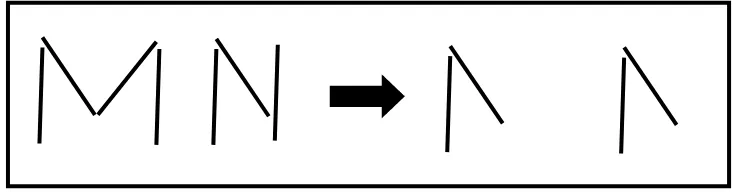
[3]Abell: N and M are equal
[4]Rafli: W and M are the same, because W is the upside down version of M. [6]Researcher: But first, how you compare N and M? Rearrange the sticks into
the letters according to the students’ construction
Abell used the similar strategy to show the angles are in the same size, he removed two sticks from M and one stick from N to make both letters appear in the same shape (see figure 4).
The students gave different answers related to which letter that had the biggest angle. In the discussion the students agreed that the biggest angle and the smallest angle had to be in the same figure (N), if they took into account the reflex angles. It was evidence that, the students have grasped the concept of reflex angles at this point.
In the second task, we asked the students to observe the angle magnitudes in several
letters that had parallel sticks. Students written works and their verbal explanations suggested that the students could easily give an explanation about angles similarity when 90° angles were involved (E, F, H, and U) and used acute angle (sharpness/opening) as a benchmark in their attempts to explain the similarity when there wasn t right-angle involved (N and Z). The students were able to reason using their existing knowledge in the attempt to show the similar angles in the letter Z. They argued that, they could reshape the letter Z into a diamond shape in order to make clear the similar angles (see figure 5 . The students reasons were based on the fact that the opposite angles in a parallelogram are in the same size.
CONCLUSION
The central question of this study is how we support seventh-grade students to comprehend the magnitude of angles through reasoning activities. Here, we showed how the designed activities could stimulate students to reason about important aspects of angle and its magnitude. After a summary of the results, we discuss limitation of this study and suggestions for further study.
In the teaching experiments, students constructed the upper case letters using matchsticks and reasoned about the angles magnitudes in those letters. The word opening appeared when students argued about how they selected the letters that have
the smallest and the biggest angles. At first, students didn t take into account the reflex
angles of the letters that they chose. In the classroom discussion, students reconsidered their selections and claimed that the biggest and the smallest angles in this context had to be in a same letter. This showed how students grasp the concept of reflex angle by seeing an angle figure as representation of two angles. We claimed that letting students investigate the angles in the letters that have parallel sticks could support their comprehension about angle similarity. In the simple situation where the letters only have right-angles on them (e.g. E, F, H, U, etc.), the students found it easier to explain
about the similarity. For the letters that don t have the right-angle on them (e.g. N, M, S and Z), most of the students were still able to indicate the similar angles in those letters. Students also tried to show that the corresponding angles in those letters are in the same magnitude, by applying reshaping and comparing the opening strategies. The actual teaching and learning activities in this lesson, suggest that the situation allowed the students to infer the similarity between angles on a parallel-transversal situation.
According to the expositions above, we can conclude that, the design lesson can help students to understand the definitions of angle, grasp the sense of angle magnitude, and comprehend the important concepts of angles. The results of this study also suggest that the use of contextual problems/situations plays a crucial role in the process of knowledge acquisition. Based on our findings, the use of contextual problems/situations in the teaching and learning process provided students with ground for thinking and prepared them for the advancement of knowledge. In addition to that, we also found that
students own ideas in the learning process have an important contribution to the students development. (owever, to generate a learning process that based on students
own ideas, extensive discussion and communication during the learning process are needed.
involved in this study had less time to study the design before she performed the teaching experiment (second cycle). It might be because of the time limitation for the teacher to study the design. She reported that the presented problems in the design were too difficult for her students. She also found it difficult to orchestrate the classroom discussions, especially a discussion that discussed about a problem that had no unique solution. Therefore, another question for further research is how we can help the teacher to successfully teach this topic.
REFERENCES
Devichi, C., &Munier, V. (2013). About the concept of angle in elementary school: Misconceptions and teaching sequences. The Journal of Mathematical Behavior, 32(1), 1-19.
Dimitric, R. M. (2012). On angles and angle measurements.The Teaching of Mathematics, 15(2), 133-140.
Fyhn, A. B. . A climbing class reinvention of angles.Educational Studies in Mathematics, 67(1), 19-35.
Gravemeijer, K. (2004). Local Instruction Theories as Means of Support for Teachers in Reform Mathematics Education. Mathematical Thinking and Learning, 6(2), 105-128.
Keiser, J. M. (2004). Struggles with developing the concept of angle: comparing
sixth-grade students discourse to the history of the angle concept. Mathematical Thinking and Learning, 6 (3), 285-306.
Mitchelmore, M. (1997).Children s informal knowledge of physical angle situations.Learning and Instruction, 7(1), 1-19.
Mitchelmore, M. & White, P. (1998). Development of angle concepts: a framework for research. Mathematics Educational Research Journal, 10 (3), 4-27.
Mitchelmore, M. & White, P. (2000).Development of angle concepts by progressive abstraction and generalization.Educational Studies in Mathematics, 41, 209 -238.
Munier, V. & Merle, H. (2009). Interdisciplinary mathematics-physics approaches to teaching the concept of angle in elementary school. International Journal of Science Education, 31 (14), 1857-1895.
Sbaragli, S., &Santi, G. .Teacher s choices as the cause of misconceptions in the
learning of the concept of angle.JornalInternacional de EstudosemEducaçãoMatemática, 4(2).
Treffers, A. (1987). Three Dimensions. A Model of Goal and Theory Description in Mathematics Instruction the Wiskobas Project. Dordrecht: Reidel Publishing Company.
Van den Akker, J., Gravemeijer, K., McKenney, S., &Nieveen, N. (2006).Introducing educational design research.Educational design research, 3-7.