Penyelesaian persamaan panas satu dan dua dimensi dengan menggunakan metode Beda Hingga

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. PENYELESAIAN PERSAMAAN PANAS SATU DAN DUA DIMENSI DENGAN MENGGUNAKAN METODE BEDA HINGGA. Tugas Akhir. Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika. Oleh: Fransisca Amelia Putri Karina NIM: 133114015. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS SANATA DHARMA YOGYAKARTA 2018.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. SOLUTION OF ONE AND TWO-DIMENSIONAL HEAT EQUATIONS USING FINITE DIFFERENCE METHODS. Final Paper. Presented as Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Sains Mathematics Study Program. Written by: Fransisca Amelia Putri Karina Student ID: 133114015. MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY SANATA DHARMA UNIVERSITY 2018. ii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. I'UGAS AKHIR. PENYELESAIAN PERSAIIAAFI IIANAS SATti Drll{ D[iA DIh,{trNSI SE. NGAI{ Mf,. }l G G UNAfufu\*. }{ETOD E BEDA HI}{G GA. Oleh: Fransisca Ainelia Putri Kar"ina. Ntrh{: I33l I4015. /,. -+* re oeynKof$Y. 1tslp. iii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. TUGAS AKHIR. PE. T'I. Y E T,ESA IA |t.i PE R SA. DENGAN. &TE s{CG. N.,I. AA. i\ PA]!\IAS SATLJ DATq DTIA DIIIIII,NS I. [-]I{A}CAI{ EIET'ODE BEDA T{IF{ GGA. Dipersiapkan dan ditulis oieh: Fransisca Arnelia Putri Karina. NIM:. 133114015. Telah dipertahankan di depan Panitia Penguji pada. tanggal. 4. Oktotrer 2018. dan dinyatakan memeftrhi syarat. Susunan Paititia Penguji. Nama Lengkap. Ketua : Sekretaris. :. Ir. Petrus Kanisius Fui'rvadi, M.l'. Lli*tono, Ph.D. ,. Anggota. :. Sucli Mungkasi. S.Si.. M.N{atli Sc.,. Yog3,'akarta,4f .OnoU*r 20 I. {,/. I. Irakultas Sailrs dan 'Ileknoiogi. ilniversitas Sanata Dhanna l)ekan,. ,044S.Si." M.Matli,Sc.. Ph D.). iv. ,/.,. a Ph.D. i ":1-1 .f;.jtt*-:.*&..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. HALAMAN PERSEMBAHAN. “Janganlah hendaknya kamu kuatir tentang apapun juga, tetapi nyatakanlah dalam segala hal keinginanmu kepada Allah dalam doa dan permohonan dengan ucapan syukur (Filipi 4:6)”. Karya ini kupersembahkan kepada Tuhan Yesus Kristus yang senantiasa menyertai dan memberi kekuatan, kedua orang tua tercinta dan adik-adik tersayang.. v.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. ABSTRAK Panas merupakan salah satu elemen penting yang terdapat dalam dunia ini. Energi panas dapat berpindah-pindah apabila di dalam suatu media terdapat perbedaan suhu. Pada tugas akhir ini akan dibahas tentang proses perpindahan panas pada penampang satu dimensi dan dua dimensi. Dalam penelitian ini objek yang akan diteliti adalah penampang batang homogen untuk permasalahan satu dimensi dan penampang lempeng persegi homogen untuk permasalahan dua dimensi. Tujuan dari penelitian dan penulisan tugas akhir ini adalah menghitung distribusi suhu pada penampang batang homogen satu dimensi dan menghitung distribusi suhu pada penampang lempeng persegi homogen dua dimensi. Dalam perhitungan distribusi suhu akan melibatkan persamaan diferensial parsial. Teknik yang akan dipakai untuk menyelesaikan persamaan diferensial parsial adalah metode numerik. Konduksi panas pada penampang batang homogen dan lempeng persegi telah ditentukan oleh persamaan panas satu dimensi dan dua dimensi. Secara matematis, kedua persamaan tersebut merupakan persamaan diferensial parsial parabolik. Kedua persamaan tersebut akan diselesaikan dengan menggunakan pendekatan metode beda hingga skema eksplisit. Perhitungan distribusi suhu dilakukan dengan menentukan nilai-nilai syarat awal dan syarat batas. Selanjutnya, perhitungan distribusi suhu tersebut akan disimulasikan menggunakan program MATLAB, dengan demikian akan diperoleh hasil dan kesimpulan.. Kata kunci: persamaan panas, metode beda hingga, penampang batang homogen, penampang lempeng persegi.. vi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. ABSTRACT Heat is one of the important elements found in this world. Heat energy can move around if there is a temperature difference in a medium. In this final project, the process of heat transfer in one-dimensional and two-dimensional cross sections will be discussed. In this research, the object to be studied is a homogeneous cross section for one-dimensional problems and a homogeneous square plate section for two-dimensional problems. The purpose of this research and final project is to calculate the temperature distribution on a one-dimensional homogeneous cross section and calculate the temperature distribution on a twodimensional homogeneous square plate cross section. The calculation of temperature distribution will involve partial differential equations. The technique that will be used to solve partial differential equations is numerical method. Heat conduction in a homogeneous cross section and square plate has been determined by one-dimensional and two-dimensional heat equations. Mathematically, the two equations are parabolic partial differential equations. Both of these equations will be solved using the explicit finite difference method. Calculation of temperature distribution will be done by determining the values of the initial conditions and boundary conditions. Furthermore, the calculation of temperature distribution will be simulated using the MATLAB program, thus results and conclusions will be obtained.. Keywords: heat equation, finite difference method, homogeneous cross section, square plate cross section.. vii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. PERNYATAAI\ KEASLIAN KARYA Saya rnenyatakan dengan sesunggulmya. bahu,a tugas akhir yang saya. tulis ini. ticlak rlernuat karya atau bagian karya orang lain. kecuali yang disebutkan dalarn. Daftar Pustaka, sebagairnana layaknya karya ilrniah. Yogyakalta, .-8.. o*,ooer 2018. Fransisca Amelia Putri Karina. viii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. PERNYATAAN PERSETUJ UAN. PUBLIKASI KAIIYA ILNIIAH UNTUK KEPENTINGAN AKADENTIS. Yang bertanda tangan di barveh ini. saya nrahasiswa Universitas Sanata Dhaltna:. Nama. : Fransisca Amelia Putri Kalina. NIM. :13311-+015. Demi pengernbangan ilmu pcngetahuan. saya rnembet'ikan kepada Petpustakaan Universitas Sanata Dharma karya. ilniah. saya yang ber-judul:. PENYELESAIAN PERSAMAAN PANAS SATU DAN DUA DIN,IENSI DENGAN MENGGUNAI(AN NIETODE BEDA HINGGA beserta perangkat yang diperlukan (bila ada). Dengan dernikian. saya memberikan. kepada Perpustakaan Universitas Sanata Dharma untuk tnenyimpan, urengalihkan. ke clalam bentuk. rneclia lain, mengelolanya dalam bentuk pangkalan data,. mendistribusikan sccara terbatas dan mempublikasikannya cli Internet atau meclia. lain untuk kepentingan akadernis tanpa perlu meminta ijin dari saya traupun memberikan royalti kepacla saya selarna tetap mencantumkan nalna saya sebagai penulis.. Demikian pernyataan ini saya buat clengan sebenarnya.. Dibuat di Yogyakarta Pada tanggaf ,. ... 8. ..Oktober 201 8. Yang menyatakan,. Fransisca Amelia Putri Karina. ix.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. KATA PENGANTAR. Puji dan syukur kepada Tuhan Yesus Kristus, atas berkat dan rahmat melimpah yang selalu diberikan kepada penulis sehingga penulis dapat menyelesaikan tugas akhir ini. Tugas akhir ini disusun sebagai salah satu syarat untuk mendapatkan gelar Sarjana Sains dari Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma, Yogyakarta. Dalam penulisan tugas akhir ini, banyak rintangan yang penulis hadapi. Namun demikian, dengan penyertaan Tuhan dan dukungan yang diberikan dari berbagai pihak pada akhirnya tugas akhir ini dapat diselesaikan. Oleh karena itu, penulis ingin mengucapkan terima kasih kepada: 1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D. selaku Dekan Fakultas Sains dan Teknologi sekaligus dosen pembimbing, 2. Bapak YG. Hartono, S.Sc., M.Sc., Ph.D. selaku Ketua Program Studi Matematika, Universitas Sanata Dharma, 3. Ibu M. V. Any Herawati, S.Si., M.Si., selaku Dosen Pembimbing Akademik, 4. Romo Prof. Dr. Frans Susilo, SJ., Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., Bapak Dr. rer. nat. Herry P. Suryawan, S.Si., M.Si. selaku dosen Program Studi Matematika yang telah memberikan ilmu-ilmu yang sangat berguna dalam penulisan tugas akhir ini, 5. kedua orang tua tercinta (Ignatius Triatmoko Ari Handoko dan Emiliana Sriningsih) dan kedua adik tercinta (Cicilia Afira Putri Karina dan Aloysius Andrian Herlambang H), 6. teman-teman tercinta, mahasiswa/i Program Studi Matematika angkatan 2013 yang selalu kompak dan mendukung satu sama lain, Novita Tania, S.Si. dan Ni Luh Putu Stephanie S.Psi. yang selalu memberikan semangat tiada henti, 7. Benediktus Romario Anugerah Agung Gumelar atas dukungan dan kesabarannya yang sangat luar biasa, 8. keluarga besar Alexander Triyanto dan keluarga besar Hadisusanto, atas doa dan semangatnya, serta. x.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. 9.. seu-rua. pihak yang ticlak dapiit disebutkan satu persatu.. Semoga segala bentuk dukungan. bantuan, clan perhatian .vang telah diberikan ntendapat balasan dari Tr-Lhan Yesus Kristus. Penulis tnenyadari bahr,r,a tugas akhir. ini masih. ktitik. ban-vak. rnemiliki kekurangan. Oleh kiirena itu. penulis mengharapkan. clan saran demi rnenyempurnakair tugas akhir. ini.. Scn"roga tugas. akhir ini. clapat berrnanlaat bagi para pernbaca.. Yogyakarta, ..3... oktober 2018 Penulis. Frarilsisca. xi. Amelia. Karina.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR ISI. HALAMAN JUDUL .................................................................................................... i HALAMAN JUDUL DALAM BAHASA INGGRIS ................................................. ii HALAMAN PERSETUJUAN PEMBIMBING ......................................................... iii HALAMAN PENGESAHAN .................................................................................... iv HALAMAN PERSEMBAHAN .................................................................................. v ABSTRAK .................................................................................................................. vi ABSTRACT ............................................................................................................... vii PERNYATAAN KEASLIAN KARYA ................................................................... viii LEMBAR PERNYATAAN PERSETUJUAN ........................................................... ix PERSETUJUAN PUBLIKASI KARYA ILMIAH .................................................... ix KATA PENGANTAR ................................................................................................. x DAFTAR ISI.............................................................................................................. xii DAFTAR GAMBAR ................................................................................................ xiv BAB I PENDAHULUAN ............................................................................................ 1 A. Latar Belakang .................................................................................................... 1 B. Rumusan Masalah ............................................................................................... 2 C. Batasan Masalah .................................................................................................. 2 D. Tujuan Penulisan ................................................................................................. 2 E. Metode Penulisan ................................................................................................ 2 F. Manfaat Penulisan ............................................................................................... 3 G. Sistematika Penulisan .......................................................................................... 3. xii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB II FUNGSI, TURUNAN, DAN INTEGRAL ..................................................... 5 A. Turunan Fungsi .................................................................................................... 5 B. Persamaan Diferensial ......................................................................................... 6 C. Pendekatan Numeris untuk Penyelesaian Persamaan Diferensial ....................... 8 D. Integral ............................................................................................................... 19 BAB III METODE NUMERIS UNTUK PERSAMAAN PANAS SATU DIMENSI ............................................................................................................................... 22 A. Penurunan Persamaan Panas ............................................................................. 22 B. Metode Beda Hingga untuk Persamaan Panas Satu Dimensi ........................... 25 C. Skema Eksplisit Persamaan Panas Satu Dimensi .............................................. 27 BAB IV METODE NUMERIS UNTUK PERSAMAAN PANAS DUA DIMENSI ............................................................................................................................... 40 A. Metode Beda Hingga untuk Persamaan Panas Dua Dimensi ............................ 40 B. Skema Eksplisit Persamaan Panas Dua Dimensi .............................................. 43 C. Hasil Simulasi untuk Persamaan Panas Dua Dimensi ....................................... 46 BAB V KESIMPULAN DAN SARAN .................................................................... 48 A. Kesimpulan ........................................................................................................ 48 B. Saran .................................................................................................................. 48 DAFTAR PUSTAKA ................................................................................................ 50 LAMPIRAN ............................................................................................................... 51. xiii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR GAMBAR Gambar 2.1 Tiga pendekatan perhitungan turunan numerik ............................... 11. Gambar 3.1 Ilustrasi aliran panas dalam suatu ruang. (Sumber: Oneil,2014) ..... 22 Gambar 3.2 Kondisi suhu awal pada contoh 3.1. ................................................ 35 Gambar 3.3 Hasil simulasi dari penyelesaian contoh 3.1 dengan menggunakan metode beda hingga dimana. dan saat. detik. ...................... 35. Gambar 3.4 Kondisi suhu awal pada contoh 3.2 ................................................. 38 Gambar 3.5 Hasil simulasi dari penyelesaian contoh 3.2 dengan menggunakan metode beda hingga dimana. dan saat. detik. ...................... 39. Gambar 4.1 Hasil simulasi dari penyelesaian persamaan panas dua dimensi dengan menggunakan metode beda hingga........................................................... 47. xiv.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB I PENDAHULUAN. Dalam bab ini akan dibahas mengenai latar belakang, rumusan masalah, batasan masalah, tujuan penulisan, metode penulisan, manfaat penulisan, dan juga sistematika penulisan yang akan dilakukan pada penulisan tugas akhir ini. A. Latar Belakang Panas adalah salah satu elemen penting yang dibutuhkan dalam kehidupan manusia. Panas merupakan salah satu energi yang dapat berpindah-pindah. Perpindahan panas merupakan masalah yang kompleks, karena di dalamnya melibatkan banyak parameter. Perpindahan panas adalah ilmu yang menjelaskan tentang perpindahan energi yang bisa terjadi karena adanya perbedaan suhu di antara material. Proses perpindahan panas mengalir dari daerah yang memiliki suhu lebih tinggi ke daerah yang memiliki suhu lebih rendah. Perpindahan panas dapat terjadi dengan tiga cara, yaitu: konduksi, konveksi, dan radiasi. Konduksi adalah proses perpindahan dari daerah yang bersuhu tinggi ke daerah yang bersuhu rendah dalam satu medium (padat, cair atau gas) secara hantaran. Konveksi adalah perpidahan panas yang terjadi karena adanya aliran. Radiasi adalah proses perpindahan dari benda bersuhu tinggi ke benda yang bersuhu rendah secara pancaran. Dalam tugas akhir ini akan dibahas mengenai proses perpindahan panas. Benda yang akan dipakai untuk penelitian adalah sebuah batang homogen yang pada batas-batas dan titik-titik tertentu telah diketahui suhunya. Penelitian ini akan dilakukan untuk persamaan panas satu dimensi, yaitu. dan persamaan panas dua dimensi. (. 1. ).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 2. dengan. adalah kepadatan batang,. adalah konstanta panas spesifik pada batang,. adalah konstanta untuk konduktivitas termal batang, bebas untuk domain ruang,. adalah variabel. adalah variabel bebas untuk waktu dan. adalah fungsi yang bergantung pada bergantung pada. dan. dan , serta. adalah fungsi yang. dan .. B. Rumusan Masalah Rumusan masalah dalam tugas akhir ini adalah: 1. Bagaimana memperoleh persamaan panas satu dimensi? 2. Bagaimana menyelesaikan persamaan panas satu dimensi secara numeris dengan menggunakan metode beda hingga? 3. Bagaimana menyelesaikan persamaan panas dua dimensi secara numeris dengan menggunakan metode beda hingga?. C. Batasan Masalah Dalam tugas akhir ini akan dicari penyelesaian numeris dari persamaan panas pada dimensi satu dan dimensi dua. Model yang berdimensi lebih tinggi tidak dibahas. Penyelesaian numeris dari persamaan panas hanya menggunakan satu metode numeris yaitu metode beda hingga.. D. Tujuan Penulisan Tujuan dari penulisan tugas akhir ini adalah: 1. mencari persamaan panas satu dimensi beserta perluasannya untuk dua dimensi, 2. mencari penyelesaian numeris dari persamaan model yang didapat dengan metode beda hingga.. E. Metode Penulisan Metode penulisan yang digunakan dalam penyusunan tugas akhir ini adalah studi pustaka, yaitu dengan mempelajari buku-buku dan jurnal. Selain itu,.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 3. dilakukan juga praktik simulasi numeris dengan menggunakan program MATLAB.. F. Manfaat Penulisan Manfaat penulisan tugas akhir ini adalah penulis. mendapatkan. pengetahuan baru, dengan mengetahui bagaimana cara memperoleh persamaan panas. Dengan adanya penulisan ini, diharapkan pembaca juga dapat lebih memahami tentang masalah konduksi panas yang ada dalam dunia nyata.. G. Sistematika Penulisan Sistematika penulisan dalam tugas akhir ini adalah: BAB I PENDAHULUAN A. Latar Belakang Masalah B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Metode Penulisan F. Manfaat Penulisan G. Sistematika Penulisan. BAB II FUNGSI, TURUNAN, DAN INTEGRAL A. Turunan Fungsi B. Persamaan Diferensial C. Pendekatan Numeris untuk Penyelesaian Persamaan Diferensial D. Integral. BABIII METODE NUMERIS UNTUK PERSAMAAN PANAS SATU DIMENSI A. Penurunan Persamaan Panas B. Metode Beda Hingga untuk Persamaan Panas Satu Dimensi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 4. C. Skema Eksplisit Persamaan Panas Satu Dimensi. BAB IVMETODE NUMERIS UNTUK PERSAMAAN PANAS DUA DIMENSI A. Metode Beda Hingga untuk Persamaan Panas Dua Dimensi B. Skema Eksplisit Persamaan Panas Dua Dimensi C. Hasil Simulasi untuk Persamaan Panas Dua Dimensi. BAB V PENUTUP A. Kesimpulan B. Saran. DAFTAR PUSTAKA.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB II FUNGSI, TURUNAN, DAN INTEGRAL Dalam bab ini akan ditulis landasan teori yang akan digunakan untuk menulis tugas akhir ini. Bab ini akan terdiri dari 4 subbab, yaitu: Turunan Fungsi, Persamaan Diferensial, Pendeketan Numeris, dan Integral. A. Turunan Fungsi. Definisi 2.1 Fungsi adalah suatu relasi khusus himpunan. antara elemen-elemen dalam suatu. dengan elemen-elemen dalam himpunan . Kekhususannya terletak. dalam dua hal, yaitu: (1). Setiap elemen dalam himpunan. berelasi dengan suatu elemen. dalam himpunan . (2). Elemen dalam himpunan. himpunan. yang berelasi dengan elemen dari. itu adalah tunggal.. Definisi 2.2 Turunan fungsi. didefinisikan sebagai berikut :. Aturan Rantai Jika. dan. mempunyai turunan, maka fungsi komposisi. juga. mempunyai turunan, yaitu (. Jika. dan. ). , maka dengan notasi Leibniz,. diturunkan terhadap , yaitu. 5. dapat.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 6. B. Persamaan Diferensial. Definisi 2.3 Persamaan adalah suatu relasi yang menyatakan dua kuantitas atau besaran bernilai sama.. Contoh 2.1 (1) 5 – 3 = 1 + 1 (2). Definisi 2.4 Persamaan diferensial adalah persamaan yang melibatkan variabel-variabel tak bebas dan turunan-turunannya terhadap variabel-variabel bebas.. Contoh 2.2 Persamaan sistem pegas massa. dengan. adalah massa,. massa. Karena. tetapan pegas,. koefisien redaman, dan. posisi. adalah fungsi dari , maka persamaan diatas dapat ditulis juga. sebagai. atau dalam bentuk yang lebih ringkas lagi,.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 7. .. Definisi 2.5 Persamaan diferensial biasa adalah persamaan diferensial yang melibatkan turunan biasa beserta satu atau lebih variabel tak bebas terhadap satu variabel bebas.. Contoh2.3 (1) (2) y’ = (3). +. (4) (5). Variabel bebas untuk contoh (1) sampai (5) adalah , sedangkan peubah (variabel) terikatnya adalah , yang merupakan fungsi dari , atau ditulis sebagai. .. Definisi 2.6 Persamaan diferensial parsial adalah persamaan diferensial yang melibatkan turunan parsial dari satu atau lebih variabel tak bebas terhadap lebih dari satu variabel bebas.. Contoh 2.4 (1) (2). (yang dalam hal ini (yang dalam hal ini.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 8. Variabel bebas untuk contoh (1) adalah terikatnya adalah. dan. yang merupakan fungsi dari. , sedangkan peubah (variabel) dan. , atau ditulis sebagai. . Sedangkan peubah bebas untuk contoh (2) adalah. ,. , dan ,. sedangkan peubah terikatnya adalah , yang merupakan fungsi dari , , dan , atau ditulis sebagai. .. Persamaan diferensial parsial diklarifikasikan menjadi tiga jenis, yaitu eliptik, hiperbolik dan parabolik. Diketahui persamaan diferensial parsial orde dua, sebagai berikut:. dimana. Persamaan diferensial parsial tersebut dikatakan:  eliptik jika  hiperbolik jika  parabolik jika. .. C. Pendekatan Numeris untuk Penyelesaian Persamaan Diferensial. Definisi 2.7 Andaikan [. ] Misalkan. [. ],. dan semua turunannya [. ], maka untuk nilai-nilai. , kontinu di dalam selang disekitar. dan. dapat dijabarkan (diekspansi) ke dalam deret Taylor:. .. Contoh 2.5 Tentukan ekspansi fungsi. =. ke dalam deret Taylor di sekitar. =1.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 9. Penyelesaian: Tentukan turunan =. terlebih dahulu sebagai berikut:. ,. =. ,. =. ,. = =. , ,. dan seterusnya.. Berdasarkan Definisi 2.3,. Bila dimisalkan. dihampiri dengan deret Taylor sebagai berikut:. = , maka. .. Penurunan Numeris dengan Menggunakan Tiga Jenis Hampiran. Dipandang fungsi. . Akan ditentukan hampiran untuk turunan. fungsi tersebut menggunakan hampiran beda maju, beda mundur, dan beda pusat.. 1. Hampiran Beda Maju Menggunakan beda maju, turunan. terhadap variabel. didefinisikan oleh.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 10. atau untuk. tertentu,. .. 2. Hampiran Beda Mundur Menggunakan beda mundur, turunan. terhadap variabel. didefinisikan. oleh. atau untuk. tertentu,. .. 3. Hampiran Beda Pusat Menggunakan beda pusat, turunan. atau untuk. terhadap variabel. didefinisikan oleh. tertentu,. . Tafsiran geometri dari ketiga jenis hampiran diatas diperlihatkan pada Gambar 2.1..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 11. 𝑦. 𝑦. 𝑦 𝑦 𝑦 𝑦. 𝑓 𝑥. 𝑦. 𝑓 𝑥. 𝑦. 𝑥. 𝑥. 𝑥. 𝑥. 𝑥. 𝑥. (a). 𝑥. (b). 𝑦 𝑦. 𝑦. 𝑓 𝑥. 𝑦. 𝑥. 𝑥. 𝑥. 𝑥. (c). Gambar 2.1 (a) Hampiran beda maju. (b) Hampiran beda mundur. (c) Hampiran beda pusat.. Penurunan Rumus Turunan dengan Deret Taylor Misalkan diberikan titik-titik. yang dalam hal ini. 𝑥.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 12. dan. kemudian akan dihitung. yang dalam hal ini. dengan. ketiga pendekatan yang telah disebutkan sebelumnya (maju, mundur, pusat).. 1. Hampiran Beda Maju Uraikan. di sekitar. :. (2.3). yang dalam hal ini, Untuk nilai-nilai. di. dan. persamaan rumusnya menjadi : (2.4). yang dalam hal ini. ..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 13. 2. Hampiran Beda Mundur Uraikan. di sekitar. :. (2.5). yang dalam hal ini, Untuk nilai-nilai. di. dan. persamaan rumusnya menjadi : (2.6). yang dalam hal ini. .. 3. Hampiran Beda Pusat Kurangkan persamaan (2.3) dan persamaan (2.5) :.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 14. yang dalam hal ini, Untuk nilai-nilai. di. dan. persamaan rumusnya menjadi :. (2.7). yang dalam hal ini. Menentukan Orde Galat. Pada penurunan rumus turunan numerik dengan deret Taylor, rumus galat dalam penurunan rumus turunan numerik dapat langsung diperoleh. Tetapi dengan polinom interpolasi harus dicari rumus galat tersebut dengan bantuan deret Taylor.. Contoh 2.6 Tentukan rumus galat dan orde dari rumus turunan numeris hampiran beda pusat:. Nyatakan. (galat) sebagai ruas kiri persamaan, lalu ekspansi ruas kanan dengan. deret Taylor di sekitar. :.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 15. *(. ) (. )+. (. ). (2.8). Jadi, hampiran beda pusat memiliki galat. , dengan. orde. Teorema 2.1 (Teorema Sisa) Jika. [. kontinu pada [. (i) ( ii ) [. ] dan fungsi. [. ]. memenuhi syarat – syarat:. ] ada untuk setiap. ] ada titik. yang terletak di antara. dan. [. ], maka untuk setiap. sehingga. (2.9).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 16. atau dapat disingkat menjadi. dimana. dan. disebut polinomial Taylor dan. disebut sisa, nilai koreksi atau kesalahan. Taylor. Bukti dari teorema sisa deret Taylor dapat dilihat pada buku karangan Darmawijaya (2011).. Teorema 2.2 (Deret Taylor) [. Jika. ] dan fungsi. ( i ) Fungsi. kontinu pada [. ( ii ). ada,. [. [. ]. memenuhi sifat – sifat:. ] ]. maka untuk nilai – nilai. dapat diperluas ke dalam deret Taylor:. [ Jika di misalkan. maka. ]. dapat juga ditulis sebagai. [. ]. di sekitar.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 17. Deret di dalam teorema (2.5) tersebut dinamakan deret Taylor fungsi titik. di sekitar. disebut deret Maclaurin, yaitu. [. ]. Contoh 2.7 Deretkan fungsi. ke dalam deret Taylor di sekitar titik. Penyelesaian: Tentukan turunan. terlebih dahulu sebagai berikut. oleh karena itu. Jika dimisalkan. , maka. Contoh 2.8 Deretkan masing-masing fungsi. dan. ke dalam deret Maclaurin. Penyelesaian: a) Beberapa turunan adalah. sudah dihitung pada contoh 2.9. Deret Maclaurin dari.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 18. b) Untuk menentukan deret Maclaurin dari turunan. , kita harus menentukan. terlebih dahulu sebagai berikut:. maka diperoleh. Sehingga deret Maclaurin dari. adalah. c) Untuk menentukan deret Maclaurin dari dari. , tentukan terlebih dahulu turunan. sebagai berikut:. sehingga deret Maclaurin dari. adalah.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 19. ∑. D. Integral. Definisi 2.8 Fungsi. disebut suatu anti turunan dari. semua. dalam .. pada interval jika. untuk. Contoh 2.9 Sebagai contoh definisi di atas, misalkan . Jadi, jika dikatakan bahwa. , maka. fungsi yang didefinisikan oleh. merupakan turunan dari , dan. Anti turunan dinotasikan dengan. , maka. adalah anti turunan dari .. sebagaimana digunakan oleh. Leibniz, kita seringkali akan memakai istilah integral tak tentu sebagai ganti anti turunan (Purcell, 1981).. Contoh 2.10 Cari anti turunan dari. Penyelesaian:. ∫. 1. Integral Tentu Untuk menghitung luas di bawah kurva aproksimasi,. yaitu. dengan. membagi. interval. , dapat dilakukan dengan [. ]. oleh. partisi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 20. ke dalam. subinterval yaitu [. ][. ]. Panjang subinterval interval ke- ditulis dengan dipilih sebarang. dari [. ][. ]. [. [. ]. Selanjutnya ]dengan. . Total. luas di bawah kurva dapat dihitung dengan ∑ interval [. yang disebut jumlahan Riemann fungsi. ], sebagai pendekatan luas daerah di bawah kurva. atas sumbu. pada dan di. . Semakin banyak subinterval seragam yang diguanakn artinya. , maka semakin baik pula aproksimasi luasan tersebut dan semakin dekat dengan. luasan. yang. sebenarnya.. Dengan. demikian,. luas. daerah. =. ∑. Definisi 2.9 Misalkan. suatu fungsi yang didefinisikan pada selang tertutup [. ]. Jika. ∑ Ada, maka nilai limit tersebut dinamakan integral tentu. dari. ke , dan ditulis. sebagai ∫. ∑. 2. Teorema Dasar Kalkulus. Teorema 2.3(Teorema Nilai Rata-Rata). Jika suatu fungsi. kontinu pada interval [. sehingga ∫. ] maka ada µ di antara. dan.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 21. ∫. Teorema 2.4 (Teorema Dasar Kalkulus I). Jika. suatu fungsi yang kontinu pada selang tertutup [. ], maka fungsi. yang ditentukan oleh ∫ dapat diturunkan pada [. ] dan merupakan suatu antiturunan , artinya ∫. [. ]. Teorema 2.5 (Teorema Dasar Kalkulus II). Jika suatu fungsi anti turunan. yang kontinu pada selang tertutup [. khusus, sehingga. ] dan. suatu. , maka. ∫ Ketiga teorema diatas telah di buktikan dan dapat dilihat pada buku karangan Thomas (2010)..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB III METODE NUMERIS UNTUK PERSAMAAN PANAS SATU DIMENSI Dalam bab ini akan dibahas mengenai metode numeris untuk persamaan panas satu dimensi. Subbab yang ada dalam bab ini, yaitu: Penurunan Persamaan Panas, Metode Beda Hingga untuk Persamaan Panas Satu Dimensi, dan Skema Eksplisit Persamaan Panas Satu Dimensi. A. Penurunan Persamaan Panas. Persamaan panas disebut juga sebagai persamaan difusi.Persamaan panas bisa didapatkan dengan merumuskan persamaan aliran panas. Aliran panas diilustrasikan pada Gambar 3.1.. Gambar 3.1 Ilustrasi aliran panas dalam suatu ruang. (Sumber: Oneil,2014) Sebuah batang dengan massa jenis konstan, yaitu . Memiliki penampang seragam dengan area A. Permukaan lateral dari batang tersebut terisolasi, jadi tidak ada panas yang keluar di seluruh permukaan ini. Letakkan sumbu sepanjang. , pada batang dan asumsikan bahwa pada waktu yang diberikan,. suhunya sama sepanjang setiap penampang yang tegak lurus dengan sumbu , walaupun mungkin bervariasi dari satu penampang ke penampang lain. Akan diturunkan persamaan untuk. , suhu pada penampang dari batang pada ,. pada waktu . Dalam konteks difusi, Misal. disebut fungsi distribusi densitas.. adalah konstanta panas spesifik pada material batang, yang. menyatakan berapa jumlah energi panas yang dibutuhkan untuk satuan unit massa suatu benda dalam menaikkan suhu 1 derajat pada batang. Ruas batang antara dan. mempunyai massa. . Jika suhunya akan dinaikkan dari 22. ke.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 23. , maka energi yang diperlukan sebanyak. . Jadi total energi. yang terbutuhkan adalah ∫. .. Jumlah energi panas dalam ruas pada waktu dapat meningkat dengan dua cara: energi panas mengalir ke dalam segmen sampai ujung batang (hal ini mengubah fluks dari energi) dan atau ada sumber energi panas lain dalam ruas batang. Tingkat perubahan dari suhu dalam ruas terhadap waktu adalah Fluks=. ∫. .. Asumsikan untuk saat ini tidak ada sumber atau energi yang hilang dalam batang, maka (3.1). Fluks =∫. Sekarang misalkan. adalah jumlah dari energi panas per-satuan. daerah yang mengalir melintasi penampang melintang pada arah. pada waktu , ke. yang meningkat. Maka fluks dari energi ke dalam ruas antara. pada waktu. dan. adalah tingkat aliran ke dalam ruas melintasi daerah pada. dikurangi tingkat dari aliran keluar ruas melintasi daerah pada. ,. (Gambar. 3.1). Sehingga didapatkan Fluks = atau dapat ditulis sebagai berikut Fluks=. .. (3.2). Sekarang ingat kembali hukum pendingin Newton, yang menyatakan bahwa energi panas mengalir dari daerah yang lebih hangat ke daerah yang lebih dingin dan banyak energi panas berbanding dengan perbedaan suhu di antara kedua titik. Hal ini berarti.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 24. Konstanta positif dari. disebut juga konduktivitas panas dari batang. Tanda. negatif pada persamaan ini berdasarkan fakta bahwa energi mengalir dari ruas yang lebih hangat ke ruas yang lebih dingin. Substitusi. ke dalam. persamaan (3.2) untuk memperoleh Fluks =. (. ). Tulis persamaan di atas sebagai Fluks =∫. (. ). (3.3). .. Dari persamaan (3.1) dan (3.3) untuk fluks, didapat. ∫. ∫. (. ). Ruas kanan pindah ke ruas kiri, sehingga didapat. ∫. ∫. (. ). Selanjutnya konstanta yang sama dikeluarkan ∫. [. Bagi persamaan di atas dengan ∫. (. )]. dan tulis persamaan tersebut sebagai. [. (. (. )]. ).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 25. dimana. merupakan koefisien difusi.. B. Metode Beda Hingga untuk Persamaan Panas Satu Dimensi. Dalam mencari solusi suatu persamaan diferensial parsial, metode yang sering digunakan adalah metode beda hingga. Hal ini disebabkan mudahnya mendekati persamaan diferensial parsial dengan pendekatan deret Taylor-nya dan diperoleh persamaan beda maju, beda mundur, dan beda pusat.. Misalkan dikethaui. dan. Dipandang persamaan panas. satu dimensi, yaitu:. (3.4). atau.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 26. Persamaan diferensial parsial di atas akan ditentukan jenisnya dengan cara klasifikasi persamaan diferensial parsial orde dua. Di sini persamaan (3.4) adalah. dan. dan. dari. , diperoleh. sehingga persamaan (3.4) merupakan persamaan diferensial parsial yang berjenis parabolik. Persamaan (3.4) sering disebut sebagai persamaan panas satu dimensi karena hanya memiliki satu variabel ruang yaitu konstanta positif,. adalah variabel waktu, dan. menyatakan suhu yang bergantung pada. variabel. adalah fungsi yang. terhadap variabel bebas. dan turunan kedua variabel tak bebas. dinotasikan dengan. merupakan. dan .. Turunan pertama variabel tak bebas dinotasikan dengan. , dengan. terhadap. .. 1. Keakuratan Skema Beda Maju Dipandang deret Taylor. Karena. di sekitar titik , yaitu. adalah bilangan yang sangat kecil,. sehingga dapat diabaikan dan diperoleh (3.5).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 27. dengan. . Yang berarti rumus turunan. beda maju mempunyai keakuratan. , yaitu memiliki keakuratan tingkat satu.. 2. Keakuratan Skema Beda Pusat Dipandang deret Taylor. dan. di sekitar titik ,. yaitu (3.6) (3.7). Persamaan (3.6) dan (3.7) dijumlahkan. Karena. adalah bilangan yang sangat kecil, sehingga dapat. diabaikan dan diperoleh (3.8). dengan. .. mempunyai keakuratan. Yang berarti rumus turunan beda maju. , yaitu memiliki keakuratan tingkat dua.. C. Skema Eksplisit Persamaan Panas Satu Dimensi Dipandang persamaan panas satu dimensi, yaitu:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 28. atau dapat ditulis. dengan syarat awal. dan syarat batas. Penampang batang homogen satu dimensi dengan panjang , akan dibagi ke dalam panjang. interval dengan masing-masing panjang Domain diambil menjadi persegi. panas dan gelombang). Titik-titik. dan tiap -interval dari (untuk persamaan. menjadi. Sementara, untuk titik-titik menjadi. Terakhir, ditulis (3.9). Suatu diskretisasi beda hingga untuk persamaan panas tersebut dengan menggunakan skema beda maju terhadap waktu dan beda pusat terhadap ruang, yaitu: (3.10). Dengan menggunakan persamaan (3.9), skema eksplisit untuk persamaan panas dapat dituliskan kembali menggunakan persamaan (3.10). Sehingga didapat.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 29. (3.11). Perhatikan bahwa. diubah menjadi. dan. .. Jadi, [. ]. [. Selanjutnya kedua ruas dikali dengan [. Misalkan. ]. ]. , diperoleh. [. ]. (3.12). , maka persamaan (3.12) menjadi [. Kedua ruas dijumlahkan dengan. ]. (3.13). , maka diperoleh [. ]. atau (3.14). dimana. dan. .. Dalam menyelesaikan persamaan panas, diperlukan syarat tambahan yaitu syarat awal dan syarat batas. Persamaan (3.9) memenuhi syarat awal yaitu:. dimana. , untuk. Persamaan (3.9) juga memenuhi syarat-syarat batas, yaitu:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 30. Syarat Kestabilan Metode Beda Hingga Skema Eksplisit (FTCS) untuk Persamaan Panas Dalam subbab ini akan di analisis skema eksplisit metode beda hingga untuk persamaan panas yang sudah diperoleh dengan menggunakan skema beda maju terhadap waktu dan skema beda pusat terhadap ruang. Disini. .. Analisis Stabilitas Fourier-von Neumann Ingat kembali persamaan (3.13), yaitu: [. ]. dengan syarat awal. dan syarat batas. dimana Misalkan (3.15). Substitusikan persamaan (3.15) ke dalam persamaan (3.13), sehingga diperoleh. = [. ]. = [. ]. = [. Selanjutnya kedua ruas dikalikan dengan. ]. sehingga diperoleh.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 31. Perhatikan bahwa. sehingga. (. ). (. ). Solusi dari persamaan (3.13) dengan syarat-syarat batas adalah. dimana (. (. )). dengan. Syarat Kestabilan Solusi Solusi dikatakan stabil jika | | |. (. (. ))|. dengan menggunakan sifat nilai mutlak, diperoleh (. (. ( ( Perhatikan bahwa. )). ( (. )) )). dan.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 32. (. ). sehingga. Jadi, syarat kestabilan solusi harus memenuhi pertidaksamaan. Sehingga jika. diketahui, maka. sebaiknya dipilih sedemikian sehingga:. Contoh 3.1 Diberikan. untuk. ,. {. Diambil. dan. Hitunglah:. a). b) Dengan rumus. dan hasil yang diperoleh di a), hitunglah.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 33. Penyelesaian: a) Pada saat. detik. 0 10(2) = 20. 10(4) = 40. 10(6) = 60. 10(8) = 80. 10(10) = 100. -10(12) + 200 = 80. -10(14) + 200 = 60. -10(16) + 200 = 40. -10(18) + 200 = 20. -10(20) + 200 = 0. b) Penyelesaian dengan menggunakan persamaan (3.14) dan jawaban pada a).. . Di sini. Dihitung terlebih dahulu untuk Dengan demikian. . Saat. diperoleh:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 34. = 20 + (40 – 2(20) + 0) = 20 =. = 40 + (60 – 2(40) + 20) = 40. =. = 60 + (80 – 2(60) + 40) = 60. =. = 80 + (100 – 2(80) + 60) = 80. =. = 100 + (80 – 2(100) + 80) = 90. =. = 80 + (60 – 2(80) + 100) = 80. =. = 60 + (40 – 2(60) + 80) = 60. =. = 40 + (20 – 2(40) + 60) = 40. =. = 20 + (0 – 2(20) + 40) = 20.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 35. Gambar 3.2 Kondisi suhu awal pada contoh 3.1.. Gambar 3.3 Hasil simulasi dari penyelesaian contoh 3.1 dengan menggunakan metode beda hingga dimana. dan saat. detik..

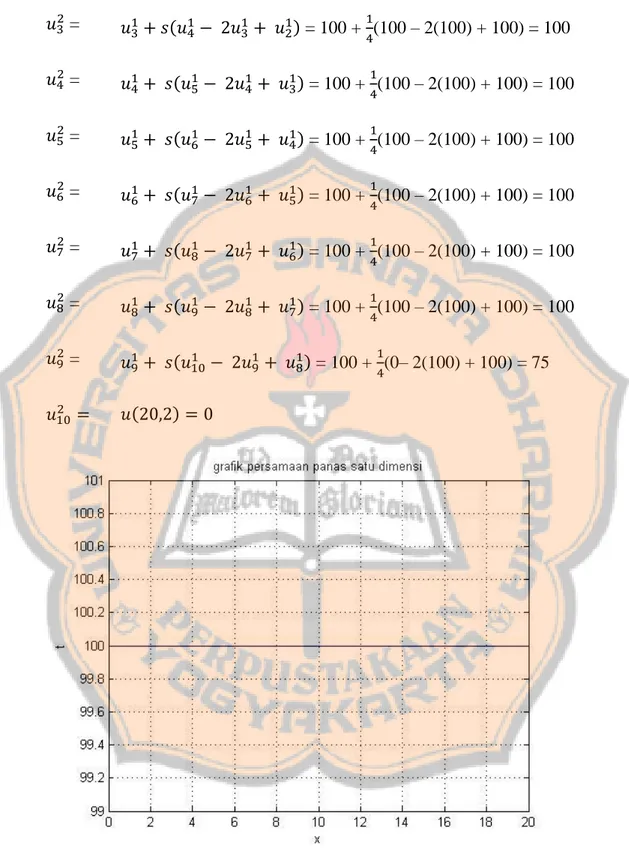
PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 36. Kondisi awal distribusi suhu ditunjukkan pada Gambar 3.2. Hasil simulasi dari penyelesaian model konduksi panas pada batang homogen dengan metode beda hingga menggunakan program MATLAB untuk contoh 3.1 ditunjukkan pada Gambar 3.3. Hasil simulasi persamaan panas satu dimensi tersebut berhenti pada saat akhirnya adalah. detik, kurva suhu menuju. secara seragam.. Contoh 3.2 Diberikan. untuk 0. ,. , .. Diambil. dan. .. Hitunglah: a) b) Dengan rumus. dan hasil yang diperoleh di a), hitunglah. c) Dengan rumus. dan hasil yang diperoleh di b), hitunglah. Penyelesaian: a) Pada saat. detik. b) Penyelesaian dengan menggunakan persamaan (3.14) dan jawaban pada a).. . Di sini. Dihitung terlebih dahulu untuk . Dengan demikian. . Saat. , diperoleh:. dan.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 37. = 100 + (100 – 2(100) +100) = 100 =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100– 2(100) + 100) = 100. c) Untuk. = 100 + (100 – 2(100) +0) = 75 =. = 100 + (100 – 2(100) + 100) = 100.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 38. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (100 – 2(100) + 100) = 100. =. = 100 + (0– 2(100) + 100) = 75. Gambar 3.4 Kondisi suhu awal pada contoh 3.2.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 39. Gambar 3.5 Hasil simulasi dari penyelesaian contoh 3.2 dengan menggunakan metode beda hingga dimana. dan saat. detik.. Kondisi awal distribusi suhu ditunjukkan pada Gambar 3.4. Hasil simulasi dari penyelesaian model konduksi panas pada batang homogen dengan metode beda hingga menggunakan program MATLAB untuk contoh 3.2 ditunjukkan pada Gambar 3.5. Hasil simulasi persamaan panas satu dimensi tersebut berhenti pada saat akhirnya adalah. tik, kurva suhu menuju. secara seragam..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB IV METODE NUMERIS UNTUK PERSAMAAN PANAS DUA DIMENSI. Dalam bab ini akan dibahas mengenai metode numeris untuk persamaan panas dua dimensi. Subbab yang ada dalam bab ini, yaitu: Metode Beda Hingga untuk Persamaan Panas Dua Dimensi, Skema Eksplisit Persamaan Panas Dua Dimensi, dan Hasil Simulasi.. A. Metode Beda Hingga untuk Persamaan Panas Dua Dimensi. Pada bab sebelumnya telah dibahas tentang metode beda hingga untuk persamaan panas satu dimensi. Dalam bab ini akan dibahas tentang metode beda hingga untuk persamaan panas dua dimensi, dimana terdapat dua dimensi ruang yaitu. dan .. Dipandang persamaan panas dua dimensi, yaitu ( dengan. dan. (4.1). ). adalah konstanta positif.. 1. Keakuratan Skema Beda Maju Dipandang deret Taylor. di sekitar titik , yaitu. 40.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 41. Karena. adalah bilangan yang sangat. kecil, sehingga dapat diabaikan dan diperoleh (4.2). dengan. . Yang berarti rumus. turunan beda maju mempunyai keakuratan. , yaitu memiliki keakuratan. tingkat satu.. 2. Keakuratan Skema Beda Pusat Dipandang deret Taylor. dan. di sekitar titik. , yaitu (4.3). (4.4). Persamaan (4.3) dan (4.4) dijumlahkan. Karena. adalah bilangan yang sangat kecil, sehingga dapat. diabaikan dan diperoleh (4.5).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 42. dengan. . Yang berarti rumus turunan beda maju. mempunyai keakuratan. , yaitu memiliki keakuratan tingkat dua.. Dipandang deret Taylor. dan. di sekitar titik. , yaitu (4.6). (4.7). Persamaan (4.6) dan (4.7) dijumlahkan. Karena. adalah bilangan yang sangat kecil, sehingga dapat. diabaikan dan diperoleh (4.8). dengan mempunyai keakuratan. . Yang berarti rumus turunan beda maju , yaitu memiliki keakuratan tingkat dua..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 43. B. Skema Eksplisit Persamaan Panas Dua Dimensi Dipandang persamaan panas dua dimensi, yaitu: (. ). atau dapat ditulis (. ). dengan syarat batas. dan syarat awal. Penampang batang homogen dua dimensi dengan panjang panjang tinggi ,. , akan dibagi ke dalam. dan. interval dengan masing-masing panjang. dan tiap -interval dari panjang . Titik-titik. Titik-titik. menjadi. Sementara itu, titik-titik menjadi. dan. Domain diambil menjadi persegi menjadi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 44. Terakhir, ditulis (. (3.9). ). Suatu diskretisasi beda hingga untuk persamaan panas tersebut dengan menggunakan skema beda maju terhadap waktu dan beda pusat terhadap ruang, yaitu:. (. (3.10) ). Dengan menggunakan persamaan (3.9), skema eksplisit untuk persamaan panas dapat dituliskan kembali menggunakan persamaan (3.10). Sehingga didapat (. ). (. (. ). (. ). Perhatikan bahwa. (. ). (. ). diubah menjadi. menjadi. , dan. (3.11) ). ,. diubah. .. Jadi, (. ). (. Selanjutnya kedua ruas dikali dengan. ). , diperoleh.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 45. (. ). (. ) (3.12). Selanjutnya kedua ruas ditambahkan dengan. , sehingga diperoleh. (. ). Kemudian kumpulkan variabel-variabel yang sejenis (. ) ((. (. ). (. )). ). (. )). ) ((. dimana (. Kedua ruas dikurangi. ). , didapatkan (. ). Keluarkan variabel (. ). Sehingga diperoleh syarat kestabilan (. ).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 46. Solusi akhirnya adalah ((. ). ) (3.13). ((. dimana. ). ,. (. dan. )). .. Dalam menyelesaikanpersamaan panas, diperlukan syarat tambahan yaitu syarat awal dan syarat batas. Misalnya diambil syarat awal :. dan misalkan diketahui syarat-syarat batas :. dimana. , untuk. dan. , untuk. C. Hasil Simulasi untuk Persamaan Panas Dua Dimensi Dalam subbab ini akan diperlihatkan hasil dari permasalahan panas dua dimensi, yang telah disimulasikan dengan menggunakan program MATLAB. Hasil simulasi tersebut ditunjukkan dalam Gambar 4.1..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 47. Gambar 4.1 Hasil simulasi dari penyelesaian persamaan panas dua dimensi dengan menggunakan metode beda hingga.. Gambar di atas merupakan penyelesaian dari persamaan panas melalui plat dimensi 1x1 dengan material perak yang mempunyai. ,. . Penyelesaian ini berdasarkan kondisi batas ,. ,. , dan ,. dan nilai awal. . Untuk. mencapai suhu steady, plat membutuhkan waktu setidaknya 1070 detik. Sebagai catatan, dalam simulasi di atas, digunakan. ,. , dan. . Di sini, titik A (0.25, 0.25) diberi warna merah, titik B (0.5, 0.5) diberi warna hijau, dan titik C (0.75, 0.75) diberi warna biru..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB V KESIMPULAN DAN SARAN Bab ini merupakan bab terakhir dari tugas akhir ini. Dalam bab ini, subbab yang ada yaitu kesimpulan dan saran. A. Kesimpulan Perpindahan panas merupakan suatu proses, dimana perpindahan energi tersebut mengalir dari suhu yang tinggi ke suhu yang lebih rendah. Proses perpindahan panas tersebut dapat diketahui dengan melihat distribusi suhunya. Perhitungan distribusi suhu diperlukan persamaan diferensial, solusi persamaan diferensial dapat dicari dengan berbagai macam metode. Namun demikian, pada tugas akhir ini metode yang digunakan adalah metode beda hingga. Pada BAB III dibahas tentang solusi dari permasalahan panas satu dimensi, dimana bahan penelitiannya adalah batang homogen. Penampang batang homogen satu dimensi ini memiliki panjang interval yang berhingga dan titik-titik tertentu telah diketahui suhunya. Pada BAB IV dibahas tentang solusi dari permasalahan panas dua dimensi, bahan penelitiannya adalah plat perak. Perhitungan pada BAB III dan BAB IV dilakukan dengan cara mengolah nilai dari titik-titik yang telah diketahui, untuk mendapatkan nilai di titik-titik selanjutnya. Perhitungan tersebut selanjutnya disimulasikan menggunakan program MATLAB. Berdasarkan perhitungan manual ataupun menggunakan program, hasil analisis yang diperoleh adalah semakin banyak interval yang digunakan maka distribusi suhu semakin akurat. Namun demikian, hal tersebut memerlukan selang waktu perhitungan komputasi yang cukup lama.. B. Saran Tugas akhir ini membahas tentang penyelesaian masalah konduksi panas pada media homogen satu dimensi dan dua dimensi. Dalam tugas akhir ini, penyelesaian masalah konduksi panas tersebut diselesaikan dengan menggunakan. 48.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 49. metode beda hingga. Untuk program MATLAB dua dimensi hanya dikerjakan menggunakan metode beda maju terhadap waktu satu langkah (metode Euler). Penulis mengharapkan pada waktu yang akan datang, akan ada yang melanjutkan tugas akhir ini dengan menggunakan metode lain yang lebih akurat. Untuk program MATLAB dua dimensi bisa dicoba menggunakan metode Runge-Kutta orde kedua terhadap waktu..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR PUSTAKA. Darmawijaya, S. (2011). Barisan dan Deret. Yogyakarta: Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Gadjah Mada. Mohamed, A.M. (2016). Heat Diffusion in 2D Square Plate Using Finite Difference Method with Steady-State Solution. Numerical Analysis-Course Project.. (https://www.mathworks.com/matlabcentral/fileexchange/55058-. 2d-heat-equation-using-finite-difference-method-with-steady-state-solution) Munir, R. (2008). Metode Numerik. Bandung: Informatika Bandung. O’Neil, P.V. (2014). Beginning Partial Differential Equations. New Jersey: John Wiley & Sons, Inc. Purcell, E J. (1981). Kalkulus dan Geometri Analitis, edisi ketiga. Jakarta: Erlangga. Suparno, P. (2009). Pengantar Termofisika. Yogyakarta: Universitas Sanata Dharma. Tarwidi, D. dan Pudjaprasetya, S.R. (2013).Godunov Method for Stefan Problems with Enthalpy Formulations.East Asian Journal on Applied Mathematics, 3(2): 107-119. Thomas, G. B. (2010). Thomas’ Calculus Early Transcendentals. Boston: Pearson Education. Wou, K. K. T. (2018). Penyelesaian Masalah Konduksi Panas Pada Media Heterogen Menggunakan Metode Beda Hingga.Yogyakarta.. 50.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. LAMPIRAN Di bawah ini di lampirkan beberapa program MATLAB yang digunakan pada saat mengerjakan tugas akhir ini. A. Program Metode Beda Hingga untuk Persamaan Panas Satu Dimensi dengan 1. Contoh kasus dimana ujung-ujung batang kawat homogen dipertahankan pada suhu 00C. clc clear dx=2; x=0:dx:60; n=length(x); uL=0*x; uB=0*x; dt=0.0005*dx; k=1; s=k*dt/dx^2; for i=1:n if x(i)<=30 uB(i)=10*x(i); else x(i)>30 uB(i)=-10*x(i)+600; end end plot(x,uB) hold on ylim([0 300]) pause(0.1) tFinal=1; Nt=tFinal/dt; for j=1:Nt uL=uB; for i=2:n-1 uB(i)=s*(uL(i+1)-2*uL(i)+uL(i-1))+uL(i); end uB(1)=0; uB(n)=0; plot(x,uB) title('grafik persamaan panas satu dimensi') 51.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 52. xlabel 'x' ylabel 't' hold on grid on ylim([0 300]) pause(0.1) t=j*dt; end 2. Contoh kasus dimana ujung-ujung batang kawat homogen dipertahankan pada suhu 00C, dengan kondisi suhu awal 1000C. clc clear close all dx=2; x=0:dx:20; n=length(x); uL=0*x; uB=0*x; dt=0.05*dx; k=1; s=k*dt/dx^2; for i=1:n uB(i)=100; end plot(x,uB) ylim([0 200]) pause(0.1) tFinal=100; Nt=tFinal/dt; for j=Nt; uL=uB; for i=2:n-1 uB(i)=k*s*(uL(i+1)-2*uL(i)+uL(i-1))+uL(i); end uB(1)=0; uB(n)=0; plot(x,uB) title('grafik persamaan panas satu dimensi') xlabel 'x' ylabel 't' hold on grid on ylim ([0 200]).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 53. pause(0.1) t=j*dt; end B. Program Metode Beda Hingga untuk Persamaan Panas Dua Dimensi clear; close all; clc; %% 1-Inputs section %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%% %%%% Please select your material, enter your parameters and your initial conditions %%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%% % %%% ** Uncomment if needed ** % name=('Aluminium'); Material name % conductivity = 204.3; thermal conductivity (j/m.C.sec) % spacific_heat = 910; specific heat (j/kg.C) % denisty = 2700.0; density (kg/m^3) % %%% ** Uncomment if needed ** % name=('Copper'); Material name % conductivity = 401; thermal conductivity (W/m.K) % spacific_heat = 390; specific heat (J/kg K) % denisty = 8940; density (kg/m^3) %%% name=('Silver'); Material name conductivity = 629; thermal conductivity (W/m.K) spacific_heat = 233; specific heat (J/kg K) denisty = 10490; density (kg/m^3). -- Aluminum --. % % % % %. -- Copper --. % % % % %. -- Silver --. % %%% -- Custom Material -** Uncomment and enter your values if needed **. % % % %. %.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 54. % name=('Custom Material'); Material name % conductivity = ; thermal conductivity (W/m.K) % spacific_heat = ; specific heat (J/kg K) % denisty = ; density (kg/m^3) %% Lx= 1; Ly= 1; Nx=40; Ny=40; T_initial= 100;%0 nodes ( the whole plate ) T_east = 100;%150 side ( at y=0 "Dirichlet T_west = 100;%300 side ( at y=Ly "Dirichlet T_north = 100;%50 side ( at x=0 "Dirichlet T_south = 0;%100 ; side ( at x=Lx "Dirichlet. % % % %. % % % %. plate plate nodes nodes. width (m) length (m) in x direction in y direction. % Initial temperature in all % temperature on the upper Conditions" ) % temperature on the lower Conditions" ) % temperature on the left Conditions" ) % temperature on the right Conditions" ). t_end=100 ; simulation (sec) dt=0.6 ;. % final time for visual. tolerence = 0.5; simulation (0.5 deg Celesius) tolerence_ss=0.001; section (0.1 deg Celesius). % tolerence for numerical. % time step (1 sec). % tolerence for steady state. %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%% From here, You don't need to modify %%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%% %% 2- Constants Section k=1; % iteration counter err_SS_max(k)=1; % initial error err_SS_min(k)=1; % initial error dx=Lx/Nx; % delta x dy=Ly/Ny; % delta y.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 55. n_time=round(t_end/dt); % number of iterrations for time alpha = conductivity/(spacific_heat*denisty); % alpha (1/sec) T_max=max([T_east T_west T_north T_south T_initial]); % Max T to set axes limits in plotting T_min=min([T_east T_west T_north T_south T_initial]); % Min T to set axes limits in plotting Solution_type=questdlg('Which method you want to solve the time derivative with ?','Question','Euler','2nd order RungeKutte','Euler'); % solve with 2nd order Runge Kutte in time or 2 to solve with Euler if dt<= 1/(2*alpha*((1/dx^2)+(1/dy^2))) % test the stability condition else fprintf('Error, the stability condition is not met\nPlease return to "Inputs Section" and choose a "dt" smaller than %f \n',1/(2*alpha*((1/dx^2)+(1/dy^2)))) return end message=msgbox('Your computer is now solving the problem, Please wait..... '); % Busy message % ----------------- Initial Conditions for finite difference section --------------T=zeros(Nx+2,Ny+2,75000); % set max iterations 75,000 due to memory limitations (T variable takes maximum 1GB in memory) T(:,1,:)=T_south; T(:,Ny+1,:)=T_north; T(:,Ny+2,:)=T_north; % Redundant, it has no effect in calculations but is required in plotting section T(Nx+1,:,:)=T_east; T(Nx+2,:,:)=T_east; % Redundant, it has no effect in calculations but is required in plotting section T(1,:,:)=T_west; T(:,:,1)=T_initial; % ------------------- Initial Conditions for steady state section ------------------Tss=zeros(Nx+2,Ny+2); Tss2=zeros(Nx+2,Ny+2); Tss(:,1)=T_south; Tss2(:,1)=T_south; Tss(:,Ny+1)=T_north; Tss2(:,Ny+1)=T_north; Tss(:,Ny+2)=T_north; Tss2(:,Ny+2)=T_north; % Redundant, it has no effect in calculations but is required in plotting section Tss(Nx+1,:)=T_east; Tss2(Nx+1,:)=T_east; Tss(Nx+2,:)=T_east; Tss2(Nx+2,:)=T_east; % Redundant, it has no effect in calculations but is required in plotting section Tss(1,:)=T_west; Tss2(1,:)=T_west;. %% 3- Steady-State section.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 56. while err_SS_max(k)>=tolerence_ss || err_SS_min(k)>=tolerence_ss for i=2:Nx looping for j=2:Ny. %. Tss2(i,j)=0.25*(Tss(i+1,j)+Tss(i,j+1)+Tss(i1,j)+Tss(i,j-1)); end end k=k+1; % update k err_SS_max(k)=abs(max(max(Tss2-Tss))); % calculate error err_SS_min(k)=abs(min(min(Tss2-Tss))); % calculate error Tss=Tss2; % update T end. %% 4- Finite difference section (Using 2nd order Runge Kutte or Euler in time) k=1; switch Solution_type case'2nd order Runge-Kutte' err_R_k_max(k)=100; % initial error err_R_k_min(k)=100; % initial error while err_R_k_max(k)>=tolerence || err_R_k_min(k)>=tolerence for i=2:Nx for j=2:Ny k1=alpha*(((T(i-1,j,k)2*T(i,j,k)+T(i+1,j,k))/dx^2)+((T(i,j-1,k)2*T(i,j,k)+T(i,j+1,k))/dy^2)); Tk=T(:,:,k)+k1*dt; k2=alpha*(((Tk(i-1,j)2*Tk(i,j)+Tk(i+1,j))/dx^2)+((Tk(i,j-1)2*Tk(i,j)+Tk(i,j+1))/dy^2)); T(i,j,k+1) =T(i,j,k)+(dt/2)*(k1+k2); end end k=k+1; err_R_k_max(k)=abs(max(max(T(:,:,k)-Tss))); %calculate error err_R_k_min(k)=abs(min(min(T(:,:,k)-Tss))); %calculate error if round(err_R_k_max(k),5)==round(err_R_k_max(k-1),5) && err_R_k_max(k)~= 0 % Test solution convergence errordlg('The solution is not converging, Please choose a larger tolerence','Tolerence Error'); close(message) return.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 57. end if round(err_R_k_min(k),5)==round(err_R_k_min(k-1),5) && err_R_k_min(k)~= 0 % Test solution convergence errordlg('The solution is not converging, Please choose a larger tolerence','Tolerence Error'); close(message) return end end case'Euler' err_E_max(k)=100; % initial error err_E_min(k)=100; % initial error while err_E_max(k)>=tolerence || err_E_min(k)>=tolerence for i=2:Nx for j=2:Ny T(i,j,k+1) =T(i,j,k)+dt*alpha*(((T(i-1,j,k)2*T(i,j,k)+T(i+1,j,k))/dx^2)+((T(i,j-1,k)2*T(i,j,k)+T(i,j+1,k))/dy^2)); end end k=k+1; err_E_max(k)=abs(max(max(T(:,:,k)-Tss))); %calculate error err_E_min(k)=abs(min(min(T(:,:,k)-Tss))); %calculate error if round(err_E_max(k),5)==round(err_E_max(k-1),5) && err_E_max(k)~= 0 % Test solution convergence errordlg('The solution is not converging, Please choose a larger tolerence','Tolerence Error'); close(message) return end if round(err_E_min(k),5)==round(err_E_min(k-1),5) && err_E_min(k)~= 0 % Test solution convergence errordlg('The solution is not converging, Please choose a larger tolerence','Tolerence Error'); close(message) return end end case [] close(message) msgbox('Error, Please re-run the code and choose Euler or 2nd order Runge-Kutte to continue the solution') return end T=T(:,:,1:k); % delete the unused assigned zero layers SStime=k*dt; % steady state time close(message) % close the busy message.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 58. %% 5- Printed results section fprintf('This is the solution of the heat equation through out a plate of diamensions %i X %i of material %s \n',Lx,Ly,name); fprintf('The solution is based on "Dirichlet Boundry Conditions" with initial values \n') fprintf('T(x,0,t)=%i , T(x,%i,t)=%i , T(0,y,t)=%i , T(%i,y,t)=%i , T(x,y,0)=%i \n',T_south,Ly,T_north,T_west,Lx,T_east,T_initial) fprintf('The plate takes %i seconds to reach steady-state temperature with tolerence %0.2f \n',round(SStime),tolerence); fprintf('Now, Simulation is running with final time %i seconds and step %0.2f second \n',t_end,dt). %% 6- Plotting section x=zeros(1,Nx+2);y=zeros(1,Ny+2); for i = 1:Nx+2 x(i) =(i-1)*dx; end for i = 1:Ny+2 y(i) =(i-1)*dy; end % %%%. %Generate the plate. -------------- Constant plot ----------------. subplot(2,2,3) hold on title(sprintf('Temperature at steady state time : %i seconds ',round(SStime))) surf(x,y,Tss) plot3( Lx/4, Ly/4,T_max,'ko','markerfacecolor','r') % plot red point plot3( Lx/2, Ly/2,T_max,'ko','markerfacecolor','g') % plot green point plot3(3*Lx/4,3*Ly/4,T_max,'ko','markerfacecolor','b') % plot blue point plot3( Lx/4, Ly/4,T_min,'ko','markerfacecolor','r') % plot red point plot3( Lx/2, Ly/2,T_min,'ko','markerfacecolor','g') % plot green point plot3(3*Lx/4,3*Ly/4,T_min,'ko','markerfacecolor','b') % plot blue point cb=colorbar; caxis([T_min T_max]); view(90,-90); xlim([0 Lx+dx]); xlabel('Length'); ylim([0 Ly+dy]); ylabel('Width'); zlim([T_min T_max]); zlabel('Temprature'); drawnow hold off subplot(2,2,4) hold on.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 59. title(sprintf('Temperature at steady state time : %i seconds ',round(SStime))) scatter(k,Tss(floor(Nx/4),floor(Ny/4)),'ko','markerfacecolor','r '); val=(sprintf(' T = %0.2f ',Tss(floor(Nx/4),floor(Ny/4)))); text(k,Tss(floor(Nx/4),floor(Ny/4)),val,'HorizontalAlignment','L eft'); scatter(k,Tss(floor(Nx/2),floor(Ny/2)),'ko','markerfacecolor','g '); val=(sprintf(' T = %0.2f ',Tss(floor(Nx/2),floor(Ny/2)))); text(k,Tss(floor(Nx/2),floor(Ny/2)),val,'HorizontalAlignment','r ight'); scatter(k,Tss(floor(3*Nx/4),floor(3*Ny/4)),'ko','markerfacecolor ','b'); val=(sprintf(' T = %0.2f ',Tss(floor(3*Nx/4),floor(3*Ny/4)))); text(k,Tss(floor(3*Nx/4),floor(3*Ny/4)),val,'HorizontalAlignment ','Left'); axis tight; xlabel('Time Iterations'); ylim([T_min T_max]); ylabel('Temperature'); legend('Red Point','Green Point ','Blue Point ','Location','northwest') drawnow hold off %%%. ------------ Animated plot ----------. for j=1:n_time subplot(2,2,1) surf(x,y,T(:,:,j)) hold on title(sprintf('Temperature at time : %i seconds ',round(j*dt))) plot3( Lx/4, Ly/4,T_max,'ko','markerfacecolor','r') % plot red point plot3( Lx/2, Ly/2,T_max,'ko','markerfacecolor','g') % plot green point plot3(3*Lx/4,3*Ly/4,T_max,'ko','markerfacecolor','b') % plot blue point plot3( Lx/4, Ly/4,T_min,'ko','markerfacecolor','r') % plot red point plot3( Lx/2, Ly/2,T_min,'ko','markerfacecolor','g') % plot green point plot3(3*Lx/4,3*Ly/4,T_min,'ko','markerfacecolor','b') % plot blue point cb=colorbar; caxis([T_min T_max]); view(90,-90); xlim([0 Lx+dx]); xlabel('Length'); ylim([0 Ly+dy]); ylabel('Width'); zlim([T_min T_max]); zlabel('Temprature'); drawnow hold off subplot(2,2,2) hold on.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 60. title(sprintf('Temperature at time : %i seconds ',round(j*dt))) scatter(j,T(floor((Nx+2)/4),floor((Ny+2)/4),j),'r.'); scatter(j,T(ceil((Nx+2)/2),ceil((Ny+2)/2),j),'g.'); scatter(j,T(ceil(3*(Nx+2)/4),ceil(3*(Ny+2)/4),j),'b.'); axis tight; xlabel('Time Iterations'); axis tight; ylabel('Temperature'); legend('Red Point','Green Point ','Blue Point ','Location','northwest') drawnow hold off end.