Studi Perbandingan Perpindahan Panas
Menggunakan Metode Beda Hingga
dan Crank-Nicholson
Durmin, Drs. Lukman Hanafi, M.Sc
Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Teknologi Sepuluh Nopember (ITS)
Jl. Arief Rahman Hakim, Surabaya 60111 [email protected]
Abstrak—Di dalam suatu benda yang memiliki perbedaan temperatur maka akan terjadi perpindahan energi atau perpindahan panas dari bagian yang bertemperatur tinggi ke bagian yang bertemperatur lebih rendah. Proses perpindahan panas tersebut dapat diketahui oleh distribusi temperaturnya. Perhitungan distribusi temperatur melibatkan persamaan diferensial parsial.Salah satu teknik yang digunakan untuk menyelesaikan persamaan diferensial parsial adalah dengan metode numerik.Metode numerik adalah teknik yang digunakan untuk menyelesaikan permasalahan yang diformulasikan secara matematis dengan operasi aritmatika biasa (tambah, kurang, bagi dan kali).Secara matematis persamaan perpindahan panas adalah termasuk dalam persamaan parabolik. Persamaan panas satu dimensi ini kemudian diselesaikan dengan menggunakan pendekatan metode Beda Hingga skema Eksplisit dan Crank Nicholson dan membandingkan kedua metode tersebut, untuk penyelesaian sistem persamaan yang terbentuk dari metode Crank-Nicholson yang berbentuk matriks tridiagonal digunakan metode sapuan ganda Choleski. Dari hasil perhitungan yang diperoleh diketahui bahwa panas berpindah menuju bagian tengah benda dan temperatur menurun sebagai fungsi waktu karena adanya perpindahan panas.
Kata Kunci—Metode Beda Hingga, Metode Crank-Nicholson, Persamaan Diferensial Parsial, Perpindahan Panas
I. PENDAHULUAN
Perpindahan panas yang terjadi di dalam bumi merupakan persoalan kompleks karena melibatkan banyak parameter.Sehingga penyelesaian persoalan perpindahan panas di alam ini memerlukan asumsi-asumsi untuk menyederhanakan permasalahan.
Perpindahan panas (heat transfer) adalah ilmu untuk mengamati perpindahan energi yang terjadi karena adanya perbedaan suhu diantara benda atau material[2]. Energi ini tidak dapat diukur atau diamati secara langsung tetapi arah perpindahannya dan pengaruhnya dapat diamati dan diukur.
Banyak model matematika perpindahan panas yang merupakan persamaan diferensial parsial.Penyelesaian persamaan diferensial parsial dapat dilakukan dengan beberapa metode.Pemilihan metode pendekatan berdasarkan pada tujuan dan kompleksitas masalah.
Pada Tugas Akhir ini akan dikaji proses perpindahan panas satu dimensi dimana objek penelitiannya adalah suatu simulasi domain bidang yang pada batas-batas dan titik-titik tertentu diketahui temperaturnya[9]. Pendekatan yang dipakai adalah dengan membandingkan metode Beda Hingga dan metode Crank-Nicholson.
II. TINJAUAN PUSTAKA A. Perpindahan Panas
Panas mengalir dari benda bertemperatur lebih tinggi ke benda bertemperatur lebih rendah. Laju perpindahan panas yang melewati benda padat sebanding dengan gradien temperatur atau beda temperatur persatuan panjang.
Mekanisme perpindahan panas sendiri dapat terjadi secara konduksi, konveksi, dan radiasi.
Perpindahan panas secara konduksi adalah proses perpindahan panas dari daerah bersuhu tinggi ke daerah bersuhu rendah dalam satu medium (padat, cair atau gas), atau antara medium–medium yang berlainan yang bersinggungan secara langsung. Dinyatakan dengan:
𝑞 = −𝑘𝐴𝑑𝑇
𝑑𝑥 (1) dimana:
𝑞 = Laju perpindahan panas (𝑤), 𝐴 = Luas penampang dimana panas
mengalir(𝑚2),
𝑑𝑇/𝑑𝑥= Gradien suhu pada penampang, atau laju perubahan suhu 𝑇 terhadap jarak dalam arah aliran panas 𝑥,
𝑘 = Konduktivitas thermal bahan (𝑤/𝑚0𝐶).
Perpindahan panas secara konveksi adalah perpindahan energi dengan kerja gabungan dari konduksi panas, penyimpanan, energi dan gerakan mencampur. Proses terjadi pada permukaan padat (lebih panas atau dingin) terhadap cairan atau gas (lebih dingin atau panas). Dinyatakan dengan:
𝑞 = ℎ𝐴 ∆𝑇 (2) dimana :
𝑞 = Laju perpindahan panas konveksi
(𝑤),
ℎ = Koefisien perpindahan panas konveksi(𝑤/𝑚20𝐶),
𝐴 = Luas penampang (𝑚2) ,
∆𝑇 = Perubahan atau perbedaan suhu ( 𝐶; 𝐹0 0 ).
Perpindahan panas secara radiasi adalah proses perpindahan panas dari benda bersuhu tinggi ke benda yang bersuhu lebih rendah, bila benda–benda itu terpisah didalam ruang (bahkan dalam ruang hampa sekalipun). Dinyatakan dengan: 𝑞 = 𝛿𝐴 𝑇14– 𝑇24 (3) dimana: 𝛿 = Konstanta Stefan-Boltzman 5,669 x10-8𝑤/𝑚2𝑘4 , 𝐴 = Luas penampang, 𝑇 = Temperatur.
B. Persamaan Diferensial Parsial
Banyak permasalahan dalam bidang ilmu terapan, fisika, dan teknik dimodelkan secara matematis dengan menggunakan persamaan deferensial parsial [6].
Persamaan deferensial parsial memiliki bentuk umum:
𝐴∅𝑥𝑥 + 𝐵∅𝑥𝑦 + 𝐶∅𝑦𝑦 = 𝑓 𝑥, 𝑦, ∅, ∅𝑥, ∅𝑦 , (4)
dimana 𝐴, 𝐵, dan 𝐶 adalah konstan yang disebut dengan quasilinear.
Terdapat tiga tipe dari persamaan quasilinear yaitu:
a. If 𝐵2– 4𝐴𝐶 < 0, persamaan disebut dengan
persamaan elips.
b. If 𝐵2– 4𝐴𝐶 = 0, persamaan disebut dengan
persamaan parabolik.
c. If 𝐵2– 4𝐴𝐶 > 0, persamaan disebut dengan
persamaan hiperbolik.
Salah satu persamaan parabolik adalah model satu dimensi untuk perpindahan panas pada sebuah batang yang diisolasi dengan panjang 𝐿(gambar 1). Persamaan panas dengan temperatur 𝑢(𝑥, 𝑡) dalam batang pada posisi 𝑥 dan waktu 𝑡dinyatakan dengan:
ĸ𝑢𝑥𝑥(𝑥, 𝑡) = 𝜎𝜌𝑢𝑡(𝑥, 𝑡) , 0 < 𝑥 < 𝐿, 0 < 𝑡 < ∞,(5)
dengan distribusi temperatur awal pada 𝑡 = 0adalah 𝑢(𝑥, 0) = 𝑓(𝑥),𝑡 = 0,0 ≤ 𝑥 ≤ 𝐿,
dan nilai batas pada ujung-ujung batang 𝑢(0, 𝑡) = 𝑐1 untuk𝑥 = 0dan 0 ≤ 𝑡 < ∞,
𝑢(𝐿, 𝑡) = 𝑐2 untuk𝑥 = 𝐿 dan 0 ≤ 𝑡 < ∞.
Konstanta ĸ adalah koefisien dari konduktifitas thermal bahan, 𝜎 adalah panas spesifik, 𝜌 berat jenis material batang, dan 𝑐 konstan.
Untuk penyelesaian persamaan diferensial parsial jenis parabolik ini persamaan perpindahan panas berdimensi satu diatas (persamaan (5)) disederhanakan menjadi:
𝑢𝑡 𝑥, 𝑡 = 𝑐2𝑢𝑥𝑥 𝑥, 𝑡 (6)
berlaku untuk daerah 0 ≤ 𝑥 ≤ 𝐿, waktu 𝑡 ≥ 0, dengan syarat-syarat batasnya adalah[5]:
𝑢𝑡(𝑥, 𝑡) = 𝑢𝑥𝑥(𝑥, 𝑡),0 ≤ 𝑥 ≤ 1, 𝑡 ≥ 0,
𝑢(𝑥, 0) = 𝑓(𝑥), (syarat awal), 𝑢 0, 𝑡 = 𝑢 1, 𝑡 = 0, (syarat batas).
Gambar 1. Model persamaan panas untuk temperatur dalam sebuah batang yang diisolasi
C. Metode Beda Hingga
Untuk dapat menggunakan metode beda hingga dibutuhkan Deret Taylor.
Deret Taylor fungsi satu variabel disekitar 𝑥 diberikan sebagai: 𝑓 𝑥 + ℎ = 𝑓 𝑥 + 𝑓′ 𝑥 ℎ + 𝑓 ′′(𝑥) 2! ℎ 2+ ⋯ atau 𝑓 𝑥 − ℎ = 𝑓 𝑥 − 𝑓′ 𝑥 ℎ + 𝑓 ′′(𝑥) 2! ℎ 2− ⋯ (7) Deret Taylor inilah yang merupakan dasar pemikiran metode beda hingga untuk menyelesaikan persamaan diferensial parsial secara numerik.
Dari deret Taylor ini dikenal tiga pendekatan beda hingga.
Pendekatan beda maju (forward difference): 𝑓′ 𝑥 ≈𝑓 𝑥 + ℎ − 𝑓(𝑥)
ℎ (8) Pendekatan beda mundur (backward difference):
𝑓′ 𝑥 ≈𝑓 𝑥 − 𝑓(𝑥 − ℎ)
ℎ (9) Pendekatan beda pusat (center difference):
𝑓′ 𝑥 ≈𝑓 𝑥 + ℎ − 𝑓(𝑥 − ℎ)
2ℎ (10) Untuk turunan kedua ditinjau deret Taylor hingga nilai ℎ yang berderajat dua. Pemotongan dilakukan pada ℎ yang berderajat tiga.
D. Metode Beda Hingga untuk Persamaan Panas Metode Beda Hingga sangat sering dipakai untuk mencari solusi suatu persamaan diferensial parsial (PDP). Hal ini disebabkan mudahnya mendekati PDP dengan pendekatan deret Taylor-nya dan diperoleh persamaan beda. Idenya adalah membawa domain PDP ke dalam domain komputasi yang berupa grid. Untuk menyederhakan penulisan, sering dituliskan dengan notasi indeks.Indeks subscript pertama sebagai variabel ruang dan subscript kedua sebagai variabel waktu.
Jadi
𝑢 𝑥, 𝑦 ~𝑢𝑖,𝑗,
𝑢 𝑥, 𝑡 ~𝑢 𝑖∆𝑥, 𝑗∆𝑡 ~𝑢𝑖,𝑗.
1. Metode FTCS (Forward Time Center Space) Metode FTCS sering disebut dengan metodeEksplisit bagi persaman difusi. Pada metode ini, Beda Maju terhadap waktu (forward time) diterapkan pada 𝑢𝑡dengan akurasi 𝑂 ∆𝑡 .dan metode
Beda Pusat (Backward Difference) diterapkan pada 𝑢𝑥𝑥dengan akurasi 𝑂 ∆𝑥2 dengan ∆𝑥 = ℎdan ∆𝑡 =
𝑘.
Gambar 2.Skema Eksplisit untuk persamaan panas Penerapan Beda Maju terhadap 𝑢𝑡 di titik
𝑖, 𝑗,lihat gambar 2, diperoreh 𝑢𝑡 𝑥, 𝑡 =
𝑢𝑖,𝑗 +1− 𝑢𝑖,𝑗
𝑘 , (11) penerapan Beda Pusat terhadap 𝑢𝑥𝑥 diperoleh
𝑢𝑥𝑥 𝑥, 𝑡 =
𝑢𝑖+1,𝑗− 2𝑢𝑖,𝑗+ 𝑢𝑖−1,𝑗
ℎ2 , (12)
sehingga dari persamaan (6) diperoleh persamaan beda berikut: 𝑢𝑡 𝑥, 𝑡 = 𝑐2𝑢𝑥𝑥 𝑥, 𝑡 , 𝑢𝑖,𝑗 +1− 𝑢𝑖,𝑗 𝑘 = 𝑐 2𝑢𝑖+1,𝑗 − 2𝑢𝑖,𝑗 + 𝑢𝑖−1,𝑗 ℎ2 ,
dengan menuliskan ruas kiri pada titik 𝑖, 𝑗 + 1, yang merupakan titik yang belum diketahui nilainya, menjadi 𝑢𝑖,𝑗 +1= 𝑢𝑖,𝑗+ 𝑐2 𝑘 ℎ2 𝑢𝑖+1,𝑗− 2𝑢𝑖,𝑗+ 𝑢𝑖−1,𝑗 , dengan substitusi 𝑟 = 𝑐2 𝑘 ℎ2 , menjadi 𝑢𝑖,𝑗 +1= 1 − 2𝑟 𝑢𝑖,𝑗+ 𝑟 𝑢𝑖+1,𝑗 + 𝑢𝑖−1,𝑗 . (13)
. Skema Eksplisit konvergen dan stabil jika 0 ≤ 𝑐2 𝑘
ℎ2≤
1 2 ,
sehingga nilai k harus memenuhi pertidaksamaan berikut
𝑘 ≤1 2
ℎ2
𝑐2 .
2. Metode Implisit BTCS (Backward Time Center Space)
Metode BTCS memiliki akurasi 𝑂 ∆𝑡, ∆𝑥2 .
Dengan ∆𝑥 = ℎdan ∆𝑡 = 𝑘, persamaan beda untuk persamaan panas dengan menggunakan metode BTCS adalah dengan menerapkan Beda Mundur terhadap waktu (backward time) pada 𝑢𝑡 dan dengan metode
Beda Pusat diterapkan pada 𝑢𝑥𝑥.
Gambar 3.Skema Implisit untuk persamaan panas Dengan menerapkan Beda Mundur terhadap 𝑢𝑡dititik 𝑖, 𝑗 + 1, lihat gambar 3, diperoleh
𝑢𝑡 𝑥, 𝑡 =
𝑢𝑖,𝑗 +1− 𝑢𝑖,𝑗
𝑘 , (14) dan dengan menerapkan Beda Pusat terhadap 𝑢𝑥𝑥 ,
diperoleh
𝑢𝑥𝑥 𝑥, 𝑡 =
𝑢𝑖+1,𝑗 +1− 2𝑢𝑖,𝑗 +1+ 𝑢𝑖−1,𝑗 +1
ℎ2 , (15)
sehingga dari persamaan (6)
𝑢𝑡 𝑥, 𝑡 = 𝑐2𝑢𝑥𝑥 𝑥, 𝑡 ,
diperoleh persamaan beda 𝑢𝑖,𝑗 +1− 𝑢𝑖,𝑗
𝑘 =
𝑐2 𝑢𝑖+1,𝑗 +1− 2𝑢𝑖,𝑗 +1+ 𝑢𝑖−1,𝑗 +1
ℎ2 ,
dengan menuliskan ruas kiri pada titik 𝑖, 𝑗, yang merupakan titik yang sudah diketahui nilainya, menjadi 𝑢𝑖,𝑗 = 𝑐2 𝑘 ℎ2 −𝑢𝑖+1,𝑗 +1+ 2𝑢𝑖,𝑗 +1− 𝑢𝑖−1,𝑗 +1 +𝑢𝑖,𝑗 +1 , dengan substitusi 𝑟 = 𝑐2 𝑘 ℎ2 , 𝑢𝑖,𝑗 = −𝑟𝑢𝑖+1,𝑗 +1+ 2𝑟𝑢𝑖,𝑗 +1− 𝑟𝑢𝑖−1,𝑗 +1 +𝑢𝑖,𝑗 +1 , disederhanakan menjadi
j
u
u
j+1 j 𝑢𝑖,𝑗 = 1 + 2𝑟 𝑢𝑖,𝑗 +1 – 𝑟 𝑢𝑖+1,𝑗 +1+ 𝑢𝑖−1,𝑗 +1 . (16) 3. Metode Crank-NicholsonDari persamaan (6), dengan menerapkan Beda Pusat terhadap waktu (center time) untuk menghampiri 𝑢𝑡di titik grid 𝑖, 𝑗 +
1
2 , dengan ∆𝑥 = ℎdan ∆𝑡 = 𝑘,
lihat gambar 4, diperoleh 𝑢𝑡(𝑥, 𝑡) = 𝑢𝑖,𝑗 +1− 𝑢𝑖,𝑗 2(1 2𝑘) , disederhanakan menjadi 𝑢𝑡 𝑥, 𝑡 = 𝑢𝑖,𝑗 +1− 𝑢𝑖,𝑗 𝑘 . (17)
Gambar 4.Skema Crank-Nicholson untuk persamaan panas
Sedangkan 𝑢𝑥𝑥 di titik grid 𝑖, (𝑗 + 1
2) dihampiri
dengan pendekatan suku derivatif ruang pada waktu 𝑗 +1
2 dianggap sebagai nilai rata-rata derivatif pada
waktu 𝑗dan 𝑗 + 1.
Dengan menerapkan Beda Pusat terhadap 𝑢𝑥𝑥
dititik 𝑖, 𝑗 + 1 (pada waktu 𝑗 + 1), diperoleh 𝑢𝑥𝑥 𝑥, 𝑡 = 𝑐2
𝑢𝑖+1,𝑗 +1− 2𝑢𝑖,𝑗 +1+ 𝑢𝑖−1,𝑗 +1
ℎ2 ,
(18) dan untuk 𝑢𝑥𝑥 di titik 𝑖, 𝑗 (pada waktu𝑗)
𝑢𝑥𝑥 𝑥, 𝑡 = 𝑐2
𝑢𝑖+1,𝑗− 2𝑢𝑖,𝑗 + 𝑢𝑖−1,𝑗
ℎ2 , (19)
sehingga diperoleh persamaan beda untuk metode Crank-Nicholson yaitu 𝑢𝑖,𝑗 +1− 𝑢𝑖,𝑗 𝑘 = 𝑐2 2 𝑢𝑖+1,𝑗 +1− 2𝑢𝑖,𝑗 +1+ 𝑢𝑖−1,𝑗 +1 ℎ2 +𝑢𝑖+1,𝑗− 2𝑢𝑖,𝑗 + 𝑢𝑖−1,𝑗 ℎ2 . (20) Persamaan (20) disederhanakan menjadi
𝑢𝑖+1,𝑗− 𝑢𝑖,𝑗 = 𝑐2 𝑘 2ℎ2 𝑢𝑖+1,𝑗 +1− 2𝑢𝑖,𝑗 +1+ 𝑢𝑖−1,𝑗 +1 + 𝑢𝑖+1,𝑗− 2𝑢𝑖,𝑗 + 𝑢𝑖−1,𝑗 , dengan substitusi 𝑟 = 𝑐2 𝑘 ℎ2 , menjadi 2(𝑢𝑖+1,𝑗− 𝑢𝑖,𝑗) = 𝑟 𝑢𝑖+1,𝑗 +1− 2𝑢𝑖,𝑗 +1 + 𝑢𝑖−1,𝑗 +1 + 𝑢𝑖+1,𝑗− 2𝑢𝑖,𝑗 + 𝑢𝑖−1,𝑗 ,
dengan mengumpulkan waktu 𝑗 + 1 ke ruas kiri dan waktu 𝑗 ke ruas kanan, menjadi
2 + 2𝑟 𝑢𝑖,𝑗 +1− 𝑟 𝑢𝑖+1,𝑗 +1+ 𝑢𝑖−1,𝑗 +1 =
2 − 2𝑟 𝑢𝑖,𝑗+ 𝑟 𝑢𝑖+1,𝑗+ 𝑢𝑖−1,𝑗 . (21)
Dengan demikian metode Crank-Nicholson memiliki akurasi 𝑂 ∆𝑡2, ∆𝑥2 .
III. PEMBAHASAN
Untuk menerapkan metode tersebut dalam perhitungan dibuat suatu simulasi domain bidang yaitu sebuah benda logam batang yang diisolasi secara membujur dengan panjang 1 kemudian pada ujung-ujung batang dipertahankan temperaturnya 00C. Temperatur awal pada batang diberikan oleh fungsi 𝑓 𝑥, 𝑡 = 4𝑥 − 4𝑥2, lihat gambar 5, dengan kata lain
dari persamaan (6) dengan kondisi awal 𝑢 𝑥, 0 = 𝑓 𝑥 = 4𝑥 − 4𝑥2, untuk 𝑡 = 0 dan 0 ≤ 𝑥 ≤ 1 dan
kondisi batas𝑢(0, 𝑡) = 𝑢(1, 𝑡) = 0 untuk 𝑥 = 0 dan𝑥 = 1,dan 0 ≤ 𝑡 ≤ 0.20.
Disini kita mengambil ukuran ∆𝑥 = ℎ = 0.2 dan ∆𝑡 = 𝑘 = 0.02 dan untuk nilai 𝑐 = 1, maka 𝑟 = 0.5, dimana 𝑟 = 𝑐2 𝑘
ℎ2 .Agar lebih mudah untuk
perhitungan gambar 5 dapat dibuat grid dengan kisi-kisi berinterval sama seperti gambar 6 [4]. Jadi dengan ℎ = 0.2 titik-titik grid menjadi 𝑛 = 6 kolom dan dengah 𝑘 = 0.02 titik-titik grid menjadi 𝑚 = 11 baris.
Gambar 5. Batang logam yang diisolasi
A. Penyelesaian dengan Metode Eksplisit
Pada skema eksplisit, variabel pada waktu 𝑗 + 1dihitung berdasarkan variabel pada waktu𝑗yang sudah diketahui.
Penerapan metode Eksplisit, dengan menggunakan persamaan (13)dengan 𝑟 = 0.5, menghasilkan
𝑢𝑖,𝑗 +1 = 0.5𝑢𝑖+1,𝑗+ 0.5𝑢𝑖−1,𝑗, (22)
untuk𝑗 = 0 berlaku kondisi awal, 𝑗 = 0, 𝑖 berjalan dari 𝑖 = 0 sampai 𝑖 = 5,
𝑖 = 0,1,2,3,4,5 (gambar 6), yaitu untuk kondisi awal: 𝑗 = 0 𝑖 = 0,𝑢0,1= 𝑓 𝑥 = 4𝑥 − 4𝑥2 = 4 0.00 − 4(0.00)2= 0.00 𝑖 = 1,𝑢1,1= 𝑓 𝑥 = 4𝑥 − 4𝑥2 = 4 0.20 − 4(0.20)2= 0.64 𝑖 = 2,𝑢2,1= 𝑓 𝑥 = 4𝑥 − 4𝑥2 = 4 0.40 − 4(0.40)2= 0.96 𝑖 = 3,𝑢3,1= 𝑓 𝑥 = 4𝑥 − 4𝑥2 = 4 0.60 − 4(0.60)2= 0.96
𝑖 = 4,𝑢4,1 = 𝑓 𝑥 = 4𝑥 − 4𝑥2
= 4 0.80 − 4(0.80)2= 0.64
𝑖 = 5,𝑢5,1 = 𝑓 𝑥 = 4𝑥 − 4𝑥2
= 4 1.00 − 4(1.00)2= 0.00.
Untuk selanjutnya hitungan dilakukan dengan memasukan nilai dari titik-titik yang sudah diketahui ke persamaan (22) untuk mendapatkan nilai dari titik-titik berikutnya, dan hitungan dilakukan dari 𝑖 = 1 sampai dengan 𝑖 = 4 dan dari 𝑗 = 1 sampai 𝑗 = 10 karena adanya syarat batas.Dari perhitungan keseluruhan dengan Metode Eksplisit didapat Tabel 1.
Gambar 6. Grid untuk gambar 5
B. Penyelesaian dengan Metode Crank-Nicholson Skema Crank-Nicholson merupakan pengembangan dari skema Eksplisit dan skema Implisit. Pada skema Eksplisit, pendekatan solusi 𝑢𝑖,𝑗 +1 dihitung menggunakan jaringan titik 𝑖, 𝑗.
Sedangkan pada skema Implisit pendekatan solusi 𝑢𝑖,𝑗dihitung menggunakan jaringan titik 𝑖, 𝑗 + 1, pada
skema Crank-Nicholson pendekatan solusi 𝑢𝑖,𝑗 +1
dihitung menggunakan jaringan titik 𝑖, 𝑗 dan jaringan titik 𝑖, 𝑗 + 1.
Tabel 1. Hasil perhitungan distribusi temperatur menggunakan metode Eksplisit dengan 𝑟 = 0.5
Penerapan metode Crank-Nicholson, dengan menggunakan persamaan (21) dengan 𝑟 = 0.5, menghasilkan:
−0.5𝑢𝑖−1,𝑗 +1+ 3𝑢𝑖,𝑗 +1− 0.5𝑢𝑖+1,𝑗 +1
= 0.5𝑢𝑖−1,𝑗+𝑢𝑖,𝑗+ 0.5𝑢𝑖+1,𝑗. 23
Untuk 𝑗 = 0 berlaku kondisi awal, sama halnya dengan penyelesaian pada skema Eksplisit, untuk 𝑗 = 0, 𝑖 berjalan dari 𝑖 = 0 sampai 𝑖 = 5, 𝑖 = 0,1,2,3,4,5, dan 𝑗 = 0,1,2,3,4,5,6,7,8,9,10, sehingga diperoleh nilai awal yang sama dengan penyelesaian pada metode Eksplisit. Selanjutnya perhitungan dilakukan dengan memasukan nilai awal dan nilai batas pada persamaan (23), untuk 𝑗 = 1,2,3,4,5,6,7,8,9,10, dan 𝑖 = 1,2,3,4, untuk 𝑖 = 0 dan 𝑖 = 5 tidak perlu dihitung karena nilainya sudah diketahui dari nilai batas.
Misal untuk 𝑗 = 1 dan 𝑖 = 1,2,3,4 diperoleh sistem persamaan, empat persamaan dengan 4 variabel yang tidak diketahui: 3𝑢1,2− 0.5𝑢2,2 = 1.12, −0.5𝑢1,2+ 3𝑢2,2− 0.5𝑢3,2 = 1.76, −0.5𝑢2,2+ 3𝑢3,2− 0.5𝑢4,2= 1.76, −0.5𝑢3,2+ 3𝑢4,2= 1.12. (24) Sistem persamaan (24) dapat ditulis dalam bentuk matriks tridiagonal, yang kemudian penulis selesaikan dengan menggunakan metode sapuan ganda Choleski, sehingga diperoleh nilai titi-titik yang dicari. Dengan cara yang sama kemudian dilakukan perhitungan untuk 𝑗 = 2,3,4,5,6,7,8,9,10, dengan 𝑖 = 1,2,3,4, sehingga diperoleh nilai seluruh titik grid yang dicari.Hasil perhitungan disajikan pada Tabel 2.
Tabel 2. Hasil perhitungan distribusi temperatur menggunakan metode Crank-Nicholson dengan 𝑟 = 0.5
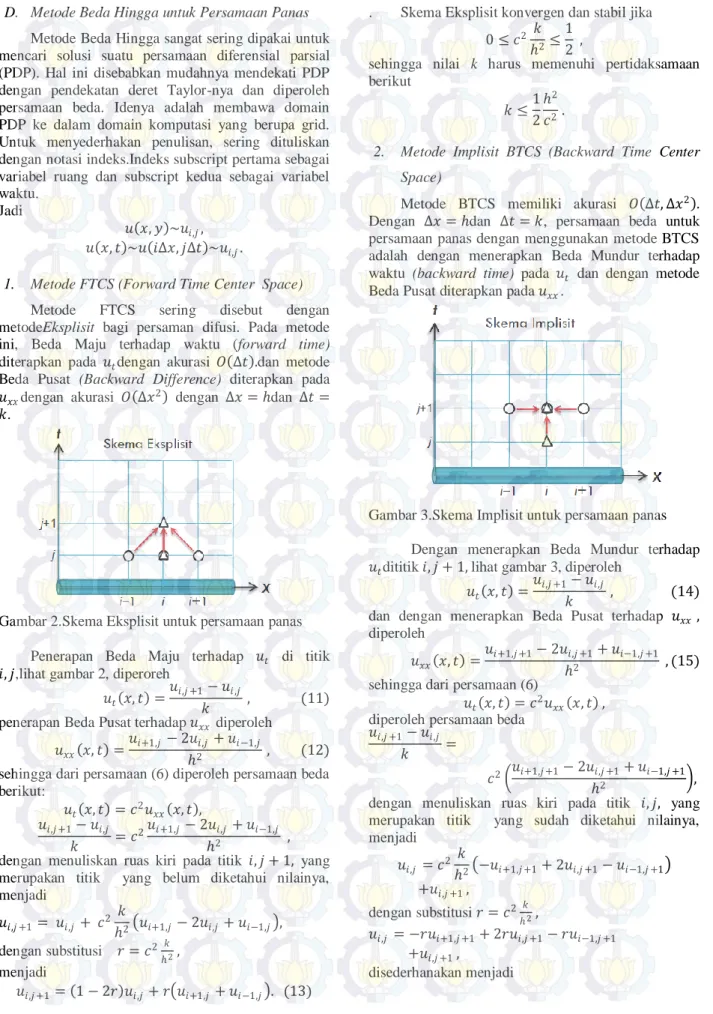
Untuk grafik perbandingan metode Eksplisit dan Crank-Nicholson diberikan berikut ini:
Gambar 7. Grafik nilai temperatur𝑢(𝑥, 𝑡)
keterangan: * : dengan Metode Eksplisit
o : dengan Metode Crank-Nicholson Gambar 8. Grafik nilai temperatur 𝑢(𝑥, 𝑡) terhadap
jarak (𝑥)
keterangan: * : dengan Metode Eksplisit
o : dengan Metode Crank-Nicholson Gambar 9. Grafik nilai temperatur 𝑢(𝑥, 𝑡) terhadap
waktu (𝑡)
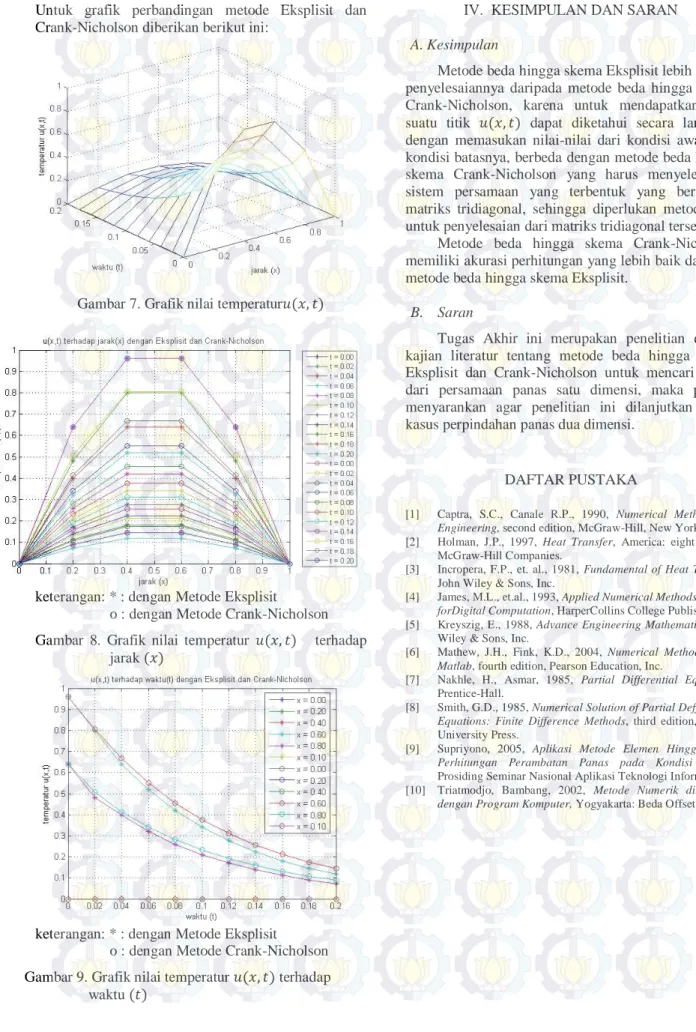
IV. KESIMPULAN DAN SARAN A. Kesimpulan
Metode beda hingga skema Eksplisit lebih mudah penyelesaiannya daripada metode beda hingga skema Crank-Nicholson, karena untuk mendapatkan nilai suatu titik 𝑢(𝑥, 𝑡) dapat diketahui secara langsung dengan memasukan nilai-nilai dari kondisi awal, dan kondisi batasnya, berbeda dengan metode beda hingga skema Crank-Nicholson yang harus menyelesaikan sistem persamaan yang terbentuk yang berbentuk matriks tridiagonal, sehingga diperlukan metode lagi untuk penyelesaian dari matriks tridiagonal tersebut.
Metode beda hingga skema Crank-Nicholson memiliki akurasi perhitungan yang lebih baik daripada metode beda hingga skema Eksplisit.
B. Saran
Tugas Akhir ini merupakan penelitian dengan kajian literatur tentang metode beda hingga skema Eksplisit dan Crank-Nicholson untuk mencari solusi dari persamaan panas satu dimensi, maka penulis menyarankan agar penelitian ini dilanjutkan untuk kasus perpindahan panas dua dimensi.
DAFTAR PUSTAKA
[1] Captra, S.C., Canale R.P., 1990, Numerical Methods for Engineering, second edition, McGraw-Hill, New York. [2] Holman, J.P., 1997, Heat Transfer, America: eight edition,
McGraw-Hill Companies.
[3] Incropera, F.P., et. al., 1981, Fundamental of Heat Transfer, John Wiley & Sons, Inc.
[4] James, M.L., et.al., 1993, Applied Numerical Methods forDigital Computation, HarperCollins College Publishers. [5] Kreyszig, E., 1988, Advance Engineering Mathematics, John
Wiley & Sons, Inc.
[6] Mathew, J.H., Fink, K.D., 2004, Numerical Methods using Matlab, fourth edition, Pearson Education, Inc.
[7] Nakhle, H., Asmar, 1985, Partial Differential Equations, Prentice-Hall.
[8] Smith, G.D., 1985, Numerical Solution of Partial Defferential Equations: Finite Difference Methods, third edition, Oxford University Press.
[9] Supriyono, 2005, Aplikasi Metode Elemen Hingga untuk Perhitungan Perambatan Panas pada Kondisi Tunak, Prosiding Seminar Nasional Aplikasi Teknologi Informasi. [10] Triatmodjo, Bambang, 2002, Metode Numerik dilengkapi