Kelas XII MATEMATIKA WAJIB. Tujuan Pembelajaran. Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.

(1)

1.

2.

3.

4.

5.

6. Dapat menentukan kedudukan titik, garis, dan bidang dalam ruang.

Dapat menentukan jarak titik ke titik.

Dapat menentukan jarak titik ke garis.

Dapat menentukan jarak titik ke bidang.

Dapat menentukan jarak garis sejajar bidang.

Dapat menyelesaikan masalah sehari-hari terkait geometri ruang.

Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.

Tujuan Pembelajaran

Kurikulum 2013 Revisi

A. Kedudukan Titik, Garis, dan Bidang dalam Ruang

1. Pengertian Titik, Garis, dan Bidang a. Titik

b. Garis

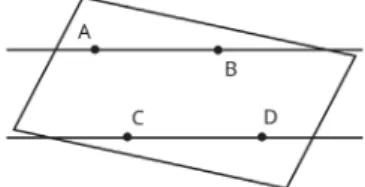
Titik merupakan sesuatu yang memiliki kedudukan, tetapi tidak mempunyai ukuran. Sebuah titik dilukiskan dengan tanda noktah dan diberi huruf kapital.

Contohnya adalah titik Q berikut.

Garis merupakan himpunan titik-titik yang hanya memiliki ukuran panjang, tetapi tidak memiliki ukuran lebar. Garis berdimensi satu. Nama garis dapat ditentukan dengan memakai huruf kecil atau dengan menyebutkan nama segmen garis dari titik pangkal ke titik ujung. Contohnya adalah garis g dan garis AB berikut.

Gambar 1. Titik Q

Kelas XII

MATEMATIKA WAJIB

Geometri Ruang

(2)

c. Bidang

Bidang merupakan himpunan titik-titik yang memiliki ukuran panjang dan lebar.

Bidang berdimensi dua. Nama bidang dapat ditentukan dengan memakai huruf atau simbol yang dituliskan di pojok bidang atau dengan menyebutkan titik-titik sudut dari bidang tersebut. Contohnya adalah bidang ABCD.

Gambar 2. Garis g dan garis AB

Gambar 3. Bidang ABCD

Gambar 4. Sebuah bidang dari tiga titik sebarang

Gambar 5. Sebuah bidang dari sebuah garis dan sebuah titik

2. Aksioma Garis dan Bidang

Aksioma merupakan pernyataan yang disepakati kebenarannya. Terdapat beberapa aksioma, yaitu sebagai berikut.

Melalui dua buah titik sebarang hanya dapat dibuat sebuah garis lurus.

Jika sebuah garis lurus dan sebuah bidang datar mempunyai dua titik persekutuan, maka garis lurus itu terletak seluruhnya pada bidang tersebut.

Melalui tiga buah titik sebarang hanya dapat dibuat sebuah bidang.

Sebuah bidang ditentukan oleh tiga titik sebarang yang tidak segaris.

Sebuah bidang ditentukan oleh sebuah garis dan sebuah titik yang terletak di luar garis tersebut.

Dari aksioma-aksioma tersebut, dapat diturunkan beberapa dalil berikut.

a.

b.

c.

a.

b.

(3)

Gambar 6. Sebuah bidang dari dua buah garis berpotongan

Gambar 7. Sebuah bidang dari dua buah garis sejajar.

Gambar 8. Titik A berimpit dengan titik B

Gambar 10. Titik A terletak pada garis g

Gambar 11. Titik A tidak terletak pada garis g Gambar 9. Titik A tidak berimpit dengan titik B

Sebuah bidang ditentukan oleh dua buah garis berpotongan.

Sebuah bidang ditentukan oleh dua buah garis sejajar.

c.

d.

3. Kedudukan Titik Terhadap Titik, Garis, dan Bidang a. Kedudukan Titik Terhadap Titik

b. Kedudukan Titik Terhadap Garis 1.) Titik berimpit dengan titik

1.) Titik terletak pada garis atau garis melalui titik

2.) Titik tidak terletak pada garis atau titik di luar garis

Suatu titik dikatakan terletak pada garis jika titik tersebut dapat dilalui oleh garis.

Suatu titik dikatakan terletak di luar garis jika titik tersebut tidak dapat dilalui oleh garis.

2.) Titik tidak berimpit dengan titik

(4)

Gambar 12. Titik A terletak pada bidang W

Gambar 13. Titik A tidak terletak pada bidang W

Gambar 14. Garis g dan h saling berimpit

Gambar 15. Garis g dan h saling sejajar

c. Kedudukan Titik Terhadap Bidang

1.) Titik terletak pada bidang atau bidang melalui titik

2.) Titik tidak terletak pada bidang atau bidang tidak melalui titik

Suatu titik dikatakan terletak pada bidang jika titik tersebut dapat dilalui oleh bidang.

4. Kedudukan Garis Terhadap Garis dan Bidang a. Kedudukan Garis Terhadap Garis

1.) Garis berimpit dengan garis

2.) Garis sejajar dengan garis

Aksioma Dua Garis Sejajar

Dua buah garis dikatakan saling berimpit jika garis tersebut terletak pada satu garis lurus, sehingga hanya terlihat sebagai satu garis lurus saja.

Dua buah garis dikatakan saling sejajar jika kedua garis tersebut terletak pada sebuah bidang dan tidak akan pernah berpotongan bahkan jika garis tersebut diperpanjang sampai tak berhingga.

Melalui sebuah titik yang berada di luar sebuah garis, hanya dapat dibuat

sebuah garis yang sejajar dengan garis itu.

(5)

Gambar 16. Garis a sejajar b dan c

Gambar 17. Garis a, b, dan c terletak pada sebuah bidang

Gambar 19. Garis g dan h saling berpotongan

Gambar 20. Garis g dan h saling bersilangan Gambar 18. Garis a dan b menembus bidang

α 3.) Garis berpotongan dengan garis

4.) Garis bersilangan dengan garis Dalil-Dalil tentang Dua Garis Sejajar

Dua buah garis dikatakan berpotongan jika kedua garis tersebut terletak pada satu bidang dan mempunyai sebuah titik persekutuan.

Dua buah garis dikatakan bersilangan (tidak sejajar dan tidak berpotongan) jika kedua garis tersebut tidak memiliki titik potong dan tidak terletak pada sebuah bidang.

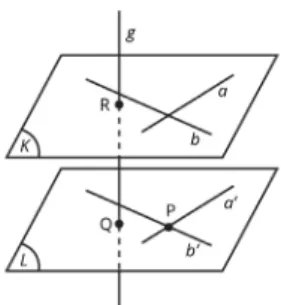
Jika garis a sejajar garis b dan garis b sejajar garis c, maka garis a sejajar dengan garis c.

Jika garis a sejajar garis b dan memotong garis c, garis b sejajar garis a dan juga memotong garis c, maka garis a, b, dan c terletak pada sebuah bidang.

Jika garis a sejajar garis b dan garis b menembus bidang α, maka garis a juga

menembus bidang α.

(6)

Gambar 21. Garis h terletak pada bidang W

Gambar 22. Garis h sejajar bidang W

b. Kedudukan Garis Terhadap Bidang

1.) Garis terletak pada bidang atau bidang melalui garis

2.) Garis sejajar bidang atau bidang sejajar garis

Sebuah garis dikatakan terletak pada bidang jika garis dan bidang tersebut sekurang-kurangnya memiliki dua titik potong atau titik persekutuan.

Sebuah garis dikatakan sejajar bidang jika garis dan bidang tersebut tidak memiliki satu pun titik potong atau titik persekutuan.

Gambar 23. Garis g sejajar dengan bidang

α

Gambar 24. Garis potong antara bidang

α

dan β sejajar terhadap garis g

Dalil-Dalil tentang Dua Garis Sejajar

Jika garis g sejajar dengan garis h dan garis h terletak pada bidang α, maka garis g sejajar dengan bidang α.

Jika bidang α melalui garis g dan garis g sejajar terhadap bidang β, maka garis potong antara bidang α dan bidang β akan sejajar terhadap garis g.

Jika garis g sejajar garis h dan garis h sejajar bidang α, maka garis g sejajar

terhadap bidang α.

(7)

Gambar 22. Garis h sejajar bidang W

3.) Garis menembus atau memotong bidang

Sebuah garis dikatakan memotong atau menembus bidang jika garis dan bidang tersebut hanya mempunyai sebuah titik potong atau titik persekutuan.

Titik persekutuan ini dinamakan juga titik tembus.

Gambar 26. Garis g dan h sejajar terhadap bidang

α

Jika bidang α dan bidang β berpotongan dan masing-masing sejajar terhadap garis g, maka garis potong antara bidang α dan bidang β akan sejajar dengan garis g.

Gambar 28. Bidang W dan bidang V saling berimpit

Gambar 29. Bidang W dan bidang V saling sejajar

5. Kedudukan Bidang Terhadap Bidang a. Bidang berimpit dengan bidang

b. Bidang sejajar dengan bidang

Dalil-Dalil tentang Dua Bidang Sejajar

Dua bidang (misalkan bidang W dan bidang V) dikatakan berimpit jika setiap titik yang terletak di bidang W juga terletak pada bidang V.

Dua bidang dikatakan sejajar jika kedua bidang tersebut tidak mempunyai satu pun titik persekutuan.

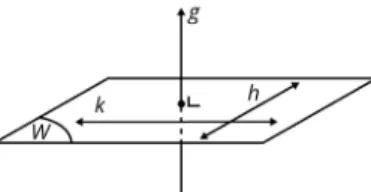
1.) Dua buah bidang akan sejajar jika keduanya tegak lurus pada sebuah garis lurus

atau pada garis-garis lurus sejajar.

(8)

Gambar 30. Bidang K dan L saling sejajar karena keduanya tegak lurus pada sebuah garis lurus

Gambar 31. Bidang K dan L saling sejajar karena terdapat sepasang garis berpotongan yang juga sejajar

Gambar 32. Bidang K dan L saling sejajar karena terdapat garis-garis yang sejajar pada kedua bidang

Gambar 33. Bidang L dapat dibuat melalui titik P di luar bidang K

2.)

3.)

4.)

Dua buah bidang akan sejajar jika sepasang garis berpotongan pada bidang yang satu sejajar dengan garis berpotongan pada bidang lainnya.

Semua garis-garis melalui titik P di luar bidang K yang sejajar dengan bidang K terletak pada sebuah bidang L yang sejajar dengan bidang K.

Melalui titik P di luar bidang K hanya dapat dibuat sebuah bidang yang sejajar

dengan bidang K.

(9)

Gambar 34. Bidang M memotong bidang K dan L yang saling sejajar

5.) Jika dua buah bidang sejajar dipotong oleh bidang ketiga, maka garis-garis potongnya akan selalu sejajar.

Gambar 35. Bidang V dan W saling berpotongan

Gambar 36. Bidang

α

, β, dan γ yang saling berpotongan

c. Bidang berpotongan dengan bidang

d. Tiga bidang berpotongan

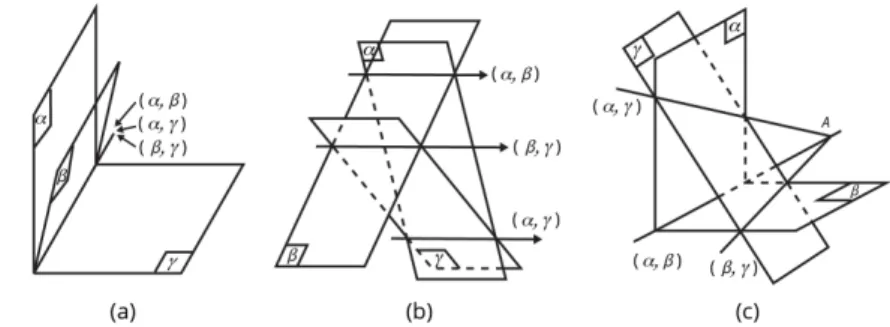
Dua bidang dikatakan berpotongan jika kedua bidang tersebut tepat memiliki sebuah garis persekutuan.

Jika tiga buah bidang (α, β, dan γ) berpotongan serta memiliki tiga buah garis persekutuan, kemungkinan kedudukan dari ketiga garis persekutuan tersebut adalah berimpit (Gambar a), sejajar (Gambar b), atau melalui sebuah titik (Gambar c).

6. Dalil-Dalil tentang Kedudukan Titik, Garis, dan Bidang dalam Ruang

Jika garis g menembus tegak lurus bidang W, maka garis g tegak lurus dengan semua garis yang terletak pada bidang W.

a.

(10)

Gambar 37. Garis g tegak lurus dengan semua garis yang terletak pada bidang W

Jika garis k dan h tidak sejajar dan tegak lurus dengan garis g, serta k dan h terletak pada bidang W, maka bidang W tegak lurus dengan garis g.

Pada kubus ABCD.EFGH, tentukan:

a. kedudukan titik B;

b. kedudukan garis AB; dan c. kedudukan bidang ABCD.

a. Kedudukan titik B pada kubus tersebut antara lain adalah sebagai berikut.

Titik B tidak berimpit dengan titik A, C, D, E, F, G, dan H.

Titik B terletak pada garis AB, BC, dan BF.

Titik B terletak pada bidang ABCD, BCGF, dan ABFE.

Perhatikan gambar berikut.

Pembahasan:

b.

Contoh Soal 1

(11)

Perhatikan kubus ABCD.EFGH berikut.

(1) Garis AG dan rusuk DH saling bersilangan.

(2) Garis EC menembus bidang CDEF.

(3) Bidang ACF dan ACGE saling sejajar.

(4) Garis AC bersilangan tegak lurus dengan garis FD.

Pernyataan yang benar adalah ….

b. Kedudukan garis AB pada kubus tersebut antara lain adalah sebagai berikut.

c. Kedudukan bidang ABCD pada kubus tersebut antara lain adalah sebagai berikut.

Garis AB berpotongan dengan garis AD, BC, AE, dan BF. Hal ini dikarenakan garis-garis tersebut terletak pada sebuah bidang dan memiliki tepat sebuah titik persekutuan.

Garis AB sejajar dengan garis DC, EF, dan HG. Hal ini dikarenakan garis-garis tersebut terletak pada sebuah bidang dan tidak memiliki titik persekutuan.

Garis AB bersilangan dengan garis FC, CG, EH, ED, HD, dan lainnya. Hal ini dikarenakan garis-garis tersebut tidak berpotongan dan tidak pula sejajar (tidak terletak pada satu bidang).

Garis AB terletak pada bidang ABCD dan ABFE. Hal ini dikarenakan garis AB dan bidang-bidang tersebut memiliki dua titik persekutuan atau titik potong, yaitu titik A dan titik B.

Garis AB memotong bidang BCGF dan ADHE. Hal ini dikarenakan garis AB dengan bidang tersebut hanya memiliki satu titik persekutuan atau titik potong, yaitu titik B pada bidang BCGF dan titik A pada bidang ADHE.

Garis AB sejajar dengan bidang CDHG dan EFGH. Hal ini dikarenakan garis AB dan bidang-bidang tersebut tidak memiliki satu pun titik persekutuan.

Bidang ABCD sejajar dengan bidang EFGH. Hal ini dikarenakan kedua bidang tersebut tidak memilki satu pun titik persekutuan atau titik potong.

Bidang ABCD berpotongan dengan bidang ABFE, BCGF, CDHG, dan ADHE. Hal ini dikarenakan bidang ABCD dan bidang-bidang tersebut memiliki tepat sebuah garis persekutuan.

Contoh Soal 2

(12)

Perhatikan masing-masing pernyataan berikut.

(1) Garis AG dan rusuk DH saling bersilangan.

(2) Garis EC menembus bidang CDEF.

(3) Bidang ACF dan ACGE saling sejajar

Dua garis dikatakan bersilangan (tidak berpotongan dan tidak sejajar) jika kedua garis tersebut tidak terletak pada sebuah bidang. Pada gambar terlihat bahwa garis AG dan rusuk DH tidak terletak pada sebuah bidang, tidak sejajar, dan tidak pula berpotongan.

Ini berarti, garis AG dan rusuk DH saling bersilangan (pernyataan benar).

Sebuah garis dikatakan menembus atau memotong bidang jika garis tersebut dan bidang hanya memiliki satu titik persekutuan (titik potong). Pada gambar terlihat bahwa garis EC tidak menembus bidang CDEF, melainkan garis tersebut terletak pada bidang CDEF (pernyataan salah).

Dua bidang dikatakan saling sejajar jika kedua bidang tersebut tidak memiliki satu pun titik persekutuan (titik potong). Pada gambar terlihat bahwa bidang ACF dan ACGE memiliki titik persekutuan, sehingga kedua bidang tersebut berpotongan (pernyataan salah).

Pembahasan:

(13)

(4) Garis AC bersilangan tegak lurus dengan garis FD.

Untuk membuktikan apakah garis AC bersilangan tegak lurus dengan garis FD, perhatikan gambar berikut.

Oleh karena bidang MDNF adalah belah ketupat, maka kedua diagonalnya saling tegak lurus. Ini berarti, garis MN tegak lurus dengan garis FD. Oleh karena garis MN sejajar dengan garis AC, maka garis AC bersilangan tegak lurus dengan garis FD (pernyataan benar).

Jadi, pernyataan yang benar adalah (1) dan (4).

Misalkan titik P adalah titik potong garis FH dan EG, serta titik Q adalah titik potong garis BD dan AC.

Tarik garis PQ yang berpotongan dengan garis FD di tengah-tengah, yaitu di titik R.

Tarik garis MN melalui titik R yang sejajar dengan AC.

Lukis belah ketupat MDNF.

B. Jarak Titik ke Titik

Misalkan terdapat titik A dan titik B sebagai berikut.

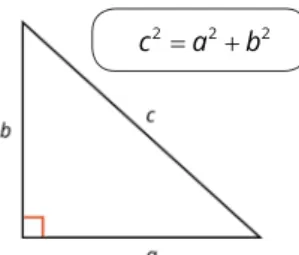
Jarak titik ke titik atau jarak antara dua titik merupakan panjang garis yang menghubungkan kedua titik tersebut. Cara umum yang sering digunakan dalam mencari jarak titik ke titik adalah dengan mengamati posisi kedua titik tersebut, lalu membuat garis bantu sehingga terbentuk suatu bangun datar segitiga siku-siku. Selanjutnya, panjang garis yang dicari ditentukan dengan menggunakan teorema Pythagoras berikut.

Gambar 39. Titik A dan titik B

(14)

Jika diketahui dua titik misalkan titik A dan B dengan koordinat berturut-turut adalah

(

1 1 1

)

A x y z, ,

dan

B

(

x y z2, ,2 2

) , jarak titik A ke titik B dapat ditentukan dengan menggunakan rumus berikut.

Kubus ABCD.EFGH memiliki panjang rusuk 6 cm. Jika titik P berada di tengah-tengah rusuk HE, jarak titik B ke titik P adalah ….

Contoh Soal 3

Perhatikan gambar berikut.

Diagonal bidang = rusuk 2 = 6 2

Diketahui panjang rusuk kubus = 6 cm. Ini berarti, AB = AE = HE = 6 cm.

Oleh karena titik P berada di tengah-tengah HE, maka PE = ½ . HE = ½ . 6 = 3 cm.

Perhatikan bahwa BE merupakan diagonal bidang kubus. Pada kubus, berlaku:

Dengan menggunakan teorema Pythagoras pada segitiga BEP yang siku-siku di E, diperoleh:

Ini berarti, BE 6 2 cm = Pembahasan:

Gambar 40. Segitiga siku-siku sebagai alat bantu

2 2 2

c =a +b

(

1 2

) (

² 1 2

) (

² 1 2

)

²

AB = x −x + y −y + z z−

(15)

Kubus ABCD.EFGH memiliki panjang rusuk 12 cm. Titik P berada di tengah-tengah rusuk GH dan titik Q berada di

₃¹

rusuk AD sedemikian sehingga AQ : QD = 1 : 2. Jarak antara titik P dan titik Q adalah ….

Contoh Soal 4

Perhatikan gambar berikut.

Dengan menggunakan teorema Pythagoras, diperoleh:

Panjang QR pada segitiga RDQ (siku-siku di D)

Diketahui panjang rusuk kubus = 12 cm. Ini berarti, AD = PR = CD = 12 cm.

Misalkan titik R adalah titik tengah CD, sehingga RD = ½.CD = ½.12 = 6 cm.

Oleh karena titik Q berada di

¹

3

rusuk AD, maka AQ = ¹⁄

3

. AD = ¹⁄

3

.12 = 4 cm dan QD =

²⁄

3

. AD = ²⁄

3

.12 = 8 cm.

Jadi, jarak titik B ke titik P adalah 9 cm.

Pembahasan:

( )

2 2

BP BE PE 6 2 3 72 9 81 9 cm

= +

=

2 2

QR = RD + QD

= 6 + 8

= 36 + 64

= 100

=10 cm

(16)

A

A' K

C. Jarak Titik Ke Garis

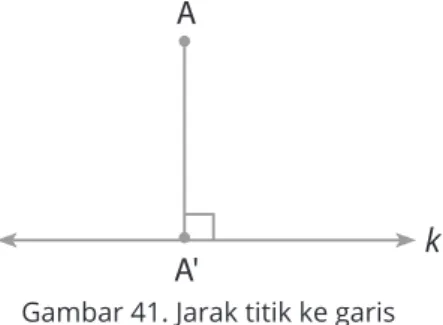
Jarak titik ke garis didefinisikan sebagai ruas garis tegak lurus yang menghubungkan garis dengan titik tersebut.

Jarak titik A ke garis k adalah ruas garis AA’, yaitu ruas garis tegak lurus yang menghubungkan garis k dengan titik A.

k

Jarak titik H pada garis AC adalah ….

Contoh Soal 5

Perhatikan gambar berikut.

Pembahasan:

H E

A 18 cm B

D C F

G

E

D C H'

F H G

Jadi, jarak antara titik P dan titik Q adalah 2 61 cm . Panjang PQ pada segitiga PRQ (siku-siku di R)

Gambar 41. Jarak titik ke garis

2 2

PQ = QR +PR = 10 +12 = 100 + 144 = 244 = 4(61) = 2 61 cm

(17)

Garis HH’ adalah garis tegak lurus yang menghubungkan titik H dengan AC.

Perhatikan diagonal bidang DB.

Perhatikan segitiga siku-siku HDH’.

Contoh Soal 6

Jarak D ke garis HP adalah ….

Dengan menggunakan persamaan luas segitiga, diperoleh:

Perhatikan dengan baik bahwa segitiga HDP adalah segitiga siku-siku di D dengan DP =

9 2

dan HP =

9 6

.

Jarak titik D ke HP adalah panjang garis DD’ pada gambar berikut:

Perhatikan gambar berikut.

Pembahasan:

A B

D C

E F

P

18 cm

G H

D P

D' H

DH’= 1 2 DB = = 9

1 2 18 2

2 HH’= DH’ +DH 9 +18 cm

2 2

= ( )

=

2 9 6

Jadi, jarak titik H pada garis AC adalah 9 6 cm .

(18)

Jarak titik H ke bidang BCGF adalah ….

Contoh Soal 7

Perhatikan gambar berikut.

Pembahasan:

A 8 cm B

D C

E F

G H

A 8 cm B

D C

E F

G H

D. Jarak Titik Ke Bidang

Jarak titik ke bidang pada bangun dimensi tiga didefinisikan sebagai ruas garis terpendek tegak lurus bidang yang menghubungkan titik dengan bidang tersebut.

P

A'

Jarak titik A ke bidang persegi adalah ruas garis AA’.

Jadi, jarak titik D ke garis HP adalah cm.

Gambar 42. Jarak titik ke bidang

(19)

Jarak titik T pada bidang ABCD adalah ….

Jarak titik H ke bidang BCGF adalah garis HG karena garis HG adalah garis terpendek yang menghubungkan titik H tegak lurus bidang BCGF.

Jadi, jarak titik H ke bidang BCGF adalah 8 cm.

Perhatikan limas persegi beraturan tersebut. Garis T' akan membagi garis diagonal bidang AC menjadi 2 ruas garis yang sama panjang, sehingga:

Dengan demikian, panjang TT' adalah sebagai berikut.

Jadi, jarak titik T pada bidang ABCD adalah

94

cm.

Jarak titik T pada bidang ABCD adalah ruas garis TT’ yang tegak lurus bidang ABCD sebagaimana gambar berikut.

Contoh Soal 8

Perhatikan gambar limas persegi beraturan berikut.

Pembahasan:

A 10 cm B

D C T

12 cm

A 10 cm B

D C T'

T

12 cm

(20)

Ini bearti:

Dengan demikian, diperoleh:

Pada limas beraturan, titik Q disebut sebagai titik berat segitiga yang terbentuk dari perpotongan garis-garis berat. Titik Q selalu membagi garis berat AP dengan perbandingan AQ : QP = 2 : 1. Pada segitiga ABC, berlaku:

BP = BC = 6

1 2

A Q C

B P D

12 cm 8 3cm

Contoh Soal 9

Jarak titik D pada alas limas segitiga beraturan tersebut adalah ….

Jarak titik D pada alas limas segitiga beraturan adalah ruas garis DQ yang tegak lurus terhadap bidang ABC.

Perhatikan gambar berikut ini.

Pembahasan:

A C

B D

12 cm 8 3cm

(21)

Perhatikan segitiga siku-siku AQD yang siku-siku di Q. Pada segitiga tersebut, berlaku:

Jadi, jarak titik D pada alas limas segitiga adalah 12 cm.

Jarak titik C pada bidang BDG adalah ….

Cara lain untuk mencari jarak titik C ke bidang BDG adalah sebagai berikut.

Cari bidang melalui C dan berpotongan dengan BDG, misalnya ABCD.

Tarik garis tegak lurus BD yang melalui titik C dan terletak pada bidang BDG.

Pada gambar tersebut, garisnya adalah PC ⊥ BD dan PG ⊥ BD.

Bidang ABCD adalah salah satu bidang yang melalui C dan berpotongan dengan BDG di sepanjang garis BD.

Perhatikan gambar berikut.

Pembahasan:

A 6 cm B

D C

E F

G H

A 6 cm B

D C

E F

G H

A 6 cm B

C P

D

E F

G H

Contoh Soal 10

(22)

E. Jarak Garis Sejajar Bidang

Jarak suatu garis yang sejajar bidang adalah panjang ruas garis yang menghubungkan garis tersebut dan bidang secara tegak lurus.

k

A A'

V

Dengan menggunakan prinsip luas segitiga, diperoleh:

Jadi, jarak titik C pada bidang BDG adalah 2 3 cm.

Jarak titik C pada BDG menjadi jarak titik C pada garis PG, yaitu garis CC’.

Perhatikan segitiga siku-siku GCP siku-siku di C, dimana

A 6 cm B

C P

D C'

E F

G H

(23)

Pada gambar tersebut garik k sejajar bidang V. Jarak garis k pada bidang V adalah ruas AA’ yang menghubungkan garis k dan bidang V. Pada prinsipnya, jarak garis yang sejajar bidang dapat diubah dengan menghitung jarak titik pada garis ke bidang tersebut.

Jarak garis AD pada bidang TBC adalah ….

Ambil titik P pada garis AD, sehingga P titik tengah AD.

Dengan menggunakan teorema Pythagoras, diperoleh:

Perhatikan segitiga TPQ yang merupakan segitiga sama kaki dengan TP = TQ.

Contoh Soal 11

Perhatikan gambar berikut ini.

Pembahasan:

A 8 cm B

6 cm 15 cm

D C T

A B

Q D C

T

P

P'

8 cm 6 cm

15 cm

P Q

R T

P'

(24)

A B D C

E F

P

G H

Perhatikan segitiga GPQ yang siku-siku di titik P.

P

P' G

Misal kita ambil titik P pada garis AP. Sekarang, kita akan menghitung jarak titik P pada bidang BDG. Titik P terletak pada bidang ACGE yang tepat memotong BDG secara tegak lurus di garis GQ.

A B

D C

E F

P

G H

Perhatikan gambar berikut.

Dengan menggunakan prinsip kesamaan luas segitiga, diperoleh:

Jadi, jarak garis AD pada bidang TBC adalah

⁴⁰

9 3

cm.

Diketahui kubus ABCD.EFGH dengan panjang rusuk 24 cm. Jika titik P adalah pusat bidang EFGH, jarak antara garis AP ke bidang BDG adalah ….

Pembahasan:

Contoh Soal 12

Q

(25)

Dengan menggunakan persamaan luas segitiga, diperoleh:

Jadi, jarak garis AP pada bidang BDG adalah

8 3

cm.

F. Menyelesaikan Masalah Sehari-hari Terkait Geometri Ruang

Konsep geometri ruang banyak diaplikasikan dalam kehidupan sehari-hari. Sebagai contoh, para arsitektur yang merancang bangunan modern, harus menghitung dahulu segala sesuatunya dengan sangat teliti agar didapatkan bangunan yang kokoh dan menakjubkan. Para arsitektur akan membuat gambar, sketsa, ataupun model bangunan dengan menggunakan konsep geometri ruang.

Konsep geometri ruang juga dapat diilustrasikan pada kejadian-kejadian di sekitar kita.

Misalkan terdapat dua ekor burung yang masing-masing bertengger pada kabel listrik yang sama dengan posisi berbeda. Kabel listrik dapat diilustrasikan sebagai garis dan burung sebagai titik. Dengan demikian, kejadian ini dapat dianalogikan sebagai sebuah titik yang terletak pada suatu garis. Contoh lainnya adalah pada permainan sepak bola.

Misalkan bola adalah titik dan lapangan adalah bidang. Dalam konsep kedudukan titik terhadap bidang, ketika bola berada di luar lapangan, berarti titik terletak di luar bidang (tidak melalui bidang).

Contoh Soal 13

Ani memelihara seekor burung kenari yang diletakkan di dalam sangkar berbentuk kubus

dengan luas permukaan 9.600 cm². Pada saat kenari tersebut bermain dalam sangkar,

tiba-tiba makanannya terlempar dan tersangkut di salah satu sudut atas sarang. Posisi

kenari saat itu berada di tengah-tengah alas sangkar. Kenari ingin mengambil makanannya

itu. Jarak terdekat agar makanan tersebut dapat diambil oleh kenari adalah .…

(26)

Ini berarti, rusuk kubus = 40 cm. Dengan demikian, panjang CG = 40 cm.

Perhatikan bahwa AC merupakan diagonal bidang. Pada kubus, berlaku:

Ini berarti AC = 40 2 cm. Dengan demikian, PC = 1 . AC = . 40 2 = 20 2 1

2 2 cm.

Dengan menggunakan teorema Pythagoras pada segitiga GPC (siku-siku di C), diperoleh:

Jadi, jarak terdekat agar makanan tersebut dapat diambil oleh kenari adalah 20 6 cm . Diketahui luas permukaan kubus = Lp

kubus

= 9.600 cm². Misalkan r = rusuk kubus, maka:

2 2

2

6 9.600 6

9.600 6 1.600

1600 40

kubus

Lp r r

r r

r r r

= × ×

⇔ = ×

⇔ =

Misalkan sangkar burung tersebut adalah kubus ABCD.EFGH, dengan posisi kenari di titik P dan posisi makanan yang tersangkut di titik G. Situasi pada soal dapat digambarkan sebagai berikut.

Jarak terdekat agar makanan tersebut dapat diambil oleh kenari sama dengan panjang ruas garis PG. Untuk menentukan panjang ruas garis PG, tentukan dahulu panjang rusuk kubusnya.

Pembahasan:

Diagonal bidang = rusuk 2

= 40 2

( )

2 2

PG = PC + CG = 20 2 + 40

= 800 + 1600 = 2400 = 400 (6) = 20 6 cm

(27)

Contoh Soal 14

Lapangan futsal indoor dipasangi jaring-jaring pembatas, sehingga terlihat seperti balok tanpa tutup dengan panjang 24 m, lebar 16 m, dan tinggi 12 m. Seorang pemain ingin menendang bola. Posisi bola ada di pojok lapangan seberang gawang. Tinggi gawang adalah ¹⁄

3

dari tinggi jaring-jaring dan posisi tengah gawang berada di tengah-tengah salah satu sisi lebar lapangan. Ketika bola ditendang, ternyata tepat mengenai posisi tengah atas gawang. Jarak tendangan pemain tersebut adalah ….