Institutional Repository | Satya Wacana Christian University: Enkripsi dan Dekripsi Data Teks Menggunakan Advanced Encryption Standard (AES) Untuk Management Password T1 622010002 BAB II

5 BAB II

DASAR TEORI

Pada bagian ini akan dibahas mengenai dasar teori yang digunakan dalam pembuatan sistem yang akan dirancang dalam skripsi ini.

2.1. Enkripsi dan Dekripsi

Proses menyandikan plaintext menjadi ciphertext disebut enkripsi (encryption) atau

enciphering (standard nama menurut ISO 7498-2) sedangkan proses mengembalikan

ciphertext mejadi plaintext disebut dekripsi (decryption) atau deciphering (standard ISO

7498-2).[2]

Plaintext merupakan pesan atau data dalam bentuk aslinya yang dapat terbaca. Sedangkan Ciphertext merupakan pesan dalam bentuk tersembunyi. [1]

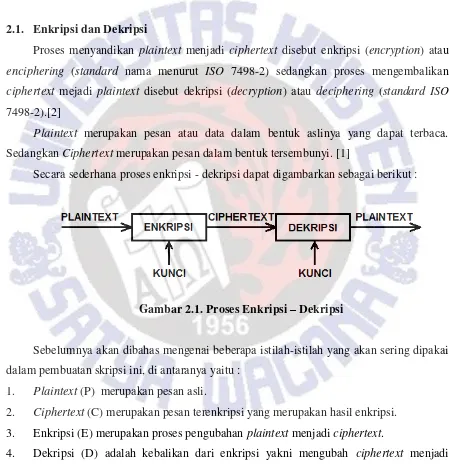
Secara sederhana proses enkripsi - dekripsi dapat digambarkan sebagai berikut :

Gambar 2.1. Proses Enkripsi – Dekripsi

Sebelumnya akan dibahas mengenai beberapa istilah-istilah yang akan sering dipakai dalam pembuatan skripsi ini, di antaranya yaitu :

1. Plaintext (P) merupakan pesan asli.

2. Ciphertext (C) merupakan pesan terenkripsi yang merupakan hasil enkripsi. 3. Enkripsi (E) merupakan proses pengubahan plaintext menjadi ciphertext.

4. Dekripsi (D) adalah kebalikan dari enkripsi yakni mengubah ciphertext menjadi

plaintext, sehingga berupa data awal/asli.

6

Secara umum operasi enkripsi dan dekripsi dapat diterangkan secara matematis sebagai berikut :

EK (P) = C (Proses Enkripsi) DK (C) = P (Proses Dekripsi)

Pada saat proses enkripsi kita menyandikan pesan P dengan suatu kunci K lalu dihasilkan pesan C. Sedangkan pada proses dekripsi, pesan C tersebut diuraikan dengan menggunakan kunci K sehingga dihasilkan pesan P yang sama seperti pesan sebelumnya.

Terdapat dua jenis metode berdasarkan kunci yang akan digunakan saat proses enkripsi maupun dekripsi yaitu:

1. Algoritma Simetrik

Algoritma Simetrik adalah algoritma yang menggunakan kunci yang sama untuk proses enkripsi maupun dekripsi. Dengan kata lain proses enkripsi dapat dihitung menggunakan kunci dekripsi dan begitu pula sebaliknya, proses dekripsi dapat dihitung menggunakan kunci enkripsi. Pada algoritma simetrik diperlukan kesepakatan antara pengirim dan penerima pesan pada suatu kunci sebelum dapat berkomunikasi secara aman. Algoritma simetrik dikelompokkan menjadi dua jenis, yaitu stream cipher dan block cipher. Stream cipher beroperasi bit per bit pada suatu waktu. Sedangkan block cipher

beroperasi per kelompok-kelompok bit yang disebut blok pada suatu waktu.

2. Algoritma Asimetrik

7 2.2. Advanced Encryption Standard (AES)

Pada skripsi ini akan membahas Algoritma Simetrik lebih lanjut dikarenakan menggunakan metode Advanced Encryption Standard (AES) lebih baik dibanding dengan metode seperti Data Encryption Standard (DES) ataupun yang lainya yang ada pada algoritma simetrik.

Pemilihan metode AES karena AES dinilai memiliki keamanan yang lebih baik daripada sistem sandi DES. [1] Untuk itu NIST (National Institute of Standards and Technology) membuat sayembara untuk menggantikan DES dengan sebuah sistem penyandian yang disebut Advanced Encryption Standard pada tanggal 12 September 1997.

NIST memberikan spesifikasi AES, yaitu harus memiliki panjang blok 128 bit dan mampu mendukung panjang kunci 128,192,256. [1]

Setelah beberapa seleksi, NIST memilih sistem penyandian Rijndael yang dikembangkan oleh Joan Daemen dan Vincent Rijment sebagai sistem penyandian AES

pada tahun 2000. [1]

AES merupakan standar enkripsi dekripsi dengan kunci simetris yang menggantikan pendahulunya yaitu DES. Jenis AES terbagi 3, yaitu AES-128, AES-192 dan AES-256. Angka-angka yang berada di belakang kata AES merupakan panjang kunci yang digunakan pada tiap-tiap AES.

Selain itu AES-128 round yang digunakan sebanyak 10 round, AES-192 menggunakan 12 round, dan AES-256 menggunakan 14 round.

2.3. Contoh Perhitungan

Pada contoh perhitungan akan dijelaskan tahap – tahap perhitungan AES, baik untuk proses enkripsi maupun dekripsi.

2.3.1Menghitung Enkripsi AES

8

Secara garis besar, desain enkripsi AES dapat diberikan oleh gambar dibawah ini.

State

AddRoundKey

SubBytes

ShiftRows

MixColumns

AddRoundKey

SubBytes

ShiftRows

MixColumns

AddRoundKey

SubBytes

ShiftRows

AddRoundKey

State Pra Ronde

Ronde 1

Ronde 2

Ronde 10 dst

Ekspansi Kunci AES

Kunci Asli

Ekspansi Kunci ke-1

Ekspansi Kunci ke-2

Ekspansi Kunci ke-10

dst

Gambar 2.2. Struktur Enkripsi AES [1]

Pada awalnya teks asli direorganisasi sebagai sebuah state. Kemudian sebelum ronde 1 dimulai blok teks asli dicampur dengan kunci ronde ke-0 (transformasi ini disebut

9

Berikut ini merupakan tabel konstan Rcon dalam hexadecimal: Tabel 2.1. Tabel Konstan Rcon [1]

01 02 04 08 10 20 40 80 1b 36 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00

Berikut merupakan cara memperoleh ekspansi kunci sebelum digunakan dalam proses perhitungan AES.

2b 28 ab 09 a0 88 23 2a 7e ae f7 cf fa 54 a3 6c 15 d2 15 4f fe 2c 39 76 16 a6 88 3c 17 b1 39 05

Kolom terakhir kunci awal ditukar ke atas satu kali menjadi :

cf 8a

4f Disubtitusi menjadi 84

3c eb

09 01

Setelah itu disubtitusi dengan tabel SubBytes kemudian di XOR dengan kolom ke-1 dan di XOR dengan kolom ke-1 pada tabel konstan Rcon sehingga menjadi :

2b 8a 01 a0

7e XOR 84 XOR 00 = fa

15 eb 00 fe

16 01 00 17

10

Lalu ambil data pada kolom ke-2 kunci awal dan di XOR dengan hasil sebelumnya.

28 a0 88

ae XOR fa = 54

d2 fe 2c

a6 17 b1

Lalu ambil data pada kolom ke-3 kunci awal dan di XOR dengan hasil sebelumnya.

ab 88 23

f7 XOR 54 = a3

15 2c 39

88 21 39

Lalu ambil data pada kolom ke-4 kunci awal dan di XOR dengan hasil sebelumnya

09 23 2a

cf XOR a3 = 6c

4f 39 76

3c 39 05

Dan langkah diatas diulang dengan kolom ke-2 tabel konstan Rcon hingga selesai (kolom ke-10 tabel konstan Rcon).

Berikut merupakan contoh data beserta perhitungan untuk masing-masing tahapan yang dilakukan pada AES:

a. Pre Round (Data xor Key)

Data asli : Key awal: Hasil:

11 b. SubBytes

Pada tahap ini hasil dari pre round disubtitusi dengan tabel berikut: (Contoh: Data dengan hex 19 disubtitusi dengan tabel subtitusi menjadi d4)

Tabel 2.2. Tabel Subtitusi untuk Transformasi Subbytes [1]

0 1 2 3 4 5 6 7 8 9 a b c d e f

0 63 7c 77 7b f2 6b 6f c5 30 01 67 2b fe d7 ab 76

1 ca 82 c9 7d fa 59 47 f0 ad d4 a2 af 9c a4 72 c0

2 b7 fd 93 26 36 3f f7 cc 34 a5 e5 f1 71 d8 31 15

3 04 c7 23 c3 18 96 05 9a 07 12 80 e2 eb 27 b2 75

4 09 83 2c 1a 1b 6e 5a a0 52 3b d6 b3 29 e3 2f 84

5 53 d1 00 ed 20 fc b1 5b 6a cb be 39 4a 4c 58 cf

6 d0 ef aa fb 43 4d 33 85 45 f9 02 7f 50 3c 9f a8

7 51 a3 40 8f 92 9d 38 f5 bc b6 da 21 10 ff f3 d2

8 cd 0c 13 ec 5f 97 44 17 c4 a7 7e 3d 64 5d 19 73

9 60 81 4f dc 22 2a 90 88 46 ee b8 14 de 5e 0b db

a e0 32 3a 0a 49 06 24 5c c2 d3 ac 62 91 95 e4 79

b e7 c8 37 6d 8d d5 4e a9 6c 56 f4 ea 65 7a ae 08

c ba 78 25 2e 1c a6 b4 c6 e8 dd 74 1f 4b bd 8b 8a

d 70 3e b5 66 48 03 f6 0e 61 35 57 b9 86 c1 1d 9e

e e1 f8 98 11 69 d9 8e 94 9b 1e 87 e9 ce 55 28 df

f 8c a1 89 0d bf e6 42 68 41 99 2d 0f b0 54 bb 16

Sehingga data setelah hasil pre-round di subtitusi dengan tabel menjadi: d4 e0 b8 1e

27 bf b4 41

11 98 5d 52

ae f1 e5 30

c. ShiftRows

Pada tahap ini data yang dihasilkan pada tahap sebelumnya (SubBytes) digeser ke kiri sesuai dengan gambar di bawah ini:

12

Sehingga data setelah hasil SubBytes di ShiftRows menjadi:

d. MixColumns

[

] [

] [ ]

Syarat:

- Jika msb data berawalan dengan 1 maka di left shift dan xor tetap

- Jika msb data berawalan dengan 0 maka di left shift tapi xor dihilangkan. - Tetapan untuk pengali 02 yaitu disubtitusi menjadi “xor1B”

- Karena 03 (11) merupakan 10 xor 01 maka akan dipecah menjadi pengali 02 (yang berarti juga akan disubtitusi menjadi xor 1B) dan 01

Contoh perhitungan perkaliannya: 1. Perhitungan untuk baris ke-1

 d4 . 02

 11010100 xor 00011011

 10101000 (di left shift dan xor tetap)  00011011 XOR

 10110011  bf . 03

 10111111 . ( 10 xor 01)

 (10111111 . 10) xor (10111111 . 01)  (01111110 xor 00011011) xor 10111111  01100101 xor 10111111

 11011010 d4 e0 b8 1e

bf b4 41 27

5d 52 11 98

13  5d . 01

 01011101 . 01  01011101  30 . 01

 00110000 . 00000001  00110000

 Lalu hasil masing-masing di xor semua menjadi 10110011

11011010 01011101 00110000 xor

00000100 (dalam hex = 04)

2. Perhitungan untuk baris ke-2  d4 . 01

 11010100 . 00000001  11010100

 bf . 02

 10111111 . 10

 01111110 . 10 (di left shift dan xor tetap)  01111110 xor 00011011

 01100101  5d . 03

 (01011101 . 10) xor (01011101 . 01)

 10111010 (xor 1B dihilangkan) xor 01011101  11100111

 30 . 01

14

 Lalu hasil masing-masing di xor semua menjadi 11010100

01100101 11100111 00110000 xor 01100110

3. Perhitungan untuk baris ke-3  d4 . 01

 11010100 . 01  11010100  bf . 01

 10111111 . 01  10111111  5d . 02

 01011101 . 10

 10111010 (hanya di left shift, xor dihilangkan)  30 . 03

 (00110000 . 10) xor (00110000 . 01)  (01100000) xor (00110000)

 01010000

 Lalu hasil masing-masing di xor semua menjadi 11010100

15 4. Perhitungan untuk baris ke-4

 d4 . 03

 (11010100 . 10) xor (11010100 . 01)  (10101000 xor 00011011) xor (11010100)  10110011 xor 11010100

 01100111  bf . 01

 10111111 . 01  10111111  5d . 01

 01011101 . 01  01011101  30 . 02

 00110000 . 10

 01100000 (hanya di left shift, xor dihilangkan)  Lalu hasil masing-masing di xor semua menjadi

16 [

] [

] [ ]

Sehingga data setelah hasil ShiftRows di MixColumns menjadi: 04 e0 48 28

66 cb f8 06

81 19 d3 26

e5 9a 7a 4c

e. AddRoundKey

Pada tahap ini hasil dari MixColumns di XOR dengan hasil Round Key ke-1 04 e0 48 28 a0 88 23 2a

66 cb f8 06 fa 54 a3 6c

81 19 d3 26 fe 2c 39 76

e5 9a 7a 4c 17 b1 39 05

Sehingga hasilnya a4 68 6b 02

9c 9f 5b 6a

7f 35 ea 50

17 2.3.2Menghitung Dekripsi AES

Untuk proses dekripsi AES dapat diilustrasikan seperti berikut: State

AddRoundKey

InvSubBytes

InvShiftRows

InvMixColumns

AddRoundKey

InvSubBytes

InvShiftRows

InvMixColumns

AddRoundKey

InvSubBytes

InvShiftRows

AddRoundKey

State Ronde 10

Ronde 9

Ronde 1

Pre - Ronde

Ekspansi Kunci AES dst

dst

Ekspansi Kunci ke-9 Kunci Asli

Ekspansi Kunci ke-1

Ekspansi Kunci ke-10

Gambar 2.4. Struktur Dekripsi AES [1]

Secara ringkas algoritma dekripsi merupakan kebalikan algoritma enkripsi AES. Algoritma dekripsi AES menggunakan transformasi invers semua transformasi dasar yang digunakan pada algoritma enkripsi AES. Setiap transformasi dasar AES memiliki transformasi invers, yaitu: InvSubBytes, InvShiftRows dan InvMixColumns. AddRoundKey

18

Berikut merupakan contoh tahapan masing-masing proses saat proses dekripsi: 1. PreRound

Ciphertext: 39 02 dc 19

25 dc 11 6a

84 09 85 0b

1d fb 97 32

Di XOR dengan AddRoundKey

d0 c9 e1 b6

14 ee 3f 63

f9 25 0c 0c

a8 89 c8 a6

Dihasilkan: e9 cb 3d af

31 32 2e 09

7d 2c 89 07

b5 72 5f 94

2. Round 1

a. InvShiftRow

Proses InvShiftRow ini merupakan kebalikan dari ShiftRow.

19

Sehingga hasil dari PreRound di InvShiftRow menjadi: e9 cb 3d af

09 31 32 2e

89 07 7d 2c

72 5f 94 b5

b. InvSubBytes

Proses InvSubBytes sebenarnya sama dengan proses SubByte hanya saja tabel yang digunakan yaitu tabel InvSubBytes seperti berikut:

Tabel 2.3. Tabel Subtitusi untuk Transformasi InvSubBytes [1]

0 1 2 3 4 5 6 7 8 9 a b c d e f

0 52 09 6a d5 30 36 a5 38 bf 40 a3 9e 81 f3 d7 fb

1 7c e3 39 82 9b 2f ff 87 34 8e 43 44 c4 de e9 cb

2 54 7b 94 32 a6 c2 23 3d ee 4c 95 0b 42 fa c3 4e

3 08 2e a1 66 28 d9 24 b2 76 5b a2 49 6d 8b d1 25

4 72 f8 f6 64 86 68 98 16 d4 a4 5c cc 5d 65 b6 92

5 6c 70 48 50 fd ed b9 da 5e 15 46 57 a7 8d 9d 84

6 90 d8 ab 00 8c bc d3 0a f7 e4 58 05 b8 b3 45 06

7 d0 2c 1e 8f ca 3f 0f 02 c1 af bd 03 01 13 8a 6b

8 3a 91 11 41 4f 67 dc ea 97 f2 cf ce f0 b4 e6 73

9 96 ac 74 22 e7 ad 35 85 e2 f9 37 e8 1c 75 df 6e

a 47 f1 1a 71 1d 29 c5 89 6f b7 62 0e aa 18 be 1b

b fc 56 3e 4b c6 d2 79 20 9a db c0 fe 78 cd 5a f4

c 1f dd a8 33 88 07 c7 31 b1 12 10 59 27 80 ec 5f

d 60 51 7f a9 19 b5 4a 0d 2d e5 7a 9f 93 c9 9c ef

e a0 e0 3b 4d ae 2a f5 b0 c8 eb bb 3c 83 53 99 61

f 17 2b 04 7e ba 77 d6 26 e1 69 14 63 55 21 0c 7d

Jika hasil dari InvShiftRow disubtitusi dengan tabel di atas maka akan dihasilkan eb 59 8b 1b

40 2e a1 c3

f2 38 13 42

20 c. AddRoundKey

Dari hasil InvSubBytes kemudian di XOR dengan AddRoundKey ac 19 28 57

77 fa d1 5c

66 dc 29 00

f3 21 41 6e

sehingga dihasilkan: 47 40 a3 4c

37 d4 70 9f

94 e4 3a 42

ed a5 a6 bc

d. InvMixColumns

[

] [

] [ ]

Untuk baris yang ke-1:  0e . 47 =

Hex 0e = binary 00001110 (Di pola polynomial = x3+x2+x) Hex 47 = binary 01000111 (Di pola polynomial = x6+x2+x+1)  (x3+x2+x) (x6+x2+x+1)

 x9+x5+x4+x3+x8+x4+x3+x2+x7+x3+x2+x  x9+x8+x7+x5+x3+x

 x.x8+x8+x7+x5+x3+x

21  0b . 37 =

Hex 0b = binary 00001011 (Di pola polynomial = x3+x+1) Hex 37 = binary 00110111 (Di pola polynomial = x5+x4+x2+x+1)  (x3+x+1)(x5+x4+x2+x+1)

 x8+x7+x5+x4+x3+x6+x5+x3+x2+x+x5+x4+x2+x+1  x8+x7+x6+x5+1

 x4+x3+x+1+x7+x6+x5+1

 x7+x6+x5+x4+x3+x (binary: 11111010 hex: fa)

 0d . 94 =

Hex 0d = binary 00001101 (Di pola polynomial = x3+x2+1) Hex 94 = binary 10010100 (Di pola polynomial = x7+x4+x2)  (x3+x2+1)( x7+x4+x2)

 x10+x7+x5+x9+x6+x4+x7+x4+x2  x10+x9+x6+x5+x2

 x2 . x8 + x.x8 + x6+x5+x2

 x2(x4+x3+x+1)+x(x4+x3+x+1)+x6+x5+x2  x6+x5+x3+x2+ x5+x4+x2+x+x6+x5+x2  x5+x4+x3+x2+x (binary 00111110 hex: 3e)

 09 . ed =

Hex 09 = binary 00001001 (Di pola polynomial = x3+1)

Hex ed = binary 11101101 (Di pola polynomial = x7+x6+x5+x3+x2+1)  (x3+1)(x7+x6+x5+x3+x2+1)

 x10+x9+x8+x6+x5+x3 + x7+x6+x5+x3+x2+1  x10+x9+x8+x7+x2+1

 x2 . x8 + x.x8 + x8+x7+x2+1

22

 Setelah itu masing-masing hasil di xor menjadi:

10000111 xor 11111010 xor 00111110 xor 11000100 = 10000111 (dalam hex: 87)

Untuk baris ke-2:  09 . 47

Hex 09 = binary 00001001 (Di pola polynomial = x3+1) Hex 47 = binary 01000111 (Di pola polynomial = x6+x2+x+1)  (x3+1)(x6+x2+x+1)

 x9+x5+x4+x3+x6+x2+x+1  x9+x6+ x5+x4+x3+x2+x+1  x.x8+x6+ x5+x4+x3+x2+x+1

 x(x4+x3+x+1)+x6+ x5+x4+x3+x2+x+1  x5+x4+x2+x+ x6+ x5+x4+x3+x2+x+1  x6+x3+1 (binary = 01001001 hex = 49)

 0e . 37

Hex 0e = binary 00001110 (Di pola polynomial = x3+x2+x) Hex 37 = binary 00110111 (Di pola polynomial = x5+x4+x2+x+1)  (x3+x2+x)(x5+x4+x2+x+1)

 x8+x7+x5+x4+x3+x7+x6+x4+x3+x2+ x6+x5+x3+x2+x  x8+x3+x

 x4+x3+x+1+ x3+x

 x4+1 (binary = 00010001 hex = 11)

 0b . 94

Hex 0b = binary 00001011 (Di pola polynomial = x3+x+1) Hex 94 = binary 10010100 (Di pola polynomial = x7+x4+x2)  (x3+x+1)(x7+x4+x2)

23  x10+x8+x4+x3+x2

 x2 . x8 + x8+x4+x3+x2

 x2(x4+x3+x+1)+ (x4+x3+x+1)+ x4+x3+x2  x6+x5+x3+x2+x+1+x2

 x6+x5+x3+x+1 (binary = 01101011 hex: 6b)

 0d . ed

Hex 0d = binary 00001101 (Di pola polynomial = x3+x2+1)

Hex ed = binary 11101101 (Di pola polynomial = x7+x6+x5+x3+x2+1)  (x3+x2+1)( x7+x6+x5+x3+x2+1)

 x10+x9+x8+x6+x5+x3+ x9+x8+x7+x5+x4+x2+ x7+x6+x5+x3+x2+1  x10+x5+x4+1

 x2 . x8 + x5+x4+1

 x2(x4+x3+x+1) + x5+x4+1  x6+x5+x3+x2+x5+x4+1

 x6+x4+x3+x2+1 (binary : 01011101 hex : 5d)

 Setelah itu masing-masing hasil di xor menjadi:

01001001 xor 00010001 xor 01101011 xor 01011101 = 01101110 (dalam hex: 6e)

Untuk baris ke-3  0d . 47

Hex 0d = binary 00001101 (Di pola polynomial = x3+x2+1) Hex 47 = binary 01000111 (Di pola polynomial = x6+x2+x+1)  (x3+x2+1)( x6+x2+x+1)

 x9+x5+x4+x3+ x8+x4+x3+x2+ x6+x2+x+1  x9+x8+x6+x5+x+1

 x.x8+x8+ x6+x5+x+1

24

 x5+x4+x2+x+ x4+x3+x+1+ x6+x5+x+1  x6+x3+x2+x (binary: 01001110 hex: 4e)

 09 . 37

Hex 09 = binary 00001001 (Di pola polynomial = x3+1)

Hex 37 = binary 00110111 (Di pola polynomial = x5+x4+x2+x+1)  (x3+1)( x5+x4+x2+x+1)

 x8+x7+x5+x4+x3+ x5+x4+x2+x+1  x8+x7+x3+x2+x+1

 x4+x3+x+1+x7+x3+x2+x+1

 x7+ x4+ x2 (binary: 10010100 hex: 94)

 0e . 94

Hex 0e = binary 00001110 (Di pola polynomial = x3+x2+x) Hex 94 = binary 10010100 (Di pola polynomial = x7+x4+x2)  (x3+x2+x)( x7+x4+x2)

 x10+x7+x5+x9+x6+x4+ x8+x5+x3  x10+x9+ x8+ x7+x6+x4 +x3

 x2 . x8 + x.x8 + x8+ x7+x6+x4 +x3

 x2(x4+x3+x+1)+x(x4+x3+x+1)+( x4+x3+x+1)+ x7+x6+x4 +x3  x6+x5+x3+x2+ x5+x4+x2+x+ x4+x3+x+1+ x7+x6+x4 +x3  x7+x4 +x3+1 (binary: 10011001 hex: 99)

 0b . ed

Hex 0b = binary 00001011 (Di pola polynomial = x3+x+1)

Hex ed = binary 11101101 (Di pola polynomial = x7+x6+x5+x3+x2+1)  (x3+x+1)( x7+x6+x5+x3+x2+1)

 x10+x9+x8+x6+x5+x3+x8+x7+x6+x4+x3+x+x7+x6+x5+x3+x2+1  x10+x9+x4+x3+x+x6+x2+1

25

 x2(x4+x3+x+1)+x(x4+x3+x+1)+ x6+x4+x3+x2+x+1  x6+x5+x3+x2+ x5+x4+x2+x+ x6+x4+x3+x2+x+1  x2+1 (binary: 00000101 hex: 05)

 Setelah itu masing-masing hasil di xor menjadi:

01001110 xor 10010100 xor 10011001 xor 00000101 = 01000110 (dalam hex: 46)

Untuk baris ke-4  0b . 47

Hex 0b = binary 00001011 (Di pola polynomial = x3+x+1) Hex 47 = binary 01000111 (Di pola polynomial = x6+x2+x+1)  (x3+x+1)(x6+x2+x+1)

 x9+x5+x4+x3+ x7+x3+x2+x+ x6+x2+x+1  x9+x7+x6+x5+x4+1

 x.x8+x7+x6+x5+x4+1

 x(x4+x3+x+1)+ x7+x6+x5+x4+1  x5+x4+x2+x+ x7+x6+x5+x4+1

 x7+x6+x2+x+1 (binary: 11000111 hex: c7)

 0d . 37

Hex 0d = binary 00001101 (Di pola polynomial = x3+x2+1) Hex 37 = binary 00110111 (Di pola polynomial = x5+x4+x2+x+1)  (x3+x2+1)( x5+x4+x2+x+1)

 x8+x7+x5+x4+x3+ x7+x6+x4+x3+x2+ x5+x4+x2+x+1  x8+x6+x4+x+1

 (x4+x3+x+1)+x6+x4+x+1

26  09 . 94

Hex 09 = binary 00001001 (Di pola polynomial = x3+1) Hex 94 = binary 10010100 (Di pola polynomial = x7+x4+x2)  (x3+1)(x7+x4+x2)

 x10+x7+x5+x7+x4+x2  x2.x8+x5+x4+x2

 x2(x4+x3+x+1)+ x5+x4+x2  x6+x5+x3+x2+x5+x4+x2

 x6+x4+x3 (binary: 01011000 hex: 58)

 0e . ed

Hex 0e = binary 00001110 (Di pola polynomial = x3+x2+x)

Hex ed = binary 11101101 (Di pola polynomial = x7+x6+x5+x3+x2+1)  (x3+x2+x)(x7+x6+x5+x3+x2+1)

 x10+x9+x8+x6+x5+x3+ x9+x8+x7+x5+x4+x2+ x8+x7+x6+x4+x3+x  x10+x8+x2+x

 x2.x8+x8+x2+x

 x2.(x4+x3+x+1)+ (x4+x3+x+1)+ x2+x  x6+x5+x3+x2+x4+x3+x+1+ x2+x

 x6+x5+x4+1 (binary: 01110001 hex: 71)  Setelah itu masing-masing hasil di xor menjadi:

27 [

] [

] [ ]

Sehingga data setelah hasil AddRoundKey di InvMixColumns menjadi: 87 f2 4d 97

6e 4c 90 ec

46 e7 4a c3