Problems in Real Analysis Advanced Calculus on The Real Axis

(1)

(2)

(3)

Teodora-Liliana T. R˘adulescu

Vicen¸tiu D. R˘adulescu

Titu Andreescu

Problems in Real Analysis

(4)

Department of Mathematics Fratii Buzesti National College Craiova 200352

Romania

[email protected]

Simion Stoilow Mathematics Institute Romanian Academy

Bucharest 014700 Romania

[email protected] Titu Andreescu

School of Natural Sciences and Mathematics University of Texas at Dallas

Richardson, TX 75080 USA

[email protected]

ISBN: 978-0-387-77378-0 e-ISBN: 978-0-387-77379-7 DOI: 10.1007/978-0-387-77379-7

Library of Congress Control Number: 2009926486

Mathematics Subject Classification (2000): 00A07, 26-01, 28-01, 40-01

permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden.

The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights.

Printed on acid-free paper

This work may not be translated or copied in whole or in part without the written

Springer Dordrecht Heidelberg London New York

(5)

to do mathematics. And what does it mean

doing mathematics? In the first place it

means to be able to solve mathematical

problems.

—George P´olya (1887–1985)

We come nearest to the great when we are

great in humility.

(6)

This carefully written book presents an extremely motivating and original approach, by means of problem-solving, to calculus on the real line, and as such, serves as a perfect introduction to real analysis. To achieve their goal, the authors have care-fully selected problems that cover an impressive range of topics, all at the core of the subject. Some problems are genuinely difficult, but solving them will be highly rewarding, since each problem opens a new vista in the understanding of mathematics. This book is also perfect for self-study, since solutions are provided.

I like the care with which the authors intersperse their text with careful reviews of the background material needed in each chapter, thought-provoking quotations, and highly interesting and well-documented historical notes. In short, this book also makes very pleasant reading, and I am confident that each of its readers will enjoy reading it as much as I did. The charm and never-ending beauty of mathematics pervade all its pages.

In addition, this little gem illustrates the idea that one cannot learn mathematics without solving difficult problems. It is a world apart from the “computer addiction” that we are unfortunately witnessing among the younger generations of would-be mathematicians, who use too much ready-made software instead or their brains, or who stand in awe in front of computer-generated images, as if they had become the essence of mathematics. As such, it carries a very useful message.

One cannot help comparing this book to a “great ancestor,” the famedProblems and Theorems in Analysis, by P´olya and Szeg˝o, a text that has strongly influenced generations of analysts. I am confident that this book will have a similar impact.

Hong Kong, July 2008 Philippe G. Ciarlet

(7)

If I have seen further it is by standing on the shoulders of giants. —Sir Isaac Newton (1642–1727), Letter to Robert Hooke, 1675

Mathematical analysis is central to mathematics, whether pure or applied. This discipline arises in various mathematical models whose dependent variables vary continuously and are functions of one or several variables. Real analysis dates to the mid-nineteenth century, and its roots go back to the pioneering papers by Cauchy, Riemann, and Weierstrass.

In 1821, Cauchy established new requirements of rigor in his celebratedCours d’Analyse. The questions he raised are the following:

– What is a derivative really? Answer: a limit. – What is an integral really? Answer: a limit. – What is an infinite series really? Answer: a limit.

This leads to

– What is a limit? Answer: a number.

And, finally, the last question:

– What is a number?

Weierstrass and his collaborators (Heine, Cantor) answered this question around 1870–1872.

Our treatment in this volume is strongly related to the pioneering contributions in differential calculus by Newton, Leibniz, Descartes, and Euler in the seventeenth and eighteenth centuries, with mathematical rigor in the nineteenth century pro-moted by Cauchy, Weierstrass, and Peano

in the integral calculus developed by Riemann and Darboux.

Due to the huge impact of mathematical analysis, we have intended in this book to build a bridge between ordinary high-school or undergraduate exercises and more difficult and abstract concepts or problems related to this field. We present in this volume an unusual collection of creative problems in elementary mathematical anal-ysis. We intend to develop some basic principles and solution techniques and to offer a systematic illustration of how to organize the natural transition from problem-solving activity toward exploring, investigating, and discovering new results and properties.

ix

(8)

The aim of this volume in elementary mathematical analysis is to introduce, through problems-solving, fundamental ideas and methods without losing sight of the context in which they first developed and the role they play in science and partic-ularly in physics and other applied sciences. This volume aims at rapidly developing differential and integral calculus for real-valued functions of one real variable, giving relevance to the discussion of some differential equations and maximum prin-ciples.

The book is mainly geared toward students studying the basic principles of math-ematical analysis. However, given its selection of problems, organization, and level, it would be an ideal choice for tutorial or problem-solving seminars, particularly those geared toward the Putnam exam and other high-level mathematical contests. We also address this work to motivated high-school and undergraduate students. This volume is meant primarily for students in mathematics, physics, engineering, and computer science, but, not without authorial ambition, we believe it can be used by anyone who wants to learn elementary mathematical analysis by solving prob-lems. The book is also a must-have for instructors wishing to enrich their teach-ing with some carefully chosen problems and for individuals who are interested in solving difficult problems in mathematical analysis on the real axis. The volume is intended as a challenge to involve students as active participants in the course. To make our work self-contained, all chapters include basic definitions and properties. The problems are clustered by topic into eight chapters, each of them containing both sections of proposed problems with complete solutions and separate sections including auxiliary problems, their solutions being left to our readers. Throughout the book, students are encouraged to express their own ideas, solutions, generaliza-tions, conjectures, and conclusions.

The volume contains a comprehensive collection of challenging problems, our goal being twofold: first, to encourage the readers to move away from routine exercises and memorized algorithms toward creative solutions and nonstandard problem-solving techniques; and second, to help our readers to develop a host of new mathematical tools and strategies that will be useful beyond the classroom and in a number of applied disciplines. We include representative problems proposed at various national or international competitions, problems selected from prestigious mathematical journals, but also some original problems published in leading publi-cations. That is why most of the problems contained in this book are neither standard nor easy. The readers will find both classical topics of mathematical analysis on the real axis and modern ones. Additionally, historical comments and developments are presented throughout the book in order to stimulate further inquiry.

Traditionally, a rigorous first course or problem book in elementary mathematical analysis progresses in the following order:

Sequences

(9)

However, the historical development of these subjects occurred in reverse order:

Cauchy(1821)⇐=Weierstrass(1872)⇐= Newton (1665)

Leibniz (1675) ⇐=

Archimedes Kepler (1615) Fermat (1638)

This book brings to life the connections among different areas of mathematical analysis and explains how various subject areas flow from one another. The vol-ume illustrates the richness of elementary mathematical analysis as one of the most classical fields in mathematics. The topic is revisited from the higher viewpoint of university mathematics, presenting a deeper understanding of familiar subjects and an introduction to new and exciting research fields, such as Ginzburg–Landau equa-tions, the maximum principle, singular differential and integral inequalities, and nonlinear differential equations.

The volume is divided into four parts, ten chapters, and two appendices, as follows:

Part I. Sequences, Series, and Limits Chapter 1. Sequences

Chapter 2. Series

Chapter 3. Limits of Functions

Part II. Qualitative Properties of Continuous and Differentiable Functions Chapter 4. Continuity

Chapter 5. Differentiability

Part III. Applications to Convex Functions and Optimization Chapter 6. Convex Functions

Chapter 7. Inequalities and Extremum Problems

Part IV. Antiderivatives, Riemann Integrability, and Applications Chapter 8. Antiderivatives

Chapter 9. Riemann Integrability

Chapter 10. Applications of the Integral Calculus Appendix A. Basic Elements of Set Theory

Appendix B. Topology of the Real Line

(10)

Key features of this volume:

– contains a collection of challenging problems in elementary mathematical analysis;

– includes incisive explanations of every important idea and develops illuminating applications of many theorems, along with detailed solutions, suitable cross-references, specific how-to hints, and suggestions;

– is self-contained and assumes only a basic knowledge but opens the path to com-petitive research in the field;

– uses competition-like problems as a platform for training typical inventive skills; – develops basic valuable techniques for solving problems in mathematical

ana-lysis on the real axis;

– 38 carefully drawn figures support the understanding of analytic concepts; – includes interesting and valuable historical account of ideas and methods in

analysis;

– contains excellent bibliography, glossary, and index.

The book has elementary prerequisites, and it is designed to be used for lecture courses on methodology of mathematical research or discovery in mathematics. This work is a first step toward developing connections between analysis and other math-ematical disciplines, as well as physics and engineering.

The background the student needs to read this book is quite modest. Anyone with elementary knowledge in calculus is well-prepared for almost everything to be found here. Taking into account the rich introductory blurbs provided with each chapter, no particular prerequisites are necessary, even if a dose of mathematical so-phistication is needed. The book develops many results that are rarely seen, and even experienced readers are likely to find material that is challenging and informative.

Our vision throughout this volume is closely inspired by the following words of George P´olya [90] (1945) on the role of problems and discovery in mathematics:

Infallible rules of discovery leading to the solution of all possible mathematical problems would be more desirable than the philosopher’s stone, vainly sought by all alchemists. The first rule of discovery is to have brains and good luck. The second rule of discovery is to sit tight and wait till you get a bright idea. Those of us who have little luck and less brain sometimes sit for decades. The fact seems to be, as Poincar´e observed, it is the man, not the method, that solves the problem.

Despite our best intentions, errors are sure to have slipped by us. Please let us know of any you find.

August 2008 Teodora-Liliana R˘adulescu

(11)

We acknowledge, with unreserved gratitude, the crucial role of Professors Cather-ine Bandle, Wladimir-Georges Boskoff, Louis Funar, Patrizia Pucci, Richard Stong, and Michel Willem, who encouraged us to write a problem book on this subject. Our colleague and friend Professor Dorin Andrica has been very interested in this project and suggested some appropriate problems for this volume. We warmly thank Professors Ioan S¸erdean and Marian Tetiva for their kind support and useful discus-sions.

This volume was completed while Vicent¸iu R˘adulescu was visiting the Univer-sity of Ljubljana during July and September 2008 with a research position funded by the Slovenian Research Agency. He would like to thank Professor Duˇsan Repovˇs for the invitation and many constructive discussions.

We thank Dr. Nicolae Constantinescu and Dr. Mirel Cos¸ulschi for the profes-sional drawing of figures contained in this book.

We are greatly indebted to the anonymous referees for their careful reading of the manuscript and for numerous comments and suggestions. These precious con-structive remarks were very useful to us in the elaboration of the final version of this volume.

We are grateful to Ann Kostant, Springer editorial director for mathematics, for her efficient and enthusiastic help, as well as for numerous suggestions related to previous versions of this book. Our special thanks go also to Laura Held and to the other members of the editorial technical staff of Springer New York for the excellent quality of their work.

We are particularly grateful to copyeditor David Kramer for his guidance, thor-oughness and attention to detail.

V. R˘adulescu acknowledges the support received from the Romanian Research Council CNCSIS under Grant 55/2008 “Sisteme diferent¸iale ˆın analiza neliniar˘a s¸i aplicat¸ii.”

(12)

Foreword. . . vii

Preface. . . ix

Acknowledgments. . . xiii

Abbreviations and Notation . . . xix

Part I Sequences, Series, and Limits 1 Sequences. . . 3

1.1 Main Definitions and Basic Results . . . 3

1.2 Introductory Problems . . . 7

1.3 Recurrent Sequences . . . 18

1.4 Qualitative Results . . . 30

1.5 Hardy’s and Carleman’s Inequalities . . . 45

1.6 Independent Study Problems . . . 51

2 Series. . . 59

2.2 Elementary Problems . . . 66

2.3 Convergent and Divergent Series . . . 73

2.4 Infinite Products . . . 86

3 Limits of Functions. . . 115

3.2 Computing Limits . . . 118

(13)

Part II Qualitative Properties of Continuous and Differentiable Functions

4 Continuity . . . 139

4.1 The Concept of Continuity and Basic Properties . . . 139

4.2 Elementary Problems . . . 144

4.3 The Intermediate Value Property . . . 147

4.4 Types of Discontinuities . . . 151

4.5 Fixed Points . . . 154

4.6 Functional Equations and Inequalities . . . 163

4.7 Qualitative Properties of Continuous Functions . . . 169

5 Differentiability. . . 183

5.1 The Concept of Derivative and Basic Properties . . . 183

5.2 Introductory Problems . . . 198

5.3 The Main Theorems . . . 218

5.4 The Maximum Principle . . . 235

5.5 Differential Equations and Inequalities . . . 238

Part III Applications to Convex Functions and Optimization 6 Convex Functions . . . 263

6.2 Basic Properties of Convex Functions and Applications . . . 265

6.3 Convexity versus Continuity and Differentiability . . . 273

7 Inequalities and Extremum Problems . . . 289

7.1 Basic Tools . . . 289

7.2 Elementary Examples . . . 290

7.3 Jensen, Young, H¨older, Minkowski, and Beyond . . . 294

7.4 Optimization Problems . . . 300

Part IV Antiderivatives, Riemann Integrability, and Applications 8 Antiderivatives . . . 313

8.1 Main Definitions and Properties . . . 313

8.3 Existence or Nonexistence of Antiderivatives . . . 317

(14)

9 Riemann Integrability. . . 325

9.1 Main Definitions and Properties . . . 325

9.3 Classes of Riemann Integrable Functions . . . 337

9.4 Basic Rules for Computing Integrals . . . 339

9.5 Riemann Iintegrals and Limits . . . 341

10 Applications of the Integral Calculus. . . 373

10.1 Overview . . . 373

10.2 Integral Inequalities . . . 374

10.3 Improper Integrals . . . 390

10.4 Integrals and Series . . . 402

10.5 Applications to Geometry . . . 406

Part V Appendix A Basic Elements of Set Theory. . . 417

A.1 Direct and Inverse Image of a Set . . . 417

A.2 Finite, Countable, and Uncountable Sets . . . 418

B Topology of the Real Line. . . 419

B.1 Open and Closed Sets . . . 419

B.2 Some Distinguished Points . . . 420

Glossary . . . 421

References. . . 437

(15)

Abbreviations

We have tried to avoid using nonstandard abbreviations as much as possible. Other abbreviations include:

AMM American Mathematical Monthly

GMA Mathematics Gazette, Series A

MM Mathematics Magazine

IMO International Mathematical Olympiad

IMCUS International Mathematics Competition for University Students MSC Mikl´os Schweitzer Competitions

Putnam The William Lowell Putnam Mathematical Competition

SEEMOUS South Eastern European Mathematical Olympiad for University Students

Notation

We assume familiarity with standard elementary notation of set theory, logic, algebra, analysis, number theory, and combinatorics. The following is notation that deserves additional clarification.

N the set of nonnegative integers(N={0,1,2,3, . . .})

N∗ the set of positive integers(N∗={1,2,3, . . .})

Z the set of integer real numbers(Z={. . . ,−3,−2,−1,0,1,2,3, . . .})

Z∗ the set of nonzero integer real numbers(Z∗=Z_{\ {}0})

Q the set of rational real numbers

Q=_m

n; m∈Z, n∈N∗,mandnare relatively prime

R the set of real numbers

R∗ the set of nonzero real numbers(R∗=R_{\ {}0})

R+ the set of nonnegative real numbers(R+= [0,+∞))

R the completed real lineR=R_{∪ {−}∞,+∞_}

(16)

C the set of complex numbers e limn→∞1+1_nn=2.71828. . . supA the least upper bound of the setA_⊂R infA the greatest lower bound of the setA_⊂R

x₊ the positive part of the real numberx(x₊=max{x,0})

x₋ the negative part of the real numberx(x₋=max{−x,0}) |x_| the modulus (absolute value) of the real numberx(|x_|=x++x−) {x_} the fractional part of the real numberx(x= [x] +{x_})

Card(A) cardinality of the finite setA

dist(x,A) the distance fromx_∈Rto the setA_⊂R(dist(x,A) =inf{|x₋a_|;a_∈A_})

IntA the set of interior points ofA_⊂R

f(A) the image of the setAunder a mappingf f−1(B) the inverse image of the setBunder a mappingf

f_◦g the composition of functionsf andg:(f_◦g)(x) = f(g(x)) n! nfactorial, equal ton(n₋1)···1 (n_∈N∗)

(2n)!! 2n(2n₋2)(2n₋4)···4·2 (n_∈N∗)

(2n+1)!! (2n+1)(2n₋1)(2n₋3)···3_·1 (n_∈N∗) lnx log_ex(x>0)

x_րx0 x→x0∈Randx<x0

x_ցx0 x→x0∈Randx>x0

lim sup

n→∞

xn lim n→∞

sup

k≥n

xk

lim inf

n→∞ xn nlim→∞

inf

k_≥nxk

f(n)(x) nth derivative of the functionf atx

Cn(a,b) the set ofn-times differentiable functionsf:(a,b)→Rsuch that f(n)is continuous on(a,b)

C∞(a,b) the set of infinitely differentiable functionsf :(a,b)→R

(C∞(a,b) =∞

n=0Cn(a,b))

Δf the Laplace operator applied to the functionf :D_⊂RN_→R

Δf=∂

2_f

∂x2

1

+∂

2_f

∂x2

2

+···+∂

2_f

∂x2

N

Landau’s notation f(x) =o(g(x))asx_→x0if f(x)/g(x)→0 asx→x0

f(x) =O(g(x))asx_→x0if f(x)/g(x)is bounded in a neighborhood ofx0

f_∼gasx_→x0if f(x)/g(x)→1 asx→x0

Hardy’s notation f _≺≺gasx_→x0if f(x)/g(x)→0 asx→x0

(17)

Sequences

As far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality.

—Albert Einstein (1879–1955)

Abstract. In this chapter we study real sequences, a special class of functions whose domain is the setNof natural numbers and range a set of real numbers.

1.1 Main Definitions and Basic Results

Hypotheses non fingo. [“I frame no hypotheses.”]

Sir Isaac Newton (1642–1727)

Sequences describe wide classes of discrete processes arising in various applica-tions. The theory of sequences is also viewed as a preliminary step in the attempt to model continuous phenomena in nature. Since ancient times, mathematicians have realized that it is difficult to reconcile the discrete with the continuous. We under-stand counting 1,2,3, . . .up to arbitrarily large numbers, but do we also under-stand moving from 0 to 1 through the continuum of points between them? Around 450

essential way. As he put it in his paradox of dichotomy:

course) before it arrives at the end.

Aristotle,Physics, Book VI, Ch. 9

A sequence of real numbers is a function f :N_→R(or f :N∗_→R). We usually writean(orbn,xn, etc.) instead of f(n). If (an)n≥1is a sequence of real numbers

and ifn1<n2<···<nk<···is an increasing sequence of positive integers, then

the sequence(ank)k≥1is called asubsequenceof(an)n≥1.

n n_≥1is said to benondecreasing(resp.,

increas-ing) ifan≤an+1(resp.,an<an+1), for all n≥1. The sequence(an)n≥1is called

“>”) instead of “≤” (resp., “<”).

3

©

nonincreasing (resp.,decreasing) if the above inequalities hold with “≥” (resp.,

_

BC, Zeno thought not, because continuous motion involves infinity in an

DOI: 10.1007/978-0-387-77379-7_1, A sequence of real numbers(a )

Springer Science + Business Media, LLC 2009

Problems in Real Analysis: Advanced Calculus on the Real Axis,

There is no motion because that which is moved must arrive at the middle (of its

(18)

1

0 1 2 3 N

y

y = l + ε

y = l − ε

x

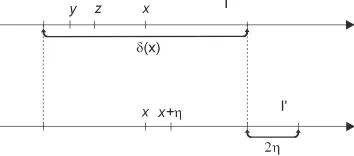
Fig. 1.1 Adapted from G.H. Hardy,Pure Mathematics, Cambridge University Press, 1952.

We recall in what follows some basic definitions and properties related to sequences. One of the main notions we need in the sequel is that ofconvergence. Let(an)n≥1 be a sequence of real numbers. We say that(an)n≥1 is aconvergent

sequenceif there existsℓ∈R(which is called thelimit of(an)n≥1) such that for

each neighborhoodN _of_ℓ_{, we have}_a_n_∈N _{for all}_n_≥_N_{, where}_N_{is a positive} integer depending onN_{. In other words,}₍_a_n₎_n_≥₁_{converges to}_ℓ_{if and only if for} eachε>0 there exists a natural numberN=N(ε)such that_|an−ℓ|<ε, for all

n_≥N. In this case we write limn→∞an=ℓoran→ℓasn→∞. The concentration of

an’s in the strip(ℓ−ε, ℓ+ε)forn≥Nis depicted in Figure 1.1.

Example. Define an= (1+1/n)n, bn= (1+1/n)n+1, cn=∑nk=01/k!. Then

(an)n_≥1and(cn)n_≥1 are increasing sequences, while(bn)n_≥1 is a decreasing

seq-uence. However, all these three sequences have the same limit, which is denoted by e (e=2.71828. . .). We will prove in the next chapter that e is an irrational number. Another important example is given by the following formula due to Stirling, which asserts that, asymptotically,n! behaves likenne−n√2πn. More precisely,

lim

n→∞

n!

nn_e₋n√₂_π_n =1.

Stirling’s formula is important in calculating limits, because without this asymptotic property it is difficult to estimate the size ofn! for largen. In this capacity, it plays an important role in probability theory, when it is used in computing the probable outcome of an event after a very large number of trials. We refer to Chapter 9 for a complete proof of Stirling’s formula.

We say that the sequence of real numbers(an)n_≥1has limit+∞(resp.,−∞) if

to eachα_∈Rthere corresponds some positive integerN0such thatn≥N0implies

an>α(resp.,an<α). Wedo notsay that(an)n≥1converges in these cases.

An elementα_∈Ris called anaccumulation pointof the sequence(an)n≥1⊂R

if there exists a subsequence(ank)k≥1such thatank→α asnk→∞.

(19)

Karl Weierstrass (1815–1897). It seems that this theorem was revealed for the first time in Weierstrass’s lecture of 1874.

Bolzano–Weierstrass Theorem. A bounded sequence of real numbers has a convergent subsequence.

However, some additional assumptions can guarantee that a bounded sequence converges. An important criterion for convergence is stated in what follows.

Monotone Convergence Theorem.Let(an)n_≥1be a bounded sequence that is monotone. Then(an)n_≥1is a convergent sequence. If increasing, thenlimn→∞an=

sup_nan, and if decreasing, thenlimn→∞an=infnan.

In many arguments a central role is played by the following principle due to Cantor.

Nested Intervals Theorem.Suppose thatIn= [an,bn]are closed intervals such thatIn+1⊂In, for alln≥1. Iflimn→∞(bn−an) =0, then there is a unique real numberx0that belongs to everyIn.

A sequence(an)n≥1of real numbers is called aCauchy sequence[Augustin Louis

Cauchy (1789–1857)] if for every ε>0 there is a natural number Nε such that |am−an|<ε, for allm,n≥Nε. A useful result is that any Cauchy sequence is a bounded sequence. The following strong convergence criterion reduces the study of convergent sequences to that of Cauchy sequences.

Cauchy’s Criterion.A sequence of real numbers is convergent if and only if it is a Cauchy sequence.

Let (an)n≥1 be an arbitrary sequence of real numbers. The limit inferior of

(an)n≥1(denoted by lim infn→∞an) is the supremum of the set X ofx∈Rsuch

that there are at most a finite numbers of n_∈N∗for whichan<x. The limit

su-periorof(an)n≥1(denoted by lim supn→∞an) is the infimum of the setY ofy∈R

such that there are finitely many positive integersnfor whichan>y. Equivalent

characterizations of these notions are the following:

(i) ℓ=lim sup_n_→_∞an(ℓ∈R) if and only if wheneverα< ℓthe set{n≥N∗;an>

α_}is infinite, and wheneverℓ <β the set{n_≥N∗;an>β}is finite;

(ii) ℓ=lim sup_n_→∞anif and only ifℓ=infm≥1supn≥man.

Exercise.Formulate the above characterizations for lim infn→∞an.

The limit inferior and the limit superior of a sequencealwaysexist, possibly in R. Moreover, the following relations hold:

lim inf

n→∞ an≤lim sup_n_→_∞ an, lim inf

n→∞(an+bn)≥lim infn→∞ an+lim infn→∞ bn, lim sup

n→∞ (

an+bn)≤lim sup n→∞

an+lim sup n→∞

bn.

The existence of the limit of a sequence is closely related to “lim inf” and “lim sup.” More precisely, the sequence (an)n≥1 has a limit if and only if

lim infn→∞an=lim supn→∞an.

(20)

Theorem.Let(an)n≥1be a sequence of positive numbers. Then

lim inf

n→∞

an+1

an ≤

lim inf

n→∞ n √

an≤lim sup n→∞

n √

an+1

an .

The above result implies, in particular, that if limn→∞(an+1/an) =ℓ, with 0≤ ℓ≤∞, then limn→∞√nan=ℓ.

Example.The above theorem implies that limn→∞an=1, wherean=√nn. We

can give an elementary proof to the fact thatan>an+1, for alln≥3. Indeed, define

bn= (an/an+1)n(n+1), for alln≥2. Thenbn>bn−1forn≥2 is equivalent ton2=

a2n_n >an_n+₊1₁a_nn−₋1₁=n2₋1. It remains to show thatbn>1 for alln≥3. This follows

from the fact that(bn)n≥2is increasing, combined withb3=34/43=81/64>1.

A sequence that is not convergent is called adivergentsequence. An important example of a divergent sequence is given byan=1+1/2+1/3+···+1/n,n≥1.

Indeed, since(an)n≥1is increasing, it has a limitℓ∈R∪ {+∞}. Assuming thatℓis

finite, it follows that

1 2+

1 4+

1 6+···=

1 2

1+1

2+ 1

3+··· →

ℓ

2 asn→∞.

This means that

1 1+

1 3+

1

5+···→

ℓ

2 asn→∞,

which is impossible because 1/1>1/2, 1/3>1/4, 1/5>1/6, and so on. Con-sequently,an→+∞as n→∞. The associated series 1+1/2+1/3+1/4+··· is

usually called theharmonic series. Furthermore, ifp<1 we have 1/np>1/n, for alln_≥2. It follows that the sequence(an)n≥1defined byan=∑nk=11/kpdiverges,

too. The situation is different ifp>1. In this case, the sequence(an)n_≥1defined as

above is convergent. Indeed,

a2n+1=1+

1 2p+

1

4p+···+

1

(2n)p

+

1 3p+

1

5p+···+

1

(2n+1)p

<1+

1 2p+

1

4p+···+

1

(2n)p

+

1 2p+

1

4p+···+

1

(2n)p

=1+an

2p+

an

2p<1+2 1−p_a

2n+1,

becausean<a2n+1. Thus(1−21−p)a2n+1<1. Sincep>1, we have 1−21−p>0.

Hence a2n+1<(1−21−p)−1 for alln≥1. So, the sequence(an)n≥1 (for p>1)

is increasing and bounded above by(1−21−p)−1_{, which means that it converges.}

The corresponding limit limn→∞∑nk=11/kp=∑n∞=11/npis denoted byζ(p)(p>1)

(21)

of mathematics (“Millennium Problems,” as designated by the Clay Mathematics Institute; seehttp://www.claymath.org/millennium/).

The following result (whose “continuous” variant is l’Hˆopital’s rule for differen-tiable functions) provides us a method to compute limits of the indeterminate form 0/0 or∞/∞. This property is due to Otto Stolz (1859–1906) and Ernesto Ces`aro (1859–1906).

Stolz–Ces`aro Lemma.Let(an)n_≥1and(bn)n_≥1be two sequences of real num-bers.

(i) Assume that an→0 and bn→0 as n→∞. Suppose, moreover, that (bn)n≥1 is decreasing for all sufficiently largenand there exists

lim

n→∞

an+1−an

bn+1−bn

=:ℓ∈R.

Then there existslimn→∞an/bnand, moreover,limn→∞an/bn=ℓ.

(ii) Assume thatbn→+∞asn→∞and that(bn)n_≥1is increasing for all sufficiently largen. Suppose that there exists

lim

n→∞

an+1−an

bn+1−bn

=:ℓ∈R.

Then there existslimn→∞an/bnand, moreover,limn→∞an/bn=ℓ.

1.2 Introductory Problems

Nature not only suggests to us problems, she suggests their solution.

Henri Poincar´e (1854–1912)

We first prove with elementary arguments the following basic result.

Arithmetic–Geometric Means (AM–GM) Inequality.For any positive num-bersa1,a2, . . . ,anwe have

a1+a2+···+an

n ≥

n √

a1a2···an.

Replacingak withak√na1···an (for 1≤k≤n), we havea1a2···an=1, so it

is enough to prove thata1+a2+···+an≥n. We argue by induction. Forn=1

the property is obvious. Passing fromnton+1, we can assume thata1≤1≤a2.

Hence(1−a1)(a2−1)≥1, that is,a1+a2≥1+a1a2.Next, we setb1=a1a2and,

for anyk=2, . . . ,n, we setbk=ak+1. Henceb1b2···bn=1. So, by the induction

hypothesis,

(22)

It follows that

a1+a2+···+an+1≥a1a2+1+a3+···+an+1≥n+1.

The AM–GM inequality also implies a relationship between the harmonic mean and the geometric mean: for any positive numbersa1,a2, . . . ,anwe have

n

1 a1 +

1 a2+···+

1 an

≤√n_a

1a2···an.

The following easy exercise shows the importance of elementary monotony argu-ments for deducing the value of the limit of a convergent sequence.

1.2.1. LetA1,A2, . . . ,Akbe nonnegative numbers. Compute

lim

n→∞(A

n

1+An2+···+Ank)1/n.

Solution.Without loss of generality, we may assume thatA1=max{A1, . . . ,Ak}.

ThereforeAn₁_≤An₁+···+An_k_≤kAn₁. It follows that

A1= lim n_→∞(A

n

1)1/n≤_nlim

→∞(A

n

1+···+Ank)1/n≤_nlim

→∞(kA

n

1)1/n=A1,

which shows that the limit sought isA1:=min{Aj; 1≤j≤k}. ⊓⊔

Comments.We easily observe that the above result does not remain true if we do not assume that the numbersA1, . . . ,Ak are nonnegative. Moreover, in such a

case it is possible that the sequence defined byBn:=An₁+···+An_k1/nis not even

convergent (give an example!).

We have already provided some basic examples of convergent and divergent sequences. The next exercise shows how, by means of monotony principles, we can construct further examples of such sequences.

1.2.2. Prove thatlimn→∞√nn!= +∞andlimn→∞√nn!/n=e−1. Solution.We first observe that(2n)!≥∏k2n=nk≥nn+1. Hence

2n

(2n)!≥ 2√nnn+1_≥√_n _and 2n+1

(2n+1)!≥ 2n+√1nn+1_≥√_n_.

For the last part we take into account that for any sequence(an)n≥1of positive

numbers we have

lim inf

n→∞

an+1

an ≤

lim inf

n→∞ n √

n √

an+1

an .

Taking an = n!/nn and using limn→∞1+n−11/n =e, we conclude that limn→∞√nn!/n=e−1. An alternative argument is based on the Stolz–Ces`aro lemma applied toan=log(n!/nn)andbn=nand using again limn→∞1+n−11/n=e.

(23)

A nonobvious generalization of the above property is stated below. Our proof applies subtle properties of real-valued functions (see Chapter 5) but we strongly suggest that the reader refine the monotony arguments developed above.

Independent Study.Prove that for real numberp_≥0we have

lim

n→∞

11p_·₂2p_···_nnp1/np+1 n1/(p+1) =e−

1/(p+1)2

.

Particular case:

lim

n→∞

11·22···nn1/n

2

n1/2 =e

−1/4_.

Hint.Use the mean value theorem. For instance, in the particular case p=2, apply the Lagrange mean value theorem to the functionf(x) = (x3_ln_x₎_/₃₋_x3_/_{9 on}

the interval[k,k+1], 1≤k_≤n.

We have seen above that √nn!→∞asn_→∞. A natural question is to study the asymptotic behavior of the difference of two consecutive terms of this sequence. The next problem was published in 1901 and is due to the Romanian mathemati-cian Traian Lalescu (1882–1929), who wrote one of the first treatises on integral equations.

1.2.3. Find the limit of the sequence(an)n_≥2defined byan= n+1

(n+1)!−√n

n!.

Solution.We can writean= n

√

n!(bn−1), wherebn= n+1

(n+1)!/√n

n!. Hence

an=

n √

n!

n · bn−1

lnbn ·

lnbn_n. (1.1)

But limn→∞√nn!/n=e−1, sobn→1 asn→∞. On the other hand,

lim

n→∞b

n n=_nlim_→_∞

(n+1)!

n! · 1 n+1

(n+1)!=e. (1.2)

So, by (1.1) and (1.2), we obtain thatan→e−1asn→∞. ⊓⊔

Remark.In the above solution we have used the property that ifbn→1 asn→∞

then(bn−1)/lnbn→1 asn→∞. This follows directly either by applying the Stolz–

Ces`aro lemma or after observing that

lim

n→∞

bn−1

lnbn

= lim

n→∞

1

ln[1+ (bn−1)]1/(bn−1)

= 1

ln e=1.

Independent Study.Letpbe a nonnegative real number. Study the convergence of the sequence(xn)n≥1defined by

xn=

11p·22p···(n+1)(n+1)p1/(n+1)

p+1

−11p·22p···nnp1/n

p+1

(24)

We already know that the sequence(sn)n≥1defined bysn=1+1/2+···+1/n

diverges to+∞. In what follows we establish the asymptotic behavior forsn/nas

n_→∞. As a consequence, the result below implies that limn→∞n(1−√nn) =∞.

1.2.4. Consider the sequence(sn)n≥1defined bysn=1+1/2+···+1/n. Prove that

(a) n(n+1)1/n<n+sn, for all integersn>1; (b) (n₋1)n−1/(n−1)<n₋sn, for all integersn>2.

Solution.(a) Using the AM–GM inequality we obtain

n+sn

n =

(1+1) + 1+1

2

+···+ 1+1

n

>

(1+1)·

1+1

2 ···

1+1 n

1/n

= (n+1)1/n.

(b) By the definition of(sn)n≥1we have

n₋sn

n₋1 =

1−12

+···+ 1−1n

n₋1 >

1−1

2 ···

1−1_n

1/(n−1)

=n−1/(n−1).

⊓ ⊔

The following exercise involves a second-order linear recurrence.

1.2.5. Letα_∈(0,2). Consider the sequence defined by

xn+1=αxn+ (1−α)xn−1, for alln≥1.

Find the limit of the sequence in terms ofα,x0, andx1.

Solution.We havexn−xn−1= (α−1)(xn−xn−1). It follows thatxn−xn−1=

(α₋1)n₋1₍_x

1−x0). Therefore

xn−x0= n

∑

k=1

(x_k₋x_k₋₁) = (x1−x0) n

∑

k=1

(α−1)k−1_.

Now, using the assumptionα∈(0,2), we deduce that

lim

n→∞xn=

(1−α)x0+x1

2−α . ⊓⊔

Next, we discuss a first-order quadratic recurrence in order to establish a neces-sary and sufficient condition for convergence in terms of the involved real parameter.

1.2.6. Letabe a positive number. Define the sequence(xn)n_≥0by

(25)

Find a necessary and sufficient condition such that the sequence is convergent.

Solution.If limn→∞xn=ℓthenℓ=a+ℓ2, that is,

ℓ=1±

√ 1−4a

2 .

So, necessarily,a_≤1/4.

Conversely, assume that 0<a_≤1/4. Fromxn+1−xn=x2n−x2n−1it follows that

the sequence(xn)is increasing. Moreover,

xn+1=a+x2n<

1 4+

1 4=

1 2,

provided thatxn<1/2. This shows that the sequence is bounded, so it converges.

⊓ ⊔ The above result is extended below to larger classes of quadratic nonlinearities. The close relationship between boundedness, monotony, and convergence is pointed out and a complete discussion is developed in the following exercise.

1.2.7. Let f(x) =1/4+x₋x2. For anyx_∈R, define the sequence(xn)n≥0 by

x0=xandxn+1=f(xn). If this sequence is convergent, letx∞be its limit.

(a) Show that ifx=0, then the sequence is bounded and increasing, and compute its limitx∞=ℓ.

(b) Find all possible values ofℓ and the corresponding real numbersxsuch that

x∞=ℓ.

Solution.(a) We have

f(x) =1

2−

x₋1

2

2 ,

so xn≤1/2, for alln≥1. This inequality also shows that(xn)n≥0 is increasing.

Passing to the limit, we obtain

ℓ=1

2−

ℓ−1

2

2 .

Since all the terms of the sequence are positive, we deduce thatℓ=1/2.

(b) By the definition off it follows that

f(x)≤x, for allx_{≤ −}1

2,

and

f(x)≤ −1

(26)

We now prove that ifx_∈(−1/2,3/2), then the sequence converges and its limit equals 1/2. Indeed, in this case we have

f(x)−1 2 <

x₋1

2 .

It follows that

xn+1−

1 2 <

x₋1

2 n

→0 asn_→∞. ⊓⊔

The next exercise gives an example of a convergent sequence defined by means of an integer-valued function. We invite the reader to establish more properties of the function·:[0,∞)→N.

1.2.8. For any integern_≥1, letnbe the closest integer to√n. Compute

lim

n→∞

n

∑

j=1

2j+2−j

2j .

Solution.Since(k₋1/2)2₌_k2₋_k₊₁_/_{4 and}₍_k₊₁_/₂₎2₌_k2₊_k₊₁_/_{4, it}

fol-lows thatn=kif and only ifk2₋k+1≤n_≤k2+k. Hence

lim

n→∞

n

∑

j=1

2j+2−j

2j =

∞

∑

k=1

∑

j=k

2j+2−j

2j =

∞

∑

k=1

k2+k

∑

n=k2₋_k₊₁

2k+2−k 2n

=

∞

∑

k=1

(2k+2−k)(2−k2+k−2−k2−k) =

∞

∑

k=1

(2−k(k−2)−2−k(k+2))

=

∞

∑

k=1

2−k(k−2)− ∞

∑

k=3

2−k(k−2)=3. ⊓⊔

We give below a characterization of the sequences having a certain growth prop-erty. As in many cases, monotony arguments play a central role.

1.2.9. (i) Let(an)n≥1be a sequence of real numbers such thata1=1andan+1>

3an/2for alln_≥1. Prove that the sequence(bn)n≥1defined by

bn=

an

(3/2)n−1

either has a finite limit or tends to infinity.

(ii) Prove that for allα>1there exists a sequence(an)n_≥1with the same properties such that

lim

n→∞

an

(3/2)n−1=α.

International Mathematical Competition for University Students, 2003

Solution.(i) Our hypothesisan+1>3an/2 is equivalent to bn+1>bn, and the

(27)

(ii) For anyα>1 there exists a sequence 1=b1<b2<··· that converges toα.

Choosingan= (3/2)n−1bn, we obtain the required sequence(an)n≥1. ⊓⊔

Qualitative properties of a sequence of positive integers are established in the next example.

1.2.10. Consider the sequence(an)n≥1defined byan=n2+2.

(i) Find a subsequence ank

k≥1such that ifi<jthenani is a divisor ofanj.

(ii) Find a subsequence such that any two terms are relatively prime.

Solution.(i) For any integerk_≥1, takenk=2(3

k₊₁₎_/2

. Thenank=2

23n+1 and the conclusion follows.

(ii) Consider the subsequence(bn)n≥1defined byb1=3,b2=b21+2, and, for any

integern_≥3,bn= (b1···bn−1)2+2. ⊓⊔

The Stolz–Ces`aro lemma is a powerful instrument for computing limits of seq-uences (always keep in mind that it gives only asufficientcondition for the exis-tence of the limit!). A simple illustration is given in what follows.

1.2.11. The sequence of real numbers(xn)n_≥1satisfieslimn→∞(x2n+x2n+1) =

315andlimn→∞(x2n+x2n₋1) =2003. Evaluatelimn→∞(x2n/x2n+1).

Harvard–MIT Mathematics Tournament, 2003

Solution.Setan=x2nandbn=x2n+1and observe that

an+1−an

bn+1−bn

= (x2n+2+x2n+1)−(x2n+1+x2n) (x2n+3+x2n+2)−(x2n+2+x2n+1)−→

2003₋315 315−2003=−1,

asn_→∞. Thus, by the Stolz–Ces`aro lemma, the required limit equals−1. ⊓⊔ Remark.We observe that the value of limn→∞(x2n/x2n+1)doesnotdepend on

the values of limn→∞(x2n+x2n+1)and limn→∞(x2n+x2n−1)but only on the

con-vergence of these two sequences.

We refine below the asymptotic behavior of a sequence converging to zero. The proof relies again on the Stolz–Ces`aro lemma, and the method can be extended to large classes of recurrent sequences.

1.2.12. Let (an)n≥1 be a sequence of real numbers such that limn→∞an∑nk=1

a2_k=1. Prove thatlimn→∞(3n)1/3an=1.

I. J. Schoenberg, Amer. Math. Monthly, Problem 6376

Solution.Setsn=∑nk=1ak2. Then the conditionansn→1 implies thatsn→∞and

an→0 asn→∞. Hence we also have thatansn−1→1 asn→∞. Therefore

s3_n₋s3_n₋₁=a2_n(s2_n+snsn−1+s2n−1)→3 asn→∞. (1.3)

Thus, by the Stolz–Ces`aro lemma,s3_n/n_→3 asn_→∞, or equivalently, limn→∞n−2/3

(28)

We study in what follows a sequence whose terms are related to the coefficients of certain polynomials.

1.2.13. Fix a real numberx=−1±√2. Consider the sequence(sn)n≥1defined bysn=∑nk=0akxksuch thatlimn→∞sn=1/(1−2x−x2). Prove that for any integer

n_≥0, there exists an integermsuch thata2_n+a2_n₊₁=am.

Solution.We have 1 1−2x₋x2=

1 2√2

√ 2+1 1−(1+√2)x+

√ 2−1 1−(1−√2)x

and

1

1+ (1±√2)x=nlim→∞

n

∑

k=0

(1±√2)k_xk_.

Therefore

an=

1 2√2

(√2+1)n+1

−(1−√2)n+1_.

A straightforward computation shows thata2_n+a2_n₊₁=a2n+2. ⊓⊔

The following (not easy!) problem circulated in the folklore of contestants in Romanian mathematical competitions in the 1980s. It gives us an interesting prop-erty related to bounded sequences ofrealnumbers. Does the property given below remain true ifbnare not real numbers?

1.2.14. Suppose that (an)n_≥1 is a sequence of real numbers such that

limn→∞an=1and(bn)n_≥1is a bounded sequence of real numbers. Ifkis a positive integer such thatlimn→∞(bn−anbn+k) =ℓ, prove thatℓ=0.

Solution.(C˘alin Popescu). Letb=lim infn→∞bnandB=lim supn→∞bn. Since

(bn)n≥1is bounded, bothbandBare finite. Now there are two subsequences(bpr) and(bqr)of(bn)n≥1such thatbpr →bandbqr →Basr→∞. Sincean→1 and

bn−anbn+k→ℓasn→∞, it follows that the subsequences(bpr+k)and(bqr+k)of

(bn)n_≥1tend tob−ℓandB−ℓ, respectively, asr→∞. Consequently,b−ℓ≥band

B₋ℓ≤B, henceℓ=0. ⊓⊔

Elementary trigonometry formulas enable us to show in what follows that a very simple sequence diverges. A deeper property of this sequence will be proved in Problem 1.4.26.

1.2.15. Setan=sinn, for anyn≥1. Prove that the sequence(an)n_≥1is divergent.

Solution.Arguing by contradiction, we assume that the sequence(an)n≥1is

con-vergent. Leta=limn→∞sinn. Using the identity

sin(n+1) =sinncos 1+cosnsin 1

we deduce that the sequence(cosn)converges and, moreover,

(29)

whereb=limn→∞cosn. Using now

cos(n+1) =cosncos 1−sinnsin 1

we deduce that

b=bcos 1−asin1.

These two relations implya=b=0, a contradiction, sincea2+b2=1. ⊓⊔

Under what assumption on the functionfone can deduce that a sequence(an)n≥1

converges, provided the sequence(f(an))n≥1is convergent? The next exercise offers

a sufficient condition such that this happens.

1.2.16. Let(an)n≥1be a sequence of real numbers such thatan≥1for allnand the sequencean+a−n1

n_≥1converges. Prove that the sequence(an)n≥1is conver-gent.

Solution.Leta=lim infn→∞anandA=lim supn→∞an. Then bothaandAexist

and are finite. Indeed, ifA= +∞then we obtain a contradiction froman+a−n1>an

and our hypothesis that the sequencean+a−n1

n≥1is bounded (since it is

conver-gent).

Arguing by contradiction, assume thatA>a. Choose subsequences(ank)k≥1and

(amk)k≥1such thatank→Aask→∞andamk→aask→∞. Thereforeank+1/ank→A+ 1/Aask_→∞andamk+1/amk→a+1/aask→∞. But the sequence

an+a−n1

n≥1

is convergent to some limitℓ. It follows that

ℓ=A+1

A=a+

1

a.

Thus,(A₋a)((Aa₋1) =0. Hence eitherA=aorAa=1 and both are impossible sinceA>a_≥1. ⊓⊔

1.2.17. Given a sequence(an)n≥1such thatan−an−2→0asn→∞, show that

lim

n→∞

an−an−1

n =0.

Solution.Forε>0, letn0be sufficiently large that|an−an₋2|<εfor alln≥n0.

We have

an−an−1= (an−an−2)−(an−1−an−3) + (an−2−an−4)

− ···+{(an0+2−an0)−(an0+1−an0−1)}.

Thus

|an−an−1| ≤(n−n0)ε+|an0+1−an0−1|

and so(an−an−1)/ntends to zero asn→∞. ⊓⊔

1.2.18. Let

Sn= n

∑

k=1

1+ k

n2−1

.

(30)

Solution.We first observe that for allx>−1,

x

2+x< √

1+x₋1<x

2.

Hence, settingx=k/n2, we obtain

k

2n2₊_k<

1+ k

n2−1<

k

2n2.

Therefore

n

∑

k=1

k

2n2₊_k<Sn<

1 2n2

n

∑

k=1

k.

We have

1 2n2

n

∑

k=1

k=n(n+1)

4n2 →

1

4 asn→∞.

On the other hand,

lim

n→∞

1 2n2

n

∑

k=1

k₋

n

∑

k=1

k

2n2₊_k

=lim

n→∞

n

∑

k=1

k2

2n2₍₂_n2₊_k₎.

But

n

∑

k=1

k2

2n2₍₂_n2₊_k₎< n

∑

k=1

k2

4n4=

n(n+1)(2n+1)

24n4 .

We deduce that

lim

n_→∞

1 2n2

n

∑

k=1

k₋

n

∑

k=1

k

2n2₊_k

=0

and

lim

n_→∞

n

∑

k=1

k

2n2₊_k=

1 4,

hence the desired conclusion. ⊓⊔

1.2.19. Let(xn)n≥1be a sequence and setyn=xn−1+2xnfor alln≥2. Suppose that the sequence(yn)n≥2converges. Show that the sequence(xn)n≥1converges.

Solution.Let ˜y=limn→∞ynand set ˜x=y˜/3. We show that ˜x=limn→∞xn. For

ε>0 there is a positive integern0such that for alln≥n0,|yn−y˜|<ε/2. Hence

ε/2>|yn−y˜|=|xn−1+2xn−3 ˜x|=|2(xn−x˜) + (xn−1−x˜)|

≥2|xn−x˜| − |xn−1−x˜|.

Thus,|xn−x˜|<ε/2+ (1/2)|xn−1−x˜|, which can be iterated to give

|xn+m−x˜|<

ε 4

m

∑

i=1

2−i

+2−(m+1)|xn₋1−x˜|<

ε 2+2

−(m+1)_|_x

(31)

By takingmlarge enough, 2−(m+1)|xn−1−x˜|<ε/2. Thus for all sufficiently large

k,|xk−x˜|<ε. ⊓⊔

1.2.20. (i) Let(an)n≥1be a bounded sequence of real numbers such thatan=0 for alln_≥1. Show that there is a subsequence(bn)n≥1of(an)n≥1such that the sequence(bn+1/bn)n≥1converges.

(ii) Let (an)n≥1 be a sequence of real numbers such that for every subsequence

(bn)n≥1of(an)n≥1,limn→∞|bn+1/bn| ≤1. Prove that(an)n≥1has at most two limit points. Moreover, if these limit points are not equal and if one of them is

t, then the other is−t.

Solution.(i) We distinguish two cases.

CASE1: there existsε>0 such that for infinitely manyk,|a_k_{| ≥}ε. Let(bn)n_≥1be

the subsequence of(an)n_≥1consisting of thoseakwith|ak| ≥ε. Then|bn+1/bn| ≤

(sup_k|ak|)/εfor alln.

CASE2: for everyε>0 there is an integerNε such that for allk≥Nε,|ak|<ε.

Then there is a subsequence(bn)n_≥1of(an)n_≥1such that|bn+1|<|bn|.

In both cases, the sequence of ratios(bn+1/bn)n≥1is bounded, and thus by the

Bolzano–Weierstrass theorem there exists a convergent subsequence.

(ii) By hypothesis it follows that the sequence(an)n_≥1is bounded. Now suppose

that(an)n_≥1has at least two distinct limit pointssandt, wheres=−t. Then

there are subsequences(bp)p_≥1and(cq)q_≥1of(an)n_≥1converging tosandt

respectively. Let(dj)j≥1be the following subsequence of(an)n≥1:

dj=

bp if jis odd (that is,d1=b1,d3=b2, . . .),

cq if jis even (that is,d2=c1,d4=c2, . . .).

Then limj→∞|dj+1/dj|does not exist. This contradiction concludes the proof. ⊓⊔

1.2.21. Let(an)n≥1be a sequence of real numbers such thatlimn→∞(2an+1−

an) =ℓ. Prove thatlimn→∞an=ℓ.

Solution.We first show that the sequence(an)n≥1is bounded. Since the sequence

(2an+1−an)n≥1is bounded (as a convergent sequence), there existsM>0 such that

|a1| ≤M and for alln≥1,|2an+1−an| ≤M. We prove by induction that|an| ≤M

for alln. Indeed, suppose that|an| ≤M. Then

|an+1|=

an+ (2an+1−an)

2

≤

1

2(|an|+|2an+1−an|)≤M.

This concludes the induction and shows that(an)n≥1is bounded.

Taking lim sup in

an+1=

an+ (2an+1−an)

2 ,

we obtain

lim sup

n→∞ an≤

lim sup_n_→_∞an+ℓ

(32)

This yields lim supn→∞an≤ℓ. Similarly, we deduce that lim infn→∞an≥ℓ. We

conclude that limn→∞an=ℓ. ⊓⊔

1.2.22. Prove that a countably infinite set of positive real numbers with a finite nonzero limit point can be arranged in a sequence(an)n_≥1such that (a1/nn )n_≥1is convergent.

P. Orno, Math. Magazine, Problem 1021

Solution.Let(xn)n≥1denote the real numbers of concern and letabe a nonzero

finite limit point. ChooseAsuch that 1/A<a<Aand leta1denote thexnof

small-est subscript that lies in the interval(1/A,A). Assuminga1,a2, . . . ,a_k₋₁ to have been chosen, leta_kbe thexnof smallest subscript different from then−1 already

chosen lying in the interval(A−√n_,_A√n₎_{. Since}_a _{is a limit point, such an}_x

n can

be found, and sinceA√n_→∞andA−√n_→0, we deduce that everyxneventually is

included in an interval of the form(A−√n,A√n)and will therefore eventually be-come part of the sequence(an)n≥1. For eachn we have 1/A

√_n

<an<A

√_n and therefore(1/A)1/√n_<_a1/n

n <A1/

√

n_{. But lim}

n→∞A1/ √

n₌_lim

n→∞(1/A)1/ √

n₌₁

and therefore limn→∞a1/nn =1. ⊓⊔

1.3 Recurrent Sequences

Mathematics is trivial, but I can’t do my work without it.

Richard Feynman (1918–1988)

Recurrent sequences are widely encountered in nature, and they should be seen as a major step toward thediscretizationof variouscontinuousmodels. One of the most famous recurrent sequences goes back to Leonardo Fibonacci (1170–1250). About 1202, Fibonacci formulated his famous rabbit problem, which led to the Fibonacci sequence 1,1,2,3,5,8,13, . . .. The terms of this sequence have beautiful properties, mainly related to thegolden ratio. At the same time, it appears in several applica-tions in biology, including leaves and petal arrangements, branching plants, rabbit colonies, and bees’ ancestors (see Figure 1.2). It seems that the Fibonacci recurrence

Fn=Fn−1+Fn−2was first written down by Albert Girard around 1634 and solved by

de Moivre in 1730. Bombelli studied the equationyn=2+1/yn−1in 1572, which

is similar to the equationzn=1+1/zn−1satisfied by ratios of Fibonacci numbers,

(33)

Number of ancestors

1

2

3

5

8

13

Fig. 1.2 Bees have Fibonacci-number ancestors.

the seventeenth century. Sir Thomas Harriet (1560–1621) invented the calculus of finite differences, and Henry Briggs (1556–1630) applied it to the calculation of logarithms. It was rediscovered by Leibniz around 1672. Sir Isaac Newton, Leon-hard Euler (1707–1783), Joseph-Louis Lagrange (1736–1813), Carl Friedrich Gauss (1777–1855), and many others used this calculus to study interpolation theory. The theory of finite differences was developed largely by James Stirling (1692–1770) in the early eighteenth century. Recurrence relations were extended to the study of several sequences. A celebrated example is related to the cooperative recurrences

xn= (xn−1+yn−1)/2 andyn=√xn−1yn−1, which were associated by Lagrange with

the evaluation of elliptic integrals.

In this section we are interested in the study of recurrent sequences that are not necessarily linear.

The first example gives an interesting connection with Euler’s indicator function.

1.3.1. Consider the sequence(an)n≥1defined bya1=1,a2=2,a3=24, and

an=

6a2_n₋₁an−3−8an−1a2n₋2

an−2an−3

for alln_≥4.

Show that for alln,anis an integer that is multiple ofn.

Solution.We have _a

n