BAB 1
PENDAHULUAN
1.1 Latar Belakang
Permasalahan transportasi merupakan permasalahan yang sering terjadi dalam kehidupan sehari-hari. Transportasi merupakan bentuk khusus dari program linier yang digunakan untuk memecahkan masalah yang berhubungan dengan transportasi (pengangkutan) untuk meminimalkan biaya, jarak tempuh dan sebagainya sehingga dapat memaksimalkan laba/keuntungan yang diperoleh. Metode transportasi merupakan suatu metode yang digunakan untuk mengatur dostribusi dari beberapa sumber ke tempat-tempat yang membutuhkan barang. Pendistribusian barang yang harus diatur sedemikian rupa, karena ada perbedaan jarak atau biaya dari sumber-sumber yang ada dan tempat-tempat yang membutuhkan barang. Tujuan dari masalah transportasi adalah untuk menentukan jumlah yang optimal dari brang yang akan diangkut dari berbagai sumber ke berbagai tujuan sehingga biaya transportasi total minimum.
dapat terjadi karena ketidakpastian jumlah ketersediaan bahan mentah, terjadinya kerusakan mesin produksi, dan terjadinya kegagalan saat produksi. Penurunan jumlah bahan mentah, kerusakan mesin produksi dan kegagalan produksi menyebabkan penurunan pada jumlah supply. Sedangkan ketidakpastian dari nilai demand dapat terjadi karena adanya perubahan situasi pasar. Permintaan terhadap suatu barang ketika kondisi pasar baik cenderung lebih besar dibandingkan ketika kondisi pasar buruk. Sebuah cara yang sering kali digunakan untuk menyatakan ketidakpastian ini adalah bilangan fuzzy. Bilangan fuzzy dapat disajikan dalam bentuk trapezoidal dan atau triangular.
Masalah transportasi dengan jumlah supply, jumlah demand, dan biaya angkutannya dinyatakan dengan bilangan fuzzy disebut sebagai masalah transportasi fuzzy. Nilai dari biaya angkutan, jumlah supply, dan jumlah demand dalam kehidupan sehari-hari dapat dinyatakan dengan suatu interval crisp. Karena nilai dari biaya angkutan, jumlah supply, dan jumlah demand tidak selalu pasti, maka nilai dari biaya angkutan, jumlah supply, dan jumlah demand yang awalnya dalam bentuk crisp dapat dinyatakan dengan suatu interval yang tidak pasti, yaitu interval fuzzy.
Dalam menyelesaikan masalah transportasi fuzzy, tabel fuzzy harus diubah terlebih dahulu ke bentuk linier agar lebih mudah dalam mengerjakannya.Adapun teknik yang digunakan untuk menyelesaikan masalah transportasi fuzzy yaitu dengan menggunakan pendekatan teknik Robust Ranking. Teknik Robust Ranking merupakan suatu teknik yang digunakan untuk mengubah masalah transportasi fuzzy menjadi permasalahan transportasi linier. Setelah masalah transportasi fuzzy telah diubah menjadi masalah transportasi linier, maka dalam menentukan solusi yang optimal dapat diselesaikan dengan metode alternatif yaitu metode Zero Suffix. (Fegade, 2012:)
transportasi lalu memilih minimum dari permintaan dan persediaan dilanjutkan mengalokasikannya ke dalam tablo. Pencarian suffix value ini tetap berlanjut sampai semua baris dan kolom sudah jenuh. Berdasarkan uraian diatas, maka
penulis memberi tulisan ini dengan judul “Kajian tentang Metode Zero Suffix Menggunakan Teknik Robust Ranking pada Masalah Transportasi dengan Variabel Fuzzy”.
1.2 Perumusan Masalah
Perumusan masalah yang akan dibahas adalah bagaimana metode Zero Suffix sebagai metode pendekatan dalam menyelesaikan masalah transportasi dengan variabel fuzzy.
1.3 Batasan Masalah
Batasan masalah dalam penelitian ini adalah:
1. Masalah yang akan diteliti merupakan masalah transportasi seimbang atau masalah transportasi tidak seimbang.
2. Masalah transportasi dengan variabel fuzzy-nya mempunyai fungsi keanggotaan berbentuk trapezoidal dan triangular.
3. Metode yang digunakan adalah metode Zero Suffix dengan menerapakan pendekatan teknik Robust Ranking dalam mengubah masalah transportasi fuzzy menjadi masalah transportasi linier.
1.4 Tujuan Penelitian
1.5 Manfaat Penelitian
Manfaat penelitian ini adalah:
1. Untuk menambah wawasan penulis dalam memecahkan masalah transportasi dengan variabel fuzzy menggunakan metode Zero Suffix. 2. Sebagai tambahan informasi dan referensi bacaan untuk mahasiswa
matematika, terlebih bagi mahasiswa yang hendak melakukan penelitian serupa.
1.6 Tinjauan Pustaka
Transportasi adalah variasi khusus dari program linear yang digunakan untuk mengatur distribusi dari sumber-sumber yang menyediakan barang yang sama, ke tempat-tempat yang membutuhkan barang secara optimal. (Pangestu et al, 1984). Tranportasi digunakan untuk mencari solusi optimal dari masalah distribusi barang. Tahun 1939, L.V. Kantorovitch mempelajari berbagai masalah yang berhubungan dengan transportasi. Kemudian, tahun 1941 F.L. Hitchcock merumuskan model matematika dari masalah transportasi yang kini menjadi model baku yang sering disebut model Hitchcock. T.C. Koopmans tahun 1949 dan G.B. Dantzig tahun 1951 juga turut mengembangkan metode transportasi.
Charnes dan Cooper (1961) memperkenalkan program tujuan ganda sebagai pendekatan untuk menyelesaikan masalah yang tidak dapat diselesaikan dengan program linear yang disebabkan oleh tujuan yang bertentangan. Kemudian Ijiri (1965) dan Jaaskelainen (1969) melanjutkan dan melengkapinya sehingga dapat dipakai secara operasional.
Sebelum menentukan penyelesaian dari masalah transportasi terlebih dahulu dibentuk model matematikanya. Model umum matematik program linier untuk masalah transportasi sebagai berikut:
∑ ∑
Kendala:
Pemasokan: ∑
Permintaan: ∑
(David, 1984)
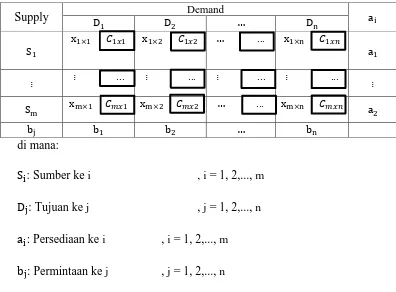
Pemodelan masalah transportasi dapat dilihat sebagai berikut:
Tabel 1. Gambaran Umum Masalah Transportasi
di mana:
: Sumber ke i , i = 1, 2,..., m
: Tujuan ke j , j = 1, 2,..., n
: Persediaan ke i , i = 1, 2,..., m
: Permintaan ke j , j = 1, 2,..., n
: Biaya transportasi per unit barang dari asal i ke tujuan j, i = 1, 2,..., m
, ,j = 1, 2,..., n
: Biaya unit barang yang diangkut dari asal i ke tujuan j, i = 1, 2,..., m
Supply Demand
...
... ... ... ...
, j = 1, 2,..., n
(Tofan, 2013)
Selanjutnya yang membedakan masalah transportasi menjadi dua macam, yaitu masalah transportasi seimbang dan transportasi tidak seimbang (Parlin, 1997). Masalah transportasi seimbang adalah masalah biaya angkutan barang dimana jumlah barang yang dipasok dari tempat asal sama dengan jumlah barang yang diminta di tempat tujuan (Parlin, 1997). Sedangkan masalah transportasi tidak seimbang adalah masalah dimana persediaan lebih besar dari permintaan atau sebaliknya (Tofan, 2013).
Istilah fuzzy lahir dari gagasan seorang guru besar pada University of California, Barkley, Amerika Serikat, Prof. Lotfi Asker Zadeh. Sejak tahun 1960 Zadeh telah merasa bahwa sistem analisis matematika tradisional yang dikenal sampai saat itu bersifat terlalu eksak sehingga tidak dapat berfungsi dalam banyak masalah dunia nyata yang seringkali amat kompleks. Pada akhirnya di tahun 1965
Zadeh mempublikasikan karangan ilmiahnya berjudul “Fuzzy Set”. Terobosan baru yang diperkenalkan oleh Zadeh ini telah memperluas konsep himpunan klasik menjadi himpunan fuzzy yang dapat mempresentasikan nilai-nilai ketidakpastian yang ditemui dalam kehidupan nyata.
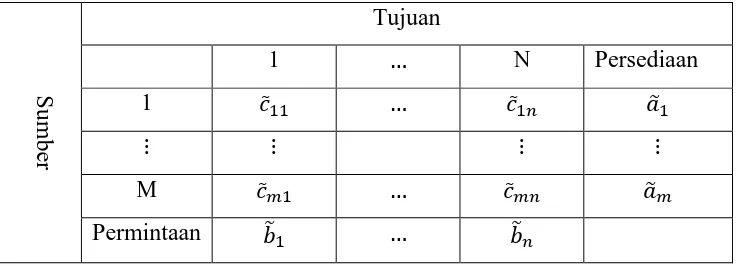
Untuk menyelesaikan masalah transformasi dengan variabel fuzzy, maka harus dimodelkan dulu ke dalam suatu tabel, adapun fungsi tujuan dari masalah transportasi dengan variabel fuzzy adalah:
Minimumkan:
Tabel 2 Masalah Transportasi dengan Variabel F uzzy
di mana:
m = jumlah dari titik persediaan
n = jumlah dari titik permintaan
̃ = jumlah tidak pasti dari unit barang yang dikirimkan dari titik persediaan i ke titik permintaan j, i = 1, 2,..., m
, j = 1, 2,..., n
̃ = biaya tidak pasti per unit barang yang didistribusikan dari
titik persediaan i ke titik permintaan j, i = 1, 2,..., m
, j = 1, 2,..., n
̃ = persediaan tidak pasti pada titik persediaan ke i , j = 1, 2,..., m
̃ = persediaan tidak pasti pada titik persediaan ke j , i = 1, 2,..., n
(Pandian, 2010)
Metode untuk menyelesaikan masalah transportasi dengan variabel fuzzy dengan metode Zero Suffix yang telah diberikan oleh Jayaraman dan Jahirhussian (2013). Dalam menggunakan metode ini diperlukan pemahaman tentang suatu teknik yang menginterpretasikan suatu bilangan fuzzy ke dalam suatu bilanngan crisp. Interpretasi dari bilangan fuzzy tersebut disebut dengan ranking dan dengan menggunakan ranking dari bilangan fuzzy itu. Teknik ini disebut dengan Robust Ranking Technique dengan persamaan sebagai berikut:
∫
di mana:
: nilai tengah dari interval [ ]
: Perhitungan batas atas dan batas bawah dari himpunan fuzzy Q
Misalkan terdapat himpunan permintaan fuzzy, himpunan persediaan fuzzy, atau himpunan biaya fuzzy dengan adalah triangular, maka:
{ }
Misalkan terdapat himpunan permintaan fuzzy, himpunan persediaan fuzzy, atau himpunan biaya fuzzy dengan adalah trapezoidal, maka:
{ }
(Fegade, 2012)
1.7 Metodologi Penelitian
Penelitian ini adalah penelitian literatur yang disusun dengan langkah-langkah berikut:
1. Menjelaskan tentang masalah transportasi.
2. Menjelaskan tentang dua macam masalah transportasi ( masalah seimbang atau tidak seimbang).
3. Menjelaskan tentang fuzzy.
4. Menjelaskan tentang masalah transportasi dengan variabel fuzzy. 5. Mengambil sebuah contoh kasus transportasi dengan variabel
fuzzy-nya mempunyai fungsi keanggotaan berbentuk trapezoidal dan triangular.
6. Mengubahnya menjadi persamaan transportasi dengan variabel fuzzy-nya mempunyai fungsi keanggotaan berbentuk trapezoidal dan triangular.
7. Melinierkan persamaan transportasi variabel fuzzy-nya mempunyai fungsi keanggotaan berbentuk trapezoidal dan triangular dengan teknik Robust Rangking.
9. Membahas hasil penyelesaian ( hasil yang diperoleh). 10.Membuat kesimpulan.
1.8 Kerangka Pemikiran
Adapun kerangka pemikiran dalam penelitian ini sebagai berikut:
Masalah Transportasi
Masalah Seimbang Masalah Tidak Seimbang
Fuzzy
Triangual Trapezoidal
Masalah Transportasi dengan Variabel Fuzzy
Metode Zero Suffix
Masalah Transportasi Linier
Teknik Robust Ranking
Solusi
Pembahasan