Syamsul Bahri Teori Pengoptimuman

Mata kuliah Teori Pengoptimuman merupakan salah satu mata kuliah pilihan bagi mahasiswa Program Studi Matematika Universitas Mataram yang disajikan pada semester 5 dengan bobot 3 SKS. Dengan melihat obyek dan bobot dari mata kulian ini, materi-materi yang disajikan dipilih sedemikian hingga mahasiswa yang telah lulus mata kuliah ini memiliki sejumlah kemampuan dasar yang berkaitan dengan teori dasar yang berkaitan dengan metode pengoptimuman dan penerapannya.

Buku ini dikemas dalam enam bab. Bab I berisi tentang apa dan bagaimana terkait dengan teori pengoptimuman, dilengkapi dengan landasan matematika yang berisi teori-teori yang mendukung dalam teknik pengoptimuman. Bab II tentang teknik-teknik pengoptimuman tanpa menggunakan konsep kalkulus. Bab III mengupas tentang tehnik pengoptimuman untuk kasus optimasi tanpa kendala. Bab IV membahas tentang tentang tehnik pengoptimuman untuk kasus optimasi yang berkendala. Bab V membahas tentang topik khusus yang berkaitan dengan program geometrik dan pada Bab VI membahas tentang topik program dinamik.

Buku ini disajikan dengan bahasa sederhana disertai dengan pembahasan contoh-contoh yang terkait dengan topik yang diuraikan. Pada setiap babnya disediakan beberapa soal latihan. Mahasiswa diharapkan mempelajari dengan baik dan cermat setiap metoda dan cara yang dilakukan dalam pemecahan soal-soal pada contoh yang diberikan dan mengerjakan semua latihan yang ada.

Akhirnya, kami menyampaikan terima kasih kepada Dekan FMIPA Universtas Mataram yang memberikan kesempatan kepada kami untuk menyusun buku ini. Kemudian sebagai penyusun kami menyadari kemungkinan adanya kekeliruan atau kesalahan pada buku ini, dengan hati terbuka kami menerima segala kritikan dan saran demi perbaikan buku ini.

Kata Pengantar

Bab 1. Pendahuluan

1.1. Pendahuluan

1.2. Landasan Matematika 1.2.1. Norma

1.2.2. Invers Matriks

1.2.3. Karakteristik Nilai Eigen 1.2.4. Fungsi dan Diferensial

1.2.5.Himpunan Konveks dan Fungsi Konveks

1.3. Kondisi Optimal untuk Masalah Optimasi Tidak Berkendala 1.4. Latihan

Bab 2. Optimasi Tanpa Kalkulus

2.1. Ketaksamaan Rata-Rata Aritmatika dan Geometri 2.2. Optimasi Menggunakan Ketaksamaan AM-GM 2.3. Ketaksamaan Cauchy

2.4. Hasil Kali Dalam untuk Matriks Bujur Sangkar 2.5. Latihan

Bab 3 Optimasi Tanpa Kendala

2.1. Metode Steepest-Descent 2.2. Metode Newton

2.3. Metode Gauss-Newton 2.4. Latihan

Bab 4. Optimasi Berkendala

4.1. Kendala

4.2. Klasifikasi Permasalahan Optimasi Berkendala

4.2.2 Program Kuadratik (Quadratic Programming) 4.2.3 Program Konveks (Convex Programming)

4.2.4 Bentuk Umum Permasalahan Optimasi Berkendala 4.3. Metode Transformasi

4.4. Pengganda Lagrange (Lagrange Multiplier)

4.4.1 Pengganda Lagrange untuk Permasalahan Kendala Persamaan 4.4.2 Kasus Khusus : Fungsi Kuadratik dengan Kendala Linear

4.4.3 Metode Lagrange untuk Kendala Pertidaksamaan 4.5. Teorema Karush-Kuhn-Tucker

4.6 . Latihan

Bab 5. Program Geometrik

5.1 Pendahuluan

5.2 Posinomial

5.3 Program Geometri Tanpa Kendala

5.3.1 Tingkat Kesulitan (degree of difficulty) 5.3.2 Syarat Cukup untuk Solusi PG

5.4 Solusi Program Geometri Menggunakan Ketaksamaan Aritmatik-Geometrik

5.5 Relasi Primal-Dual dan Syarat Cukup untuk Kasus Tanpa Kendala 5.6 Permasalahan Optimasi Berkendala

5.7 Penyelesaian Permasalahan Program Geometrik Berkendala 5.8 Latihan

Bab 6. Program Dinamik

6.1 Pendahuluan

6.2 Definisi Program Dinamik

6.3 Sifat atau Karakteristik Program Dinamis 6.4 Multi Tahapan Proses Pengambilan Keputusan

6.5 Konsep Suboptimalisasi dan Prinsip Optimalitas dalam Permasalahan Program Dinamik

6.6 Metode Kalkulus untuk Penyelesaian Program Dinamik

BAB 1

PENDAHULUAN

1.1 Pendahuluan

Teori optimasi merupakan salah satu subyek dalam matematika terapan, matematika komputasi, dan riset operasi yang memiliki ranah aplikasi yang cukup luas pada berbagai bidang seperti sains, enginering, ekonomi dan bisnis, keuangan, militer, dan sebagainya. Secara khusus, teori dan metode optimasi merupakan suatu alat untuk menentukan solusi optimal dari suatu permasalah nyata yang didefinisikan secara matematika menggunakan metode ilmiah dan alat-alat (teori atau metode) yang terkait dalam penentuan solusi optimal tersebut.

Penyelesaian permasalahaan optimasi merupakan suatu langkah ilmiah penentuan solusi optimal atau terbaik terhadap suatu permasalahan nyata yang terdiri atas serangkaian kegiatan yang meliputi penyusunan model matematika yang terkait dengan masalah yang dipecahkan. Model matematika ini berkaitan dengan proses pendefinisian variabel yang merepresentasikan permasalahan yang dihadapi, penentuan fungsi tujuan, dan fungsi kendala.

Secara umum, model optimasi diberikan oleh Persamaan (1.1.1) berikut ini. Min ( ) dengan f x x X, atau Min ( )f x

x X



 (1.1.1)

dengan x menyatakan variabel keputusan (decision variable), f x( ) menyatakan fungsi tujuan (objective function), dan n

X  menyatakan himpunan kendala (constrain set) atau daerah feasibel (feasible region). Secara khusus, permasalahan optimasi dapat dibedakan atas dua tipe, yaitu optimasi tanpa kendala dan optimasi berkendala. Permasalahan optimasi tanpa kendala diberikan oleh Persamaan (1.1.2) berikut :

Min ( )f x x X

(1.1.2)

Min ( )

dengan E dan I berturut-turut menyatakan himpunan indeks untuk kendala berupa persamaan (equality constraints) dan kendala berbentuk pertidaksamaan (inequality

constraints).

1.2 Landasan Matematika

Pada sub bagian ini akan diuraikan beberapa konsep matematika yang menjadi dasar pengembangan teori dan metode pengoptimuman, seperti norma, matriks, fungsi, diferensial, himpunan dan fungsi konveks.

1.2.1 Norma

Pada buku ini, notasi n

 dan n

 berturut-turut menyatakan ruang berdimensi n

atas lapangan real dan lapangan kompleks. Untuk n



atau n



x  menyatakan n -tupel, x



x x₁, ,₂ ,xn



dengan xiatau xi฀; i1, 2,, .n

Definisi berikut akan memberikan pengertian tentang terminologi norma. Definisi 1.1 Misalkan , n

x y dan sebarang. Fungsi : n 

   disebut

norma, jika memenuhi pernyataan berikut ini :

(i). x 0, dan x 0 jika dan hanya jika x0, (ii). x  x ,

(iii). xy  x  y .

Untuk n,

Secara umum, untuk suatu bilangan bulat p didefinisikan Norma-lp sebagai berikut:

disebut norma matriks, jika memenuhi pernyataan berikut ini :

(i). A 0, dan A 0 jika dan hanya jika A0, (ii). A  A ,

(iii). A B  A  B .

Berkaitan dengan norma-lppada (1.2.1), norma-lpuntuk matriks adalah sebagai berikut :

Secara khusus, beberapa definisi norma yang sudah sering dan umum digunakan adalah (1). Norma maksimum atas vektor kolom:

1 ₁

(2). Norma maksimum atas vektor baris:

1 ₁

Selanjutnya berdasarkan definisi norma tersebut di atas, didefinisikan konsep jarak sebagai berikut.

Definisi 1.3 Misalkan , n

x y . Jarak antara titik x dan y pada ruang n,

dinotasikan dengan d x y( , ), merupakan suatu fungsi ( , ) : n n

d x y    yang

Berdasarkan definisi norma, berikut ini adalah karakteristik dari fungsi jarak.

Definisi 1.4 Misalkan , , n

x y z .

(i). d x y( , )0 dan d x y( , )0 jika dan hanya jika x y,

(ii). d x z( , )d x y( , )d y z( , ), (iii).d x y( , )d y x( , ).

Selanjutnya berikut akan diberikan beberapa terminologi konvergensi barisan vektor pada n

dan barisan matriks pada ruangm n .

Definisi 1.5 Misalkan x_k n, untuk setiap n bilangan asli. Barisan vektor

 

x_k dikatakan konvergen ke-x, jika

lim n 0

n x  x (1.2.6)

Selanjutnya, misalkan m n k

A   , untuk setiap m n, . Barisan matriks

 

Ak dikatakan konvergen ke A, jika

lim n 0

n A A  (1.2.7)

Definisi 1.6 Barisan

 

xk n dikatakan barisan Cauchy, jika untuk setiap  0

terdapat indeks N sehingga x_n x_m , untuk setiap n m, N.

Atau, untuk setiap n m, Nberlaku

,

lim n m 0

n m x x  (1.2.8)

1.2.2 Invers Matriks

Pada subbagian ini akan diuraikan beberapa teorema dasar yang berkaitan dengan invers dan invers yang diperumum (generalized inverse) dari matriks.

Teorema 1.7 [Sun dan Yuan, 2006:9]

Misalkan . konsisten norma matriks dengan I 1 dan En n sebarang. Jika

1

1 adalah nonsingular dan memenuhi





Teorema 1.8 [Sun dan Yuan, 2006:10]

Misalkan , n n

1.2.3 Karakteristik Nilai Eigen

Pada subbab ini, akan diuraikan beberapa terminologi yang terkait dengan nilai eigen, khususnya yang terkait dengan matriks definit positif, matriks definit negatif, dan matriks simetrik indefinit.

Definisi 1.9 Misalkan An n suatu matriks dan n, 0

x x . Bilangan 

disebut nilai eigen dari matriks A, jika memenuhi kesamaan berikut:

Axx (1.2.14)

Definisi 1.10 Radius spektral dari matriks A didefinisikan dengan

1

( ) _i

i n

A maks

 

 

 (1.2.15)

Misalkan matriks n n

A  dengan nilai–nilai eigen  ₁, ₂,, ._n Vektor eigen yang berkorespondensi dengan nilai eigen yang berbeda dari matriks A adalah bebas linear.

Definisi 1.11 Misalkan An n adalah matriks simetrik dan n v . (1). Matriks A disebut definit positif jika T 0

v Av , untuk setiap v0. (2). Matriks A disebut semidefinit positif jika T 0

v Av .

(3). Matriks A disebut definit negatif jika A definit positif atau T 0

v Av , untuk

setiap v0.

(4). Matriks A disebut semidefinit negatif jika A semidefinit negatif atau T 0 v Av . (5). Matriks A disebut indefinit, jika A bukan semidefinit positif atau semidefinit

negatif.

Misalkan n n

A  adalah matriks simetrik. Beberapa karakteristik dari matiks A

adalah sebagai berikut :

(1). Semua nilai eigen dari A adalah bilangan real.

(2). Vektor eigen yang berkorespondensi dengan nilai-nilai eigen yang berbeda dari matriks A adalah ortogonal.

Berdasarkan Definisi 1.10, beberapa karakteristik yang terkait dengan matriks simetrik definit posifif, semidefinit positif, definit negatif dan semidefinit negatif. Misalkan n n

A  adalah matriks simetrik.

(1). Matriks A adalah definit positif jika dan hanya jika semua nilai eigen dari matriks A adalah positif.

(2). Matriks A adalah semidefinit positif jika dan hanya jika semua nilai eigen dari matriks A adalah non negatif.

(3). Matriks A adalah definit negatif jika dan hanya jika semua nilai eigen dari matriks A adalah negatif.

(5). Matriks A adalah indefinit jika dan hany jika nilai eigen dari matriks A ada yang positif dan sekaligus yang negatif.

1.2.4 Fungsi dan Diferensial

Misalkan n

x dan  0. Sekitaran- (neighborhood) dari vektor x didefinisikan dengan





( ) n|

N x  y ฀y x  (1.2.16)

Misalkan n

D dan xD. Titik x disebut titik interior dari D, jika terdapat sekitaran- dari x sedemikian hingga N x_( )D. Himpunan semua titik interior dari himpunan D dinotasikan dengan Int D( ). Oleh karenanya, Int D( )D. Jika setiap titik pada D adalah titik interior atau Int D( )D, maka himpunan D adalah himpunan buka.

Titik n

x D  disebut titik akumulasi atau titik limit, jika   0,

( ) D .

N x_    ini berarti, terdapat subbarisan

 

k n

x pada D sehingga k n

x x. Himpunan semua titik limit dari D disebut tutupan (closore) dari D, dinotasikan dengan

D. Jelas bahwa DD. Selanjutnya, jika DD atau setiap titik limit pada D dimuat oleh D maka D adalah himpunan tutup.

Himpunan n

D disebut terbatas, jika terdapat bilangan real M sedemikian hingga x M, untuk setiap xD. Selanjutnya, himpunan n

D dikatakan himpunan kompak, jika D tutup dan terbatas.

Fungsi : n

f   disebut kontinu di titik n,

Fungsi kontinu : n

f  dikatakan kontinu terdiferensial di titik n,

c jika

atau Matriks Jacobian untuk fungsi f di titik n

x didefinisikan dengan

Jika f kontinu terdiferensial di setiap titik pada himpunan buka n

D maka f disebut kontinu terdiferensial pada D dan dinotasikan dengan f C D1( ). Secara umum, jika fungsi kontinu _{f x( ), dan ( ),f x f}' ''_{( ),x ,f}(p)_{( )x ada dan kontinu untuk setiap titik pada} himpunan D, maka dinotasikan dengan p( ).

f C D

Fungsi kontinu terdifensial : n

f   dikatakan mempunyai turunan kedua yang kontinu di n

Matriks Hessian dari fungsi f,2f, didefinisikan sebagai matriks simetris berukuran n n dengan elemen sebagai berikut

2

1.2.5 Himpunan Konveks dan Fungsi Konveks

1.2.5.1 Himpunan Konveks

maka himpunan S disebut himpunan konveks.

Secara umum, himpunan n

S disebut himpunan konveks, jika untuk setiap 1, ,2 , m

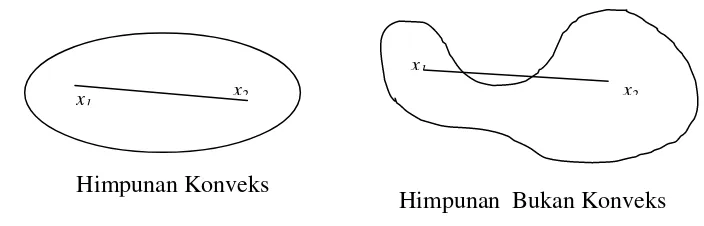
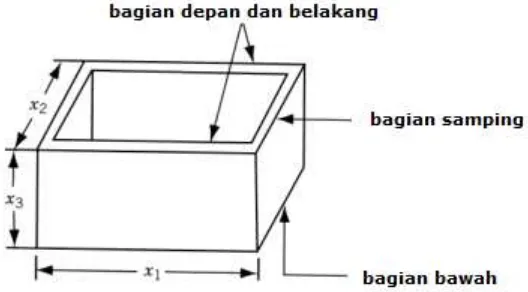
Secara geometri, Definisi 1.11 mengindikasikan bahwa jika x x₁, ₂Smaka segmen garis antara x₁ dan x₂ berada pada himpunan S, sebagaimana di ilustrasikan pada Gambar 1 berikut:

Gambar 1. Ilustrasi himpunan konveks dan himpunan bukan konveks

Pada Gambar 1, himpunan yang pertama (bagian kiri) terlihat bahwa x₁ dan x₂

serta semua titik pada ruas garis x x_{1 2} berada pada himpunan S, tetapi pada himpunan kedua (bagian kanan), x₁ dan x₂berada pada himpunan S, tetapi ada bagian pada ruas garis x x_{1 2}yang berada di luar himpunan S.

Beberapa karakteristik himpunan konveks adalah sebagai berikut : 1) Misalkan S₁ dan S₂ adalah himpunan konveks pada n

(a). S₁S₂ adalah himpunan konveks.

(b). S₁S₂ 



x₁x ₂|x₁S x₁, ₂S₂



adalah himpunan konveks. 2) Jika n

S adalah himpunan konveks maka

(a). Himpunan interior dari S, Int(S), adalah himpunan konveks. (b). Tutupan (closure) dari himpunan S adalah himpunan konveks.

1.2.5.2 Fungsi Konveks

Definisi 1.13 Misalkan Sn dan S  merupakan himpunan konveks, serta fungsi

: n.

f S  Jika untuk setiap x x₁, ₂S dan setiap 

 

0,1 berlaku

1 2 1 2

( (1 ) ) ( ) (1 ) ( ),

f x   x f x   f x (1.2.21)

maka fungsi f disebut fungsi konveks pada S.

Selanjutnya, jika terdapat c0 sedemikian hingga untuk setiap x x₁, ₂Sberlaku

2

1 2 1 2 1 2

1

( (1 ) ) ( ) (1 ) ( ) ,

2

f x   x f x   f x  c x x (1.2.22)

maka fungsi f disebut fungsi konveks secara seragam (uniformly) pada S.

Jika fungsi f pada S merupakan fungsi konveks (konveks seragam), maka invers dari fungsi f yaitu

 

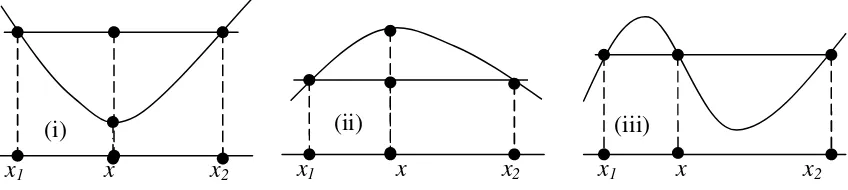
f merupakan fungsi konkaf /concave (konkaf seragam) pada S, seperti yang di ilustrasikan pada Gambar 2.

Gambar 2 Ilustrasi grafik (i) fungsi konveks, (ii) fungsi konkaf, dan (iii) bukan fungsi konveks dan konkaf

Secara geometri, berdasarkan ilustrasi pada Gambar 2, fungsi konveks dapat diinterpretasikan sebagai suatu fungsi yang grafiknya berada di bawah ruas garis yang

x1 x x2

x1 x x2

(i)

x1 x x2

(ii)

x1 x x2

menghubungkan titik



x f x₁, ( )₁



dan titik



x₂, ( )f x₂



untuk setiap x



x x₁, ₂



. Sebaliknya, grafik fungsi konkaf berada di atas ruas garis yang menghubungkan titik



x f x1, ( )1



dan titik



x2, ( )f x2



untuk setiap x



x x1, 2



.

Suatu fungsi : n

f S   dikatakan fungsi konveks tegas (strictly convex) pada S, jika

( ( )) ( ) ( ( ) ( )), ,

f x yx  f x  f y  f x x yS.

Selanjutnya teorema berikut akan memberikan hubungan antara fungsi konveks dengan matriks Hessian.

Teorema 1.14 Misalkan Sn suatu himpunan konveks yang tidak kosong dan misalkan pula f : S kontinu terdiferensial dua kali, f C S2( ).

1) Fungsi f adalah fungsi konveks jika dan hanya jika matriks Hessian yang berkaitan dengan fungsi f adalah matriks semidefinit positif untuk setiap titik di S.

2) Fungsi f adalah fungsi konveks tegas, jika matriks Hessian yang berkaitan dengan

fungsi f adalah matriks definit positif untuk setiap titik di S.

3) Fungsi f konveks seragam jika dan hanya jika matriks Hessian yang berkaitan

dengan fungsi f adalah matriks definit positif seragam untuk setiap titik di S, yaitu

terdapat konstanta m0 sehingga

2 ₂

(x) , dan

T n

m u  u f u  x S u

1.3 Kondisi Optimal untuk Masalah Optimasi Tidak Berkendala

Pada subbab ini, misalkan permasalahan optimasi tidak berkendala diberikan sebagai berikut:

min ( ), n

f x x (1.23)

Definisi 1.15 Titik x disebut titik minimum lokal (local minimizer),, jika terdapat

0

  sedemikian hingga ( ) ( ), n

f x  f x  x  dan xx . Kemudian, Titik x

disebut titik minimum lokal tegas (strict local minimizer), jika terdapat  0

sedemikian hingga ( ) ( ), , n ,

f x  f x  x  xx dan xx  .

Definisi 1.16 Titik x disebut titik minimum global (global minimizer), jika

( ) ( ), n

f x  f x  x  . Kemudian, Titik x disebut titik minimum global tegas (strict

global minimizer), jika ( ) ( ), , n dan .

f x  f x  x  xx

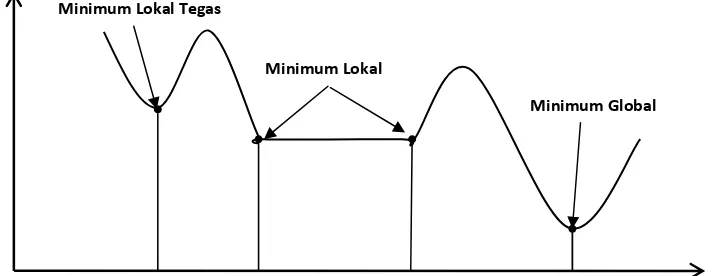
Secara geometri, ilustrasi definisi minimum lokal, minimum lokal tegas dan minimum global dapat dilihat pada Gambar 3. Pada tataran aplikasi, kebanyakan algoritma yang diajukan digunakan untuk menentukan minimum lokal. Sedangkan untuk minimum global merupakan pekerjaan yang cukup sulit, kecuali untuk beberapa fungsi tertentu yang sudah dikenal karakteristiknya, seperti fungsi kuaratik atau fungsi polinomial pada umumnya.

Gambar 3. Ilustrasi minimum lokal, minimum lokal tegas dan minimum global Salah satu konsep yang sangat penting dalam menemukan lokasi minimum lokal adalah arah descent (descent direction) yang didefinisikan sebagai berikut.

Definisi 1.17 Misalkan : n

f   terdiferensial di titik n.

x Jika terdapat vektor

n

d sehingga

( ), 0,

f x d

  (1.24)

maka d disebut arah descent dari fungsi f di titik x. Minimum Lokal Tegas 

Minimum Lokal  

Kondisi pada teorema berikut merupakan syarat perlu suatu fungsi f memiliki minimum lokal di titik n.

x

Teorema 1.18 (Syarat Perlu untuk Turunan Pertama)

Misalkan : D n

f  kontinu terdiferensial pada himpunan buka D. Jikax*D

adalah titik minimum lokal dari (1.23) maka berlaku

 

0. f x

   _(1.25)

Teorema 1.19(Syarat Perlu untuk Turunan Kedua) Misalkan Dn matriks semidefinit positif.

Teorema 1.20(Syarat Cukup untuk Turunan Kedua)

Misalkan D n

x  disebut titik stasioner (titik kritis) untuk fungsi terdiferensial f, jika f x

 

* 0.

Teorema 1.22 Misalkan n

S suatu himpunan konveks tak kosong dan fungsi

:

(2). Jika f fungsi konveks tegas maka x*Smerupakan satu-satunya titik minimum global.

1.4 Latihan

1. Misalkan A adalah matriksnon singular berukuran n n . Buktikan bahwa

1

x Ax

A

 .

2. Tunjukkan dengan induksi matematika bahwa himpunan n

S adalah himpunan

adalah himpunan konveks.

4. Misalkan



2



konveks, tetapi himpunan D belum tentu himpunan konveks.

BAB 2

OPTIMASI TANPA KALKULUS

(

OPTIMIZATION WITHOUT CALCULUS

₎

Pembahasan tentang tehnik atau metode optimasi, biasanya kita tidak terlepas dari syarat turunan pertama dan kedua dari suatu fungsi, sistem persamaan linier, operator nonlinier, ukuran jarak dan sebagainya. Bahkan beberapa mahasiswa atau kita pada umumnya sering kali menganggap bahwa optimasi merupakan suatu topik atau pokok bahasan yang penyelesaiannya bergantung pada aplikasi dari turunan dan kalkulus pada umumnya.

Pada bab ini, kita akan mendiskusikan optimasi tanpa menggunakan prinsip dan tehnik kalukulus, khususnya teori tentang diferensial. Pembahasan tehnik atau metode optimasi pada bab ini didasarkan pada ketaksamaan rata-rata Aritmatika-Geometri dan ketaksamaan Cauchy.

2.1 Ketaksamaan Rata-Rata Aritmatika dan Geometri

Sebelum kita membahas tentang ketaksamaan yang melibatkan hubungan antara rata-rata aritmatika dan rata-rata, berikut diberikan terminologi tentang rata-rata aritmatia dan geometri secara parsial.

Definisi 2.1 Jika x x₁, ,₂ ,xn adalah bilangan real positif maka :

(1). Rata-rata aritmatika terhadap n data x x₁, ,₂ ,xn adalah

1 2 1

( n)

AM x x x

n

   _ , (2.1.1)

(2). Rata-rata geometri terhadap n data x x₁, ,₂ ,xn adalah 1/ 1 2

GM ( . . . ) n n x x x

 _ . (2.1.2)

Teorema 2.2 Misal diberikan x x₁, ,₂ ,xn adalah bilangan positif. Hubungan antara

rata-rata aritmatika(AM) dan rata-rata geometri (GM) diberikan oleh ketaksamaan

berikut :

Ketaksamaan (2.1.3) dikenal dengan ketaksamaan rata-rata aritmatika dan geometri (arithmetic mean-geometric mean)yang dikenal dengan AM-GM.

Teorema 2.3 Perumuman dari Ketaksamaan AM-GM

Misalkan x x₁, ,₂ ,xn adalah n bilangan positif dan misalkan pula a a1, 2,,anadalah bilangan-bilangan positif dengan sifat

1



Perumuman dari ketaksamaan AM-GM adalah

2.2 Optimasi Menggunakan Ketaksamaan AM-GM

Ilustrasi penggunaan AM-GM untuk penyelesaian permasalahan optimasi adalah sebagai berikut :

2.2.1 Contoh 1

Tentukan nilai minimun dari fungsi f x y( , ) 12 18 xy,

x y

   dengan dan x y merupakan dua bilangan positif.

 

Ketaksamaan pada (2.2.1) berimplikasi bahwa nilai minimum fungsi 12 18

Kesamaan pada (2.2.2) memberikan x2 dan y3 sehingga diperoleh nilai minimum untuk fungsi f x y( , ) 12 18 xy

x y

   adalah 18.

2.2.2 Contoh 2

Tentukan nilai maksimum dari fungsi ( , )f x y xy(72 3 x4 )y dengan dan x y

merupakan dua bilangan positif.

Perhatikan bahwa fungsi ( , )f x y xy(72 3 x4 )y terdiri atas tiga suku, yaitu x y, , dan 72 3 x4y, serta jumlah ketiga suku-suku tersebut bukanlah suatu konstanta. Tetapi, kalau dimodifikasi menjadi 3x4y(72 3 x4 )y memberikan hasil yang konstan yaitu 72. Dengan demikian fungsi ( , )f x y dapat ditulis kembali menjadi

  

maksimum dari fungsi ( , )f x y terjadi jika masing-masing suku tak konstan dari fungsi

( , )

f x y pada (2.2.3) adalah 24.

Akibatnya diperoleh nilai x8 dan y6. Substitusi nilai x dan y pada fungsi ( , )

f x y memberikan nilai maksimum untuk fungsi

8; 6

2.2.3 Contoh 3

Tentukan nilai minimum dari fungsi f x y( , ) 4x x₂ 4y

y x

   dengan dan x y

merupakan dua bilangan positif.

Untuk kasus ini, tulis fungsi f x y( , ) 4x x₂ 4y

Selanjutnya, tulis kembali fungsi ( , )f x y sebagai berikut

2

Selanjutnya, berdasarkan ketaksamaan AM-GM berlaku

 

Dengan menulis kembali (2.2.4) menjadi

2

Berdasarkan persamaan (2.2.5) dan (2.2.6) maka diperoleh 1 ( , ) 2

4 f x y  . Dengan

demikian diperoleh nilai minimum dari fungsi ( , )f x y adalah 8, yaitu ketika masing-masing suku pada (2.1.5) bernilai 2.

2.3 Ketaksamaan Cauchy Definisi 2.4 Misalkan , n

1 1 2 2

, n n

x y x y x y x y . (2.3.1)

(2). Norma vektor xndidefinisikan dengan

,

x  x x . (2.3.2)

Definisi 2.5 Misalkan , n

x y dengan x



x x₁, ₂,,xn



dan y



y y1, 2,,yn



.

Ketaksamaan Cauchy berkaitan dengan vektor x dan y memenuhi

,

x y  x y (2.3.3)

Ruas kiri akan sama dengan ruas kanan, jika terdapat asehingga xay.

Permasalahan optimasi yang menggunakan ketaksamaan Cauchy sebagai alat penyelesaiannya diperlihat oleh contoh-contoh berikut ini.

Contoh 1.

Tentukan nilai terbesar dan terkecil dari fungsi

( , , ) 2 3 6 ,

f x y z  x y z (2.3.4)

jika titik ( , , z)x y memenuhi 2 2 2 1

x y z  .

Berdasarkan ketaksamaan Cauchy, kita peroleh

2 2 2 2 2 2 2

(2  3 6 )(x y z ) (2 x3y6 ) ,z (2.3.5) Karena syarat x2y2z2 1maka ruas kiri pada (2.3.5) sama dengan 49. Akibatnya nilai fungsi ( , , z)f x y berada pada interval [ 7,7] dan kesamaan pada (2.3.5) terjadi ketika vektor (2,3,6) paralell terhadap vektor ( , , )x y z , yaitu

2 3 6

x y z

  . (2.3.6)

Kesamaan (2.3.6) memberikan xt, 3 2 ,

y t dan z3t dengan 2 4 9.

t  Akibatnya, nilai terkecil dari ( , , )f x y z  7, pada saat nilai 2

7

x  dan nilai terbesar dari

( , , ) 7

f x y z  , ketika nilai 2.

7

Contoh 2.

Permasalahan mendasar pada teori estimasi adalah mengestimasi nilai konstanta c, jika diberikan sejumlah J data zj  c vj, 1, 2,j ,J dengan vj,j merupakan variabel acak yang merepresentasikan suatu gangguan (noise) atau kesalahan pengukuran (measurement error). Jika diasumsikan nilai harapan (ekspetasi) untuk nilai vj,j adalah E v( )j 0, nilai vj,j tidak saling berkorelasi atau E v v( , )j k 0, untuk jk dan varians dari vjadalah

2 2 ( )j 0. E v   Estimator linier untuk c diberikan oleh

1

Dengan demikian, ini berarti bahwa bj harus meminimumkan

2 2

dengan kendala

1

Untuk menyelesaikan permasalahan ini, kita akan menggunakan ketaksamaan Cauchy. Pandang kesamaan

Ketaksamaan Cauchy memberikan

dengan tanda sama dengan terpenuhi jika dan hanya jika terdapat suatu konstanta, sebut

Berdasarkan persamaan (2.3.9) diperoleh

2

Akhirnya memberikan nilai untuk estimator

2

2.4 Hasil Kali Dalam untuk Matriks Bujur Sangkar

Trace untuk suatu matriks persegi M, notasi trM, adalah jumlah elemen-elemen matriks M yang berada di bawah diagonal utamanya. Jika diberikan matriks persegi A dan B atas lapangan  (semua elemennya merupakan bilangan real).

Trace dari perkalian matriks T

B A mendefinisikan hasil kali dalam, , ( TA).

A B tr B

Hasil kali dalam pada matriks dapat digunakan untuk mendefinisikan norma pada matriks, yang dikenal dengan norma Frobenius, yaitu :

, ( T ).

A  A A  tr A A (2.4.1)

Berikut akan diberikan sebuah teorema yang berlaku pada suatu matriks simetri (Teorema Fan). Namun sebelum itu akan diuraikan dulu beberapa terminologi yang akan digunakan dalam teorema tersebut.

Misalkan S adalah suatu matriks simetris. Definisikan ( ) n, ( )



₁, ₂, ,



n

S S

 _     _ 

adalah vektor yang elemen-elemennya merupakan nilai eigen dari matriks simetris S,

dan D( ( )) S merupakan matriks diagonal yang elemennya adalah elemen dari ( ) S . Berdasarkan definisi ini, dapat ditunjukkan bahwa

( )

S   S . (2.4.2)

Misalkan pula



( )S



menyatakan vektor dari nilai eigen S yang diurut dengan urutan tidak naik.

Teorema 2.6 (Teorema Fan)

Jika S dan R adalah dua matriks simetris sebarang maka berlaku

( ) [ ( )],[ ( )] , tr SR   S  R

dengan tanda sama dengan terpenuhi jika dan hanya jika terdapat matriks ortogonal U

sedemikian hingga

([ ( )]) T,

SUD  S U

dan

([ ( )]) T.

RUD  R U

Akibat dari Teorema Fan, jika matriks S dan R adalah matriks diagonal, maka berlaku ( ), ( )S R [ ( )],[ (R)]S

2.5 Latihan

1. Misalkan A menyatakan rata-rata aritmatika dari himpunan berhingga bilangan positif P, dengan x dan y berturut-turut menyatakan unsur terkecil dan terbesar dari himpunan P.

Buktikan bahwa xy A x(  y A), dan kesamaan terjadi jika dan hanya jika .

x y A

2. Minimumkan fungsi

2 2

1 4

( ) 4

f x x x

x x

   

untuk setiap x bilangan positif.

Petunjuk : pandang dua suku pertama dan dua suku terakhir secara terpisah.

3. Tentukan nilai maksimum dari fungsi 2 ( , ) ,

f x y x y jika x dan y memenuhi 6x5y45.

Petunjuk : Tulis 6x3x3x.

4. (Ketaksamaan Young) Misalkan p dan q adalah bilangan positif yang lebih besar dari 1 dan memenuhi 1 1 1.

p q Jika x dan y adalah dua bilangan positif maka

,

p q

x y xy

p q

 

dengan kesamaan terjadi jika dan hanya jika p q.

x  y

BAB 3

OPTIMASI TANPA KENDALA

(

UNCONSTRAINED OPTIMIZATION

₎

Permasalahan optimasi tanpa kendala dapat dibedakan atas dua metode, yaitu metode pencarian (search methods) dan metode gradien (gradient methods). Namun secara umum, khususny untuk permasalahan multidimensi, metode pencarian kurang efisien. Oleh karenanya pada buku ini hanya akan dibahas tentang metode gradien.

Metode gradien merupakan salah satu metode optimasi yang berdasarkan pada informasi gradient fungsi yang akan dioptimalkan pada suatu titik tertentu. Pada bagian ini, kita akan fokus pada tiga metode gradien yang umum yaitu :

(a). Metode Steepest-Descent (b). Metode Newton

(c). Metode Gauss-Newton

3.1 Metode Steepest-Descent

Misal diberikan suatu permasalahan optimasi

F = ( ), untuk n.

Min Min f x x (3.1.1)

Berdasarkan aturan pada Deret Taylor,

1 2

( ) ( ) T T ,

F  F f x  f x g   H (3.1.2)

dan  0. Perubahan F dalam fungsi  diberikan oleh

. T

F g 

 _ (3.1.3)

Operasi kali pada ruas kanan (3.1.3) adalah kali skalar atau hasil kali dalam (dot product) antara vektor g dan vektor  .

Jika



1g2



T n

g g g dan



1 2



T n

1

cos n

i i i

F g g  



 





dengan  menyatakan sudu antara vektor g dan vektor  , dan

 

1

2 . T

g  g g (3.1.4)

3.1.1 Arah Ascent dan Descent

Perhatikan plot kontur pada Gambar 3.1. Jika x dan x dua titik yang berdekatan pada kontur A, maka untuk  0 berlaku

cos 0

F g  

   (3.1.5)

Karena F merupakan konstanta pada kontur. Dengan demikian dapat disimpulkan bahwa besaran sudut  antara vektor g dan vektor  sama dengan 900. Akibatnya gradien di titik x adalah ortogonal dengan kontur A, seperti yang diilustrasikan pada Gambar 3.1. Selanjutnya, untuk setiap , F bernilai maksimum (positif) jika 0, dan  merupakan arah dari fungsi g.

Pada sisi lain, F bernilai maksimum (negatif) jika   , dan  menyatakan arah dari fungsi g. Gradien gdan gberturut-turut menyatakan arah steepest ascent dan steepest descent. Secara mendasar definisi terkait dengan hal ini diberikan sebagai berikut.

3.1.2 Metode Dasar

Misalkan f x( ) adalah fungsi kontinu di sekitaran titik x. Jika d menyatakan arah steepest-descent di titik X di titik x, yaitu

d  g maka perubahan sebesar  di titik x diberikan oleh

,

d

  untuk suatu 0

akan mengurangi nilai fungsi ( ).f x Maksimum pengurangan nilai fungsi ( )f x dapat dipandang sebagai permasalahan mencari solusi permasalahan

( )

Min F f x d

   (3.1.6)

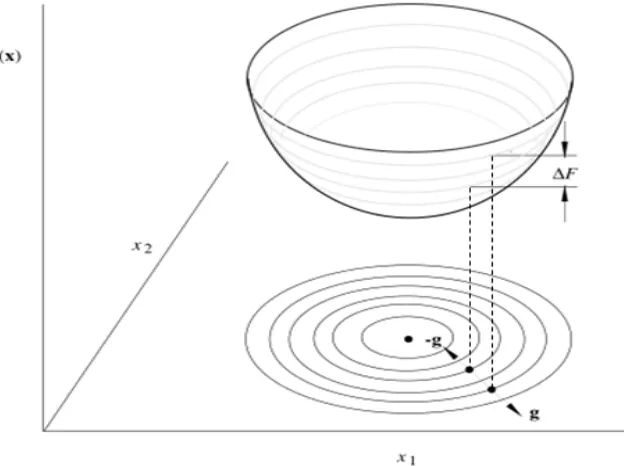
sebagaimana diilustrasikan seperti pada Gambar 3.2 dan Gambar 3.3.

Gambar 3.3 Arah Steepest Descent dan Steepest Ascent. Sumber : Antoniou dan Lu (2007:122).

Jika keadaan dari suatu titik x ke suatu titik optimum x* yang menyebabkan nilai f(x) minimum, maka melalui metode stepest descent arah pencarian ditentukan oleh nilai  seperti diilustrasikan pada Gambar 3.3. Akibatnya, permasalahan dimensi banyak (multi-dimensional) semula dapat diselesaikan dengan permasalahan dimensi satu Persamaan (3.1.1).

Pada kenyataannya, d bukanlah titik yang berada pada arah _x* _{dan selanjutnya} prosedur iterasi harus digunakan untuk menentukan solusi yaitu _x*_{. Dimulai dari titik}

0,

x arah d d₀  g dapat ditentukan dan nilai  yang meminimumkan



0 0 0



f x  d , sebut ₀ dapat ditentukan. Selanjutnya titik x₁ x₀ _{0 0}d dapat ditentukan dan selanjutnya dapat dilanjutkan melalui proses iterasi

1 .

k k k k

x _ x  d (3.1.7)

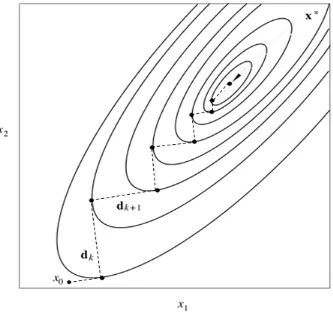
positif kecil. Proses iterasi ini seperti diilustrasikan pada Gambar 3.4. Perhatikan bahwa pola trayektori dari titik awal menuju titik solusi mengikuti pola zig-zag tetapi saling tegak lurus.

Gambar 3.4 Arah Steepest Descent dan Steepest Ascent. Sumber : Antoniou dan Lu (2007:124).

Algoritma Steepest-Descent adalah sebagai berikut : Langkah 1.

Input x₀ dan tetapkan nilai toleransi (bilangan positif cukup kecil).

Tetapkan k = 0;

Langkah 2.

Hitung gradien gk dan tetapkan dk  gk. Langkah 3.

Tentukan k, nilai  yang meminimumkan f x( kdk)

Langkah 4. memberikan formula penentuan nilai k, jika diberikan H matriks Hessian untuk ( )f x adalah dengan menggunakan formula (Antoniou dan Lu, 2007:125) :



Algoritma Steepest-Descent tanpa Line Search : Langkah 1.

Input x₁ dan tetapkan nilai toleransi (bilangan positif cukup kecil).

Langkah 2.

Hitung gradien g_k.

Langkah 3.

Tetapkan d_k  g_kdan k k₁.

Hitung f  f x( k gk).

Tentukan nilai k berdasarkan Persamaan (3.1.10) Langkah 4.

untuk m menyatakan nilai eigen terkecil dari Hessian Hk dan Mmenyatakan nilai eigen terbesar dari Hessian Hk.

3.2 Metode Newton

Metode Newton (Newton-Raphson) dibangun berdasarkan aproksimasi kuadratik dari deretTaylor. Jika  menyatakan gangguan untuk titik x, fungsi

Turunan fungsi (f x) respek terhadap parameter _k,k 1, 2,,n dan seting hasil turunan tersebut sama dengan nol akan memberikan kyang meminimumkan nilai fungsi (f x), yaitu :

2 1

0, untuk 1, 2, , n

i i

k i k

f f

k n

x  x x 

 

  





   (3.2.2)

Dalam notasi matriks , Persamaan (3.2.2) dapat ditulis

g  H Atau,

1

H g

 _{ } 

(3.2.3)

Persamaan (3.2.3) memiliki solusi, jika memenuhi kondisi berikut ini. 1) MatriksHessian non singular.

2) Aproksimasi pada Persamaan (3.2.1) valid.

Secara sederhana, metode Newton-Raphson merupakan suatu metode optimasi untuk meminimumkan suatu fungsi : n ,

f   yaitu menentukan variabel _x* sedemikian hingga f x( ) 0.* 

3.2.1 Metode Newton untuk Satu Variabel

Pada kasus ini, permasalahan optimasi yang dilakukan adalah meminimumkan fungsi satu variabel. Misal fungsi :f   diberikan dan akan diminimumkan, yaitu mencari x*yang meminimumkan fungsi f , yaitu f x( )*  f x( ) untuk setiap

.

x D  Untuk mencari x*dilakukan dengan menyelesaikan persamaan f x'( ) 0. Seting g(x) f x'( )dan terapkan metode Newton-Rapson pada fungsi ( ).g x Oleh karenanya, permasalahan ini dapat dipandang sebagai permasalahan mencari x*

1

3.2.2 Metode Newton untuk Multivariabel

Algoritma Newton-Raphson untuk menentukan akar dari fungsi : n n

f  

mengikuti iterasi berikut ini :





1

1 [ ]( ) ( ),

k k k k

x _ x  J g x  g x (3.2.6)

dengan J[g x]( )menyatakan matriks jacobian dari turunan parsial orde satu, j ( ),k j tentukan akar dari fungsi g. Kemudian, tahapan iterasi Algoritma Newton-Raphson diberikan oleh

1

 J[ adalah matriks Hessian dari turunan parsian kedua dari fungsi f.

Selanjutnya, jika 2

( ), dan ( ) merupakan arah descent karena memenuhi T T 1 0

k k k k k

Algoritma Metode Newton

Langkah 1.

Input x₀n dan tetapkan nilai toleransi  (bilangan positif cukup kecil).

Tetapkan k = 0

Langkah 2.

Jika gk , maka slesai! Langkah 3.

Selesaikan Gk  gk untuk setiap sk Langkah 4.

Tetapkan x_k1x_ks_k; dan hitung f_k1 f x( _k1).

Langkah 5.

Tetapkan k  k 1, dan ulangi langkah 2-4.

Teorema berikut memberikan syarat cukup untuk konvergensi metode Newton. Teorema 3.1 [Teorema Konvergensi Metode Newton (Sun dan Yuan, 2006)]

Misalkan f C2 dan x cukup dengan solusi permasalahan minimasi k

*

x dengan

* ( ) 0.

g x  Jika matriks Hessian G x definit positif dan ( )* G x memenuhi kondisi ( )

Lipschitz,

( ) (y) , untuk suatu dan , ij ij

G x G  xy  i j (3.2.9)

dengan G x menyatakan elemen baris ke-i dan kolom ke-j pada matriks G(x) maka _ij( )

untuk setiap k, algoritma Newton (3.2.8) adalah well-defined; dibangun oleh barisan

 

xk konvergen ke *_.

x

3.3 Metode Gauss-Newton

Pada banyak permasalahan optimasi, fungsi obyektif diberikan dalam bentuk fungsi terhadap vektor,

1 2

[ ( ) ( ) ( )]T m

Dengan ( ), 1, 2,f xj j ,m adalah fungsi dengan variabel bebas x.

Pada permaalahan seperti ini, fungsi bernilai real F dapat ditulis dalam bentuk 2

Pada kasus ini, jika F dapat diminimumkan menggunakan algoritma multi-dimensi tanpa kendala, maka fungsi f xj( ) secara individu adalah minimum dalam bentuk

least-squares. Metode mencari solusi optimal untuk kasus seperti ini dikenal dengan metode Gauss-Newton.

Jika diberikan sejumlah fungsi, f xj( ), j1, 2,,m dengan n

x , maka matriks Jakobian diberikan oleh

1 1 1

Bilangan m yang menyakan banyaknya fungsi mungkin saja lebih banyak dari jumlah variabel elemen x, yaitu bilangan n.

Melalui pendiferensialan fungsi F pada Persamaan (3.3.2) respek terhadap variabel , 1, 2,x i_i  ,n memberikan

Dalam bentuk matriks dapat ditulis

Sehingga gradien dari fungsi F, notasi gF, diberikan oleh 2 T

F

g  J f (3.3.4)

Jika diasumsikan bahwa 2 ( ) maka Persamaan (3.3.5) menjadi

2

Selanjutnya, Hessian dari matriks F, notasi HF, dapat diperoleh 2 T

F

H  J J (3.3.7)

Karena gradien dan Hessian dari F sudah diketahui, maka relasi rekursif metode Newton diberikan oleh persamaan berikut ini.

1

Sebelum Algoritma Newton dibahas, berikut akan diberikan Algoritma Matthews dan Davies sebagai algoritma yang mendasari Algoritma Newton, sebagai berikut :

Set m=k-1, l_mm 1. If h_mm 0, set h_mm h₀₀.

Langkah 2.1

For ik k, 1,,n do:

Set ljm hjm /hmm, hjm 0.

Langkah 2.1.1

For t=k, k+1, ... , n do: Set hit hitl him mt

If 0hkk h₀₀, set h00hkk. Langkah 3.

Set l_nn 1.

If hnn0, set hnn h00.

For i=1,2, ... , n set dii hii.

Selesai !

Selanjutnya, Adapun Algoritma Newton sebagaimana yang telah diuraikan di atas adalah sebagai berikut :

Algoritma Metode Gauss-Newton Langkah 1.

Input x₀n dan tetapkan nilai toleransi  (bilangan positif cukup kecil).

Tetapkan k = 0

Langkah 2.

Hitung fjk  f xj( ), k j1, 2,,m dan Fk Langkah 3.

Hitung , 2 T , k k k k

J g  J f dan 2 T . k k k

H  J J

Langkah 4.

Hitung Lkdan Dk menggunakan algoritma Matthews dan

Davies.

Hitung yk  L gk k dan  1 T

k k k k

d L D y .

Langkah 5.

Tentukan _k, nilai  yang meminimumkan F x( _k d_k).

Langkah 6.

Hitung f_{j k( 1),}untuk j1, 2,,m dan F_k1

Langkah 7.

Jika F_k1F_k  maka kerjakan

Output x*xk₁, fj k₍ ₁₎( )x* untuk j1, 2,,m dan Fk1.

Selesai. Jika Tidak,

3.4. Latihan

1. Gunakan metode Steepest-Descent untuk menyelesaikan permasalahan berikut :

(a). 2 2 2. Untuk soal No. 1.(b) : dengan menggunakan induksi, tunjukkan bahwa

1

Selanjutnya, tentukan titik x* sedemikian hingga nilai (x)f minimum. 3. Diberikan masalah minimasi

2 2

1 2 1 2 1 2

min 0, 2x x  x x 2, 2x 2, 2x 2, 2.

(a). Tentukan titik x* yang memenuhi kondisi turunan pertama, yaitu *

'( ) 0.

f x 

(b). Tunjukkan bahwa titik _x*_{pada (a) merupakan titik minimum global !} (c). Jika titik awal, 0

0 0

x    

 , berapa banyak iterasi steepest-descent dilakukan agar dicapai titik optimal dengan  _{10 .}10

4. Selesaikan permasalahan minimasi,

2 2 2 2 2 2 2

1 2 3 1 2 1 3

( ) ( 5) ( 8) ( 7) 2 4

f x  x   x   x   x x  x x ,

menggunakan algoritma steepest-descent.

(a). Mulai dengan x₀ 



1 1 1



Tdan  10 .6 Verifikasi solusi tersebut dengan menggunakan kondisi turunan kedua.

(b). Sama dengan no. (a), dengan x₀  



2,3 0 0 .



T (c). Sama dengan no. (a), dengan x₀ 



0 2 12 .



T 5. Selesaikan permasalahan minimasi berikut

2 2 2 2

1 2 1 2

( ) ( 1) ( 1)

jika  106 dengan titik awal



4 4 ,

 

T 4 4 , 4

 

T 4 , dan



T



4 4



T menggunakan algoritma steepest-descent, kemudian bandingkan hasilnya jika menggunakan algoritma Steepest-Descent tanpa Line Search.

BAB 4

OPTIMASI BERKENDALA

(

CONSTRAINED OPTIMIZATION

₎

Pada bab ini akan diuraikan beberapa hal yang terkait dengan prinsip, metode, dan algoritma yang berkaitan dengan permasalahan optimasi dengan kendala (constrained optimization).

4.1 Kendala

Bentuk umum permasalahan optimasi berkendala adalah menentukan vektor * n

x  yang meminimumkan suatu fungsi,

( ),

Min f x (4.1.1)

dengan kendala (subject to) :

1( ) 0, untuk 1, 2, , .

a x  i  p (4.1.2)

( ) 0, untuk 1, 2, , . j

c x  j  q (4.1.3)

Kesamaan pada (4.1.2) disebut kendala persamaan (equality constraints) dengan dan ketaksamaan pada (4.1.3) disebut kendala pertidaksamaan (inequality constraints).

Permasalahan optimasi dengan fungsi obyektif/fungsi tujuan (objective function) dan kendala (4.1.2) dan (4.1.3) yang diasumsikan mempunyai turunan kedua dan

kontinu, yaitu 2

( ), ( ) untuk 1, 2, , dan 1, 2, , . i j

a x c x C i  p j  q Misalkan D menyatakan daerah feasibel untuk permasalan (4.1.1), yaitu himpunan semua titik-titik yang memenuhi (4.1.2) dan (4.1.3) :



| ( )i 0, untuk 1, 2, , dan ( ) 0, untuk j 1, 2,j , q



D x a x  i  p c x    (4.1.4)

4.1.1 Kendala Persamaan

Misalkan beberapa kendala persamaan diberikan 1( ) 0

( ) 0 p

a x

a x





mendefinisikan suatu permukaan (hypersurface) pada n.

 Dalam notasi vektor, Persamaan (4.1.5) dapat ditulis menjadi

1 2

( ) [ ( ) ( ) ( )]T 0. p

a x  a x a x  a x  (4.1.6)

Defini 4.1

Suatu titik x disebut titik regular (regular point) dari kendala (4.1.5), jika titik x

memenuhi Persamaan (4.1.5) dan vektor kolom a x₁( ),a x₂( ),,a xp( ) adalah

bebas linear.

Berdasarkan Definisi 4.1, Suatu titik regularxdari suatu kendala persamaan, jika titik xtersebut memenuhi kesamaan (4.1.5) dan matriks Jacobian

1 2

 memiliki rank baris yang penuh. Karena n

x maka matriks Jacobian Jeberukuran np. Oleh karenanya, agar titik n

x

menjadi titik regular dari kendala (4.1.5) maka haruslah ukuran pn. Selanjutnya, jika pn, pada banyak kasus jumlah vektor n

x yang memenihi Persamaan (4.1.5) adalah finit dan permasalahan optimasi (4.1.1) mempunyai solusi trivial.

Contoh 4.2

Diskusikan dan sketsalah daerah feasibel yang memenuhi kendala persamaan berikut : 1 3 1 0

Matriks Jacobian untuk kendala (4.1.7a) dan (4.1.7b) adalah sebagai berikut :

1 2

Perhatikan, Kesamaan pada (4.1.7b) dapat ditulis kembali menjadi





2 2

1 1 2 1

x  x  (4.1.8)

Dalam bentuk persamaan parameter dalam t, Persamaan (4.1.8) dapat ditulis menjadi 1 1 cos( )

x   t (4.1.9a)

2 sin( )

x  t (4.1.9b)

jika Persamaan (4.1.9) dihubungkan dengan Persamaan (4.1.7a) akan memberikan 3 2 cos( )

x   t (4.1.9c)

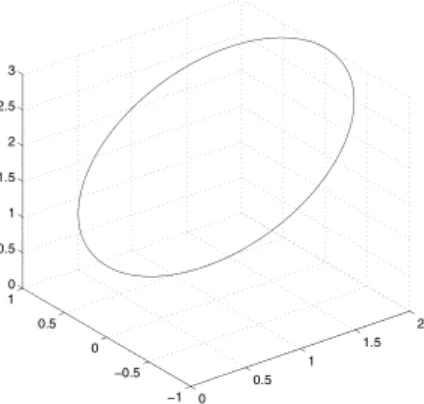
Persamaan parameter (4.1.9a)-(4.19c) dengan parameter t pada [0, 2 ] menghasilkan kurva seperti pada Gambar 4.1 berikut ini.

Gambar 4.1 Kurva representasi dari kendala Persamaan (4.1.7)

Pada kasus tertentu, permasalahan optimasi memiliki kendala ( )a xi semuanya dalam bentuk persamaan linear. Oleh karenanya, Persamaan (4.1.5) menjadi sistem persamaan linear yang dapat diekspresikan menjadi

Axb (4.1.10)

dengan p n

A  yang secara numerik sama dengan Jacobian, yaitu AJ_e, dan 1

p

adalah titik regular, jika rank(A) = p. Jika rank(A) = p’< p, maka terdapat dua kemungkinan yaitu :

 

Jika Persamaan (4.1.11) terpenuhi, maka terdapat kontradiksi diantara kesamaan yang ada pada sistem (4.1.11). Oleh karena perlu dilakukan reduksi untuk menghilangkan yang dua atau lebih kesamaan yang kontradiksi tersebut. Jika Persamaan (4.1.12) yang terpenuhi dengan rank(A) = p’maka dengan manipulasi aljabar Persamaan (4.1.10) dapat direduksi menjadi sistem yang ekivalen yang terdiri atas p’kendala kesamaan linear, yaitu

Ketika rank(A) = p’, secara numerik terdapat cara untuk mereduksi Persamaan (4.1.10) menjadi (4.1.13) yaitu dengan menerapkan singular-value decomposition



Sederhanakan kendala persamaan berikut ini: 1 2 3 4

Persamaan (4.1.16), dapat ditulis dalam notasi matriks Axb sebagai berikut : 1 pada (4.1.16) dapat direduksi menjadi 2 kesamaan saja, melalui penerapan SVD pada matriks A dengan

0, 2717 0,8003 0,5345 0,1365 0,5818 0,8018 0,9527 0,1449 0, 2673 U

0,1463 0,3171 0, 6331 0, 6908 0, 6951 0, 6284 0,3161 0,1485 0, 6402 0,3200 0, 6322 0, 2969

Selanjutnya, berdasarkan Persamaan (4.1.14) dan (4.1.15) diperoleh

1 2 3 4

2,1770x 10,3429x 9,5255x 4,3540x 5, 7135 (4.1.17a)

1 2 3 4

0,5106x 1, 0118x 0,5152x 1, 0211x 3, 0587

4.1.2 Kendala Pertidaksamaan

Pada sub bab ini akan diuraikan tentang permasalahan optimasi dengan kendala pertidaksamaan. Diberikan himpunan kendala sebagai berikut :

1 2

( ) 0 ( ) 0

( ) 0 q

c x c x

c x

 



 (4.1.18)

Berbeda dengan banyaknya kendala sama dengan, banyaknya kendala pertidaksamaan,

q, tidak harus lebih kecil dari banyaknya komponen x, yaitu n. Sebagai contoh, jika diberikan suatu kasus dengan kendala ( ),c xj untuk setiap 1 j q sebagai fungsi linear maka kendala pada (4.1.18) merepresentasikan polihedron dengan q facets dan

banyaknya facets pada polihedron adalah tak berhingga (unlimited).

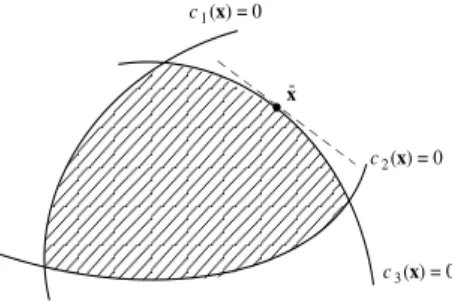
Terhadap kendala pertidaksamaan, terdapat dua isu pokok yang termuat pada (4.1.18). Berkaitan dengan titik feasibel x, kendala pertidaksamaan (4.1.18) dapat dibagi dua klasifikasi, yaitu himpunan kendala dengan ( )c xj 0 dan himpunan kendala dengan ( )c xj 0. Himpunan kendal dengan sifat ( )c xj 0disebut dengan kendala aktif (active constraints) himpunan kendala dengan sifat ( )c xj 0 disebut dengan kendala tidak aktif (inactive constraints). Sebagai ilustrasi perhatikan Gambar 4.2 berikut ini.

Berdasarkan ilustrasi pada Gambar 4.2, c x₁( ) dan c x₂( ) merupakan kendala tidak aktif, dan kendala c x₃( ) merupakan kendala aktif.

Pendekatan lain berkaitan dengan kendala pertidak samaan adalah mengkonversi kendala tersebut menjadi kendala sama dengan. Sebagai ilustrasi, diberikan permaslahan optimasi sebagai berikut :

( ), n

Min f x x , (4.1.19a)

dengan kendala : c x_i( ) 0, untuk  i1, 2,,q. (4.1.19b) Kendala pada (4.1.19b) dapat ditulis dalam bentuk lain, yaitu

 Kendala (4.1.20b) dapat dieliminasi menggunakan substitusi variabel

2

, untuk 1 . i i

y y  i q

Jika kita misalkan

 _{ }

maka permasalahan optimasi (4.1.19) dapat ditulis menjadi  

( ), n q

Min f x xE  (4.1.21a) dengan kendala :



( ) 0, untuk 1, 2, , i

c x  i  q (4.1.21b)

Sebagai ilustrasi, kita dapat menuliskan kendala pertidaksamaan (4.1.18) dalam bentuk matriks sebagai berikut :

0

Cx (4.1.22)

dengan q n _{dan .}q1

C  d  Misalkan D



x Cx| d



dan asumsikan bahwa 1, 2 .

x x D Untuk 

 

0,1 , titik xx₁ (1 )x₂ memenuhi Persamaan (4.1.22) karena

1 (1 ) 2

(1 )

Cx Cx Cx

d d d

 

 

  

    (4.1.23)

Dengan demikian , Cxdmendefinisikan suatu himpunan konveks.

4.2 Klasifikasi Permasalahan Optimasi Berkendala

Sebelum kita membahas tentang klasifikasi permasalahan optimasi berkendala, berikut diberikan beberapa terminologi yeng berperan dalam diskusi tentang hal tersebut. Pada pembahasan selanjutnya, himpunan D menyatakan daerah feasibel untuk permasalahan optimasi (4.1.1)-(4.1.3), dan himpunan *





* : x

B  x xx  untuk suatu  0disebut bola yang berpusat di _x* _{dengan jari-jari .}

Definisi 4.4 Titik x disebut titik minimum lokal untuk permasalahan optimasi (4.1.1)-* (4.1.3), jika terdapat bola B sehingga _x* D_x* B_x*D bukan himpunan kosong dan



*



*

( ) min ( ) : _x . f x  f x xD

Definisi 4.5 Titik x disebut titik minimum lokal untuk permasalahan optimasi (4.1.1)-* (4.1.3), jika x*D dan f x( )* min



f x( ) :xD



.

Definisi 4.6 Titik x disebut titik minimum lokal kuat * (strong local minimizer) jika

terdapat bola B sehingga _x* D_x* B_x*D bukan himpunan kosong dan *

x adalah titik

pembuat minimum pada D_x*

4.2.1 Program Linear (Linear Programming)

( ) T

Min f x c x (4.2.1a)

dengan kendala :

Axb (4.2.1b)

0

x (4.2.1c)

untuk suatu n1, p n, dan p 1.

c  A  b  Pada permasalahan LP, kita ingin menentukan vektor x*yang meminimumkan fungsi tujuan ( )f x dengan kendala berupa fungsi linear pada (4.2.1b) dan kendala (batasan) non negatif pada (4.2.1c).

Selanjutnya, permasalahan LP dapat juga diberikan dalam bentuk tidak standar berikut ini.

T

Min c x (4.2.2a)

dengan kendala :

Axb . (4.2.2b)

Dengan menggunakan variabel dummy (slack variable) vektor yAx b , maka Persamaan (4.2.2b) dapat ditulis menjadi

Ax y b (4.2.3a)

dan

0

y . (4.2.3b)

Selanjutnya, jika kita ekspresikan variabel x sebagai selisih dua variabel non negatif, vektor x 0dan vektor x 0, yaitu :

xxx dan misalkan

 x x x y





          

maka fungsi tujuan (4.2.2a) menjadi

 ₀ 

T

T T

c x _c c _x



_{A A I x}



_{b dan x}_0.

Berdasarkan konstruksi variabel di atas, permasalahan optimasi tidak standar dapat ditulis dalam bentuk standar sebagai berikut :

 T

Min c x (4.2.4a)

dengan kendala

 Axb (4.2.4b)

 ₀

x (4.2.4c)

dengan dan 





.

0 c

c c A A A I

   

 _{ }   

   



4.2.2 Program Kuadratik (Quadratic Programming)

Bentuk umum dari permasalahan kuadratik (QP) adalah sebagai berikut : 1

min ( ) 2

T T

f x  x Hxx pc (4.2.5a)

dengan kendala

Axb (4.2.5b)

Cxd (4.2.5c)

Pada banyak kasus , Hessian dari fungsi f(x), H, adalah semidefinit positif. Hal ini berimplikasi bahwa ( )f x fungsi konveks dan daerah feasibel yang ditentukan oleh Persamaan (4.2.5b) dan (4.2.5c) selalu konveks.

4.2.3 Program Konveks (Convex Programming)

Terdapat beberapa tipe atau model permasalahan CP, namun pada bab ini kita akan mendiskusikan model yang sering digunakan dalam penerapan sains dan teknik yaitu :

4.2.4 Bentuk Umum Permasalahan Optimasi Berkendala

Permasalahan optimasi berkendala (4.1.1)-(4.1.3) dapat dipandang sebagai permasalahan optimasi dalam bentuk umum (GCO), jika ( )f x berupa fungsi nonlinear berorde lebih besar dari orde dua, dan bukan konveks global atau paling sedikit terdapat satu kendal yang tidak konveks.

Contoh 4.7 Diberikan permasalahan optimasi berikut

2 3

dengan kendala :

1

Selidiki apakah permasalahan tersebut di atas termasuk dalam kelas GCO. Solusi :

3 2 pada titik x, sehingga ( )f x tidak konveks pada daerah feasibel dan permasalahan optimasi di atas termasuk dalam GCO.

4.3 Metode Transformasi

Metode transformasi merupakan salah satu metode penyelesaian masalah optimasi berkendala ke dalam permasalahan optimasi tanpa kendala.

4.3.1 Eliminasi Variabel

4.3.1.1 Kendala Persamaan Linear Diberikan permasalahan optimasi

min ( )f x (4.3.1a) semua solusi Persamaan (4.3.1b) dengan karakterisasi



[ n ]

xA b  I A A  (4.3.2) Dengan A menotasikan pseudo-invers Moore-Penrose dari A, In matriks identitas berukuran nn, dan  adalah vektor parameter berdimensi sebarang. Solusi yang diekpresikan oleh Persamaan (4.3.2) dapat disederhanakan menggunakan dekomposisi SVD. Selanjutnya, karena matriks A mempunyai rank penuh, rank A( ) p, dekomposisi SVD menghasilkan