Teori Dualitas dan Penerapannya (Duality Theory and Its Application)

1

TEORI DUALITAS DAN PENERAPANNYA

(DUALITY THEORY AND ITS APPLICATION)

TEORI DUALITAS DAN PENERAPANNYA

(DUALITY THEORY AND ITS APPLICATION)

Amelia Kurniawati, ST., MT.

Goal

•

Memahami perbedaan bentuk Primal dan

Dual

•

Memahami hubungan antara persamaan

Primal dan Dual

•

_{Memahami cara pemecahan masalah}

3

Outline

①

Teori dualitas

5

Teori dualitas

•

_{Ide dasar:}

–

_{Setiap masalah pemrograman linier}

mempunyai satu pemrograman linier yang

terkait yang disebut

dual

.

–

_{Solusi pada masalah pemrograman liniear}

originalnya juga memberikan solusi bagi

dualnya.

–

_{Jika suatu solusi masalah pemrograman linier}

dipecahkan dengan

simplex method,

pada

Pemrograman linier dual simetris

•

_{Suatu pemrograman linier dikatakan dalam}

bentuk

simetris

jika

–

semua variabel dibatasi tak negatif

–

_{semua pembatas dalam bentuk}

pertidaksamaan

•

untuk masalah maksimasi, bentuk

7

Masalah primal

Z

=

c

₁

x

₁

+

c

₂

x

₂

+ … +

c

_n

x

_n

a

₁₁

x

₁

+

a

₁₂

x

₂

+ … +

a

_1n

x

_n



b

₁

a

₂₁

x

₁

+

a

₂₂

x

₂

+ … +

a

_2n

x

_n



b

₂

.

.

.

a

_m1

x

₁

+

a

_m2

x

₂

+ … +

a

_mn

x

_n



b

_m

x

₁

≥0,

x

₂

≥0,…,

x

_n

≥0

dengan pembatas

Masalah dual

W

=

b

₁

y

₁

+

b

₂

y

₂

+ … +

b

_m

y

_m

a

₁₁

y

₁

+

a

₂₁

y

₂

+ … +

a

_m1

y

_m

≥

c

₁

a

₁₂

y

₁

+

a

₂₂

y

₂

+ … +

a

_m2

y

_n

≥

c

₂

.

.

.

a

y

+

a

y

+ … +

a

y

≥

c

Masalah primal-dual

Primal

Max Z = 3x₁ + 2x₂

dengan pembatas-pembatas: x₁ + 2x₂  6

2x₁ + x₂  8 – x₁ + x₂  1

x₂



2

Dual

Min W = 6y₁ + 8y₂ + y₃ + 2y₄

dengan pembatas-pembatas:

y₁ + 2y₂ – y₃ ≥ 3 2y₁ + y₂ + y₃ + y₄ ≥ 2

11

Hubungan primal-dual

• _{Koefisien fungsi tujuan untuk masalah primal menjadi} konstanta ruas kanan bagi dual.

• _{Konstanta ruas kanan dari primal menjadi koefisien} fungsi tujuan bagi dual.

• _{Pertidaksamaan untuk pembatas dibalik untuk kedua}

masalah.

• _{Tujuan diubah dari maksimasi untuk primal menjadi}

minimasi untuk dual.

• _{Tiap kolom dalam primal menjadi baris (pembatas) pada} dual; sehingga jumlah pembatas dual sama dengan

jumlah variabel primal.

• _{Tiap baris (pembatas) dalam primal berkaitan dengan} kolom pada dual; sehingga satu variabel dual berkaitan dengan satu pembatas primal.

13

Beberapa teorema dalam

teori dualitas

•

Weak duality theorem

•

_{Optimality criterion theorem}

•

_{Main duality theorem}

Teorema 1:

Weak duality theorem

(1)

Misalkan diberikan program linier primal-dual simetris:

P: max

Z

=

cx

,

Ax



b

,

x

≥

0

D: min

W

=

yb

,

yA

≥

c

,

y

≥

0

Nilai fungsi tujuan dari masalah minimimasi (dual)

15

Teorema 1:

Weak duality theorem

(2)

Bukti

Misalkan:

x0 : vektor solusi layak untuk primal y0 : vektor solusi layak untuk dual

Akan dibuktikan bahwa: y0b ≥ cx0

Karena x0 adalah layak untuk primal, maka Ax0  b, x0 ≥ 0 (1) Karena y0 _{adalah layak untuk dual, maka y}0_{A ≥ c, y}0 _{≥ 0 (2)}

Perkalian kedua sisi pertidaksamaan (1) dengan y0  y0Ax0  y0b Perkalian kedua sisi pertidaksamaan (2) dengan x0 : y0Ax0  cx0

Teorema 1:

Weak duality theorem

(3)

•

_{Konsekuensi 1:}

– _{Nilai fungsi tujuan dari masalah maksimasi (primal)}

untuk sebarang solusi layak merupakan batas bawah dari nilai minimum fungsi tujuan dual.

•

_{Konsekuensi 2:}

– _{Nilai fungsi tujuan dari masalah minimasi (dual) untuk}

sebarang solusi layak (dual) merupakan batas atas dari nilai maksimum fungsi tujuan primal.

•

_{Konsekuensi 3:}

17

Teorema 1:

Weak duality theorem

(4)

•

Konsekuensi 4:

– _{Jika masalah dual adalah layak dan nilai fungsi}

tujuannya tak terbatas (dalam hal ini, min W -), maka masalah primal adalah tak layak.

•

_{Konsekuensi 5:}

– _{Jika masalah primal adalah layak dan dualnya tak}

layak maka masalah primal tersebut adalah tak terbatas.

•

_{Konsekuensi 6:}

– _{Jika masalah dual adalah layak dan primalnya adalah}

Teorema 1:

Weak duality theorem

(4)

- Ilustrasi #1

Primal

Max Z = 3x₁ + 2x₂

dengan pembatas-pembatas: x₁ + 2x₂  6

2x₁ + x₂  8 – x₁ + x₂  1



Dual

Min W = 6y₁ + 8x₂ + y₃ + 2y₄

dengan pembatas-pembatas:

y₁ + 2y₂ – y₃ ≥ 3 2y₁ + y₂ + y₃ + y₄ ≥ 2

19

Teorema 1:

Weak duality theorem

(4)

- Ilustrasi #1

x adalah solusi layak untuk primal. Nilai fungsi tujuan primal Z = cx0 = 12

y

adalah solusi layak untuk dual

Nilai fungsi tujuan dual W = y0_{b = 40}

Disini Z = cx0  _y0_{b = W dan memenuhi weak duality}

theorem.

Berdasarkan Konsekuensi (1), nilai minimum W untuk dual tidak dapat lebih kecil dari 12.

Teorema 1:

Weak duality theorem

(4)

- Ilustrasi #2

Memaksimumkan Z = 4x₁ + x₂

dengan pembatas-pembatas:

x₁ – x₂  2 -3x₁ + x₂  3

x₁ ≥ 0, x₂ ≥ 0

Meminimumkan W = 2y₁ + 3y₂

dengan pembatas-pembatas:

y₁ – 3y₂ ≥4 - y₁ + y₂ ≥ 1

y₁ ≥ 0, y₂ ≥ 0

21

Teorema 1:

Weak duality theorem

(4)

- Ilustrasi #2

x

₁

x

₂

Solusi primal

Teorema 1:

Weak duality theorem

(4)

- Ilustrasi #2

y

₂

Solusi dual

23

Teorema 2:

Optimality criterion theorem

(1)

Jika terdapat solusi layak

x

0

dan

y

0

untuk masalah

pemrograman linier dual simetris sedemikian hingga

nilai fungsi tujuannya adalah sama,

Teorema 2:

Optimality criterion theorem

(2)

Bukti

Misalkan x adalah sebarang solusi layak bagi masalah primal. Maka berdasarkan Teorema 1,

cx  y0b

Tetapi ini diberikan bahwa cx0 = y0b.

Oleh karena itu cx  cx0 untuk semua solusi layak bagi masalah primal. Per definisi, x0 _{adalah optimal bagi primal.}

25

Teorema 3:

Main duality theorem

Teorema 4:

Complemantary slackness theorem

(1)

Misalkan diberikan program linier primal-dual simetris:

P: max

Z

=

cx

,

Ax



b

,

x

≥

0

D: min

W

=

yb

,

yA

≥

c

,

y

≥

0

dimana

A

: matriks (

m

x

n

)

b

: vektor kolom (

m

x 1)

c

: vektor baris (1 x

n

)

27

Teorema 4:

Complemantary slackness theorem

(2)

Misalkan:

x

0

: vektor solusi layak untuk primal

y

0

: vektor solusi layak untuk dual

Maka

x

0

dan

y

0

adalah optimal untuk masalah

masing jika dan hanya jika

Teorema 4:

Complemantary slackness theorem

(3)

Bukti:

( u adalah vektor slack untuk primal

29

Teorema 4:

Complemantary slackness theorem

(4)

Perkalian (1) dengan y0  y0Ax0 + y0u0 = y0b (3) Perkalian (2) dengan x0  y0Ax0 – v0x0 = cx0 (4)

Pengurangan (3) dengan (4)  y0u0 + v0x0 = y0b – cx0 (5)

Untuk membuktikan Teorema 4, harus diperlihatkan bahwa x0 dan y0 adalah solusi optimal bagi masing-masing masalah primal dan dual jika dan hanya jika

Teorema 4:

Complemantary slackness theorem

(5)

Bagian 1

Diasumsikan bahwa x0 dan y0 adalah solusi optimal dan harus dibuktikan bahwa Persamaan (6) adalah benar.

Karena x0 dan y0 adalah optimal, berdasarkan Teorema 3 maka cx0 = y0b.

Oleh karena itu, Persamaan (5) menjadi Persamaan (6)

31

Teorema 4:

Complemantary slackness theorem

(6)

Bagian 2

Diasumsikan bahwa Persamaan (6) adalah benar dan

akan dibuktikan bahwa x0 _{dan y}0 _{adalah solusi optimal bagi} masing-masing masalah primal dan dual

Karena Persamaan (6) benar, maka Persamaan (5) menjadi y0b – cx0.

y0_u0 _{+ v}0_x0 _{= y}0_{b – cx}0  _y0_{b = cx}0

Complementary slackness

condition

Persamaan (6) : v0_x0 _{+ y}0_u0 _{= 0 dari complementary slackness}

theorem dapat disederhanakan sebagai berikut:

v_j0x

j0 = 0 untuk semua j = 1, 2, …, n

y_i0u

i0 = 0 untuk semua i = 1, 2, …, m

dengan memperhatikan hal-hal berikut:

33

Complementary slackness condition

①

Jika suatu variabel primal (

x

_j0

) adalah positif, maka

pembatas dual yang bersesuaian memenuhi

persamaan pada titik optimalnya (yaitu,

v

_j0

= 0)

②

Jika suatu pembatas primal adalah

strick

inequality

pada titik optimal (yaitu,

u

_j0

> 0), maka

variabel dual yang bersesuaian (

y

_i0

) harus nol.

③

Jika suatu variabel dual (

y

_i0

) adalah positif maka

pembatas primal yang bersesuaian memenuhi

persamaan pada titik optimalnya (yaitu,

u

_i0

= 0)

④

Jika suatu pembatas dual adalah

strick inequality

pada titik optimal (yaitu

v

_i0

> 0), maka variabel

Ilustrasi (1)

Primal

Max Z = 3x₁ + 2x₂

dengan pembatas-pembatas: x₁ + 2x₂  6

2x₁ + x₂  8 – x₁ + x₂  1

x₂



2

Dual

Min W = 6y₁ + 8x₂ + y₃ + 2y₄

dengan pembatas-pembatas:

y₁ + 2y₂ – y₃ ≥ 3 2y₁ + y₂ + y₃ + y₄ ≥ 2

35

Ilustrasi (2)

Primal

(Penambahan slack variable)

Max Z = 3x₁ + 2x₂

(Penambahan slack variable)

Ilustrasi (3)

37

Ilustrasi (4)

Dengan metode simplex diperoleh solusi optimal

untuk masalah primal sebagai berikut:

Ilustrasi (5)

Dengan penerapan

complementary slackness condition

,

solusi optimal bagi dual ditentukan sebagai berikut

39

Ilustrasi (6)

Kondisi (1), (2), (5) dan (6) mengimplikasikan:

Penerapan

complementary

slackness condition

•

_{Digunakan untuk mencari solusi primal optimal dari}

suatu solusi dual optimal, dan sebaliknya.

•

_{Digunakan untuk memverifikasi apakah suatu solusi}

layak adalah optimal untuk masalah primal.

•

_{Digunakan untuk menginvestigasi ciri-ciri umum dari}

solusi optimal pada masalah primal dan dual

dengan menguji hipotesis-hipotesis yang berbeda.

•

_Kuhn-Tucker

_{optimality condition}

_untuk

41

Karakteristik pokok

hubungan primal-dual

Primal Dual

A Matriks pembatas Transpos dari matriks _pembatas

b Konstanta ruas kanan Vektor biaya

c Vektor biaya Konstanta ruas kanan

Fungsi tujuan Max Z = cx Min W = yb

Pertidaksamaan pembatas Ax  b yA ≥ c

Interpretasi ekonomi dari

solusi dual (1)

•

_{Dalam pandangan ekonomi, solusi dual optimal}

dapat diinterpretasikan sebagai harga yang

dibayarkan untuk sumberdaya pembatas.

•

_{Berdasarkan Teorema 3 (}

_{main duality}

_{), nilai}

optimal bagi primal dan dual adalah sama.

•

_Jika

_x

0

dan

y

0

masing-masing adalah solusi

43

Interpretasi ekonomi dari

solusi dual (2)

•

Dengan kata lain, nilai optimal dari masalah

Interpretasi ekonomis dari

solusi dual (3)

• _{Misalkan diasumsikan bahwa level sumberdaya 1 (yaitu,} b₁) diubah.

• _{Maka, untuk variasi kecil dalam perubahan nilai b1,}

katakan b₁, perubahan dalam nilai optimal dari

pemrograman linier Z0 diberikan oleh y

10(b1).

• _{Dengan kata lain, nilai optimal dari variabel dual untuk}

tiap pembatas primal memberikan perubahan bersih (net change) dalam nilai optimal dari fungsi tujuan untuk

peningkatan satu satuan dalam konstanta ruas kanan.

45

Contoh interpretasi solusi dual

(1)

Memaksimumkan Z = 3x₁ + 2x₂

dengan pembatas-pembatas:

x₁ + 2x₂  6 (Bahan A) 2x₁ + x₂  8 (Bahan B)

– x₁ + x₂  1 (Selisih permintaan cat interior dan eksterior)

x₂  2 (Permintaan cat interior)

x₁ ≥ 0

x₂ ≥ 0

Contoh interpretasi solusi dual

(2)

Dual:

Meminimumkan W = 6y₁ + 8x₂ + y₃ + 2y₄

dengan pembatas-pembatas:

y₁ + 2y₂ – y₃ ≥ 3 2y₁ + y₂ + y₃ + y₄ ≥ 2

47

Contoh interpretasi solusi dual

(3)

y₄ = 0  shadow price untuk pembatas permintaan cat interior, yaitu

Masalah primal-dual tak simetris (1)

Memaksimumkan Z = 4x₁ + 5x₂

dengan pembatas

3x₁ + 2x₂  20 4x₁ – 3x₂ ≥ 10 x₁ + x₂ = 5 x ≥ 0

49

Masalah primal-dual tak simetris (2)

Memaksimumkan Z = 4x₁ + 5x₃ – 5x₄

dengan pembatas

3x₁ + 2x₃ – 2x₄  20 – 4x₁ + 3x₃ – 3x₄  – 10 x₁ + x₃ – x₄  5 – x₁ – x₃ + x₄  – 5 x₁, x₃, x₄ ≥ 0

Masalah primal-dual tak simetris (2)

Meminimumkan W = 20w₁ – 10w₂ +5w₃ – 5w₄

dengan pembatas

3w₁ – 4w₂ + w₃ – w₄ ≥ 4 2w₁ + 3w₂ + w₃ – w₄ ≥ 5 – 2w₁ – 3w₂ – w₃ + w₄ ≥ – 5

w , w , w , w ≥ 0

51

Masalah primal-dual tak simetris (2)

Meminimumkan W = 20y₁ + 10y₂ +5y₃

dengan pembatas

3y₁ + 4y₂ + y₃ ≥ 4 2y₁ – 3y₂ + y₃ = 5

y₁ ≥ 0 y₂  0

y₃ tak dibatasi tanda

Masalah Dual

Tabel primal-dual secara umum

Primal (maksimasi) Dual (minimasi)

Matriks koefisien A Transpos matriks koefisien Vektor ruas kanan Vektor biaya

Vektor harga c Vektor ruas kanan

Pembatas ke-i adalah persamaan Variabel dual y_i tak dibatasi tanda Pembatas ke-i bertipe  Varibel dual y_i ≥ 0

Pembatas ke-i bertipe ≥ Varibel dual y_i  0

53

Catatan (1)

•

Teorema (1), (2), (3), dan (4) dari teori

dualitas berlaku juga bagi primal-dual tak

simetris.

•

_{Complementary slackness condition}

_juga

Catatan (2)

Misalkan diberikan masalah pemrograman linier dalam bentuk standar

Memaksimumkan Z = cx

dengan pembatas

Ax = b x ≥ 0

Masalah dual

Meminimumkan W = yb

dengan pembatas

yA ≥ c

55

Menentukan solusi dual optimal (1)

•

Solusi dual optimal dapat ditentukan

dengan

complementary slackness

condition

•

_{Solusi dual optimal dapat juga diperoleh}

Menentukan solusi dual optimal (2)

Meminimumkan

Z

=

cx

dengan pembatas

Ax

=

b

57

Menentukan solusi dual optimal (3)

Misalkan :

Solusi primal optimal :

dimana

x

_B

: varabel basis

Menentukan solusi dual optimal (4)

Nilai minimum

Z

=

cx

*

=

c

B

x

B

=

c

B

B

-1

b

Karena

B

menunjukkan basis optimal, maka koefisien

biaya relatif ( ) yang berkaitan dengan variabel basis

harus tak negatif

j

c

0







_{j j}

j

c

c

_

P

untuk semua

j

59

Menentukan solusi dual optimal (5)

Dalam notasi matrix:

c

-



A

≥

0

atau



A



c

yang merupakan pembatas pemrograman linier dual.

Menentukan solusi dual optimal (6)

Nilai fungsi tujuan dual yang berkaitan dengan solusi

layak adalah

W

=

yb

=



b

=

c

_B

B

-1

b

yang sama dengan nilai minimum

Z

.

61

Ilustrasi menentukan

solusi dual optimal (1)

Primal (Dalam bentuk standar)

Ilustrasi menentukan

solusi dual optimal (2)

Dengan metode

revised simplex

, solusi optimal untuk primal:

63

Ilustrasi menentukan

solusi dual optimal (3)

Simplex multiplier

optimal :







1/3,4/3,0,0



 memenuhi pembatas dual, dan nilai fungsi tujuannya:

W = 6(1/3) + 8(4/3) + 1(0) + 2(0) = 38/3

yang bersesuaian dengan nilai optimal untuk masalah primal.

Oleh karena itu,

y₁ = 1/3, y₂ = 3/4, y₃ = 0, y₄ = 0  optimal untuk dual.

Simplex multiplier yang bersesuaian dengan tabel (primal) optimal

65

Masalah Pemrograman Linier

(Primal) dalam Bentuk Standar

Minimasi

Z

=

cx

dengan pembatas

Ax

=

b

x

≥

0

A

: matrix (

m

x

n

)

P

: vektor kolom dari matrix

A

B

: matrix basis untuk masalah primal

Basis Layak Primal

Basis

B

: basis layak primal (

primal feasible basis

)



B

-1

b

≥

0

B

: basis layak primal



nilai variabel basis:

B

-1

b

solusi layak basis

x

_B

=

B

-1

b

67

Kondisi Optimalitas (1)

Untuk memeriksa apakah basis layak

B

adalah optimal



hitung koefisien fungsi tujuan relatif

(

c

j

)

j j

j

c

c

_

_

πP

j

= 1, …,

n



=

c

_B

B

-1

:

simplex multiplier

Basis layak primal

B

adalah optimal



c

_j

_

0

Kondisi Optimalitas (2)

Maksimasi

W

=

yb

dengan pembatas

yA



c

69

Kondisi Optimalitas (3)

Pembatas dual

yA



c

dapat ditulis:



P

1

,

P

2

,



,

P

n

 



c

1

,

c

2

,



,

c

n



y

j j

c

yP

_

0





_j

j

Kondisi Optimalitas (4)

Jika basis layak primal

B

: basis optimal bagi masalah primal



simplex multiplier



=

c

_B

B

-1

memenuhi

0





_j

j

c

yP

j = 1, …, n

Implikasi





: layak bagi masalah dual

Nilai fungsi tujuan dual

W

=



b

=

c

_B

B

-1

b

sama dengan

71

Basis Dual Layak (1)

Basis

B

untuk masalah primal

Minimasi

Z

=

cx

dengan pembatas

Ax

=

b

x

≥

0

layak dual (

dual feasible

)



c

–

c

_B

B

-1

A

≥

0

Basis Dual Layak (2)

Basis

B

untuk masalah primal : layak primal dan layak dual



Basis

B

: basis optimal

Solusi optimal untuk primal :

x

_B

=

B

-1

b

,

x

N

=

0

Solusi optimal untuk dual :

y

=

c

_B

B

-1

73

Catatan

•

_{Akar dari pemecahan masalah pemrograman}

linier



mendapatkan solusi basis

B

yang layak

primal dan layak dual

•

Metode simplex

_

bergerak dari satu basis

layak primal ke basis yang lain hingga basis

tersebut menjadi layak dual

– _{Metode simplex primal (primal simplex method)}

•

Metode simplex dual (

dual simplex method

)

_

Rincian Metode Simplex Dual (1)

Pemrograman linier bentuk standar:

Minimasi

Z

=

cx

75

Rincian Metode Simplex Dual (2)

•

Metode simplex dual menggunakan tabel

yang sama dengan metode simplex

primal.

•

_{Dalam semua tabel, koefisien fungsi}

tujuan relatif dipertahankan tak negatif

(Untuk maksimasi, dipertahankan tak

positif)

•

_{Konstanta ruas kanan tidak perlu tak}

negatif.

)

(

c

_j

j

Rincian Metode Simplex Dual (3)

•

_{Algoritma mulai dengan membuat elemen}

ruas kanan menjadi tak negatif, dengan pada

saat yang sama menjaga koefisien tak

negatif.

•

Algoritma berhenti jika semua konstanta ruas

kanan telah tak negatif.

j

77

Rincian Metode Simplex Dual (4)

Pemilihan Variabel Basis

yang Keluar Basis

Pilih variabel basis yang membuat solusi saat ini menjadi

tidak layak

dengan kata lain

Pilih variabel basis yang nilai solusinya negatif

79

Pemilihan Variabel Non Basis yang

Masuk Basis (1)

Kolom pivot dipilih sedemikian rupa sehingga memenuhi

dua kondisi sebagai berikut:

1. Ketidaklayakan primal berkurang (atau paling sedikit,

tidak bertambah jelek).

Atau

, paling sedikit konstanta ruas kanan pada baris

r

menjadi positif pada tabel berikutnya



Variabel non basis (

x

_j

) dengan koefisien negatif

Pemilihan Variabel Non Basis yang

Masuk Basis (2)

2. Tabel berikutnya setelah operasi pivot harus tetap

layak dual.

Dapat dijamin jika variabel non basis yang masuk

basis dipilih dengan aturan rasio sebagai berikut:

81

Ilustrasi Metode Simplex Dual

Meminimumkan Z = x₁ + 4x₂ + 3x₄

dengan pembatas

x₁ + 2x₂ – x₃ + x₄ ≥ 3 – 2x₁ – x₂ + 4x₃ + x₄ ≥ 2 x₁, x₃, x₃, x₄ ≥ 0

Meminimumkan Z = x₁ + 4x₂ + 3x₄

dengan pembatas

x₁ + 2x₂ – x₃ + x₄ – x₅ = 3 – 2x₁ – x₂ + 4x₃ + x₄ – x₆ = 2 x₁, x₃, x₃, x₄, x₅, x₆ ≥ 0

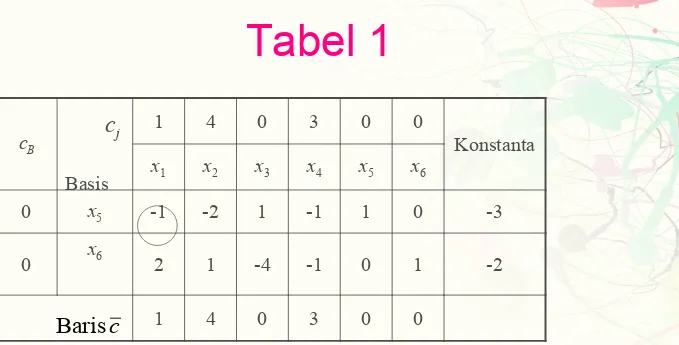
Tabel 1

c_B 1 4 0 3 0 0 _Konstanta x₁ x₂ x₃ x₄ x₅ x₆

0 x5 -1 -2 1 -1 1 0 -3

0 x6 2 1 -4 -1 0 1 -2

1 4 0 3 0 0

c

Baris Basis

83

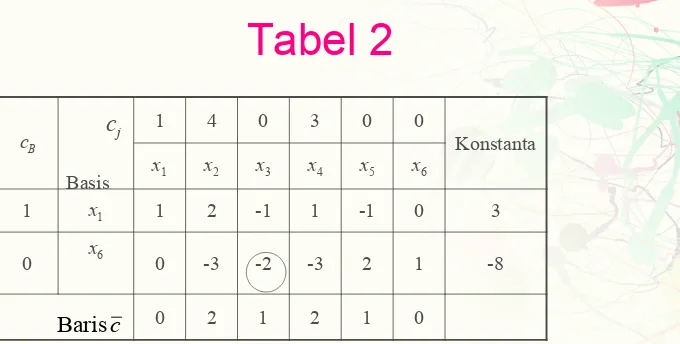
Tabel 2

c_B 1 4 0 3 0 0 _Konstanta x₁ x₂ x₃ x₄ x₅ x₆

1 x1 1 2 -1 1 -1 0 3

0 x6 0 -3 -2 -3 2 1 -8

0 2 1 2 1 0

c

Baris Basis

c_j

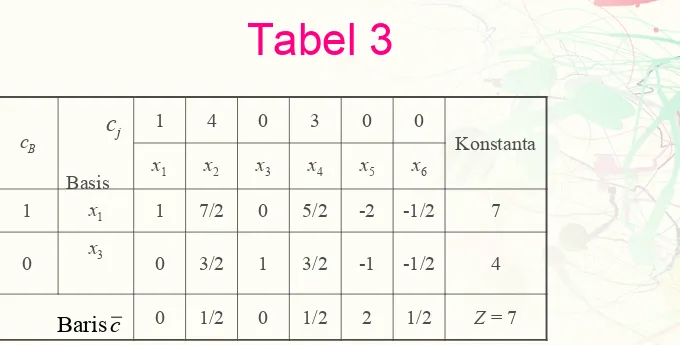
Tabel 3

c_B 1 4 0 3 0 0 _Konstanta x₁ x₂ x₃ x₄ x₅ x₆

1 x1 1 7/2 0 5/2 -2 -1/2 7

0 x3 0 3/2 1 3/2 -1 -1/2 4

0 1/2 0 1/2 2 1/2 Z = 7

c

Baris Basis

85

Mengidentifikasi Ketidaklayakan

Primal dalam Metode Simplex Dual

•

_{Dalam metode simplex dual}

_

_selalu

terdapat solusi layak bagi dual.

•

_{Metode simplex dual mengenali}

ketidaklayakan primal jika aturan rasio

gagal mengidentifikasi variabel non basis

yang masuk basis

Memecahkan Masalah Maksimasi

dengan Metode Simplex Dual

Dalam masalah maksimasi



Kondisi optimalitas:

Koefisien fungsi tujuan

(

c

_j

)

_

0

Misal,

b

_r

_

0

dan

x

_r

: variabel keluar basis

Variabel non basis yang masuk basis



dipilih sedemikian

rupa sehingga elemen baris tetap tak positif pada

iterasi berikutnya.

c

87

Penerapan metode simplex dual

•

Analisis sensitivitas (

sensitivity analysis

) dan

pemrograman parametrik (

parametric

programming

)

•

Algoritma pemrograman bilangan bulat

(

integer programming

algorithms

)

•

Algoritma pemrograman non linier (

nonlinear

programming algorithm

)

•

Varian dari metode simplex:

primal-dual