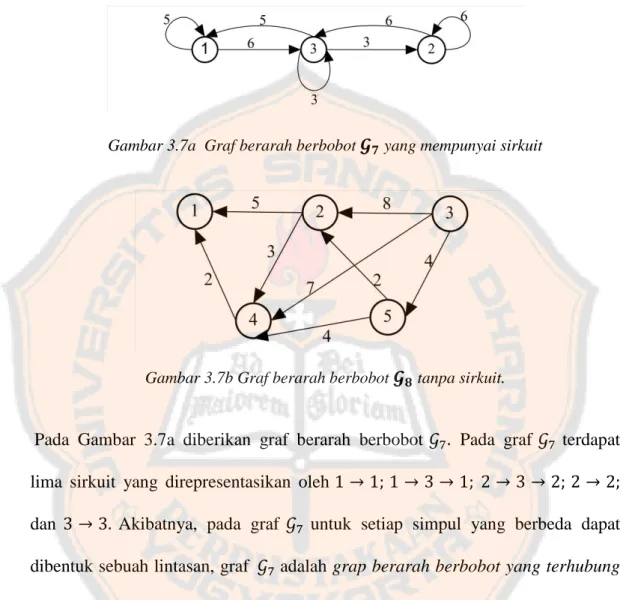
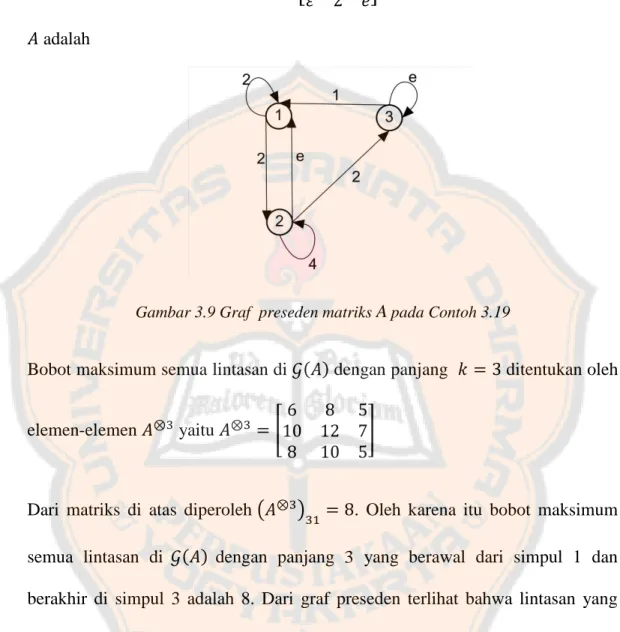
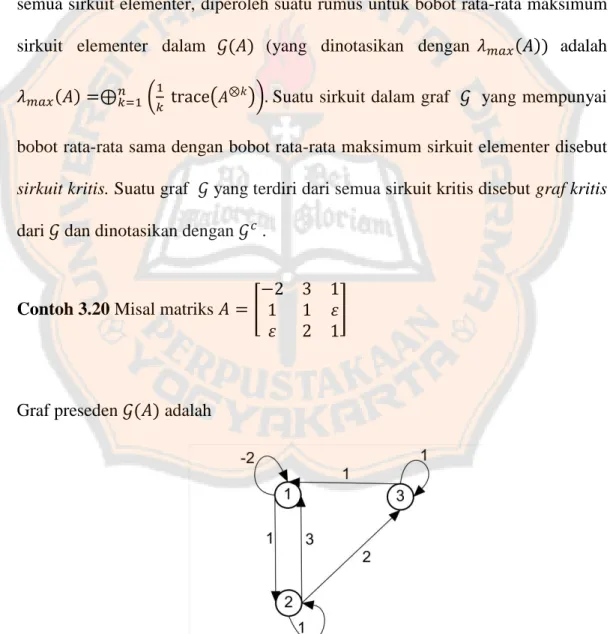
Aljabar max-plus dan aplikasinya pada suatu rute bus Transjogja

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. ALJABAR MAX-PLUS DAN APLIKASINYA PADA SUATU RUTE BUS TRANSJOGJA. SKRIPSI Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika Program Studi Matematika. Disusun Oleh:. Johny Decky Sasambe 113114005. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS SANATA DHARMA YOGYAKARTA 2015 i.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. MAX-PLUS ALGEBRA AND ITS APPLICATION ON A TRANSJOGJA BUS ROUTE. PAPER Presented as Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Matematika in Mathematics Study Program. By:. Johny Decky Sasambe 113114005. MATEMATICS STUDY PROGRAM DEPARTEMEN OF MATEMATICS FACULTY OF SAINS AND TECHNOLOGY SANATA DHARMA UNIVERSITY YOGYAKARTA 2015. ii.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. SKRIPSI ALJABAR MAX-PLUS DAN. iii.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. iv.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. HALAMAN PERSEMBAHAN. Non Scholae Sed Vitae Discimus. Tugas Akhir ini kupersembahkan untuk: Tarekat MSC Provinsi Indonesia, Ibu dan kakak-kakakku yang tercinta, Para seminaris di SMA Seminari Xaverius Kakaskasen Tomohon, Rekan-rekan mahasiswa Matematika Universitas Sanata Dharma, Para pecinta Matematika.. v.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. vi.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. vii.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. ABSTRAK. Aljabar max-plus adalah semilapangan idempoten. Aljabar max-plus, dengan operasi maksimum dan penjumlahan sebagai operasi dasarnya mempelajari tentang matriks, graf, serta nilai eigen dan vektor eigen. Beberapa topik yang dapat disebutkan adalah konsep matriks iredusibel, graf preseden, nilai eigen dan vektor eigen dari matriks persegi yang iredusibel. Suatu matriks persegi disebut iredusibel jika graf presedennya terhubung kuat. Oleh karena itu jika diberikan suatu graf maka dapat dibentuk suatu matriks persegi, dan dapat ditentukan nilai eigen dan vektor eigen dari matriks tersebut. Dalam aplikasinya pada suatu rute bus Transjogja, teori nilai eigen dan vektor eigen matriks persegi yang iredusibel di aljabar max-plus digunakan sebagai alat untuk menganalisa apakah dapat disusun jadwal keberangkatan bus yang periodik pada rute pilihan. Artinya, jika dipilih suatu rute, dibuat graf preseden dari rute pilihan dan disusun sinkronisasi berdasarkan data di lapangan, dapat dibangun suatu model matematika yang menghasilkan suatu matriks serta nilai eigen dan vektor eigennya. Dengan mengintepretasikan nilai eigen sebagai periodisasi keberangkatan setiap bus dan vektor eigen sebagai waktu awal keberangkatan bus pada setiap halte, dapat disusun suatu jadwal bus yang periodik pada rute pilihan tersebut. Hasil pemodelan menunjukkan bahwa belum dapat disusun suatu jadwal periodik untuk rute pilihan. Hal ini sebabkan karena matriks yang dihasilkan adalah matriks tak iredusibel. Akibatnya dari matriks tersebut, diperoleh vektor eigen yang memuat elemen tak real. Konsekuensinya adalah waktu awal keberangkatan bus tidak bisa ditentukan dan hal ini berpengaruh juga pada penentuan waktu keberangkatan sesudahnya. Akibatnya jadwal periodik untuk rute pilihan belum bisa dibuat. Kata Kunci: nilai eigen, vektor eigen, graf preseden, matriks irudisibel.. viii.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. ABSTRACT Max-plus algebra is an idempotent semilfield. Max-plus algebra, with maximum and addition operation on real numbers as its basic operations, explores matrices, graphs, eigenvalues and eigenvectors. Some of the topics that may be mentioned are the concept of irreducible matrices, precedence graph, eigenvalues and eigenvectors of a irreducible square matrix. A square matrix is called irreducible if its precedence graph is strongly connected. Therefore, if given a graph, a square matrix can be formed and eigenvalues and eigenvectors of the matrix can be determined. In its application on one bus route Transjogja, the theory of eigenvalues and eigenvectors of a irreducible square matrix in max-plus algebra is used as a tool to analyze whether periodic bus departure timetable on a selected route can be made. That is, if a route is selected, precedence graphs of the selected route, and synchronization according to the data obtained are made, it can be constructed a mathematical model that results in a matrix and its eigenvalues and eigenvectors. By interpreting eigenvalues as departure periodization of each bus and eigenvectors as first time of departure of buses at every bus stop, it can be constructed a periodic bus schedule on the selected route. Modelling results show that a periodic schedule for the selected route still can not be made. This is because the resulting matrix is not a irreducible matrix. As a result, the eigenvector of the matrix contains elements which are not real numbers. Thus first time of departure of buses can not be determined and this influences the determination of the else following departure time. Consequently, periodic schedule for the selected route still can not be made. Keywords: eigenvalues, eigenvectors, precedence graph, irreducible matrix.. ix.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. KATA PENGANTAR. Puji dan syukur kepada Tuhan yang telah memberikan rahmat dan berkatNya kepada penulis, sehingga tugas akhir ini dapat diselesaikan dengan baik. Banyak pergumulan dan tantangan yang dialami selama proses penyelesaian tugas akhir ini, namun berkat bantuan dan dukungan dari berbagai pihak, akhirnya tugas akhir ini dapat diselesaikan dengan baik. Oleh karena itu, pada kesempatan ini, penulis ingin mengucapkan terima kasih banyak atas dukungan dan bimbingannya kepada: 1. Bapak Dr. Marcellinus Andy Rudhito, S.Pd. selaku dosen pembimbing Tugas Akhir. 2. Bapak Y.G. Hartono, Ph.D. selaku Ketua Program Studi Matematika Universitas Sanata Dharma. 3. Ibu Paulina Heruningsih Prima Rosa, S.Si., M.Sc. selaku Dekan Fakultas Sains dan Teknologi Universitas Sanata Dharma. 4. Bapak dan Ibu Dosen Program Studi Matematika Universitas Sanata Dharma. 5. Tarekat MSC Propinsi Indonesia dan para konfraterku yang tercinta. 6. Teman-teman sekomunitas GRIYA CHEVALIER Palagan – Yogyakarta. 7. Keluargaku: ibu yang tercinta dan kakak-kakakku yang selalu mendoakan dan mendukung saya. 8. Teman-teman matematika 2011 Universitas Sanata Dharma, Bayu, Herry, Ensi dan Indra.. x.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. 9. Kakak-kakak angkatan 2008, 2009, 2010 dan adik-adik angkatan 2012, 2013 dan 2014 yang pernah menjadi teman selama masa-masa perkuliahan. 10. Semua pihak yang tak dapat disebutkan satu persatu, atas segala bantuan dan dukungannya. Penulis menyadari bahwa masih banyak kekurangan dalam tugas akhir ini. Oleh karena itu penulis mengharapkan kritik dan saran yang dapat membangun dan menyempurnakan tugas akhir ini. Akhirnya, penulis berharap agar tugas akhir ini dapat memberikan wawasan dan pengetahuan baru bagi para pembaca.. Yogyakarta 26 Juni 2015 Penulis. xi.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. DAFTAR ISI. HALAMAN JUDUL DALAM BAHASA INDONESIA ....................................... i HALAMAN JUDUL DALAM BAHASA INGGRIS ............................................ ii HALAMAN PERSETUJUAN PEMBIMBING…………………………………iii HALAMAN PENGESAHAN……………………………………………………iv HALAMAN PERSEMBAHAN…………………………………………………..v PERNYATAAN KEASLIAN KARYA…………………………………………vi LEMBAR PERSETUJUAN PUBLIKASI KARYA ILMIAH………………….vii ABSTRAK .......................................................................................................... viii ABSTRACT .......................................................................................................... ix KATA PENGANTAR ............................................................................................ x DAFTAR ISI ........................................................................................................ xii BAB I PENDAHULUAN ...................................................................................... 1 A. Latar Belakang............................................................................................ 1 B. Perumusan Masalah .................................................................................... 5 C. Pembatasan Masalah .................................................................................. 5 D. Tujuan Penulisan ........................................................................................ 6 E. Manfaat Penulisan ...................................................................................... 6 F. Metode Penulisan ....................................................................................... 7 G. Sistematika Penulisan ................................................................................. 7 BAB II. LANDASAN TEORI ............................................................................... 9 A. Himpunan dan Operasi Biner ..................................................................... 9 1. Himpunan ............................................................................................... 9 2. Operasi Biner ........................................................................................ 11 B. Grupoid, Semigrup dan Monoid ............................................................... 16 C. Semigelanggang ....................................................................................... 19 D. Semilapangan ........................................................................................... 25 E. Vektor dan Matriks Pada Himpunan Bilangan Real ................................ 26 BAB III ALJABAR MAX-PLUS ........................................................................ 30. xii.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. A. Definisi Aljabar Max-Plus ........................................................................ 30 B. Notasi di ℝ𝑚𝑎𝑥 ........................................................................................ 35 C. Sifat Operasi di ℝ𝑚𝑎𝑥 ............................................................................. 38 D. Vektor dan Matriks di ℝ𝑚𝑎𝑥 ................................................................... 40 1. Vektor di ℝ𝑚𝑎𝑥 ................................................................................... 40 2. Matriks di ℝ𝑚𝑎𝑥 .................................................................................. 41 E. Matriks dan Graf di ℝ𝑚𝑎𝑥 ....................................................................... 52 1. Konsep Dasar Graf ............................................................................... 52 2. Matriks dan Graf di ℝ𝑚𝑎𝑥 ................................................................... 62 F. Nilai Eigen dan Vektor Eigen Matriks di ℝ𝑚𝑎𝑥 ..................................... 70 BAB IV APLIKASI ALJABAR MAX-PLUS PADA SUATU RUTE BUS TRANSJOGJA ........................................................ 78 A. Gambaran Singkat Rute Bus Transjogja .................................................. 78 B. Rute Pilihan .............................................................................................. 83 C. Graf Rute Pilihan ...................................................................................... 84 D. Sinkronisasi .............................................................................................. 90 E. Model Matematika dari Rute Pilihan ....................................................... 93 F. Menghitung Nilai Eigen dan Vektor Eigen .............................................. 96 BAB V KESIMPULAN DAN SARAN ............................................................... 99 A. Kesimpulan ............................................................................................... 99 B. Saran ....................................................................................................... 100 DAFTAR PUSTAKA ......................................................................................... 101. xiii.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. BAB I PENDAHULUAN. Pada bab ini dijelaskan tentang latar belakang penulisan, perumusan masalah, pembatasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan dan sistimatika penulisan. A. Latar Belakang Struktur aljabar adalah suatu himpunan tak kosong yang dilengkapi dengan satu atau lebih operasi biner. Struktur aljabar ini secara berurutan dinotasikan dengan S ,* atau S ,, . Contoh struktur aljabar adalah grup, gelanggang dan lapangan. Akan tetapi selain grup, gelanggang dan lapangan yang telah dijelaskan pada saat perkuliahan, terdapat struktur aljabar yang lebih sederhana yaitu, grupoid, semigrup, monoid, semigelanggang dan semilapangan. Grupoid merupakan struktur aljabar yang paling sederhana. Grupoid adalah himpunan tak kosong yang dilengkapi dengan satu operasi biner. Semigrup adalah grupoid yang memenuhi sifat asosiatif terhadap operasi biner yang terdefinisi pada himpunan yang dimaksud. Dalam semigrup jika operasi binernya bersifat komutatif, semigrup dikatakan semigrup komutatif. Sedangkan Monoid adalah semigrup yang memiliki elemen identitas. Semigelanggang dan semilapangan mempunyai struktur yang berbeda dengan grupoid, semigrup dan monoid. Semigelanggang adalah struktur aljabar. 1.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. yang dilengkapi dengan dua operasi biner yaitu + dan  dan memenuhi syaratsyarat berikut: terhadap operasi pertama, semigrupnya adalah semigrup komutatif dan memiliki elemen identitas; terhadap operasi kedua, semigrupnya adalah monoid dan mempunyai elemen penyerap; dan operasi kedua bersifat distributif kiri dan distributif kanan terhadap operasi pertama. Dalam semigelanggang sifat operasi biner menentukan sifat semigelanggangnya. Oleh karena itu jika suatu semigelanggang (𝑆, +,  ) terhadap operasi biner  berlaku ∀𝑎, 𝑏 ∈ 𝑆, 𝑎  𝑏 = 𝑏  𝑎 maka semigelanggangnya disebut semigelanggang komutatif. Sedangkan, jika suatu semigelanggang (𝑆, +,  ) terhadap operasi pertamanya berlaku ∀𝑎 ∈ 𝑆 maka 𝑎 + 𝑎 = 𝑎, semigelanggangnya disebut semigelanggang idempoten. Konsep tentang semigelanggang di atas menjadi dasar penjelasan bagi struktur aljabar lain, yaitu semilapangan. Suatu semigelanggang disebut semilapangan jika semigelanggang tersebut adalah semigelanggang komutatif dengan setiap elemen yang bukan elemen identitas terhadap operasi pertama mempunyai invers terhadap operasi kedua; atau dengan kata lain suatu semigelanggang komutatif (𝑆, +,  ) adalah semilapangan jika ∀𝑥 ∈ 𝑆\{0} mempunyai invers terhadap operasi  yaitu (∀𝑥 ∈ 𝑆\{0} )(∃𝑥 −1 ∈ 𝑆), 𝑥  𝑥 −1 = 𝑥 −1  𝑥. Dengan demikian semilapangan adalah semigelanggang komutatif yang mendapat syarat tambahan, yaitu invers terhadap operasi kedua untuk setiap elemen yang bukan elemen identitas terhadap operasi pertama. Suatu semilapangan adalah semilapangan idempoten jika operasi biner pertama bersifat idempoten.. 2.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Salah satu contoh semilapangan adalah aljabar max-plus. Aljabar maxplus adalah salah satu contoh semilapangan idempoten. Aljabar max-plus, dengan operasi maksimum dan penjumlahan sebagai operasi dasarnya mempelajari tentang matriks, graf, serta nilai eigen dan vektor eigen dan lain sebagainya. Istilah aljabar max-plus diambil dari nama operasinya, yaitu operasi penjumlahan yang dinotasikan dengan ⊕ dan operasi perkalian yang dinotasikan dengan ⊗. Dalam aljabar max-plus operasi ⊕ didefinisikan sebagai maksimum, dan operasi ⊗ didefinisikan sebagai operasi penjumlahan biasa untuk bilangan real. Munculnya teori aljabar max-plus dilatarbelakangi oleh berkembangnya bidang riset operasi pada tahun 1950 yang menekankan pencarian solusi optimal. Oleh karena itu, aljabar max-plus dengan operasi maximum, membawa harapan baru dalam dunia riset operasi untuk mencapai solusi optimal (Andersen, 2002). Dalam perkembangannya aljabar max-plus sebagai sarana riset operasi untuk mencapai solusi yang optimal telah digunakan dengan baik untuk memodelkan dan menganalisis secara aljabar masalah-masalah jaringan, misalnya jaringan transportasi, sistem manufaktur, dan lain sebagainya. Contoh penggunaan model max-plus dalam masalah jaringan dapat dilihat pada Modeling Bus Bounching with Petri Nets and Max-Plus Algebra (Newcomb, 2014), Penentuan Waktu Produksi Tercepat pada Mesin Produksi Jamu (Kharisma, 2013), Optimisasi Jadwal Pemesanan Bakpia Patok Jaya “25” (Arifin, 2012) dan lain sebagainya. Dalam karya tulis ini, aljabar max-plus digunakan untuk memodelkan suatu rute transportasi bus Transjogja. Salah satu masalah yang ditemukan adalah keluhan para pengguna mengenai ketidakpastian kedatangan bus di setiap halte,. 3.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. terkadang cepat, terkadang cukup lama bahkan saat tiba di halte, bus telah penuh dengan penumpang. Dengan sistem yang ada saat ini, para pengguna jasa bus Transjogja seringkali harus menunggu bus dengan ketidakpastian. Berdasarkan informasi tersebut, pada bagian akhir karya tulis ini akan dikaji model aljabar max-plus untuk mendesain jadwal bus Transjogja yang periodik sebagai solusi atas masalah yang dihadapi masyarakat. Proses pemodelan ini dimulai dengan mengambil sampel sederhana yaitu memodelkan salah satu rute bus Transjogja. Pemilihan rute ini dilakukan secara acak, yaitu dengan menentukan empat halte utama yang menjadi halte awal dan halte akhir dari suatu rute. Selanjutnya berdasarkan data lapangan akan dibangun lintasanlintasan yang menghubungkan keempat halte utama dan membentuk sebuah graf dari rute pilihan. Berdasarkan graf dari rute pilihan, selanjutnya dibuat sinkronisasi yang menjadi landasan untuk menyusun model matematika. Dari model matematika tersebut dapat dibentuk suatu matriks yang merupakan representasi dari graf rute pilihan. Matriks yang diperoleh akan dianalisa dengan menggunakan nilai eigen dan vektor eigen. Nilai eigen dan vektor eigen yang diperoleh adalah output yang diharapkan. Berdasarkan uraian di atas, yang diharapkan dari karya tulis ini adalah penguasaan konsep aljabar max-plus dan aplikasinya untuk membuat model matematika bagi masalah yang ditemukan dalam rute pilihan. Pemodelan matematika tersebut diarahkan untuk menghasilkan suatu analisa pada suatu rute bus Transjogja dan mengambil kesimpulan berdasarkan hasil analisa yaitu. 4.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. apakah dimungkinkan dibuat suatu jadwal bus Transjogja yang periodik untuk rute pilihan. B. Perumusan Masalah Dalam karya tulis ini, penulis akan memfokuskan perhatian pada konsep dasar aljabar max-plus, sifat-sifatnya dan aplikasinya. Inti tulisan tersebut dapat dituangkan dalam empat pertanyaan berikut: 1. Apa itu aljabar max-plus? 2. Apa yang dimaksud dengan nilai eigen dan vektor eigen dari suatu matriks iredusibel dalam aljabar max-plus? 3. Bagaimana membuat model matematika untuk suatu rute pilihan bus Transjogja berdasarkan teori aljabar max-plus? C. Pembatasan Masalah Berdasarkan rumusan masalah di atas, fokus utama karya tulis ini adalah penjelasan tentang konsep dasar aljabar max-plus dan aplikasinya pada suatu rute bus Transjogja. Oleh karena itu, pertama-tama akan diuraikan secara teoretis landasan-landasan teori yang menjadi dasar pembahasan tentang aljabar maxplus. Teori-teori tersebut mencakup konsep tentang himpunan, operasi biner dan sifat-sifatnya, semigrup, semigelanggang, semilapangan serta konsep dasar tentang vektor dan matriks pada himpunan semua bilangan real. Selanjutnya akan dijelaskan konsep aljabar max-plus dan sifat-sifatnya yang mencakup definisi aljabar max-plus, operasi dan sifat operasi aljabar max-plus, matriks dalam aljabar max-plus, graf dalam aljabar max-plus, nilai eigen dan vektor eigen dalam. 5.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. aljabar max-plus. Pada bagian akhir akan diperkenalkan aplikasi aljabar max-plus pada suatu rute bus Transjogja. D. Tujuan Penulisan Berdasarkan rumusan masalah di atas, tujuan dari karya tulis ini adalah pertama, mempelajari, mendalami dan menuliskan kembali konsep tentang aljabar max-plus; kedua menyusun model matematika untuk suatu rute bus Transjogja berdasarkan teori aljabar max-plus. E. Manfaat Penulisan Hasil karya tulis diharapkan dapat bermanfaat bagi: 1. Penulis Menambah dan memperdalam konsep pengetahuan dan keilmuan tentang aljabar max-plus dan aplikasinya. 2. Lembaga Sebagai tambahan pustaka untuk rujukan penelitian dan bahan perkuliahan tentang aljabar max-plus. 3. Pembaca/Masyarakat a. Sebagai bahan pembelajaran dan pengetahuan mengenai aljabar max-plus, dan diharapkan dapat menjadi rujukan untuk penelitian yang akan datang. b. Diperoleh analisis suatu rute bus Transjogja dengan tujuan peningkatan kualitas pelayanan pada masyarakat.. 6.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. F. Metode Penulisan Dalam proses penyelesaian karya tulis ini, penulis menggunakan dua metode penulisan, yaitu studi literatur dan penelitian lapangan. Studi literatur digunakan untuk menjelaskan landasan teori pada Bab II, konsep tentang aljabar max-plus pada Bab III dan penyusunan model matematika pada Bab IV. Sedangkan penelitian lapangan digunakan untuk mengumpulkan data yang digunakan ketika menyusun model matematika pada Bab IV. G. Sistematika Penulisan Secara garis besar, karya tulis ini terdiri atas lima bagian, yaitu: 1. Bab I Pendahuluan Pada bagian ini diuraikan tentang latar belakang, perumusan masalah, pembatasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan dan sistimatika penulisan. 2. Bab II Landasan Teori Pada bagian ini dijelaskan teori-teori yang digunakan sebagai dasar penjelasan aljabar max-plus. Teori-teori tersebut mencakup himpunan, operasi biner dan sifat-sifatnya, semigrup, semigelanggang, semilapangan serta konsep tentang vektor dan matriks pada himpunan semua bilangan real. 3. Bab III Pembahasan Pada bagian ini dijelaskan konsep dasar aljabar max-plus yang mencakup definisi aljabar max-plus, operasi dan sifat operasi aljabar maxplus, vektor dan matriks dalam aljabar max-plus, graf dalam aljabar max-plus serta konsep nilai eigen dan vektor eigen suatu matriks dalam aljabar max-plus.. 7.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. 4. Bab IV Aplikasi Pada bagian ini dijelaskan tentang aplikasi aljabar max-plus pada suatu rute bus Transjogja. Oleh karena itu, pada bagian ini dibuat model matematika untuk suatu rute bus Transjogja berdasarkan teori aljabar max-plus. Pemodelan matematika tersebut mencakup penentuan rute pilihan, pembuatan graf rute pilihan, penyusunan sikronisasi berdasarkan graf rute pilihan, penyusunan model matematika berdasarkan sinkronisasi yang buat, penentuan matriks yang direpresentasikan oleh graf rute pilihan berdasarkan model matematika yang diperoleh; penghitungan nilai eigen dan vektor eigen serta penarikan kesimpulan berdasarkan nilai eigen dan vektor eigen yang diperoleh. 5. Bab V Penutup Bagian ini berisi kesimpulan karya tulis ini serta saran untuk penulisan lebih lanjut.. 8.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. BAB II LANDASAN TEORI. Pada bab ini dijelaskan teori-teori yang digunakan sebagai dasar untuk menjelaskan teori aljabar max-plus pada Bab III. Penjelasan pada bab ini mencakup gambaran singkat tentang himpunan, definisi dan sifat-sifat operasi biner, definisi elemen identitas dan elemen invers himpunan, grupoid, semigrup, monoid, semigelanggang dan semilapangan. Pada bagian akhir akan dijelaskan secara singkat juga vektor dan matriks serta nilai eigen dan vektor eigen pada himpunan semua bilangan real. A. Himpunan dan Operasi Biner Pada bagian ini dijelaskan tentang himpunan dan operasi biner. Penjelasan tentang himpunan mencakup definisi himpunan, keanggotaan himpunan serta definisi dan contoh operasi gabungan dua himpunan. Sedangkan penjelasan tentang operasi biner mencakup definisi operasi biner dan sifatsifatnya. Penjelasan tentang himpunan dan operasi biner dirangkum dari Fraleigh (2003); Durbin (2009), Whitelaw (1995), dan Hungerford (2002). 1. Himpunan Himpunan adalah sekumpulan objek yang mempunyai syarat tertentu dan jelas. Objek ini selanjutnya dinamakan anggota atau elemen dari himpunan itu.. 9.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Syarat tertentu dan jelas dalam menentukan anggota suatu himpunan ini sangat penting agar himpunan tersebut terdefinisi dengan baik (well-defined set). Berikut ini diberikan beberapa contoh himpunan. Contoh 2.1 1. Himpunan semua mahasiswa program studi matematika angkatan 2011. 2. Himpunan lima huruf pertama dalam abjad 3. Himpunan empat bilangan asli yang pertama. Nama suatu himpunan biasanya dinyatakan dengan huruf besar 𝐴, 𝐵, 𝐶 dan sebagainya. Sedangkan untuk melambangkan anggota himpunan digunakan huruf kecil 𝑎, 𝑏, 𝑐, 𝑥 dan sebagainya. Untuk menyatakan himpunan digunakan simbol "{… }". Dengan demikian himpunan pada Contoh 2.1 di atas dapat ditulis sebagai berikut: Contoh 2.2 1. 𝐴 = {𝐼𝑛𝑑𝑟𝑎, 𝐽𝑜ℎ𝑛𝑦, 𝐵𝑎𝑦𝑢, 𝐸𝑛𝑠𝑖} 2. 𝐵 = {𝑎, 𝑏, 𝑐, 𝑑, 𝑒} 3. 𝐶 = {1, 2, 3, 4} Selanjutnya, notasi untuk keanggotaan suatu himpunan dapat dinyatakan sebagai berikut: Misalkan 𝐴, adalah suatu himpunan. a. Jika 𝑎 adalah objek pada himpunan 𝐴 maka 𝑎 dikatakan sebagai anggota 𝐴 dan ditulis 𝑎 ∈ 𝐴.. 10.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. b. Jika 𝐴 tidak mempunyai anggota maka 𝐴 disebut himpunan kosong, dan dinotasikan dengan 𝐴 = { } c. Jika 𝐴 mempunyai sekurang-kurangnya satu anggota maka 𝐴 disebut himpunan tak kosong. Selanjutnya, akan dijelaskan operasi gabungan dua himpunan. Gabungan himpunan 𝐴 dan 𝐵 adalah himpunan yang memuat himpunan 𝐴 atau 𝐵 yang dinotasikan 𝐴 ∪ 𝐵 = {𝑎|𝑎 ∈ 𝐴 ⋁ 𝑎 ∈ 𝐵}. Berikut ini diberikan contoh operasi gabungan dua himpunan. Contoh 2.3. Misalkan terdapat 𝐴 = {2, 4, 6, 8, 10} dan 𝐵 = {1, 2, 3, 4, 5} maka. 𝐴 ∪ 𝐵 = {1, 2, 3, 4, 5, 8, 10}. 2. Operasi Biner Pada bagian ini dijelaskan operasi biner dan sifat-sifatnya. Penjelasan pada bagian ini mencakup definisi operasi biner dan sifat-sifatnya, yakni sifat tertutup, komutatif, asosiatif, distributif, idempoten – definisi elemen identitas dan elemen invers. Penjelasan pada bagian ini dimulai dengan memberikan definisi hasil kali silang. Definisi 2.1 Misalkan 𝐴1 , 𝐴2 , … , 𝐴𝑛 adalah himpunan tak kosong. Himpunan semua 𝑛 tupel terurut pada himpunan 𝐴1 , 𝐴2 , … , 𝐴𝑛 disebut hasil kali silang dan dinotasikan dengan 𝐴1 × 𝐴2 × … × 𝐴𝑛 = {(𝑎1 , 𝑎2 , … , 𝑎𝑛 )|𝑎𝑖 ∈ 𝐴𝑖 , 𝑖 = 1, … , 𝑛}.. 11.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Setelah didefinisikan hasil kali silang, selanjutnya akan didefinisikan operasi biner. Definisi 2.2 Misalkan 𝑆 adalah himpunan tidak kosong. Operasi biner ∗ pada himpunan 𝑆 adalah pemetaan 𝑆 × 𝑆 pada 𝑆. Menurut Definisi 2.2 terdapat dua sifat dasar operasi biner; pertama terdefinisi dengan baik (well-defined) yaitu untuk setiap pasangan terurut (𝑎, 𝑏) ∈ 𝑆 × 𝑆 dipasangkan tepat satu dengan elemen di 𝑆. Kedua, sifat tertutup yaitu untuk setiap 𝑎, 𝑏 ∈ 𝑆, (𝑎 ∗ 𝑏) ∈ 𝑆. Berikut ini diberikan contoh sifat operasi biner pada suatu himpunan. Contoh 2.4 Misalkan ℤ adalah himpunan semua bilangan bulat yang dilengkapi dengan operasi penjumlahan dan perkalian. Akan ditunjukkan bahwa operasi penjumlahan dan perkalian adalah operasi biner di ℤ. Berdasarkan Definisi 2.2 maka ∀(𝑎, 𝑏) ∈ ℤ, (𝑎 + 𝑏) dapat dipasangkan tepat satu anggota ℤ . Selanjutnya ∀(𝑎, 𝑏) ∈ ℤ, 𝑎 + 𝑏 ∈ ℤ.. Jadi ℤ tertutup. terhadap operasi penjumlahan. Selanjutnya a, b   ℤ, a  b  juga well-difined dan a, b   ℤ , a  b  ℤ. Jadi ℤ tertutup terhadap operasi perkalian. Jadi, operasi penjumlahan dan perkalian adalah operasi biner di ℤ. Contoh 2.5 Misalkan ℕ adalah himpunan semua bilangan bulat positif. Pada ℕ didefinisikan operasi ∗ dengan ketentuan 𝑎 ∗ 𝑏 = 𝑎 − 𝑏. Karena 3 dan 5 ada di ℕ dan 3 − 5 = −2 ∈ ℕ maka ℕ tidak tertutup terhadap operasi biner ∗ . Jadi operasi ∗ bukan operasi biner pada ℕ. 12.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Selanjutnya akan dijelaskan dan diberikan contoh sifat-sifat operasi biner pada suatu himpunan. Definisi 2.3 (Sifat Komutatif Operasi Biner) Operasi biner ∗ pada suatu himpunan tak kosong S bersifat komutatif, jika dan hanya jika (∀𝑎, 𝑏 ∈ 𝑆), 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎. Contoh 2.6. Misalkan ℝ adalah himpunan semua bilangan real. Akan. ditunjukkan bahwa operasi penjumlahan dan perkalian pada ℝ adalah komutatif. Berdasarkan sifat operasi penjumlahan bilangan real jika diambil sebarang 𝑎, 𝑏 ∈ ℝ , berlaku 𝑎 + 𝑏 = 𝑏 + 𝑎. Selanjutnya berdasarkan sifat operasi perkalian bilangan real jika diambil sebarang 𝑎, 𝑏 ∈ ℝ , maka 𝑎 × 𝑏 = 𝑏 × 𝑎. Jadi berdasarkan Definisi 2.3 operasi penjumlahan dan perkalian di ℝ komutatif. Definisi 2.4 (Sifat Asosiatif Operasi Biner) Suatu operasi biner ∗ pada suatu himpunan tak kosong S bersifat asosiatif jika dan hanya jika (∀𝑎, 𝑏, 𝑐 ∈ 𝑆), (𝑎 ∗ 𝑏) ∗ 𝑐 = 𝑏 ∗ (𝑎 ∗ 𝑐). Contoh 2.7 Misalkan ℝ adalah himpunan semua bilangan real. Akan ditunjukkan bahwa operasi penjumlahan dan perkalian di ℝ asosiatif. Berdasarkan sifat operasi penjumlahan bilangan real jika diambil sebarang 𝑎, 𝑏, 𝑐 ∈ ℝ, berlaku (𝑎 + 𝑏) + 𝑐 = 𝑏 + (𝑎 + 𝑐). Selanjutnya berdasarkan sifat operasi perkalian bilangan real jika diambil sebarang 𝑎, 𝑏, 𝑐 ∈ ℝ, berlaku (𝑎 × 𝑏) × 𝑐 = 𝑏 × (𝑎 × 𝑐).. 13.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Jadi berdasarkan Definisi 2.4 operasi penjumlahan dan perkalian pada ℝ bersifat asosiatif. Definisi 2.5 (Sifat Distributif Operasi Biner) Misalkan operasi biner  dan ∗ terdefinisi pada himpunan S . 1. Jika (∀𝑎, 𝑏, 𝑐 ∈ 𝑆), 𝑎 ∘ (𝑏 ∗ 𝑐) = (𝑎 ∘ 𝑏) ∗ (𝑎 ∘ 𝑐), maka di 𝑆 berlaku sifat distributif kiri operasi ∘ terhadap operasi ∗ 2. Jika (∀𝑎, 𝑏, 𝑐 ∈ 𝑆), (𝑎 ∗ 𝑏) ∘ 𝑐 = (𝑎 ∘ 𝑐) ∗ (𝑏 ∘ 𝑐), maka di 𝑆 berlaku sifat distributif kanan operasi ∘ terhadap operasi ∗. Contoh 2.8 Misalkan ℝ adalah himpunan semua bilangan real. Berdasarkan sifat operasi pada bilangan real jika diambil sebarang 𝑎, 𝑏, 𝑐 ∈ ℝ, berlaku 𝑎 × (𝑏 + 𝑐) = (𝑎 × 𝑏) + (𝑎 × 𝑐) dan (𝑎 + 𝑏) × 𝑐 = (𝑎 × 𝑐) + (𝑏 × 𝑐). Jadi berdasarkan Definisi 2.5 operasi perkalian terhadap penjumlahan di ℝ bersifat distributif kiri dan distributif kanan. Definisi 2.6 (Sifat Idempoten Operasi Biner) Suatu operasi biner ∗ pada himpunan 𝑆 bersifat idempotent jika dan hanya jika (∀𝑎 ∈ 𝑆), 𝑎 ∗ 𝑎 = 𝑎. Contoh 2.9 Misalkan ℕ adalah himpunan semua bilangan asli. Untuk setiap 𝑎 ∈ ℕ didefinisikan operasi biner ∗ sehingga 𝑎 ∗ 𝑏 = elemen yang lebih kecil atau sama dengan 𝑎 atau 𝑏, berlaku 𝑎 ∗ 𝑎 = 𝑎 dan 𝑏 ∗ 𝑏 = 𝑏. Jadi berdasarkan Definisi 2.6 ℕ idempoten.. 14.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Setelah didefinisikan operasi biner dan sifat-sifatnya, selanjutnya akan didefinisikan elemen identitas dan elemen invers pada suatu himpunan tak kosong S . Definisi 2.7 Suatu himpunan tak kosong 𝑆 dikatakan mempunyai elemen identitas terhadap operasi biner ∗ jika ada elemen 𝑒 ∈ 𝑆 sedemikian sehingga (∀𝑎 ∈ 𝑆), 𝑎 ∗ 𝑒 = 𝑒 ∗ 𝑎 = 𝑎. Contoh 2.10 Misalkan ℝ adalah himpunan semua bilangan real. Akan ditunjukkan bahwa ℝ mempunyai elemen identitas terhadap operasi penjumlahan dan perkalian. Ambil sebarang 𝑎 ∈ ℝ, 𝑎 + 𝑒 = 𝑎 ⟺ 𝑎 + 𝑒 − 𝑎 = 𝑎 − 𝑎 ⟺ 𝑒 = 0 ∈ ℝ Ambil sebarang (𝑎 ∈ ℝ), (𝑎 ≠ 0) maka berlaku 1. 1. 𝑎 × 𝑒 = 𝑎 ⇔ 𝑎 × 𝑒 × 𝑎 = 𝑎 × 𝑎 ⇔ 𝑒 = 1 ∈ ℝ. Untuk 𝑎 = 0, ∃1 ∈ ℝ maka berlaku 𝑎 × 1 = 0 × 1 = 1 × 0 = 0. Jadi berdasarkan Definisi 2.7 dapat disimpulkan bahwa 0 adalah elemen identitas terhadap operasi penjumlahan di ℝ; dan 1 adalah elemen identitas terhadap operasi perkalian di ℝ. Definisi 2.8 Misalkan himpunan tak kosong 𝑆 terhadap operasi biner ∗ mempunyai elemen identitas, yaitu 𝑒. Suatu elemen 𝑏 ∈ 𝑆 dikatakan invers dari 𝑎 ∈ 𝑆 terhadap operasi biner ∗ jika dan hanya jika 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎 = 𝑒 Contoh 2.11 Misalkan ℝ adalah himpunan semua bilangan real. Akan ditunjukkan bahwa ℝ mempunyai elemen invers terhadap operasi penjumlahan dan ℝ\{0} mempunyai elemen invers terhadap operasi perkalian.. 15.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Ambil sebarang 𝑎 ∈ ℝ, 𝑎 + (−𝑎) = 0. Jadi −𝑎 adalah elemen invers terhadap operasi penjumlahan di ℝ. Ambil sebarang 𝑏 ∈ ℝ\{0}, 𝑏 ≠ 0 sehingga berlaku bahwa 𝑏 × 𝑏1 = 1 ∈ ℝ\{0}. 1. Jadi 𝑏 adalah elemen invers terhadap operasi perkalian di ℝ\{0}. Setelah dijelaskan konsep himpunan dan operasi biner, selanjutnya dijelaskan tentang struktur aljabar sebagai suatu himpunan yang tak kosong yang dilengkapi satu atau dua operasi biner. B. Grupoid, Semigrup dan Monoid Struktur aljabar adalah suatu himpunan tak kosong S yang dilengkapi dengan satu atau lebih operasi biner. Struktur aljabar di atas berturut-turut dinotasikan dengan (𝑆,∗) dan (𝑆, +,  ). Struktur aljabar yang paling sederhana adalah grupoid, semigrup, dan monoid. Grupoid adalah himpunan tak kosong yang dilengkapi dengan satu operasi biner. Semigrup adalah himpunan tak kosong yang dilengkapi dengan satu operasi biner dan operasi binernya bersifat asosiatif. Monoid adalah semigrup yang mempunyai elemen identitas. Berikut ini diberikan contoh struktur aljabar grupoid, semigrup dan monoid. Contoh 2.12 Misalkan ℕ adalah himpunan semua bilangan asli terhadap operasi penjumlahan. Berdasarkan sifat operasi penjumlahan bilangan asli diketahui bahwa ℕ tertutup dan well-defined terhadap operasi penjumlahan. Jadi ℕ adalah grupoid terhadap operasi penjumlahan. Contoh 2.13 Akan ditunjukkan bahwa (ℕ, +) adalah semigrup. Pada Contoh 2.12 telah ditunjukkan bahwa (ℕ, +) well-defined dan tertutup. Hal ini berarti 16.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. cukup diselidiki apakah operasi penjumlahan di ℕ asosiatif; dan diketahui bahwa operasi penjumlahan bilangan asli bersifat asosiatif. Jadi (ℕ, +) adalah semigrup. Contoh 2.14. Misalkan ℤ adalah himpunan semua bilangan bulat. Akan. ditunjukkan bahwa (ℤ, +) adalah monoid. Untuk menunjukkan (ℤ, +) adalah monoid harus ditunjukkan bahwa (ℤ, +) adalah semigrup dan (ℤ, +) mempunyai elemen identitas terhadap operasi penjumlahan. Diketahui bahwa di ℤ operasi penjumlahan bersifat tertutup dan asosiatif. Jadi ℤ adalah semigrup. Sekarang akan ditunjukkan bahwa ℤ punya elemen identitas terhadap operasi penjumlahan. Ambil sebarang 𝑎 ∈ ℤ, berdasarkan Definisi 2.7 bahwa 𝑎 + 𝑒 = 𝑎 ⟺ 𝑎 + 𝑒 − 𝑎 = 𝑎 − 𝑎 ⟺ 𝑒 = 0. Jadi terbukti bahwa ℤ mempunyai elemen identitas terhadap operasi penjumlahan, yaitu 0. Jadi (ℤ, +) adalah monoid. Selanjutnya penjelasan dilanjutkan dengan memberi fokus pada semigrup. Penjelasan dimulai dengan mendefinisikan suatu grupoid sebagai semigrup. Definisi 2.9 Suatu grupoid S adalah semigrup jika operasi binernya bersifat asosiatif . Definisi 2.9 menjelaskan bahwa tidak semua grupoid adalah semigrup. Pada Contoh 2.13 di atas telah ditunjukkan bahwa suatu grupoid (ℕ, +) adalah semigrup. Berikut ini akan diberikan contoh yang menjelaskan bahwa tidak semua grupoid adalah semigrup.. 17.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Contoh 2.15 Misalkan (𝐺,∗) adalah grupoid. Operasi biner dari himpunan 𝐺 terdefinisi seperti dalam tabel berikut: Tebel 2.1 Tabel Operasi Biner Himpunan 𝐺. (𝐺,∗). a. B. C. d. A. b. C. D. a. B. d. A. B. c. C. a. B. C. d. D. c. D. A. b. Akan ditunjukkan bahwa (𝐺,∗) bukan semigrup. Hal itu berarti bahwa terdapat elemen di 𝐺 jika dioperasikan dengan operasi yang terdefinisi pada 𝐺 tidak asosiatif. Ambil sebarang 𝑎, 𝑎, 𝑎 ∈ 𝐺 maka (𝑎 ∗ 𝑎) ∗ 𝑎 = 𝑎 ∗ (𝑎 ∗ 𝑎). 𝑏∗𝑎 =𝑎∗𝑏 𝑑≠𝑐 Berdasarkan hasil operasi di atas, G bukan semigrup. Selanjutnya akan dijelaskan dan diberikan contoh semigrup komutatif. Definisi 2.10 Semigrup (𝑆,∗) adalah semigrup komutatif jika operasi biner ∗ bersifat komutatif. Contoh 2.16 Misalkan ℕ adalah himpunan semua bilangan asli. Pada Contoh 2.13 telah dibuktikan bahwa (ℕ, +) adalah semigrup terhadap operasi penjumlahan. Sekarang akan ditunjukkan bahwa (ℕ, +) adalah semigrup komutatif. Diketahui bahwa operasi penjumlahan pada bilangan asli komutatif.. 18.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Maka berdasarkan Definisi 2.10 dapat disimpulkan bahwa (ℕ, +) adalah semigrup komutatif. Dari penjelasan di atas dapat disimpulkan bahwa semigrup adalah himpunan tak kosong yang dilengkapi dengan satu operasi biner yang bersifat tertutup, terdefinisi dengan baik dan bersifat asosiatif. Suatu semigrup adalah komutatif jika operasinya komutatif. Penjelasan tentang semigrup dirangkum dari Howie (1995), Harju (1996) dan Kandasamy (2002). C. Semigelanggang Pada Bagian B telah dijelaskan struktur aljabar dengan satu operasi biner. Pada bagian ini akan dijelaskan struktur aljabar dengan dua operasi biner yang dinotasikan dengan (𝑆, +,  ) . Salah satu contoh struktur aljabar dengan dua operasi. biner. adalah. semigelanggang.. Penjelasan. selanjutnya. tentang. semigelanggang dirangkum dari Howie (1995), Harju (1996), dan Heidergott, dkk (2005). Penjelasan pada bagian ini dimulai dengan menjelaskan elemen penyerap pada grupoid dan definisi semigelanggang. Definisi 2.11. Suatu elemen 𝑎 dalam suatu grupoid (𝑆,∗) disebut elemen penyerap terhadap operasi biner ∗ jika ∀𝑥 ∈ 𝑆 berlaku 𝑎 ∗ 𝑥 = 𝑥 ∗ 𝑎 = 𝑎. Definisi 2.12 Suatu semigelanggang S ,, adalah suatu himpunan tak kosong 𝑆 yang dilengkapi dengan dua operasi biner, yaitu + dan  yang memenuhi aksioma-aksioma berikut:. 19.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. 1. (𝑆, +) adalah monoid komutatif dengan elemen identitasnya θ 2. (𝑆,  ) adalah monoid dengan elemen identitasnya 𝑒 3. Elemen identitas 𝜃 adalah elemen penyerap terhadap operasi biner  . 4. Operasi biner  bersifat distributif kiri dan distributif kanan terhadap operasi biner +. Selanjutnya akan dijelaskan contoh himpunan tak kosong dengan dua operasi dan merupakan semigelanggang. Contoh 2.17 Misalkan ℝ adalah himpunan semua bilangan real yang dilengkapi dengan operasi penjumlahan dan perkalian. Akan ditunjukkan bahwa (ℝ, +,×) adalah semigelanggang. Berdasarkan Definisi 2.12 akan ditunjukkan bahwa: 1. (ℝ, +) adalah monoid komutatif Diketahui ℝ adalah himpunan bilangan real. Ada empat sifat yang harus diselidiki untuk menunjukkan bahwa (ℝ, +) adalah monoid komutatif yaitu sifat tertutup, sifat asosiatif, sifat komutatif dan keberadaan elemen identitas. Ambil sebarang 𝑎, 𝑏 ∈ ℝ, maka berlaku bahwa 𝑎 + 𝑏 ∈ ℝ. Jadi ℝ tertutup terhadap operasi biner +. Selanjutnya pada Contoh 2.7 telah ditunjukkan bahwa operasi penjumlahan di ℝ asosiatif. Selanjutnya pada Contoh 2.6 telah ditunjukkan juga bahwa operasi penjumlahan di ℝ komutatif. Akhirnya pada Contoh 2.10 telah ditunjukkan bahwa ℝ terhadap operasi penjumlahan mempunyai elemen identitas, yaitu 0. Jadi (ℝ, +) adalah semigrup komutatif dengan elemen identitasnya 0.. 20.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. 2. (ℝ,×) adalah monoid Diketahui ℝ adalah himpunan bilangan real. Ada tiga sifat yang harus ditunjukkan untuk membuktikan bahwa (ℝ,×) adalah monoid yaitu sifat tertutup, sifat asosiatif, dan keberadaan elemen identitas. Ambil sebarang ∀𝑎, 𝑏 ∈ ℝ, berlaku bahwa 𝑎 × 𝑏 ∈ ℝ . Jadi ℝ tertutup terhadap operasi perkalian. Selanjutnya pada Contoh 2.7 telah ditunjukkan bahwa operasi perkalian di ℝ asosiatif. Akhirnya pada Contoh 2.10 telah ditunjukkan bahwa ℝ terhadap operasi perkalian mempunyai elemen identitas, yaitu 1. Jadi terbukti (ℝ,×) adalah monoid. 3. Akan ditunjukkan bahwa elemen 0 adalah elemen penyerap terhadap operasi perkalian. Diketahui bahwa 0 ∈ ℝ dan 0 adalah elemen identitas terhadap operasi + di ℝ. Ambil sebarang a  ℝ maka 0 × 𝑎 = 𝑎 × 0 = 0 . Jadi 0 adalah elemen penyerap terhadap operasi × di ℝ. 4. Akan ditunjukkan operasi perkalian di (ℝ, +,×) bersifat distributif kiri dan distirbutif kanan terhadap operasi penjumlahan. Pada Contoh 2.8 telah ditunjukkan bahwa operasi perkalian di (ℝ, +,×) bersifat distributif kiri dan distirbutif kanan terhadap operasi penjumlahan. Jadi berdasarkan 1, 2, 3 dan 4 (ℝ, , ) adalah semigelanggang. Selanjutnya dijelaskan dua semigelanggang yang memiliki sifat khusus, yaitu semigelanggang komutatif dan semigelanggang idempoten. Definisi 2.13 Suatu semigelanggang (𝑆, +,  ) adalah semigelanggang komutatif jika operasi biner  bersifat komutatif.. 21.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Contoh 2.18 Akan ditunjukkan bahwa (ℝ, , ) adalah semigelanggang komutatif.. Pada Contoh 2.17 telah ditunjukkan bahwa (ℝ, , ) adalah. semigelanggang. Jadi cukup ditunjukkan bahwa di ℝ berlaku sifat komutatif terhadap operasi perkalian. Pada Contoh 2.6 telah ditunjukkan bahwa operasi perkalian di ℝ komutatif. Karena (ℝ, , ) adalah semigelanggang dan terhadap operasi perkalian ℝ komutatif maka (ℝ, , ) adalah semigelanggang komutatif. Definisi 2.14 Suatu semigelanggang (𝑆, +,  ) disebut semigelanggang idempoten jika operasi biner + bersifat idempoten. Contoh 2.19 Misalkan ℝ+ adalah himpunan semua bilangan real tak negatif. Pada ℝ+ didefinisikan operasi minimum yang dinotasikan dengan ⊖ dan operasi perkalian bilangan real yang dinotasikan dengan ⊙, sehingga ∀𝑎, 𝑏, 𝑐 ∈ ℝ+ berlaku 𝑎 ⊖ 𝑏 = min(𝑎, 𝑏) dan 𝑎 ⊙ 𝑏 = 𝑎 × 𝑏. Akan ditunjukkan bahwa (ℝ+ ,⊖, ⨀) adalah semigelanggang idempoten. Pertama harus ditunjukkan bahwa (ℝ+ ,⊖, ⨀) adalah semigelanggang. Untuk menunjukkan bahwa (ℝ+ ,⊖, ⨀) adalah semigelanggang, harus ditunjukkan bahwa: 1. (ℝ+ ,⊖) adalah monoid komutatif. Ambil sebarang 𝑎, 𝑏, 𝑐 ∈ ℝ+ maka berlaku a. 𝑎 ⊝ 𝑏 = min(𝑎, 𝑏) ∈ ℝ+ . Jadi ℝ+ tertutup. b. (𝑎 ⊖ 𝑏) ⊝ 𝑐 = min(min(𝑎, 𝑏), 𝑐) = min(𝑎, 𝑏, 𝑐) = min(𝑎, min(𝑏, 𝑐)) = 𝑎 ⊝ (𝑏 ⊝ 𝑐) Jadi ℝ+ asosiatif terhadap operasi ⊝.. 22.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. c. 𝑎 ⊖ 𝑏 = min(𝑎, 𝑏) = min(𝑏, 𝑎) = 𝑏 ⊝ 𝑎 . Jadi ℝ+ bersifat komutatif terhadap operasi ⊝. d. Misalkan (ℝ+ ,⊖) mempunyai elemen identitas, yaitu 𝑒. Berdasarkan Definisi 2.7 maka (𝑎 ⊖ 𝑏) + 𝑒 = 𝑎 ⊖ 𝑏 min(𝑎, 𝑏) + 𝑒 = min(𝑎, 𝑏) min(𝑎, 𝑏) + 𝑒 − min(𝑎, 𝑏) = min(𝑎, 𝑏) − min(𝑎, 𝑏). 0e 0 e  0. Jadi 0 adalah elemen identitas di (ℝ+ ,⊖). Jadi berdasarkan a, b, c dan d terbukti bahwa (ℝ+ ,⊖) adalah monoid komutatif dengan elemen identitas 0. 2. (ℝ+ , ⨀) adalah monoid. Ambil sebarang 𝑎, 𝑏, 𝑐 ∈ ℝ+ maka berlaku a. 𝑎 ⊙ 𝑏 = 𝑎 × 𝑏 ∈ ℝ+ . Jadi ℝ+ tertutup terhadap operasi ⊙. b. (𝑎 ⊙ 𝑏)⨀𝑐 = (𝑎 × 𝑏) × 𝑐 = 𝑎 × 𝑏 × 𝑐 = 𝑎 × (𝑏 × 𝑐) = 𝑎 ⊙ (𝑏 ⊙ 𝑐) Jadi ℝ+ asosiatif terhadap operasi ⊙. c. Ambil sebarang a adalah elemen identitas di (ℝ+ , ⨀). Berdasarkan Definisi 2.7 maka untuk 𝑎 ≠ 0 berlaku 𝑎 ⊙ 𝑒 = 𝑎 ⟺ 𝑎 × 𝑒 = 𝑎 ⟺ 𝑎 × 𝑒 × 𝑎1 = 𝑎 × 𝑎1 ⟺ 𝑒 = 1 Untuk 𝑎 = 0. Diketahui 1 ∈ ℝ+ , maka 0 × 1 = 1 × 0 = 0. Jadi 1 adalah identitas di (ℝ+ , ⨀).. 23.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Berdasarkan a, b dan c, dapat disimpulkan bahwa (ℝ+ , ⨀) adalah monoid dengan elemen identitas adalah 1. 3. Diketahui bahwa 0 ∈ ℝ+ dan 0 adalah elemen identitas terhadap operasi ⊖ di ℝ+ . Ambil sebarang a  ℝ+ , maka berlaku 0 ⊙ 𝑎 = 𝑎 ⊙ 0 = 0 . Jadi 0 adalah elemen penyerap terhadap operasi ⊙ di ℝ+ . 4. Operasi biner ⨀ di (ℝ+ ,⊖, ⨀) bersifat distributif kiri dan distributif kanan terhadap operasi biner ⊖. Ambil sebarang 𝑎, 𝑏, 𝑐 ∈ ℝ+ maka berlaku: 1) (𝑎 ⊖ 𝑏) ⊙ 𝑐 = min(𝑎, 𝑏) × 𝑐 = min(𝑎 × 𝑐, 𝑏 × 𝑐) = (𝑎 ⊙ 𝑐) ⊖ (𝑏 ⊙ 𝑐) 2) 𝑎 ⊙ (𝑏 ⊝ 𝑐) = 𝑎 × min(𝑏, 𝑐) = min(𝑎 × 𝑏, 𝑎 × 𝑐) = (𝑎 ⊙ 𝑏) ⊝ (𝑎 ⊙ 𝑐) Berdasarkan a, b maka disimpulkan bahwa operasi ⨀ bersifat distributif kiri dan distributif kanan terhadap ⊖ di (ℝ+ ,⊖, ⨀). Berdasarkan 1, 2, 3 dan 4 terbukti bahwa (ℝ+ ,⊖, ⨀) adalah semigelanggang. Selanjutnya akan ditunjukkan bahwa operasi ⊖ idempoten. Ambil sebarang 𝑎 ∈ ℝ+ maka berlaku 𝑎 ⊖ 𝑎 = 𝑚𝑖𝑛(𝑎, 𝑎) = 𝑎. Jadi operasi ⊖ idempoten. Karena (ℝ+ ,⊖, ⨀) adalah semigelanggang dan operasi ⊖ idempoten, (ℝ+ ,⊖, ⨀) adalah semigelanggang idempoten. Dari penjelasan di atas dapat disimpulkan bahwa semigelanggang adalah struktur aljabar yang dilengkapi dengan dua operasi biner dan memenuhi aksioma: terhadap operasi pertama membentuk monoid komutatif; terhadap operasi kedua membentuk monoid; elemen identitas terhadap operasi pertama merupakan elemen penyerap terhadap operasi kedua dan operasi kedua bersifat 24.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. distributif kiri dan distributif kanan terhadap operasi pertama. Suatu semigelanggang adalah komutatif, jika operasi keduanya komutatif; dan semigelanggang adalah idempoten jika operasi pertama idempoten. D. Semilapangan Struktur aljabar terakhir yang akan dijelaskan adalah semilapangan. Semilapangan adalah semigelanggang komutatif yang mendapat tambahan sifat khusus, yaitu untuk setiap elemen yang bukan elemen identitas terhadap operasi pertama mempunyai elemen invers terhadap operasi kedua. Definisi formal semilapangan dijelaskan oleh dua definisi berikut: Definisi 2.15 Suatu semigelanggang komutatif (𝑆, +,  ) disebut semilapangan jika setiap elemen di 𝑆 yang bukan elemen identitas 𝜃 mempunyai invers terhadap operasi biner  yaitu ∀𝑎 ∈ 𝑆\{𝜃}, ∃𝑎−1 sehingga 𝑎  𝑎−1 = 𝑒, dengan 𝑒 adalah elemen identitas terhadap operasi  . Definisi 2.16 Suatu semilapangan (𝑆, +,  ) adalah semilapangan idempoten jika operasi  bersifat idempoten. Selanjutnya diberikan contoh semigelanggang komutatif yang merupakan semilapangan idempoten. Contoh 2.20 Misalkan Himpunan ℝ ∪ 𝜀 dengan ℝ adalah himpunan semua bilangan real; Misalkan juga di ℝ ∪ 𝜀 didefinisikan 𝑒 = 0 dan 𝜀 = −∞ serta dua operasi biner yang belaku di himpunan ℝ ∪ 𝜀, operasi  dan dan operasi  yang didefinisikan sebagai berikut: ∀𝑎, 𝑏 ∈ ℝ ∪ 𝜀, 𝑎 ⊕ 𝑏 = max(𝑎, 𝑏) dan 𝑎 ⊗ 𝑏 = 𝑎 + 𝑏.. 25.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Himpunan ℝ ∪ 𝜀 yang dilengkapi dengan operasi biner  dan  adalah semilapangan idempotent. Himpunan ini kemudian dikenal dengan sebutan aljabar max-plus. Bukti lengkap Contoh 2.20 ini akan dijelaskan pada Bab III. E. Vektor dan Matriks Pada Himpunan Bilangan Real Pada bagian ini dijelaskan definisi tentang vektor dan matriks pada himpunan bilangan real serta nilai eigen dan vektor eigen dari matriks real. Pembahasan dimulai dengan memberikan definisi tentang lapangan dan ruang vektor. Definisi 2.17 Lapangan adalah semilapangan yang mempunyai elemen invers terhadap operasi pertama. Definisi 2.18 Misalkan 𝐹 adalah lapangan. Himpunan 𝐹 adalah ruang vektor jika untuk setiap 𝑎, 𝑏 ∈ 𝐹 dan sebarang skalar 𝑘 ∈ ℝ berlaku 𝑎 + 𝑏 ∈ 𝐹 dan hasil kali 𝑘  𝑎 ∈ 𝐹. Salah satu contoh lapangan adalah himpunan bilangan real ℝ dengan operasi. penjumlahan dan operasi perkalian dan disebut lapangan real ℝ .. Menurut Definisi 2.17 dan Definisi 2.18 jika ℝ𝑛 = ℝ × ℝ × … × ℝ = {𝒂 = (𝑎1 , 𝑎2 , … , 𝑎𝑛 )|𝑎𝑖 ∈ ℝ, 𝑖 = 1, … , 𝑛} dan pada ℝ𝑛 didefinisikan operasi: . Penjumlahan: 𝒂 + 𝒃 = (𝑎1 , 𝑎2 , … , 𝑎𝑛 ) + (𝑏1 , 𝑏2 , … , 𝑏𝑛 ) = (𝑎1 + 𝑏1 , 𝑎2 + 𝑏2 , … , 𝑎𝑛 + 𝑏𝑛 ). . Perkalian dengan skalar 𝛼 di ℝ 𝛼 × 𝒂 = 𝛼 × (𝑎1 , 𝑎2 , … , 𝑎3 ). 26.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. = (𝛼 × 𝑎1 , 𝛼 × 𝑎2 , … , 𝛼 × 𝑎3 ) maka ℝ𝑛 merupakan ruang vektor atas lapangan real ℝ , 𝒂 = (𝑎1 , 𝑎2 , … , 𝑎𝑛 ) disebut vektor real (Anton, 2005). Setelah dijelaskan vektor real di ℝ𝑛 , selanjutnya akan dijelaskan konsep matriks pada himpunan bilangan real, nilai eigen dan vektor eigen pada matriks real. Penjelasan dimulai dengan memberikan definisi tentang matriks. Definisi 2.19 Matriks adalah susunan bilangan berbentuk segiempat. Bilanganbilangan dalam susunan itu disebut elemen-elemen dari matriks tersebut (Anton, 2005). Definisi 2.20 Ordo atau ukuran matriks adalah banyaknya baris 𝑖  banyaknya kolom 𝑗 dalam matriks itu (Kolman, 2001). Selanjutnya jika 𝐴 adalah matriks berukuran 𝑚 × 𝑛 maka elemen yang terletak pada baris ke- 𝑖 dalam kolom ke- 𝑗 matriks 𝐴 dinotasikan dengan 𝑎𝑖𝑗 atau [𝐴]𝑖𝑗 dengan 𝑖 = 1, … , 𝑚 dan 𝑗 = 1, … , 𝑛. Bentuk umum matriks 𝐴 berukuran 𝑚 × 𝑛 dituliskan sebagai berikut:.  a11 a A   12    a m1. a12 a 22  am2.  a1n   a 2 n       a mn . Untuk penjelasan selanjutnya matriks yang dijelaskan adalah matriks yang elemen-elemennya adalah himpunan semua bilangan real. Himpunan matriks real berukuran 𝑚 × 𝑛 dinotasikan dengan ℝ𝑚𝑥𝑛 . Berikut ini beberapa tipe matriks, yaitu: 27.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. 1. Jika semua elemen matriks 𝐴 bernilai nol maka matriks 𝐴 disebut matriks nol. 2. Matriks dengan banyaknya baris dan banyaknya kolom sama disebut matriks persegi. Matriks persegi dengan baris dan kolom sebanyak 𝑛 disebut matriks persegi berukuran 𝑛 × 𝑛. Jika matriks 𝐴 = [𝑎𝑖𝑗 ] adalah matriks persegi berukuran 𝑛 × 𝑛 maka elemen-elemen 𝑎11 , 𝑎22, … , 𝑎𝑛𝑛 disebut elemen diagonal utama matriks 𝐴. 3. Suatu matriks persegi berukuran 𝑛 × 𝑛 disebut matriks identitas jika elemen diagonal utamanya 1 dan elemen lainnya 0. Matriks identitas berukuran 𝑛 × 𝑛 dinotasikan dengan 𝐼𝑛 . Setelah dijelaskan konsep tentang matriks, selanjutnya akan dijelaskan definisi operasi-operasi pada matriks. Definisi 2.21 1. Untuk 𝐴, 𝐵 ∈ ℝ𝑚𝑥𝑛 maka 𝐴 + 𝐵 = [𝑎𝑖𝑗 + 𝑏𝑖𝑗 ], dengan 𝐴 + 𝐵 ∈ ℝ𝑚𝑥𝑛 . 2. Untuk 𝐴 ∈ ℝ𝑚𝑥𝑝 dan 𝐵 ∈ ℝ𝑝𝑥𝑛 maka 𝐴 × 𝐵 = 𝐶 dengan 𝐶 ∈ ℝ𝑚𝑥𝑛 dan. cij  k 1 aik bkj untuk 𝑖 = 1, … , 𝑚 dan 𝑗 = 1, … , 𝑛. p. 3. Untuk sebarang matriks 𝐴 ∈ ℝ𝑚𝑥𝑛 dan sebarang skalar 𝑠 ∈ ℝ maka 𝑠 × 𝐴 = [𝑠 × 𝑎𝑖𝑗 ] dengan 𝑠 × 𝐴 ∈ ℝ𝑚𝑥𝑛 . Setelah didefinisikan tiga operasi pada matriks di atas, berikut ini akan didefinisikan operasi pangkat pada matriks. Definisi 2.22 Misalkan A adalah matriks persegi berordo 𝑛 dan 𝑝 adalah bilangan bulat positif maka operasi pangkat pada matriks didefinisikan. 28.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. 𝐴𝑝 = ⏟ 𝐴 ×𝐴 ×…× 𝐴 𝑝. Berdasarkan Definisi 2.21, 𝐴𝑝 dapat ditulis juga sebagai berikut 𝐴𝑝 = 𝐴 × ⏟ 𝐴 × 𝐴 × … × 𝐴 = 𝐴 × 𝐴𝑝−1 𝑝−1. Untuk p  0 maka A0  I n . Selanjutnya akan dijelaskan definisi nilai eigen dam vektor eigen matriks. Definisi 2.23 Misalkan 𝐴 adalah suatu matriks berordo 𝑛 × 𝑛, suatu vektor 𝒙 ≠ 𝟎 di ℝ𝑛 disebut vektor eigen dari matriks 𝐴 jika 𝐴𝒙 = 𝜆𝒙 untuk suatu skalar 𝜆. Skalar 𝜆 disebut nilai eigen (Anton, 2005). Setelah menjelaskan konsep himpunan, operasi biner, semigrup, semigelanggang, semilapangan, vektor dan matriks pada himpunan bilangan real, selanjutnya konsep-konsep tersebut akan digunakan sebagai landasan untuk menjelaskan teori aljabar max-plus yang akan dijelaskan pada bab selanjutnya.. 29.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. BAB III ALJABAR MAX-PLUS. Pada bab ini dijelaskan tentang konsep dasar aljabar max-plus yang mencakup definisi aljabar max-plus, operasi dalam aljabar max-plus dan sifatsifatnya, vektor dan matriks dalam aljabar max-plus, graf dalam aljabar max-plus, nilai eigen dan vektor eigen dalam aljabar max-plus. Penjelasan tentang topiktopik di atas dijelaskan dalam definisi-definisi dan teorema serta dilengkapi dengan contoh-contoh penjelas tentang topik-topik yang bersangkutan. A. Definisi Aljabar Max-Plus Secara singkat aljabar max-plus dapat didefinisikan sebagai himpunan ℝ ∪ {𝜀} dengan ℝ adalah himpunan semua bilangan real yang dilengkapi dengan operasi maksimum dan operasi penjumlahan dan membentuk semilapangan. Secara matematika, definisi tentang aljabar max-plus dijelaskan lebih lanjut dalam definisi dan teorema-teorema berikut ini. Definisi 3.1 Notasi ℝℰ menunjuk pada himpunan ℝ ∪ {𝜀} dengan ℝ adalah himpunan semua bilangan real (Bacelli, 2001). Definisi 3.2 Didefinisikan 𝜀 = −∞ dan 𝑒 = 0 maka ∀𝑎, 𝑏 ∈ ℝℰ , operasi ⊕ dan operasi ⊗ didefinisikan sebagai berikut: 𝑎 ⊕ 𝑏 = max(𝑎, 𝑏) dan 𝑎 ⊗ 𝑏 = 𝑎 + 𝑏. 30.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Didefinisikan juga bahwa max(𝑎, 𝜀) = max(𝜀, 𝑎) = 𝑎 dan 𝑎 + 𝜀 = 𝜀 + 𝑎 = 𝜀 sehingga untuk setiap 𝑎 ∈ ℝℰ , dapat dituliskan 𝑎 ⊕ 𝜀 = 𝜀 ⊕ 𝑎 = 𝑎 dan 𝑎 ⊗ 𝜀 = 𝜀 ⊗ 𝑎 = 𝜀. Dalam Heidergott, cs, 2006 himpunan ℝℰ yang dilengkapi operasi ⊕ dan ⊗ disebut aljabar max-plus dan dinotasikan dengan ℝ𝑚𝑎𝑥 = (ℝ𝜀 ,⊕,⊗). Pada penjelasan selanjutnya sebutan dan notasi ini digunakan dalam karya tulis ini untuk menyederhanakan penyebutan aljabar max-plus. Selanjutnya akan diberikan beberapa contoh penggunaan operasi ⊕ dan ⊗ dalam perhitungan . Contoh 3.1 Perhatikan contoh operasi ⊕ dan ⊗ yang digunakan pada masalah berikut: 5 ⊕ 2 = max(5,2) = 5 5 ⊕ 𝜀 = max(5, 𝜀) = 5 5 ⊗ 𝜀 = 5 + (−∞) = −∞ 𝑒 ⊕ 2 = max(0,2) = 2 3⊗𝑒 =3+0= 3 4 ⊗ 8 = 4 + 8 = 12 Setelah dijelaskan definisi tentang ℝ𝑚𝑎𝑥 , berikut ini akan dijelaskan dua teorema yang menjelaskan sifat dasar ℝ𝑚𝑎𝑥 .. 31.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Teorema 3.3 ℝ𝑚𝑎𝑥 adalah semigelanggang komutatif dan idempoten (Bacelli, 2001). Bukti Akan dibuktikan bahwa ℝ𝑚𝑎𝑥 adalah semigelanggang komutatif dan idempoten. Untuk membuktikan ℝ𝑚𝑎𝑥 adalah semigelanggang komutatif dan idempoten maka dibuktikan bahwa 1. ℝmax adalah semigelanggang. Untuk membuktikan bahwa (ℝ𝑚𝑎𝑥 ,⊕,⊗) adalah semigelanggang ditempuh langkah-langkah berikut: a. Akan dibuktikan (ℝ𝑚𝑎𝑥 ,⊕) adalah monoid komutatif. Oleh karena itu ∀𝑎, 𝑏, 𝑐 ∈ ℝ𝑚𝑎𝑥 berlaku: i.. Operasi ⊕ di ℝ𝑚𝑎𝑥 asosiatif, yaitu: (𝑎 ⊕ 𝑏) ⊕ 𝑐 = max(max(𝑎, 𝑏), 𝑐) = max(𝑎, 𝑏, 𝑐) = max(𝑎, max(𝑏, 𝑐)) = 𝑎 ⊕ (𝑏 ⊕ 𝑐). ii.. Operasi ⊕ di ℝ𝑚𝑎𝑥 komutatif, yaitu: 𝑎 ⊕ 𝑏 = max(𝑎, 𝑏) = max(𝑏, 𝑎) = 𝑏 ⊕ 𝑎. iii. Terdapat elemen 𝜀 = −∞ ∈ ℝ𝑚𝑎𝑥 , sedemikian hingga 𝑎 ⊕ 𝜀 = max(𝑎, −∞) = max(−∞, 𝑎) = 𝑎. Jadi berdasarkan Definisi 2.7 terbukti bahwa 𝜀 = −∞ adalah elemen identitas dari (ℝ𝑚𝑎𝑥 ,⊕). Berdasarkan i, ii, dan iii terbukti bahwa (ℝ𝑚𝑎𝑥 ,⊕) adalah monoid komutatif dengan elemen identitas, yaitu 𝜀 = −∞. 32.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. b. Akan dibuktikan bahwa (ℝ𝑚𝑎𝑥 ,⊗) adalah monoid. Oleh karena itu ∀𝑎, 𝑏, 𝑐 ∈ ℝ𝑚𝑎𝑥 , berlaku: i. Operasi ⊗ di ℝ𝑚𝑎𝑥 asosiatif, yaitu: (𝑎 ⊗ 𝑏) ⊗ 𝑐 = 𝑎 + 𝑏 + 𝑐 = 𝑎 + 𝑏 + 𝑐 = 𝑎 ⊗ (𝑏 ⊗ 𝑐) ii. Terdapat elemen e  0 di ℝ𝑚𝑎𝑥 sehingga 𝑎 ⊗ 𝑒 = 𝑎 + 0 = 0 + 𝑎 = 𝑎. Jadi berdasarkan Definisi 2.7 terbukti bahwa e  0 adalah elemen identitas dari (ℝ𝑚𝑎𝑥 ,⊗). Jadi, berdasarkan i dan ii terbukti bahwa (ℝ𝑚𝑎𝑥 ,⊗) adalah monoid dengan elemen identitas e  0. c. Akan dibuktikan di ℝ𝑚𝑎𝑥 terdapat elemen penyerap terhadap operasi ⊗ Diketahui bahwa −∞ ∈ ℝ𝑚𝑎𝑥 dan −∞ adalah elemen identitas terhadap operasi ⊕ di ∈ ℝ𝑚𝑎𝑥 . Ambil sebarang 𝑎 ∈ ℝ𝑚𝑎𝑥 , berdasarkan Definisi 2.11 berlaku 𝑎 ⊗ −∞ = −∞ ⊗ 𝑎 = −∞. Jadi    adalah elemen penyerap terhadap operasi ⊗ di ℝ𝑚𝑎𝑥 . d. Operasi ⊗ bersifat distributif terhadap ⊕, a, b, c  ℝ𝑚𝑎𝑥 berlaku: i. Sifat distributif kanan, yaitu: (𝑎 ⊕ 𝑏) ⊗ 𝑐 = max(𝑎, 𝑏) + 𝑐 = max(𝑎 + 𝑐, 𝑏 + 𝑐) = (𝑎 ⊗ 𝑐) ⊕ (𝑏 ⊗ 𝑐) ii. Sifat distributif kiri, yaitu: 𝑎 ⊗ (𝑏 ⊕ 𝑐) = 𝑎 + 𝑚𝑎𝑥 (𝑏, 𝑐) = 𝑚𝑎𝑥 (𝑎 + 𝑏, 𝑎 + 𝑐) = (𝑎 ⊗ 𝑏) ⊕ (𝑎 ⊗ 𝑐) Kesimpulan: berdasarkan a, b, c dan d terbukti bahwa ℝ𝑚𝑎𝑥 adalah semigelanggang.. 33.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. 2. Selanjutnya. akan. ditunjukkan. bahwa ℝ𝑚𝑎𝑥 adalah. semigelanggang. komutatif. Berdasarkan Definisi 2.13 untuk membuktikan ℝ𝑚𝑎𝑥 adalah semigelanggang komutatif harus ditunjukkan bahwa ℝ𝑚𝑎𝑥 adalah semigelanggang dan operasi kedua pada ℝ𝑚𝑎𝑥 komutatif. Pada bagian (1) telah ditunjukkan bahwa ℝ𝑚𝑎𝑥 adalah semigelanggang. Selanjutnya akan ditunjukkan bahwa operasi kedua di ℝ𝑚𝑎𝑥 komutatif. Ambil sebarang 𝑎, 𝑏 ∈ ℝ𝑚𝑎𝑥 , 𝑎 ⊗ 𝑏 = 𝑎 + 𝑏 = 𝑏 + 𝑎 = 𝑏 ⊗ 𝑎. Jadi, untuk sebarang 𝑎, 𝑏 ∈ ℝ𝑚𝑎𝑥 operasi ⊗ komutatif. Berdasarkan bagian (1) dan (2) terbukti bahwa ℝ𝑚𝑎𝑥 adalah semigelanggang. komutatif. 3. Yang terakhir akan dibuktikan bahwa ℝ𝑚𝑎𝑥 adalah semigelanggang idempoten. Berdasarkan Definisi 2.14 untuk membuktikan ℝ𝑚𝑎𝑥 adalah semigelanggang idempoten, harus ditunjukkan ℝ𝑚𝑎𝑥 adalah semigelanggang dan operasi pertama pada ℝ𝑚𝑎𝑥 idempoten. Pada bagian (1) telah ditunjukkan bahwa ℝ𝑚𝑎𝑥 adalah semigelanggang. Selanjutnya akan ditunjukkan bahwa operasi ⊕ pada ℝ𝑚𝑎𝑥 idempoten. Ambil sebarang 𝑎 ∈ ℝ𝑚𝑎𝑥 , 𝑎 ⊕ 𝑎 = max(𝑎, 𝑎) = 𝑎. Jadi untuk sebarang 𝑎 ∈ ℝ𝑚𝑎𝑥 , operasi ⊕ idempoten. Terbukti bahwa ℝ𝑚𝑎𝑥 adalah semigelanggang idempoten. Kesimpulan: Berdasarkan 1, 2, dan 3 terbukti bahwa ℝ𝑚𝑎𝑥 adalah semigelanggang komutatif dan idempoten.. 34. ∎.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Selanjutnya akan dijelaskan juga teorema yang menjelaskan bahwa ℝ𝑚𝑎𝑥 adalah suatu semilapangan. Teorema 3.4 ℝ𝑚𝑎𝑥 adalah suatu semilapangan (Bacelli, 2001). Bukti Akan ditunjukkan bahwa ℝ𝑚𝑎𝑥 adalah suatu semilapangan. Berdasarkan Teorema 3.3 telah dibuktikan bahwa ℝ𝑚𝑎𝑥 adalah suatu semigelanggang komutatif. Oleh karena itu, untuk membuktikan ℝ𝑚𝑎𝑥 adalah semilapangan, cukup dibuktikan bahwa di ℝ𝑚𝑎𝑥 untuk setiap elemen yang bukan elemen identitas −∞ mempunyai invers terhadap operasi ⊗. Ambil sebarang 𝑎 ∈ ℝ𝑚𝑎𝑥 \{−∞}, ∃𝑎−1 = −𝑎 ∈ ℝ𝑚𝑎𝑥 maka berlaku 𝑎 ⊗ 𝑎−1 = 𝑒 atau 𝑎 + (−𝑎) = 0. Jadi terbukti bahwa ℝ𝑚𝑎𝑥 adalah ∎. semilapangan.. Berdasarkan Teorema 3.3 dan Teorema 3.4 dapat disimpulkan bahwa ℝ𝑚𝑎𝑥 adalah himpunan ℝ𝜀 yang dilengkapi dengan operasi ⊕ dan ⊗ serta membentuk semilapangan idempoten. B. Notasi di ℝ𝒎𝒂𝒙 Dalam rangka memahami operasi biner dalam ℝ𝑚𝑎𝑥 maka perlu diperkenalkan notasi yang berlaku dalam ℝ𝑚𝑎𝑥 . Pada Definisi 3.2 di atas, telah diperkenalkan dua operasi yang dinotasikan dengan ⊕ dan ⊗. Dalam Definisi 3.2 juga telah dijelaskan bahwa operasi ⊕ dan ⊗ dalam aljabar biasa didefinisikan sebagai operasi maksimum untuk operasi ⊕; dan penjumlahan untuk operasi ⊗. Dengan demikian cara sederhana untuk memahami sifat-sifat. 35.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. operasi dalam ℝ𝑚𝑎𝑥 adalah menganalogikannya dengan operasi yang berlaku dalam aljabar biasa. Misalkan, dalam ℝ𝑚𝑎𝑥 terdapat operasi biner “  ” (baca: O bagi) sebagai invers dari operasi ⊗. Dengan menganalogikannya pada aljabar biasa, operasi biner  sebagai invers dari operasi ⊗ dapat dianalogikan dengan invers dari operasi penjumlahan dalam aljabar biasa, yaitu pengurangan. Oleh karena itu operasi 𝑎  𝑏 dalam ℝ𝑚𝑎𝑥 dapat diselesaikan dengan menggunakan aljabar biasa, yaitu 𝑎 − 𝑏. Notasi untuk operasi lainnya di ℝ𝑚𝑎𝑥 diberikan dalam tabel analogi notasi operasi berikut: Tabel. 3.1 Analogi Notasi ℝ𝑚𝑎𝑥 Notasi ℝ𝒎𝒂𝒙. Notasi Aljabar Biasa. ⊕. max( ). ⊗. +. . −. √. /. 𝑒. 0. 𝜀. −∞. Selanjutnya pada tabel berikut diberikan beberapa contoh penggunaan notasi dalam ℝ𝑚𝑎𝑥 dan cara pengoperasiaannya.. 36.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Tabel 3.2 Contoh Penggunaan Notasi Operasi dalam ℝ𝑚𝑎𝑥 ℝ𝒎𝒂𝒙. Aljabar Biasa. =. 4⊕7. max(4,7). 7. 1⊕2⊕3⊕4⊕5. max(1, 2, 3, 4, 5). 5. 4⊗5. 4+5. 9. 4⊕𝜀. max(4, 𝜀). 4. 𝜀⊗4. 𝜀+4. . −5 ⊗ 2. −5 + 2. −3. 𝑒⊗5. 05. 5. 3⊗2 = 3 ⊗ 3. 3+3. 6. 𝑒 ⊗2 = 2⊗0. 2×0= 0×2. 0. (4 ⊗ 7)  (4 ⊕ 7). 4 + 7 − max(4,7). 4. 3 × max(2,3) atau (2 ⊕ 3)⊗3 = 2⊗3 ⊕ 3⊗3. max(3 × 2, 3 × 3). 9. 8 𝑒. 8−0. 8. 𝑒 5. 0−5. −5. 2. 14⁄ 2. 7. 5. 25⁄ 5. 5. √14 √25. Pembahasan pada Bagian B di atas dirangkum dari Bacelli (2001) dan Heidergott, dkk (2006).. 37.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. C. Sifat Operasi di ℝ𝒎𝒂𝒙 Definisi 3.2, Teorema 3.3 dan Teorema 3.4 telah menjelaskan sifat-sifat operasi biner dalam ℝ𝑚𝑎𝑥 . Kemudian pada Bagian B juga telah dijelaskan notasi operasi dalam ℝ𝑚𝑎𝑥 dan cara pengoperasiannya. Oleh karena itu, pada bagian ini akan dijelaskan sifat-sifat operasi yang belum dijelaskan pada Bagian A dan Bagian B. Contoh 3.2 Perhatikan masalah dalam contoh berikut 4 ⊗ −7 ⊕ 5 ⊗ 2. Sebelum menyelesaikannya, masalah pada Contoh 3.2 di atas harus dipahami sebagai (4 ⊗ −7) ⊕ (5 ⊗ 2).Oleh karena itu, solusi yang tepat untuk masalah ini adalah (4 ⊗ −7) ⊕ (5 ⊗ 2) = max(4 + (−7), 5 + 2) = 7. Dalam Contoh 3.2 diperlihatkan bahwa terdapat analogi antara sifat operasi ⊕ dan operasi ⊗ dalam ℝ𝑚𝑎𝑥 dengan sifat operasi + dan operasi − dalam aljabar biasa, yaitu dalam hal urutan pengoperasiaan, jika tidak ada tanda kurung operasi ⊗ mempunyai prioritas (atau lebih kuat) daripada operasi ⊕ (Heidergott dkk, 2006). Pangkat 𝑛 ∈ ℕ ∪ {0} dengan ℕ adalah himpunan semua bilangan asli, dari elemen 𝑎 ∈ ℝ𝑚𝑎𝑥 dinotasikan dengan 𝑎⊗𝑛 . Notasi 𝑎 ⊗𝑛 didefinisikan sebagai berikut: 𝑎⊗0 ; = 0 dan 𝑎⊗𝑛 ≔ 𝑎 ⊗ 𝑎𝑛−1 , untuk 𝑛 = 1, 2, … Didefinisikan juga 𝜀 ⊗0 ≔ 0 dan 𝜀 ⊗𝑛 : = 𝜀, untuk 𝑛 = 1, 2, … Diperhatikan. bahwa. a  n  aa  a a  a ... a  na,  ...   a  a n. n. dengan 𝑛𝑎 adalah operasi perkalian pada bilangan real. Sifat pangkat dalam ℝ𝑚𝑎𝑥 mempunyai prioritas tertinggi dibandingkan dengan operasi ⊕ dan ⊗.. 38.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Berdasarkan operasi pangkat ℝ𝑚𝑎𝑥 dan sifat operasi akar pada aljabar 𝑏. biasa, maka dapat dijelaskan cara menghitung operasi √𝑎 di ℝ𝑚𝑎𝑥 . Dalam 𝑏. ℝ𝑚𝑎𝑥 operasi √𝑎 didefinisikan dengan menggunakan definisi akar pada aljabar biasa dan kemudian menganalogikan operasi pangkat biasa dengan operasi pangkat dalam ℝ𝑚𝑎𝑥 . Maka dapat dijelaskan 𝑏. √𝑎 = 𝑥 ⟺ 𝑎 = 𝑥 𝑏. Dengan menganalogikan 𝑥 𝑏 ke bentuk pangkat di ℝ𝑚𝑎𝑥 , maka 𝑎. 𝑎 = 𝑥 ⊗𝑏 ⟺ 𝑎 = 𝑏𝑥 ⟺ 𝑥 = 𝑏. Penjelasan lebih lanjut mengenai pangkat dalam ℝ𝑚𝑎𝑥 dapat dilihat dalam teorema berikut. Teorema 3.5 (Farlow, 2009) Untuk setiap 𝑚, 𝑛 ∈ ℕ; dengan ℕ adalah himpunan semua bilangan asli dan untuk setiap 𝑎, 𝑏 ∈ ℝ𝑚𝑎𝑥 , berlaku 1. 𝑎⊗𝑚 ⊗ 𝑎⊗𝑛 = 𝑎⊗(𝑚⊗𝑛) 2. (𝑎⊗𝑚 ). ⊗𝑛. = 𝑎⊗(𝑚. ⊗𝑛 ). 3. 𝑎⊗1 = 𝑎 4. 𝑎⊗𝑚 ⊗ 𝑏 ⊗𝑚 = (𝑎 ⊗ 𝑏)⊗𝑚 Bukti Ambil sebarang 𝑚, 𝑛 ∈ ℕ dan 𝑎, 𝑏 ∈ ℝ𝑚𝑎𝑥 , sedemikian sehingga 1. 𝑎⊗𝑚 ⊗ 𝑎⊗𝑛 = 𝑚𝑎 + 𝑛𝑎 = (𝑚 + 𝑛)𝑎 = 𝑎⊗(𝑚⊗𝑛) 2. (𝑎⊗𝑚 ). ⊗𝑛. = (𝑚𝑎)⊗𝑛 = 𝑛(𝑚𝑎) = (𝑛𝑚)𝑎 = 𝑎 ⊗(𝑚. 3. 𝑎⊗1 = 1𝑎 = 𝑎 39. ⊗𝑛 ).

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. 4. 𝑎⊗𝑚 ⊗ 𝑏 ⊗𝑚 = 𝑚𝑎 + 𝑚𝑏 = 𝑚(𝑎 + 𝑏) = (𝑎 ⊗ 𝑏)⊗𝑚. ∎. Contoh 3.3 Hitunglah operasi ℝ𝑚𝑎𝑥 berikut ini 1.. 5⊗3 = 3 × 5 = 15 1. 1. 2. 8⊗2 = 2 × 8 = 4 3. 2⊗3 ⊗ 2⊗2 = (3 × 2) + (2 × 2) = 6 + 4 = 10 4. (3⊗2 ). ⊗3. = 3 × 2 × 3 = 18. D. Vektor dan Matriks di ℝ𝒎𝒂𝒙 Pada bagian ini akan dijelaskan vektor dan matriks pada ℝ𝑚𝑎𝑥 yang mencakup definisi vektor di ℝ𝑚𝑎𝑥 , definisi matriks di ℝ𝑚𝑎𝑥 dan operasi matriks di ℝ𝑚𝑎𝑥 serta sifat-sifatnya. Penjelasan pada bagian ini dirangkum dari Farlow (2009), Bacelli (2001), Heidergott, dkk (2006), Rudhito. (2003), Andersen. (2002). 1. Vektor di ℝ𝒎𝒂𝒙 Berikut ini akan didefinisikan ℝ𝑛𝑚𝑎𝑥 berdasarkan ℝ𝑚𝑎𝑥 sebagai ℝ𝑛𝜀 = ℝ𝜀 × … × ℝ𝜀 = {𝒂 = (𝑎1 , … , 𝑎𝑛 )|𝑎𝑖 ∈ ℝ𝜀 , 𝑖 = 1, … , 𝑛} dan pada ℝ𝑛𝜀 didefinisikan: a. Operasi ⊕: 𝒂 ⊕ 𝒃 = (𝑎1 , 𝑎2 , … , 𝑎𝑛 ) ⊕ (𝑏1 , 𝑏2 , … , 𝑏𝑛 ) = (𝑎1 ⊕ 𝑏1 , 𝑎2 ⊕ 𝑏2 , … , 𝑎𝑛 ⊕ 𝑏𝑛 ) b. Operasi ⊗ dengan skalar 𝛼 di ℝ𝜀 𝛼 ⊗ 𝒂 = 𝛼 ⊗ (𝑎1 , 𝑎2 , … , 𝑎𝑛 ) = (𝛼 ⊗ 𝑎1 , 𝛼 ⊗ 𝑎2 , … , 𝛼 ⊗ 𝑎𝑛 ) 𝒂 ∈ ℝ𝑛𝑚𝑎𝑥 disebut vektor pada ℝ𝑚𝑎𝑥 . 40.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Definisi 3.6 Dua vektor 𝒂 dan 𝒃 di ℝ𝑛𝑚𝑎𝑥 dikatakan sama jika elemen-elemen yang bersesuaian sama. Selanjutnya vektor 𝒂 di ℝ𝑛𝑚𝑎𝑥 ditulis sebagai vektor kolom, yaitu suatu vektor yang dihasilkan dengan mentranspose vektor 𝒂. 2. Matriks di ℝ𝒎𝒂𝒙 Dalam aljabar linear, untuk ℝ adalah himpunan semua bilangan real, dapat dibentuk suatu matriks 𝐴 berukuran 𝑚 × 𝑛 yang entri-entrinya adalah elemen-elemen di ℝ. Demikian juga dalam ℝ𝑚𝑎𝑥 dapat dibentuk suatu matriks 𝐴 berukuran 𝑚 × 𝑛 dengan entri-entrinya adalah elemen di ℝ𝑚𝑎𝑥 . Selanjutnya matriks yang dijelaskan adalah matriks di ℝ𝑚𝑎𝑥 . Himpunan matriks 𝑚 × 𝑛 untuk 𝑚, 𝑛 ∈ ℕ dengan ℕ adalah himpunan semua bilangan asli dinotasikan dengan ℝ𝑚×𝑛 𝑚𝑎𝑥 . Sedangkan untuk 𝑚 = 𝑛 matriks. A di atas didefinisikan sebagai matriks persegi. Himpunan matriks 𝑛 × 𝑛 untuk n  ℕ dengan ℕ adalah himpunan semua bilangan asli dinotasikan dengan ℝ𝑛×𝑛 𝑚𝑎𝑥 .. Selanjutnya akan dijelaskan tentang operasi matriks. Pada Bagian A dan Bagian B telah dijelaskan tentang operasi ⊕ dan ⊗ pada ℝ𝑚𝑎𝑥 . Kedua operasi tersebut dapat diperluas untuk operasi matriks. Seperti pada matriks real, operasi matriks atas ℝ𝑚𝑎𝑥 juga memiliki tiga operasi dasar. Dalam definisi berikut dijelaskan tiga operasi matriks di ℝ𝑚𝑎𝑥 . Definisi 3.7 Diberikan ℝ𝑚×𝑛 𝑚𝑎𝑥 ≔ {𝐴 = [𝑎𝑖𝑗 ]|𝑎𝑖𝑗 ∈ ℝ𝑚𝑎𝑥 }, untuk 𝑖 = 1, … , 𝑚 dan untuk 𝑗 = 1, … , 𝑛. Diketahui 𝛼 ∈ ℝ dan 𝐴, 𝐵 ∈ ℝ𝑚×𝑛 𝑚𝑎𝑥 .. 41.

PLAGIAT PLAGIATMERUPAKAN MERUPAKANTINDAKAN TINDAKANTIDAK TIDAKTERPUJI TERPUJI. Secara berturut-turut didefinisikan 𝛼 ⊗ 𝐴 dan 𝐴 ⊕ 𝐵 adalah matriks yang unsur ke-𝑖𝑗-nya adalah (𝛼 ⊗ 𝐴)𝑖𝑗 = 𝛼 ⊗ 𝑎𝑖𝑗 dan (𝐴 ⊕ 𝐵)𝑖𝑗 = 𝑎𝑖𝑗 ⊕ 𝑏𝑖𝑗 untuk 𝑖 = 1, … , 𝑚 dan untuk 𝑗 = 1, … , 𝑛. 𝑝×𝑛 Diketahui matriks 𝐴 ∈ ℝ𝑚×𝑝 𝑚𝑎𝑥 dan 𝐵 ∈ ℝ𝑚𝑎𝑥 .. Didefinisikan 𝐴 ⊗ 𝐵 adalah matriks yang unsur ke-𝑖𝑗-nya adalah (𝐴 ⊗ 𝐵 )𝑖𝑗 = ⊕𝑝𝑘=1 𝑎𝑖𝑘 ⊗ 𝑏𝑘𝑗 untuk 𝑖 = 1, … , 𝑚 dan untuk 𝑗 = 1, … , 𝑛. Setelah definisi operasi matriks di atas, selanjutnya diberikan contoh cara mengoperasikan matriks. Contoh 3.4. Perhatikan operasi matriks berikut 4⊗1 4⊗𝜀 4+1 4+𝜀 1 𝜀 5 𝜀 4 ⊗ [ 2 −2] = [ 4 ⊗ 2 4 ⊗ −2] = [ 4 + 2 4 + −2] = [ 6 2] 4 ⊗ 0.5 4 ⊗ 3 4 + 0.5 4 + 3 0.5 3 4.5 7 2 0 [4 1 6 𝜀. 2⊕6 6 3 𝜀 5 3] ⊕ [2 0 7] = [4 ⊕ 2 6⊕4 4 7 5 8. 0⊕3 5⊕𝜀 1 ⊕ 0 3 ⊕ 7] 𝜀⊕7 8⊕5. max(2,6) max(0,3) max(5, 𝜀) =[max(4,2) max(1,0) max(3,7) ] max(6,4) max(𝜀, 7) max(8,5) 6 3 = [4 1 6 7 [. 5 7] 8. 2 3 2⊗2⊕3⊗1⊕2⊗1 2 3 2 ] ⊗ [1 1 ] = [ 1⊗2⊕0⊗1⊕4⊗1 1 0 4 1 2 =[. 4⊕4⊕3 5⊕4⊕4 ] 3⊕1⊕5 4⊕1⊕6. 42. 2⊗3⊕3⊗1⊕2⊗2 ] 1⊗3⊕0⊗1⊕4⊗2.