FORMULASI ENUMERASI PADA MODEL JARINGAN
INTERKONEKSI LUCAS-HYPERCUBE
Ernastuti
Pusat Studi Komputasi Matematika Universitas Gunadarma Jl. Margonda Raya 100 Depok
E-mail: [email protected]
Abstrak: Lukas-Hypercube (LH) adalah model topologi jaringan interkoneksibaruyang dapat direpresentasikan sebagai graf, di mana himpunan simpulnya dibangun secara rekursif seperti model jaringan Hypercube dengan dua subgraf di dalamnya masing-masing isomorfis ke model jaringan Lucas cube, dan himpunan busurnya dibangun dengan metode jarak Hamming. Penelitian ini bertujuan ingin membuktikan
LH adalah termasuk dalam model jaringan keluarga Fibonacci Cube, yaitu dengan cara memperlihatkan parameter enumerasi jumlah simpul dan busur dalam LH dapat dinyatakan sebagai fungsi satuan bilangan Fibonacci. Metode penelitian dilakukan dengan memperlihatkan enumerasi jumlah simpul dan busur dalam LH. Dalam penelitian, keterhubungan antara simpul-simpul, pembangunan formulasi enumerasi jumlah simpul dan busurdianalisis melalui lemma-lemma dan teorema yang keseluruhannya dilakukan dengan pendekatan teori graf kombinatorik himpunan string biner. Hasil analisis menunjukkan bahwa formulasi enumerasi dari jumlah simpul dan jumlah busur pada
LH masing-masing dapat dinyatakan dengan fungsi satuan bilangan Fibonacci.
Kata kunci: bilangan fibonacci, hypercube, lucas cube, jarak hamming, string biner, subgraf bentukan hypercube.
Abstract: Lucas-Hypercube (LH) is a new model of interconnection network topology that can be represented as a graph, where the set of vertices is constructed recursively as Hypercube network model with two sub graphs in which each of them is isomorphic to the Lucas cube, and the set of edges is built with the Hamming distance method. The research in this paper aims to prove that LH is classified in the network model of Fibonacci Cube family, by showing the parameter enumeration of the number of vertices and edges in the LH can be expressed as a unit function of the Fibonacci numbers. In this research, the relationship between the vertices, building formulations of enumerating the number of vertices and edges are analyzed through the lemmas and theorems that the whole approaches are performed with the combinatorial graph theory of binary strings. The analysis showed that the formulation of enumerating the number of vertices and edges can be expressed by the unit function of Fibonacci numbers respectively.
Key words: fibonacci number, hypercube, lucas cube, hamming distance, bynary string, induced subgraph of hypercube.
PENDAHULUAN
Latar belakang penelitian ini adalah adanya salah satu masalah mendasar dalam sistem multiprosesor yaitu pada pendisainan topologi (model) jaringan interkoneksi. Jaringan interkoneksi ini disediakan bagi prosesor-prosesor untuk saling dapat mengirim pesan (message) antara satu prosesor dengan prosesor lainnya di dalam jaringan. Pesan-pesan ini dapat berupa data-data yang diperlukan prosesor lain untuk melakukan suatu komputasi. Setiap prosesor idealnya dapat mengirim pesan secara langsung tanpa melewati prosesor lainnya.
Studi pendisainan topologi jaringan interkoneksi komputer mendapat perhatian yang cukup meningkat pada beberapa dekade terakhir ini (Baskoro,2007). Dalam studi tersebut, graf (graph) atau digraf (directedgraph)
umumnya digunakan sebagai model dari jaringan interkoneksi, bergantung pada apakah arah (direction) memegang peranan penting atau tidak dalam jaringan. Simpul (vertex) pada graf atau digraf menyatakan elemen prosesor dan busur (edge) atau sisi berarah menyatakan saluran komunikasi dalam jaringan. Model jaringan (struktur graf) yang dipilih akan menjadi faktor yang menentukan kemampuan kinerja sistem jaringan komputer dalam melakukan sebuah pekerjaan komputasi. Idealnya, model jaringan yang dipilih sedapat mungkin adalah model jaringan yang terbaik. Namun, membandingkan satu jaringan interkoneksi dengan jaringan interkoneksi lain secara abstrak merupakan pekerjaan yang terkenal sulit (Parhami,2001:12(1)74-80) dan (Wilkinson,2008). Sementara itu Liszka (1997) mengatakan bahwa:
"Scientically determining the best network is as difficult as saying with certainty that one animal is better than another". Membandingkan kelebihan dan/atau kekurangan di antara model-model jaringan interkoneksi sangatlah relatif, tergantung pada teknologi implementasi perangkat keras, skema perjalanan data, beban-kerja komputasi, distribusi data/tugas, dan parameter-parameter arsitektur, sistem atau aplikasi lainnya. Para peneliti sampai saat ini termotivasi untuk mengusulkan model-model jaringan baru atau perbaikan model jaringan lama dengan memperlihatkan kelebihan-kelebihan, dan juga menawarkan evaluasi kinerja dalam konteks yang berbeda-beda.
Para peneliti membandingkan model-model jaringan tersebut melalui suatu analisis dari berbagai parameter, di antaranya, untuk sifat struktural: derajat (degree), diameter, radius dan center; untuk sifat enumerasi: jumlah simpul, busur dan siklus persegi (square); untuk sifat konektifiti: konektifitas simpul dan busur; untuk sifat hamiltonisiti: jalur dan siklus Hamiltonian; untuk sifat penanaman (embedding): diantaranya penanaman linear array, ring, 2D mesh, tree, hypercube; scalability; modularity; regularity; potential bottleneck; fault tolerance; dan recursive decompotion.
Model-model jaringan interkoneksi multiprosesor yang populer saat ini antara lain adalah linear array, ring, hypercube, tree, mesh dan star. Model-model ini dapat dilihat pada Gambar 1. Model-model ini adalah model jaringan yang umum digunakan di bidang komputasi paralel, namun saat ini model jaringan hypercube paling banyak menarik perhatian dan diteliti seraca intensif. Jumlah simpul hypercube berdimensi n adalah 2n dan jumlah busurnya n*2n-1.
Hypercube mempunyai sifat-sifat istimewa, yaitu simpul dan busurnya simetri (derajat setiap simpulnya sama), mempunyai struktur rekursif yang sederhana (hypercube berisi dua subgraf yang juga hypercube), mempunyai jalur dan siklus Hamiltonian dan kepadanya dapat ditanam model jaringan lain seperti linear array, ring, mesh dan tree secara efisien. Di samping keistimewaannya hypercube ternyata mempunyai kelemahan pada ukuran jumlah prosesor. Ketika dimensi hypercube diperbesar, jumlah prosesornya meningkat secara eksponensial. Hal ini dikarenakan jumlah prosesor dalam hypercube berdimensi-n adalah 2n. Kenyataan ini sangat membatasi alternatif pilihan jumlah simpul dalam graf atau ukuran sistem yang akan dibangun.
Sebagai contoh, untuk mengaktifkan sistem jaringan interkoneksi dengan 21 prosesor, maka harus menggunakan hypercube 32 prosesor. Hal ini berarti terdapat 11 prosesor aktif tapi tidak dioperasikan. Untuk mengatasi persoalan ini para peneliti termotivasi untuk mendisain model-model jaringan baru yang ukurannya (jumlah simpulnya) lebih kecil dari 2ntetapi masih tetap memiliki sifat-sifat istimewa hypercube. Berarti model-model jaringan ini haruslah model jaringan incomplete-hypercube atau disebut subgraf bentukan (induced) hypercube yang setiap simpulnya terhubung.
Model-model jaringan subgraf bentukan hypercube yang memiliki hampir semua sifat istimewa hypercube telah diperkenalkan oleh para peneliti dalam dua dekade ini, yaitu: Fibonacci cube (FC) diperkenalkan oleh Hsu pada tahun 1993 (Hsu,1993;4 (1):3-12), extended Fibonacci cube (EFC) diperkenalkan oleh Wu pada tahun 1997 (Wu, 1997; 8 (12):1203-1210)) dan Lucas cube (LC) diperkenalkan oleh Munarini pada tahun 2002 (Munarini, 2002:4 (39:12-21), dan Extended Lucas Cube (ELC) oleh Ernastuti tahun 2008:25_36). FC, EFC, LC dan ELC masing-masing adalah model jaringan incomplete hypercube yang merupakan subgraf bentukan dari hypercube. Semuanya adalah graf terhubung. Jumlah simpul FC, EFC, LC dan ELC jauh lebih sedikit dari hypercube (sekitar 1/5 jumlah simpul hypercube). Untuk sejumlah N simpul, jumlah busur FC, EFC, LC, dan ELC
parameter formulasi jumlah node, jumlah edge dan jumlah square, di mana masing-masing formulasi dianalisa dengan membangun teorema dan lemma-lemma. Keseluruhan analisa dilakukan melalui pendekatan teori graf kombinatorik himpunan string biner.
Topologi dan Graf Kombinatorik
Sebuah string biner panjang n adalah barisan a1, a2, …, an dengan ai {0,1}. Sebuah string Fibonacci panjang n adalah string biner a1, a2, …, an yang tidak mengandung dua bit ‘1’ berurutan. Berikut adalah semua string Fibonacci dengan panjang 3: {000, 001, 010, 100 ,101}. Jarak Hamming diantara dua string biner A dan B yang masing-masing panjangnya n adalah jumlah dari posisi bit berbeda diantara keduannya; notasi jarak Hamming antara A dan B adalah H(A,B). Contoh: H(001,100) = 2. Sebuah graf G=(V,E) terdiri dari himpunan simpul V dan himpunan busur E; sebuah busur adalah suatu pasngan tidak terurut (x,y), di mana xy VG. Untuk menghindari pengertian yang ambigu, V dan E dalam garaf G masing-masing dinotasikan VG dan EG. Sebuah jalur (path) pada suatu graf G=(VG,EG) adalah barisan (x1, x2, …, xn), xi VG sedemikian sehingga (x1, x2,), (x2, x3), …, (xn-1, xn) adalah busur-busur dalam EG dimana xi masing-masing berbeda. Jumlah busur dalam dalam suatu jalur disebut panjang (length) jalur. Graf G dikatakan terhubung jika terdapat paling sedikit ada satu jalur diantara setiap pasang simpul dalam G. Graf K(VK,EK ) adalah subgraf bentukan (induced subgraph) dari graf G(VG,EG) jika memenuhi aturan berikut: VK VG , dan untuk setiap busur (s,t) EG , di mana s,t VK , busur (s,t) juga EK. Bilangan Fibonacci didefinisikan dengan f1 = f2 = 1, dan untuk n •'3d3, fn = fn-1+ fn-2.
Tabel 1. Bilangan Finonacci ke 1 sampai ke 9 sekitar kurang 1/5 dari jumlah busur hypercube. Walaupun
ketiga model jaringan ini tidak simetris dan hubungan konektiftas sangat rendah (sparse), semuanya mempunyai keistimewaan; yaitu mempunyai struktur rekursif yang menarik.
Penelitian-penelitian (Baril,2005: 348:189-199), (Klavzar, 2005299):145-153), (Wu,1997), (Hsu, 1993), (Munarini, 2002), (Ernastuti, 2008) dalam mendisain topologi jaringan interkoneksi FC, EFC, LC dan ELC, semuanya menggunakan graf kombinatorik sebagai modelnya, yaitu graf yang simpulnya adalah objek kombinatorik himpunan string biner dan busurnya menghubungkan dua string biner bila mempunyai jarak Hamming satu. Menurut Klavzar (2005), karena parameter enumerasi dapat dinyatakan dalam satuan bilangan Fibonacci, maka graf-graf FC, EFC, LC dan ELC dapat dikelompokkan sebagai satu keluarga graf kubus Fibonacci (Fibonacci cube). Struktur graf FC dibangun dari suatu formulasi dekomposisi rekursif yang inisialnya berdasarkan himpunan simpul FC sendiri. Struktur graf EFC dibangun dari formulasi dekomposisi rekursif yang mirip dengan FC tetapi inisialnya berdasarkan himpunan simpul EFC sendiri. Sedangkan struktur LC dibangun dari formulasi dekomposisi rekursif yang berbeda dengan FC tetapi inisialnya menggunakan himpunan simpul FC. Sedangkan ELC formulasi dekomposisi rekursif mirip dengan LC dengan inisial berdasarkan himpunan simpul EFC.
Terlihat formulasi-formulasi dekomposisi rekursif tersebut dapat dikembangkan dengan berbagai cara kombinasi antara rekursif dan inisialnya. Berdasarkan peluang pengembangannya, maka peneliti tertarik mendisain suatu topologi jaringan interkoneksi baru yaitu dengan membangun formulasi dekomposisi rekursif yang sama dengan hypercube dan mengambil inisialnya adalah himpunan simpul LC. Model topologi baru ini dinamakan Lucas-hypercube (LH). Untuk membuktikan bahwa disain topologi jaringan interkoneksi baru LH juga termasuk keluarga graf Fibonacci cube, maka pada makalah ini khusus membahas penjabaran memperoleh formulasi enumerasi Lucas-Hypercube khususnya
n Bilangan Fibonacci fn 1 2 3 4 5 6 7 8 9 1 1 2 3 5 8 13 21 34
Pada penelitian ini, graf hypercube dimensi-n yang dinotasikan dengan Q(n), didefinisikan secara rekursif sebagai berikut:
Definisi 1: Untuk n •'3d 0, Hypercube Q(k) = (VQ(n);EQ(n)),
n VQ (n), himpunan simpul-simpul berlabel string biner dalam Q (n) didefinisikan secara rekursif sebagai
VQ (n) =
0.VQ (n - 1) U1. VQ (n - 1) if n > 2
_
{
nDua simpul x,y V Q(n) dihubungkan oleh suatu busur dalam
E Q(n) jika dan hanya didefinisikan secara rekursif H (x,Y) = 1
{1} if n = 1 (2.1)
φ
if n = 0Gambar 2. Contoh graf-graf hypercube Q(n), masing masing untuk n = 1, 2, 3,4.
Definisi 2: (Hsu, 1993) Untuk n •'3d 0, Fibonacci cube FC(k) = (VFC(n);EFC(n)),
n VFC (n), himpunan simpul-simpul berlabel string biner dalam FC (n) didefinisikan secara rekursif sebagai
VFC (n) =
0.VFC (n - 1) U1. VFC (n - 2) if n > 3
{
nDua simpul x,y V FC(n) dihubungkan oleh suatu busur dalam
E FC(n) jika Hamming H (x,y) = 1
{0,1} if n = 3, (2.2)
φ
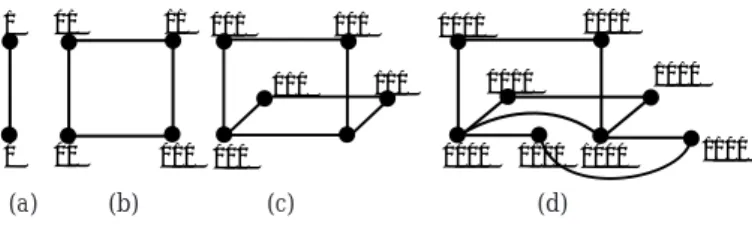
if n = 0 {λ} if n = 1,2Gambar 3. contoh graf-graf Fibonacci cube FC(n), masing masing untuk n = 3, 4, 5, 6.
(a) (b) (c) (d)
Keterangan: Fibonacci cube (a) FC(3), (b) FC(4), (c) FC(5) and (d)
FC(6) 1 0 01 00 001 000 101 100 010 0001 0000 0101 0100 1000 1010 1001 1 0 10 00 100 000 010 010 001 111 110 011 100 000 0010 010 001 0111 0110 011 1000 1010 1101 001 111 110 1011 1100
simpulnya didefinisikan secara rekursif seperti model jaringan Hypercube dengan basis pembangunannya terdiri atas dua subgraf yang isomorfis ke model jaringan LC. Model jaringan baru ini dinamakan dengan Lucas Hypercube (LH).
Usulan definisi model topologi jaringan LH, sebagai berikut: Untuk n •'3d 0, Lucas hypercube LH(k) = (VLH(n);ELH(n)), didefinisikan sebagai
• VLH (n), himpunan simpul-simpul berlabel string biner
dalam LH(n), didefinisikan secara rekursif sebagai: VLH(n) = 0 · VLC(n •'2d 1) •'3f 1 · VLC(n•'2d1), n>3, di mana VLH(0)= { }; VLH(1)= VLH(2)={ };VLH(3)={0,1}. • Dua simpul x, y •'3f VLH(n) dihubungkan oleh suatu busur dalam LH(n) jika dan hanya jika jarak Hamming H(x,y) = 1.
Gambar 5. model jaringan Lucas-Hypercube pada n = 3, 4, 5, 6.
Desain atau model jaringan baru yang dibangun pada penelitian ini didefinisikan dengan cara membentuk suatu formulasi rekursif yang mirip dengan formulasi rekursif model jaringan Hypercube, di mana himpunan simpul LC sebagai kondisi inisialnya. Dengan kata lain formulasi
1 0 01 00 010 1001 0000 1000 1010 0001 001 010 11 000 101 110 0010 0100 1100 (a) (b) (c) (d)
Keterangan: Lucas Hypercube (a) LH(3), (b) LH(4), (c) LH(5)
and (d) LH(6)
Metode atau langkah-langkah penelitian untuk mengetahui kinerja model jaringan baru LH dilakukan serangkaian kegiatan analisis sebagai berikut: Langkah pertama dalam rangkaian kegiatan penelitian ini adalah membuktikan bahwa model jaringan LH adalah graf terhubung, yaitu harus dibuktikan terlebih dahulu bahwa terdapat paling sedikit satu jalur diantara setiap pasang simpul di dalam LH Membuktikan LH adalah graf terhubung merupakan hal yang sangat penting. Karena bila LH terbukti bukan graf terhubung maka parameter jumlah busur, diameter, radius, center dan Hamiltoniciti tidak dapat diturunkan.
Langkah kedua; menentukan formulasi enumerasi pada model jaringan LH yang akan dinyatakan dengan satuan bilangan Fibonacci. Bila LH adalah subgraf bentukan hypercube dan formulasi enumerasi terbukti dapat dinyatakan dengan satuan dari bilangan Fibonacci, maka
LH dikatakan termasuk sebagai anggota dari kelompok keluarga Fibonacci cube. Pada langkah kedua ini akan dibuktikan bahwa LH adalah decomposable dan terdapat busur-busur yang menghubungkan antara dua subgraf kiri dan kanan dalam LH. Pembuktian ini diperlukan untuk memperoleh parameter formulasi enumerasi: jumlah simpul, dan jumlah busur pada LH. Formulasi enumerasi sangat penting untuk menetapkan perluasan (extendable) ukuran model jaringan.
PEMBAHASAN Karakteristik Jaringan
Perbandingan karakteristik model-model jaringan interkoneksi Hypercube, FC, EFC, dan LC untuk parameter-parameter dekomposisi rekursif, Hamiltonisiti, enumerasi jumlah simpul, busur dan siklus persegi, network cost, dan penanaman suatu linear array, ring dan 2D mesh yang mengacu pada paper-paper (Hsu, 1993), (Wu,1997), (Munarini dkk, 2001), (Klavzar, 2005), (Baril dkk, 2005), dan (Ernastuti, 2008) seperti berikut: Perbandingan Formula Dekomposisi Rekursif Perbandingan definisi formula dekomposisi rekursif dari hypercube, FC, EFC, LC dan ELC diperlihatkan pada Tabel 2 berikut:
Tabel 2. Perbandingan definisi formula dekomposisi rekursif dari hypercube, FC, EFC, LC
n 3 4 5 n> 6 VQ(n-2) {0,1} {00,01,10,11}{000,001,011,100,101,111,110} 0.VQ(n-1) u1.VQ(n-1)
VFC(n) {0,1} {00,01,10} {000,001,010,100,101} 0.VFC(n-1) u10.VFC(n-2) VEFC(n) {0,1} {00,01,10,11} {000,001,010,011,100,101} 0.VEFC(n-1) u10.VEFC(n-2) VLC(n) {0,1} {00,01,10} {000,001,010,100,} 0.VFC(n-1) u10.VFC(n-3).0
Dari Tabel 2 terlihat bahwa VFC(n) {0; 1}n-2, VEFC(n) {0; 1}n-2, dan VLC(n) {0; 1}n-2, untuk setiap
n> 3. Ini berarti FC(n), EFC(n) dan LC(n) masing-masing
adalah subgraf dari hypercube Q (n-2).n > 3. Dari aturan jarak Hamming untuk busur terlihat bahwa ketiga graf tersebut adalah subgraf-subgraf bentukan dari hypercube. Sebuah FC(n) mengandung dua sugraf saling lepas yang isomorfis ke FC (n-1) dan FC(n-2), sebuah EFC(n) mengandung dua sugraf saling lepas yang isomorfis ke EFC(n-1) dan EFC(n-2). Sebuah LC(n) mengandung dua sugraf saling lepas yang isomorfis ke FC(n-1) dan FC
(n-3). Formulasi untuk ELC(n): VELC(3) = {0,1}; VELC(4) = {00,01,11,01}; VELC (n) = 0. VEFC(n-1) U 10.
VEFC (n-3).0.
Perbandingan Formulasi Enumerasi
Formulasi-formulasi jumlah simpul, busur dan siklus persegi dari FC, EFC dan LC yang dinyatakan berdasarkan bilangan Fibonacci. Notasi |A| menyatakan jumlah elemen dalam himpunan A, seperti terlihat sebagai berikut: Proposisi 1. (Hsu, 1993) Formulasi jumlah simpul pada FC untuk n • |VFC(n) | = fn.
Proposisi 2. (Klavzar, 2005) Formulasi jumlah busur pada FC untuk n • 3, |EFC(n)| = (n 2fn-1 +2(n fn-2 )/5
Proposisi 3. (Klavzar, 2005) Formulasi jumlah siklus persegi pada FC untuk n • 3
| S (FC (n)) | = - 3(n-2) fn-1+ ((n-2)2 + 3(n-2)) fn-2 25 10 50
Proposisi 4. (Klavzar, 2005) Formulasi jumlah simpul, busur dan siklus persegi pada EFC untuk n • 3 |VEFC(n) | = | VFC(n-1) | × |V (Q(1)| = 2fn-1 | EEFC(n) | = | VFC(n-1) |×|V (Q(1)|+|EEFC(n-1)|×|V (Q(1)| = f n-1+2|EFC(n-1) |; | S( E F C ( n ) )| = | VF C (n1 )| × | S(Q( 1 )|+| EE F C ( n - 1 ) |×|E(Q(1)|+|S(EFC(n 1))|× |V (Q(1)| = |EFC(n-1) | + 2|S(FC(n1)|.
Proposisi 5. (Klavzar,2005) Formulasi jumlah simpul pada LC untuk n = 3, 4, 5, 6.
|VLC(3) | = 2, |VLC(4) | = 3, |VLC(5) | = 4 dan |VLC(6) | = 7. Untuk n • 7, |VLC(n)| = fn fn-4.
Proposisi 6. (Klavzar, 2005) Formulasi jumlah busur pada LC untuk n = 3, 4, 5, 6
|ELC(3))| = 1, |ELC(4) | = 4, dan |ELC(5)| = 3. Untuk n • LC(n)| = |EFC(n-1)| + |EFC(n-3))| + |VFC(n-3) |.
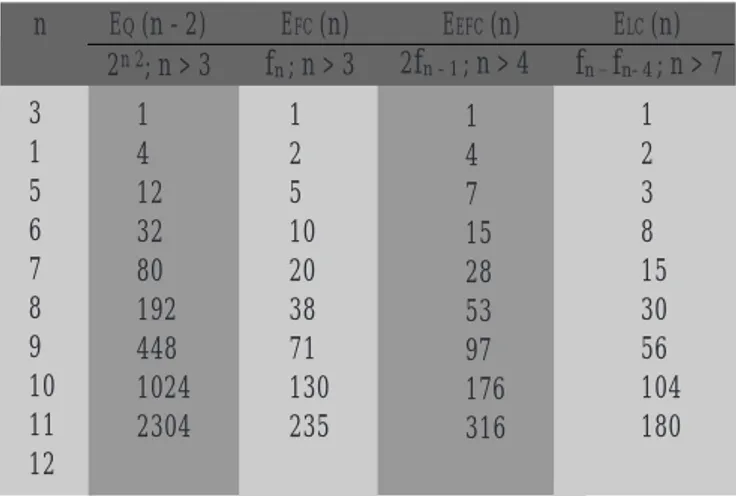
Tabel 3. Tabel jumlah busur-busur hypercube, FC(n), EFC(n), dan LC(n). 3 4 5 6 7 1 4 12 32 80 1 2 5 10 20 1 4 7 15 28 1 2 3 8 15 n EQ (n - 2) EFC (n) EEFC (n) ELC (n) 8 9 10 11 192 448 1024 2304 38 71 130 235 53 97 176 316 30 56 104 180
Tabel 4. Tabel jumlah simpul-simpul hypercube, FC, EFC, dan LC 3 1 5 6 7 8 9 10 11 12 1 4 12 32 80 192 448 1024 2304 1 2 5 10 20 38 71 130 235 1 4 7 15 28 53 97 176 316 1 2 3 8 15 30 56 104 180 n EQ (n - 2) EFC (n) EEFC (n) ELC (n) 2n 2; n > 3 fn; n > 3 2fn - 1; n > 4 fn _ fn- 4; n > 7
Hasil dan Pembahasan
Untuk membuktikan bahwa LH adalah graf terhubung, digunakan metode kontradiksi yaitu: suatu graf G(VG,EG) adalah graf tidak tehubung jika himpunan simpul VG dapat dipartisi menjadi dua himpunan bagian tidak kosong V1 dan V2 yang saling lepas sedemikian sehingga tidak terdapat busur dalam G yang menghubungkan sebuah simpul dalam V1 dengan sebuah simpul dalamV2. Setelah itu, dibuktikan terdapat busur diantara V1 danV2, sehingga teorema tersebut gugur.
Lemma 1. Untuk n > 3, LH(n) berisi dua subgraf saling lepas yang masing-masing isomorfis ke LC(n _ 1). Bukti. Pada Defnisi 2.3 diperlihatkan bahwa, untuk n > 3 , VLC(n) berisi simpul-simpul berlabel string biner, dimana interkoneksi LC diatur berdasarkan jarak Hamming pada string-string biner tersebut. Misalkan L(n) adalah sebuah subgraf bentukan dari 0 · VLC(n 1) dan M(n) adalah subgraf bentukan dari 1 · VLC(n _ 1). Jelas kedua L(n) dan M(n) masing-masing adalah subgraf dari LH(n) yang simpul-simpulnya masing-masing berlabel string biner panjang (n _ 2). Berdasarkan proposisi 3.1, yaitu: VLH(n) = 0 · VLC(n _ 1) · VLC(n_1) , di mana VLC(n _ 1) adalah himpunan simpul-simpul dalam LC(n _ 1), maka jelaslah setiap simpul di dalam VLC(n _ 1) mempunyai label
string biner panjang (n_2). Dengan kata lain, (s,t) LC (n_1) jika dan hanya jika (s,t) (n_1), karena s dan t masing-masing mempunyai bit awal (prefix) "0" yang sama dalam urutan order-(n_2) yang tidak mempengaruhi nilai jarak Hammingnya. Dengan demikian, L(n) adalah isomorfis ke LC(n_1). Begitu juga dengan cara yang sama, M(n) adalah isomorfis ke LC(n_1); Karena setiap i VLC(n_1) dan j 1 · VLC(n_1) mengakibatkan i < j dipandang dari bilangan bulat dalam basis biner, maka L(n) M(n) U φ 1001 0000 1000 1010 0001 0010 0100 1100 L(6) M(6)
Gambar 6. Contoh Subgraf L(6) dan M(6) yang masing-masing isomorfis ke LC(5)
Sudah dibuktikan LH(n) mengandung dua subgraf saling lepas yang masing-masing isomorfis ke LC(n_1). Sekarang hanya perlu membuktikan bahwa terdapat busur yang menghubungkan kedua subgraf tersebut. Menurut proposisi 2.5, jumlah simpul di dalam LC(n) adalah
fn _ fn - 4, dimana fn adalah bilangan Fibonacci.
Teorema yang menunjukkan jumlah busur dalam LH (dalam satuan bilangan Fibonacci) yang menghubungkan subgraf L ke subgraf M; sekaligus juga membuktikan bahwa LH adalah graf terhubung sebagai berikut: Teorema 1. Untuk sebarang n • 5, di dalam LH(n), terdapat fn-1_ fn-5 busur yang menghubungkan subgraf bentukan dari 0 · VLC(n_1) ke subgraf bentukan dari 1· VLC(n_1). Bukti. Berdasarkan proposisi 3.1, untuk n • 5, VLH (n_1)= 0· VLH(n _ 1)UVLH(n_1). Setiap simpul pada L yaitu subgraf bentukan {0 · VLC(n_1)} dihubungkan dengan sebuah busur ke M yaitu subgraf bentukan {1·VLC(n_ 1)}. Hal ini disebabkan karena masing-masing x L mempunyai bit awal (prefx) "0" dan y M mempunyai bit awal (prefx) "1". Sedangkan subgraf bentukan dari L adalah isomorfis ke subgraf bentukan dari LC(n _1), sehingga jumlah simpul dalam L adalah
U
U
|L| =|VLC(n_1)|. Maka jelaslah terdapat fn-1 _ fn-5busur yang menghubungkan subgraf bentukan dari 0·VLC(n_1) kesubgraf bentukan 1·VLC(n_1).
LH sudah dibuktikan terdiri dari 2 himpunan yang saling lepas, dengan cara membuktikan lebih dulu bahwa LH berisi dua sugbraf yang masing-masing isomorfis ke LC. Karena LH(n) terdiri dari 2 LC(n-1) yang terhubung, dan terdapat fn-1 _ fn-5busur yang menghubungkan subgraf bentukan dari 0·VLC(n_1) kesubgraf bentukan 1·VLC (n_1), serta LC(n_1) adalah subgraf bentukan dari hypercube, maka LH juga subgraf bentukan dari hypercube.
Hasil pembangunan formulasi jumlah simpul berdasarkan himpunan simpul dari dua subgraf L(n) dan M(n) yang saling lepas di dalam LH(n) sebagai berikut: Akibat 1 Untuk n • 3, |VLH(n)| = 2 * |VLC(n _1)| = 2 * (f n-1 _ fn-5).
Bukti. Berdasarkan proposisi 3.1: untuk n • 5, VLH(n) = 0· VLH(n_1) U VLH(n_1), dan berdasarkan lemma 4.1: ELC(n) berisi dua subgraf saling lepas yang masing-masing isomorfis ke LC(n_1). Kemudian {0·VLH(n_1)} 1·VLH(n_1)} = {}, maka jelas, |VLH(n)| = |VLH(n_ 1)| + |VLH(n_1| = 2 * |VLC(n_1)| = 2 * (fn-1_fn-5).
Hasil pembangunan formulasi jumlah busur berdasarkan himpunan busur dari dua subgraf L(n) dan M(n) yang saling lepas di dalam LH(n) dan busur-busur yang menghubungkan kedua subgraf tersebut sebagai berikut:
Akibat 2. Untuk n • 5, |ELH(n)| = |ELC(n _1)| + |ELC(n_ 1| + |VLC(n_1)|.
Bukti. Dari proposisi 3.1: : untuk n • 5, VLH(n) = 0· VLH(n_1) 1· VLH(n_1) , lemma 4.1. dan Teorema 4.2, jelaslah |ELH(n)| = |ELC(n_1)| + |ELC(n_1| + |VLC(n_1)| = 2*((n_2fn-1+2(n_1)fn-2)/5) + (fn-1_fn-5).
PENUTUP Kesimpulan
1. Hasil analisis menunjukkan bahwa formulasi enumerasi model jaringan Lucas-hypercube (LH) terbukti dapat dinyatakan dengan satuan fungsi bilangan Fibonacci, yaitu: (a) Jumlah simpul Lucas-hypercube adalah
2 * (fn-1 _ fn-5), (b) Jumlah ruas Lucas-hypercube adalah 2*((n _ 2fn-1+2(n _ 1)fn-2)/5) + (fn-1 _ fn-5).
2. Formulasi enumerasinya dapat dinyatakan dalam satuan bilangan Fibonacci dan struktur grafnya merupakan subgraf bentukan Hypercube maka model jaringan Lucas Hypercube termasuk dalam kelompok keluarga Fibonacci cube.
Saran
Formulasi jumlah simpul dan jumlah busur ini akan digunakan untuk penelitian selanjutnya yaitu menghitung parameter lainnya di dalam model jaringan Lucas Hypercube (LH) antara lain jumlah siklus square.diameter, center, jalur Hamiltonian, dan penanaman model jaringan linear array dan mesh
Acknowledgment
Penulis mengucapkan terimakasih kepada Direktorat Penelitian Pengabdian Masyarakat (DP2M), Direktorat Jenderal Pendidikan Tinggi (DIKTI) yang telah mendanai penelitian ini melalui program Hibah Fundamental 2012, dan juga kepada Lembaga Penelitian Universitas Gunadarma yang telah memberikan dukungan dan menyediakan fasilitas sarana dan prasarana. DAFTAR PUSTAKA
Baskoro. ET Mengenalkan Indonesia Melalui Teori Graf. thesis, Pidato Ilmiah Guru Besar Institut Teknologi Bandung. 2007. Baril. JL & Vajnovzki, V. Minimal change list for Lucas strings and some graph theoritic consequneces. Elsevier Thoritical Computer Science, 2005
Cong, B & Zheng, SQ and Sharma, S, On simulation of linear arrays, rings and 2-d meshes on Fibonacci cube networks. 1993 Ernastuti & Ravi A Salim.. On Enumerative Properties of Extended Lucas Cube: A New Interconnection Network. International Journal of Computational and Mathematical Sciences, Tokyo, Japan, May 26-28, 2010. WASET,, 2010
Ernastuti & RA.Salim.. Complexity Analysis of Data Routing Algorithms in Extended Lucas Cubes, Web Based Information Technologies and Distributed Systems, Atlantis Ambient and Pervasive Inteligence Vol.2, Word Scientific Book, 2010 Ernastuti & B. H Widjaja & D.Kerami. Extended Lucas Cube: A New Hamiltonian Graph, Journal of the Indonesian Mathematical Society, Volume 14, No.1 April 2008, 2008.
Ernastuti & Belawati. WH. Hamiltonicity on interconnection network: Extended Lucas Cube. Proceeding of The International Conference On Soft Com puting, Inteligent System and Information Technology, 2007
Ernastuti & Juarna. A.. Model jaringan interkoneksi Extended Lucas Cube. Proceeding of National Conference On Computer Science and Information Technology, 2007
Ernastuti & Juarna. A. On a new family of _bonacci-like cubes: Extended Lucas Cube. Abstract of The International Conference On Graph Theory and Information Security, 2007. Ernastuti & Vajnovszki, V Embeddings of linear arrays, rings and 2-d meshes on Exten2-de2-d Lucas Cube. Proceeding of The International Conference OnElectrical Engineering and Informatics, 2007,
Hsu. WJ,. Fibonacci cube - a new interconnection topology. IEEE Trans. On Parallel and Distributed Systems, 1993 Klavzar, S, On median nature and enumerative properties of Fibonacci-like cubes. Elsevier Discrete Mathematics, 2005. Liszka, KJ & Antonio,JK & Siegel, HJ. Problems with comparing intercon-nection networks: Is an alligator better than an armadillo? IEEE Concurency,1997.
Munarini, E, Cippo, CP & Salvi, NZ, 2001. On the Lucas cube. Fibonacci Quarterly, 2002.
Munarini, E, On the Lucas cubes. Fibonacci quart, 2002. Parhami. B, A unified formulation of honeycomb and diamond networks. IEEE Transaction on Parallel and distributed systems, 2001. Wilkinson, B & Allen, M..Parallel Programming: techniques and applications using networked workstations and parallel computers. Prentice Hall. 2008
Wu, J,. Extended Fibonacci cubes. IEEE Trans. on Parallel and Dsitributed Systems,1997