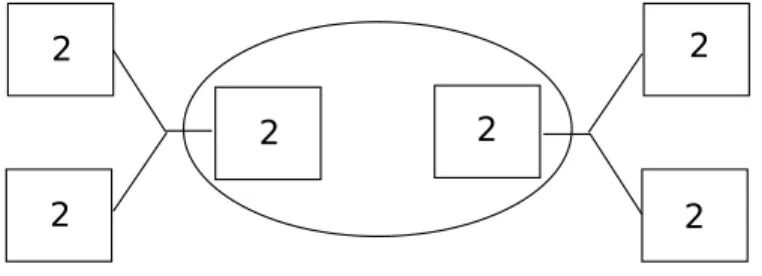
31 3.4 The periodic matrix τIR,ij of the Seiberg-Witten curve is equal to a second. Right: Quiver representation of the gauge theory SUp2q ˆSUp2q associated with two bi-fundamental hypermultiplets.

Outline
The Higgs branch of the modulus space is a hyper-Kahler manifold and receives no quantum correction. Thanks to the N “2 supersymmetry, the low-energy effective action can be written in terms of a single holomorphic function Fpaq called the prepotential.
Seiberg-Witten solution
Originally, the Seiberg-Witten curve was obtained by an educated guess based on electric-magnetic duality and the singularity structure of the module space. In the next section, we will use a slightly different form based on the M-theoretic construction of the Seiberg-Witten theory.
N “ 2 gauge theory from M5-branes on a Riemann surface
UV-curves and Hitchin systems
- Unitary gauge group
- Symplectic/orthogonal gauge group
We insert a stack of ˜NM5-branes wrapping the six-dimensional manifold R4ˆC.˜ The positions of these M5-branes in the cotangent bundle determine the Seiberg-Witten curve Σas the subspace T˚C. More specifically, the Seiberg-Witten curve is embedded in the cotangent bundle T˚C of the Gaiott curve C with the holomorphic differentialv.

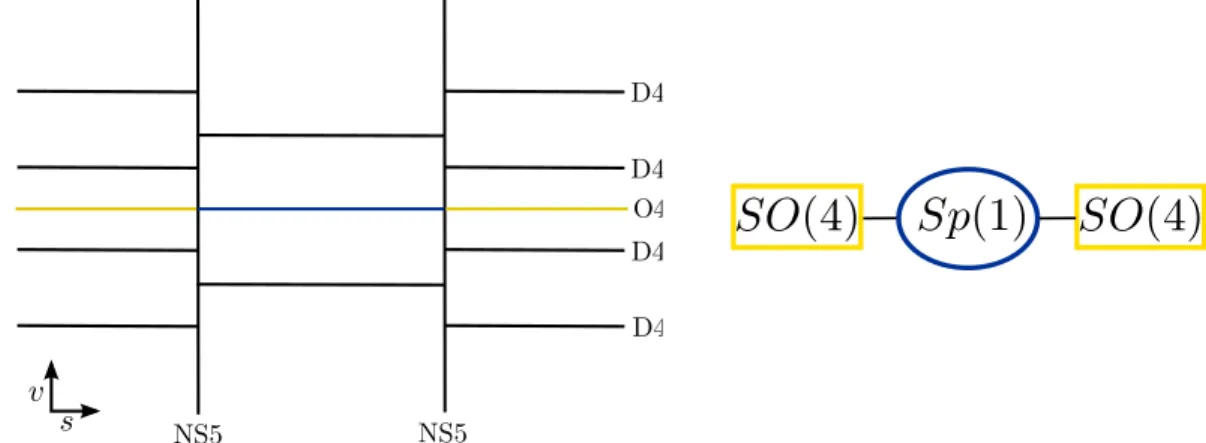
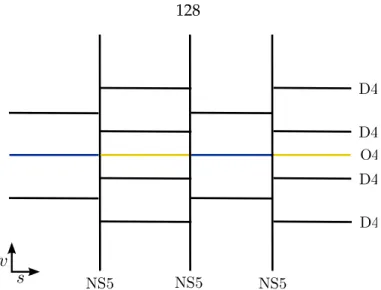
In order to obtain a pure N “ 2 Yang-Mills theory, we need to place the 5d Yang-Mills theory on a segment with an appropriate semi-BPS boundary condition at both ends. When Gis is classical, the 5d Yang-Mills theory can be realized on coincident D4-branes, preferably on top of the O4-plane.
S-duality
Instanton corrections to the N “2-gauge theory, with Nf hypermultiplications in the fundamental representation of the gauge group, are calculated by the instanton partition function. Their action can best be understood from the famous ADHM construction of the instanton moduli space [54].
Instanton counting
ADHM construction
The vector spaces VandW are k and N-dimensional, respectively, with a natural action of the double group Upkq and the frame group UpNq. The universal bundle is obtained by varying the ADHM parameters of the cards in the complex (3.15).
Ω-background and equivariant integration
For SppNq, the weights of the equivariant torus action on the vector spaces V and W are given by. In general, the equivariant index of a gauge multiplet is given by the character of the tangent space of the module space [30].
One-instanton contribution for arbitrary gauge group
One-instanton contribution
The space of holomorphic functions on ˜MG,1 was known to mathematicians, for example using the fact that ˜MG,1 is the orbit of the maximum weight vector in CunderGC. The conclusion is that, as a representation of Up1q2ˆG, we decompose the space of holomorphic functions on MG,1 as
Hilbert series of the one-instanton moduli space
Here, ∆ is the set of roots, ∆l is the set of long roots, ∆ is the set of positive roots, ~ρ is the Weyl vector, and spwq is the sign of an element of the Weyl group W. The difference~ρpGq ´~ρpG0q of The Weyl vectors of GandG0 are perpendicular to all~αi ofG0 and are therefore proportional to´~α0.
N “ 2 SCFT and renormalization scheme
Infrared versus ultraviolet
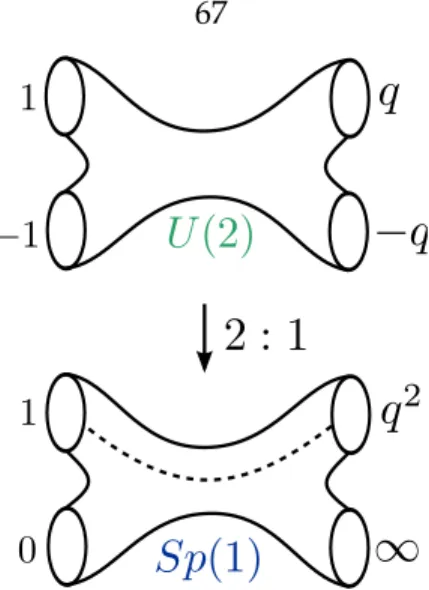
Since the Seiberg-Witten curve determines the masses of BPS particles in the low-energy limit of the gauge theory N “ 2 , its periodic matrix τIR is a physical quantity that must be independent of the chosen renormalization scheme. The Nekrasov distribution function agrees if it is expressed in terms of the classical periodic matrix τIR. This is just a double cover [90] of the better-known parameterization of the SUp2qSeiberg-Witten curve.
Examples
- Spp1q versus Up2q : the asymptotically free case
- Spp1q versus Up2q : the conformal case
- SOp4q versus Up2q ˆ Up2q instantons
- Spp1q ˆ Spp1q versus Up2q ˆ Up2q instantons
The instanton partition function for the pureSOp4q gauge theory is similar to that of the pureUp2q ˆUp2q theory15. The off-diagonal entry in the period matrix represents a mixture of the two gauge groups. Note that this mapping is independent of the Coulomb branch moduli and the mass parameters, as it should be.
UV-IR relation and N “ 2 geometry
SO{Sp versus U geometries
Furthermore, the boundary conditions for the Hitchin differentials at punctures of both models should be related by the mapping that identifies the corresponding fabric representations. This especially relates the eigenvalues of the Seiberg-Witten differential at punctures of both models. Nevertheless, there should be a corresponding isomorphism of Hitchin systems for two models of the same gauge theory.
Examples
- Spp1q versus Up2q geometry
- SOp4q versus Up2q ˆ Up2q geometry
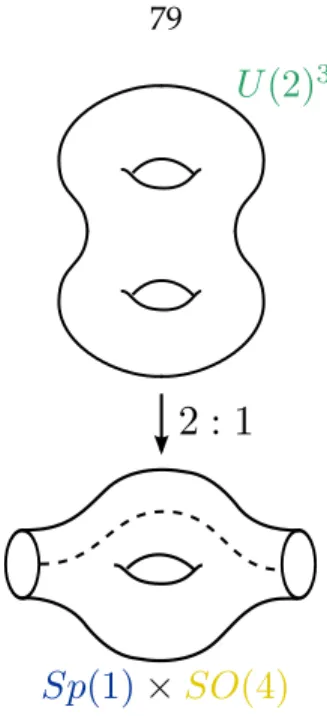
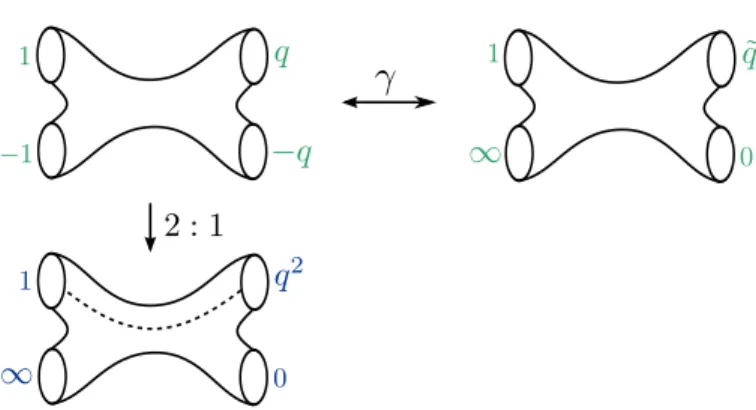
Since this leaves the complex structure of the UV curve invariant, the gauge theory is invariant under such transformations. The Seiberg-Witten curve is a quadruple cover of a four-holed sphere with complex structure parameter ˜qSOp4q. As shown in Figure 3.9, this time the double cover of the UV-curve torus is branched with two holes.
Instanton counting for half-hypermultiplets
Half-hypermultiplets
So, apart from the obvious possibility of combining a chiral and an anti-chiral multiplet into a full hypermultiplet, we can also consider a single half-hypermultiplet in a pseudo-real representation of the gauge group G. On the contrary, a single half-hypermultiplet in the fundamental representation of SUp2q3 contains four chiral fermions in each SUp2q representation. A half-hypermultiplet that transforms under the bifundamental SOˆSpis into a pseudo-real representation of the gauge group G“SOˆSpand is also free of the Witten anomaly.
Instanton counting for half-hypermultiplets
The path integral of the theory of semihypermultiplets is localized to the solutions of the Dirac equation (3.113), which are invariant with respect to τ. Thus, we can find the basis of the solution space of the Dirac equation, on which τ acts with the eigenvalue˘1. Multiplying the solutions of the Dirac equation therefore takes us from one semi-hypermultiplet to another.
Instanton contribution for the Sp ˆ SO bifundamental
In this section we will review some basic properties of 2-dimensional conformal field theory. When the theory is invariant on scale1, we obtain from the conservation of the dilational current jµ “ Tµνxν. Expanding the product operator (OPE) of the stress-energy tensor with other fields tells you how the fields transform under the conformal group.
Representations of Virasoro Algebra
The dimension of the space Mph,cqpNq is given by the Euler function ppNq, which counts the number of partitions of N. There may be a set of zero vectors in the Verma module which are orthogonal to all states inMph,cq. The positivity of the norm (or unitarity) constrains the value of central charge and highest weight to be . 4.27) Note that in the latter case only a limited number of highest weights are allowed.
Free Field Theory
It does not change the OPE of the fields, but changes the stress-energy tensor to Now the central charge becomes "1´12Q2, so it shields the central charge of the original system. An advantage of the free boson construction in the 4d/2d correspondence is that the relationship between the Coulomb branch parameters in the 4d gauge theory is directly given by the zero states of the free bosons.
Conformal Block
We will discuss this in Section 5.5.1, where we relate it to the trifundamental half-hypermultiplet appearing in Sicilian gauge theories.
W -algebras
Chiral Blocks and Twisted Representations
Since the spectrum of the CFT decomposes into representations of the W-algebra, we can use generalized branch identities to relate correlation functions of (W-)descendant fields to correlation functions of (W-)primary fields. In the case of the Virasoro algebra, we can always reduce them to just functions of prime fields. With the above remarks, the result is then independent of the theory's three-point functions, i.e. it depends only on the kinematics of the theory.
Free field realization of W -algebras
Simply laced W-algebras
- A n
- D n
- E 6
One can show that the singular part of the OPE of Rpn`1q with ˜s˘i is a total derivative, which means that the Upkqpzq is indeed in the centralizer of the screening charges. Again one can show that Vpnq and the Up2kq are independent, giving us a set of generators of the correct weights [110, 111]. Note that an operatorOpzq commutes with the screening costQi if and only if it has the form.
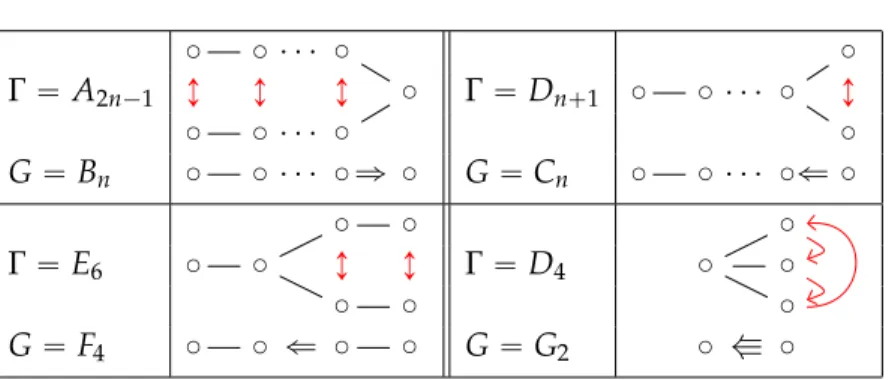
Twisted sectors of the simply-laced W-algebras
Basic properties of the Verma module
Remember that the tubes of the UV curve are related to the ADE gauge group of theN “2 gauge theory, and the holes in the UV curve are related to matter. The symmetry of the two-dimensional theory must be related to the ADE gauge set. Additionally, the two-dimensional operators that fit into the UV curve holes must encode the flavor symmetries of the corresponding matter multiples.
Pure YM case
Identification of the coherent state
Under the correspondence of Nekrasov's partition functions and conformal blocks of W-algebras, the key relation is that the vev of the W-currents must become the fieldsφpwiqpzq in the limit1,2!a:. 5.5) The fieldsφpwiqpzqhave two singularitiesz "0,8, which means that there is a statexG|at z" 8and a state|Gyatz "0. W0pwiq|~wy “wpwiq|wy~ (5.6) where the eigenvalueswpwiq must be equal to the vevupwiq to some quantization error involving1,2 5.7) When Gis is non-simply aligned, the conditions (2.27) to (2.29) imply that|Gyis in the Verma module generated by the Zr-twisted vacuum| wy~ of WpΓq algebra determined by. W0pwˆiq|~wy "wpwˆiq|wy~ (5.8) where the eigenvalueswpwˆiq must be equal to the vevupwˆiqup to the quantization error involving1,2. 5.9) Then we must have the relation. 5.10).
Coherent state at the lowest level
To obtain the norm of the ~ Gaiotto states of the twisted Zr sector, we simply look for the descendants of level-1{r and take the corresponding element of the Kac-Shapovalov matrix. To evaluate the Kac-Shapovalov matrix, write the W generators in terms of free bosons and expand as. To calculate it, we need to find states of the form : pJjqm :´1{r, which can be found from the original prescription of OPE-normal order, that is, by subtracting the singular part of the correlator for the m bosons.
Comparison
- A n
- D n
- B n
- C n
- G 2
- F 4
Now we evaluate the Kac-Shapovalov matrix to obtain the norm of the coherent state. We find that they correspond to the norm of the corresponding coherent states up to the numerical constants. The Gaiotto-Whittaker state norm is given as the reciprocal of the above expression.
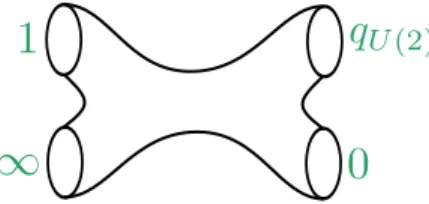
SO ´ Sp quiver
The SOp4q and Spp1q AGT correspondence
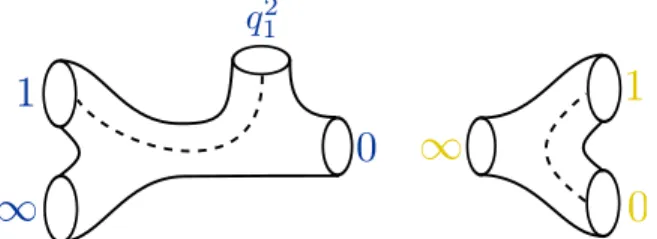
Inner tubes without twist line (yellow) correspond to SOp4q and carry two copies of the Virasoro algebra. A tube with a twisted line corresponds to the aSpp1qgauge group, and the weight of the twisted primary in the channel corresponds to its single Coulomb branch parameter. A tube without a twist line corresponds to a SOp4qgauge group, and the two weights of the untwisted primary in the channel correspond to the two Coulomb branch parameterssa1anda2.
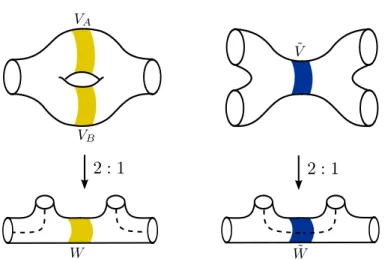
Correlators for the W p2, 2q algebra and the cover trick
The exact map from base to cover thus depends on the positions of the intersections. We can relate the stress-energy tensor on coverTpzq˜ to the two copies on the base in the following way. This means that at the coverage point there is a fieldφ, which is an untwisted representation of Virasoro.
Examples
- Spp1q versus Up2q correlators
- SOp4q versus Up2q ˆ Up2q correlators
Returning to the computation of the conformal block, if we do not know the full cover map, then we must decompose the conformal block into three-point functions with curve fields. From (5.57) we see that any coordinate transformation on the UV curve leads to a product of prefactors of the form pf1qh. Up to spurious prefactors introduced by the mapping to the cover, (5.65) is thus given by the conformal block of the two pierced torus expressed in terms of qSOp4q.
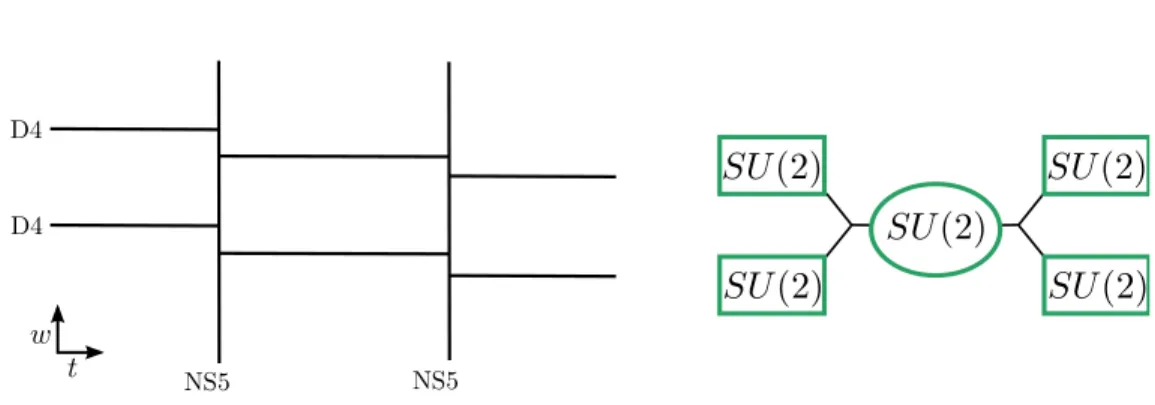
Linear Sp{SO quivers
UV-curves for linear Sp{SO quivers
One example of the connection between linear Spp1q{SOp4q quivers and generalizedSUp2qquiver theories is illustrated in Figure 5.10. As illustrated in Figure 5.11, we find that the UV curve for the generalized A1koker theory is a double coverage of the UV curve for the corresponding linear D2koker theory. This is a branched double overlay over the UV curve of the linear SOp4q{Spp1qquiver theory illustrated below.
Sp ˆ SO bifundamental
Test of the Spp1q ˆ SOp4q AGT correspondence
- Spp1q ˆ SOp4q instantons
- Spp1q ˆ SOp4q correlators
To calculate the rightmost correlator, we can continue as in Subsection 5.3.3.2 and map it to a cover correlator of the form (5.68). The prefactor counter on the other hand is the same prefactor we already found in the Spp1q calculation. We verified that the instanton partition function and the chiral block match up to the order pk1,k2q “ p1, 2q up to a modulus-independent spurious factor using the same identifications of the previous examples.
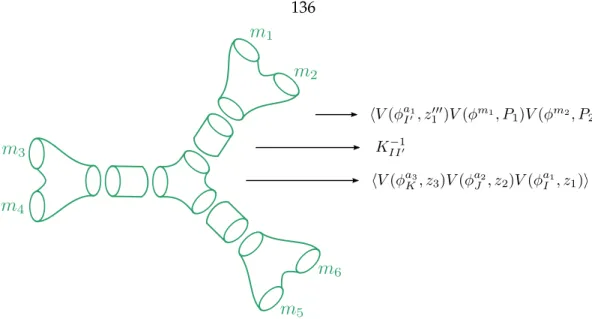
Sicilian quivers
CFT building blocks for Sicilian quivers
- Three-point functions
- Partition function for the trifundamental coupling
On the CFT side, this means that the three-point function must be symmetric under permutations of the insertion points. Similarly, it can be obtained from the equivariant index of the Dirac operator in the instanton background (see Appendix E). It has been checked by a direct calculation of the partition function [131] using the recursive structure of the instanton partition function [55, 132].
Due to poles of the form (B.8), theφi will take values in chains, just as in the UpNq case. For the root˘12pe1´e2q, note that no box can be attached to the e1`e2 2 box because of the zeros in the counter.