Analisis Numerik Materi- 02

Analisis Numerik

Materi- 02

“ ^DERET

TAYLOR

2

1. Persamaan deret Taylor

Let’s start with the first set of slides

4

Pendahuluan

Deret Taylor merupakan dasar untuk menyelesaikan masalah dalam analisis numerik, terutama penyelesaian persamaan diferensial. Jika suatu fungsi𝑓 𝑥 diketahui di titik 𝑥_𝑖 dan semua turunan dari 𝑓terhadap 𝑥diketahui pada titik tersebut dinyatakan nilai 𝑓 pada titik𝑥_𝑖+1 yang terletak pada jarak∆𝑥 dari titik𝑥_𝑖.

𝑓 𝑥_𝑖+1 = 𝑓 𝑥_𝑖 + 𝑓^′ 𝑥_𝑖 ^∆𝑥

1! + 𝑓^′′ 𝑥_𝑖 ^∆𝑥2

2! +𝑓^′′′ 𝑥_𝑖 ^∆𝑥3

3! +…....+𝑓^𝑛 𝑥_𝑖 ^∆𝑥𝑛

𝑛! + 𝑅_𝑛 (2.1)

Dengan:

𝑓 𝑥_𝑖 : fungsi di titik𝑥_𝑖 𝑓 𝑥_𝑖+1 : fungsi di titik𝑥_𝑖+1

𝑓^′, 𝑓^′′, … 𝑓^𝑛 : turunan pertama, kedua,…,ke n dari fungsi

∆𝑥 : langkah ruang, yaitu jarak antara𝑥_𝑖 dan 𝑥_𝑖+1 𝑅_𝑛 : kesalahan pemotongan

! : operator faktorial, artinya 3! = 1x2x3; 4!=1x2x3x4

Pendahuluan

Dalam persamaan (2.1) yang mempunyai pemotongan 𝑅

_𝑛

diberikan oleh:

𝑅

_𝑛

= 𝑓

^𝑛+1

𝑥

_𝑖 ^{∆𝑥𝑛+1}

𝑛+1 !

+ 𝑓

^𝑛+2

𝑥

_𝑖 ^{∆𝑥𝑛+2}

𝑛+2 !

+ ⋯ (2.2)

Persamaan (2.1) yang mempunyai suku sebanyak tak terhingga akan memberikan perkiraan nilai suatu fungsi sesuai dengan penyelesaian

eksaknya. Dalam praktek sulit memperhitungkan semua suku tersebut dan

biasanya hanya diperhitungkan beberapa suku pertama saja.

1. Memperhitungkan satu suku pertama (orde nol)

Apabila hanya diperhitungkan satu suku pertama dari ruas kanan, maka Persamaan (2.1) dapat ditulis dalam bentuk:

𝑓 𝑥_𝑖+1 ≈ 𝑓 𝑥_𝑖 (2.3)

Pada persamaan (2.3) yang disebut sebagai perkiraan orde nol, nilai 𝑓 pada titik 𝑥_𝑖+1 sama dengan pada titik 𝑥_𝑖. Perkiraan tersebut adalah benar jika fungsi yang diperkirakan adalah suatu konstan. Jika fungsi tidak konstan, maka harus diperhitungkan suku-suku berikutnya dari deret taylor.

6

2. Memperhitungkan dua suku pertama (orde 1)

Bentuk deret taylor orde satu, yang memperhitungkan dua suku pertama , dapat ditulis dalam bentuk:

𝑓 𝑥

_𝑖+1

= 𝑓 𝑥

_𝑖

+ 𝑓

^′

𝑥

_𝑖 ^∆𝑥

1!

(2.4)

Yang merupakan bentuk persamaan garis lurus (linier)

3. Memperhitungkan tiga suku pertama (orde 2)

Deret Taylor yang memperhitungkan tiga suku pertama dari ruas kanan dapat ditulis menjadi:

𝑓 𝑥

_𝑖+1

= 𝑓 𝑥

_𝑖

+ 𝑓

^′

𝑥

_𝑖 ^∆𝑥

1!

+ 𝑓

^′

′ 𝑥

_𝑖 ^∆𝑥2

2!

(2.5)

Persamaan (2.5) disebut perkiraan orde dua.

8

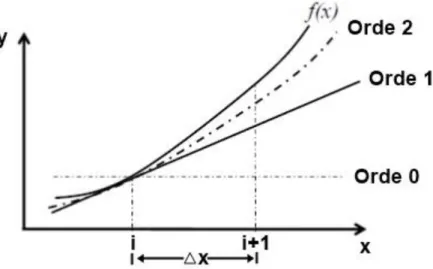
Gambar 1 menunjukkan perkiraan suatu fungsi dengan deret Taylor secara grafis. Perkiraan orde 0, 1, dan 2 berturut-turut adalah garis horisontal, garis lurus miring, dan kurva lengkung.

Gambar 1 Perkiraan suatu fungsi dengan Deret Taylor

2. Kesalahan Pemotongan (Truncation error)

Let’s start with the second set of slides

Pendahuluan

Deret Taylor akan memberikan perkiraan suatu fungsi dengan benar jika semua suku dari deret tersebut diperhitungkan. Dalam praktek hanya beberapa suku pertama saja yang diperhitungkan sehingga hasil perkiraan tidak tepat seperti pada penyelesaian analitik atau eksak. Ada kesalahan karena tidak diperhitungkannya suku-suku terakhir dari deret Taylor. Kesalahan ini disebut

dengan kesalahan pemotongan (truncation error, 𝑹_𝒏), yang ditulis dalam bentuk:

𝑹_𝒏 = 𝑶(∆𝒙^𝒏+𝟏)

Indeks n menunjukkan bahwa deret yang diperhitungkan adalah sampai pada suku ke n, sedang superskrip n+1 menunjukkan bahwa kesalahan pemotongan mempunyai orde n+1. Notasi

𝑂(∆𝑥^𝑛+1) berarti bahwa kesalahan pemotongan mempunyai orde∆𝑥^𝑛+1; atau kesalahan adalah sebanding dengan interval ∆𝒙pangkat x+1. Kesalahan pemotongan tersebut adalah kecil apabila:

1. Interval ∆𝑥 adalah kecil,

2. Memperhitungkan lebih banyak suku dari deret Taylor

Pada perkiraan orde satu, besarnya kesalahan pemotongan adalah:

𝑂 ∆𝑥² = 𝑓^′′ 𝑥_𝑖 ^∆𝑥2

2! + 𝑓^′′′ 𝑥_𝑖 ^∆𝑥3

3! + ⋯ (2.6)

CONTOH 1

Diketahui suatu fungsi𝑓 𝑥 = 𝑥³ − 𝑥² + 0,5𝑥 + 1 gunakan deret Taylor orde nol, satu, dua, dan tiga;

perkirakan fungsi tersebut pada titik 𝑥_𝑖+1= 0,5

berdasarkan nilai fungsi pada titik𝑥_𝑖. Titik 𝑥_𝑖+1= 0,5 berada pada jarak ∆𝑥= 0,5 dari titik𝑥_𝑖 = 0.

12 𝑖 − 1 𝑖 𝑖 + 1

∆𝑥 ∆𝑥

𝑛 + 1

𝑛 − 1 𝑛

𝑡

𝑥

∆𝑡

Gambar 2 Jaringan titik hitungan sistem ruang waktu (x-y)

Karena bentuk fungsi sudah diketahui, maka dapat dihitung nilai𝑓(𝑥)antara 0 dan 0,5.

Untuk𝑥_𝑖= 0 maka : 𝑓 𝑥 = 0 = (0)³− 0 ² + 0,5 0 + 1 = 1,0

Untuk𝑥_𝑖+1= 0,5 maka: 𝑓 𝑥 = 0,5 = (0,5)³− 0,5 ² + 0,5 0,5 + 1 = 1,125 Jadi nilai eksak untuk 𝑓 𝑥 = 0,5 adalah 1,125

Apabila digunakan deret Taylor orde nol, maka berdasarkan Persamaan (2.3) didapatkan:

𝑓 𝑥_𝑖+1 = 0,5 ≈ 𝑓(𝑥_𝑖 = 0) ≈ 1 Kesalahan pemotongan adalah:

𝜀_𝑒 = 𝐸_𝑒

𝑝 × 100% = 1,125 − 1,0

1,125 × 100% = 11,1%

Penyelesaian Contoh 1:

^{𝑓 𝑥 = 𝑥3 − 𝑥2+ 0,5𝑥 + 1}

1,125 = 𝑏𝑒𝑟𝑎𝑝𝑎 𝑠𝑢𝑘𝑢? 𝑠𝑢𝑝𝑎𝑦𝑎 𝑑𝑖𝑑𝑎𝑝𝑎𝑡𝑘𝑎𝑛 1,125 𝑑𝑒𝑛𝑔𝑎𝑛 𝑝𝑒𝑟𝑠𝑒𝑛𝑡𝑎𝑠𝑒 𝑘𝑒𝑠𝑎𝑙𝑎ℎ𝑎𝑛 0%

14

Apabila digunakan deret Taylor orde satu, nilai 𝑓(𝑥_𝑖+1 = 0,5)dapat dihitung dengan menggunakan persamaan (2.4). Pertama kali dihitung turunan fungsi di titik 𝑥_𝑖 = 0:

𝑓^′ 𝑥_𝑖 = 0 = 3𝑥² − 2𝑥 + 0,5

= 3(0)²−2 0 + 0,5 = 0,5 Sehingga diperoleh:

𝑓 𝑥_𝑖+1 = 𝑓 𝑥_𝑖 + 𝑓^′ 𝑥_𝑖 ∆𝑥 1!

= 1 + 0,5 ×^0,5

1 = 1,25 Kesalahan pemotongannya adalah:

𝜀_𝑒 = 𝐸_𝑒

𝑝 × 100% = 1,125 − 1,25

1,125 × 100% = −11,1%

Lanjutan Penyelesaian Contoh 1:

^{𝑓 𝑥 = 𝑥3− 𝑥2+ 0,5𝑥 + 1}

Apabila digunakan deret Taylor orde dua, nilai 𝑓(𝑥_𝑖+1 = 0,5)dapat dihitung dengan menggunakan persamaan (2.5). Pertama kali dihitung turunan fungsi di titik𝑥_𝑖 = 0 :

𝑓^′′ 𝑥_𝑖 = 0 = 6𝑥 − 2

= 6 0 − 2 = −2 Sehingga diperoleh:

𝑓 𝑥_𝑖+1 = 𝑓 𝑥_𝑖 + 𝑓^′ 𝑥_𝑖 ∆𝑥

1! + 𝑓^′′ 𝑥_𝑖 ∆𝑥² 2!

= 1 + 0,5 ×^0,5

1 − 2 × ^0,52

1×2 = 1,0 Kesalahan pemotongannya adalah:

𝜀_𝑒 = 𝐸_𝑒

𝑝 × 100% = 1,125 − 1,0

1,125 × 100% = 11,1%

Lanjutan Penyelesaian Contoh 1:

𝑓^′ 𝑥_𝑖 = 0 = 3𝑥²− 2𝑥 + 0,5

16

Apabila digunakan deret Taylor orde tiga, persamaan (2.1) menjadi:

𝑓 𝑥_𝑖+1 = 𝑓 𝑥_𝑖 + 𝑓^′ 𝑥_𝑖 ^∆𝑥

1! + 𝑓^′′ 𝑥_𝑖 ^∆𝑥2

2! +𝑓^′′′ 𝑥_𝑖 ^∆𝑥3

3!

Turunan ketiga dari fungsi adalah:

𝑓^′′′ 𝑥_𝑖 = 0 = 6 Sehingga diperoleh:

𝑓 𝑥_𝑖+1 = 1 + 0,5 ×0,5

1 − 2 × 0,5²

1 × 2 + 6 × 0,5³

1 × 2 × 3 = 1,125 Kesalahan pemotongannya adalah:

𝜀_𝑒 = 𝐸_𝑒

𝑝 × 100% = 1,125 − 1,125

1,125 × 100% = 0%

Terlihat bahwa dengan menggunakan deret Taylor orde tiga, hasil penyelesaian numerik sama dengan nilai eksak.

Lanjutan Penyelesaian Contoh 1:

𝑓^′′ 𝑥_𝑖 = 0 = 6𝑥 − 2 →

Apabila hitungan dilakukan untuk pias-pias berikutnya dengan∆𝑥 = 0,5 sampai 𝑥 = 2, akan diperoleh hasil seperti ditunjukkan dalam Tabel 1 dan Gambar 3.

Hitungan dilakukan dengan menggunakan software excel.

Lanjutan Penyelesaian Contoh 1:

𝑥

Eksak Orde 0 Orde 1 Orde 2 Orde 3

∆𝑥 𝑓(𝑥_𝑖) 𝑓(𝑥_𝑖+1) 𝜀_𝑒(%) 𝑓′(𝑥_𝑖) yi+1 𝜀_𝑒(%) 𝑓′′(𝑥_𝑖) yi+1 𝜀_𝑒(%) 𝑓′′′(𝑥_𝑖) yi+1 𝜀_𝑒(%)

0 0,5 1,000 1 0 0,5 1 0 -2 1 0,0 6 1 0

0,5 0,5 1,125 1 11,1 0,25 1,25 -11,1 1 1 11,1 6 1,125 0

1 0,5 1,500 1 33,3 1,5 1,25 16,7 4 1,375 8,3 6 1,5 0

1,5 0,5 2,875 1 65,2 4,25 2,25 21,7 7 2,75 4,3 6 2,875 0

2 0,5 6,000 1 83,3 8,5 5 16,7 10 5,875 2,1 6 6 0

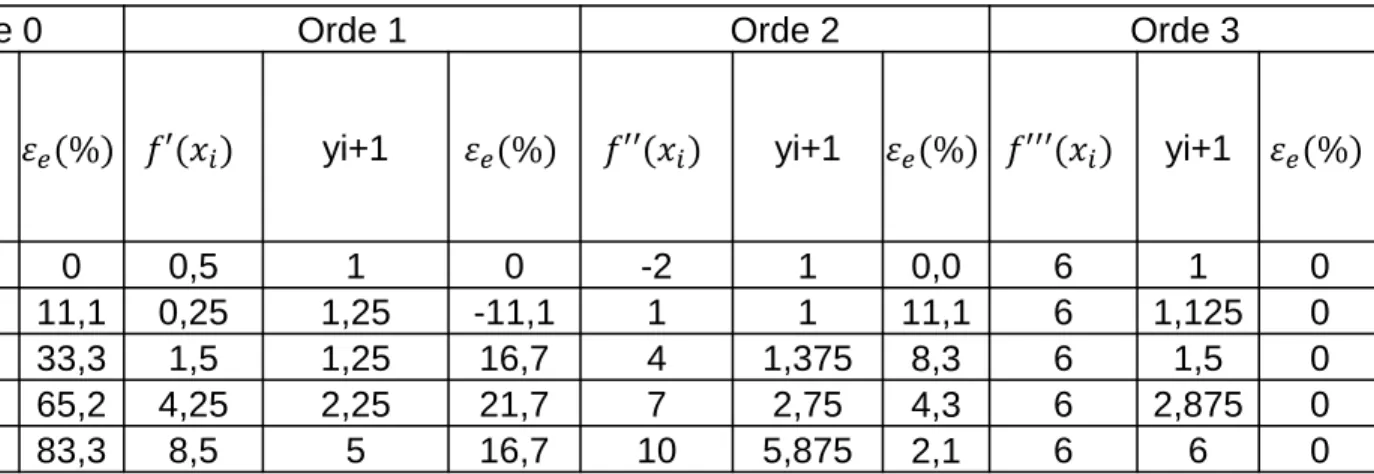
Tabel 1. Perkiraan fungsi deret Taylor orde 0,1,2 dan 3

18

Dari tabel dan gambar tersebut, terlihat bahwa semakin tinggi orde dari deret Taylor, semakin kecil kesalahan yang terjadi. Pada 𝑥 = 2, kesalahan relatif

terhadap nilai eksak (𝜀_𝑒) dari penggunaan orde 0,1,2 dan 3 berturut-turut adalah 83,3%, 16,7%, 2,1% dan 0%. Deret Taylor orde tiga memberikan hasil yang sama dengan nilai eksak. Pada Gambar 3, kurva nilai eksak dan hasil deret taylor orde 3 berimpit.

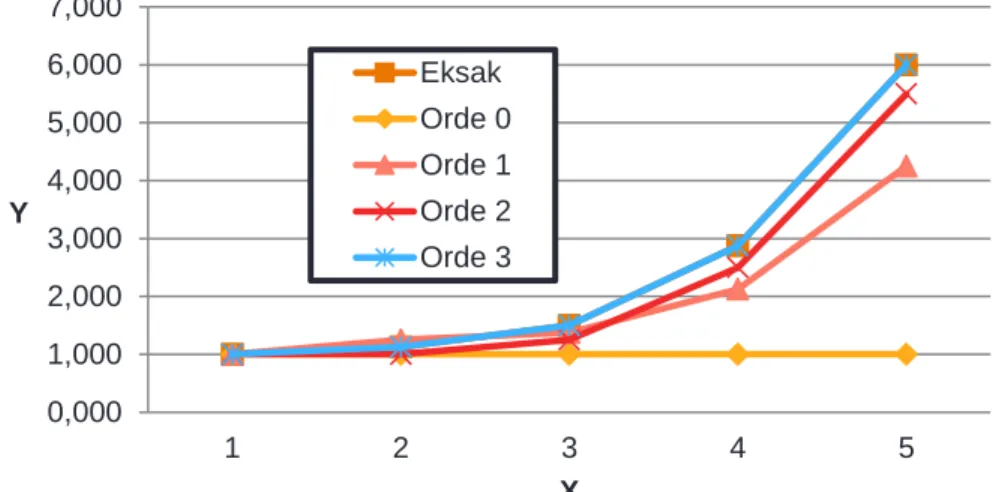
Lanjutan Penyelesaian Contoh 1:

Gambar 3. Perkiraan fungsi dengan deret Taylor orde 0,1,2 dan 3

0,000 1,000 2,000 3,000 4,000 5,000 6,000 7,000

1 2 3 4 5

Y

X Eksak Orde 0 Orde 1 Orde 2 Orde 3

“ Diferensial Numerik

Diferensial numerik digunakan untuk memperkirakan bentuk diferensial kontinyu menjadi bentuk diskret.

Diferensial numerik ini banyak digunakan untuk

menyelesaikan persamaan diferensial. Bentuk tersebut

dapat diturunkan berdasarkan deret Taylor

1. Diferensial turunan pertama

Let’s start with the first set of slides

21

Pendahuluan

Deret Taylor (Persamaan 2.1) dapat ditulis dalam bentu:

𝑓 𝑥_𝑖+1 = 𝑓 𝑥_𝑖 + 𝑓′ 𝑥_𝑖 ∆𝑥 + 𝑂(∆𝑥²) (2.7) Atau

𝜕𝑓

𝜕𝑥 = 𝑓^′ 𝑥_𝑖 =^{𝑓 𝑥𝑖+1 −𝑓(𝑥𝑖)}

∆𝑥 − O(∆𝑥) (2.8)

Seperti ditujukkan gambar 3 dan persamaan 2.8, turunan pertama dari𝑓terhadap𝑥di titik𝑥_𝑖 didekati oleh kemiringan garis yang melalui titik B (𝑥_𝑖, 𝑓 𝑥_𝑖 ) dan titik C (𝑥_𝑖+1, 𝑓 𝑥_𝑖+1 ).

22

Pendahuluan

Bentuk diferensial dari Persamaan (2.8) dsebut diferensial maju orde satu. Disebut diferensial maju karena menggunakan data pada titik𝑥_𝑖 dan𝑥_𝑖+1untuk memperhitungkan diferensial. Jika data yang digunakan adalah di titik𝑥_𝑖 dan𝑥_𝑖−1, maka disebut diferensial mundur dan deret Taylor menjadi:

𝑓 𝑥_𝑖−1 = 𝑓 𝑥_𝑖 − 𝑓^′ 𝑥_𝑖 ^∆𝑥

1! + 𝑓′′ 𝑥_𝑖 ^∆𝑥2

2! − 𝑓′′′ 𝑥_𝑖 ^∆𝑥3

3! + ⋯ (2.9)

Atau

𝑓 𝑥_𝑖−1 = 𝑓 𝑥_𝑖 − 𝑓^′ 𝑥_𝑖 ∆𝑥 + 𝑂(∆𝑥²) (2.10)

𝜕𝑓

𝜕𝑥 = 𝑓^′ 𝑥_𝑖 = ^{𝑓 𝑥𝑖 −𝑓(𝑥𝑖−1)}

∆𝑥 + 𝑂(∆𝑥²) (2.11)

Apabila data yang digunakan untuk memperkirakan diferensial fungsi adalah pada titik𝑥_𝑖−1dan 𝑥_𝑖+1, maka perkiraannya disebut diferensial terpusat. Persamaan (2.1) dikurangi persamaan (2.9) didapatkan:

𝑓 𝑥_𝑖+1 = 𝑓 𝑥_𝑖 − 2𝑓^′ 𝑥_𝑖 ∆𝑥 + 2f′′′ 𝑥_𝑖 ^∆𝑥3

3! +… (2.12)

Atau

𝜕𝑓

𝜕𝑥 = 𝑓^′ 𝑥_𝑖 = ^{𝑓 𝑥𝑖+1 −𝑓(𝑥𝑖−1)}

2∆𝑥 − 𝑓′′ 𝑥_𝑖 ^∆𝑥2

6 + ⋯

Pendahuluan

atau

𝜕𝑓

𝜕𝑥 = 𝑓^′ 𝑥_𝑖 = ^{𝑓 𝑥𝑖+1 −𝑓(𝑥𝑖−1)}

2∆𝑥 − O(∆𝑥²) (2.13)

Dari persaman (2.13) terlihat bahwa kesalahan pemotongan beroder∆𝑥²; sedangkan pada diferensial maju dan mundur berorde∆𝑥kecil, nilai kesalahan pemotongan yang berorde 2 yaitu O(∆𝑥²) lebih kecil dari orde 1 yaitu O(∆𝑥). Hal ini menunjukkan bahwa perkiraan diferensial terpusat lebih teliti dibandingkan diferensial maju atau mundur. Keadaan ini juga apat dilihat pada Gambar 4. Kemiringan garis yang melalui titik A dan C (diferensial terpusa) hampir sejajar dengan kemiringan garis singgung dari fungsi di titik𝑥_𝑖; dibandingkan dengan kemiringan garis singgung yang melalui titik A dan B (diferensial mundur) atau titik B dan C (diferensial maju).

2. Diferensial turunan kedua

Let’s start with the second set of slides

Turunan kedua dari fungsi dapat diperoleh dengan menjumlahkan Persamaan 2.1 dengan persamaan 2.9:

𝑓 𝑥

_𝑖+1

+ 𝑓 𝑥

_𝑖−1

= 2𝑓 𝑥

_𝑖

+ 2𝑓

^′′

𝑥

_𝑖

∆𝑥

²

2! + 2𝑓′′′′ 𝑥

_𝑖

∆𝑥

⁴

4! + ⋯ Atau

𝑓′′ ∆𝑥

_𝑖

= 𝑓 𝑥

_𝑖+1

− 2𝑓 𝑥

_𝑖

+ 𝑓 𝑥

_𝑖−1

∆𝑥

²

− 𝑓′′′′ 𝑥

_𝑖

∆𝑥

²

12 − ⋯ Atau

𝜕²𝑓

𝜕𝑥²

= 𝑓 𝑥

_𝑖

=

^{𝑓 𝑥𝑖+1 −2𝑓 𝑥𝑖 +𝑓 𝑥𝑖−1}

∆𝑥²

− 𝑂 ∆𝑥

²

(2.14)

Dari uraian di atas dapat disimpulkan bahwa bentuk diferensial dapat diubah

dalam bentuk diferensial numerik (beda hingga).

3. Diferensial turunan lebih tinggi

Let’s start with the thirth set of slides

Dengan cara serupa seperti telah diberikan di depan, dapat diturunkan diferensial turunan yang lebih tinggi seperti diberikan berikut ini.

1. Diferensial turunan ketiga :

𝜕³𝑓

𝜕𝑥³

= 𝑓(𝑥

_𝑖

) ≈

^{𝑓 𝑥𝑖+2 −2𝑓 𝑥𝑖+1 +2𝑓 𝑥𝑖−1 −𝑓(𝑥𝑖−2)}

2∆𝑥³

(2.15)

2. Diferensial turunan keempat :

𝜕⁴𝑓

𝜕𝑥⁴

= 𝑓(𝑥

_𝑖

) ≈

^{𝑓 𝑥𝑖+2 −4𝑓 𝑥𝑖+1 +6𝑓 𝑥𝑖 −4𝑓 𝑥𝑖−1 +𝑓(𝑥𝑖−2)}

∆𝑥⁴

(2.16)

CONTOH 2

Diketahui suatu fungsi

𝑓 𝑥 = 𝑥

³

− 𝑥

²

+ 0,5𝑥 + 1.

Perkirakan turunan pertama

(kemiringan kurva) dan turunan kedua dari persamaan tersebut di titik 𝑥=0,5 dengan menggunakan langkah ruang

∆𝑥 = 0,5.

28

Secara analitis turunan pertama dan kedua dari fungsi adalah:

𝑓′ 𝑥_𝑖 = 0,5 = 3𝑥² − 2𝑥 + 0,5 = 3 0,5 ² − 2 0,5 + 0,5 = 0,25 𝑓′′ 𝑥_𝑖 = 0,5 = 6𝑥 − 2 = 6 0,5 − 2 = 1

Dengan∆𝑥 = 0,5dapat dihitung nilai fungsi pada titik𝑥_𝑖−1, 𝑥_𝑖, dan 𝑥_𝑖+1: 𝑥_𝑖−1 = 0 → 𝑓 𝑥_𝑖−1 = 0³ − 0² + 0,5 × 0 + 1 = 1,0

𝑥_𝑖 = 0,5 → 𝑓 𝑥_𝑖 = 0,5³ − 0,5² + 0,5 × 0,5 + 1 = 1,125 𝑥_𝑖+1 = 1,0 → 𝑓 𝑥_𝑖+1 = 1,0³ − 1, 0² + 0,5 × 1,0 + 1 = 1,5 Perkiraan turunan pertama dengan diferensial mundur:

𝑓 0,5 = 𝑓 𝑥_𝑖 − 𝑓(𝑥_𝑖−1)

∆𝑥 = 1,125 − 1,0

0,5 = 0,25 Perkiraan turunan pertama dengan diferensial maju:

𝑓 0,5 = 𝑓 𝑥_𝑖+1 − 𝑓(𝑥_𝑖)

∆𝑥 = 1,5 − 1,125

0,5 = 0,75

Penyelesaian Contoh 2:

30

Perkiraan turunan pertama dengan diferensial terpusat:

𝑓 0,5 = 𝑓 𝑥_𝑖+1 − 𝑓(𝑥_𝑖−1)

2∆𝑥 = 1,5 − 1,0

2 × 0,5 = 0,5 Perkiraan turunan kedua:

𝑓 𝑥_𝑖 = 𝑓 𝑥_𝑖+1 − 2𝑓 𝑥_𝑖 + 𝑓 𝑥_𝑖−1

∆𝑥² = 1,5 − 2𝑥1,125 + 1,0

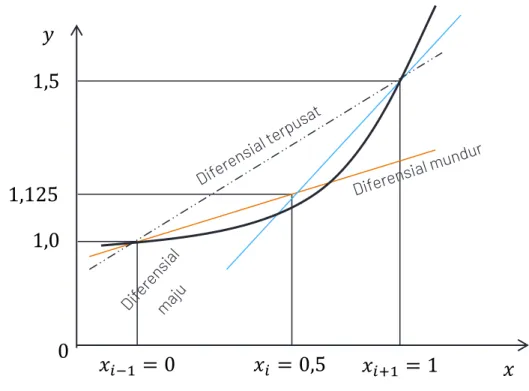
0,5² = 1,0 Gambar 4 menunjukkan kemiringan analisis di titik𝑥 = 0,5dan perkiraan turunan fungsi di titik tersebut.

Lanjutan Penyelesaian Contoh 2:

Gambar 4. Perkiraan Kemiringan Fungsi

Lanjutan Penyelesaian Contoh 2:

𝑥 𝑦

1,5

1,125 1,0

0 𝑥_𝑖−1 = 0 𝑥_𝑖 = 0,5 𝑥_𝑖+1 = 1

4. Turunan Terhadap Variable

Let’s start with the fourth set of slides Lain

Telah dipelajari pada slide sebelumnya tentang deret Taylor untuk suatu fungsi yang hanya mengandung satu variable bebas. Apabila fungsi mengandung lebih dari satu variabel bebas, seperti f(x,y), maka bentuk deret Taylor menjadi:

𝑓 𝑥

_𝑖+1

, 𝑦

_𝑗+1

= 𝑓 𝑥

_𝑖

, 𝑦

_𝑗

+

^𝜕𝑓

𝜕𝑥

∆𝑥

1!

+

^𝜕𝑓

𝜕𝑦

∆𝑦

1!

+

^𝜕2𝑓

𝜕𝑥²

∆𝑥²

2!

+

^𝜕2𝑓

𝜕𝑦²

∆𝑦²

2!

+ ⋯ (2.17) Dengan cara yang sama seperti telah dijelaskan di depan, turunan pertama terhadap variabel x dan y berturut-turut dapat ditulis dalam bentuk (diferensial maju):

𝜕𝑓

𝜕𝑥

≈

^{𝑓 𝑥𝑖+1,𝑦𝑗 −𝑓(𝑥𝑖,𝑦𝑗)}

∆𝑥

(2.18)

𝜕𝑓

𝜕𝑦

≈

^{𝑓 𝑥𝑖,𝑦𝑗+1 −𝑓(𝑥𝑖,𝑦𝑗)}

∆𝑦

(2.19)

34

Untuk menyederhanakan penulisan, bentuk 𝑓(𝑥

_𝑖

, 𝑦

_𝑗

) ditulis 𝑓

_𝑖,𝑗

dengan subskrip 𝑖 dan 𝑗 menunjukkan komponen dalam arah sumbu 𝑥 dan sumbu 𝑦. Apabila fungsi berada dalam sistem tiga dimensi (sistem koordinat 𝑥, 𝑦, 𝑧); maka 𝑓(𝑥

_𝑖

, 𝑦

_𝑗

, 𝑧

_𝑘

) ditulis menjadi 𝑓

_{𝑖,𝑗,𝑘}

. Dengan cara seperti itu maka Persamaan (2.15) dan 2.16) dapat ditulis menjadi:

𝜕𝑓

𝜕𝑥

≈

^{𝑓𝑖+1,𝑗−𝑓𝑖,𝑗}

∆𝑥

(2.20)

𝜕𝑓

𝜕𝑦

≈

^{𝑓𝑖,𝑗+1−𝑓𝑖,𝑗}

∆𝑦

(2.21)

Untuk diferensial terpusat bentuk di atas menjadi:

𝜕𝑓

𝜕𝑥

≈

^{𝑓𝑖+1,𝑗−𝑓𝑖−1,𝑗}

2∆𝑥

(2.22)

𝜕𝑓

𝜕𝑦

≈

^{𝑓𝑖,𝑗+1−𝑓𝑖,𝑗−1}

2∆𝑦

(2.23)

Dengan cara yang sama, turunan kedua terhadap x dan y dapat ditulis menjadi

𝜕²𝑓

𝜕𝑥² ≈ ^{𝑓𝑖−1,𝑗−2𝑓𝑖,𝑗+𝑓𝑖+1,𝑗}

∆𝑥² (2.24)

𝜕²𝑓

𝜕𝑦² ≈ ^{𝑓𝑖,𝑗−1−2𝑓𝑖,𝑗+𝑓𝑖,𝑗+1}

∆𝑦² (2.25)

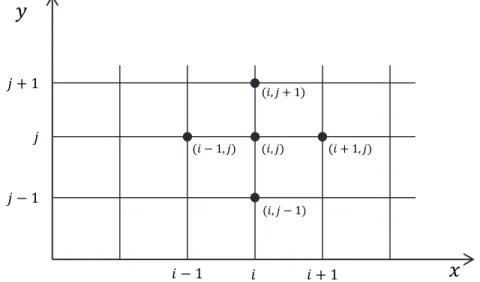
Gambar 4 menunjukkan jaringan titik hitung untuk fungsi yang berada dalam sistem koordinat𝑥dan𝑦 (dua dimensi).

𝑦

𝑖 − 1 𝑖 𝑖 + 1 𝑥

𝑗 − 1 𝑗 𝑗 + 1

(𝑖, 𝑗 + 1)

(𝑖, 𝑗)

(𝑖, 𝑗 − 1)

(𝑖 + 1, 𝑗) (𝑖 − 1, 𝑗)

Gambar 4 Jaringan titik hitungan dalam sistem dua dimensi (x-y)

36

Sering dijumpai permasalahan dimana suatu fungsi selain tergantung pada ruang juga tergantung pada waktu, misalnya pada aliran tidak permanen seperti banjir atau pasang surut dan perambatan panas. Dalam hal ini turunan fungsi 𝑓(𝑥, 𝑡) terhadap waktu (𝑡) dapat ditulis dalam bentuk:

𝜕𝑓

𝜕𝑡

≈

^𝑓𝑖

𝑛+1−𝑓_𝑖^𝑛

∆𝑡

(2.26)

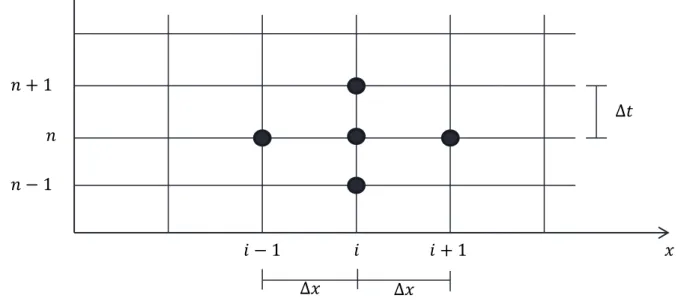
Dalam persamaan 2.23 superskrip 𝑛 menunjukkan bahwa varibel 𝑓 merupakan

fungsi waktu. Gambar 5 adalah jaringan hitungan yang digunakan untuk

memperkirakan diferensial parsiil fungsi 𝑓 terhadap 𝑥 dan 𝑡.

𝑖 − 1 𝑖 𝑖 + 1

∆𝑥 ∆𝑥

𝑛 + 1

𝑛 − 1 𝑛

𝑡

𝑥

∆𝑡

Gambar 5 Jaringan titik hitungan sistem ruang waktu (x-y)

CONTOH 3

Tulis bentuk persamaan diferensial parsiil berikut, yang merupakan

persamaan perambatan panas pada batang, dalam bentuk persamaan diferensial numerik.

𝜕𝑇

𝜕𝑡

= 𝐾

^𝜕2𝑇

𝜕𝑥²

(1)

38

Dengan menggunakan cara seperti telah dijelaskan di depan, bentuk turunan pertama terhadap 𝑡dan turunan kedua terhadap𝑥dapat ditulis dalam bentuk:

𝜕𝑇

𝜕𝑡 ≈𝑇_𝑖^𝑛+1 − 𝑇_𝑖^𝑛

∆𝑡

𝜕²𝑇

𝜕𝑥² ≈𝑇^𝑛_𝑖+1− 2𝑇_𝑖^𝑛+ 𝑇^𝑛_𝑖−1

∆𝑥² Sehingga persamaan (1) menjadi:

𝑇_𝑖^𝑛+1− 𝑇_𝑖^𝑛

∆𝑡 = 𝐾_𝑖^𝑛𝑇^𝑛_𝑖−1− 2𝑇_𝑖^𝑛 + 𝑇^𝑛_𝑖+1

∆𝑥² Atau

𝑇_𝑖^𝑛+1 = 𝑇_𝑖^𝑛 +𝐾_𝑖∆𝑡

∆𝑥² (𝑇^𝑛_𝑖−1− 2𝑇_𝑖^𝑛 + 𝑇^𝑛_𝑖+1)

Penjelasan lebih rinci mengenai penyelesaian persamaan diferensial parsiil diberikan dalam Bab tersendiri

Penyelesaian Contoh 3:

40

Thanks!

Any questions?