Computational methods for simulating and parameterizing nucleic acid secondary structure thermodynamics and kinetics

I would like to thank my committee chair, Tom Miller, for his continued support and tireless focus on achieving our shared goals. I would like to thank Erik Winfree and Garnet Chan for their supportive and entertaining discussions, as well as their positivity towards even my most speculative ideas. Finally, I would like to thank Zhen-Gang Wang for the open views he has provided.

I would like to thank Jining Huang for his positivity, networking expertise and tailor-made clusters. I would like to thank Kaleigh Durst, Grace Shin, Zhewei Chen, Heyun Li, Mikhail Hanewich-Hollatz, Lisa Hochrein, and Melinda Kirk for the fun and helpful conversations. I would also like to thank George Rossman for his support in changing departments and charting my own research path.

Lastly, but most importantly for me, I would like to thank my family for their support throughout school, and to Vicky and Willow for staying through it all. In this work, we develop a unified framework for the construction and understanding of dynamic programming algorithms for complexes of interacting nucleic acid strands.

INTRODUCTION

Nucleic acid secondary structures

Unpseudoknotted structures

Dynamic programming algorithms

Abstract evaluation algebras

Simulation of secondary structure kinetics

Stochastic simulation
Kinetics including coaxial and dangle stacking contributions

Computational parametrization of secondary structure models

Simulation design and choice
Molecular dynamics methodologies
Thermodynamic and kinetic regression

Conclusions

In such a model, the free energy of a secondary structure is parameterized as the sum of loop free energies, which in turn are defined solely by the identities and order of the bases in the loop, i.e. of the fundamental statistical mechanics of the isothermal isobaric ensemble, the complex partition function can be computed as a Boltzmann summation over the ensemble Γ(𝜙) of secondary structures compatible with sequence𝜙:. 1.2) where 𝑘𝐵 is the Boltzmann constant, 𝑇 the temperature and Δ𝐺(𝜙, 𝑠) the structure free energy. 1.3) Here 𝑄𝑖, 𝑗 is the partition function of the subsequence [𝑖:𝑗], and Δ𝐺𝑖, 𝑗 is the free energy of base pairing bases𝑖 and 𝑗.

The idea is that the possible configurations are those of [𝑖:𝑗-1] when the size of the considered sequence is increased by one (by including base 𝑗). Calculation of complex free partition functions is perhaps one of the most essential tools for understanding nucleic acid thermodynamics. To continue, it is useful to consider the essential logic of the counting problem for secondary structures.

In summary, we first develop the covariance matrix Γ𝑟® using the functional forms of the nearest neighbor free energy model. We then consider the joint reduction of the conditional variance of the complex free energy Δ𝐺(𝜙) over a set of representative sequences𝜙.

Figure 1.2: Secondary structure notation. (a) Example (single-stranded) secondary struc- struc-ture

BIBLIOGRAPHY

IMPROVED ALGORITHMS FOR THE EQUILIBRIUM ANALYSIS OF NUCLEIC ACID COMPLEXES

Physical model

Complex ensemble and test tube ensembles
Loop-based free energy model
Coaxial and dangle stacking subensembles within complex ensembles
Symmetry correction
Free energy parameters

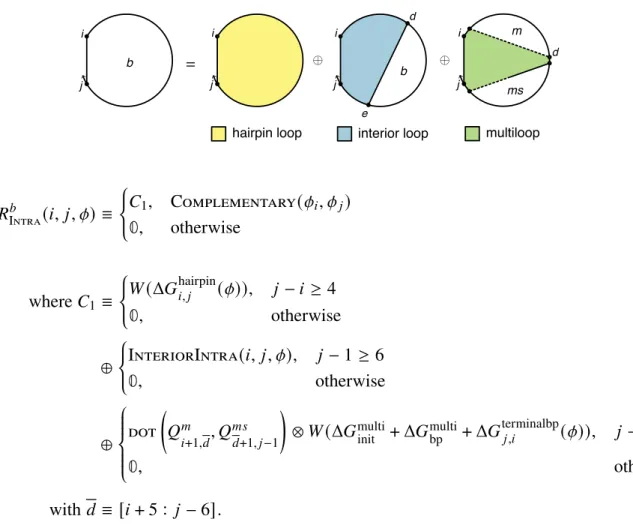
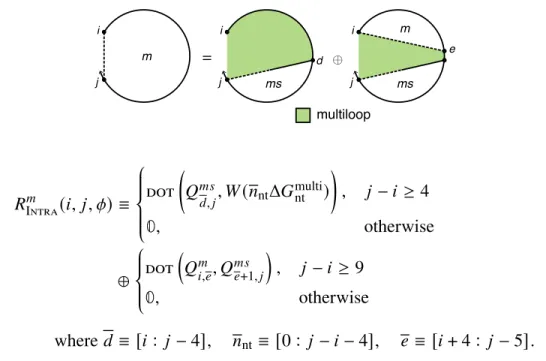
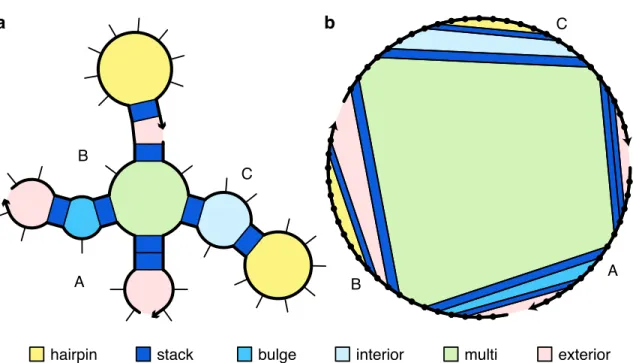
A secondary structure is not pseudo-knotted if there exists a strand arrangement for which the polymer graph has no intersecting lines (e.g., Figure 2.1b), or pseudo-knotted if all strand arrangements contain intersecting lines (e.g., the kissing loops of Figure 2.1de). The loop free energy is modeled as the sum of three series-independent penalties: (1) Δ𝐺multi. Within a multiloop or an outer loop, there is a subassembly of coaxial stacking states between adjacent closing base pairs and dangling stacking states between closing base pairs and adjacent unpaired bases.

The physical model for multiple loops and outer loops has previously been improved for the single-strand array [20] by incorporating coaxial stacking and dependent stacking terms in the free energies of multiple loops and outer loops. See Figure 2.3 for an illustration of valid aggregation states for a multiple loop (panel a) or two outer loops (panels b and c). The free energy of a multiloop or outer ring is increased by the corresponding stacking bonus Δ𝐺.

Thus, a secondary structure 𝑠 is still defined as a set of base pairs, and the stacking states within a given multiloop or outer loop are treated as a structural subensemble that contributes in a Boltzmann-weighted manner to the free energy model for the loop. For a secondary structure𝑠 ∈Γ(𝜙)with a 𝑅-fold rotational symmetry there is in 𝑅-fold reduction in distinguishable conformational space, so the free energy (2.1) must be adjusted[11] by a symmetry correction:. 2.5) Because the symmetry factor 𝑅(𝜙, 𝑠) is a global property of each secondary structure 𝑠 ∈Γ(𝜙), it is not suitable for use with dynamic programs that treat several subproblems simultaneously without access to global structural information.

Figure 2.2: Loop-based free energy model for a complex. (a) Canonical loop types for complex with strand ordering 𝜋 = ABC

Algorithm

Physical quantities
Existing dynamic programs
Unified dynamic programming framework
Recursions for the complex ensemble with coaxial and dangle stacking
Evaluation algebras for partition function, minimum free energy, and ensemble size
Overflow-safe evaluation algebra for large partition function calculations One of the challenges with calculating the partition function is the prevention of overflowOne of the challenges with calculating the partition function is the prevention of overflow
Efficient blockwise dynamic programs over subcomplexes using caching and vectorizationvectorization
Enhanced efficiency and scalability of the partition function algorithm for complex ensembles including very large complexes
Enhanced efficiency of the partition function algorithm for sets of complexes in test tube ensemblestest tube ensembles
Backtrack-free base-pairing probability matrices
Evaluation algebras and backtracking operation orders for simultaneous structure sampling, MFE structure determination, and suboptimal structurestructure sampling, MFE structure determination, and suboptimal structure

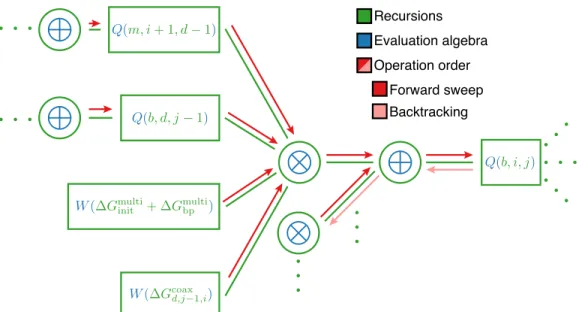
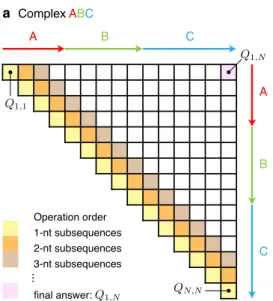
The complex ensemble size, |Γ(𝜙) |, grows exponentially with the number of nucleotides (Figure S37), 𝑁 ≡ |𝜙|, but the partition function can be computed in 𝑂(𝑁3) time and 𝑂(𝑁2) space using a dynamic program [11, 21]. The algorithm computes the subsequence partition function 𝑄𝑖, 𝑗 for each subsequence [𝑖, 𝑗] via a forward sweep from short subsequences to the full sequence (Figure 2.4), ultimately yielding the full sequence partition function, 𝑄1, 𝑁. As noted earlier for the complex ensemble without coaxial and dangling stacking, the recursion diagrams of the partition function of Figure 2.5a can be expressed equivalently as the.

Using quadruple precision (128-bit) arithmetic, the maximum expressible number increases to ≈104932 (platform dependent), allowing partition function calculations for complexes up to ≈22,000 nt. Calculation of the partition function for a complex of 3 strands, each with a different random sequence of uniform length. Calculation of the distribution function and equilibrium complex concentration for a group of tubes containing 𝑀 types of chains forming all complexes up to 𝐿max chains.

Empirically, after computing the partition function 𝑄(𝜙) at a cost of 𝐶𝑄, computing the equilibrium base-pairing probability matrix 𝑃(𝜙) costs an additional 𝐶𝑃 ≈1.5–3𝐶𝑄 (Figure S40). After computing the partition function 𝑄(𝜙) for a strand [6] or complex [11], a structural 𝑠pattern can be randomly sampled from the structural ensemble Γ(𝜙) by backtracking through the matrix of subsequence partition functions.

Figure 2.4: Operation order for partition function dynamic program over a complex ensem- ensem-ble with 𝑁 nucleotides.

Conclusions

Motivated by the central use case where a set of structures is needed for averaging or clustering, here we develop a simultaneous sampling approach that samples A given recursion element may contribute to a large number of sample structures (e.g., if has a deep well in the free energy landscape), so we perform backtracking using a next-priority data structure that reduces computational effort by ensuring that all samples of any given element of the recursion are performed during one visit to single in that recursion element (see section S4.4). With the simultaneous sampling algorithm, we observe order-of-magnitude speedups over sequential sampling for 𝐽over≈ S 103 (Figure 2.15) and empirical complexity ∼

Methods summary .1 Implementation.1Implementation

Trials

Resources

NUPACK source code
NUPACK Python module

An algorithm for computing nucleic acid base pairing probabilities including pseudoknots.Journal of Computational Chemistry. A set of nearest neighbor parameters for predicting the enthalpy change of RNA secondary structure formation. The equilibrium partition function and base pair bond probabilities for RNA secondary structure. Biopolymers: Original research on biomolecules.

A unified display of polymer, dumbbell, and oligonucleotide DNA for nearest-neighbor thermodynamics. Proceedings of the National Academy of Sciences. Thermodynamic parameters of an extended nearest-neighbor model for the formation of RNA duplexes with Watson-Crick base pairs.

EFFICIENT SIMULATION OF NUCLEIC ACID SECONDARY STRUCTURE STOCHASTIC KINETIC TRAJECTORIES

MOLECULAR DYNAMICS METHODS FOR SIMULATING NUCLEIC ACID BASE-PAIRING REACTIONS

COMPUTATIONAL PARAMETERIZATION OF EQUILIBRIUM AND KINETIC NUCLEIC ACID SECONDARY STRUCTURE MODELS

ADDITIONAL DETAILS FOR IMPROVED ALGORITHMS FOR THE EQUILIBRIUM ANALYSIS OF NUCLEIC ACID COMPLEXES

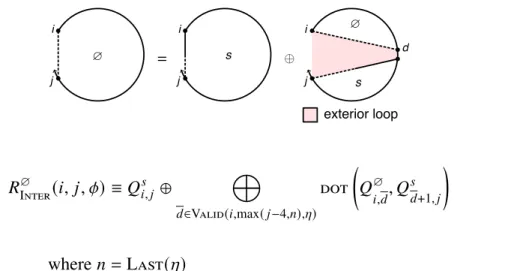
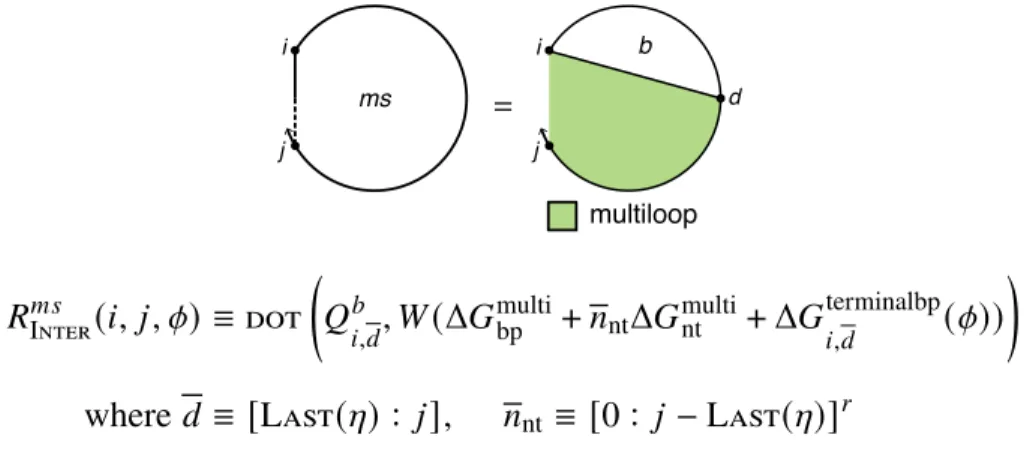
For non-coaxial and dependent recursions (Section S2.3), the terms Δ𝐺allcoax( [𝜙], 𝜔)andΔ𝐺alldangle ( [𝜙], 𝜔) are neglected. For a given 𝑖 and 𝑗, every valid string leads to a dot product between range𝑑 of row𝑖 and range+1 of column 𝑗 (e.g., the recursion of Figure S8 contains a dot product for every valid string𝑑). To compute the matrix entry𝑖, 𝑗for an interstring block with nickname𝜂, the function Valid(𝑖, 𝑗 , 𝜂) (Algorithm S2) returns the set of valid intervals{𝑑1, 𝑑2,.

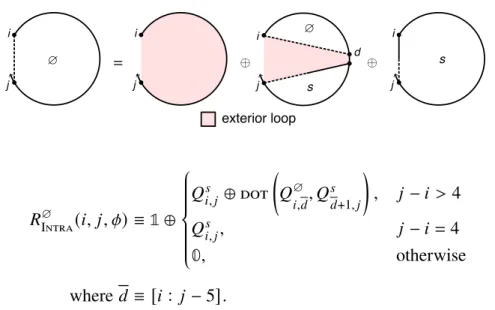
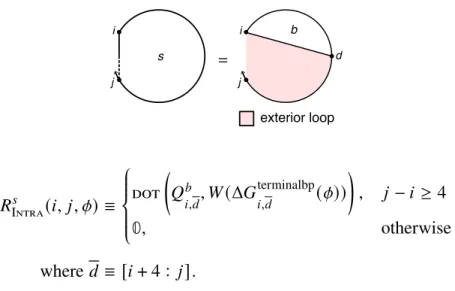
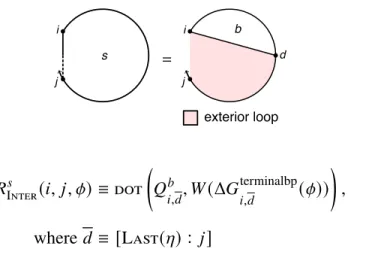
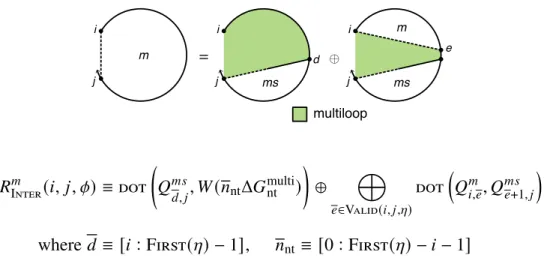
There are one or more additional terminal base pairs in the interval [𝑖, 𝑒] (the straight dashed line indicates that 𝑖 and 𝑒 may or may not be paired); the contribution of the subsequence[𝑖, 𝑒] is included with the element𝑄𝑚. For a given interstrand block with alias indices𝜂, the function Valid returns the set of valid vectorization ranges{𝑑1, 𝑑2,. This final base pair starts at 𝑑 and ends in the interval [𝑑 + 1, 𝑗] (shown by a straight half-dashed/half-dashed line between 𝑑 and 𝑗); the contribution of the subsequence [𝑑 , 𝑗] is included with the element 𝑄𝑚 𝑠.

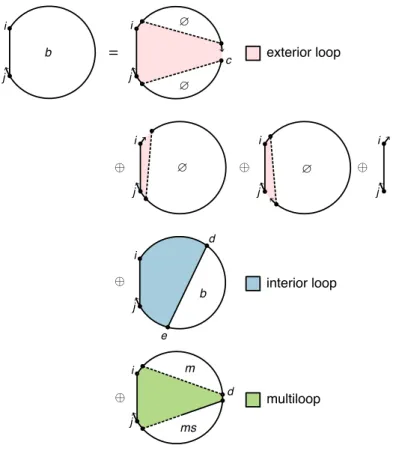
For the outer recursions defined earlier and with multiple loops without coaxial and dependent stacking (see Section S2.3), the elementary entity of the recursion was a terminal base pair (a base pair that terminates a doublet to form part of the loop external or multi-loop) . The left recursion handles the case when there is a dependent aggregation state involving the terminal base pair 𝑗 ·𝑖 (depicted as a dotted straight line between +1, 𝑗 −𝑙−1] (depicted as a dashed line between +1 and 𝑗 −𝑙 −1).The recursion on the right handles the case where there is a dependent stacking state involving the terminal base pair 𝑗 ·𝑖 (described as a straight dotted line between 𝑖+𝑘 and 𝑗− − 𝑙−1] (depicted as a dashed line between 𝑒 and 𝑗−𝑙−1).

Also note that 𝑅𝑚 𝑠 is an efficiency wrapper of the 𝑅𝑚 𝑑-recursion (the 30 most dangling stack states in a multi-loop context). Note that the 𝑅𝑚 𝑐 𝑠 recursion serves as an efficiency wrapper of the 𝑅𝑚 𝑐 recursion (here it represents the 30 most coaxial stacking states in a multi-loop context). Basic cases. The basic cases correspond to the recursion diagrams in the first row of Figure S27 and are treated with term𝐶1 in the subroutine MultiCoaxInter (recursion equation S58).

The left recursion handles the case when there is a dependent aggregation state involving the terminal base pair 𝑗·𝑖 (depicted as a straight dotted line between , 𝑗−𝑙−1](depicted as a dashed line between +1 and 𝑗 −𝑙−1).The recursion on the right handles the case when there is a dependent aggregation state involving the terminal base pair 𝑗 ·𝑖 (depicted as a straight dotted line between 𝑙−1] (depicted as a dashed line between 𝑒 and 𝑗−𝑙−1).Note that the recursion𝑅𝑚 𝑐 serves as an efficiency wrapper of the recursion