Pemodelan dan Peramalan Hari Hujan di Kota Bandung pada Tahun 2019 Berdasarkan Data Tahun 2009-2018 Menggunakan Metode

(1)

Pemodelan dan Peramalan Hari Hujan di Kota Bandung pada Tahun 2019 Berdasarkan Data Tahun 2009-2018 Menggunakan Metode

Analisis Runtun Waktu Musiman

Disusun oleh : Erena 082011833031

Dosen Pengampu :

M. Fariz Fadillah Mardianto, S.Si., M.Si

PROGRAM STUDI S1 STATISTIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS AIRLANGGA SURABAYA

2022

(2)

2

KATA PENGANTAR

Puji syukur atas kehadirat Allah Subhanahu wa Ta’ala, Tuhan Yang Maha Esa, karena berkat segala rahmat dan karunia-Nya, penulis dapat menyelesaikan makalah dengan judul “Pemodelan dan Peramalan Hari Hujan di Kota Bandung pada Tahun 2019 Berdasarkan Data Tahun 2009-2018 Menggunakan Metode Analisis Runtun Waktu Musiman”. Penyusunan makalah ini dimaksudkan untuk menyelesaikan tugas mata kuliah Analisis Runtun Waktu.

Tidak lupa penulis mengucapkan terima kasih terhadap bantuan dari pihak yang telah berkontribusi dengan memberikan sumbangan baik pikiran maupun materinya. Dan pada kesempatan ini pula penulis haturkan terima kasih sebesar – besarnya kepada Bapak M. Fariz Fadillah Mardianto, S.Si., M.Si yang telah membimbing dan memudahkan terselesaikannya makalah ini.

Penulis menyadari bahwa masih banyak kekurangan dalam penyusunan makalah ini karena keterbatasan pengetahuan dan pengalaman. Oleh karena itu, penulis sangat mengharapkan kritik dan saran pembaca agar makalah ini akan menjadi lebih baik dan bermanfaat bagi kedepannya.

Surabaya, 12 Juni 2022

Penulis

(3)

3 DAFTAR ISI

KATA PENGANTAR ... 2

DAFTAR ISI ... Error! Bookmark not defined. DAFTAR TABEL ... 4

DAFTAR GAMBAR ... 5

BAB I PENDAHULUAN ... 6

1.1 Latar Belakang ... 6

1.2 Rumusan Masalah ... 6

1.3 Tujuan Penelitian ... 7

1.4 Manfaat Penelitian ... 7

BAB II TINJAUAN PUSTAKA ... 8

2.1 Hujan ... 8

2.2 Hari Hujan ... 8

2.3 Analisis Runtun Waktu ... 8

2.4 Model-Model Analisis Runtun Waktu ... 11

2.4 Peramalan ... 14

2.5 MAPE (Mean Absolute Percentage Error) ... 14

BAB III METODE PENELITIAN... 16

3.1 Metode dan Sumber Data Penelitian ... 16

3.2 Variabel Penelitian ... 16

3.3 Langkah – Langkah Analisis Data ... 16

BAB IV ANALISIS DAN PEMBAHASAN ... 19

4.1 Deskripsi Data ... 19

4.2 Identifikasi Kestasioneran Data ... 19

4.3 Identifikasi Model Analisis Runtun Waktu ... 23

4.4 Pemilihan Model Terbaik ... 25

4.5 Uji Asumsi Residual ... 27

4.6 Persamaan Model ARIMA(1,1,1)(0,1,1)¹² Probabilistik ... 29

4.7 Forecasting Hari Hujan Kota Bandung ... 29

4.8 MAPE Hari Hujan Kota Bandung ... 30

BAB V PENUTUPAN ... 32

5.1 Kesimpulan ... 32

5.2 Saran ... 32

DAFTAR PUSTAKA ... 33

LAMPIRAN ... 34

(4)

4

DAFTAR TABEL

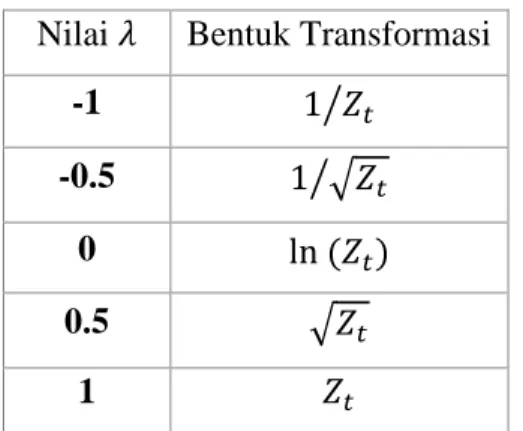
Tabel 2.1 Nilai λ dan Bentuk Transformasi Box-Cox yang Bersesuaian ... 9

Tabel 2.2 Kategori Nilai MAPE ... 15

Tabel 4.1 Hasil Identifikasi Model Analisis Runtun Waktu Musiman ... 25

Tabel 4.2 Estimasi Parameter ARIMA Hari Hujan Kota Bandung ... 25

Tabel 4.3 Perbandingan Hasil Forecasting dengan Hari Hujan Kota Bandung... 30

Tabel 4.4 Perhitungan Nilai MAPE ... 31

(5)

5

DAFTAR GAMBAR

Gambar 4.1 Statistik Deskriptif Data Hari Hujan Kota Bandung ... 19

Gambar 4.2 Grafik Time Series Data Hari Hujan Kota Bandung ... 19

Gambar 4.3 Grafik Trend Analysis Data Data Hari Hujan Kota Bandung ... 20

Gambar 4.4 Plot ACF Data Data Hari Hujan Kota Bandung ... 20

Gambar 4.5 Plot PACF Data Hari Hujan Kota Bandung ... 20

Gambar 4.6 Uji ADF Data Hari Hujan Kota Bandung ...... 21

Gambar 4.7 Plot Box-Cox Plot Box-Cox Hari Hujan Kota Bandung ... 21

Gambar 4.8 Trend Analysis Plot Data Hasil Differencing 1 ... 22

Gambar 4.9 Uji ADF Data Hasil Differencing 1 ... 22

Gambar 4.10 Plot ACF Data Hasil Differencing 1 ... 22

Gambar 4.11 Plot PACF Data Differencing 1 ... 23

Gambar 4.12 Trend Analysis Plot Data Hasil Differencing Musiman Lag 12 ... 23

Gambar 4.13 Uji ADF Data Hasil Differencing Musiman Lag 12 ... 24

Gambar 4.14 Plot ACF Data Hasil Differencing Musiman Lag 12... 24

Gambar 4.15 Plot PACF Data Hasil Differencing Musiman Lag 12 ... 24

Gambar 4.16 Output Ljung-Box Test ARIMA(1,1,1)(0,1,1)¹² Probabilistik ... 27

Gambar 4.17 Plot ACF Residual ARIMA(1,1,1)(0,1,1)¹² Probabilistik ... 27

Gambar 4.18 Plot PACF Residual ARIMA(1,1,1)(0,1,1)¹² Probabilistik ... 28

Gambar 4.19 Uji Normalitas Residual Model ARIMA(1,1,1)(0,1,1)¹² Probabilistik ... 28

Gambar 4.20 Hasil Peramalan Hari Hujan Kota Bandung Bulan Januari – Mei 2019 ... 30

Gambar 4.21 Time Series Plot dengan Hasil Peramalan Hari Hujan Kota Bandung... 30

(6)

6 BAB I PENDAHULUAN 1.1 Latar Belakang

Kota Bandung terletak di wilayah Jawa Barat dan merupakan Ibukota Propinsi Jawa Barat. Kota Bandung mempunyai nilai strategis terhadap daerah-daerah di sekitarnya.

Wilayah Kota Bandung berbatasan langsung dengan Kabupaten Bandung di sebelah timur, selatan dan utara (sebagian), Kabupaten Bandung Barat di sebelah utara, dan Kota Cimahi di sebelah barat. Bandung dikenal sebagai wilayah atau daerah yang ada di dataran tinggi yang dikelilingi oleh pegunungan. Menjadikannya sebagai kawasan yang memiliki suhu udara yang sangat sejuk.

Seperti kota-kota di Indonesia lainnya, wilayah Bandung mengalami 2 musim, yaitu musim hujan dan musim kemarau. Di antara musim hujan dan musim kemarau terdapat masa peralihan atau masa pancaroba. Pada musim hujan, jarang terlihat matahari karena hampir sepanjang hari cuacanya berawan, mendung, atau hujan. Sehingga pada musim hujan, banyak masyarakat sedikit terganggu untuk melakukan aktivitasnya dikarenakan turunnya hujan. Di setiap bulan pun banyaknya hari hujan tidak selalu sama. Sehingga harus terlebih dahulu memperkirakan di bulan apakah yang paling sedikit turun hujan agar dapat meminimalisir gangguan saat beraktivitas.

Berdasarkan uraian-uraian di atas, penulis tertarik untuk melakukan penelitian terkait peramalan hari hujan bulanan yang ada di Kota Bandung pada bulan Januari – Mei 2019 dengan metode analisis runtun waktu menggunakan model ARIMA seasonal.

Diharapkan dengan adanya peramalan ini mampu memberikan pengetahuan ke pada masyarakat terkait gambaran atau ramalan hari hujan yang ada di Kota Bandung pada bulan Januari – Mei 2019. Oleh karena itu, judul yang akan penulis gunakan dalam penelitian ini adalah “Peramalan Hari Hujan di Kota Bandung pada Tahun 2019 Berdasarkan Data Tahun 2009-2018 Menggunakan Metode Analisis Runtun Waktu Musiman”.

1.2 Rumusan Masalah

Berdasarkan latar belakang yang telah diuraikan diatas, maka pokok masalah yang akan dirumuskan dalam penelitian ini adalah sebagai berikut:

1. Bagaimana gambaran data hari hujan Kota Bandung pada tahun 2009 – 2018?

(7)

7

2. Bagaimana model ARIMA musiman yang tepat untuk meramalkan hari hujan Kota Bandung pada bulan Januari – Mei 2019?

3. Bagaimana hasil peramalan (forecasting) hari hujan Kota Bandung pada bulan Januari – Mei 2019?

1.3 Tujuan Penelitian

Berdasarkan rumusan masalah di atas, tujuan yang hendak dicapai dalam penelitian ini adalah sebagai berikut :

1. Untuk mengetahui gambaran data hari hujan Kota Bandung pada tahun 2009 – 2018.

2. Untuk menganalisis model ARIMA musiman yang tepat untuk meramalkan hari hujan Kota Bandung pada bulan Januari – Mei 2019.

3. Untuk mendapatkan hasil peramalan (forecasting) hari hujan Kota Bandung pada bulan Januari – Mei 2019.

1.4 Manfaat Penelitian

Manfaat dari penelitian ini adalah sebagai berikut :

1. Bagi penulis, menambah pengetahuan dan wawasan mengenai pengaplikasian analisis runtun waktu (time series) dalam kehidupan sehari-hari.

2. Bagi masyarakat umum, sebagai pemberi informasi mengenai gambaran dan prediksi hari hujan bulanan di Kota Bandung.

(8)

8 BAB II

TINJAUAN PUSTAKA 2.1 Hujan

Menurut BMKG (Badan meteorologi dan Geofisika) hujan merupakan suatu bentuk presipitasi yang berwujud cair. Presipitasi ini dapat berwujud padat (salju dan es) atau aerosol (embun dan kabut). Jadi, presipitasi merupakan cairan atau zat padat yang berasal dari kondensasi yang jatuh dari awan ke permukaan bumi. Butiran-butiran air yang jatuh sampai ke permukaan bumi disebut curah hujan sedangkan butiran-butiran air yang tidak sampai ke permukaan bumi disebut virga. Butiran-butiran air hujan yang tidak sampai ke permukaan bumi disebabkan terjadinya penguapan ketika jatuh melalui udara kering (Tjasyono, 2006).

2.2 Hari Hujan

Hari hujan merupakan jumlah hari hujan yang terjadi dalam stau bulan dan diperoleh berdasarkan hasil pengukuran harian. Faktor iklim ini tidak memperhatikan berapa banyaknya hujan yang turun ke permukaan bumi, tetapi jumlah hari dimana hujan turun ke permukaan bumi dalam satu bulan (Dini, 2009).

2.3 Analisis Runtun Waktu

Runtun waktu merupakan himpunan observasi terurut dalam waktu atau dalam dimensi lain yang menurut sejarah observasinya (Dwitanto, 2011). Dengan kata lain, analisis runtun waktu merupakan suatu kumpulan data yang diaamati dengan waktu yang urut atau secara beruntun. Runtun waktu dapat dikatakan stokastik maupun deterministik.

Dikatakan runtun waktu stokastik apabila nilai-nilai masa lalu mempengaruhi sebagian niliai masa depan serta memiliki sifat yang probabilistic. Sedangkan runtun waktu dikatakan deterministik ketika deret waktu tersebut mampu diprediksi dengan tepat.

Apabila di dalam suatu proses tidak terjadi perubahan yang cenderung terhadap mean maupun varians, maka dapat dikatakan bahwa analisis runtun waktu tersebut stasioner. Namun, jika suatu analisis runtun waktu tersbeut tidak stasioner maka bisa kita selesaikan dengan menggunakan transformasi data dengan cara sebagai berikut :

1. Konsep Transformasi Box-Cox

Data yang prosesnya tidak stasioner dalam varians dapat diatasi dengan melakukan transformasi Box-Cox dengan bentuk matematis sebagai berikut.

(9)

9 𝑍_𝑡^(𝜆) =𝑍_𝑡^(𝜆)

𝜆 , 𝑑𝑒𝑛𝑔𝑎𝑛 − 1 < 𝜆 < 1

Tabel 2.1 Nilai λ dan Bentuk Transformasi Box-Cox yang Bersesuaian Nilai 𝜆 Bentuk Transformasi

-1 1⁄𝑍_𝑡

-0.5 1⁄√𝑍_𝑡 0 ln⁡(𝑍_𝑡)

0.5 √𝑍_𝑡

1 𝑍_𝑡

Data yang belum stasioner dalam varians biasanya juga belum stasioner dalam mean, sehingga untuk menstasionerkan diperlukan proses differencing setelah melakukan transformasi Box-Cox.

2. Konsep Differencing

Konsep differencing merupakan suatu proses yang dilakukan ketika suatu data tidak stasioner dalam mean. Proses ini menggunakan pengurangan pengamatan hari ini dengan pengamatan sebelumnya (𝑍_𝑡− 𝑍_𝑡−1), dengan penulisan matematisnya sebagai berikut.

∆𝑍_𝑡 = 𝑍_𝑡− 𝑍_𝑡−1⁡dan ∆²𝑍_𝑡= 𝑍_𝑡−2𝑍_𝑡−1+2𝑍_𝑡−2

Selain itu, untuk melakukan differencing dapat digunakan operator Backshift sebagai berikut :

𝐵^𝑑𝑍_𝑡= 𝑍_𝑡−𝑑

𝑊_𝑡= (1− 𝐵)^𝑑𝑍_𝑡(𝐷 =1,2) (Sediono, 2014) 3. Konsep ACF (Autocorrelation Function)

Konsep ACF memegang peran penting, khususnya untuk mendeteksi awal sebuah model dan kestasioneran data. Apabila plot ACF bergerak menurun secara lambat atau menurun secara linier maka dapat disimpulkan bahwa data belum stasioner dalam mean. ACF merupakan suatu fungsi yang menunjukkan besarnya korelasi (hubungan linier) antara pengamatam pada waktu t saat sekarang dengan pengamatan pada waktu – waktu sebelumnya (𝑡 −1, 𝑡 −2, … , 𝑡 − 𝑘) . Nilai autokorelasi sampel lag k dirumuskan sebagai :

(10)

10

𝑟_𝑘 = 𝑐𝑜𝑟𝑟(𝑍_𝑡, 𝑍_𝑡−𝑘) = 𝜌̂_𝑘 =^∑ ^(𝑍^𝑡^{−𝑍̅)(𝑍}^𝑡+1^−𝑍̅)

𝑛−𝑘 𝑡=1

∑^𝑛 (𝑍𝑡−𝑍̅)² 𝑡=1

(Sediono, 2014) 4. Konsep PACF (Partial Autocorrelation Function)

Konsep ini digunakan untuk mengukur keeratan antara 𝑍𝑡 dan 𝑍𝑡−𝑘 apabila pengaruh dari lag waktu t = 1, 2, 3, …, k-1 dianggap terpisah. Partial Autocorrelation Function adalah suatu fungsi yang menunjukkan besarnya korelasi parsial (hubungan linier secara terpisah) antara pengamatan pada waktu t saat sekarang dengan pengamatam pada waktu – waktu sebelumnya. (𝑡 −1, 𝑡 −2, … , 𝑡 − 𝑘) . Nilai autokorelasi parsial sampel lag k dirumuskan secara matematis dalam bentuk formulasi Durbin (1960) sebagai berikut :

𝜙_𝑘𝑘 =^𝜌^𝑘^−∑ ^𝜙^{𝑘−1,𝑗}^𝜌^𝑘−𝑗

𝑘−1 𝑗=1

1−∑^𝑘−1𝜙_{𝑘−1,𝑗}𝜌_𝑗 𝑗=1

(Sediono, 2014) 5. Konsep White Noise

Dalam analisis runtun waktu, White Noise biasanya identik dengan galat (dalam regresi) dan disimbolkan dengan 𝑎𝑡 yang merupakan variabel random berdistribusi IID 𝑁(0, 𝜎²) yang tidak saling berkorelasi dengan 𝛾_𝑘= 𝑐𝑜𝑣(𝑎_𝑡, 𝑎_𝑡−𝑘) =0, 𝑘 ≠0 . Sedangkan nilai 𝛾₀= 𝑐𝑜𝑣(𝑎_𝑡, 𝑎_𝑡) = 𝜎².

Dari pengertian tersebut konsep white noise adalah stasioner dengan sifat-sifat sebagai berikut :

𝛾_𝑘 = {𝜎²^𝑎

0 ⁡, 𝑘 = 0 , 𝑘 ≠ 0 𝜌_𝑘 = {1

0⁡, 𝑘 = 0 , 𝑘 ≠ 0

∅_𝑘𝑘 = {1

0⁡, 𝑘 = 0 , 𝑘 ≠ 0

Dengan demikian suatu proses dikatakan White Noise jika mean dan variansnya konstan dan saling bebas (Sediono,2014). Selanjutnya, suatu proses dapat dikatakan White Noise jika tidak ada lag yang keluar dari margin error pada plot ACF dan juga PACF.

6. Konsep Parsimony

(11)

11

Prinsip Parsimony ini mencari parameter yang minimal tetapi dapat menjelaskan model secara baik (model dengan jumlah parameter yang sedikit). Biasanya, prinsip ini digunakan setelah melakukan proses identifikasi model awal secara tentatif, kemudian melihat apakah model yang dihasilkan tersebut sudah baik (valid) atau belum. Untuk mendeteksi apakah model valid tidaknya dapat dilakukan melalui tahap- tahap berikut :

a. Uji signifikansi parameter → p-value < 5% atau uji |T| > T tabel.

b. Uji White Noise, dengan Uji Ljung Box → p-value < 5%.

c. Uji normalitas residual (Kolmogorov - Smirnov) → p-value > 5%.

d. Mencari nilai MSE (Mean Square Error) minimum dari setiap model.

e. Uji Parsimony → Mencari model valid yang paling sederhana dengan parameter minimum (Sediono, 2014).

2.4 Model-Model Analisis Runtun Waktu 1. Model Autoregressive (AR) Orde p

Proses autoregresif secara harfiah berarti regresi pada dirinya sendiri. Biasanya dalam praktek model AR hanya terjadi pada lag 1 dan lag 2 (Sediono, 2014).

Menurut Soejoeti (1987), proses autoregresif tingkat ke-p dari deret waktu {𝑍_𝑡}, disingkat AR(p), memenuhi persamaan

𝑍_𝑡 = 𝜙₁𝑍_𝑡−1+ 𝜙₂𝑍_𝑡−2+ ⋯ + 𝜙_𝑝𝑍_𝑡−𝑝+ 𝑎_𝑡 Dengan

𝑍_𝑡 : Data pada periode ke-𝑡; 𝑡 = 1,2, … 𝑛 𝑍_𝑡−𝑖 : Data pada periode ke 𝑡 − 𝑖; 𝑖 = 1,2, … 𝑝 𝑎_𝑡 : Error pada periode ke-𝑡

𝜙_𝑖 : Parameter autoregressive ke-𝑖; 𝑖 = 1,2, … 𝑝

Diasumsikan bahwa 𝑎_𝑡 saling bebas dengan 𝑍_𝑡−1, 𝑍_𝑡−1, … 2. Model Moving Average (MA) Orde q

Pada kasus berhingga bobot tak nol, diperoleh proses rerata bergerak (moving average process). Menurut Wei (2006), bentuk umum proses MA dapat dinyatakan sebagai berikut :

𝑍_𝑡 = 𝑎_𝑡− 𝜃₁𝑎_𝑡−1− 𝜃₂𝑎_𝑡−2− ⋯ − 𝜃_𝑝𝑎_𝑡−𝑝 Dengan

(12)

12 𝑍_𝑡 : Data pada periode ke-𝑡; 𝑡 = 1,2, … 𝑛 𝑎_𝑡−𝑖 : Error pada periode ke 𝑡 − 𝑖; 𝑖 = 1,2, … 𝑝 𝑎_𝑡 : Error pada periode ke-𝑡

𝜃_𝑖 : Parameter moving average ke-𝑖; 𝑖 = 1,2, … 𝑝

Biasanya dalam praktik model MA biasanya hanya terjadi pada lag ke-1 dan 2 (Sediono, 2014).

3. Model Autoregressive Moving Average (ARMA) Orde p dan q

Model ini merupakan gabungan antara AR(p) dan MA(q), sehingga dengan gabungan model tersebut maka autokorelasinya dapat dipertimbangkan baik nilai yang berturut pada periode sebelumnya dari variabel dependen yang diramalkan serta nilai berturut -turut dari residual pada periode sebelumnya. Model Autoregressive Moving Average dinyatakan ARMA(p, q) dengan bentuk umum sebagai berikut :

𝑍_𝑡 = 𝜙₀ + 𝜙₁𝑍_𝑡−1+ ⋯ + 𝜙_𝑝𝑍_𝑡−𝑝+ 𝑎_𝑡− 𝜃₁𝑎_𝑡−1− 𝜃₂𝑎_𝑡−2− ⋯ − 𝜃_𝑞𝑎_𝑡−𝑞 Dengan

𝑍_𝑡 :Data pada periode ke-𝑡; 𝑡 = 1,2, … 𝑛 𝑎_𝑡 : Error pada periode ke-𝑡

𝑎_𝑡−𝑖 : Error pada periode ke 𝑡 − 𝑖; 𝑖 = 1,2, … 𝑞 𝜃_𝑖 : Parameter moving average ke-𝑖; 𝑖 = 1,2, … 𝑞 𝜙₀ : Konstanta

𝜙_𝑖 : Parameter autoregressive ke-𝑖; 𝑖 = 1,2, … 𝑝

4. Model Autoregressive Integrated Moving Average (ARIMA)

Jika model analisis runtun waktu tidak memenuhi sifat stasioner, maka dapat dilakukan differencing pada data asli untuk menghasilkan data yang lebih mendekati atau bersifat stasioner. Model ini merupakan gabungan antara AR(p) dan MA(q), dinyatakan ARMA(p, q) dengan bentuk umum sebagai berikut :

a. Model ARIMA (p,d,q)

𝜙_𝑝(𝐵)(1 − 𝐵)^𝑑𝑍_𝑡 = 𝜙₀+ 𝜃(𝐵)𝑎_𝑡, dimana 𝜙_𝑝(𝐵) sebaga operaor AR (p), 𝜃_𝑞(𝐵) sebagai operator MA(q), dan (1 − 𝐵)^𝑑𝑍_𝑡 adalah operator dari differencing (d).

b. Model ARIMA (0,d,q)

Model ini dapat disebut juga dengan model IMA (d,q) dengan bentuk matematis sebagai berikut :

(13)

13

(1 − 𝐵)^𝑑𝑍_𝑡= 𝜃_𝑞(𝐵)𝑎_𝑡, dimana 𝜃(𝐵) = (1 − 𝜃₁𝐵 − 𝜃₂𝐵²− ⋯ − 𝜃_𝑞𝐵^𝑞) c. Model ARIMA (p,d,0)

Model ini dapat disebut juga dengan model ARI (p,d) dengan bentuk matematis sebagai berikut :

d. 𝜙_𝑝(𝐵)(1 − 𝐵)^𝑑𝑍_𝑡 = 𝑎_𝑡, dimana 𝜙(𝐵) = (1 − 𝜙₁𝐵 − 𝜙₂𝐵²− ⋯ − 𝜙_𝑝𝐵^𝑝)

5. Model ARIMA Multiplikatif

Model ARIMA multiplikatif mengandung unsur musiman dan non musiman yang dapat dinyatakan sebagai model ARIMA (𝑝, 𝑑, 𝑞)(𝑃, 𝐷, 𝑄)^𝑆. Bentuk umum dari model tersebut adalah sebagai berikut (Wei, 2006):

𝜙_𝑝(𝐵)Φ_𝑃(𝐵^𝑠)(1− 𝐵)^𝑑(1− 𝐵^𝑠)^𝐷𝑍_𝑡 = 𝜃_𝑞(𝐵)Θ_𝑄(𝐵^𝑆)𝑎_𝑡 Dengan :

𝜙_𝑝 = (1⁡ − ⁡ 𝜙₁𝐵⁡ − ⁡ 𝜙₂𝐵²− ⁡ ⋯⁡− ⁡ 𝜙_𝑝𝐵^𝑝) 𝜃_𝑞(𝐵) = (1 − 𝜃₁𝐵⁡ − ⁡ 𝜃₂𝐵²− ⁡ ⋯⁡− ⁡ 𝜃_𝑞𝐵^𝑞) Φ_𝑃(𝐵^𝑠) = (1 − Φ₁𝐵^𝑠− ⁡ Φ₂𝐵^𝑠 − ⁡ ⋯⁡− ⁡ Φ_𝑃𝐵^𝑠)

𝛩_𝑄(𝐵^𝑠) = (1 − 𝛩₁𝐵^𝑠− ⁡ 𝛩₂𝐵^𝑠− ⁡ ⋯⁡− ⁡ 𝛩_𝑄𝐵^𝑠)

Keterangan :

p, d, q : Order AR, differencing, dan MA non musiman.

P, D, Q : Order AR, differencing, dan MA musiman.

𝜙_𝑝(𝐵) : Polinomial AR(p) non musiman 𝜃_𝑞(𝐵) : Polinomial MA(q) non musiman Φ_𝑃(𝐵^𝑠) : Polinomial AR(P) musiman atau SAR 𝛩_𝑄(𝐵^𝑠) : Polinomial MA(Q) musiman atau SMA (1− 𝐵)^𝑑𝑍_𝑡 : Operator differencing non musiman

(1− 𝐵^𝑠)^𝐷𝑍_𝑡 : Operator differencing musiman 𝐵 : Operator backshift

𝑆 : 3 (triwulan), 4 (kuartal), 6 (semester), ataupun 12 (tahunan)

(14)

14 6. Model ARIMA Musiman (Seasonal)

Model analisis runtun waktu musiman dinyatakan sebagai model arima (P,D,Q) yang bentuk umumnya dapat dirumuskan sebagai berikut:

Φ_P(𝐵^𝑠)(1 − 𝐵^𝑠)^𝐷𝑍_𝑡 = Θ_𝑄(𝐵^𝑆)𝑎_𝑡 Dengan :

Φ_𝑃(𝐵^𝑠) = (1 − Φ₁𝐵^𝑠− ⁡ Φ₂𝐵^𝑠 − ⁡ ⋯⁡− ⁡ Φ_𝑃𝐵^𝑠) 𝛩_𝑄(𝐵^𝑠) = (1 − 𝛩₁𝐵^𝑠− ⁡ 𝛩₂𝐵^𝑠− ⁡ ⋯⁡− ⁡ 𝛩_𝑄𝐵^𝑠)

Keterangan :

Φ_𝑃(𝐵^𝑠) : Polinomial AR(P) musiman atau SAR 𝛩_𝑄(𝐵^𝑠) : Polinomial MA(Q) musiman atau SMA (1− 𝐵^𝑠)^𝐷𝑍_𝑡 : Operator differencing musiman

2.4 Peramalan

Peramalan (forecasting) adalah seni dan ilmu untuk memperkirakan kejadian di masa depan (Heizer dan Render, 2009). Langkah dalam metode peramalan secara umum adalah pengumpulan data, menyeleksi data dan memilih data, memilih model peramalan, menerapkan model untuk peramalan, evaluasi hasil akhir (Subagyo, 1986).

Peramalan dilakukan dengan menggunakan data historis yang selanjutnya diproyeksikan ke masa mendatang dengan menggunakan suatu bentuk model sistematis.

Manfaat dari peramalan ini yaitu mampu menganalisis suatu kondisi yang akan diteliti guna memprediksi suatu kondisi terkait hal yang diteliti di masa depan.

2.5 MAPE (Mean Absolute Percentage Error)

MAPE (Mean Absolute Percentage Error) adalah alat statistik yang digunakan untuk mengukur keakuratan suatu model statistik dalam melakukan prediksi atau peramalan.

Rumus MAPE:

𝑀𝐴𝑃𝐸 =

∑ |(𝐴_𝑡− 𝐹_𝑡) 𝐴_𝑡 |

𝑛 𝑡=1

𝑛 ×100%

Dengan,

𝐴_𝑡 = nilai data aktual 𝐹_𝑡= nilai data peramalan 𝑛 = ukuran sampel

(15)

15

Semakin kecil MAPE maka semakin akurat sebuah model dalam melakukan peramalan. Hal ini berarti sebuah model yang memiliki nilai MAPE sebesar 5%

merupakan model yang lebih baik dalam melakukan peramalan dibandingkan model lain yang memiliki MAPE sebesar 10%. Interpretasi nilai MAPE dapat dilihat dari interval nilainya sebagai berikut.

Tabel 2.2 Kategori Nilai MAPE

Range MAPE Arti Nilai

<10% Kemampuan model peramalan sangat baik 10-20% Kemampuan model peramalan baik 20-50% Kemampuan model peramalan layak

>50% Kemampuan model peramalan buruk

(16)

16 BAB III

METODE PENELITIAN 3.1 Metode dan Sumber Data Penelitian

Penelitian ini menggunakan metode penelitian kuantitatif. Data yag digunakan dalam penelitian ini adalah data hari hujan Kota Bandung pada Januari 2009 sampai Desember 2018 yang diperoleh secara sekunder dari situs web bandungkota.bps.go.id.

3.2 Variabel Penelitian

Variabel yang diolah dan dianalisis dalam penelitian ini adalah hari hujan Kota Bandung pada Januari 2009 sampai Desember 2018 yang berjumlah 120 data pengamatan.

3.3 Langkah – Langkah Analisis Data

Metode analisis data yang digunakan dalam penelitian ini adalah metode Autoregressive Integrated Moving Average (SARIMA). Langkah – langkah analisis data untuk membentuk model SARIMA dan melakukan peramalan dengan bantuan software Minitab adalah sebagai berikut.

1. Mengidentifikasi kestasioneran data dalam mean dan varians a. Membuat Trend Plot

1) Klik menu Stat → Time Series → Trend Analysis 2) Muncul kotak dialog Trend Analysis

• Variable: Hari Hujan

• Model Type : Linear 3) Lalu klik OK

b. Membuat ACF Plot

1) Klik menu Stat → Time Series → Autocorrelation..

2) Muncul kotak dialog Autocorrelation Function

• Series: Hari Hujan 3) Lalu klik OK

c. Membuat PACF Plot

1) Klik menu Stat → Time Series → Partial Autocorrelation..

2) Muncul kotak dialog Partial Autocorrelation Function

(17)

17

• Series: Hari Hujan 3) Lalu klik OK

2. Mentransformasikan data sehingga stasioner dalam mean dan varians

a. Jika data belum stasioner dalam varians, maka data ditransformasi menggunakan transformasi Box-Cox.

1) Klik menu Stat → Control Charts → Box-Cox Transformation…

2) Muncul kotak dialog Box-Cox Transformations

• Pilih All observations for a chart are in one column : Hari Hujan

• Subgroup sizes : 1 3) Klik Options

• Store transformed data in : Box-cox (C2) 4) Lalu klik OK

b) Kemudian, jika data hasil transformasi Box-Cox belum stasioner dalam mean, maka dilanjutkan dengan melakukan differencing.

1) Klik menu Stat → Time Series → Differences…

2) Muncul kotak dialog Differences

• Series : Box-cox (C2)

• Store differences in : Diff1 (C3)

• Lag : 1 3) Lalu klik OK

Gunakan data hasil differencing untuk melihat Time Series Plot, ACF dan PACF sesuai dengan langkah (1).

3. Apabila setelah di differencing plotnya masih tidak stasioner maka di differencing lagi pada musiman seperti pada langkah (2b) dengan mengisi Series : Diff1 (C3) dan Lag : 12. Kemudian gunakan data differencing lag 12 untuk melihat Time Series Plot, ACF dan PACF sesuai dengan langkah (1).

4. Menentukan orde SARIMA berdasarkan plot ACF dan PACF yang diperoleh.

5. Membuat model SARIMA dengan melakukan pemeriksaan diagnostik terhadap beberapa kemungkinan model yang diperoleh.

1) Klik menu Stat → Time Series → ARIMA..

2) Muncul kotak dialog ARIMA

(18)

18

• Centang Fit seasonal model, lalu isi Period : 12

• Isi Autoregressive, Difference, dan Moving Average pada kotak isian Nonseasonal maupun Seasonal sesuai dengan kemungkinan-kemungkinan model

3) Lalu klik OK

6. Uji normalitas residual dari model terbaik yang didapatkan a. Menampilkan data residual

• Isi Autoregressive, Difference, dan Moving Average sesuai dengan model terbaik

3) Klik Storage → centang residual → klik OK 4) Lalu klik OK

b. Uji normalitas residual

1) Klik menu Stat → Basic Statistics → Normality Test..

2) Muncul kotak dialog Normality Test

• Variable : Residuals

• Test of Normality : Kolmogorov-Smirnov 3) Lalu klik OK

7. Forecasting

• Isi Autoregressive, Difference, dan Moving Average sesuai dengan model terbaik

3) Klik Forecasts

• Lead : 5 (banyak data yang akan diramalkan)

• Origin : 120 (banyak data asli) 4) Lalu klik OK

(19)

19 BAB IV

ANALISIS DAN PEMBAHASAN 4.1 Deskripsi Data

Berdasarkan data yang diperoleh dari situs web bandungkota.bps.go.id pada Lampiran 1, maka diperoleh gambaran umum hari hujan Kota Bandung pada Januari 2009 sampai Desember 2018 sebagai berikut :

Gambar 4.1 Statistik Deskriptif Data Hari Hujan Kota Bandung

Gambar 4.1 menunjukkan bahwa rata – rata bulanan hari hujan Kota Bandung pada Januari 2009 sampai Desember 2018 adalah 19.525 hari. Hari hujan terendah adalah 1 hari, yang terjadi pada bulan Agustus 2011. Sedangkan, hari hujan tertingginya adalah 31 hari, yang terjadi pada bulan Maret 2010.

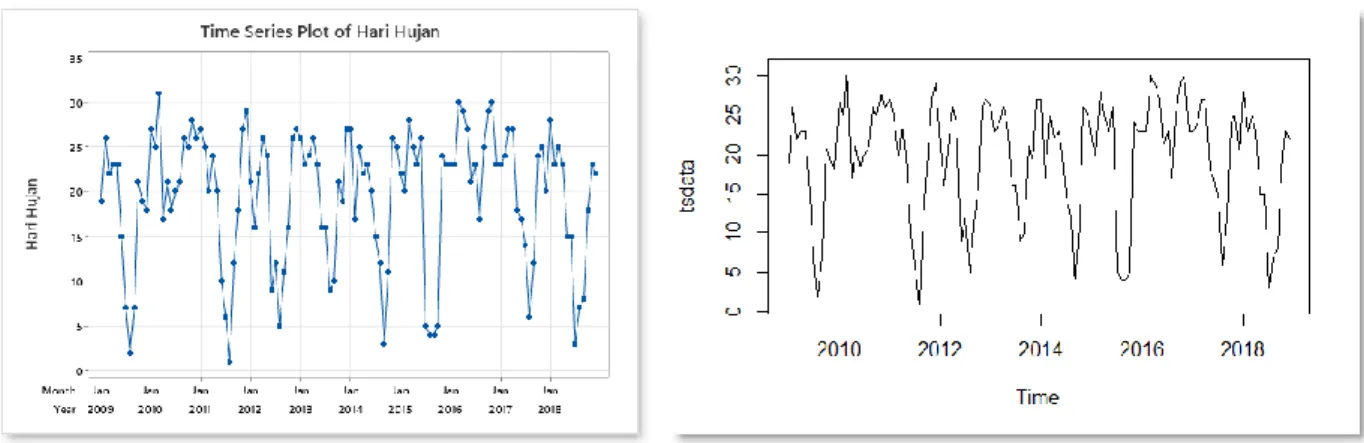
Gambar 4.2 Grafik Time Series Data Hari Hujan Kota Bandung 4.2 Identifikasi Kestasioneran Data

Dalam proses ARIMA, tahap pertama yang harus dilakukan adalah mengecek kestasioneran data dengan melihat grafik time series atau trend analysis, ACF, PACF, dan ADF (Dickey-Fuller Test) dari data hari hujan Kota Bandung tahun 2009-2018.

(20)

20

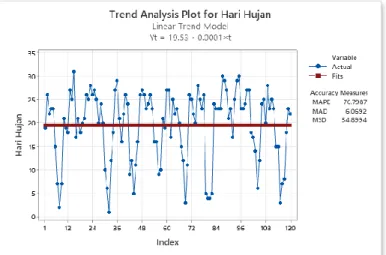
Gambar 4.3 Grafik Trend Analysis Data Hari Hujan Kota Bandung

Berdasarkan plot trend analysis pada Gambar 4.3, dapat dilihat bahwa data memiliki trend konstan sehingga data diprediksi sudah stasioner dalam varians.

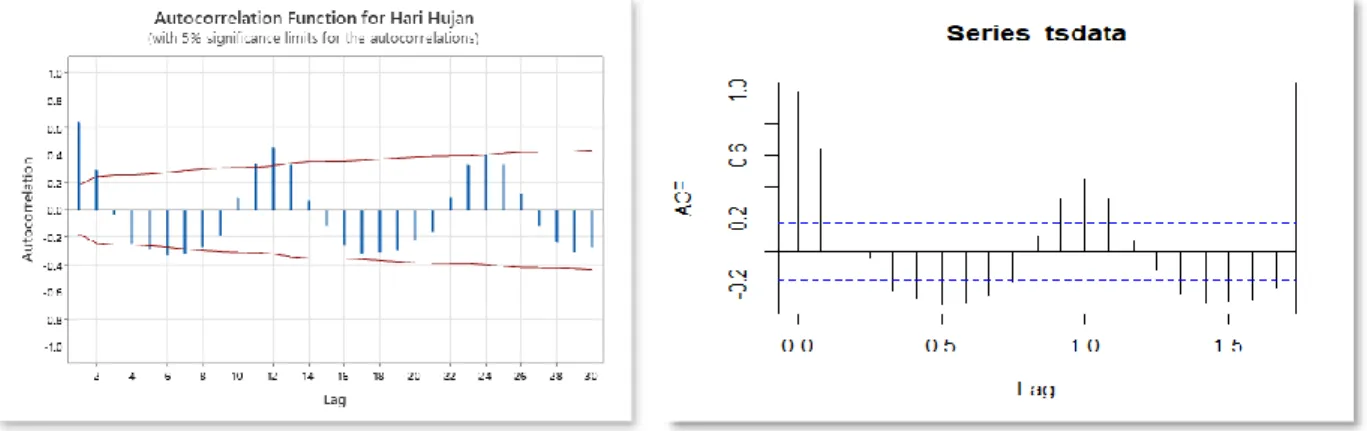
Gambar 4.4 Plot ACF Data Hari Hujan Kota Bandung

Plot ACF pada Gambar 4.4 menunjukkan turun linier lambat dan bergelombang, hal ini mengindikasikan bahwa data tidak stasioner dalam mean dan diindikasikan bahwa data tersebut adalah data musiman.

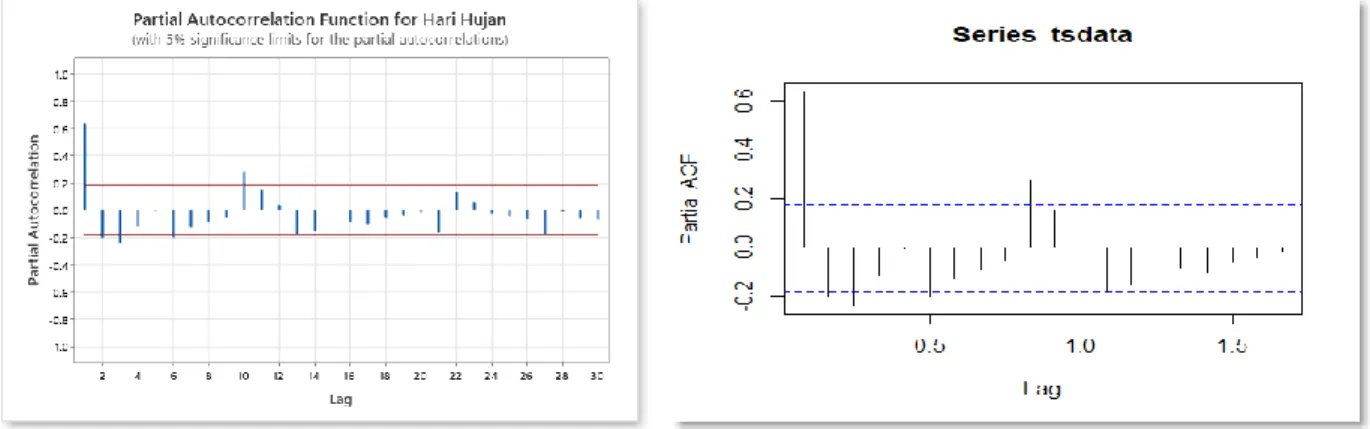
Gambar 4.5 Plot PACF Data Hari Hujan Kota Bandung Tahun 2009-2018

(21)

21

Plot PACF pada Gambar 4.5 terlihat bahwa hanya masih didapati lag selain lag musiman dan lag non musiman yang keluar dari garis significant limits. Hal tersebut juga mengidentifikasi bahwa data tidak stasioner.

Gambar 4.6 Uji ADF Data Hari Hujan Kota Bandung

Dilihat hasil uji Augmented Dickey-Fuller (ADF) pada Gambar 4.6, didapatkan P-value sebesar 0.3473 yang nilainya lebih dari taraf signifikansi alpha (5%) sehingga dapat disimpulkan data tidak stasioner dalam mean. Dari keempat gambar diatas, dapat disimpulkan bahwa data stasioner dalam varians tetapi tidak stasioner dalam mean. Selanjutnya, dilakukan transformasi Box-Cox untuk memastikan data sudah stasioner dalam varians.

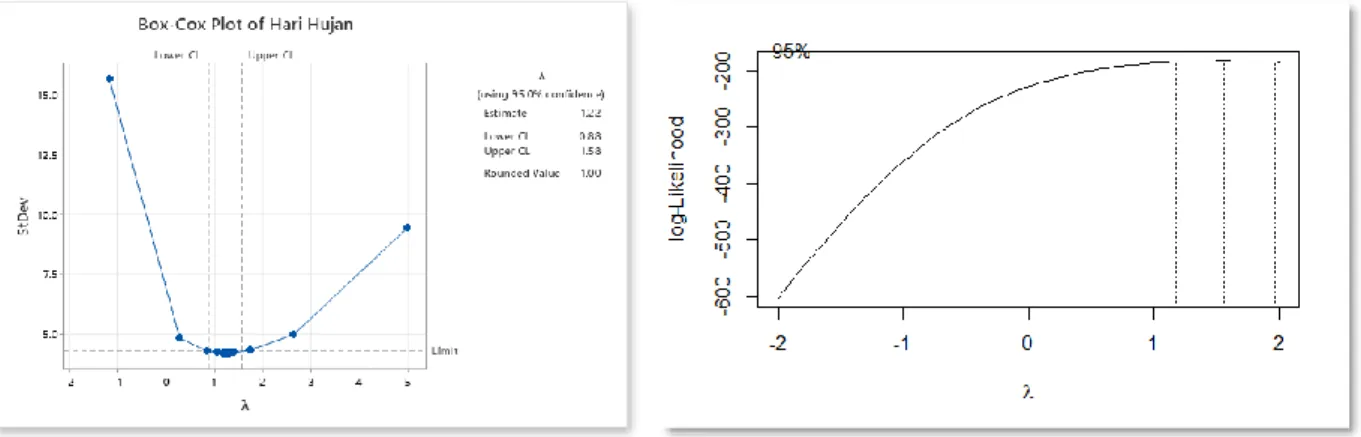
Gambar 4.7 Plot Box-Cox Hari Hujan Kota Bandung

Dari hasil transformasi Box-Cox, diketahui nilai rounded value atau lambda(𝜆) = 1. Berdasarkan Tabel 2.1, bentuk transformasi lambda(𝜆) = 1 yaitu 𝑍_𝑡. Sehingga, data tidak perlu ditransformasikan karena data sudah terbukti stasioner dalam varians tetapi tidak stasioner dalam mean.

Oleh karena data tidak stasioner dalam mean, maka dilakukan differencing pada data tersebut dan dihasilkan plot sebagai berikut.

(22)

22

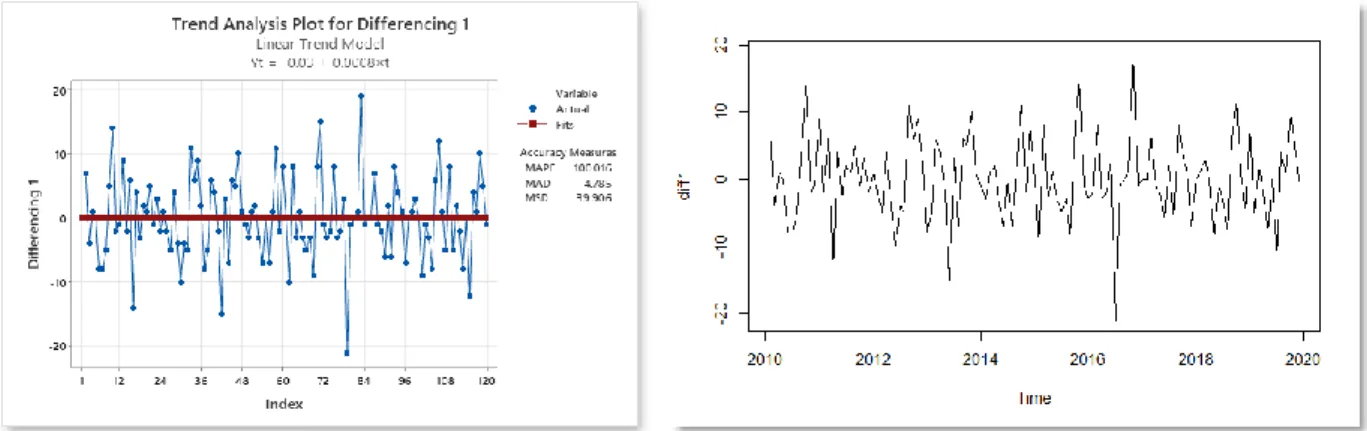
Gambar 4.8 Trend Analysis Plot Data Hasil Differencing 1

Gambar 4.9 Uji ADF Data Data Hasil Differencing 1

Berdasarkan Gambar 4.9, uji Augmented Dickey-Fuller (ADF) didapatkan P-value sebesar 0.01354 yang nilainya kurang dari taraf signifikansi alpha (5%) sehingga dapat disimpulkan data sudah stasioner, baik stasioner dalam mean maupun stasioner dalam varians. Hal tersebut menunjukkan bahwa proses differencing non musiman cukup dilakukan satu kali saja.

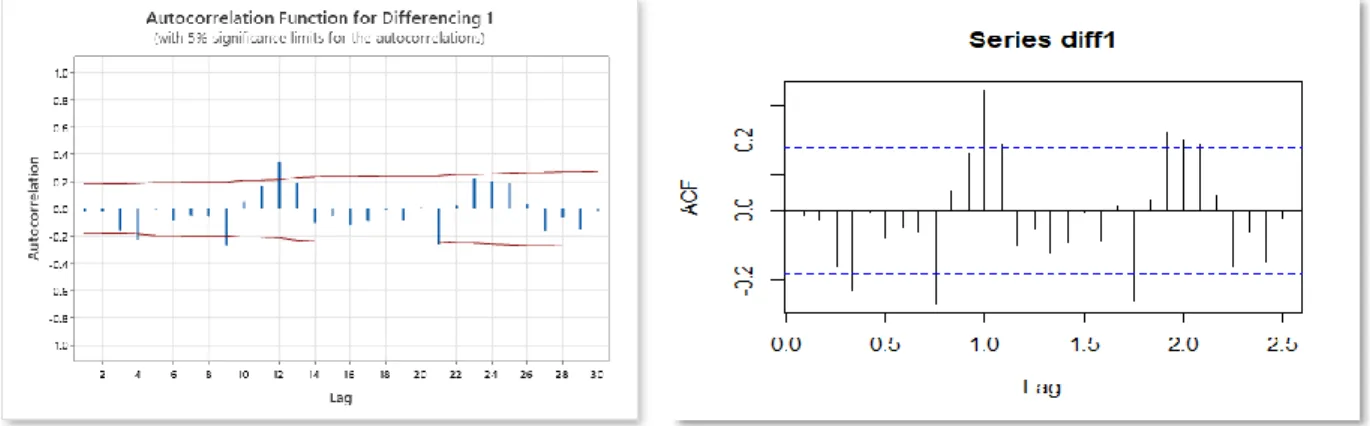
Gambar 4.10 Plot ACF Data Hasil Differencing 1

(23)

23

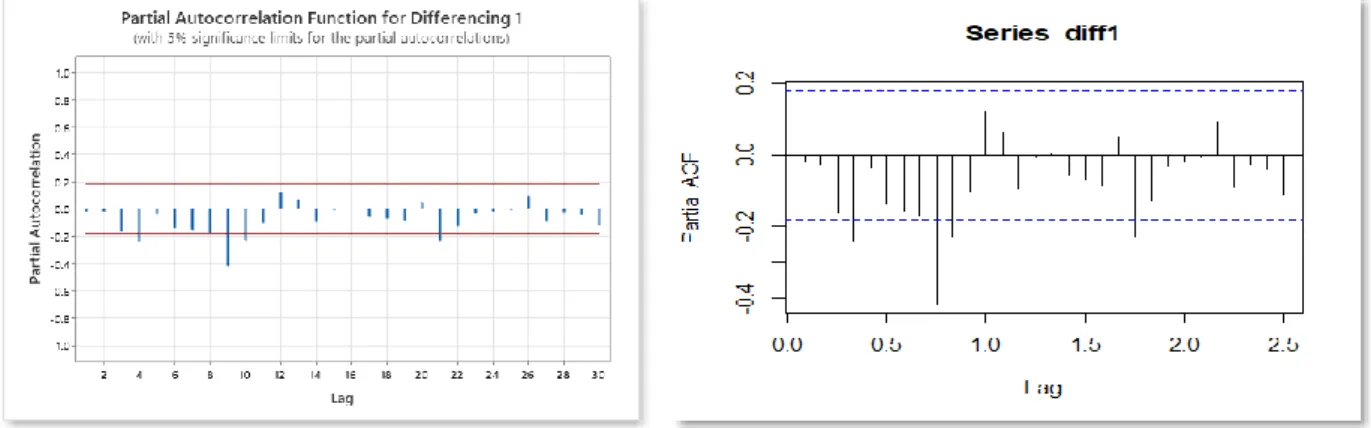
Gambar 4.11 Plot PACF Data Hasil Differencing 1

Kemudian, plot ACF menunjukkan bahwa ada beberapa lag yang keluar dari garis significant limits, yaitu, 4, 9, 12, dan 21. Adapun plot PACF yang juga menunjukkan bahwa terdapat beberapa lag yang keluar dari garis significant limits, yaitu 4, 9, 10, dan 21. Beberapa lag yang keluar termasuk dalam lag musiman. Sehingga, dapat disimpulkan bahwa data tersebut perlu dilakukan differencing musiman di lag 12. Lag 12 dipilih karena plot ACF data asli (sebelum dilakukan proses differencing) memperlihatkan bahwa lag tertinggi dalam setiap pola gelombang adalah kelipatan 12. Harapannya, didapatkan plot ACF dan PACF dengan lag non musiman dan musiman yang lebih jelas sehingga model analisis runtun waktu dapat diidentifikasi.

4.3 Identifikasi Model Analisis Runtun Waktu

Dalam tahap ini, dilakukan identifikasi model analisis runtun waktu dari data yang telah diperoleh. Setelah data berbentuk stasioner, langkah berikutnya adalah melakukan differencing musiman dengan lag 12.

Gambar 4.12 Trend Analysis Plot Data Hasil Differencing Musiman Lag 12

(24)

24

Gambar 4.13 Uji ADF Data Data Hasil Differencing Musiman Lag 12

Berdasarkan Gambar 4.12 dan Gambar 4.13, dapat dilihat bahwa data sudah tidak ada kecenderungan trend naik maupun turun dan nilai uji Augmented Dickey-Fuller (ADF) didapatkan P- value sebesar 0.01 yang nilainya kurang dari taraf signifikansi alpha (5%) sehingga dapat disimpulkan data sudah stasioner. Hal tersebut menunjukkan bahwa proses differencing musiman cukup dilakukan satu kali saja.

Gambar 4.14 Plot ACF Data Hasil Differencing Musiman Lag 12

Gambar 4.15 Plot PACF Data Hasil Differencing Musiman Lag 12

Plot ACF dan PACF data hasil differencing musiman lag 12 menunjukkan bahwa lag 1 (lag non musiman) dan lag 12 (lag musiman) keluar dari garis significance limits. Dengan demikian, beberapa model ARIMA yang dapat diperkirakan sesuai adalah sebagai berikut.

(25)

25

Tabel 4.1 Hasil Identifikasi Model Analisis Runtun Waktu Musiman

Model Nama Lain

ARIMA (0,1,1)(0,1,1)¹² IMASIMA ARIMA (0,1,1)(1,1,0)¹² IMASARI ARIMA (0,1,1)(1,1,1)¹² IMASARIMA ARIMA (1,1,0)(0,1,1)¹² ARISIMA ARIMA (1,1,0)(1,1,0)¹² ARISARI ARIMA (1,1,0)(1,1,1)¹² ARISARIMA ARIMA (1,1,1)(0,1,1)¹² ARIMASIMA ARIMA (1,1,1)(1,1,0)¹² ARIMASARI ARIMA (1,1,1)(1,1,1)¹² ARIMASARIMA 4.4 Pemilihan Model Terbaik

Syarat – syarat yang harus dimiliki model terbaik yaitu parameter – parameternya signifikan ditandai dengan p-value < α (5%), memiliki MSE (Mean Square Error) terkecil, dan memiliki residual white noise. Berikut ini adalah hasil estimasi parameter semua kemungkinan model yang disajikan dalam bentuk table.

Tabel 4.2 Estimasi Parameter ARIMA Hari Hujan Kota Bandung Model ARIMA Nilai Signifikansi

Parameter Residual MSE

(0,1,1)(0,1,1)¹²

Probabilistik MA 1 = 0.000

SMA 12 = 0.000 White Noise 24.1168 Deterministik

MA 1 = 0.000 SMA 12 = 0.000 Constant = 0.538

White Noise 24.3379

(0,1,1)(1,1,0)¹²

Probabilistik SAR 12 = 0.000

MA 1 = 0.000 White Noise 36.6581 Deterministik

SAR 12 = 0.000 MA 1 = 0.000

Constant = 0.793 Tidak White Noise ^35.1430

(0,1,1)(1,1,1)¹²

Probabilistik

SAR 12 = 0.835 MA 1 = 0.000 SMA 12 = 0.000

White Noise 24.3458

Deterministik

SAR 12 = 0.830 MA 1 = 0.000 SMA 12 = 0.000 Constant = 0.493

Tidak White Noise 24.5700

(1,1,0)(0,1,1)¹² Probabilistik AR 1 = 0.000

SMA 12 = 0.000 Tidak White Noise 25.6180 Deterministik AR 1 = 0.001

SMA 12 = 0.000 Tidak White Noise 26.3663

(26)

26

Constant = 0.721

(1,1,0)(1,1,0)¹²

Probabilistik AR 1 = 0.000

SAR 12 = 0.000 Tidak White Noise 37.2606 Deterministik

AR 1 = 0.000 SAR 12 = 0.000

Constant = 0.888 Tidak White Noise 37.6158

(1,1,0)(1,1,1)¹²

Probabilistik

AR 1 = 0.000 SAR 12 = 0.905 SMA 12 = 0.000

Deterministik

AR 1 = 0.000 SAR 12 = 0.907 SMA 12 = 0.000 Constant = 0.693

(1,1,1)(0,1,1)¹²

Probabilistik

AR 1 = 0.001 MA 1 = 0.000 SMA 12 = 0.000

White Noise 23.2889

Deterministik

AR 1 = 0.001 MA 1 = 0.000 SMA 12 = 0.000 Constant = 0.211

White Noise 23.4019

(1,1,1)(1,1,0)¹²

Probabilistik

AR 1 = 0.000 SAR 12 = 0.000

MA 1 = 0.000

White Noise 32.2114

Deterministik

AR 1 = 0.000 SAR 12 = 0.000

MA 1 = 0.000 Constant = 0.379

White Noise 32.5519

(1,1,1)(1,1,1)¹²

Probabilistik

AR 1 = 0.001 SAR 12 = 0.671

MA 1 = 0.000 SMA 12 = 0.000

White Noise 23.4583

Deterministik

AR 1 = 0.001 SAR 12 = 0,671

MA 1 = 0.000 Constant = 0.201

White Noise 23.5706 Berdasarkan hasil estimasi parameter ARIMA, telah didapatkan model yang memenuhi syarat – syarat, yaitu parameter – parameternya signifikan ditandai dengan p-value < α, memiliki MSE (Mean Square Error) terkecil, dan memiliki residual yang bersifat white noise, yaitu model ARIMA(1,1,1)(0,1,1)¹² probabilistik.

(27)

27 4.5 Uji Asumsi Residual

a. Uji Asumsi Residual White Noise

Uji Independensi residual white noise dapat dilakukan dengan menggunakan statistik uji Ljung-Box dengan hipotesis pengujian adalah sebagai berikut.

H₀: Tidak ada korelasi residual antar lag (k = 0)

H₁:Terdapat korelasi residual antar lag (Paling sedikit ada satu k ≠ 0, dengan⁡k = 1,2,3, … )

Gambar 4.16 Output Ljung-Box Test ARIMA(1,1,1)(0,1,1)¹² Probabilistik

Berdasarkan gambar 4.12 didapatan semua nilai signifikansi lag bernilai lebih dari α (5%). Sehingga dapat disimpulkan bahwa tidak terdapat korelasi residual antar lag.

Selain itu, hasil pemeriksaan apakah residual model ARIMA(1,1,1)(0,1,1)¹² Probabilistik white noise juga dapat terlihat melalui plot ACF dan PACF residual, dimana tidak ada lag yang keluar dari significance limits dalam kedua plot tersebut.

Gambar 4.17 Plot ACF Residual ARIMA(1,1,1)(0,1,1)¹² Probabilistik

(28)

28

Gambar 4.18 Plot PACF Residual ARIMA(1,1,1)(0,1,1)¹² Probabilistik b. Uji Asumsi Residual Berdistribusi Normal

Setelah mendapatkan model terbaik yaitu ARIMA(1,1,1)(0,1,1)¹² probabilistik, tahap analisis berikutnya adalah melakukan pengujian kenormalan residual. Jika residual memenuhi asumsi normalitas, maka model tepat untuk digunakan.

Perumusan hipotesis untuk melakukan pengujian tersebut adalah sebagai berikut.

H₀: Residual model berdistribusi normal H₁: Residual model tidak berdistribusi normal

Pengujian ini menggunaan metode Kolmogorov-Smirnov, dengan daerah kritis yaitu menolak H₀apabila nilai p-value < 5%.

Gambar 4.19 Uji Normalitas Residual Model ARIMA(1,1,1)(0,1,1)¹² Probabilistik

(29)

29

Pada grafik hasil pengujian residual model, terlihat bahwa sebaran data residual mengikuti garis distribusi normal. Kemudian, didapatkan nilai p-value 0.296, dimana nilai tersebut lebih besar daripada α (5%). Selanjutnya dapat diputuskan untuk menolak H₀dan ditarik kesimpulan bahwa residual model telah berdistribusi normal.

4.6 Persamaan Model ARIMA(1,1,1)(0,1,1)¹² Probabilistik

Setelah model dinyatakan tepat untuk digunakan sesuai konsep analisis runtun waktu, maka tahap selanjutnya adalah menyusun persamaan model. Persamaan dari ARIMA (1,1,1)(0,1,1)¹² probabilistik adalah sebagai berikut:

Secara umum bentuk model ARIMA (p,d,q)(P,D,Q)^S

𝜙_𝑝(𝐵)∅_𝑃(𝐵^𝑠)(1 − 𝐵)^𝑑(1 − 𝐵^𝑠)^𝐷𝑍_𝑡 = 𝛿 + 𝜃_𝑞(𝐵)Θ_𝑄(𝐵^𝑠)𝑎_𝑡⁡ Model ARIMASIMA → (1,1,1)(0,1,1)¹²

Persamaan arimanya sebagai berikut.

𝜙_𝑝(𝐵)∅_𝑃(𝐵^𝑠)(1 − 𝐵)^𝑑(1 − 𝐵^𝑠)^𝐷𝑍_𝑡 = 𝛿 + 𝜃_𝑞(𝐵)Θ_𝑄(𝐵^𝑠)𝑎_𝑡⁡ 𝜙₁(𝐵)∅₀(𝐵¹²)(1 − 𝐵)¹(1 − 𝐵¹²)¹𝑍_𝑡= 𝛿 + 𝜃₁(𝐵)Θ₁(𝐵¹²)𝑎_𝑡⁡

(1 − 𝜙₁𝐵)(1 − 𝜙₀𝐵¹²)(1 − 𝐵)¹(1 − 𝐵¹²)¹𝑍_𝑡= 𝛿 + (1 − 𝜃₁𝐵)(1 − Θ₁𝐵¹²)𝑎_𝑡 (1 − 𝜙₁𝐵)(1 − 𝐵)(1 − 𝐵¹²)𝑍_𝑡= 𝛿 + (1 − 𝜃₁𝐵)(1 − Θ₁𝐵¹²)𝑎_𝑡

(1 − 𝜙₁𝐵)⁡(1 − 𝐵¹²− 𝐵 + 𝐵¹³)𝑍_𝑡= 𝛿 + (1 − 𝜃₁𝐵 − Θ₁𝐵¹²+ 𝜃₁Θ₁𝐵¹³)𝑎_𝑡 Karena 𝐵^𝑚. 𝑍_𝑡 = 𝑍_𝑡−𝑚 dan 𝐵^𝑚. 𝑎_𝑡 = 𝑎_𝑡−𝑚, maka

(1 − 𝜙₁𝐵)⁡(𝑍_𝑡− 𝑍_𝑡𝐵¹²− 𝑍_𝑡𝐵 + 𝑍_𝑡𝐵¹³) =𝛿 +𝑎_𝑡− 𝜃₁𝐵𝑎_𝑡− Θ₁𝐵¹²𝑎_𝑡+ 𝜃₁Θ₁𝐵¹³𝑎_𝑡 (1 − 𝜙₁𝐵)⁡(𝑍_𝑡− 𝑍_𝑡−12− 𝑍_𝑡−1+ 𝑍_𝑡−13) =𝛿 +𝑎_𝑡− 𝜃₁𝑎_𝑡−1− Θ₁𝑎_𝑡−12+ 𝜃₁Θ₁𝑎_𝑡−13

𝑍_𝑡− 𝑍_𝑡−12− 𝑍_𝑡−1+ 𝑍_𝑡−13− 𝜙(𝐵𝑍_𝑡− 𝐵𝑍_𝑡−12− 𝐵𝑍_𝑡−1+ 𝐵𝑍_𝑡−13) =𝛿 +𝑎_𝑡− 𝜃₁𝑎_𝑡−1− Θ₁𝑎_𝑡−12+ 𝜃₁Θ₁𝑎_𝑡−13 𝑍_𝑡=𝛿 +𝑍_𝑡−12+ 𝑍_𝑡−1− 𝑍_𝑡−13+ 𝜙(𝑍_𝑡−1− 𝑍_𝑡−13− 𝐵𝑍_𝑡−2+ 𝐵𝑍_𝑡−14)+𝑎_𝑡− 𝜃₁𝑎_𝑡−1− Θ₁𝑎_𝑡−12+ 𝜃₁Θ₁𝑎_𝑡−13 𝑍_𝑡= 𝑍_𝑡−12+ 𝑍_𝑡−1− 𝑍_𝑡−13+ 0.369(𝑍_𝑡−1− 𝑍_𝑡−13− 𝐵𝑍_𝑡−2+ 𝐵𝑍_𝑡−14) + 𝑎_𝑡− 0.8844𝑎_𝑡−1− 0.8679𝑎_𝑡−12+ 0.76757𝑎_𝑡−13

Dengan 𝑍̇_𝑡 = 𝑍_𝑡 → bentuk transformasi apabila rounded value (𝜆) bernilai 1.

4.7 Forecasting Hari Hujan Kota Bandung

Berdasarkan persamaan model ARIMA(1,1,1)(0,1,1)¹² probabilistik yang telah dirumuskan sebelumnya, maka selanjutnya dapat dilakukan forecasting untuk memprediksi hari hujan Kota Bandund selama lima bulan ke depan, yaitu bulan Januari−Mei 2019. Berikut ini adalah penyajian hasil forecasting.

(30)

30

Gambar 4.20 Hasil Peramalan Hari Hujan Kota Bandung Bulan Januari−Mei 2019

Gambar 4.21 Time Series Plot dengan Hasil Peramalan Hari Hujan Kota Bandung

4.8 MAPE Hari Hujan Kota Bandung

Tabel 4.3 Perbandingan Hasil Forecasting dengan Hari Hujan Kota Bandung 2019 Bulan Forecast Data Asli

Januari 22.1798 24

Februari 19.9970 24

Maret 23.4073 25

April 22.2860 25

Mei 18.7367 23

Data hasil peramalan terlihat tidak memiliki perbedaan yang besar dengan data asli.

Kemudian, nilai data asli juga masih masuk dalam selang kepercayaan 95% untuk nilai forecast. Selanjutnya akan dihitung nilai MAPE (Mean Absolute Percentage Error) dan didapatan nilai sebagai berikut.

(31)

31

Tabel 4.4 Perhitungan Nilai MAPE

Data Asli Forecast |(𝐴𝑡− 𝐹𝑡) ×100⁄𝐴𝑡|

24 22.1798 7.584167

24 19.9970 16.67917

25 23.4073 6.3708

25 22.2860 10.856

23 18.7367 18.53609

Jumlah 60.02622

MAPE 12.00524

Berdasarkan hasil perhitungan MAPE pada tabel 4.4 didapatkan nila MAPE yakni 12.00524, maka dapat dikategorikan bahwa hasil forecasting (peramalan) dapat dikatakan baik karena berada di range 10-20%. Jadi, model tersebut cocok dijadikan acuan untuk memprediksi hari hujan Kota Bandung Bulan Januari−Mei 2019.

(32)

32 BAB V PENUTUPAN 5.1 Kesimpulan

Berdasarkan hasil dan pembahasan pada bab sebelumnya, maka dapat ditarik beberapa kesimpulan dari penelitian ini yaitu sebagai berikut.

1. Pada rentang waktu Januari 2009 hingga Desember 2018, hari hujan Kota Bandung cenderung fluktuatif pada setiap periode. Rata – rata bulanan hari hujan Kota Bandung adalah 19.525 hari. Hari hujan terendah adalah 1 hari, yang terjadi pada bulan Agustus 2011. Sedangkan, hari hujan tertingginya adalah 31 hari, yang terjadi pada bulan Maret 2010.

2. Model ARIMA yang sesuai untuk data hari hujan Kota Bandung Tahun 2009-2018 adalah ARIMA(1,1,1)(0,1,1)¹² probabilistik dengan bentuk model sebagai berikut.

3. Pada bulan Januari−Mei 2019, data hasil peramalan terlihat tidak memiliki perbedaan yang besar dengan data asli. Kemudian, nilai data asli juga masih masuk dalam selang kepercayaan 95% untuk nilai forecast dan nilai MAPE didapatkan 12.00524, sehingga dikategorikan bahwa hasil forecasting dikatakan baik

5.2 Saran

Berdasarkan hasil penelitian dan pembahasan, maka saran yang dapat diajukan oleh penulis, yaitu :

1. Diharapkan hasil penelitian ini dapat diaplikasikan untuk meramalkan hari hujan Kota Bandungper bulan.

2. Bagi peneliti lain yang tertarik pada permasalahan yang sama, diharapkan untuk mengevaluasi hasil penelitian saya dan meneliti faktor – faktor yang berpengaruh jumlah hari hujan Kota Bandung dengan metode yang berbeda, agar penelitian bisa memiliki ruang lingkup yang lebih luas.

𝒁_𝒕= 𝒁_{𝒕−𝟏𝟐}+ 𝒁_𝒕−𝟏− 𝒁_{𝒕−𝟏𝟑}+ 𝟎. 𝟑𝟔𝟗(𝒁_𝒕−𝟏− 𝒁_{𝒕−𝟏𝟑}− 𝑩𝒁_𝒕−𝟐+ 𝑩𝒁_{𝒕−𝟏𝟒}) + 𝒂_𝒕− 𝟎. 𝟖𝟖𝟒𝟒𝒂_𝒕−𝟏− 𝟎. 𝟖𝟔𝟕𝟗𝒂_{𝒕−𝟏𝟐}+ 𝟎. 𝟕𝟔𝟕𝟓𝟕𝒂_{𝒕−𝟏𝟑}

(33)

33

DAFTAR PUSTAKA

Budiyanto, Aris. 2022. Kota Bandung dalam Angka 2022 [Online].

https://bandungkota.bps.go.id/publication.html. Diakses pada 1 Juni 2022.

Dini, Amah Majidah. 2009. Hubungan Faktor Ikim dan Angka Insiden Demam Berdarah Dengue di Kabupaten Serang Tahun 2007 – 2008 [Online].

https://lib.ui.ac.id/file?file=digital/124268-S-5601-Hubungan%20faktor-Literatur.pdf.

Diakses pada 1 Juni 2022.

Rusdin. 2008. Pasar Modal Teori Masalah dan Kebijakan dalam Praktek. Bandung: Alfabeta.

Sediono. 2014. Diktat Kuliah Analisis Runtun Waktu. Surabaya.

Soejoeti, Zanzawi. 1987. Analisis Runtun Waktu. Jakarta: Karunika.

Tjasyono, Bayong. 2006. “Meteorologi Indonesia : Karakteristik Dan Sirkulasi Atmosfer”.

Jakarta : Badan Meteorologi dan Geofisika.

Wei, W.W.S. 2006. Time Series Analysis: Univariate and Multivariate Methods Second Edition. New Jersey: Pearson Prentice Hall.s

(34)

34 LAMPIRAN

Lampiran 1. Data Hari Hujan Kota Bandung Tahun 2010-2019

Lampiran 2. Data Hasil Differencing Diff 1

Diff Musiman

Lag 12

* *

7 *

-4 *

1 *

0 *

-8 *

-5 *

5 *

14 *

-2 *

-1 *

9 *

-2 -9

6 10

-14 -15

4 4

-3 5

2 10

1 6

5 0

-1 -15

3 5

-2 -1

1 -8

-2 0

-5 -11

4 18

-4 -8

-10 -7

-4 -6

-5 -6

11 6

6 7

9 6

2 4

-8 -9

-5 -3

6 11

4 0

-2 2

-15 -5

3 7

-7 -2

6 -5

5 -1

10 1

1 -1

-1 7

-3 2

1 -5

2 -2

-3 -1

-7 8

0 -3

-7 0

1 -5

11 6

-2 -12

8 7

0 1

Bulan Hari Hujan

2010 2011 2012 2013 2014 2015 2016 2017 2018 2019

Januari 19 27 27 21 26 27 22 23 23 28

Februari 26 25 25 16 23 17 20 23 24 23

Maret 22 31 20 22 24 25 28 30 27 25

April 23 17 24 26 26 22 25 29 27 23

Mei 23 21 20 24 23 23 23 27 18 15

Juni 15 18 10 9 16 20 26 21 17 15

Juli 7 20 6 12 16 15 5 23 14 3

Agustus 2 21 1 5 9 12 4 17 6 7

September 7 26 12 11 10 3 4 25 12 8

Oktober 21 25 18 16 21 11 5 29 24 18

November 19 28 27 26 19 26 24 30 25 23

Desember 18 26 29 27 27 25 23 23 20 22

(35)

35

-10 -7

8 7

-3 -5

1 4

-3 4

-5 -5

-3 4

-9 -10

8 -3

15 17

-1 -9

-3 -3

-2 8

8 0

-3 0

-2 -3

3 6

-21 -16

-1 2

0 9

1 -7

19 4

-1 0

0 3

0 2

7 -1

-1 2

-2 0

-6 -9

2 23

-6 -5

8 8

4 3

1 -18

-7 -6

0 0

1 1

3 -4

0 1

-9 -7

-1 5

-3 -5

-8 -2

6 -2

12 8

1 0

-5 2

8 8

-5 -6

2 -1

-2 -2

-8 1

0 1

-12 -9

4 12

1 -5

10 -2

5 4

-1 4

Lampiran 3. Output MINITAB Model ARIMA(1,1,1)(0,1,1)12 Probabilistik

(36)

36

(37)

37 Lampiran 4. Syntax Program R

Program Tugas Individu

Erena (082011833031)

require(pacman)

## Loading required package: pacman

## Warning: package 'pacman' was built under R version 4.1.3

#load packages

pacman::p_load(datasets, tseries) pacman::p_load(rio)

pacman::p_load(MASS)

#Membaca Data library(openxlsx)

## Warning: package 'openxlsx' was built under R version 4.1.3 masterdata <- read.xlsx("C:/Users/acer/Downloads/hari.xlsx") head(masterdata)

## Jumlah

## 1 19

## 2 26

## 3 22

## 4 23

## 5 23

## 6 15 tail(masterdata)

## Jumlah

## 115 3

## 116 7

## 117 8

## 118 18

## 119 23

## 120 22

summary(masterdata)

## Jumlah

## Min. : 1.00

## 1st Qu.:15.75

## Median :22.00

## Mean :19.52

## 3rd Qu.:25.00

## Max. :31.00

#Plot time series

tsdata <- ts(masterdata$Jumlah, frequency = 12, start = c(2009, 1)) tsdata

(38)

38

## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec

## 2009 19 26 22 23 23 15 7 2 7 21 19 18

## 2010 27 25 31 17 21 18 20 21 26 25 28 26

## 2011 27 25 20 24 20 10 6 1 12 18 27 29

## 2012 21 16 22 26 24 9 12 5 11 16 26 27

## 2013 26 23 24 26 23 16 16 9 10 21 19 27

## 2014 27 17 25 22 23 20 15 12 3 11 26 25

## 2015 22 20 28 25 23 26 5 4 4 5 24 23

## 2016 23 23 30 29 27 21 23 17 25 29 30 23

## 2017 23 24 27 27 18 17 14 6 12 24 25 20

## 2018 28 23 25 23 15 15 3 7 8 18 23 22 plot.ts(tsdata)

acf(tsdata)

pacf(tsdata)

(39)

39

#Cek kestasioneritasan Data library(tseries)

adf.test(tsdata,k=12)

##

## Augmented Dickey-Fuller Test

##

## data: tsdata

## Dickey-Fuller = -2.5519, Lag order = 12, p-value = 0.3473

## alternative hypothesis: stationary

#transformasi box-cox boxcox(lm(tsdata~1))

(40)

40

#diff 1

diff1 <- diff(tsdata, 1) diff1

## 2009 7 -4 1 0 -8 -8 -5 5 14 -2 -1

## 2010 9 -2 6 -14 4 -3 2 1 5 -1 3 -2

## 2011 1 -2 -5 4 -4 -10 -4 -5 11 6 9 2

## 2012 -8 -5 6 4 -2 -15 3 -7 6 5 10 1

## 2013 -1 -3 1 2 -3 -7 0 -7 1 11 -2 8

## 2014 0 -10 8 -3 1 -3 -5 -3 -9 8 15 -1

## 2015 -3 -2 8 -3 -2 3 -21 -1 0 1 19 -1

## 2016 0 0 7 -1 -2 -6 2 -6 8 4 1 -7

## 2017 0 1 3 0 -9 -1 -3 -8 6 12 1 -5

## 2018 8 -5 2 -2 -8 0 -12 4 1 10 5 -1 plot.ts(diff1)

acf(diff1,lag.max = 30)

(41)

41 pacf(diff1,lag.max=30)

adf.test(diff1,k=12)

##

## data: diff1

## alternative hypothesis: stationary library(TSA)

## Warning: package 'TSA' was built under R version 4.1.3

##

## Attaching package: 'TSA'

(42)

42

## The following objects are masked from 'package:stats':

##

## acf, arima

## The following object is masked from 'package:utils':

##

## tar eacf(diff1)

## AR/MA

## 0 1 2 3 4 5 6 7 8 9 10 11 12 13

## 0 o o o x o o o o x o o x o o

## 1 x o o x o o o o x o o x x o

## 2 o o o x o o o o x o o o o o

## 3 x x o x o o o o o o o o o o

## 4 o x x x o o o o o o o x o o

## 5 x x o o x o o o x o o x o o

## 6 x o o o x o o o o o o x o o

## 7 x o o o x o o o o o o x o o

#diff 12

diff12 <- diff(diff1, 12) diff12

## 2010 -9 10 -15 4 5 10 6 0 -15 5 -1

## 2011 -8 0 -11 18 -8 -7 -6 -6 6 7 6 4

## 2012 -9 -3 11 0 2 -5 7 -2 -5 -1 1 -1

## 2013 7 2 -5 -2 -1 8 -3 0 -5 6 -12 7

## 2014 1 -7 7 -5 4 4 -5 4 -10 -3 17 -9

## 2015 -3 8 0 0 -3 6 -16 2 9 -7 4 0

## 2016 3 2 -1 2 0 -9 23 -5 8 3 -18 -6

## 2017 0 1 -4 1 -7 5 -5 -2 -2 8 0 2

## 2018 8 -6 -1 -2 1 1 -9 12 -5 -2 4 4 plot.ts(diff12)

(43)

43 acf(diff12,lag.max = 30)

pacf(diff12,lag.max=30)

adf.test(diff12,k=12)

## Warning in adf.test(diff12, k = 12): p-value smaller than printed p- value

##

## data: diff12

## alternative hypothesis: stationary library(TSA)

eacf(diff12)