FIG. i OEFBNlTlON OF THE COORDINATE SYSTEM

T H E MOTION O F A S P H E R E IN A CYLINDER F I L L E D WITH A VISCOUS LIQUID AND WITH A DIAMETER SLIGHTLY LARGER

THAN T H E S P H E R E DIAMETER T h e s i s b y

H e r m a n u s S n e l

In P a r t i a l F u l f i l l m e n t of t h e R e q u i r e m e n t s F o r t h e D e g r e e of

A e r o n a u t i c a l E n g i n e e r

C a l i f o r n i a I n s t i t u t e of Technology P a s a d e n a , C a l i f o r n i a

1970

(Submitted D e c e m b e r 24, 1 9 6 9 )

Acknowledg ement s

The author wishes to e x p r e s s h i s gratitude to D r . P. G.

Saffman for suggesting the subject of investigation of this work, and h i s help throughout the c o u r s e of the r e s e a r c h .

Also, thanks a r e due to D r s . D. E. Coles, A. Roshko, T. Y. T. Wu and E. E. Zukoski, for their helpful suggestions.

F u r t h e r , the fine craftsmanship of Mr. L. P. B a l t h a s a r , who built the experimental apparatus i s gratefully acknowledged.

The NASA-International University Fellowship p r o g r a m and, in the closing months, the California Institute of Technology provided the financial support.

And finally, even the c a s u a l r e a d e r won't be h a r d p r e s s e d to understand the a u t h o r ' s gratitude to M r s . Elizabeth Fox, who did the magnificent typing job.

Abstract

The flow around a s p h e r e , moving under the influence of

gravity in a long cylinder filled with a viscous liquid, i s investigated, for the c a s e w h e r e the inside d i a m e t e r of the tube i s only slightly l a r g e r than the d i a m e t e r of the sphere.

F o r low Reynolds n u m b e r s , a n extension of the Christopher- son and Dowson (1 ) theory i s obtained in the f o r m of a f i r s t o r d e r Reynolds number correction. It i s shown that the fluid e x e r t s a f i r s t o r d e r i n e r t i a l force on the b a l l , tending to i n c r e a s e the eccen- t r i c i t y ratio. The sideways motion of the ball due to this f o r c e h a s been calculated approximately.

F o r v e r y high Reynolds n u m b e r s , a potential flow solution has been found i n the f o r m of a F o u r i e r s e r i e s . This solution a l s o yields a f o r c e tending to i n c r e a s e the eccentricity ratio.

Experiments have been done for i n t e r m e d i a t e Reynolds numbers. The motion of the b a l l a p p e a r s to be unstable when the Reynolds number exceeds a c r i t i c a l value (about 10).

P a r t

I Introduction

Table of Contents T i t l e

I1 Low Reynolds Number Expansion

I11 A p p r o x i m a t e S i d e w a y s M o t i o n o f t h e B a l l u n d e r the Influence of the I n e r t i a l F o r c e

IV Potential Flow Solution V Experimental Work

Appendix : The Convergence of the Potential Flow Solution R e f e r e n c e s

G r a p h s

P a g e 1 3

I. Lntroduc tion

In 1959, Christopherson and Dowson (1) considered the flow around a heavy s p h e r e , descending under the influence of gravity i n a v e r t i c a l tube filled with a viscous fluid, the d i a m e t e r of which i s only slightly bigger than the s p h e r e d i a m e t e r . It was shown that the approximate flow equations for Re = 0 and the r a t i o of tube d i a m e t e r to ball d i a m e t e r going to one, r e s u l t i n no f o r c e perpendicular to the motion, independent of the eccentricity r a t i o a t which the b a l l moves.

However, t h e r e i s one eccentricity r a t i o (about 9 8 % ) for which the r a t e of energy dissipation i s maximum, and experiments p e r f o r m e d by Christopherson and Dowson indicate that the s p h e r e will always take up that eccentricity r a t i o , r e g a r d l e s s of the initial conditions.

The work p r e s e n t e d in this thesis i s an effort to obtain a better understanding of the flow d e s c r i b e d above, for non-zero Reyn- olds n u m b e r s ,

Experiments w e r e done ( s e e Chapter V ) with a light s p h e r e , a ping-pong ball. If the Reynolds number that c h a r a c t e r i z e s the motion exceeds a c e r t a i n c r i t i c a l value, the motion of the s p h e r e a p p e a r s to be unstable: the b a l l bounces against the tube wall during the upward motion and obtains a rotational speed around the v e r t i c a l axis.

In o r d e r to get an idea about the c h a r a c t e r of the flow and p r e s s u r e field i n the region between the cylinder wall and the s p h e r e a t non-zero Reynolds number, a perturbation of the flow equations in Re::: was p e r f o r m e d . This f i r s t o r d e r i n e r t i a l c o r r e c t i o n yields a f o r c e that will i n c r e a s e the eccentricity, but doesn' t s e e m quite l a r g e

enough to account for the Christopherson and Dowson effect. T h e r e a l s o i s a force opposing horizontal motion of the ball, which in the Stokes l i m i t tends to infinity when the eccentricity r a t i o tends to one.

This f o r c e will make the ball stick close to the wall, once i t gets there,

Also, a potential flow solution in the region between the ball and the cylinder wall was found, a s an approximation of the flow a t v e r y high Reynolds number. This approximation a l s o r e s u l t s in a horizontal force, tending to i n c r e a s e the eccentricity ratio.

All the calculations w e r e done with the assumption of steady flow,

11. Low Reynolds Number Expansion

-

For the following analysis i t i s assumed that the s p h e r e moves vertically in the cylinder, a t a certain constant eccentricity ratio.

For that steady s t a t e condition the velocity and p r e s s u r e fields can be evaluated with the eccentricity r a t i o a s a p a r a m e t e r . The flow region under consideration will be the region where the distance be- tween cylinder and sphere i s of the o r d e r s f the difference in the respective diameters.

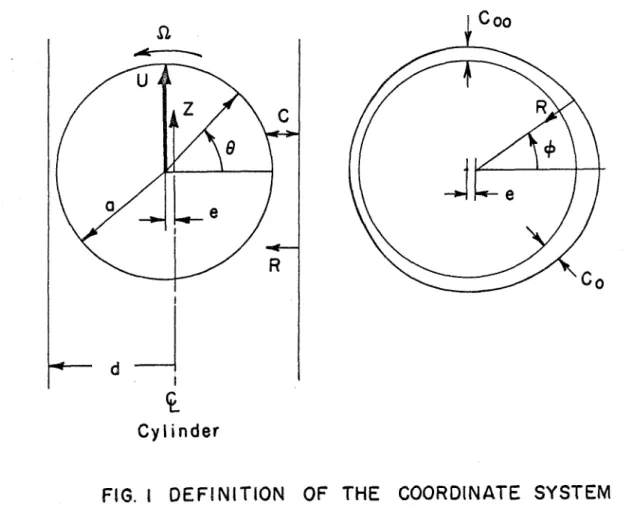
Let the radius s f the sphere be a, the radius of the cylinder d = a

+

c and the eccentricity ratio e/c ( s e e fig. 1).

00' 00

C y l i n d e r

FIG. i OEFBNlTlON OF THE COORDINATE SYSTEM

Essentially, a cylindrical p o l a r coordinate s y s t e m will be used. However, for convenience of integration this coordinate s ys-

1

a

t e m will s o m e t i m e s be slightly modified, s o that

-

_a

-

₈₈ m e a s u r e s the v a r i a n c e with the v e r t i c a l coordinate, instead of

- a

The gap

az '

width c, e x p r e s s e d in cylindrical polar s will be

7

c = c o o + e c o s p t a ( 1

-

l - z /a )

F o r c to b e of the o r d e r of c we m u s t r e q u i r e 00'

s o that to leading o r d e r i n c 00 /a

F u r t h e r m o r e , we define c O = c o o

+

^{e c s s}

p

and

-

= t e2/2a

The r a d i a l coordinate R will be m e a s u r e d f r o m the wall. In the modified coordinate s y s t e m , the expression f o r c will r e a d :

= '-00

+

^{e cos}

p +

a ( l - c o s 8) and ₈

-

^O [ ( c O 0 / a ) 1 / 2

I

c l e a r l y s i n 8

=

z/a

to leading o r d e r i n

- Coo

_a

As i s done by Christopherson and Dowson, the a x i s s y s t e m will be considered to move upward with the s p h e r e with velocity U.

The s p h e r e a l s o h a s a n angular velocity G a s i s shown i n figure 1.

The boundary conditions on the velocity a r e v = - U a t R = O

z ( a

v = 52a cos

q

a t R = c

z (b )

Since v in the gap region m u s t be of o r d e r U(-) a in o r d e r to allow

Z --,

=oo

the flux - u n a L to p a s s through a n a r e a of 2nacO0, w e can r e w r i t e

to leading o r d e r in

- Coo

_a

.

Now s o m e o r d e r of magnitude analysis can be done to obtain the right approximation of the flow equations. As we saw, v i s of

Z

o r d e r U

-

a Then, f r o m the continuity equation,

a

¹

with

- - ^-

^and

^{- a} -

¹

a R "00

a

^z

s o that v R N 0

F r o m the momentum equation in the R direction, one can show in the usual way that p does not depend on R to leading o r d e r in

- .

a When the i n e r t i a l t e r m s in the equations a r e s m a l l (the condition for which will be d i s c u s s e d l a t e r ) , -

4

m u s t balance the l a r g e s t

P ^a2 a2v

viscous t e r m in the z-momentum equation, v- Z so that 8~~ '

a

e

F r o m the go-momentum equation, with

- - ^-

one then finds in the

ap Coo

s a m e way:

c

To leading o r d e r i n

00

a

,

the v equation then r e a d s z

2 3/2

The o r d e r of magnitude of the i n e r t i a l t e r m s i s

'm

P" a ^and Ua "00

the viscous t e r m s have an o r d e r of magnitude of

%

coo3

The condition that the i n e r t i a l t e r m s be s m a l l compared to the viscous t e r m i s thus e x p r e s s e d by

One can a s s u m e a r e g u l a r perturbation expansion in Re*:

fnc = fnc ₀ t fncl

+ ...

(1 0)

w h e r e fnc stands for any of the velocity components, the p r e s s u r e ,

-

^7-

o r the quantities Q and U, and fnc

-

^{0 [fnco x} R e * ] . The z e r o th 1

o r d e r equations then reduce to the Stokes-flow equations, with a solu- tion for the p r e s s u r e field a s obtained by Chris topherson and Dowson.

In our notation:

+ o

^{b y n acosrp 12pf0}

-

= ⁰

- -

a~

C 2

C 3 (11)

C

where

fo(rp)

= j v dR

zo

⁽¹²⁾

0

We will proceed to find the f o r m s of the z e r o th o r d e r velocity components v

,

v and v

.

F r o m the z-momentum equation and

=o yo Ro

(7a) and (7b) one obtains:

Integration of (1 1 ) g' ive s

with

and

F r o m s y m m e t r y arguments one can show that in this l i n e a r c a s e i3pO/arp = 0 a t a = 0, s o that the integration constant

Then v follows f r o m

V o

2

- - -

-

P a

vqo

(18) and (7e) 8R2 a

acp

b f o ag3

v'p 0 -3Q0 sincpg

- - - --

6g3 afo)(R2- R c ) 2 - a

acp

^a

a 9

a n d v from

Ro

According to Christopherson and Dowson, one can e x p r e s s f and 52 in t e r m s of the eccentricity e and the difference in weight

0 0

of the fluid displaced and the s p h e r e , m ' g . One obtains:

and

em' g c 00 1 /2

a0

=

a

²

3 a r l L a with

3/2

C o

+

eci0/2cosq

E(cp) =

-

_Tr

I1 and

c s s ² (p I, =

s"

-r ( l + Z coscp) 1/2

dV

"00

-

9-

Then, one c a n e x p r e s s the Stokes approximation of the velocity corn- ponents in the following way:

with the functions k l

,

2,

l 1 , 2 and h defined by (13) and (18) through 1 , 2

(23).

We a r e now r e a d y to find the f i r s t o r d e r i n e r t i a l c o r r e c t i o n s fnc (10); those f o r the p r e s s u r e and the z-velocity component follow

1 f r o m :

-

T h e boundary conditions on v a r e : 1

F o r (23a) to b e t r u e , one m u s t r e q u i r e that

2

C << Re* << 1 a

After substitution of (24), (25), (26), equation (27) r e a d s

with q Z ( z , p ) =

1 1

ak 1 h k + k l X

Integrating (29) twice over R, and using (28), v can be written a s 1

follows

Defining

j-

^v _z ^{dR =} f l ( c p ) ₍₃₄₎

0 1

one can obtain an expression for

-

4'1

_a~

s i m i l a r to the e x p r e s s i o n for

- +o a~ ^,

^(11):

To facilitate the integration of this expression, the functions qi(z,

cp

) can be w r i t t e n in t e r m s of Q.

(cp

)

-

z

c k

with

2 2

e ( m ' g ) C O O 2 Q l ( ' p ) ' 2 2 6 2 c o s ' p

% P a I1

Then (35) can be w r i t t e n a s

Integration of this equation however will give an integration constant which m a y depend on

q ,

fnl

(p).

This function can be determined by

evaluating the p r e s s u r e on the top and bottom of the s p h e r e (9 =

_-

t

z),

'Tr

and requiring that the p r e s s u r e t h e r e be independent of

p.

In o r d e r to accomplish that i t i s n e c e s s a r y to u s e the modified coordinate s y s t e m (with a0 instead of z ) and the Sornrnerfeld t r a n s - formation, a s w a s done by Christopherson and Dowson to find the zeroth o r d e r p r e s s u r e a t 9 =

-

t a/2. In the modified coordinate s y s - t e m , e x p r e s s i o n (42) r e a d s

F o r the Sornmerfeld transformation we define

To leading o r d e r in

-

a one obtains

The Sommerfeld transformation defines a new angle y

One can u s e the expressions obtained with this transformation a l l the way to y =

-

t n (corresponding to 8 =

-

t n/Z) since, to leading - ^{I -} c o o l / Z o r d e r in c OO/a,

I y I

a s s u m e s the value of ^IT for every

/ e I

> 0[(-) _a

1.

This comes down to neglecting changes in the p r e s s u r e field outside coo 112

-

the region

/

⁰

I -

^{0 [ (-)} _a ] compared to changes in this region.

Then, f r o m (46) one obtains 2 1/2

de (1-n )

-

=

dy l t n c o s y and

2 1/2 (1-n ) siny sine =

l t n c o s y Equation (43) t r a n s f o r m s into

6 p L ? 1 ~ ~ ~ a ( l t n c o s y ) 12pfl ( l t n c o s y ) 2

- - * -

_(1-n ^{2 3/2} ₎

^-

_{a (1-n} ^{2 2 5/2} ₎ ^t

-

1 Qlasiny t - Q2siny 16 Q3siny ( l t n c o s y ) ( l t n c o s y 7 2 ^{t -} 35a 2 2

1

1 - n (1-n )

(49 which can be integrated to give

-

^13-

2 2

6 p , 4 cosrp(yt siny) 3pf (4yt8nsinyt2n y t n sin2y)

-

1

P1

- T

2 3 2

^-

^{a (1-n} 2 2 5/2 ⁾ l t n c o s Q2cosy

ln(*+f 2 i-

1-n

The f i r s t two t e r m s of this expression a r e odd in y, a l l the other t e r m s a r e even. Hence, to compute the p r e s s u r e difference (PI

ly

=- a

-

^(pl ) y = n 9 only the f i r s t two t e r m s a r e of importance, and the s a m e applies to the torque resulting f r o m the viscous shear s t r e s s . Using those two t e r m s then, one can proceed to compute the values of Ql and U1, s i m i l a r to the way in which ~ h r i s t o ~ h e r s o n and Dowson

computed Go and Uo. This determines f l in such a way that the con- tribution to the p r e s s u r e f r o m the f i r s t two t e r m s i s independent of

q

a t y = + r e -

Therefore, fn

, V

( ) i s determined by the condition that the p a r t of p l even in y, be also independent of

q

a t y = t - r. Hence

Defining the p a r t of p that i s even in y a s P1, we then obtain 1

=:{A 2

n l n l t n c o s y 1 -n ) t + h 2 - + - t cos 4- 1 l -n

Clearly, only this p a r t of the p r e s s u r e will contribute to any force perpendicular to the velocity U. Such a force will be expressed b y

and will be destabilizing (increasing the eccentricity r a t i o ) i f F > 0.

Now

and the integration l i m i t s on y a r e - n and n.

It i s not possible to p e r f o r m the y integration analytically, but to get an idea about the magnitude of the force, we can t r a n s f o r m

e x p r e s s i o n (52) back to the z-variable and integrate over z in the 1 /2

region of i n t e r e s t , s a y for z f r o m

-

( c O 0 a ) to (c00a)1/2. The Sorn- m e r f e l d transformation formula (46) can b e w r i t t e n a s

"00 F u r t h e r m o r e , to leading o r d e r in

-

_a

_'

Then

I t n c o s y

- - -

a 1 - n 2c

Coo

cos t 1 ncosyt1-t- O(-)

--4

^{= 3 a}

and

n n 2 2 - n

c o s y t l t

-

₄ (cos2y-1) =

2

c o s y t c o s y t

-

₂

1 2 2

- - Coo

-

²ⁿ (n c o s yt2ncosytltO(-)) a

s o that

c o s y t 1+

-q

n (cos2y-1)

1 a 2 2 2

- - - -

2n c2 (1-n )

E x p r e s s i o n (52) then t r a n s f o r m s into

to leading o r d e r i n c O O / a , and

Still, the

q

i n t e g r a t i o n cannot b e done analytically, except asymptotically, for e/cO0

<<

1. We will p r o c e e d t o evaluate F. f o r

1

that c a s e , to leading o r d e r i n e/c 0 0'

S t r a i g h t f o r w a r d manipulation shows that c o s ² 40

1, =

f

^{e 1/2 d q = 7f 4-} o [ e / c O 0 l - n ( 1 + - c o s q )

Coo

When one computes F. to leading o r d e r i n e/cO0. c l e a r l y only the

1

l a s t two t e r m s in the right-hand side of ( 5 9 ) will contribute. P e r - forming the <p integration, one finds

or:

t 2 1 4 G a

35 (T)'/2 00 a r c t g to leading o r d e r in e/cO0.

One can conclude that for s m a l l e/co0 the force due to the f i r s t o r d e r i n e r t i a l effects will always tend to i n c r e a s e the eccen- tricity ratio.

F o r e/cO0 of o r d e r one, the integration h a s been p e r f o r m e d numerically, and the r e s u l t s a r e l i s t e d below.

2 3

p(m'g) C O O

-

o r : F. =

1 2 2 4 F

971

y a F o r a = 2, c o o = 0. 1:

The computed values of

-

F a r e plotted in graph 1.

One can e x p r e s s the o r d e r of magnitude of F in t e r m s of p, p, U, c o o and a. The balance of buoyancy and p r e s s u r e forces r e q u i r e s that

F r o m expression ( 3 3 ) for vZ one can also obtain the f i r s t 1

o r d e r inertial correction of the viscous s h e a r force on the sphere, and i t s component Fv perpendicular to the velocity U. Only the p a r t of avz

/ a ~

that i s odd i n z will contribute to Fv and after differen-

1

tiating ( 3 3 ) with r e s p e c t to R and substituting ( 3 6 ) , ( 3 7 ) and ( 3 8 ) Fv

will be e x p r e s s e d a s

( 7 0 ) F v will tend to i n c r e a s e

1

^e

I

i f positive. However, i t can readily be shown that

s o that to leading o r d e r in c ₀₀ /a the sign of the p r e s s u r e f o r c e Fi d e t e r m i n e s the question of whether the f i r s t o r d e r i n e r t i a l f o r c e s a c t to i n c r e a s e o r to d e c r e a s e

/

^e

1.

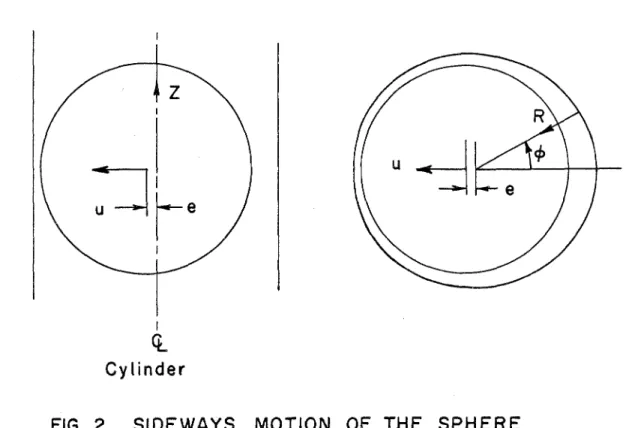
111. Approximate Sideways Motion of the Ball Under Influence of the I n e r t i a l F o r c e

If a t any t i m e during the v e r t i c a l motion the ball takes up an e c c e n t r i c position in the tube, the i n e r t i a l f o r c e F calculated in

i'

Chapter 11, will a c t to a c c e l e r a t e the ball in a horizontal direction, such that the eccentricity r a t i o i s increased. If u i s the horizontal velocity of the ball obtained by the action of F t h e r e will be a f o r c e

i'

F opposing the horizontal rno tion which f o r s m a l l enough u will b e P '

l i n e a r i n u. The condition to be satisfied for F to b e l i n e a r in u i s P

that the leading o r d e r equations governing the flow be the Stokes equations. In that c a s e F can be obtained f r o m the p r e s s u r e field

P

around the b a l l caused by p u r e horizontal motion of the ball (figure 2).

I

Q

Cylinder

FIG. 2 S I D E W A Y S M O T I O N O F THE SPHERE

- 2 1

-

The boundary conditions on the velocity a r e

w h e r e the flow region under consideration i s again

The typical Reynolds number of this motion i s

F r o m the continuity equation i t will be shown that

s o that

F will be l i n e a r in u and can be calculated f r o m the Stokes equations P

with boundary conditions a s stated above, since the Strouhal number of the motion i s of the s a m e o r d e r a s the Reynolds number.

To leading o r d e r in cO0/a. the flow equations then a r e

with boundary conditions (72) through (74).

1

With R = 0 [ c O 0 ]

,

z = ~ [ ( c ~ ~ a ) ~ ] and the boundary conditions ( 7 2 ) on v one obtains easily f r o m (75)

R'

Then, f r o m (77) i t follows that

and f r o m (87)

Hence the p r e s s u r e does not depend on R to leading o r d e r in cO0/a.

The leading o r d e r t e r m of p will depend on

q

a t z = 0, but m u s t be independent of cp a t the top and bottom of the s p h e r e and m u s t conse- quently b e a function of both z and

q.

With 8/ap of o r d e r e/cO0. i t can then b e shown f r o m (80) that

and the p - m o m e n t u m equation (76) then gives

v = 0 [ u ]

<P

^{(8 3 )}

To leading o r d e r in c OO/a, the continuity equation (75) r e d u c e s

which can b e integrated over R f r o m R = 0 to R = c to yield

using (72).

Physically, the integrated f o r m of the continuity equation h a s the following significance: consider a volume element extending f r o m the b a l l to the tubewall, with width a d p and height d z (figure 3 )

A

F l u i d f l u x

When the ball moves c l o s e r to the wall, fluid h a s to b e spilled out of

av

Coo

^avz

the contracting volume, and s i n c e

1 . 2

= 0[-

-1

a l l the fluid a

a 9

a

a~

will be spilled in the z direction, to leading o r d e r in c 00 /a.

Equation (77) can now readily be integrated to give v Using z'

the boundary conditions, (74):

Substituting this in (85) and again using the fact that vZ

=

⁰ a t R = c, one obtains a f t e r p e r f o r m i n g the integration

To find the integration constant C ( q ) that r e s u l t s f r o m inte- grating (88) over z , one has to u s e the s a m e method a s employed for integration of equation (42) ( s e e Chapter 11). In s p h e r i c a l coordi- n a t e s , (88) r e a d s

and using the Somrnerfeld transformation a s defined i n (44) through (46

1

which can be integrated to give

cosyt 'Icos2y

-12pucos(p 4

P

_{= a 2 2 +} C ( C ~ )

(1-n

Obviously p i s an even function of y, and the integration con- stant C ( q ) i s determined by the condition that p does not depend on

p

a t y =

- +

^{T .} Hence

n .

s o that

and using expression (58)

-6puacoscp

- -

-bPuacoscp

- -

-6puacosq

P = 2 2 2 (92)

C

+ -

z

+

e c o s p ) 2

(Ic

t e c o s q ) ('00 2a

to leading o r d e r in cO0/a.

The force resulting f r o m this p r e s s u r e distribution will ap-

proximately b e 1

cos2<pdq

( C

- +

e c o s q ) 2

cos 2 cp dql F = - l ~ ~ u a ~

[ l i j

P -2 c - n ( I t 5 e C O S ~ ) 2

The cp integration can be performed to give

2 -2

cos cp c e 2

e 2

s"

^{e 2 d v = 2 2} t ( 1 - 7}9t(2--1)D

e2(1-e

6

) -2

- 7 r (1t coscp) C C _-7r

i

with 1

e 2

D =- a r c t g

[(GI

^tg

_:]

,Kg

^{1 t, C}

C

The z-integration cannot be performed analytically, but one can get the o r d e r of magnitude of F by setting

-

c

=

coo.

P Then:

F i s negative, and hence opposing the sideways motion for P

and F tends to - m when e/cO0 tends to one, and one can w r i t e P

The i n e r t i a l f o r c e w a s found i n Chapter 11 to b e

. -

w h e r e F r e p r e s e n t s a n i n t e g r a l o v e r z and

q ,

and h a s the dimension of length. According to Christopherson and Dowson, one can e x p r e s s m ' g / p in t e r m s of the v e r t i c a l velocity U:

with I1

Now

"oo'l

a s defined in ( 2 3 ) and

define

Aite/coo)

then Fi can be w r i t t e n a s

The equation for the horizontal motion of the b a l l under the action of Fi and F will then be

P

Since A. and A a r e nonlinear functions of e , and u = de/dt,

1 P

equation (102) i s in fact a nonlinear second o r d e r differential equation in e ( t ) , which cannot be solved exactly, However, i t i s possible to get the o r d e r of magnitude of u by solving (102) a s i f Ai and A w e r e

P constants. The solution of the then resulting l i n e a r equation can easily be found to be

A. ^I 9n p ~ 2 a

ll ^{(- 5}

^{24nPa5/' t )}

u = -

A 4 8 p

-

^exp

mb '13 3/2

i f the ball i s a s s u m e d to be a t r e s t a t t = 0.

When the value of e/cO0 tends to one, the value of A. r e m a i n s

1

r a t h e r s m a l l (about 0. I ) , but a s we saw the value of A will tend to P

infinity. It follows that the horizontal velocity of the ball will tend to z e r o when the eccentricity ratio tends to unity, which m e a n s that the ball will be virtually locked in place c l o s e to the wall.

To find the o r d e r of magnitude of time t needed for the b a l l to t r a v e l horizontally over a distance of o r d e r coo, one can take

Ai 9a P U ~ C ~ ~ the o r d e r of magnitude of u to be

- -

A 48

.

Typical values of

TJ P

A. and A can be taken a s ..

1 P

Ai = 0.06 and A = 1 P

(approximate values at e/cO0 = 0. 5). So t follows f r o m

In that t i m e , the ball t r a v e l s vertically over a distance s

If s / a i s of o r d e r unity, one can conclude that the ball r e a c h e s the wall while i t t r a v e l s v e r t i c a l l y over a distance of o r d e r a , and then s t a y s c l o s e to the wall by v i r t u e of a n infinite Stokes d r a g f o r c e in a horizontal direction. However

i s of o r d e r 50 for m o s t of the experiments p e r f o r m e d by Christopher- son and Dowson.

When the Reynolds number i n c r e a s e s , the c h a r a c t e r of the flow will change, but i t s e e m s reasonable to a s s u m e that the i n e r t i a l f o r c e keeps growing till i t r e a c h e s the potential flow l i m i t , and that s / a d e c r e a s e s when Re* i n c r e a s e s . At the value of Re* w h e r e in the experiments the ball s t a r t s bouncing against the tube wall, the Reynolds number i s too high to m a k e s/a f r o m e x p r e s s i o n (105) a f a i r m e a s u r e of the distance travelled in a v e r t i c a l direction during the time needed for the ball to t r a v e l a distance of o r d e r c i n a

00

horizontal direction. T h e r e i s a Reynolds number a s s o c i a t e d with s/a, namely

but its values at the stage where experimentally the bouncing insta- bility occurs a r e spread over a range of 1 0 2

IV. Potential Flow Solution

If the Reynolds number a s defined in Chapter I1 i s v e r y high one can a s s u m e that the vorticity of the flow i s confined in boundary l a y e r s on the s p h e r e and cylinder wall, thin compared to the gap width. In that c a s e , the m a i n flow in the gap region m a y be consid- e r e d to b e potential flow, and the p r e s s u r e distribution around the s p h e r e can b e derived f r o m the potential flow solution.

The condition for potential flow i s that the boundary l a y e r thickness 6 i s s m a l l compared to coo. So

The p r o b l e m then reduces to

w h e r e

with the boundary condition

- 3 2 -

F r o m the continuity equation (107) it follows that

a@

^z

- _a~

and

- ^a@

^R

aR

a r e of the s a m e o r d e r . Hence, like in the low Reynolds-number c a s e

However, to s a t i s f y irrotationality we m u s t have

unless @ z i s not a function of R to f i r s t o r d e r in (-),

Coo

in which c a s e a

(1 1 1 ) can b e satisfied by the next t e r m in an expansion i n

-

_a f o r @ z . Hence, r e s t r i c t i n g the analysis to the t e r m s of leading o r d e r i n

c O O / a 9 like in the low Reynolds number c a s e ,

m u s t be satisfied by a valid solution of the potential equation.

We will now proceed to find such a solution, in the f o r m of a F o u r i e r s e r i e s , the coefficients of which a r e s e r i e s a s well. The boundary conditions (1 09) a r e c l e a r l y satisfied by a ^" s i m i l a r i t y solution'

'

^:

-

^33-

Now (1 12) and (1 13) imply

The potential equation (1 07) r e a d s

o r to leading o r d e r in c _{00 /a}

F r o m (1 1 3 ) , (1 14), (1 15) one then finds

The angular velocity component m u s t be s y m m e t r i c a l and

P

periodical in

9 ,

s o that one can w r i t e @ i n the f o r m of a F o u r i e r

q

sinus s e r i e s

Q q ⁼

g n ( ~ , z ) s i n n p n = l

and consequently

Substituting (1 18) into (1 14) one obtains

H

cosnq ⁺

3)

⁺ ( c t e c o s q )a

R n a2 R Z

N

c4e cos q

R za ^g ncosnq

=

0

a

^z _{n = l} ⁿ

It i s now c l e a r that the l a s t t e r m in (119) i s of o r d e r cO0/a t i m e s the other t e r m s and hence can be neglected. With

c o s q c o s n q = cos(n+ 1

)q +

cos(n-1)cp 2

Equation (1 19) then r e a d s

-3

ea

a2

^{g 0}

t-- 2 c o s q = 0 z

a2

Equating the coefficients of cosncp to z e r o we obtain for n = 0

-

^'80

+ -

^I c a "go ea a2g

-

0 az z

2 - 2 2 2 -

a

^{z az}

and the g e n e r a l equation, for n > 1

The conditions under which this s y s t e m i s to be solved a r e : ( a ) Q z # function ( R )

2~

-

(b) the flux condition ^$J Z c a d q =

-

^{Una 2}

0

( c ) $p = 0 i f e = 0 , s o

g n = 0 if e = 0 for all n 2 1 (125)

The equations (121) through (123) f o r m a s y s t e m of an infinite number of equations with an infinite number of unknown functions g

n '

The , s y s t e m can be solved, a s will be demonstrated, under the assump- tion that

Condition (125) implies that g l must be the p a r t i c u l a r solution of (122), and gn the p a r t i c u l a r solution of (123) for n > 1, s o that

for n 3 1. Hence the assumption (126) i s consistent with the system.

F o r e = 0, the full soPution can simply be obtained f r o m equation (1 21 ), which then r e a d s

CI

The meaning of the second index in g will become c l e a r l a t e r . 0 , 0

Writing (127) a s

i t i s clear that

where the constant A i s to b e evaluated f r o m the flux condition (124).

F o r non-zero eccentricity one has to solve the complete s y s - t e m (121) through (123). F o r s m a l l values of e/coOy one can find a f i r s t approximation of agl/azy by substituting (1 28) into (1 22):

-%

the p a r t i c u l a r solution of which i s easily found to be

The f i r s t correction of agO/az can then be obtained f r o m (121), a f t e r substitution of (1 30):

Again ag /az = 0 for e

=

0, s o ag /az m u s t be the p a r t i c u l a r

0, 1 091

solution of (1 31 ):

In the s a m e way one can continue to compute the f i r s t and next approximations of gn, and the f o r m s that one obtains suggest a general solution of the form:

The validity of this expression can easily be shown by induction f r o m equations (121) through (123), and in doing s o one obtains r e c u r s i v e relations for the constants kn, :

Using (1 18) and (1 33), one then can w r i t e the z - component of the velocity a s

F o r s u c h a solution to exist, k m u s t be bounded for either one of n, 1

the indices n , 1 tending to infinity while the other one i s fixed, s i n c e e/G

<

1. The d e t a i l s of the convergence of the s e r i e s i n the right hand side of (1 37) a r e given in the Appendix.

Finally, with k = 1, and a l l other k

'

s known f r o m (1 34)

0 , 8 n, 1

through (1 36), A can b e determined by the flux condition (124).

N

Straightforward integration of

Q,

c a gives

The p r e s s u r e distribution can then be obtained f r o m Bernoulli's equation

s i n c e v

_{R ~ R}

^{a V ~}and

9-

a avz _aV a r e of o r d e r

- coo

_{a z}

_a~

t i m e s v

-

'

along s t r e a m l i n e s and s i n c e a l l s t r e a m l i n e s come f r o m the undis- turbed,

9

independent region, one can define

with vz a s in ( 1 3 7 ) .

The resulting f o r c e on the s p h e r e can be approximated a s

before ¹

(cOOa)" 2 7

= )

]

^{PCOSP ad.}

I

^{dz (141)}

-

How many t e r m s one wants to keep in v depends on the value of z e/cO0 and on the r e q u i r e d accuracy. F o r instance i f e/c << 1 and

00

one wants F to leading o r d e r i n e/cO0, one easily obtains f r o m the g e n e r a l formulae

and

F =

4 a r c t g

-

00

42 I

V. Experimental Work a ) Apparatus

The apparatus used for the experimental work consisted of a long glass tube, vertically mounted in a f r a m e , in such a way that i t could be turned 180' about a horizontal axis.

Three different tubes w e r e used, two of which (tubes number I and 11) w e r e standard tubes with an unknown tolerance on the inside diameter. Tube number I11 was a precision bore tube, with a maxi- m u m tolerance of 0. 170 on the inside diameter. The values of length and average inside diameter of the tubes a r e listed in Table VI.

A number of ping-pong balls w e r e used a s spheres. The sphericity of the balls was crudely checked with a m i c r o m e t e r and only those with a deviation of sphericity of l e s s than 3% w e r e used.

Balls number 4 and 5, used in the precision b o r e tube, had a devia- tion of sphericity of l e s s than 0. 5%. The values of the d i a m e t e r s of the balls a r e listed in Table VII.

To change the upward velocity of the balls in the tube without having to change the viscosity of the fluid, the weight of some of the balls was increased by inserting solder w i r e through a little hole in the ball side

,

which was then sealed. This of c o u r s e changes the inertial moments of the balls, but the flow in the gap region and the forces acting on the ball will s t i l l be the same.

When a ping-pong ball remains for some time in the fluid, the m a t e r i a l of the ball side will absorb some of the fluid. The in- cr.ease of weight caused by this effect during the time needed to run the experiment a t a certain weight of the ball appears to be negligible,

- 4 0 -

even m o r e s o when the weight i s already increased by the inserted solder wire. However, in the experiments with the precision bore tube, the clearance r a t i o c/a was v e r y s m a l l and the motion seemed almost critical* already with an unweighted ball. Therefore, the effect of fluid absorption could be used to i n c r e a s e the weight of the ball ,and d e c r e a s e its upward velocity slightly. After every m e a s

-

urement, the ball was left in the tube and the experiment was repeated after some time, The absorption of fluid did not appear to have a measurable effect on the sphere radius a.

The fluids used in the tube w e r e mixtures of various amounts of glycerine with water. The viscosity of each mixture was d e t e r - mined with a precision viscometer of the falling ball type, accurate up to 1

%.

The specific gravity of each mixture was m e a s u r e d with a pycnometer and a precision balance. The balance was also used to determine the weight of the spheres for every run, except in the c a s e of the experiment in the precision bore tube.

b ) The p r o c e s s and the observed phenomena

The lower end of the tube was closed with a rubber plug and the tube was filled with fluid. The viscosity and specific gravity of the fluid w e r e determined beforehand. Then the s p h e r e was inserted a t the upper end of the tube, which was then closed and the tube was turned around. Intervals of 5 crn had been marked on the tube wall, so that the ascent velocity could be measured.

In the experiments with tubes I and 11, the tube was turned

*

See paragraph b.

three m o r e times at each weight of the ball, s o that an average over four measurements could be taken. After that the ball was taken out again, m o r e solder w i r e was inserted, and the experiment was r e - peated.

F o r the experiment with the precision bore tube, only two measurements at a time w e r e done, to make the time, needed for the measurements a t a certain weight and hence the variance in

4

weight s m a l l e r . The ball was now left in the tube, and the experi- ment was repeated after roughly half an hour.

When the Reynolds number was higher than a c r i t i c a l value ( ~ e : ~ ) , the ball obtained a spin velocity about the v e r t i c a l axis, the direction of which appeared to be random. Also, it bounced

f r o m wall to wall during the motion. The spin velocity was measured by timing a certain number of complete rotations of the ball, and the bouncing frequency by timing a certain number of times that the ball

* *

bounces off the s a m e side of the tubewall. When Re

<

R e the c r

motion appears to be smooth. Both the spin and the bouncing d i s - appear, and the ball goes up in a straight line.

When the Reynolds number i s v e r y high, o r the ball v e r y light, the bouncing frequency i s too high to be measured. In the tables of measurements in paragraph c of this chapter one can s e e that the bouncing frequency for balls 2 and 3 could only be measured when the weight of the ball was roughly over 20 grams. F o r balls

4 and 5, in the precision b o r e tube, the bouncing frequency was too high to be measured all the way to the c r i t i c a l Reynolds number, where the bouncing disappeared. With R:" tending towards Re

*

c r

f r o m above the bouncing frequency d e c r e a s e s , to go to z e r o r a t h e r

* *

suddenly when Re 4 Recr. The spin velocity f i r s t becomes v e r y e r r a t i c in magnitude, s o m e t i m e s even r e v e r s i n g i t s direction during the upward motion. It d i s a p p e a r s completely with the bouncing, for

In a l l c a s e s w h e r e t h e r e i s spin, the spin velocity s e e m s to i n c r e a s e when the b a l l bounces against the tubewall, and to d e c r e a s e again in between walls. However, due to the method of m e a s u r i n g the spin velocity, this observation could not b e established a s a fact.

A possible explanation of this behavior i s that the ball r o l l s over the wall a s i t w e r e , while i t bounces off the wall, which will be t r u e i f the direction bf approach does not coincide with the " d i r e c - tion" of the eccentricity (p =

a

in figure I ) , s e e figure 4.

FIG. 4

-

4 3 -

It i s c l e a r that t1.c- rnagnila~de of such a spin-torque will depend on the velocity of the ba1.i in the z 0 plane and on the angle a between the direction of approach and = x . Since the velocity in the horizon- t a l plane depends on the v e r t i c a l velocity U, this interpretation i s consistent with the d e c r e a s e in S2 with U on the average.

The o c c u r r e n c e of the bouncing instability a t a c e r t a i n value of ~ e * can probably be explained by the f a c t that the i n e r t i a l f o r c e a s computed in Chapter 11, h a s to grow a s a function of ~ e * , the effective Reynolds number in the gap region. At the c r i t i c a l value of ~ e * , this i n e r t i a l f o r c e gives enough momentum to the ball to m a k e i t bounce against the wall before it i s brought to r e s t by the f o r c e , opposing the horizontal motion.

The experiments, due to the lack of a c c u r a c y resulting f r o m their simplicity have to b e considered a s qualitative r a t h e r than quan- titative. However, they show that a t an

' '

intermkdiate'

'

Reynolds number, w h e r e theoretical analysis would involve the full nonlinear Navier-Stokes equations, a n instability of the described n a t u r e s e t s in

Finally, we have to point out that in the experiments I through 111, the f r e e d o m of spin about a horizontal a x i s w a s s u p p r e s s e d by the p r e s e n c e of a weight (the solder w i r e ) inside the ball. But the ex- pe-riments I V and V, in which s p h e r i c a l s y m m e t r y was p r e s e r v e d ,

suggest that this i s not a v e r y important factor for the o c c u r r e n c e of the instability.

-

^44-

c ) Data

In the following tables, the weight of the ball i s listed together with the average values of the upward velocity V , the spin about the v e r t i c a l axis and the bouncing frequency f a t that weight. Also

b

which tube and ball w e r e used for the specific experiment i s indicated, and the values of the viscosity v and density p of the fluid used.

2 2

I Tube I, ball 1, v

=

2. 1 x10- c m /sec, p

=

1. 12 gm/cm ³

m ball (gm) ~ ( c m / s e c ) a ( r a d / s e c ) fb(#/sec) cO0/a = 8 . 5 %

27.190 2. 04 0. 50 1.55 = 0.16 c m

28. 176 1. 71 0. 31 1.22

28.765 1. 56 0.12

*

^{0. 90}

28. 972 1 . 4 5 0 . 2 8

*

^{0. 81}

*

Rather e r r a t i c , deviation f r o m average value above 15%

I1 Tube 11, ball 2; v

=

4 . 35 x 1 c m /sec; 2 p = 1. 162 g n / c m 3

*:Spin becomes v e r y e r r a t i c ; deviation of 20% and m o r e f r o m average value

**

For higher velocities, f too high to be accurately measurable b

2 2

I11 Tube 11, b a l l 3; v = 4. 3 5 . 1 0 - cm

/set;

^p = 1. 162 gm/cm 3

Tube I11 M e a s u r e m e n t s in the p r e c i s i o n tube;

2 2 3.

IV: B a l l 4 , v = 1 . 2 8 x 10- c m / s e c ; p = 1 . 0 7 8 g m / c m ,

= 0.024 c m c /a = L37o 00

wobble d i s a p p e a r s a t U = 0. 54 c m / s e c

2 3

V: B a l l 5 , v = 0 . 8 1 x 1 0 ~ 2 c m / s e c , p = l . 0 3 5 g m / c m ; c / a = c o o = 0 . 0 1 8 c m cO0/a = 0.95%

wobble d i s a p p e a r s a t U = 0 . 2 9 c m / s e c VI: Tube no.

VII: B a l l no.

C r i t i c a l Reynolds n u m b e r s E x p e r i m e n t # %

R e c r

I 12. 9

I1 11, 3

T h e e x p e r i m e n t a l d a t a a r e plotted in g r a p h 2, givingS2 and f b a s a

-3.

function of ReT.

ADD endix

The convergence of the potential flow solution

Consider k to be an element of a two-dimensional m a t r i x n,Q

with n denoting the row number, and 1 the column number. Repeated executing of relation (136) then gives a relation for element k i n

n,Q t e r m s of the f i r s t ( n t 1) elements in the preceding column:

k n-2,Qi-1

- -

^{n - l k 2n n , l}

I+(--)-

2 n t l n t l , l ^{n k}

-

l 2 n

-

(-

2 )

; ; 1 ~ n - 2 , ~ + 1

(2)'

₂

n

_{n n , Q} ^{+ (- -)}

-

n k 2 n t l n t 1 , I and a f t e r j steps

+ ----

_{( -}

2 )

^{1 2 kn, Q} + ( - -) 2 n t l n t 1 , Q

-

n k

L e t n- j = 1 and u s e (1 34) and (1 35) combined:

to obtain f r o m (I)

for n 2 l and a l l I .

To evaluate k for n 3 1, (1 3 5 ) and (1 3 6 ) can be written a s n, 0

Then k

1 , o = 1 ( s e e (128))and (IV) can be written a s

-

1 3 n

kn, 0

-

^(-

2 )

_{n-j, O}

With expressions (1 34), (11) and ( V ) one can then evaluate a l l the m a t r i x elements k column b y column.

n , l E* g.,

n t l

or k

-

n, 1

- -

⁾ n(n-t-2) for n 3 1 n t IL n t l n- jt 2

n 1 jt1 Next k

n, 2 -

- ¹

j ( j t 2 )

j = l j

Bkt ( m + l )-Bk+l (0) Now

2

^{jk =}

j =1 k t 1

s t

Where Bkt i s the Bernoulli polynomial of k t 1 o r d e r , k t 1

i

B k + l ( x ) =

1

b k + l , i x (VIII), with b

=

.1

i = O ^{m , m}

F o r k = 1 one obtains

and hence

The e x p r e s s i o n s (V), (VI) and (IX) suggest a g e n e r a l form for k

n, I

( X ) Expression (X) can be shown to be valid by induction; substitute (X) into (11) to find

Using (VII) one obtains

1 n-1+2(I+1)

-

B1+1("t2)-BItl(0)

k n , ~ + l

- ( - z ) A

[ / l t i & a i

,

i1-t 1 t 1 t

t ( n t 1 )a 191j

L t l

Only the Bernoulli polynomial of o r d e r I t 1 will give a n t e r m . Since b I t l , l t l = 1, one finds

1 n - 1 t 2 ( Q t 1 )

--

LnIt l t a I

k n , ~ t l = (-

Z)

( I t l ) ! i i - l , l Kt -I--- ^{+ a} I t l , t i - 1

I

(XI) w h e r e the aI ⁺

,

' s can b e found b y evaluation of the Bernoulli poly- nomials, and consequently (X) i s true.

Clearly, for fixed I and l a r g e enough n

which tends to z e r o for n tending to infinity.

The convergence for I tending to infinity and fixed n i s h a r d e r to p r o v e since one m u s t evaluate a l l the a

'

s , for which i t i s n e c e s

-

S 9 j

s a r y to know the values of the coefficients of the Bernoulli polynomials bi, j a A g e n e r a l f o r m for b i s not known. However, i f we a s s u m e

i , j

that none of the a . ' s grow f a s t e r than I !

,

kn, I i s bounded f o r I tend-

1 7J

ing'to infinity and n fixed, and the s e r i e s in the right hand s i d e of (1 3 7 ) i s convergent.

R e f e r e n c e s

1. D. G. C h r i s t o p h e r s o n and D. Dowson: "An E x a m p l e of Minimum E n e r g y Dissipation i n Viscous Flow. P r o c e e d i n g s of the Royal Society, S e r i e s A, Vol. 251, May- June 1959, pp. 550- 564.

2. Milton Abramowitz and I r e n e A. Stegun (ed. ): "Handbook of M a t h e m a t i c a l Functions.

"

Dover P u b l i c a t i o n s , Inc.

,

New York, 1965, p. 804.