PROGRAM FISIKA pada Vektor

FISIKA 1

1

Penilaian:

 Take home quiz di LMS 30%

 Limited access ( 6 days)

 Highest grade

 Take home Assignment di LMS 10%

 UTS 30%

 UAS 30%

3 SKS:

 Perkuliahan online: 90 menit (max)

 Tutorial Sinkron (LMS): 60 menit

(min)

WHAT IS PHYSICS?

FISIKA 1

3

Materi:

 Vektor

 Integral & Diferensial Penilaian:

 Take home quiz di LMS

 Unlimited attempt

 Limited access ( 1 week)

 Highest grade

Week 1

FISIKA 1

School of Electrical Engineering, Telkom University

VEKTOR

Week 1. Part 1

5

PENGENALAN VEKTOR



Vektor merupakan sebuah besaran yang memiliki magnitudo (besar) dan arah.



Vektor digambarkan dengan menggunakan panah:

 arah panah menunjukkan arah vektor,

 panjang garisnya adalah besar (magnitudo) vektor

= (3, 4)  

x

Y

3 4

¿

 

⃗ �

₁

∨ ¿ √ ³

²

^{+ 4}

²

⁼⁵

PENULISAN VEKTOR

�= ⃗

(

^���11¹

)

�= ⃗

 

�

₁

� ^ + �

₁

^ � + �

₁

� ^

�₁ , �₁ ,�₁

�(¿)

  ¿

�= ⃗

(

^��11

)

�= ⃗

 

�

₁

� ^ + �

₁

^ �

�₁ , �₁

�(¿)

  ¿

1.

2.

3.

1.

2.

3.

Dalam 2-D Dalam 3-D

PANJANG/BESAR VEKTOR

�= ⃗

(

^��11

) ^¿

 

^{�∨ ⃗ ¿ √ �}

¹²

^{+ �}

¹²

� ⃗=

(

^���11¹

) ^¿

 

^{�∨ ⃗ ¿ √ �}

¹²

^{+ �}

¹²

^{+ �}

¹²

1.

2.

Manakah besaran-besaran yang termasuk vektor?

 Jarak atau perpindahan?

 Kecepatan atau kelajuan?

 Gaya?

 Momentum?

7

OPERASI VEKTOR

PENJUMLAHAN/PENGURANGAN VEKTOR

� ⃗=

(

^���11¹

)

^{⃗�  =}

(

^���222

)

Jika dan , maka

� ⃗−⃗�=

(

^���111⁻⁻−^���²₂²

)

�⃗  +⃗�=

(

^���111⁺⁺+^���²₂²

)

PERKALIAN SKALAR VEKTOR

� ⃗=

(

^���11¹

)

Jika ^{, maka} �  .�=⃗

(

^{���... ���11}1

)

�= ⃗

(

⁻³²¹

)

^{⃗�  =}

(

⁻⁻³¹¹

)

^{⃗�  =}

(

⁻³⁰⁴

)

^{⃗�  =}

(

¹⁴⁰

)

^{⃗�  =}

(

¹⁴⁰

)

 Diketahui:

Tentukanlah:

| -|

    |4|   |4|

| |

1.   2. 3. 4.

LATIHAN

CONTOH

9

⃗�  =

(

⁻⁻³¹¹

)

^{⃗�  =}

(

⁻¹⁰²

)

 Diketahui:

Tentukanlah:   | -|

VEKTOR POSISI

� ⃗=

(

−³²1

)

^{⃗�  =}

(

⁻⁻³¹¹

)

^{⃗�  =}

(

⁻³⁰⁴

)

^{⃗�  =}

(

¹⁴⁰

)

^⃗�= 

(

¹⁴⁰

)

Diketahui:

Jika diketahui vektor  

� ⃗

dan vektor

⃗ �

 

, maka vektor posisi

⃗

 

��=⃗ � − � ⃗

⃗ ��

 

⃗

 

��

⃗ ��

 

1.

2.

3.

VEKTOR SATUAN

Vektor satuan adalah vektor yang besarnya 1 satuan

¿

 

�∨¿ ⃗ 1

¿�∨⃗ ¿.⃗�

�=⃗ 1

¿

 

LATIHAN

� ⃗

   ^-

+ 2 ⃗ �

Tentukan vektor satuan dari

6.

4.

Tentukanlah:

� ⃗

  5.

⃗ �

 

7.

CONTOH

11

�= ⃗

(

⁻⁻⁰¹²

)

^{⃗�  =}

(

⁻¹²¹

)

. Tentukanlah

^⃗

 

^{� �}

Diketahui:

Tentukan vektor satuan dari

⃗

 

� �

OPERASI PERKALIAN VEKTOR

PERKALIAN DOT VEKTOR

� ⃗=

(

^���11¹

)

^⃗�= 

(

^���222

) ^{�∘ ⃗}

 

^{⃗ � =�}

¹

^�

²

^{+ �}

¹

^�

²

^{+ �}

¹

^�

²

Jika dan , maka

�∘ ⃗

 

⃗ � =¿ �∨¿ �∨ cos �

Perkalian DOT dua vektor yang membentuk sudut 1.

2.

3.

(Perkalian dot vektor menghasilkan besaran SKALAR)

�

 

⃗

⃗ �

 

θ Sudut antara dua vektor dapat dicari dengan:

¿�∨¿�∨¿

cos �=⃗� ∘�⃗

¿  

Proyeksi terhadap

�

 

⃗ ^⃗ _�

 

⃗ �

 

�

 

⃗

θ

Proyeksi skalar terhadap

�

 

⃗ ^⃗ �

  ^¿⃗�∘^⃗�∨¿⃗�

¿

=> 

(

 

¿ ^{�∘ ⃗} ⃗ � ¿ ^{⃗ �}

²

) ^{. � ⃗}

Proyeksi vektor terhadap

�

 

⃗ ^⃗ �

  ⁼

x >

(Hasil: Panjang x)

(Hasil: vektor posisi x)

LATIHAN

13

�= ⃗

(

⁻³²¹

)

^{⃗�  =}

(

⁻⁻³¹¹

)

^{⃗�  =}

(

⁻³⁰⁴

)

^{⃗�  =}

(

¹⁴⁰

)

^⃗�= 

(

¹⁴⁰

)

Diketahui:

Tentukanlah:

( ) 1.  

2.

3.

4.

 

⃗ �� ∘

 

⃗ ��

⃗ �� ∘

 

⃗ ��

Carilah besar sudut yang dibentuk oleh:

�

 

⃗

^dan

^⃗ _�

 

⃗ �

  ^dan

^⃗ _�

 

5.

6.

Tentukan proyeksi skalar dan vektor

�

 

⃗

^terhadap

^⃗ _�

 

⃗ �

  ^terhadap

�

 

⃗

7.

8.

CONTOH

15

� ⃗=

(

¹⁰²

)

^{⃗�  =}

(

⁻¹⁰¹

)

Diketahui:

 

Tentukanlah:

Tentukan proyeksi skalar dan vektor

�

 

⃗

^terhadap

^⃗ _�

 

OPERASI PERKALIAN SILANG (CROSS) VEKTOR

PERKALIAN CROSS VEKTOR ⃗ �

 

× ⃗ �=⃗ � =¿ ⃗ �∨ ¿ ⃗ �∨sin �

⃗

 

�

⃗ �

 

θ

⃗ �

 

⃗

 

�

⃗ �

 

θ

⃗ �

 

 Arah hasil perkalian silang selalu tegak lurus dengan arah dua vektor yang dikalikan.

 Untuk menentukan arah dari hasil perkalian silang dari dua buah vektor dapat menggunakan aturan tangan kanan.

 Ibu jari = hasil vektor

 Empat jari lain = sudut terkecil dari vektor A ke B

[1]

B

PERHITUNGAN CROSS VEKTOR

17

Diketahui:

⃗ �=

 

� � ^ + b ^ � +c � ^

⃗ �

 

= � � ^ + e ^ � + f � ^

Diketahui:

⃗ �= ^

 

� − 2 ^ � + ^ �

⃗ �=

 

3 �+ ^ ^ � − 2 � ^

CONTOH:

⃗ �

 

× ⃗ �

⃗ �

 

× � ⃗

Dengan soal yang sama pada soal di samping, tentukanlah dan

-

RESULTAN VEKTOR

x

Y

θ F

F_x = F.cos θ

F_y = F.sin θ

x

Y

60^o

F₁ = 5 N

F₂ = 5 N

F_1x = F₁.cos60^o

F_1y = F₁.sin60^o F_x = F_1x + F_2x F_y = F_1y + F_2y F_2x = F₂.cos0^o

F_2y = F₂.sin0^o

�

 

= √ ^{� � 2 + � � 2}

Hitunglah resultan gaya dari F₁ dan F₂!

�

 

= √ ^{� � 2 + � � 2}

 Resultan vektor = penjumlahan dua vektor atau lebih

Rumus resultan vektor

¿

 

� ∨¿ √ ^{∑ � 2 � + ∑ � � 2}

⃗ �

 

= ∑ ^{� � � ^ +} ∑ ^{� � ^ �}

(Bentuk skalar) (Bentuk vektor)

PENJUMLAHAN VEKTOR

19

x

Y

45^o

F₁ = 4 N

F₂ = 2 N

Hitunglah resultan gaya dari F₁ dan F₂!

RESULTAN VEKTOR

Hitunglah resultan gaya dari F₁, F₂ dan F₃!

x

Y

60^o

F₁ = 5 N

F₃ = 4 N 37^o

F₂ = 3 N

45^o

I (semua positif) II (sin positif)

III (tan positif) IV (cos positif) INGAT KUADRAN TRIGONOMETRI

F_1x = F₁.cos60^o F_1y = F₁.sin60^o

F_2x = F₂.(-cos53^o) F_2y = F₂.(+sin53^o)

F_3x = F₃.(+cos45^o) F_3y = F₂.(-sin45^o)

 Sudut yang dipakai adalah besar sudut TERHADAP SUMBU X.

 Ingat letak kuadran (ada kemungkinan fungsi sin/cos bernilai positif atau negatif)

F_x = F_1x + F_2x + F_3x F_y = F_1y + F_2y + F_3y Maka:

� = √ ^{� � 2 + � � 2}

 

⃗ �

 

= � � � ^ + � � ^ �

LATIHAN

21

Hitunglah resultan vektor!

x

Y

53^o

F₁ = 5 N F₂ = 6 N

37^o

x

Y

45^o

F₁ = 2 N F₂ = 4 N

60^o

F₃ = 10 N 30^o

x

Y

F₁ = 3 N F₃ = 4 N

45^o

F₄ = 5 N 30^o

1) 2)

3)

F₂ = 3 N

x

Y

F₁ = 3 N F₃ = 4 N

45^o

F₄ = 5 N

30^o 30^o 45^o 4)

F₂ = 4 N

Soal Cerita

 Seorang pedagang tahu berangkat dari pabrik tahu dan berkendara sejauh 5 km ke arah utara, kemudian berbelok dan melanjutkan perjalanannya pada arah 30˚ ke selatan dari timur sejauh 3 km, lalu berbelok lagi ke arah barat daya

sejauh 4 km. Berapakah perpindahannya dari pabrik tahu?

23

FISIKA 1

School of Electrical Engineering, Telkom University

Week 1. Part 2

INTEGRAL & DIFERENSIAL

BESARAN FISIS

25

 Keadaan fisis dari materi selalu dinyatakan sebagai fungsi matematis dari besaran lain yang mempengaruhinya.

�

�=� (¿)

  ¿

 S = besaran yang diukur, x = variabel yang mempengaruhi besar S.

 Besaran fisis perlu dipelajari,

sehingga dapat diketahui karakteristik fenomena tersebut.

� (� )=( � − 2 )

²

 

Contoh:

Posisi sebuah partikel dalam arah x sebagai fungsi waktu.

t (s) x (m)

0 4

1 1

2 0

3 1

4 4

5 9

6 16

PROFIL POSISI PARTIKEL TERHADAP WAKTU

REVIEW INTEGRAL DAN DIFERENSIAL

 Beberapa besaran fisis suatu fenomena dapat diketahui dari fungsi turunan/integralnya.

 Diferensial = Turunan = Bagaimana nilai suatu fungsi berubah menurut perubahan input-nya.

 Integral = anti turunan.

∫

 

^�

^�

^��= _� ¹ ₊₁ ^�

^�+1

^+�

� =� �

^�

→ ��

�� =� . � �

^�−1

TURUNAN   INTEGRAL

Contoh:

 Kecepatan adalah perubahan jarak terhadap waktu.

 Percepatan adalah perubahan kecepatan terhadap waktu.

� = ��

 

��

�= � �

��

 

�=��

�� =�²�

� �²  

Contoh Lain:

� = ��

 

��

� = ��

 

��

�

 

= ∫ ^���

�

 

= ∫ ^���

�

 

= ∫ ^���

�

 

= ∫ ^���

Usaha = Gaya x Jarak

Fluks = Medan x Luas Daya = Usaha per

satuan waktu

Arus = muatan per satuan waktu

CONTOH

27

 Sebuah partikel bergerak dengan vektor posisi x(t) = 4t + t

²

m (t dalam s).

Tentukanlah:

a. Kecepatan saat t = 1 s dan t = 10 s

b. Tentukan waktu (s) saat kecepatan bernilai 10 m/s c. Percepatan saat t = 10 s dan t = 20 s

d. Gambarlah grafik x(t), v(t) dan a(t)

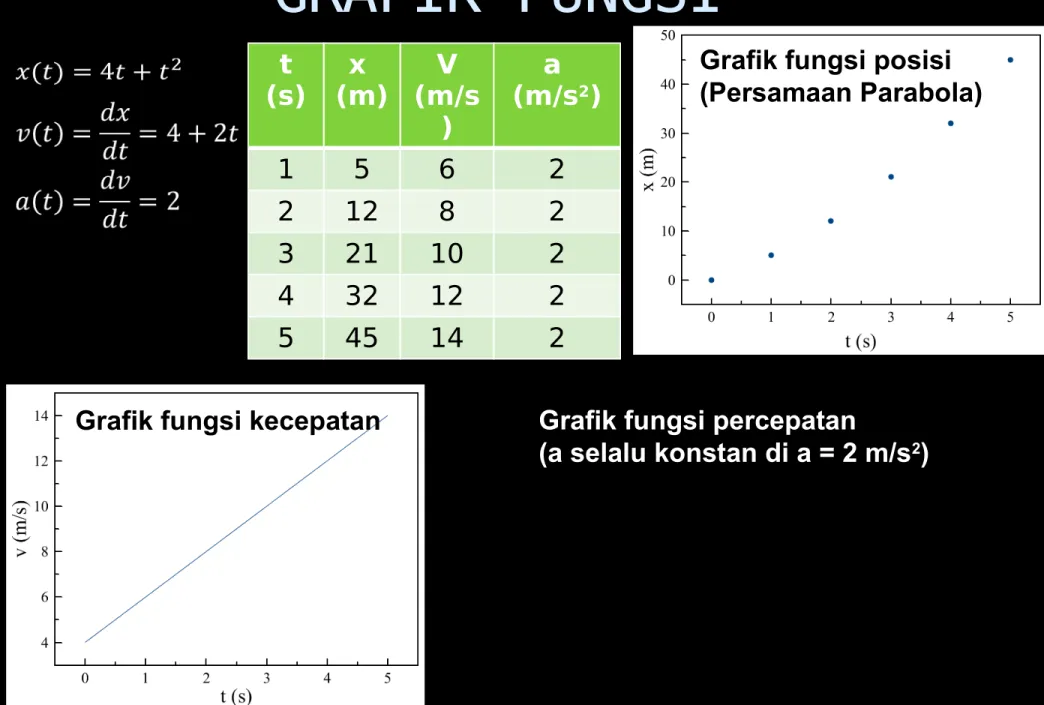
GRAFIK FUNGSI

²⁹

� ( � ) = � �

�� =4 +2 �

 

t (s)

x (m)

V (m/s

)

a (m/s²)

1 5 6 2

2 12 8 2

3 21 10 2

4 32 12 2

5 45 14 2

� ( � )= 4 � +�

²

 

� ( � ) = � �

�� =2

 

Grafik fungsi percepatan

(a selalu konstan di a = 2 m/s²) Grafik fungsi posisi (Persamaan Parabola)

Grafik fungsi kecepatan

CONTOH SOAL 2

(0, 2)

(5, 12)  Sebuah partikel bergerak dengan

profil kecepatan seperti gambar di samping. Tentukanlah:

a. Tentukan persamaan kecepatan v (t)

b. Tentukan kecepatan dan percepatan saat t = 10 s

LATIHAN

31

 Sebuah partikel bergerak dengan kecepatan v(t) = 4 - t² m/s (t dalam s). Tentukanlah:

a. Kecepatan saat t = 5 s dan t = 10 s

b. Tentukan waktu (t) saat kecepatannya bernilai 0 m/s

c. Percepatan saat t = 10 s

 Sebuah benda bergerak dengan

percepatan a = 2t – 1 (m/s²). Jika kecepatan awal benda v = 5 m/s, tentukanlah:

Fungsi kecepatan v(t)

LATIHAN

 Sebuah partikel bergerak dengan profil kecepatan seperti gambar di samping.

Tentukanlah:

a. Tentukan persamaan kecepatan v (t) b. Tentukan kecepatan dan percepatan

saat t = 10 s

(1,1) (2,4)

(5,25)

33

Danke!