This thesis is about interactions between asymmetrically informed agents, where information can be transmitted through agents' actions. The following refinements of the equilibrium concept are derived and applied to (i) a model of preliminary negotiations between litigants in a civil suit, where both parties. The state of the art on the theory side has generated predictions from equilibrium analysis, in which agents' beliefs about unknown parameters are explicitly recognized in the equilibrium concept.
Many of these predictions are a function of the leeway agents are given in their beliefs when confronted with events inconsistent with the equilibrium path; that is, events that equilibrium predicts would occur with zero probability. The general form of these constraints concerns the informativeness of the equilibrium payoffs in determining the balance sheet. For a given signaling game, we call a subset C of the set of Nash equilibria stable if for every e > 0 there exists o > 0 such that any (p,q,r) perturbation of the original game with.

DIVINE EQUILIBRIA
Particularly in generic signaling games, if an equilibrium is stable, then any perturbation has an equilibrium with payoffs close to the original equilibrium payoffs. The first intuitive constraint on beliefs that we discuss requires that R's beliefs that fall outside the equilibrium path assign positive probability only to those types of Sender that might not lose to a defection. Cho and Kreps (1986) also identify this condition and show that when an equilibrium is stable, the
Establish an equilibrium in which a Sender of type t obtains utility u (t), and, for all t e T, the probability that t m sends is zero. It states that if an equilibrium is stable, then there exist beliefs in r • that support it. We can show that in generic signaling games, if an equilibrium is stable, it can be supported.
A CHARACTERIZATION OF STABLE EQUILIBRIA
i 12. not voluntarily sending m2 is an element of <3•3), then there is an equilibrium for the perturbed game close to the original equilibrium only if the tremor induces R to take an action given m. Furthermore, if ~(t1 m2) t <3•3>, then the perturbed game has an equilibrium that is close to the original game and in which either t1 or t 2 voluntarily sends m2 • Therefore, the equilibrium in the example is stable if and only if, given m. First, we identify the set of tremors that cannot induce voluntary action in any equilibrium to the perturbed wildlife that is close to the original equilibrium.
Second, we prove that an equilibrium is stable exactly when no best response to this set of shocks causes S to voluntarily send m. For sufficiently small tremors, an equilibrium exists for the perturbed wildlife, with payoffs close to . In generic signaling games, an equilibrium is stable if and only if, for all unused signals m, A • = o.
EXTENSIONS
Farrell calls an equilibrium in which this type of deviation does not exist neologism evidence. Kreps rejects an equilibrium in which there exists a sender type that wants to defect for every action in BR(AT\J'm). It does not change our results to require R to believe that any type that sends m instead of the equilibrium signal expects to strictly benefit from it.
In the game described in Figure 2, there is a sequential equilibrium in which both S types send m1 with probability one and R takes a. Conversely, in the study of the strategic, the work of Bebchuk (1984), Samuelson (1983), P'ng and Salant (1984) has focused on correctly modeling the negotiation problem inherent in the legal process after an accident. The article is organized as follows: the next section provides an overview of the above-mentioned models of preliminary negotiations.
This model corresponds to the model below when the rule of negligence applies, although P'ng (1984) arbitrarily restricts attention to a subset of the sequential equilibria. 34; to avoid a priori restrictions on the information structure or on the strategy space of the bargaining game." The revelation principle enables Spulber to characterize the set of tentative incentive-efficient solutions to the game where both claimants have private information. Analysis of the settlement and liability issues is based on the following order of actions and events: an accident happens.
The issue in this case is the carelessness or carelessness of both parties in terms of actions directly related to the occurrence of the accident. Monetary payments to the parties from the court decision are functions of both. Definition: A sequential equilibrium for each of the above games consists of the strategies {q*(•),r*(•,•)} ford and p, and the beliefs.
DIVINE EQUILIBRIA
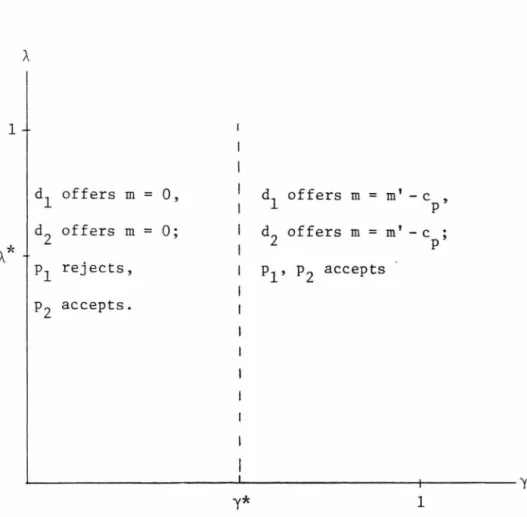
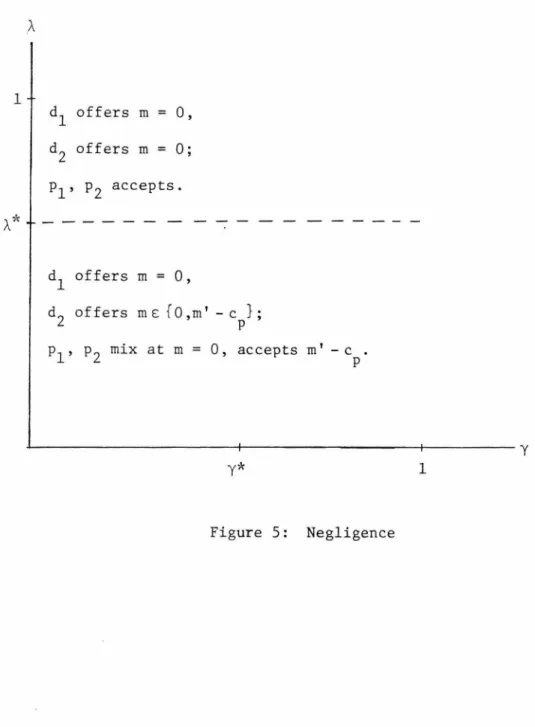
To check whether any of these union equilibria is divine, we use the following: the given equilibrium payoffs u*(d. To check for divine, we can redefine ei(;lm•> in terms of the joint bid m•. Thus, after solving for the equilibrium utility d1•s, e1<;1m•) solve To summarize the results according to the neglect rule:. i) if mA ~ cd' there is an equilibrium offer divine union at m• = max{O, mA}, which p accepts with positive probability. ii) if mA 2 0, there exist divine semi-join equilibria with joint bid m• e [O,min{mA,cd}], and where is the trial probability.
Thus, the only divine pool equilibrium offer that accepts both p1 and p2 with positive probability is at m• = m~. 2 can only make p1 indifferent for .. offers less than mA.' a condition for the existence of successive semi-pool equilibria is that. Since P1 is indifferent to m• in the semi-pool equilibrium and q*{m•ld1). which is the same as under the negligence rule.
Note that these partial derivatives are the same as in the semi-pooling equilibrium under the negligence rule multiplied by 1/r. Thus, all successive semi-merging equilibria under the rule of negligence with contributory negligence are divine. iii) if mA > 0, m ~ mA, m ~ red' there exists a semi-pooling of divine equilibria with a common supply m s [m,min{mA,rcd}] and where the probability of trial is . The sequential semi-pooling equilibria in this case will imply that p1 rejects the common offer and accepts m = m' - cp, p2 indifferent between accepting and rejecting the common offer, d. sending the joint offer with probability one, and d. 2 indifferent between the common supply and m = m' - cp.
We start by dividing the parameter space into two groups. i) Half-coupling equilibria do not exist. ii). If there exists a coupling equilibrium at m* = 0 under slcn, then there exists a coupling equilibrium at m* = 0 under sldcn;. If there is a coupling equilibrium at m• = m' cp under sldcn, then there is a coupling equilibrium at m• = m' - c p under slcn. i).
The merger equilibrium supply m• = 0 exists more often under ncn than under n. v) Semi-joining equilibria exist more often under n than under no; moreover, the set of common bids is smaller under ncn than under n.

UNIVERSALLY DIVINE EQUILIBRIA
CONCLUSION
We have seen how the applicable liability rule can affect the behavior of plaintiff and defendant in the pre-trial negotiation of a civil suit. This will give the defendant the opportunity to gain insight into the plaintiff's type before making his offer, an opportunity that does not exist in the model above. Of course one could have initially defined equilibrium and then added divinity; however, divinity grew out of the methodology of the sequential equilibrium concept and as such is easier to characterize as a refinement of sequential equilibrium.
Since the payoffs are not a function of the plaintiff's type, the plaintiff's strategy can be a nontrivial function of type i f only. 2• In this case, the (mixed) strategies of the plaintiff below can be interpreted as those that arise after expectations about p. 34; Liability, Litigation, and Incentives to Care." Mimeo, Center for Economic Policy Research, Stanford University.
34; Settlement, Litigation, and the Allocation of Litigation Costs." Cal tech Social Science Working Paper No. 34; A Reexamination of the Perfection Concept for Equilibrium Points in Extended Games." International Journal of Game Theory 4: 25-55. 34; Indictment, settlement, and trial: A theoretical analysis among alternative methods of legal fee allocation. Journal of Legal Studies 11: 55-81.
CHAPTER III. A MODEL OF ELECTORAL COMPETITION WITH INCOMPLETE INFORMATION
SYMMETRIC EQUILIBRIA
- POOLING EQUILIBRIA
- SEMI-POOLING EQUILIBRIA
- SEPARATING EQUILIBRIA
- HYBRID EQUILIBRIA
Furthermore, for the non-(pure) pooling equilibria we will investigate equilibria that are symmetric with respect to the origin (i.e., s(a) = -s(-a)), which implies that we can concentrate on the half-policy space [ 0.2 ]. One characteristic of all symmetric equilibria in the model is that the equilibrium strategy s(•) is monotonically increasing; i.e. To see this, establish an equilibrium and let ~(a) be the probability that an a-type candidate wins the election, where we suppress the other arguments of this function.
From the continuity of U(•,•), it must also be the case that a must be indifferent between the union with [a-e . 1,a) and division. To see whether or not these beliefs are reasonable, we calculate (as in Chapter II) the probability of voting for A, which makes a given type indifferent between sending the equilibrium. In general, if a e (ai,ai+l), then a gains a with probability 2- F(ai)- F(ai+l), giving an expected equilibrium utility of.
Thus, form sufficiently close to ai' ai will want to send m in opposition to ai and thereby disturb the equilibrium. If not, let a' = s(a) > a, for some a; then a' is better off sending s(a) than s(a'), since a' gets a higher utility from winning and a higher probability of winning, contradicting the assumption of an equilibrium. 2) as. Equation (7) applies with equality at a' = a; 'thus a (first-order) necessary condition for an equilibrium is that.
For both c1 and c11, we assume that there exists a type, a1 and a11, respectively, which does not care about separating and pooling. By the results in 3.2 above, we only need to consider one pooling position per semi-political space in trying to characterize the universal divine equilibrium, since more than one would suggest (as above) that some type would want to deviate from the equilibrium when we limit beliefs. To ensure an equilibrium, it must be that differentiation of the LHS of (12) with respect to the first argument in U(•,•) is non-positive:. 1 don't care to send s To ensure equilibrium, the LHS of (20) with respect to the first argument in U(•,•) must be positive (again ignoring the denominator). EXAMPLES OF SYMMETRIC EQUILIBRIUM BEHAVIOR Information: A Satisfied Expectations Model Using Contemporaneous Polls and Approval Data as Sources of Information.” Journal of Economic Theory 36:55–85.
CONCLUSION