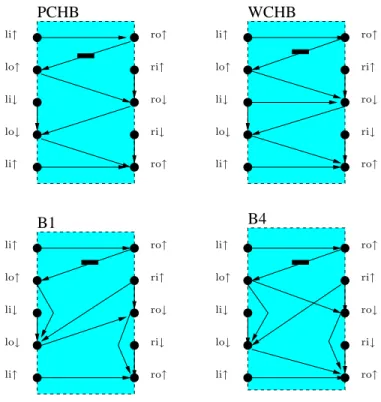
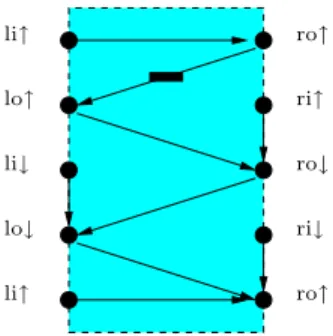
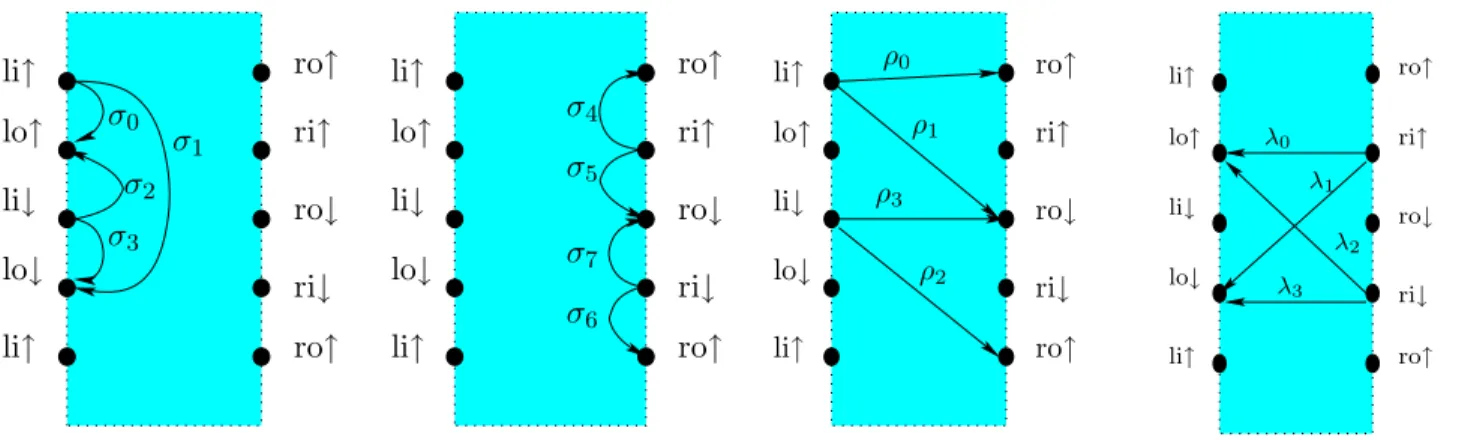
Edges: The edges of the constraint graph capture the partial order between tasks in a collection of HSE. A ring of buffers is a pipeline, such that the pipeline's active channel is also the pipeline's passive channel.
Pipelines
In order to determine the number of messages in the pipeline, it will be necessary to keep a count of how many times certain variables are allocated in the system. The number of messages in the pipeline π≡πA·πB is the sum of the number of messages in πA and πB.
Rings
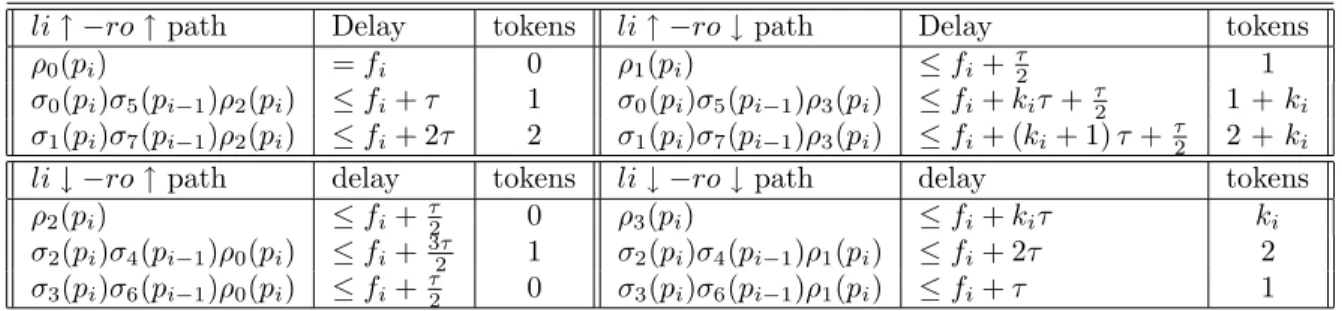
Since clo−cri is even, the number of messages placed in the ring must be integral. Letc(v) denote the number of times that command v occurs when the number of messages in πr increases by n.
Pipelines
Changing the number of messages in a ring byn∈Z changes the number of tokens on each cycle in a ring's constraint graph by an amount independent of the channel on which the ring was disconnected to insert the messages. Changing the number of messages on a ring, by an integral amount, only changes the number of messages on the cycles corresponding to F1, F2, B2, B1. If a cycle matches one of F1, F2, B2, B1 when a ring is broken on a given channel, it must match the same expression regardless of where the ring is broken.
Inspection of Tables 1 and (4) reveals that inserting a message into a ring changes the number of tokens on all cycles that match one of the expressions F1, F2, B2, B1, by the same amount. For processes with multiple passive channels and/or active channels, the static slack in the process between a specified pair of passive and active channels is defined as for a buffer where all other channels are connected to sources and sinks.
Rings
Dynamic Slack
If a ring rn consisting of π instances has dynamic laxity ds(rn, τ), then π is said to have dynamic laxity at least ds(rnn,τ). The relationship between the dynamic looseness of the ring and the number of processes on the ring is not necessarily constant. A ring consisting of n instances of π may not be able to operate in cycle time τ for all n∈N.
We consider rings composed of L(i) instances of π where L(i) is the ith smallest ∈ N, so that a ring of n instances of π can run at cycle timeτ. The dynamic slack is the maximum number of messages an instance ofπ can contain while maintaining a cycle time ofτ. We will prove a lemma that relates the dynamic slackness of a ring of buffers to the maximum number of messages in the steady state of a fastest linear execution of a pipeline obtained by disconnecting the ring.
If rn can operate at cycle time τ or less, then no fastest linear implementation of π2n contains more than ds(r2n, τ) + 1 steady-state messages. A path must have at least δ(p)τ tokens during the steady state of the fastest linear implementation π2n, where δ(p) is the delay along p. If there exists such that a ring consisting of π instances has an implementation with cycle time at most τ, then ndspip(π, τ) = dsring(π, τ).
Dynamic Threshold
The dynamic threshold,dtring(π, τ), of a pipeline,π, when part of a ring is defined as dtring(π, τ)def= lim. We first present a lemma relating the dynamic threshold of a ring consisting of instances of π to that of a ring consisting of in, i∈Ninstances of π. Consider a pipeπ for which there exists such that a loop of instances of π has cycle time at mostτ.
The dynamic threshold is the minimum number of messages that an instance of π can contain, while maintaining a cycle time of τ. Let each instance of π contain the minimum number of messages such that π can compose with itself. We will present a lemma that relates the dynamic threshold of a ring of buffers to the minimum number of messages in the steady state of a pipeline obtained by breaking the ring.
This lemma can be used to prove that the limit in Definition 13 exists and is equal to the dynamic threshold of the pipeline when it is part of a ring. If rn can operate at cycle time τ or lower, then in any fastest linear implementation of π2n, π2n. If there exists such that a ring composed of instances of π has an execution with at most cycle timeτ, then ndtpip(π, τ) =dtring(π, τ).
Buffers
We will consider systems composed of processes that have one of the four remaining reshuffles. In addition to Assumptions 1 and 2, it is assumed that the ratio of the delay to the number of tokens on cycles traversing exactly one process is at most τ. Global cycles that match one of the regular expressions (5) or (6) are referred to as forward cycles.
An acritical cycle of a system is a cycle in which the ratio of the delay along the cycle to the number of tokens in the cycle is equal to the cycle time of the system. Using the bounds from Table 2, we see that if a cycle that limits the cycle time of a ring of buffers to τ has paths of types 2 and 3, a cycle that does not contain paths of these two types also defines the system cycle time. Basic example: Table 9 lists all the paths from the input variables of the output channel to the output variables of the input channels in a two-buffer pipeline.
Examination of the table reveals that the requirement actually holds for rings of length 2 and 4. The dynamic slack (or dynamic threshold) of a pipeline of processes satisfying Assumptions 1 and 2 is the sum of the dynamic slack (or dynamic threshold ) for the processes on the pipeline. Furthermore, Lemma 9 guarantees that no local cycles force the cycle time of the system to be greater than τ.
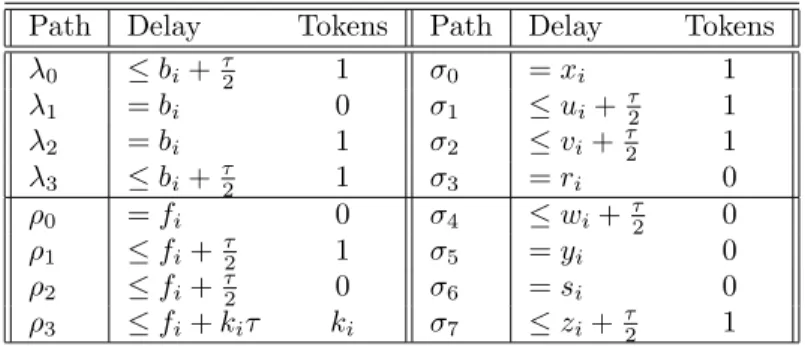
Processes with more than two channels
When these constraints hold, by considering all possibilities it can be shown that if all pipelines can simultaneously contain a number of messages greater than their dynamic threshold and less than their dynamic slack, then no local cycles limit the cycle time to be greater than τ. Similarly, an exhaustive case analysis can be used to show that if the global cycles given in Lemmas 10 and 11 do not limit the cycle time to be greater than τ, then no global cycle limits the cycle time to be greater than τ. Slack matching is an optimization performed by adding buffers to a system to reduce the system's cycle time.
If the system is not closed, sources are connected to system inputs and sinks to outputs. The environmental delays are assumed to be such that the environment does not constrain the system cycle time to be greater than the target cycle time, τ0. We will first state the constraints that can be used to determine whether a system is compatible.
We adopt the convention that an edge (u, v) represents a channel so that it is an active channel of processu and a passive channel of processv. For each pair of edges, (a, b) and (b, c) let ds(abc, τ) endt(abc, τ) denote the dynamic clearance and dynamic threshold of the process bbetween channel connected to a and connecting c at cycle is time τ. The cycle time of a system will be considered that of the slowest command in the system.
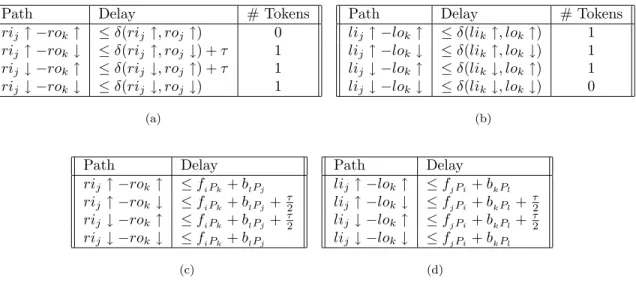
Necessary and sufficient conditions for slack matching
A system is represented by a directed graph, G= (V, E), with each vertex representing a process, and each edge a communication channel. We will refer to the closed interval, [dt(abc, τ), ds(abc, τ)] as the dynamic range of process b between channels etc. Note that the variables drabc indicate a value in the dynamic range of process b between the channel (a, b) and the channel (b, c).
For each path in the process graph between processes d such that the first edge of the path is (a, b) and the last is (e, f), the sum of Sabef and the number of initial messages in the corresponding pipeline lies within the dynamic range of on the way. If there are multiple paths in the process graph between a process a and f such that the first edge of the path is (a, b) and the last is (e, f), the Sabef variables capture the requirement that the dynamic range of the corresponding pipelines be such that there exists a number of messages that can be added to all these pipes a-f so that the number of messages in the pipe is within its dynamic range. This requirement arises from the fact that if a message is inserted into one of these pipes, a message is inserted into all pipes.
Since each communication channel is used once per cycle, the number of messages on a ring is constant. Furthermore, if two pipelines, π1 and π2, exist between a pair of processesa and b, the difference between the number of messages on the two pipelines is constant. Thus, there exists an execution such that the number of messages in any pipeline (or ring) in the system is within the dynamic range of the pipeline (or ring).
MILP for slack matching
Generating the MILP
Example I: Lutonium Fetch Loop
Example II: Control Loop of MiniMIPS
An algorithm was presented for slack matching systems consisting of processes that can be represented as collections on a recurrent SLHSE in standard form, given certain assumptions about the dynamic slack and the dynamic threshold of these processes. Sufficient conditions have been presented to ensure that the dynamic relaxation and threshold of systems composed of half-bumps satisfy these assumptions. Arguments similar to those in Section 6 can be used to provide a class of full buffers such that systems composed of these buffers satisfy Assumptions 5 and 6.
Since most real systems do not use every channel on every cycle, extending the theory to systems with conditional communication would be interesting. It would be interesting to study systems consisting of buffers with different static clearances, especially the case of systems containing both half buffers and full buffers. 4th International Conference on the Mathematics of Program Construction, Lecture Notes in Computer Science 1422, pages 272–285.
Proof of lemma 7
Proof of theorem 3
Proof of lemma 8
During steady state, the number of tokens on each path varies by up to one. The padp must have at least δ(p)τ tokens at any point during any fastest linear execution, where δ(p) is the delay along p. This corresponds to the fact that there are at least dt(r2n, τ)−1 messages inπ2n at any time during the steady state of a fastest linear execution.
Proof of theorem 4