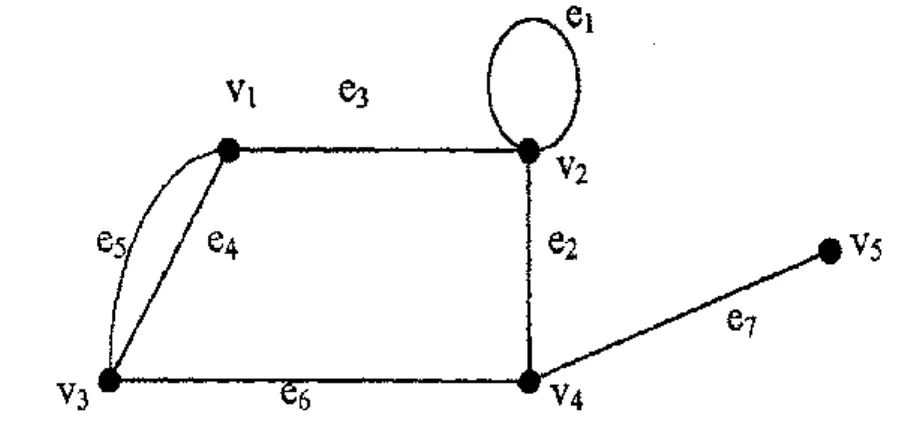
Misalnya pada Gambar 1.1 di atas tepi e2, e6 dan e7 merupakan tepi yang menempel pada titik v4. Keadaan seperti ini dapat dinyatakan dalam bentuk sederhana berupa grafik seperti terlihat pada Gambar 4.4 di bawah ini. Contoh graf yang mempunyai sisi dan loop sejajar dapat dilihat pada Gambar 6.2 berikut beserta matriks ketetanggaannya.
Lebih lanjut, grafik pada Gambar 6.4 di bawah ini bukanlah grafik sederhana karena mengandung satu lingkaran dan dua sisi sejajar.
Banyaknya atau banyaknya sisi yang menempel pada suatu titik v (lingkaran dihitung dua kali) disebut derajat titik tersebut; dilambangkan dengan d(v). Jika kita memisahkan titik-titik dengan derajat ganjil dan genap, maka jumlah ruas kiri persamaan (1) dapat dinyatakan sebagai jumlah kedua bilangan tersebut. Karena ruas kiri persamaan (2) genap dan suku pertama ruas kanan genap, maka suku kedua ruas kanan juga harus genap.
Jika dua sisi yang tidak sejajar menyentuh titik sudut yang sama, maka kedua sisinya disebut 2.
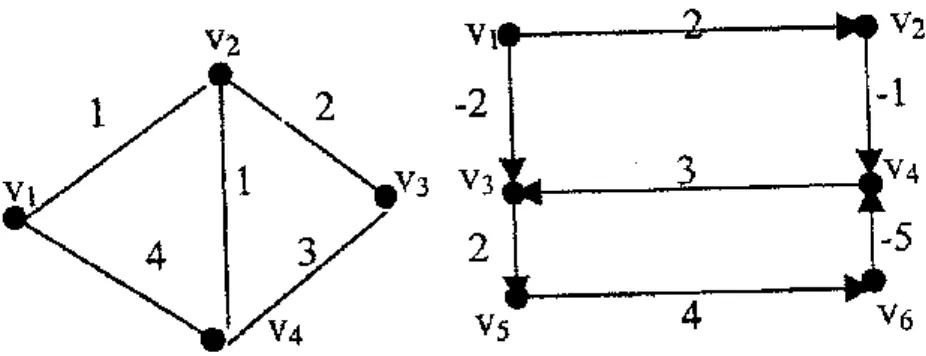
Jaringan adalah graf atau graf berarah dengan fungsi yang memetakan himpunan sisi atau sisi berarah ke himpunan bilangan real. Jaringan yang berupa graf disebut jaringan tidak berarah, sedangkan jaringan yang berupa graf berarah disebut jaringan berarah. Jika relasi yang mendefinisikan suatu graf memuat (v,v) dengan v dan V, maka nama graf tersebut berubah menjadi graf cincin, graf berarah cincin, jaringan cincin, atau multigraf cincin.
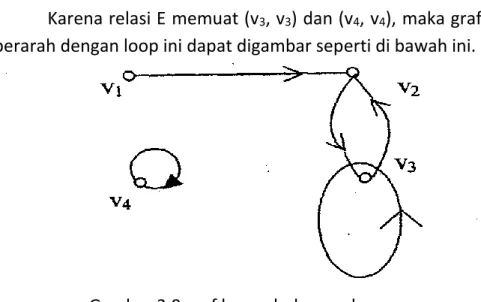
Karena relasi E mengandung (v3, v3) dan (v4, v4), maka graf berarah dengan loop ini dapat digambarkan sebagai berikut.
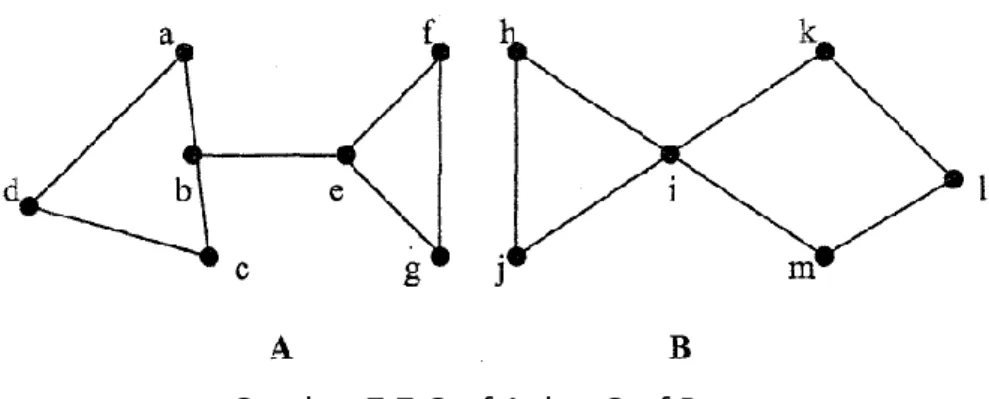
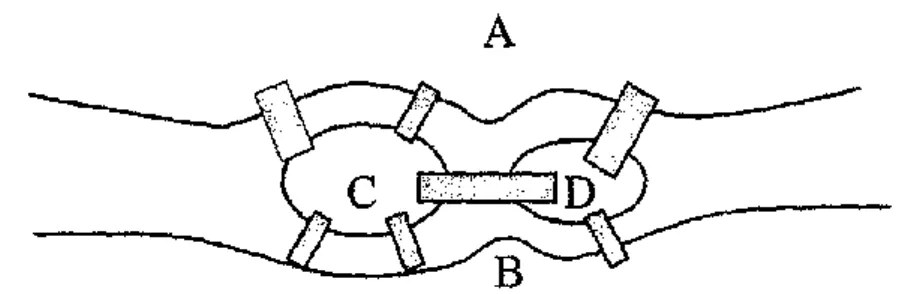
Pada gambar, lingkaran putih kecil melambangkan mikrokomputer dan lingkaran hitam kecil melambangkan komputer mini. Seseorang yang ingin mengakses jaringan harus menggunakan salah satu minikomputer yang ada bersama mikrokomputernya. Pada gambar A, B, C, D, dan E melambangkan ruangan-ruangan pada bangunan, sedangkan 0 melambangkan bagian luar bangunan.
Jika A, B, C, D, E dan 0 direpresentasikan sebagai titik-titik dan pinto yang menghubungkan antar ruangan atau antara ruang dengan bagian luar direpresentasikan sebagai sisi-sisinya, maka keadaan pada gambar di atas dapat direpresentasikan sebagai grafik seperti pada Gambar di bawah. 4.6 di bawah.
Graf G adalah himpunan tak kosong V yang memenuhi sifat non-refleksif dan simetris dari relasi R pada V. Jika G adalah graf yang didefinisikan dalam himpunan titik V dan relasi R pada V, maka (u, v ) ER menghasilkan (v, u) ER. Sisi-sisi paralel pada grafik akan menghasilkan kolom-kolom identik pada matriks kejadian.
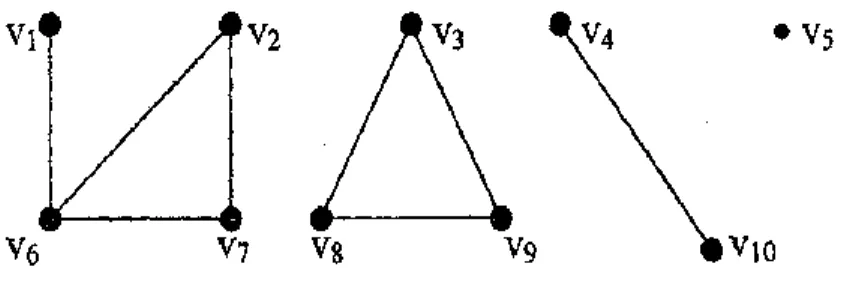
Jika suatu graf G tidak terhubung dan terdiri dari dua komponen Gl dan G2, maka matriks kejadian A(G) dari graf G dapat dituliskan sebagai berikut.
Suatu graf selain dinyatakan dalam bentuk matriks kenampakan, juga dapat dinyatakan dalam bentuk lain, yaitu matriks ketetanggaan atau matriks keterhubungan. Matriks ketetanggaan pada graf G merupakan matriks persegi berorde n, X(G) (xij) dengan elemen xij yang menyatakan banyaknya sisi yang menghubungkan titik ke-i dan titik ke-j. Dengan definisi ini, dimungkinkan untuk mendefinisikan suatu graf yang memiliki sisi atau loop sejajar dengan matriks ketetanggaan.
Elemen-elemen matriks X sepanjang diagonal utama semuanya 0 jika dan hanya jika graf matriks tersebut tidak mengandung loop: Dua graf G1 dan G2 yang tidak memiliki sisi-sisi sejajar adalah isomorfik jika dan hanya jika matriks-matriks yang berdekatan, yaitu X(G1 ) dan X(G2), saling berhubungan. Suatu graf G tidak terhubung dan terdiri dari dua komponen G1 dan G2 jika dan hanya jika matriks yang bertetangga yaitu X(G) dapat dipartisi menjadi.
Jelas bahwa distribusi ini mengakibatkan tidak adanya tepi yang menghubungkan suatu titik pada subgraf G1 dengan suatu titik pada subgraf G2. Jadi graf G selalu dapat dibentuk dengan n simpul (dan tidak memuat sisi-sisi yang sejajar sehingga Q adalah matriks yang bertetangga dengan G). Karena graf tersebut tidak mempunyai loop dan sisi yang sejajar, maka graf tersebut merupakan graf sederhana.
Karena setiap titik pada graf lengkap selalu terhubung ke titik lain melalui sebuah sisi, maka derajat setiap titik pada graf lengkap G dengan n titik adalah n-1. Jika suatu graf memuat titik-titik yang dapat diuraikan menjadi dua himpunan sedemikian rupa sehingga tidak ada sisi yang menghubungkan titik-titik dalam himpunan yang sama, maka graf tersebut disebut graf.
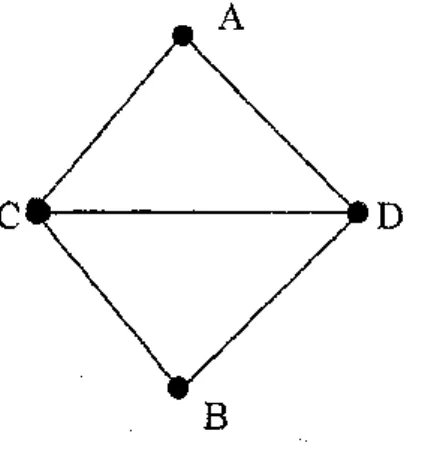
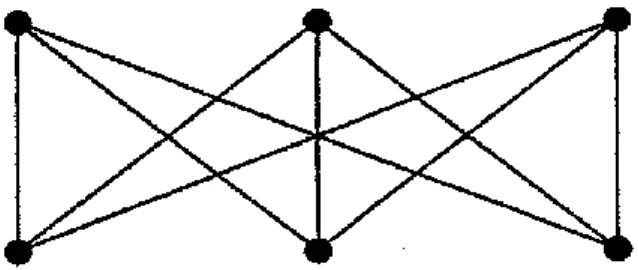
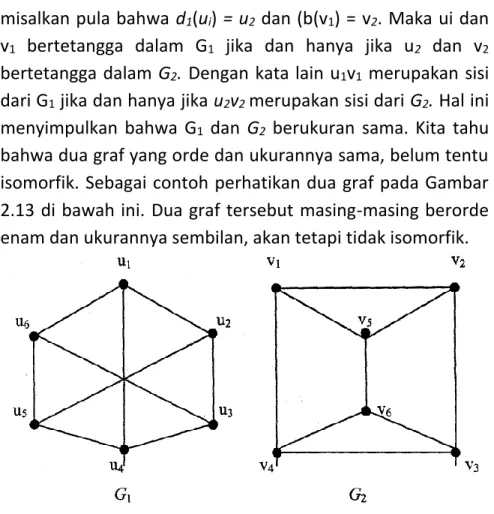
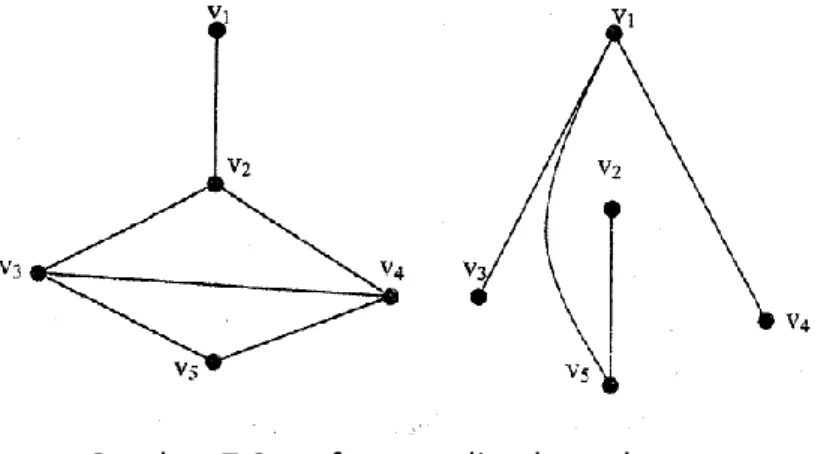
Karena titik-titik pada suatu himpunan terhubung langsung dengan setiap titik pada himpunan yang lain, maka Gambar 2.10 disebut graf bipartit lengkap K3,3. Komplemen graf G, disebut G', adalah graf yang mempunyai himpunan simpul-simpul yang sama seperti pada graf G dan mempunyai sifat bahwa dua simpul di G bertetangga jika dan hanya jika dua simpul yang sama di G' bukan bertetangga. Suatu graf G dikatakan isomorfik terhadap graf H jika terdapat pemetaan satu-ke-satu Φ (disebut isomorfisme dari V(G) ke V(H)), sehingga Φ mempertahankan tetangganya.
Konsekuensinya, tiga titik G1 yang bayangannya v1, v2, dan v5 juga harus merupakan tiga titik yang berdekatan. Jika G1 dan G2 merupakan graf isomorfik, maka derajat simpul-simpul di G1 sama persis dengan derajat simpul-simpul di G2. Titik-titik tersebut, yaitu v1, v2, …,vn, merupakan titik-titik yang bertetangga dengan v, karena u berada di sebelah x pada G1 jika dan hanya jika v berada di sebelah Φ (x) pada G2.
Suatu graf disebut terhubung apabila graf tersebut hanya terdiri atas satu bagian (komponen). Jika suatu graf tidak terhubung, maka graf tersebut terdiri dari beberapa komponen yang masing-masing merupakan graf terhubung atau titik terisolasi. Berapa banyak sisi atau simpul yang harus dihilangkan (dihilangkan) dari suatu graf tertentu agar graf tersebut menjadi graf tidak terhubung.
Node terhubung k(G) dari graf terhubung G adalah jumlah node terkecil yang penghapusannya mengakibatkan G tidak terhubung. Jika kG) ≥ k, maka graf G dikatakan terhubung ke k. Jika V1 = V2 dan dua titik di G bertetangga jika dan hanya jika dua titik yang sama di H tidak bertetangga, maka G dipanggil dari H.
Dengan menggunakan Teorema 12.14 di atas, dapat dibuktikan bahwa setiap graf planar sederhana mempunyai sebuah titik yang berderajat tidak lebih dari 5. Mewarnai suatu graf berarti mewarnai setiap simpul pada graf tersebut sehingga simpul-simpul yang berdekatan memperoleh warna yang berbeda. Jika suatu siklus memiliki jumlah titik ganjil, seperti ditunjukkan pada Gambar 14.4(a), tiga warna harus digunakan.
Sekarang titik-titik yang berdekatan dengan titik yang tadinya berwarna biru diwarnai merah. Mungkinkah salah satu titik merah ini, katakanlah titik W, berdekatan dengan titik V, yang juga berwarna merah. Jadi, setiap titik lain yang hanya berwarna merah tidak berdekatan dengan titik yang berwarna merah, karena sebaliknya terdapat siklus yang panjangnya ganjil.
Kemudian, jika dua titik berwarna biru berdekatan antara satu sama lain, maka terdapat sicius panjang ganjil. Seperti sebelum ini, tiada titik yang baru berwarna boleh terletak berhampiran titik yang sudah merah. Proses ini diulang sehingga tiada titik yang tidak berwarna terletak berhampiran titik yang diwarnakan.
Jika graf tersebut tidak terhubung, maka akan terdapat simpul-simpul yang tidak bertetangga dengan simpul-simpul yang diwarnai, sehingga belum diwarnai. Titik yang belum diwarnai dan terletak disebelah titik biru adalah titik C, D dan E sehingga diberi warna merah. Terakhir, titik G merupakan titik yang belum diwarnai dan berbatasan dengan titik merah sehingga berwarna biru.
Sekarang X adalah titik tak berwarna yang tidak berdekatan dengan titik berwarna, jadi X diwarnai merah. Berikan warna baru ini pada titik mana pun yang tidak berdekatan dengan titik lain yang diwarnai. Selain itu, pasangan titik yang mewakili daerah yang berdekatan dihubungkan oleh suatu sisi, sehingga model grafik terlihat seperti pada Gambar 5-68.
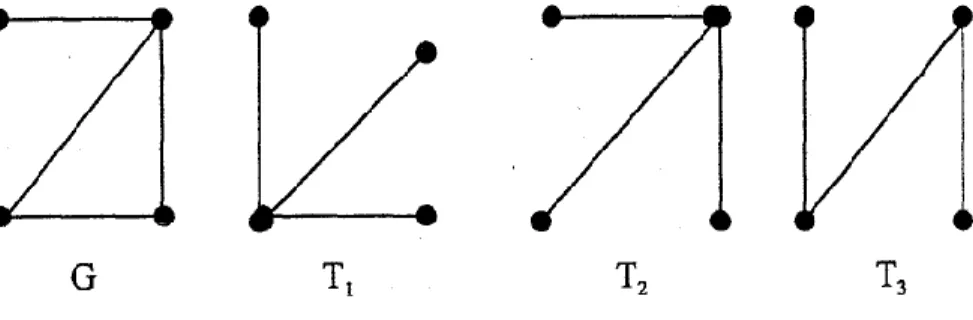
Setiap pohon bangunan di G yang tidak mempunyai tepi di e juga merupakan pohon bangunan di G - e, begitu pula setiap pohon. Jika G adalah graf berbobot, maka bobot T pohon pembangun G didefinisikan sebagai jumlah bobot semua sisi pada T. Dari semua pohon pembangun pada G, pohon pembangun yang berbobot terkecil disebut pohon pembangun minimum. , yang merupakan pohon pembangun utama.
Algoritma ini akan mencari pohon merentang minimum, jika ada, untuk graf berbobot G yang mempunyai n simpul, dengan n ≥ 2. Jika T memuat n-1 sisi, hentikan; tepi di T dan titik di S membentuk pohon konstruksi minimal.
13
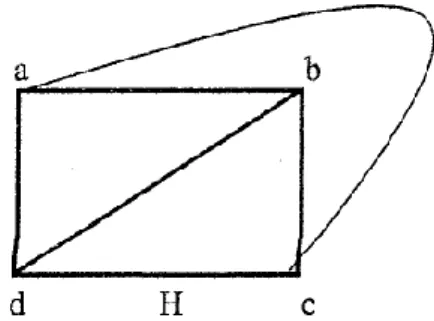
Suatu graf G disebut planar jika graf tersebut dapat digambarkan pada suatu bidang sedemikian rupa sehingga tidak ada satupun sisinya yang berpotongan, kecuali mungkin pada titik ujung sisi tersebut. Misalnya graf G pada Gambar 12.1 di bawah merupakan graf planar karena dapat digambarkan sebagai graf H; tetapi graf G bukan graf planar karena sisi ac dan bd dari G terletak di atas satu sama lain. Perhatikan bahwa graf G adalah planar jika dan hanya jika graf sederhana yang dibentuk dari G dengan menghilangkan loop dan mengganti beberapa sisi dengan sebuah sisi adalah planar.
Perhatikan graf G, bentuklah graf H dari G dengan menambahkan (mungkin nol) beberapa simpul pada beberapa sisi dari G. Terlebih lagi, jika Hl juga merupakan graf subdivisi dari G, maka H dan Hl kita sebut homeomorfik (lihat Gambar 12.2). . Kuratowski membuktikan bahwa setiap graf nonplanar harus memuat subgraf yang isomorfik terhadap subdivisi graf K3,3 atau graf K5.
Karena K3,3 dan K5 merupakan graf nonplanar, maka graf tersebut mengandung subgraf isomorfik dengan subdivisi dari K3,3 atau K5. Suatu graf G dikatakan nonplanar jika dan hanya jika G memuat subgraf yang bersifat horneomorfik dengan graf K3,3 atau K5. Graf G membagi bidang menjadi beberapa daerah yang masing-masing daerah disebut muka yang dilambangkan dengan f.
Berikut ini kita uji hubungan antara jumlah simpul, jumlah sisi, dan jumlah muka pada graf planar terhubung. Misalkan e adalah suatu sisi dalam siklus yang ada di G, maka graf H = G - e merupakan graf planar yang dihubungkan oleh k sisi.
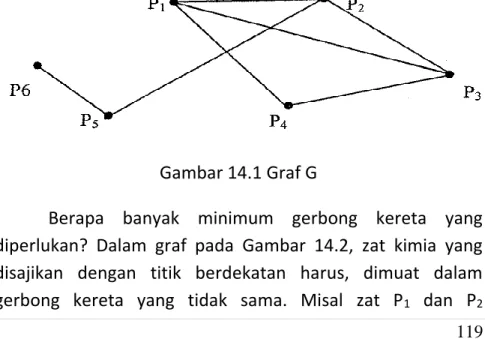
Mencari jumlah minimum gerbong kereta yang diperlukan pada Contoh 14.2 sama dengan mencari jumlah minimum warna yang diperlukan untuk mewarnai grafik pada Gambar 14.2, dimana warna tersebut mewakili gerbong kereta. Secara umum, jika suatu siklus mempunyai jumlah titik genap, maka siklus tersebut dapat diwarnai dengan dua warna. Jika Anda mencoba menggunakan pemanasan intermiten seperti yang ditunjukkan pada gambar 14.4, warna merah adalah untuk titik V1 dan V3.
Pada grafik pada Gambar 14.9(a), proses pewarnaan di atas diawali dengan memilih titik V dan mewarnainya dengan warna merah. Karena paling banyak terdapat k simpul yang bertetangga dengan W dan paling sedikit terdapat k + l warna yang tersedia, maka paling tidak ada satu warna (mungkin lebih) yang belum digunakan untuk mewarnai simpul-simpul yang bertetangga dengan W. Jadi rumusan dari Masalah graf adalah mewarnai semua simpul pada graf sehingga titik-titik yang terhubung pada sisi-sisinya mempunyai warna yang berbeda-beda.
Angka pada Gambar 14.14 menunjukkan kemungkinan penempatan warna dan terdapat juga kemungkinan penempatan lainnya.