I would also like to thank all the other employees of the department for their encouragement and help. In most common soft computing methods, the system modeling results depend on the amount of training data used.
List of Tables
Nomenclature
Mathematical Notations
Introduction
- Aim of the research
- Contribution of the thesis
- Organization of the thesis
- ORGANIZATION OF THE THESIS 5 Chapter 7: The last chapter presents a brief discussion about the research work and also draws con-
In such cases, soft computing-based modeling approaches [3] provide a viable alternative for identifying the system based on the available data. The thesis provides a detailed account of the use of soft computing techniques for system identification.
Soft Computing based Techniques for System Identification
- Neural Network based Algorithms
- NEURAL NETWORK BASED ALGORITHMS 7 characteristics of the neural network are
- Fuzzy Logic based Algorithms
- FUZZY LOGIC BASED ALGORITHMS 9 inference system (FIS) is based on the concepts of fuzzy set theory, fuzzy if-then rules and fuzzy
- Analysis with Fuzzy Inference System
- FUZZY LOGIC BASED ALGORITHMS 10
- Types of Fuzzy System
- FUZZY LOGIC BASED ALGORITHMS 11 applications of Fuzzy logic controller (FLC) in industrial processes [41–43]. The interpolation of the
- Genetic Algorithm
- GENETIC ALGORITHM 13 as a gene pool or population which can be repeatedly evolved towards a better fitness value in the next
- GENETIC ALGORITHM 14
- NEURO FUZZY APPROACH 15
- Neuro Fuzzy Approach
- NEURO FUZZY APPROACH 16 numerical data which represents the dynamic behavior of the system. System modelling based on this
- NEURO FUZZY APPROACH 17
- Adaptive Network based Fuzzy Inference System
- Forecasting Methodologies
- FORECASTING METHODOLOGIES 20 conventional learning methods like statistics based ones, the use of the evolutionary methods were also
- FORECASTING METHODOLOGIES 21 forecasting accuracy
- Research gap
- RESEARCH GAP 23 a thermal power plant. This is because in order to get the training data, the power plant has to be kept
Similarly, Saez and Cipriano [64] proposed a fuzzy model for representing the non-linearity of a process. Similarly, Chiu [77] proposed another method for the selection of inputs of the neuro-fuzzy model built for nonlinear system identification.

Research Objectives and Methodology
Objectives of the present work
Methodology of the present work
- ANFIS based methodology for modeling
- Full factorial design based methodology for optimal data selection
- V-fold based methodology for optimal data selection
Neural network training can also be repeated in a statistical experiment involving a large number of tests for optimization. This FFD methodology is used to select the critical dataset for training the ANFIS model of the real system.
METHODOLOGY OF THE PRESENT WORK 27
- Full factorial design combined with V-fold based methodology for optimal data selectiondata selection
- Model building with statistical approaches for performance study
- Genetic algorithm based fuzzy methodology
- Controller with the FFD-V-fold based methodology
Adaptive Network based Fuzzy Inference System
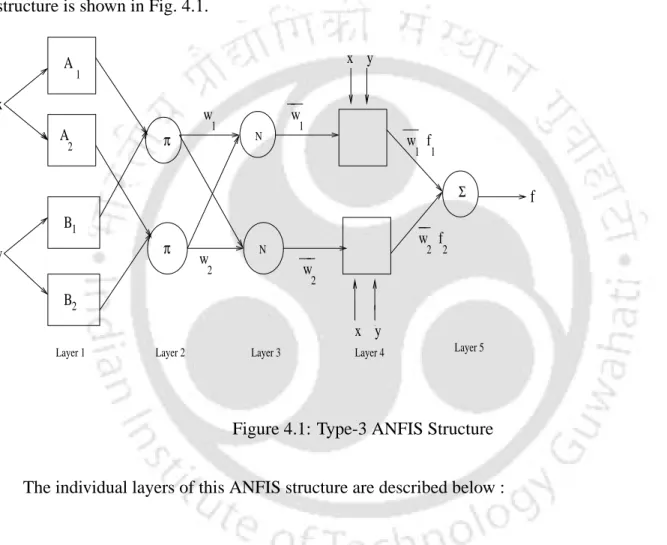
ANFIS structure
ANFIS STRUCTURE 29 fuzzy model is formed. For a first order two rule Sugeno fuzzy inference system, the two rules may be
Learning Algorithm
Derivation of the Initial Fuzzy Model
- Extracting the initial fuzzy model
DERIVATION OF THE INITIAL FUZZY MODEL 32 Subtractive Clustering Technique
DERIVATION OF THE INITIAL FUZZY MODEL 33
DERIVATION OF THE INITIAL FUZZY MODEL 34
DERIVATION OF THE INITIAL FUZZY MODEL 35
- Selection of input variables and final fuzzy model
DERIVATION OF THE INITIAL FUZZY MODEL 36 model is the Root mean square error (RMSE). The ANFIS structure of the system which is being
EXPERIMENTAL DATA 37
- Optimization of the initial fuzzy model
Experimental Data
Experimental Results and Discussion
EXPERIMENTAL RESULTS AND DISCUSSION 39
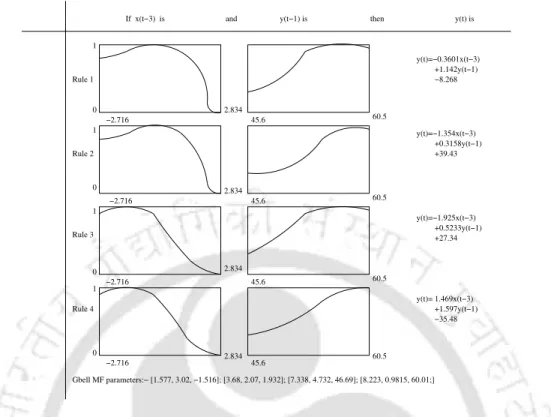
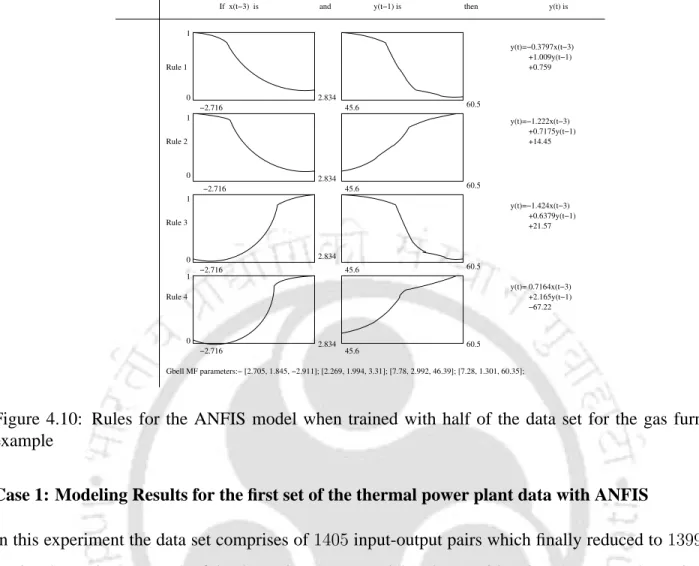
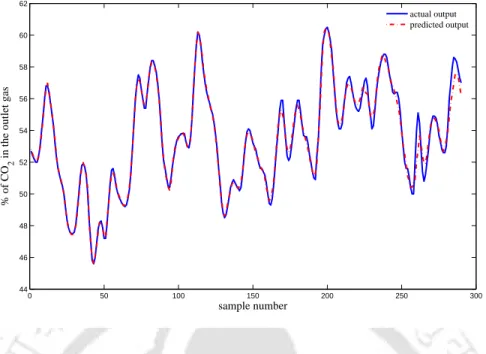
- ANFIS Model for Gas Furnace
EXPERIMENTAL RESULTS AND DISCUSSION 40
EXPERIMENTAL RESULTS AND DISCUSSION 41
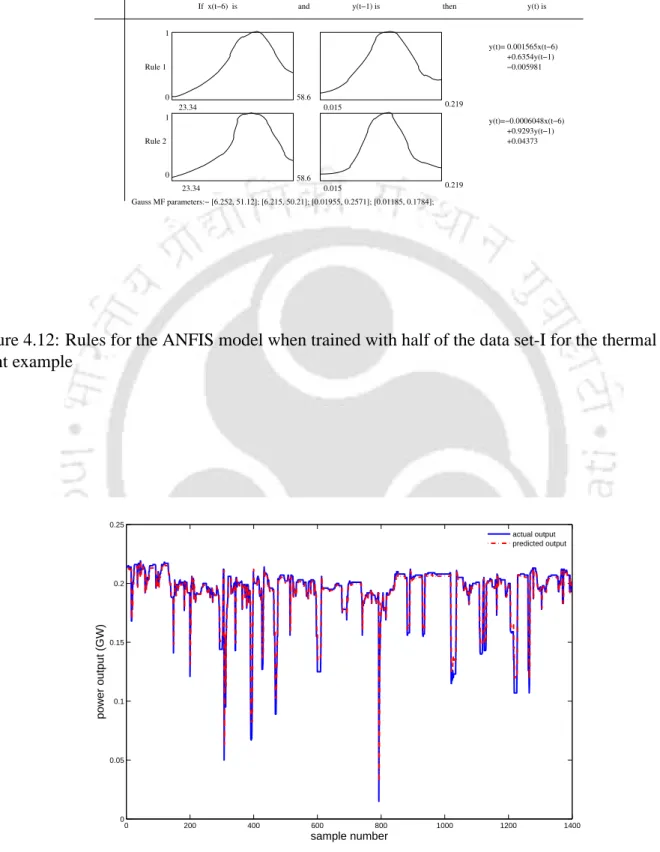
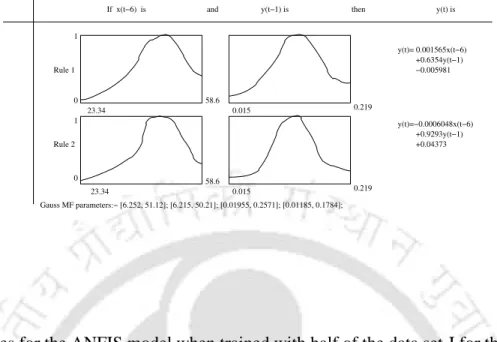
- ANFIS Model for Thermal Power Plant
EXPERIMENTAL RESULTS AND DISCUSSION 42
EXPERIMENTAL RESULTS AND DISCUSSION 43
EXPERIMENTAL RESULTS AND DISCUSSION 44
EXPERIMENTAL RESULTS AND DISCUSSION 45
Modeling Results for the first set of the thermal power plant data with ANFIS
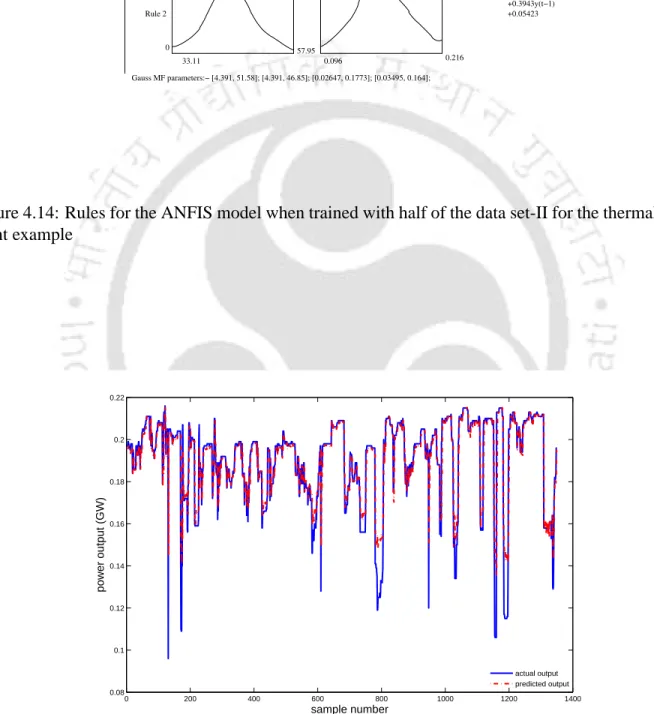
Modeling Results for the second set of the thermal power plant data with ANFIS
- EXPERIMENTAL RESULTS AND DISCUSSION 46
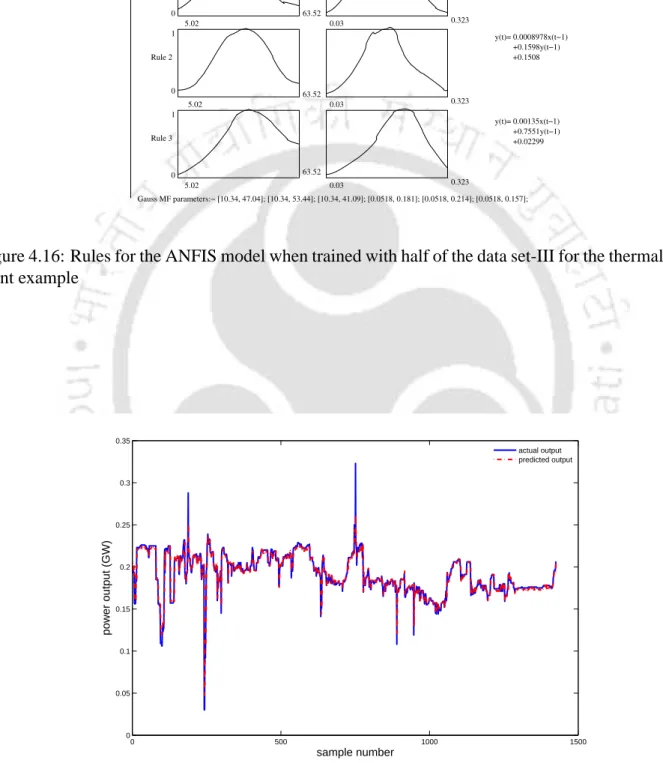
Modeling Results for the third set of the thermal power plant data with ANFIS
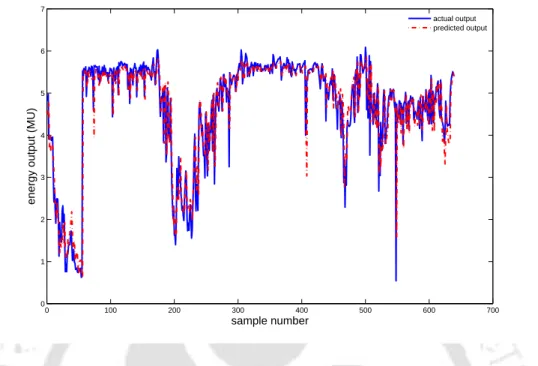
Modeling Results for the fourth set of the thermal power plant data with ANFIS
- EXPERIMENTAL RESULTS AND DISCUSSION 47
- EXPERIMENTAL RESULTS AND DISCUSSION 48
- EXPERIMENTAL RESULTS AND DISCUSSION 49
- EXPERIMENTAL RESULTS AND DISCUSSION 50
- CONCLUSIONS 51
Modeling Results for the fifth set of the thermal power plant data with ANFIS
- Conclusions
- CONCLUSIONS 52
- CONCLUSIONS 53 the existing modeling results obtained from the first 7 rows as excerpted from a table in [77], the entire
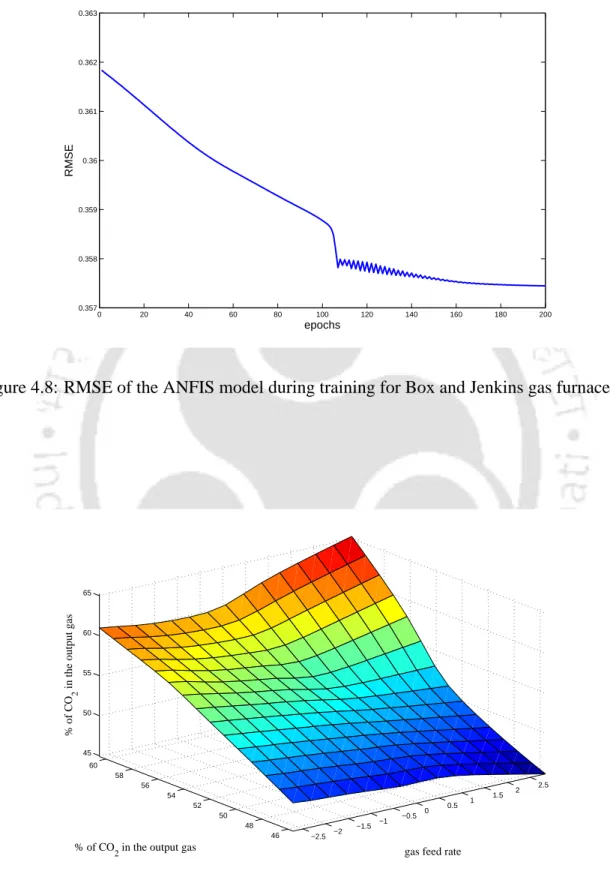
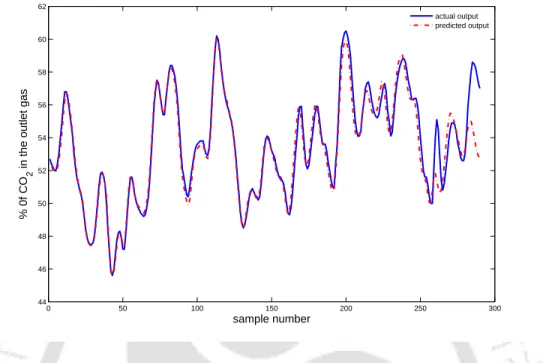
CONCLUSIONS 53the existing modeling results obtained from the first 7 rows as extracted from a table in [77], the entire existing modeling results obtained from the first 7 rows as extracted from a table in [77], the entire gas furnace dataset was used for training of the network. The modeling results of the Box and Jenkins gas furnace and the thermal power plant are shown in Fig. From the results, it can be concluded that the RMSE of the ANFIS-based model decreases as the number of training data increases.
In the ANFIS model, the backpropagation learning method is used to train the neural network for optimizing the fuzzy rules. This number can vary greatly depending on the complexity of the problem and the quality of the data, but many neural networks have been trained successfully with a smaller amount of data. Here, the optimal selection of the data set is a major problem, which is still a challenge in neural networks.
In the previous section, the modeling results of the conventional ANFIS model are shown where the training data set consists of either the whole portion or half of the available data set. The proposed ANFIS model with the optimal choice of the modeling data for training the ANFIS model is the subject of discussion in the next chapter.
Optimal Data based ANFIS Modeling
Full Factorial Design Based ANFIS Modeling
FULL FACTORIAL DESIGN BASED ANFIS MODELING 55 ANFIS
FULL FACTORIAL DESIGN BASED ANFIS MODELING 56
FULL FACTORIAL DESIGN BASED ANFIS MODELING 57 the two factors. The different levels that have been considered in the experiments are viz 2, 3 and 4
V-Fold Technique Based ANFIS Modelling
FFD-V-fold Based ANFIS Modeling
Experimental Results and Discussion
EXPERIMENTAL RESULTS AND DISCUSSION 60
- Modeling results with Full factorial design based ANFIS model
Modeling with Box and Jenkins gas furnace data
- EXPERIMENTAL RESULTS AND DISCUSSION 61
- EXPERIMENTAL RESULTS AND DISCUSSION 62
Considering only the minimum and maximum values of the input-output data pairs, first only 22 = 4 data pairs are selected. These 4 data pairs are taken around the minimum and maximum value of input-output pairs with equal representation (2 pairs around the minimum and 2 pairs around the maximum). So4(1 each around the minimum and maximum values of bothxiandyi) are now needed for additional data pairs, and these are taken around the minimum and maximum values of input-output data pairs.
Therefore, 4 more input-output data pairs are taken around the minimum and maximum of the input-output pairs. So now the 3 levels are the minimum, maximum and middle value of the data range. After three successive evaluations of 32 = 9 data pairs, EOF values of 1, 1 and 1 are obtained for xi.
After three consecutive evaluations on the 42 = 16 data pairs, EOF values of 1, 1 and 1 are obtained for yi,xiand(xi,yi) of the different levels. So with 1 data pair each around the minimum, the maximum, the centroid and each of the two cluster centers foryi,xiand(xi, yi), a value of 5.5 and 10 additional data pairs are taken making a total number of training data pairs.
Modeling with thermal power plant data (i) Data set-I
- EXPERIMENTAL RESULTS AND DISCUSSION 64 Starting initially with 4 2 = 16 data pairs and evaluating the EOF after two successive runs, the
- EXPERIMENTAL RESULTS AND DISCUSSION 65
- EXPERIMENTAL RESULTS AND DISCUSSION 66
- EXPERIMENTAL RESULTS AND DISCUSSION 67
- V-fold technique based ANFIS model
- EXPERIMENTAL RESULTS AND DISCUSSION 68 Table 5.2: Modeling results for the Box and Jenkins gas furnace data and the thermal power plant data
- Modeling results with FFD-V-fold technique based ANFIS model
Another experiment is carried out by taking all the 4 different levels of the data set, namely the minimum, the maximum, the middle value of the data series that the cluster center. The number of data pairs required for the different levels of the experiment is explained below. Here, 22 = 4 data pairs are first selected taking into account the minimum and the maximum values of the input-output data pairs.
Starting with 32 = 9 data pairs initially for the three levels of the maximum, minimum and middle values of the data pairs, the values of EOF obtained are 1, 1 and 1 after three consecutive evaluations for (xi, yi). In the third set of thermal power plant data, x(t−1) andy(t−1) were found to be the optimal inputs. In the fourth set of thermal power plant data, x(t−1)andy(t−1) were found to be optimal inputs.
In the fifth set of thermal power plant data, x(t−1) andy(t−1) were found to be optimal and are therefore used in our model. After selecting the data for the different folds, which is approximately one-eighth of the training data used in the conventional model, the results thus obtained are shown below.
Modeling results for Box and Jenkins gas furnace data
EXPERIMENTAL RESULTS AND DISCUSSION 68Table 5.2: Modeling results for Box and Jenkins gas furnace data and power plant data Table 5.2: Modeling results for Box and Jenkins gas furnace data and power plant data using the ANFIS model V-slot based.
Modeling results for the thermal power plant data (i) Data set-I
- EXPERIMENTAL RESULTS AND DISCUSSION 69 set the best result was obtained for the 2-level FFD-V-fold based ANFIS model
- EXPERIMENTAL RESULTS AND DISCUSSION 70
- EXPERIMENTAL RESULTS AND DISCUSSION 71
- EXPERIMENTAL RESULTS AND DISCUSSION 72
- EXPERIMENTAL RESULTS AND DISCUSSION 73
- EXPERIMENTAL RESULTS AND DISCUSSION 74
- CONCLUSION 75
- Conclusion
EXPERIMENTAL RESULTS AND DISCUSSION The best result was obtained with the 2-level FFD-V fold-based ANFIS model. Herex(t−1)andy(t−1) are the optimal inputs used for modeling and the least MSE was obtained for the 2-level FFD-V fold based ANFIS model. The results obtained using the ANFIS model based on the combined FFD-V fold technique are shown in Table 5.3.
In Table 5.4, the results obtained using the different models, namely conventional ANFIS, FFD-based ANFIS, V-fold based ANFIS and FFD-V-fold based ANFIS, are compared with respect to their RMSE. It can be seen from Table 5.4 that the best modeling results are obtained with the FFD-V fold based ANFIS model, as the RMSE (testing) in this case is the lowest for all different types of data. Table 5.4 shows that the FFD-V fold-based ANFIS model shows the best performance even though only about one-eighth of the dataset used in the conventional ANFIS model is selected for training.
The FFD-V-fold based ANFIS model is built based on optimally chosen data for modeling. This shows that the ANFIS model based on the training dataset selected using the FFD-V-fold technique exhibits the best prediction ability.
Statistical Models and Genetic Algorithm Based Fuzzy Model
Statistical Models
STATISTICAL MODELS 77In this chapter, some existing statistical models are adapted to the systems under study and them.
STATISTICAL MODELS 77 In this chapter some of the existing statistical models are fitted into the systems under study and they
- Auto Regressive with Exogenous Input (ARX) Model
- Auto Regressive Moving Average with Exogenous Input (ARMAX) Model
- Auto Regressive Integrated Moving Average with Exogenous Input (ARI- MAX) ModelMAX) Model
Genetic Algorithm Based Fuzzy Model
Experimental Results and Discussion
EXPERIMENTAL RESULTS AND DISCUSSION 79
- Statistical models
EXPERIMENTAL RESULTS AND DISCUSSION 80 Table 6.1: Results obtained for Statistical models using the Box and Jenkins gas furnace and the thermal
Box and Jenkins gas furnace data
Thermal power plant data (i) Data set-I
- EXPERIMENTAL RESULTS AND DISCUSSION 81
- EXPERIMENTAL RESULTS AND DISCUSSION 82
- GA based fuzzy model
- EXPERIMENTAL RESULTS AND DISCUSSION 83
- EXPERIMENTAL RESULTS AND DISCUSSION 84
- EXPERIMENTAL RESULTS AND DISCUSSION 85
- EXPERIMENTAL RESULTS AND DISCUSSION 86
- EXPERIMENTAL RESULTS AND DISCUSSION 87
- CONTROLLER USING FFD-V-FOLD BASED ANFIS MODEL 88
- Controller Using FFD-V-fold based ANFIS Model
- CONTROLLER USING FFD-V-FOLD BASED ANFIS MODEL 89 Table 6.2: Results obtained for the GA based fuzzy model using the Box and Jenkins gas furnace and
- CONTROLLER USING FFD-V-FOLD BASED ANFIS MODEL 90
- Controller Design
- CONTROLLER USING FFD-V-FOLD BASED ANFIS MODEL 91
- CONTROLLER USING FFD-V-FOLD BASED ANFIS MODEL 92 u 2 (k) = K i
- Experimental Results and Discussion
- CONCLUSION 93
- Conclusion
- CONCLUSION 94
- CONCLUSION 95
- CONCLUSION 96
- CONCLUSION 97
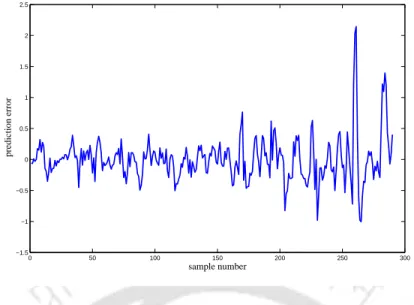
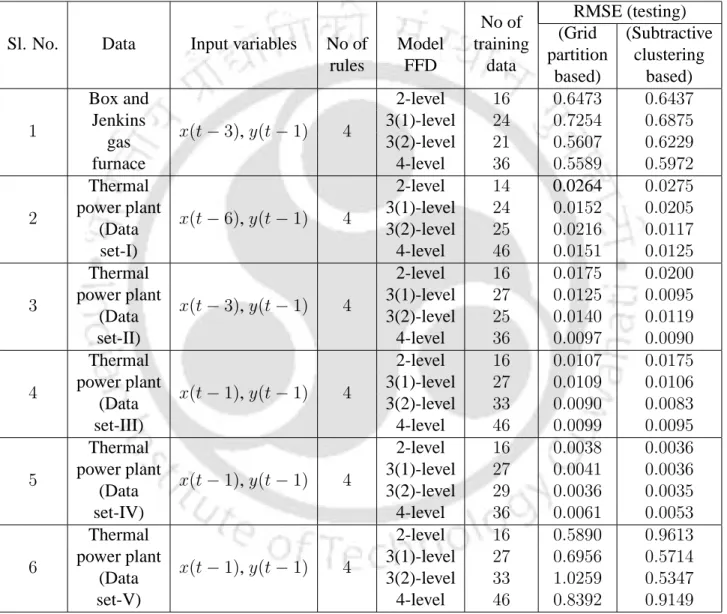
In the GA-based fuzzy model, the initial fuzzy model is built along the same lines as that of the ANFIS model. The first dataset of the thermal power plant, consisting of 699 data pairs, is used here. In this experiment, 320 data pairs are used with x(t−1)endy(t−1) as the optimal input. The predicted output of the actual and the GA-based fuzzy model versus the sample number is shown in Fig.
The performance of the proposed model is studied along with GA-based fuzzy model and ARIMAX model. In the learning phase, the ANFIS-based inverse plant model deals with the available input-output data. In the next stage, the inverse plant model based on ANFIS is used to initiate the control action.
This is called the application phase of the ANFIS-based controller and is shown in Fig. This error is the difference between the desired output and the actual output of the device.
Conclusions and Future Work
- Summary of the thesis
- Discussion
- Conclusion
- Future Work
- FUTURE WORK 102
The main advantage of the soft computing tools used in this work is that the requirement of a mathematical model is not a prerequisite. The model of the considered system can be built around the available input-output data of the system. It was also found that the performance of the proposed model is equal to the conventional statistical models used in forecasting.
The power of a critically selected input and output training data set was used to train ANFIS. The power of the input/output data used is only about one-eighth of the total number of available data sets. The correct choice of FFD levels is important because the ANFIS model is decided based on the optimal choice of these levels.
Another limitation of the model is the possible presence of outliers and noise in the dataset used for the system modeling. The emphasis was on optimal selection and use of the available data source.
Appendix A
Sample Power Plant Data
Bibliography
Tokhi, "Nonlinear modeling of a dual-rotor mimo system using radial basis function network." in Proc. Lewis, "Multi-model neural networks identification and fault detection of nonlinear systems," in Proc. See, “Identification and control of continuous nonlinear systems via dynamic neural networks,” IEEE Trans.
Ghosh, and Sachchidanand, "Fuzzy identification and control of a class of nonlinear systems," in Proc. Cipriano, "Economic predictive control based on fuzzy models for a combined cycle power plant boiler," in Proc. Juang, “Application of genetic algorithm and recurrent network for nonlinear system identification,” in Proc.
Lee, “Intelligent control of nonlinear power plant using multiobjective optimization based on immune algorithm,” in Proc. Adaptive IMC using fuzzy neural networks for control in nonlinear systems,” in Research Paper.
Related Publications by the Author
Mahanta, “ANFIS Modeling of Nonlinear Systems based on Combined FFD-V-fold Technique,” in Proceedings of IEEE International Conference on Industrial Technology, Mumbai, 15-17 Dec. Mahanta, “Full Factorial Design based ANFIS Model for Complex Sys - tems,” in Proceedings of the IEEE Annual Indian Conference, New Delhi, September. Mahanta, “ANFIS Modeling of Nonlinear Systems Based on Subtractive Clustering and V-Fold Techniques,” in Proceedings of the IEEE Annual Indian Conference, New Delhi, September 2006.
Mahanta, “ANFIS modeling of nonlinear systems based on subtractive clustering and combined FFD-V-folding technique,” in Proceedings of IEEE Annual India Conference, New Delhi, Sept. Mahanta, "Modeling of complex systems with soft computing techniques," in Proceedings of National Systems Conference, Goa, Nov 2006. Mahanta, "Statistical and Neuro-Fuzzy Technique based Modeling of Complex Systems," in Proceedings of National Systems Conference, Goa, Nov 2006.
Mahanta, “Power plant modeling using full factorial ANFIS design,” in Proceedings of IEEE International Conference on Cybernetics and Intelligent Systems, Bangkok, June 2006.
Bio-data of the Author