The astonishing connection between the asymptotic symmetries and black hole thermodynamics was realized by the scientific community about forty years ago. It is expected that the microscopic information about the black hole entropy can probably be extracted from the central charges and the zero state Q0. In these efforts, the study of the Noether charges corresponding to the asymptotic symmetries has gained enormous interest in recent times.
In this thesis we examine the various aspects of the asymptotic symmetries in gravitation theories. Interestingly, the Fourier modes of the supertranslation parameter turn out to be the unstable ones. In the semi-classical regime, we found that this instability can lead to thermalization of the horizon.
For our discussion, the time-like surface is assumed to be positioned at a finite distance outside the horizon of the black hole.
General background
The zeroth law of black hole mechanics states that the surface gravity is constant above the horizon of a stationary black hole. Now, the second law of black hole mechanics states that the surface area of the black hole horizon never decreases with time. Bekenstein argued [24,25] the entropy of a black hole to be proportional to the area of its event horizon with a multiplying factor β given by,.
While their derivation confirms Bekenstein's classical results, it does not provide much information about the microscopic description of black hole entropy. A fruitful calculation of black hole entropy using the microcanonical ensemble is presented in [32]. Other attempts have been made [36] in which the entropy of the black hole is derived by analyzing the quantum structure near the horizon.
However, the appropriate choice of this parameter can lead to the correction of the Bekenstein-Hawking entropy of the black hole.
Review on asymptotic symmetries and BMS group
Review on asymptotic symmetries and the group BMSHere∆ is the eigenvalue of the zero mode of L0 symmetry generators and can be. Finally, for an asymptotically flat spacetime, the asymptotic solutions of the metric components give the following: Review on asymptotic symmetries and the BMS group It was proved that the supertranslation is a normal subgroup of the asymptotic symptom.
On the other hand, the determinant of the metric must be invariant even after the given transformations. It has been found that the form of the near-horizon BMS4algebra [91] is different from the standard BMS4algebra derived at null infinity [74]. The entropy can be associated with this zero surface locally using the Virasoro algebra.
Review of asymptotic symmetries and BMS group symmetries of the bulk theory with the global symmetries of the limit theory.
Chapter-wise description of the thesis
- Chapter 2
- Chapter 3
- Chapter 4
- Chapter 5
- Chapter 6
Chapter wise description of the thesis connection between the horizon symmetries and the associated Goldstone modes. Here we presented the conclusion of the thesis and also discussed some interesting room for future work. Each chapter of the thesis contains several appendices which are added at the end of the respective chapter.
In the introductory chapter of the present thesis, we discussed extensively that for a generic diffeomorphism invariant gravity theory, the Noether current and charge are very important to understand the thermodynamic properties of black holes. In this regard, one of the significant results is the commutator algebra under the charges associated with the asymptotic symmetries of spacetime under study. The general strategy is to choose a subset of diffeomorphism such that under those transformations the solutions of the field equation must remain invariant near the null boundaries.
Nevertheless, from the above discussions, one would be inclined to believe that understanding the behavior of a generic null surface can not only provide the desired results of on-shell properties of the studied theory, but can also throw light on the off-shell behavior that occurs naturally in quantum theory.
Objective of the chapter
In [132], the analysis for gravity in four space-time dimensions at zero infinity was extended to include Yang-Mills fields. Recently, a unified treatment of asymptotic symmetries for the Einstein-Maxwell system for the Kerr-Newman (A)dS black hole horizon was discussed in [170]. Therefore, the asymptotic symmetry analysis for Einstein–Maxwell theory has been extended and investigated near the static or stationary horizon (see for various examples), which are solutions to Einstein's equations of motion.
So far, the symmetries of the boundary diffeomorphism have been first explored near zero infinity for the asymptotic plane of spacetime, later on the black hole horizon, which acts as the second zero boundary of spacetime. Or we can have a generic null surface that will serve as the horizon for a class of observers in any given spacetime. It has been found that not only does the thermodynamic interpretation have a black hole horizon, but every generic null surface in the theory of gravity also has this property [108].
Zero surface with (1) charge: a brief overview Einstein's equations of motion or the gauge field equation of motion will be used.
As emphasized in the introduction to this chapter, we will consider the most general zero surface, where all metric components M, hA and µAB are functions of all spacetime coordinates (u, r, x). Therefore, choosing this particular coordinate system eliminates all excess degrees of freedom and only d(d−1)/2 free functions remain in the metric tensor given by M, hA and µAB. Therefore, in general, all metric components will also be a function of electric and magnetic charges.
We can also see that there =0 surface is a zero(d−2)dimensional sphere with an elementary surface areaΣab =−d(d−2)x√. For generic charged zero surface, we also consider the following drop-off conditions for the gauge field near the surface. Therefore, it generalizes a special class of null metric obtained from the near-horizon expansion of the Kerr–Newmann black hole, which is stationary (the procedure can be followed from [ 179 ]).
Here we are considering the case where all metric coefficients depend on all space-time coordinates.
Symmetries near the null surface
Our aim now is to find the diffeomorphism vector ζa and the gauge parameter, which satisfy the conditions set above. First we solve the strong conditions (2.4) to find different components of ζa and then we impose the weak conditions (2.5) on the aforementioned solutions. The weak conditions for the metric components gvu, gvA in Eq. (2.5) give us the following constraint on the diffeomorphism parameters derived in Eq.
The ongAB drop condition does not yield any new condition (see Appendix 2.B for a detailed derivation). Therefore, any transformation that changes the position of the null surface should disappear as we approach the null surface. To find e, it is necessary to use the components of ζa, which were determined by the conditions on gab.
The above expressions are the components of the diffeomorphism symmetry vector that preserves the null surface.
Algebra of the symmetry parameters
In the next section, we will compute the various charges and their associated algebra corresponding to the diffeomorphism and U(1) gauge symmetry transformations that keep our generic charged null surface invariant.
Charge and its algebra: an off-shell analysis
For example, the space-time of a black hole has two natural sets of boundaries in the two-dimensional section of zero infinity and the horizon. So, for LL gravity, the fraction of charge on the zero surface is taken as follows [115]. This load is also determined outside the shell since no equation of motion conditions are imposed in the derivation.
But still, the amount of fabe may not be zero when calculated on the part of the closed boundary, and so one can get a non-zero charge from (2.29). Moreover, in the solution space of the full Einstein equation, such as the spacetime of a black hole, those conserved charges indicate the existence of soft hair near the black hole's horizon. At this point, let us emphasize again that our analysis does not depend on the equation of motion of the considered fields.
Before concluding our analysis, we show that the same algebra can also be obtained from the Noether charge corresponding to the surface term of the gravitational action.
Null surface: Extremal case
Null surface: An extreme case where Na is unity, normal to the boundary ∂V of the spacetime region V. In this context, we look at the diffeomorphism symmetries for a generic charged extreme null surface, which can be defined as the zero temperature limit of the non-extreme null surface considered so far . The extremity condition, which is equivalent to the zero-temperature limit, appears in the drop condition guu ∼ O(r2) as one approximation to the surface at tr=0.
The extremity condition on the metric has no influence on the configuration of the gauge field Aµ near the surface equation (2.3). Therefore, given the configurations of the metric and the measurement field in the extreme zero background, we will perform the same analysis as before with the following modified drop conditions. 2.39). Therefore, the diffeomorphism parameters derived in equation (2.8) must satisfy the modified constraint relations as follows.
As stated earlier, the radial component of the diffeomorphism vector T must be zero near the surface.
Conclusions
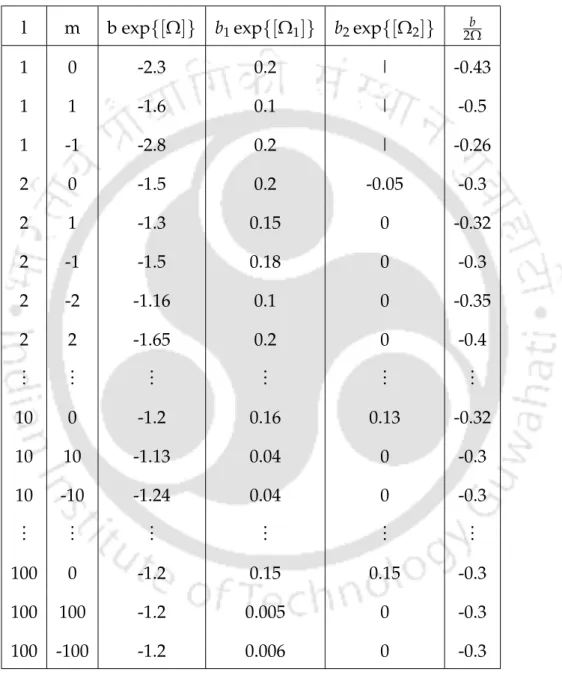
Purpose of the chapter In this chapter we will study the dynamics of those Goldstone modes. Then from the coefficients of the reflected wave Z(a,−α) and those of the transmitted wave Z(a,α) one can easily deduce the intensities that generate (PT) and (PR) as given in (3.3.25 ) . The form of the Lagrangian presented in the main text comes from this non-zero contribution.
We still considered the angular part of the anzatz solution in the form of spherical harmonics. Therefore, the components of the metric have an asymptotic form as given in (5.4.5) near the aforementioned time limit. With the components of the newly transformed metric given in (5.4.5), the first equation of (5.4.7) indicates that.