In this paper we will study the ground-state superconducting and magnetic properties of double-layer superconductors and the role of interlayer couplings in the framework of the t-J model using the variational Monte Carlo (VMC) method. The details of the phenomenon in various aspects have been extensively discussed in the past in the literature.
A preliminary survey on high-T c superconductors
A new class of material
Chapter 3 contains a study of superconducting pairing symmetry in a t-J double layer for parameter values related to double cuprates. The critical temperature of HgBa2Ca2Cu3O8+x(Hg1223) has been raised above 150◦K under very high pressure[16], and is one of the highest Tc observed so far.
Universal phase diagram
In the charge reservoir, Cu atoms form the linear Cu-O chains, which have varying oxygen content. The Cu-O chains provide and direct charge carriers for electrical conduction in the CuO2 planes[29].
Anomalous behaviour
One fact that stands out in this regard is the symmetry of the superconducting gap, ∆(k). The striking feature in the spectra below Tc is the sharpening of the peak with decreasing T.
Electronic models for high-T c superconductors
Basic electronic structure
Three-band Hubbard model
The values of the various parameters in the Hamiltonian can be obtained from electronic calculations of the band structure. The energy for double occupancy of the Cu d orbitals Ud is ~ 10.5 eV, which is very large compared to all other energies in the problem.
One-band models
In addition to the above, another model relevant to high Tc superconductors that has been extensively studied is the two-dimensional one-band Hubbard model [88]. In the strong coupling limit, the Hubbard model can be shown to reduce to the t-J model as far as low-energy excitations are concerned.
Theoretical studies of high-T c superconductors
Alternative approaches
According to this theory, superconductivity arises in the individual CuO2 layers of high-Tc superconductors as a result of pairings caused by some electronic mechanism. The c-axis conduction in the normal state of high-Tc superconductors is blocked due to the confinement property of Luttinger liquids that prohibits coherent single-particle hopping across the planes.
Success with the t-J model
It was suggested that the RGB state better describes the ground state of the hole-doped t-J model. Elementary excitations in the RGB state are obtained by breaking some singlet bonds in it.
Variational Monte Carlo studies
An exciting perspective is the application of VMC to study the finite temperature properties of the superconducting state. This has already begun in the recent past, and various aspects of the quasiparticle excitation spectrum of the Gutzwiller projected BCS wavefunction are investigated using this technique.
Interlayer coupling
Nevertheless, interlayer coupling between different CuO2 layers in cuprate superconductors affects many of their physical properties (for a review, see Ref. [55]). In the superconducting state, the tunneling of Cooper pairs across the layers is thought to play a key role in high Tc superconductors [26].
Bilayer t-J model
The effects of the interlayer exchange coupling on the magnetic excitation spectra of bilayers were studied by Kr¨uger et al [168]. Recently, in a comprehensive study, Yamase et al. explained the magnetic excitations and their anisotropy in the bilayer YBCO based on the bilayer t-J model.
The variational Monte Carlo method
- Representation of the wavefunction in real space
- Lattice boundary condition
- Calculation of the expectation values
- The Markov chain Monte Carlo method
- VMC simulation
- Verification of the VMC code
Superconductivity in the two-dimensional (2D) t-J model has been studied in considerable detail in the past using variational Monte Carlo (VMC). In the phenomenological SO(5) theory, antiferromagnetism and superconductivity are assumed to have a common microscopic origin and are treated on an equal footing[95, 191].
A QMC study of the Hubbard model doped with nonmagnetic impurities
The Quantum Monte Carlo method
We developed the numerical code for the FTQMC method for studying the Hubbard model during the current project. Here we show the verification of our codes by comparing some results for the two-dimensional Hubbard model.
Effects of nonmagnetic impurities
To test our QMC codes, we calculate the following three quantities for the Hamiltonian and compare them with the corresponding results shown in Ref. If we compare the results with those obtained for the same quantities by White et al [182], we find a very good quantitative agreement between the two, which indicates the correctness of our codes.
Two dimensional lattice
On the other hand, the increase in local moment at sites close to the impurity is due to reduced probability of double occupancy at those sites which occurs because the sites are surrounded by only three 'active' sites. The slow decrease beyond this concentration is due to the impurity-induced dilution of the lattice.
Two-leg ladder
Fig.2.7 shows the results for spin correlations along a leg for the pure ladder and the ladder doped with a non-magnetic impurity, at half filling. Apart from half-filling, the enhancement of spin correlations with impurity is nevertheless small for the temperature range considered here.
Summary
The superconducting and magnetic properties of the coexisting phase are compared with those of the pure SC state. A larger interplanar jump is found to reduce planar correlations at optimal doping, while an opposite behavior, i.e. stabilization of the superconducting state is observed in the overdoped regime, where the interplanar exchange always plays a quiescent role.
Model parameters and other numerical details
For calculating the expected values, we have taken relatively larger sample sizes to get a good precision. The size of the Hilbert space increases rapidly up to about 30% of the hole concentration and then decreases.
The superconducting state
- The gap function
- Stable pairing symmetry
- Doping dependence of the superconducting gap
- Magnetic and superconducting correlations
The optimal d-wave state energy obtained from data such as above for various values of the interplanar parameter is shown in Fig. 3.4 as a function of hole concentration. The doping dependence of the superconducting gap parameter, ˜∆d(x) of the d-wave state for different lattice sizes and interplanar parameter values is shown in fig.
Coexistence of magnetism and superconductivity
The variational wavefunction
The quasiparticle operators, d†kσdiagonalize the AF Hartree-Fock Hamiltonian (Appendix B) with a gap∆AF and are related to the electron operators by the following transformation,. For non-zero Cand∆AF∆S, the wave function describes a phase with the AF and SC state coexisting as will be shown later, while the normal state is recovered as both parameters vanish.
Optimal gap parameter and energy
The results for the optimal parameters and ground state energy in the underdoped region are shown in Fig.3.11. The corresponding optimal SC gap parameter, ˜∆d is now modified compared to its value in the pure SC wave function.
Enhanced correlations in the coexisting state
The figure shows that the energy in the coexisting state is significantly decreased near half-full compared to that in the pure SC state. It increases with increasing x in the coexisting state while the opposite behavior is observed for the case of the pure d-wave state (3.8(c)).
Summary
In the previous chapter, we investigated the properties of the two-layer t-J model for the values of the interlayer coupling parameters believed to be relevant for high-Tc superconductors. Indeed, mean-field study of the t-J model found a combination of these two hole symmetries to be favorable in bilayers[205].
The trial wavefunction and optimization scheme
In conventional methods of finding the minimum, it is difficult to take into account statistical fluctuations in the estimated values of the function. F4.2: Determination of the global minimum and corresponding optimal parameters for the energy surface shown in Fig.4.1.
Phase diagram
We observe interesting features of the boundary separating the SC and the normal phase in the overdoped region. At higher values of t⊥, the delocalization effect takes over and we observe the disappearance of the SC phase at lower values of hole doping.
Effect of interlayer couplings
Energy gaps
The dependence of the energy gap, ˜∆dz for the dz wave state from t⊥and x is shown in Fig.4.7. In this case, we observe an opposite behavior of the energy gap compared to that of ˜∆d.
Superconducting correlations
The order parameter, Φd, corresponding to the plane correlations in the d-wave state is shown in the figure. On the other hand, the superconducting correlations in the dz-wave state are found to be predominantly interplanar.
Magnetic correlations
Summary
The idea of interlayer pair tunneling (ILPT) in high Tc superconductors was introduced by Wheatley et al[211, 212] to explain the occurrence of high transition temperatures in materials. Coherent hopping of single particles between two CuO2 layers is blocked in the normal state due to the non-Fermi liquid nature.
The model
In this work, we directly calculate the energy due to the Josephson pair tunneling term in a double layer in the superconducting state, where each of the layers is described by the Gutzwiller projected d-wave BCS wavefunction with variable particle number. The results of our calculation show that the energy due to the pair tunneling is too small to have any significance at least for parameter values considered.
The variational wavefunction
The method
- Hamiltonian in real space
- Wavefunction in real space
- Controlling particle density
- Verification of the algorithm
The average number of particles, ¯N in the grand canonical wave function is determined by the variation parameters µ and ∆k. The average number of particles in the projected grand canonical BCS wavefunction is given by, .
Energy due to interlayer pair tunneling
5.6) for a bilayer as a function of the variation parameter,∆for three values of hole concentrations shown in the figures. Because of this small value of E⊥, the pair tunneling term has practically no effect on .
Summary
The dependence of the superconducting gap moment has been one of the main issues in high Tc superconductors. Interlayer pair tunneling (ILPT) is believed to play an important role in the development of the superconducting state in high Tc cuprates.
Trotter decomposition
Hubbard-Stratonovich transformation
Trace over fermionic degrees of freedom
We divided the entire imaginary time interval (0, β) into small slices of width∆. L), then both the Hubbard-Stratonovich (HS) variables si and Viσ are given a time index l. It can be shown that the trace over the fermionic degrees of freedom of the term in brackets is equal to deth.
Calculation of expectation values
If the lattice has translational symmetry, average occupancy at any site is obtained as, . each component of the spin-spin correlation function can be expressed as, hmixmxji = hmyimyji=DD. A.34) Finally, the spin susceptibility is defined as,. The unequal time correlation function is expressed in terms of the unequal time Green's function.
Diagonalization of the Hamiltonian
The antiferromagnetic quasiparticle operators dkσ are related to the electron operators ckσ, by the following transformation. B.18). The ground state of the Hamiltonian is the fully projected sea of the quasiparticles, filled up to the Fermi level.
Wavefunction with coexisting AF and SC order
It's easy to see the transformation. B.16) diagonalizes the matrix M in the following way.
Various phases in the wavefunction
Transformation of the wavefunction into real space
- Crystal structure of two well known high-T c superconductors
- Phase diagrams of two well studied high-T c superconductors
- Generic phase diagram of high-T c superconductors
- In-plane resistivity, ρ ab (T ) in high-T c superconductors
- Out-of-plane resistivity, ρ c (T ) in high-T c superconductors
- Hall coefficient, R H as a function of T for YBCO
- Anisotropy of the SC gap in high-T c superconductors
- Temperature dependence of ARPES spectra for optimally doped Bi2212
- Electronic structure of the cuprates
- The copper 3d x 2 −y 2 and oxygen 2p x,y orbitals in hole picture
- A copper oxide layer simplified to a picture in one-band model
- An SU(2) mean-field phase diagram of the two dimensional t-J model
- Comparison of RMFT results on doping dependence of the SC gap parameter
- A VMC phase diagram of the two dimensional t-J model
- Allowed momenta in the first Brillouin zone for a lattice with periodic/an-
- Verification of VMC code for t-J model
- Verification of QMC code for Hubbard model
- Enhancement of magnetic correlations around a nonmagnetic impurity in the
- Destruction of AFLRO by nonmagnetic impurities in the two dimensional
- Magnetic susceptibility as a function of temperature for the pure and impurity
- Enhancement of magnetic correlations around a nonmagnetic impurity in a
- Spin structure factor versus impurity concentration in Hubbard ladder
- Effects of nonmagnetic impurities on spin wave velocity in Hubbard ladder . 53
- Variational energy of the d-wave state in bilayer for various values of hole
- Optimal energy of the d-wave state at various hole dopings in bilayer
- Doping dependence of optimal gap parameter of the d-wave SC state in bi-
- Optimal gap parameter, ˜ ∆ d (x) of the d-wave state as a function of hole doping
- Exchange energy and hopping energy as a function of variational parameter
- Magnetic correlations in the d-wave state in bilayer and in two dimensional
- Superconducting pair-pair correlations for the d-wave state as a function of
- Superconducting order parameter for the d-wave state as a function of hole
- Optimal values of the AF and SC gap parameters as a function of hole con-
- Spin-spin correlations as a function of distance in the coexisting state
- Spin structure factor in the coexisting state
- Enhancement of superconducting correlations in the coexisting state as com-
- Optimization of two parameter variational wavefunction (first step)
- Optimization of two parameter variational wavefunction (subsequent steps) . 80
- Phase diagram for J ⊥ = 0.20
- Phase diagram for J ⊥ = 0.35
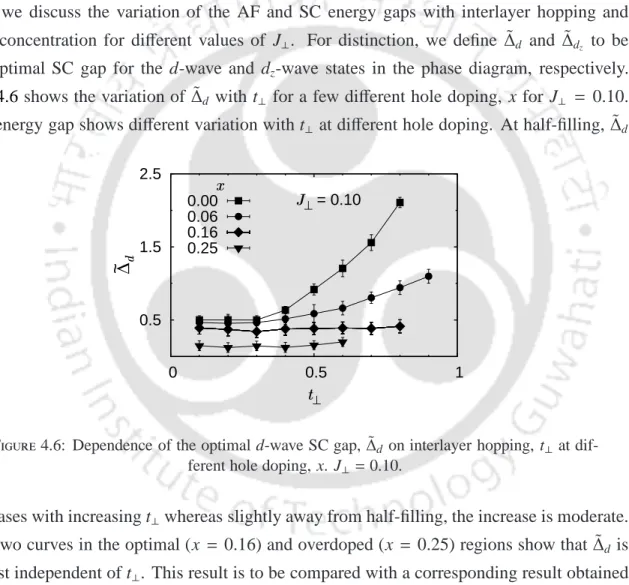
- Effects of interlayer hopping, t ⊥ on the d-wave SC gap
- Effects of interlayer hopping, t ⊥ on the d z -wave SC gap
- Doping dependence of the AF gap parameter for various t ⊥
- Effect of interlayer hopping on momentum distribution in the d-wave state
- Disruption of planar SC correlations by interlayer hopping
- Disruption of interplanar SC correlations by interlayer hopping
- Effects of interlayer hopping on superconducting correlations
- Dimension of different fixed N subspaces in a grand canonical Hilbert space
- Testing the algorithm for random walk in grand canonical Hilbert space
Tranquada, Neutronverstrooiingstudies van Antiferromagnetiese korrelasies in Cuprates, in Handbook of High-Temperature Superconductivity, geredigeer deur J. Orenstein, Optical Conductivity and Spatial Inhomogeneity in Cuprate Superconductivity, in Handbook of High-Temperature Superconductivity deur J.