An approximate single-loop chaos control method for reliability-based design optimization using conjugate gradient search direction. Raktim Biswas and Deepak Sharma. 2023) Single-loop multi-objective reliability-based design optimization using chaos control theory and moving vector with differential evolution.
Uncertainty and reliability analysis
Reliability is estimated by predicting and calculating the probability of performance function violations at any point during a system's life. The probability of occurrence of an event such as 'performance function violation' is a numerical measure of probability of failure of the system.
Reliability-based design optimization
MPP has the highest probability density on the performance function in the standard normal space. In addition, the computational efficiency also decreases exponentially as the number of random variables and performance function increases.
Motivation
The method was developed using a multi-objective DE algorithm designed using non-dominated sorting and push distance. Furthermore, another novel formulation for multi-objective RBDO is proposed using shift vector approximation and adaptive multi-objective DE for generating the reliable Pareto optimal solutions.
Objectives of the thesis
Since most real-world problems consist of multiple objectives, the next goal is to develop a multi-objective RBDO formulation in which the reliability analysis is approached using Karush Kuhn Tucker (KKT) optimal conditions. Develop a hybrid multi-objective RBDO formulation incorporating modified chaos control theory and shifting vector approximation, and solve it using adaptive DE.
Organization of the thesis
Then various RBDO methods are discussed along with basic types of reliability analysis to have a complete understanding of the subject. Finally, different types of metaheuristic algorithms used to solve single and multi-objective RBDO are discussed.
Single-objective reliability-based design optimization
Reliability-based design optimization (RBDO)
An optimal shift vector (OSV) method was proposed by Chen et al. 2013a) performing reliability analysis in the supersphere. A single loop singular vector (SLSV) (Chen et al., 1997) was proposed by transforming the probabilistic performance function into approximate deterministic performance function.
Multi-objective reliability-based design optimization
Multi-objective, multi-case RBDO was developed by Sun et al. 2017), in which a radial basis function is used to approximate the performance function and objective function responses. Multi-objective PSO is incorporated to obtain optimally reliable Pareto-optimal solutions, which are coupled with MCS for reliability analysis. Optimization is performed by multi-objective PSO, and Bayesian interference is used for reliability analysis.
Closure
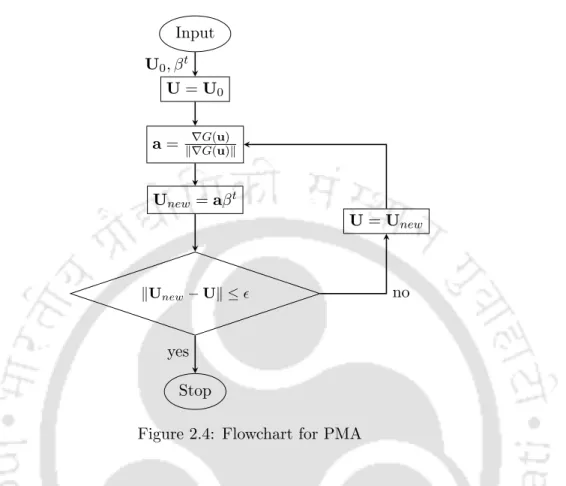
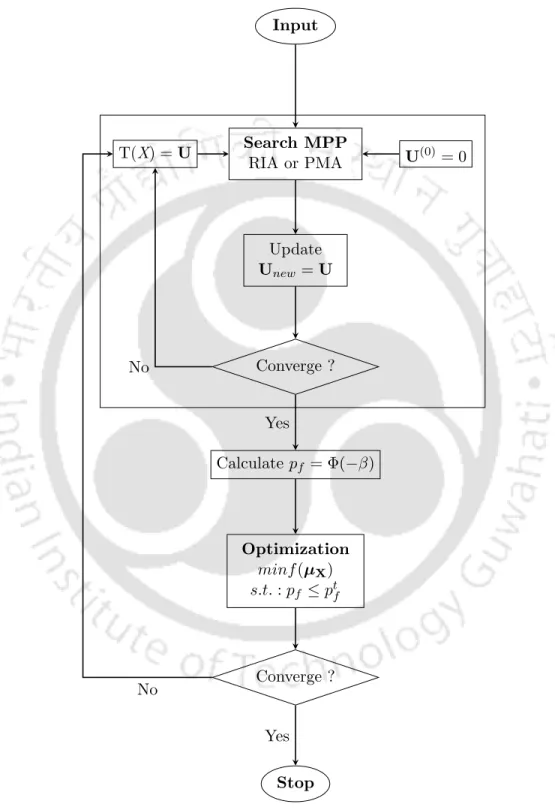
Therefore, the development of single-loop multi-objective optimization algorithms for solving RBDO problems can also be studied. The first objective of the thesis is to develop an accurate and efficient single-loop method for solving RBDO problems. A FORM-based single-loop method is coupled with the displacement vector approach of SORA (Du and Chen, 2004) to achieve this goal.
Single-loop approach
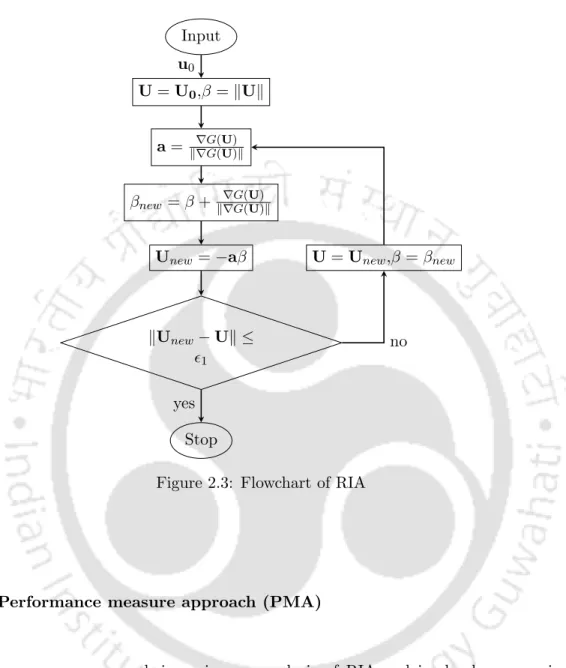
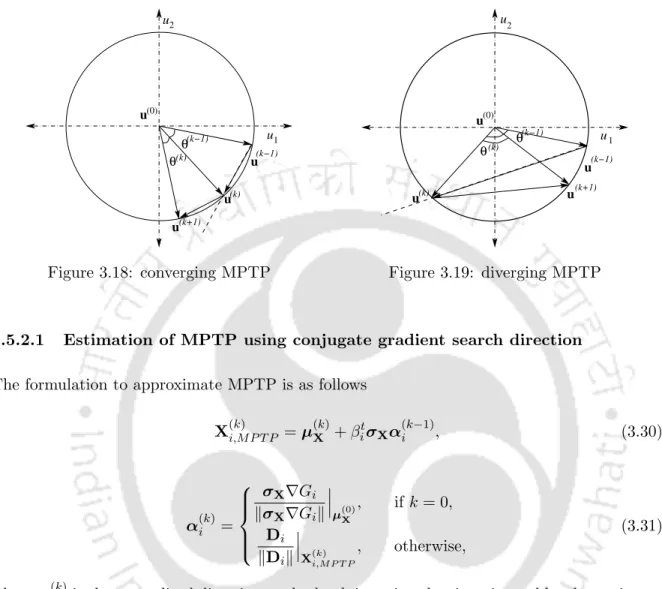
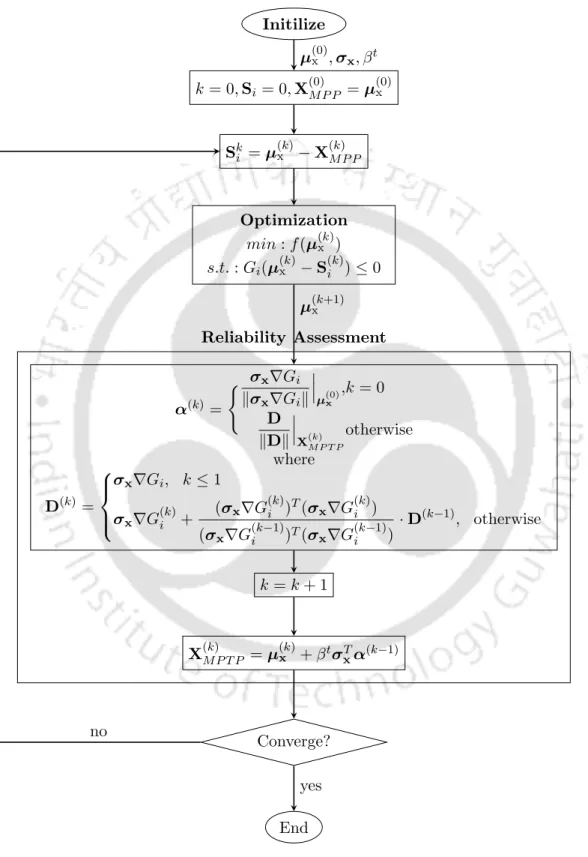
After multiplying ∥∇G(U)∥in the numerator and denominator of the right side of U, we get. It should be noted that α(k)i,X is calculated using σX and ∇Gat MPTP from the last iteration. The generation of S(k)i is an iterative process that helps to estimate the feasibility of the constraints until the reliability is met.
The proposed single-loop shifting vector method with con- jugate gradient search (SLShV-CG)jugate gradient search (SLShV-CG)
The shift vector S(k)i is updated in each iteration by the approximate MPTP, which is given as. Since CG direction is used to update the MPTP of the proposed hybrid single-loop method with the shift vector approximation of SORA method, it is referred to as SLShV-CG. The flow diagram of SLShV-CG is shown in Figure 3.2 in which all the steps are shown.
Numerical examples
It can be seen that SLShV-CG and PMA-CGA are the only methods that can evolve the solution with the desired target reliability. Graphically, it can be seen that SLShV-CG evolved the optimal solution with the desired target reliability. It can be seen from the figure that SLShV-CG converges to the optimal solution within five iterations.
Discussion
The beam is loaded with two point loads, lateral load pz and vertical load py at the tip. It can be seen from the table that SLShV-CG is found better than PMA-AMV, PMA-CGA and SORA when comparing their NFC. It can be seen that SLShV-CG requires more iterations than SLSV, SLSV-CG, ASORA and SORA.
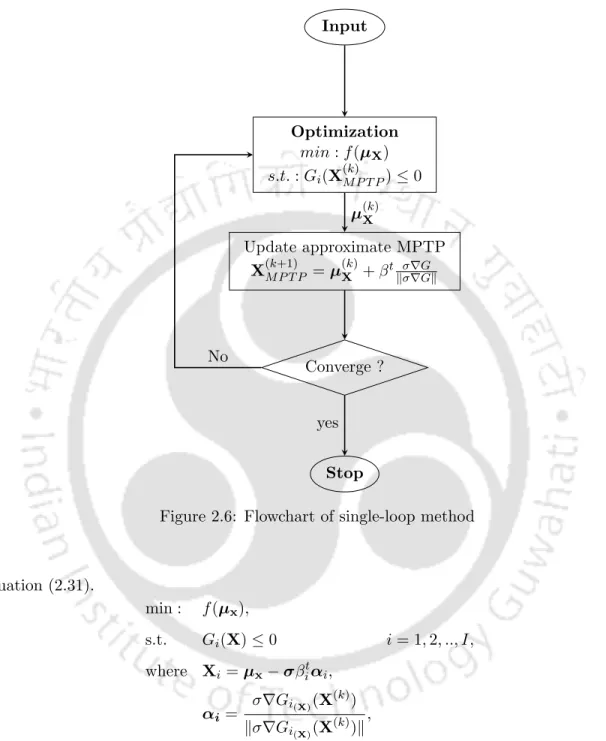
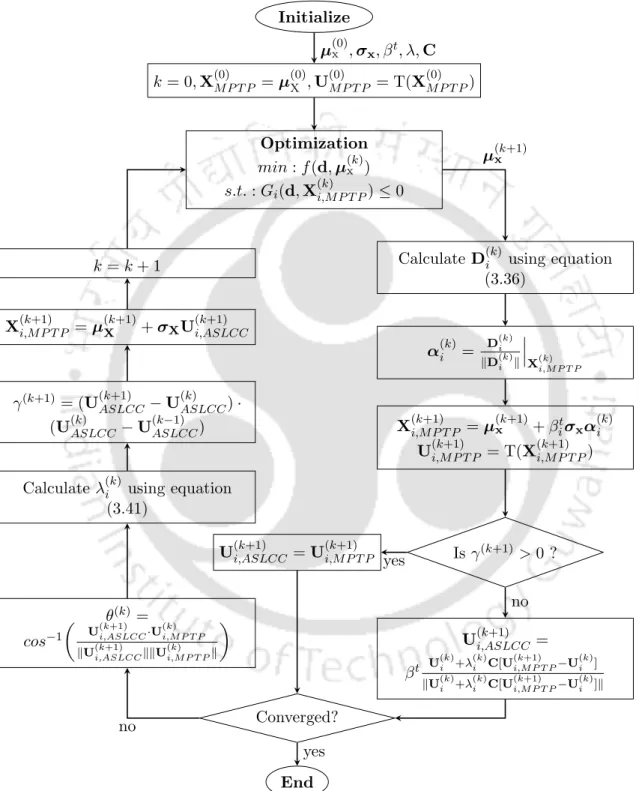
Proposed approximate single-loop chaos control (ASLCC) methodmethod
Therefore, the efficiency of the RBDO methods becomes sensitive to the initial value of the chaos control factor. When these MPTPs start to oscillate, the current MPTP of equation (3.27) is updated using chaos control theory. The chaos check factor λ(k)i is changed in each iteration using the angle condition given in equation (3.29).

Numerical examples
The six columns of Table 3.10 show that the ASLCC-2 method yields the reliable solution. The computational efficiency of the methods is quantified using the function evaluations shown in the fourth and fifth columns of Table 3.10. The calculation efficiency of the methods is shown in the fourth and fifth columns of Table 3.18.
Closure
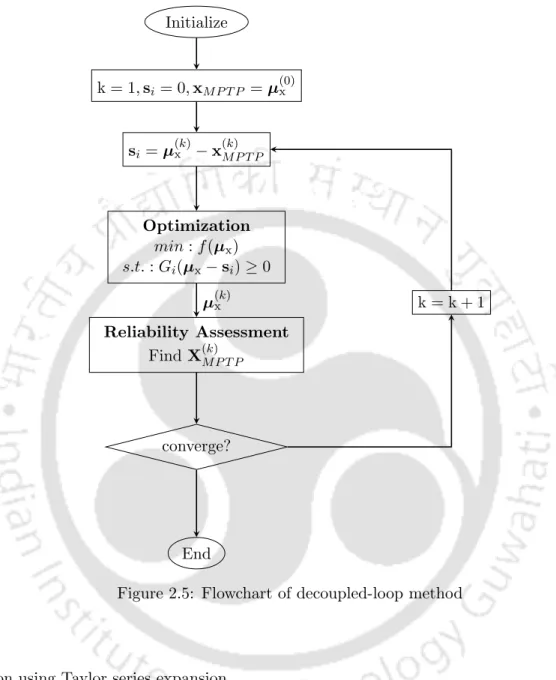
The single-loop methods discussed in Chapter 3 employ numerical optimization techniques that tend to converge to a locally optimal solution (Deb et al., 2009; Lobato et al., 2017). The single-loop methods can be improved by including approximations that can help generate reliable solutions. Therefore, the third objective of this thesis aims to develop a single-loop RBDO formulation using shifting vector approximation (see equation (3.7)) that can direct violated constraints/performance functions towards the achievable direction for the generate a reliable solution.
Differential evolution
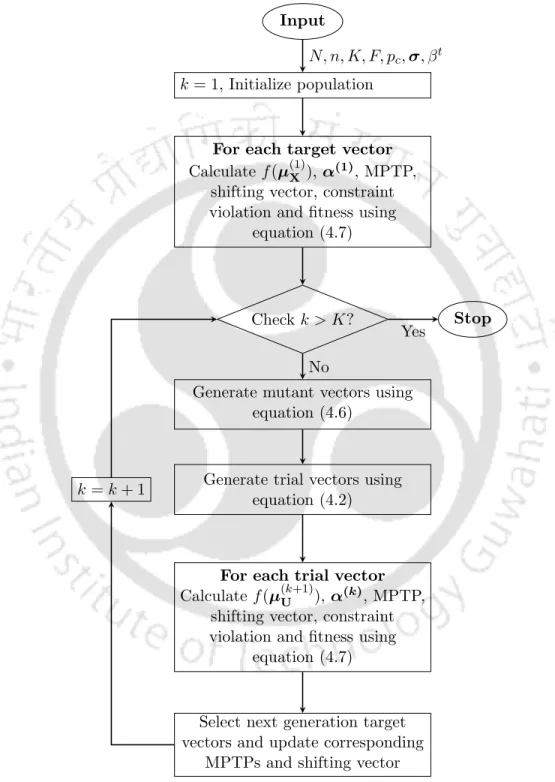
The Proposed Method and it’s Implementation
The (µ+ λ)- strategy is used to select the target vectors of the next generation, instead of using equation (4.3). It can be seen that after initialization, for each target vector, equation (4.7) is used to calculate the objective function using random variables and the fitness is determined using MPTP. Again, for each test vector, the objective function is calculated and the fitness is determined using equation (4.7).
Numerical Examples
It can be seen that the objective function value (f∗) obtained by the proposed SLADE is better than the rest of the methods. The fourth column of Table 4.3 reveals that SLADE needs more function estimates than CC and SORA. The statistical values of different runs of SLADE are shown in Table 4.10, which again shows its consistency in generating the solution for the spring design example.
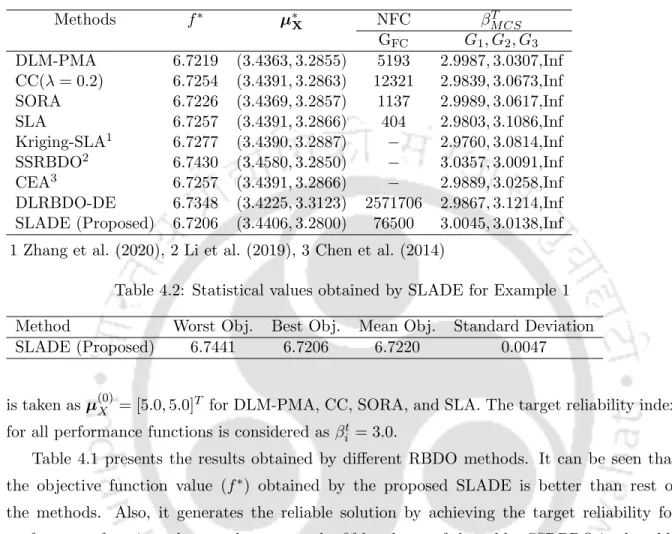
Closure
However, the number of feature estimates obtained by SLADE is much smaller than DLRBDO-DE. The formulation is solved using multi-objective DE, which is designed using non-dominant sorting and crowding distance. In the following sections, the proposed reliability-based single-loop optimization of the multi-objective design is discussed.
Proposed single-loop multi-objective RBDO formulation
In equation (5.3) U(k)i is the MPTP calculated for the first constraint in k-th generation in the standard normal space. Its value is calculated after transformation which is given as. 5.4) The formulation given in equation (5.1) is unique with respect to the literature because it was developed using the single-loop methodology which eliminates the nested double-loop formulation. Furthermore, the MPTP in the proposed formulation is estimated using the chaos control theory.
Multi-objective differential evolution using adaptive muta- tion schemetion scheme
Then, constraint violation for each constraint is calculated using the estimated MPTP by chaos control theory using equations. The µ(k)best(t) vector for each target vector is found by computing the Euclidean distance of the th target vector with respect to all non-dominated target vectors in the objective space. It is noted that the non-dominated target vectors in (k−1) and (k) generations are normalized together for the estimation of the hypervolume with respect to the dominated point T.
Numerical examples
The same observation can be seen with both methods that for larger value of βt the PO solutions become conservative and move away from the deterministic PO front. For different values of βt, it can be seen that SL-MODE shows the best performance over DL-MODE. A lot of fluctuation in HV values can be seen with both methods in terms of number of generations.
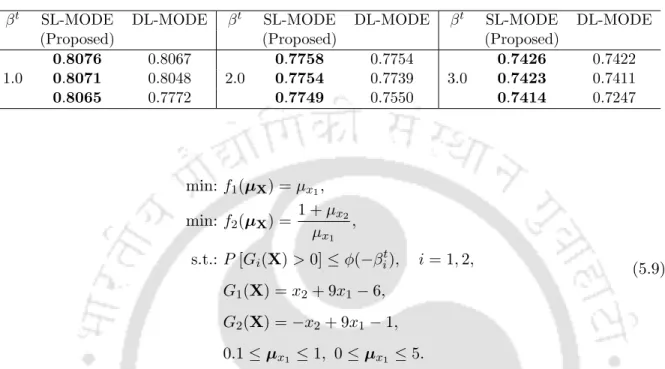
Discussion
In Example 2, a certain amount of fluctuation was observed in the convergence plot for both SL-MODE and DL-MODE. This leads to the final objective of the thesis, where changing vector is incorporated with single-loop multi-objective reliability-based design optimization.
Single-loop MORBDO formulation using chaos control and shifting vector approachshifting vector approach
Numerical Examples
It can be seen that for larger values of βt the PO solutions become conservative and move within the feasible region. In can be seen that SLMDE converged to better values of HV for different βt values. The statistical values of HV values obtained from both methods with respect to different βt are presented in Table 5.13.
Closure
It was found that SLMDE was able to generate better HV values compared to DLMDE for all the samples. The aim of the thesis was to develop efficient RBDO methods that can generate better reliable solutions compared to the existing algorithms in the literature and can reduce the computational costs of these methods. All the developed methods were tested on several mathematical and engineering benchmark examples and compared with existing RBDO methods to validate the results.
Conclusions
Many metaheuristic algorithms have been developed in the literature to obtain reliable PO solutions to multi-objective RBDO problems. Therefore, in the final objective of this thesis, both concepts are included for multi-objective RBDO formulation. In the last objective, a single-loop multi-objective reliability-based design optimization is proposed with shifting vector approximation for generating reliable PO solutions.
Recommendation for future work
A single-loop adaptive hybrid method for reliability-based design optimization using an iterative control strategy. A hybrid self-adjusting mean method for reliability-based design optimization using sufficient descent conditions. A self-adaptive modified chaos control method for reliability-based design optimization. Structural and multidisciplinary optimization.